Abstarct
An ensemble of neurons can provide a dynamic representation of external stimuli, ongoing processes, or upcoming actions. This dynamic representation could be achieved by changes in the activity of individual neurons and/or their interactions. To investigate these possibilities, we simultaneously recorded from ensembles of prefrontal neurons in non-human primates during a memory-guided saccade task. Using both decoding and encoding methods, we examined changes in the information content of individual neurons and that of ensembles between visual encoding and saccadic target selection. We found that individual neurons maintained their limited spatial sensitivity between these cognitive states, whereas the ensemble selectively improved its encoding of spatial locations far from the neurons’ preferred locations. This population-level “encoding expansion” was not due to the ceiling effect at the preferred locations and was accompanied by selective changes in noise correlations for non-preferred locations. Moreover, the encoding expansion was observed for ensembles of different types of neurons and could not be explained by shifts in the preferred location of individual neurons. Our results demonstrate that the representation of space by neuronal ensembles is dynamically enhanced prior to saccades, and this enhancement occurs alongside changes in noise correlations more than changes in the activity of individual neurons.
Keywords: neural interactions, neural representation, noise correlation, population code, response selectivity
Introduction
Over the past decade, the combination of improved techniques for large-scale recording from neuronal ensembles and novel computational methods has led to a surge of interest in understanding the contribution of population-level representations to cognitive functions such as working memory, visual attention, decision making, and categorization (Hung 2005; Cohen and Maunsell 2010; Zhang et al. 2011; Mante et al. 2013; Rigotti et al. 2013; Cunningham and Byron 2014; Parthasarathy et al. 2017). Importantly, an ensemble of neurons can represent external stimuli, ongoing processes, or upcoming actions based on the complex response of neurons contained in that ensemble (Churchland et al. 2012; Mante et al. 2013; Rigotti et al. 2013; Parthasarathy et al. 2017). This representation can be dynamically adjusted according to the task at hand, cognitive states, and the chain of ongoing events (Morcos and Harvey 2016). These adjustments could occur by changes in the response of individual neurons of an ensemble and/or through changes in how these neurons interact with each other.
On the one hand, individual neurons contributing to ensemble activity could be highly selective to external stimuli (Hubel and Wiesel 1959, 1968; Quiroga et al. 2005) or highly informative about the animal’s action (Britten et al. 1992, 1996; Shadlen et al. 1996) and thus, changes in their response could contribute to dynamic adjustments of the population representation. On the other hand, inter-neuronal correlations could influence the coding capacity of neural populations as pointed out by previous theoretical work (Shadlen and Newsome 1998; Abbott and Dayan 1999; Panzeri, Schultz, et al. 1999; Nirenberg and Latham 2003; Pola et al. 2003; Averbeck et al. 2006; Pillow et al. 2008) as well as electrophysiological studies (Zohary et al. 1994; Gutnisky and Dragoi 2008; Cohen and Maunsell 2009; Cohen and Newsome 2009; Sundberg et al. 2009; Adibi et al. 2014). For example, it has been shown that noise correlation affects signal-to-noise ratio of the population response (Zohary et al. 1994) and modulates sensory coding independently of the firing rate of individual neurons (Cohen and Maunsell 2009; Mitchell et al. 2009).
Here, we examined whether changes in the responses of individual neurons and/or their interactions contribute to dynamic adjustments of information encoded at the population level. To that end, we recorded neural activity in the Frontal Eye Field (FEF) of monkeys during a memory-guided saccade task. We utilized multisite linear array electrodes in order to record the activity of dozen neurons at the same time. The memory-guided saccade task requires encoding of the location of a target stimulus and making a saccade to the remembered location after a delay, and thus involves visual encoding, maintenance of spatial information, and saccadic target selection (3 cognitive states). Employing a combination of decoding and encoding methods to simultaneously recorded neural activity, we then examined changes in the information content of individual neurons and that of ensembles between visual encoding and saccadic target selection.
We found a spatially selective enhancement of the information content of neuronal ensembles from visual encoding to saccadic target selection. Although individual neurons maintained their limited spatial sensitivity between these 2 cognitive states, the ability of the ensemble to encode spatial locations far from the neurons’ preferred locations (i.e., locations poorly encoded by individual neurons) improved. We show that this phenomenon, which we refer to as “encoding expansion”, is accompanied by selective changes in noise correlations for the non-preferred location, and could not be explained by a shift in the preferred location of individual neurons between visual encoding and saccadic selection. Our results suggest that in order to dynamically enhance the representation of visual space prior to a saccade, the prefrontal cortex relies on changes in the interactions between neurons (both noise and signal correlations) in the population more than changes in the activity of individual neurons.
Materials and Methods
Experimental Paradigm and Recording
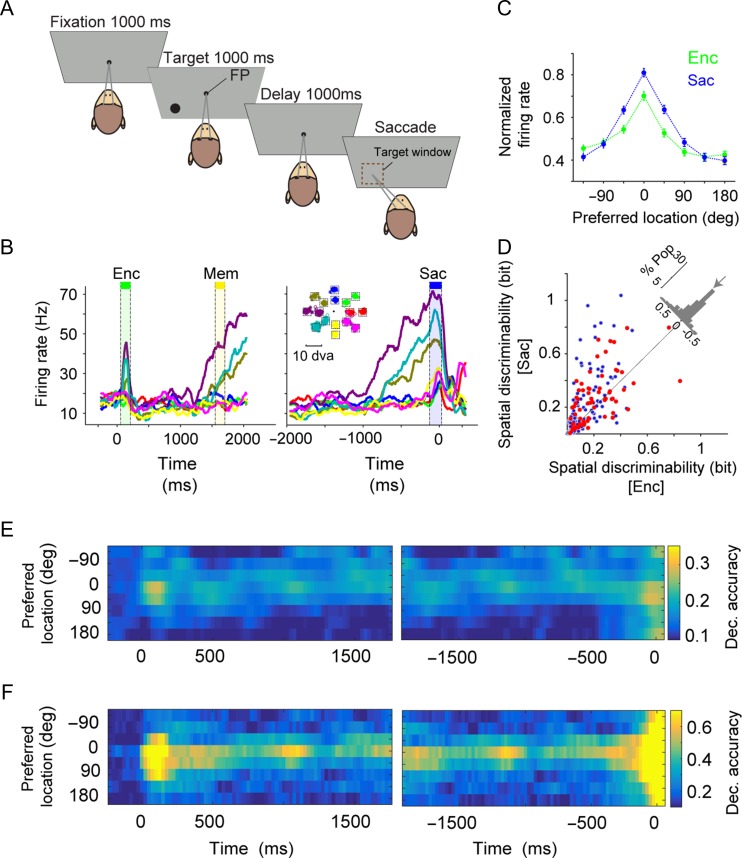
Two monkeys (macaca mulatta) were trained to perform a memory-guided saccade task (Fig. 1A). Each trial started with the monkey fixating on the fixation point, followed by the presentation of a visual target in one of 16 locations, defined with 2 possible eccentricities (7 and 14 visual degrees) and 8 different angles (0, 45, 90, 135, 180, 225, 270, and 315 degrees). Stimuli were presented on an LED-lit monitor (ASUS VG248QE: 24 in, resolution 1920×1080, refresh rate 144 Hz) positioned 28.5 cm in front of the animal’s eyes. The target remained on screen for one second, followed by 1 second of delay after which the monkey could saccade to the remembered location. We used a relatively small delay to avoid making the task too challenging with 16 possible target locations. The latter was chosen to have more read-out locations for the SVM classifier. The monkey was rewarded with a drop of juice if the saccade landed within a 2.5-degree of visual angle window centered on the target location. The neural recording was done using a multisite linear array electrode (V-probe, Plexon Inc.), allowing us to simultaneously record from 16 channels. Using a strict criterion for spike sorting, we identified 188 single-unit (1165 pairs of neurons) and 320 clusters of multiunit activity (total 508) during the 20 recording sessions (with an average of 784 trials per session).
Figure 1.
Spatial encoding of a population of FEF neurons expands beyond the space encoded by individual neurons prior to a saccade. (A) Behavioral paradigm. Each trial of the memory-guided saccade task started with fixation on a central spot for 1000 ms followed by the presentation of a visual target (black circle) for 1000 ms in one of the 16 possible locations (at 8 angles and 2 eccentricities). Disappearance of the target was followed by a 1000 ms delay, after which the central spot disappeared and the monkey made a saccade to the remembered target location. (B) The mean response of an example FEF neuron to the target presented at 8 different angles (averaged over 2 eccentricities), indicated by color in the inset. The neural response is aligned to the onset of the target (left panels) or saccade (right panel). (C) Normalized response of 188 FEF neurons (single-units) to targets presented at different angles relative to the neuron’s preferred location during visual encoding (Enc) and saccade preparation (Sac) epochs. The error bars represent s.e.m. The spatial tuning of individual neurons only slightly improved from visual encoding to saccade preparation. (D) Comparison of the spatial discriminability during visual encoding and saccade preparation for all FEF neurons (n = 188). Histogram on the diagonal shows the difference in spatial discriminability between encoding and saccade (arrow shows the median; %Pop: percent of population). FEF neurons with broad selectivity (i.e., those exhibiting selective response to target locations in all task epochs) are shown in red (n = 65). (E,F) Plot shows the decoding accuracy for different target locations based on the SVM classifier, when the activity of individual units (E) or the ensemble of units (F) recorded in an example session is used. The time course of decoding accuracy showed similar accuracy during saccade preparation and visual encoding for individual units (E) but larger accuracy by the ensemble of neurons during saccade preparation than visual encoding for non-preferred locations (F). The left (right) panels shows the results when the activity is aligned to target (saccade) onset. A 150-ms sliding time window with a 25-ms step size were used in both E and F.
General and Surgical Procedures
Two male rhesus monkeys (maccaca mulatta) were used in this experiment. All experimental procedures were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, the Society for Neuroscience Guidelines and Policies, and the Montana State Animal Care and Use Committee. Each animal was surgically implanted with a head post and recording chamber. Surgery was conducted using aseptic techniques under general anesthesia (isoflurane), and analgesics were provided during postsurgical recovery. Eye position was monitored by the Eyelink 2000 system (SR Research, Canada) at 1 kHz to allow detection of micro-saccades. However, we used a 5-ms Gaussian filter to smooth this signal and to reduce high frequency noise, since here we were only interested in detecting saccades. Eye monitoring, stimulus presentation, data acquisition, and behavioral monitoring were controlled by the Monkey Logic system (Asaad et al. 2013).
Single-Neuron Recording in the FEF
Single-neuron recordings were made in awake monkeys through a surgically implanted cubic titanium chamber (30×30 mm). The 16-site, linear V-probe electrode (125 μm distance of sites) was lowered into the cortex using a hydraulic micro-drive (Narishige group, Japan) to record the extracellular activity of single cells. During each experiment, a recording site in the FEF was first localized by the ability to evoke fixed-vector, saccadic eye movements with stimulation at currents <50 μA (Bruce et al. 1985; Merrikhi et al. 2017).
Spike Sorting Procedure
We utilized a state-of-the-art method for offline sorting. In this method, the PCA and some primitive clustering methods were applied, followed by clustering based on a competitive mixture decomposition algorithm using expectation-maximization and mixture decomposition of multivariate t-distributions (Shoham et al. 2003). Finally, we used cross-validation classifier performance to define a criterion for the accuracy of the well-isolated clusters (Barnett et al. 2016). This was done by training a binary support vector machine (SVM) classifier using 10-fold cross-validation with an equal number of samples for each pair of clusters in a given recording site. For each cluster, we adopted the minimum performance for the binary classifier separating a given cluster from other clusters as an index to measure the isolation power of that cluster. The clusters of spikes with high isolation power (>92%) were selected as well-isolated single cells (n = 188).
Individual and Population Neural Response
We computed the firing rate of individual single-unit or multiunit clusters in 3 150-ms time intervals of the experiment: the visual epoch, defined as 50–200 ms following target onset; the memory epoch, defined as 1500–1650 ms following target onset; and the saccade epoch, defined as 120 ms preceding saccade initiation to 30;ms afterward. For some analyses, the ensemble activity consisted of the activity of all simultaneously recorded units (single- and multiunits) in a given recording session. Therefore, the ensemble representation of location used for the classification analysis was a point in RN space, where N is the number of simultaneously recorded units (single and multi) in a given recording session. On average, there were 25.83 ± 1.46 units in each recording session with the range of ensemble size between 18 and 39. For all correlation analyses, however, we only considered the activity of single-units to construct ensemble activity consisting of pairs of neurons or all single-units in a given recording session. Finally, for analyses of neuron-condition pairs, the ensemble consisted of a pair of neurons and the 2 locations were represented in R2 neural space.
Neural Response Tuning Curves
In order to compute the neural response relative to each neuron’s preferred location, the 8 stimulus locations were circularly shifted such that 0 degree indicated the preferred location for each neuron. The preferred location was defined based on the maximum of the average response (neural tuning curve) during the visual encoding, memory, and saccade preparation epochs in order to avoid bias toward any epochs. To quantify the spatial tuning of individual neurons, we fit a Gaussian probability density function to the response tuning curve of each neuron and used the standard deviation of the fitted function as the measure of “tuning dispersion”.
Mutual Information and Neural Selectivity
We used mutual information (MI) as a measure to quantify the ability of the response of individual neurons to represent the target location (Shannon 1948). MI quantifies how well an ideal observer can discriminate between target locations based on the neural response. We computed MI using the neural firing rate during non-overlapping 150-ms time windows within different task epochs:
| (1) |
where s is the set of stimuli, r is the set of neural response (mean firing rate), P[r|s] is the conditional probability of neural response r given stimulus s, and p[s] and p[r] are the prior probability of stimulus s and response r, respectively. The baseline MI was computed using neural firing rates from 6 non-overlapping 150-ms time windows during the fixation interval for each pair of locations. Non-overlapping time windows were used to ensure samples used for the estimation of MI are independent. We refer to this MI as “spatial discriminability” because it quantifies the ability of single neuron to discriminate between alternative target locations.
In our study, MI values were unlikely to be affected by sampling bias for 2 reasons. First, we had a large number of trials in each condition/location (mean ± std = 99.48 ± 24.98), which results in a very small systematic error as shown previously (Panzeri and Treves 1996). Second, in our dataset, the differences between the numbers of samples for different conditions were very small (mean ± std = 8.88 ± 10.29). Nevertheless, we examined the effect of sampling bias using 2 methods. First, we equalized the number of trials for different locations before computing MI. We repeated this procedure 50 times to compute the average “equal-sample” MI. Second, we corrected for sampling bias by subtracting the first-order correction term, C1, from the MI using the following equation for C1 (Panzeri and Treves 1996):
| (2) |
where denotes the number of relevant (non-zero) response bins for stimulus s, B is number of bins, N is number of trials, and S is number of stimuli. As shown in Supplementary Figs 1–3, we found similar results using both the uncorrected and corrected MI values (both equal-sample and bias-corrected methods), which we attribute to large samples and small differences between sample sizes in our data. For these reasons, we used the uncorrected MI values for most results presented here.
Neural selectivity across different epochs was then quantified by comparing the MI for each pair of locations during sensory encoding (50–200 ms following target onset), memory (1500–1650 ms following target onset), and saccade preparation (120 ms preceding saccade initiation to 30 ms afterward), to the baseline MI. The significance of neural selectivity was determined using a 2-sided Wilcoxon rank sum test at P < 0.05.
The Support Vector Machine Classifier
We trained an SVM classifier with a linear kernel (Cortes and Vapnik 1995) using the population or individual-unit responses on a randomly selected 70% of trials as a training set. We then measured the classification accuracy of the trained classifier on the remaining 30% of trials (the test set). Training was done using the least square method and with an equal number of samples for different classes (Johan and Suykens 1998). A majority voting procedure (one-vs.-one, max-wins voting strategy) was used between every pair of classes in order to classify multi classes (Hsu and Lin 2002). To calculate the standard error of classification accuracy in a given recording session, we repeated the calculations 500 times with different sets of training and test trials in that session. For each repetition, the data was randomly partitioned into training and test sets. We trained and tested the SVM classifier with stimuli represented either in 1-dimensional (for “individual” decoding accuracy), or n-dimensional space (for “ensemble” decoding accuracy, where n is the number of units in a given recording session).
Decoding Tuning Curves
To construct decoding tuning curves during different epochs of the task, we extracted the decoding accuracy of the SVM classifier for the 8 target angles (combining the 2 eccentricities) using the confusion matrix. This was done for individual units as well as ensembles (including ensembles of both single- and multiunits or ensembles of single-units alone). Similar to a tuning curve based on single-unit activity, we also calculated the relative decoding tuning curves by circularly shifting the 8 target angles such that 0 degree indicated the preferred decoding location. The preferred decoding location was defined based on the maximum of the average decoding accuracy of locations during visual encoding, memory, and saccade preparation epochs. This was done to avoid bias toward any epochs of the experiment.
Number of Units Required for Decoding Population-Level Information in SVM Analysis
To find the sufficient number of units needed for decoding space based on ensemble activity, we sorted the simultaneously recorded units in each session based on their MI, and made a set of neural ensembles by subsequently adding new units (with decreasing MI). Using this approach, we first computed the decoding accuracy as a function of the number of included units. This function was then fitted with an exponential using the least-squares methods: , where y is the SVM performance and n is number of units. Using the outcome fit we defined the number of sufficient units equal to the number of units needed to exceed 75% of the maximum decoding accuracy. To measure the standard error of the number of sufficient units, we used a bootstrapping method that sampled the session’s ensembles with replacement (1000 times).
Computation of Signal and Noise Correlations
The signal and noise correlation between each pair of simultaneously recorded neurons (single-units only) was computed for each pair of target locations (a “neuron-condition pair”). The correlation coefficient across trials captured the total correlation for each neuron-condition pair. The signal correlation was defined as the correlation coefficient computed after randomly shuffling the order of repeated trials for each pair of target locations. We repeated the shuffling and calculation of the correlation coefficient 500 times, and used the mean of these r-values as the measure of the signal correlation for that neuron-condition pair. The noise correlation was defined by subtracting the signal correlation from the total correlation (Pachitariu et al. 2015; Tremblay et al. 2015).
In order to compute the signal and noise correlations for pairs of conditions for preferred and non-preferred target locations based on the SVM classifier tuning curves, we used the following steps. First, we calculated the average of the decoding tuning curve in visual, memory, and saccade epochs for each session based on the ensemble of single-units only. Second we labeled the location with maximal decoding accuracy (0 degree) and its closest neighbor locations (±45 degree) as the “preferred” locations, and the location on the tail of tuning curves (>90 degree) were considered the “non-preferred” locations. Finally, using these locations, we computed the noise and signal correlations across all pairs of neurons recorded during each session.
Tuning Curve for Noise Correlations
To obtain a tuning curve for noise correlations, we first determined the order of the 8 possible target locations by extracting the average decoding tuning curves of a given single-cell ensemble during visual, memory, and saccade epochs in each session. The noise correlation for a given location C was then computed by averaging the values of noise correlations in all neuron-location pairs which involved location C and its nearby locations in a given session (C ± 45 degree).
Fisher Information
To estimate the upper bound of the accuracy with which neural code can be read out by any unbiased decoding method we calculated the Fisher Information (FI) for single-units and ensemble of neurons. Here, we approximated the neural response to the presentation of target at location θ by f(θ) (the tuning curve) plus a multivariate Gaussian noise with zero mean and covariance matrix Σ(θ). Using this approximation, the FI was computed using the following equation (Abbott and Dayan 1999):
| (3) |
where and are the derivatives of the tuning curve with respect to location θ and the inverse of the covariance matrix, respectively (Seriès et al. 2004; Kanitscheider et al. 2015). For 2 adjacent locations (θ+ and θ−, ∆θ = ) we estimated the derivative of the tuning curve by . Similarly, the covariance matrix was estimated by .
We also computed the FI for the shuffled data (i.e., shuffling the order of repeated trials for each pair of target locations) in order to measure how encoded information depends on the correlation in the activity between pairs of neurons. The shuffled FI was estimated using the following equation:
| (4) |
where is the marginal variance of neural response for neuron i, and shuffled covariance matrix was obtained by putting zeros for the off-diagonal values in the covariance matrix (Kanitscheider et al. 2015).
We extracted the FI for the 8 adjacent locations (combining the 2 eccentricities). This was done for individual units as well as ensembles of multiunits. We also calculated the relative FI tuning curves by circularly shifting the 8 target angles such that 0 degree indicated the preferred decoding location. To avoid bias toward any epochs of the experiment, the preferred decoding location was defined based on the maximum of the average FI of locations during visual encoding, memory, and saccade preparation epochs.
Fisher Linear Discriminant Analysis and Joint Discriminability
In each neuron-condition pair, 2 locations were represented in a 2-dimensional neural space based on the simultaneously recorded activity of 2 neurons. We used Fisher linear discriminant analysis (LDA) to find the optimal vector for the linear discrimination between 2 conditions (locations). We then projected the location in the 2-dimensional response space into that vector (Duda et al. 2012). For an ensemble of 2 neurons, the response to stimulus s can be summarized by the 2×N response matrix Rs(s = 1, 2, and N is number of trials) and the neural response covariance matrix Cs can be represented with a 2×2 matrix. Using the response matrices, one can compute the average population response to stimulus s, (a 2×1 matrix). We calculated the optimal weight vector wopt that yields maximum discrimination between 2 target locations using the following equation:
| (5) |
where R is the difference of mean vectors of 2 conditions () and C-1 is the inverse of the sum of the covariance matrices for the 2 conditions (). After finding wopt, we projected the population response of each trial onto this optimal weight vector. This projection is a mapping from 2 dimensions to scalar. Using this method, we could estimate the distribution of projected neural response in one dimension and compute the “joint discriminability” as the MI between the projections of the neural response and the target locations. The geometric mean of MI values of single cells constituting a given pair was considered as the single-cell version of the joint discriminability, which we refer to as the “isolated” discriminability. Isolated discriminability was used as a control for measuring encoding expansion at the single-cell level (see below).
Encoding Expansion Measure
To measure population-level encoding expansion using SVM or neuron-condition pair analyses, we first defined the differential expansion index, DX, as the differential change in the information content of an ensemble between visual encoding and saccade preparation and for preferred and non-preferred locations:
| (6) |
where X indicates one of different measures of the information content of an ensemble activity and can be equal to SVMindividual, SVMensemble, discriminabilityisolated, or discriminabilityjoint. We used the difference between the preferred and non-preferred locations in order to obtain the maximum possible difference. We then subtracted the individual-unit differential expansion index (X = SVMindividual or discriminabilityisolated) from the corresponding ensemble differential expansion index (X = SVMensemble or discriminabilityjoint) in order to measure the encoding expansion specific to the population.
Statistical Analyses
Statistical analyses were performed using the Wilcoxon’s signed-rank test (for paired comparisons) or rank sum (for unpaired comparisons), unless otherwise specified. All p values are reported up to 3 digits and values below 0.001 are reported as P < 10−3.
To calculate the interquartile range (IQR) for the preferred locations of all neurons in a given session, we first computed the distance between the preferred locations for all pairs of units in a given session, which could take a value between 0 and 180, and then constructed the distribution of the angle difference in preferred locations during Enc and Sac. Using these distributions, we computed the range of tuning preferences (IQR = Q3 − Q1) within each session.
In order to directly address the relationship between the size of neuronal ensembles and the effect of pairwise correlations, we looked at rate-matched ensembles. We constructed neuronal ensembles with different numbers of neurons, and for each ensemble size we selected 100 ensembles while the mean of the MI of neurons in these ensembles was matched, that is, there was no significant difference between the mean of the MI of neurons in ensembles with different sizes. This ensured that the observed effect is not due to different overall information in different ensembles. For each ensemble, we then computed the SVM performance before and after shuffling the identity of trials belonging to the same target location for each single neuron to eliminate noise correlations while preserving single-unit tuning and signal correlations.
Results
Using 16-channel linear array electrodes, we simultaneously recorded from a population of neurons in the FEF of 2 monkeys during a memory-guided saccade task (188 single neurons, 1165 pairs of neurons; see Materials and Methods). The memory-guided saccade task (Fig. 1A) enabled us to trace the transformation of visual input into motor action (saccade), and has been classically used to determine the contribution of FEF neurons to each of these processes (Bruce and Goldberg 1985; Bruce et al. 1985). Our goal was to determine how the visual space is encoded and represented by a given ensemble of neurons and the participating individual neurons, and how this representation is dynamically adjusted as the animal transitions between visual encoding and saccadic target selection. Therefore, we analyzed the simultaneously recorded neural data to measure spatial information encoded at the single-cell and population levels during these 2 cognitive states.
Presaccadic Expansion of the Population Code
The average activity of an example recorded neuron during the memory-guided saccade task revealed the typical spatial tuning or selectivity of FEF neurons (Fig. 1B). This neuron responded differently to stimuli presented at 8 possible angles during both visual encoding (Enc; one-way ANOVA, F = 18.51, P < 10−3) and just before the saccade to the remembered location (Sac; one-way ANOVA F = 48.72, P < 10−3). However, the neural response had a larger dynamic range during saccade preparation than visual encoding. Similarly, the average normalized activity across all recorded neurons showed stronger spatial tuning during saccade preparation compared to visual encoding such that the tuning was narrower for the former epoch (Fig. 1C; tuning dispersion: Sac = 2.06 ± 0.04, Enc = 2.25 ± 0.04, P < 10−3). We found a similar difference between the spatial tuning of individual neuron’s responses during saccade preparation and visual encoding when we restricted the analysis to the population of neurons that showed a selective response to target locations in all task epochs (i.e., “broad” selectivity neurons, n = 65).
Next, we quantified the information content of individual neurons using the MI between the response and stimulus location (see Materials and Methods). We refer to this MI as “spatial discriminability”, as it quantifies the ability of individual neurons to discriminate between various target locations. For the example neuron, the spatial discriminability was greater during saccade preparation than visual encoding (spatial discriminability: Enc = 0.09 ± 0.01, Sac = 0.18 ± 0.02, P < 10−3). This difference was also observed across all neurons: the spatial discriminability was greater during saccade preparation than visual encoding for the entire population of neurons, and also for the population of neurons with broad selectivity (Encall = 0.15 ± 0.01, Sacall = 0.23 ± 0.02, P < 10−3, n = 188; Encselective = 0.21 ± 0.02, Sacselective = 0.27 ± 0.02, P = 0.007, n = 65; Fig. 1D). We found similar results using both the equal-sample and bias-corrected MI values (see Materials and Methods and Supplementary Fig. 1). This enhanced representation of saccade targets is consistent with previous studies (Bruce and Goldberg 1985) and the known role of FEF in oculomotor control.
In addition to MI, which reflects the spatial discriminability of single neurons, we employed a SVM to quantify the ability of the population of FEF units and individual FEF units to represent the target location. The decoding accuracy of the SVM measures the ability of an external observer (the classifier) to determine the location of the target based on the simultaneous activity of recorded single-units and multiunits. The SVM classifier was designed to classify 8 target angles either when all the units were considered individually (i.e., separately running the SVM for each unit, SVMindividual) or when the simultaneous activity of the ensemble of units recorded in one session was taken into account (i.e., running the SVM for each recording session, SVMensemble; see Materials and Methods). The time course of the SVM performance applied to 36 individual units recorded within a single recording session of the experiment showed similar accuracy during saccade preparation and visual encoding (Fig. 1E). However, when the activity of the ensemble of simultaneously recorded units was taken into account, the decoding accuracy during saccade preparation improved dramatically (Fig. 1F). This improvement was most pronounced for targets in locations not optimally driving individual neurons in the ensemble. More specifically, the ensemble decoding accuracy for the preferred location improved by only 0.06 between visual encoding and saccade preparation (Enc = 0.79, Sac = 0.86). In contrast, the decoding accuracy increased by 0.36 (Enc = 0.21, Sac = 0.57) for the location 180 degrees away from the preferred location. Altogether, results from this example recording session revealed a population-level enhancement of neural encoding during saccade preparation (“presaccadic expansion”) which occurred primarily for parts of space weakly encoded by the single-cell responses in either epoch.
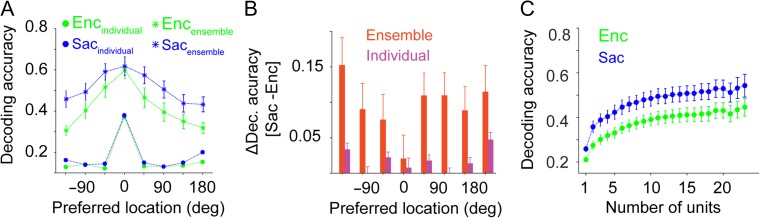
The presaccadic expansion of the neural code was consistently observed across all recording sessions. For each unit or session, we determined the preferred location based on the decoding accuracy of the SVM using the average activity across the 3 task epochs (visual, memory and presaccadic). For each unit or ensemble of units in a given session, the 8 stimulus locations were circularly shifted such that the 0 degree indicated the maximum response (preferred location; see Materials and Methods). Overall, we did not find any presaccadic change in the decoding accuracy for the preferred locations at the level of individual units considering both single- and multiunits (Δdecoding accuracyindividual = 0.0074 ± 0.0135, P = 0.722, n = 481; Fig. 2A). At the same time, non-preferred locations (>90 degrees away from the preferred location) exhibited a modest increase in decoding accuracy (Δdecoding accuracyindividual = 0.0313 ± 0.0042, P < 10−3). In contrast, when the activity of the ensemble of simultaneously recorded units (single- and multiunits) was taken into account, the decoding accuracy during the presaccadic period improved dramatically for both preferred and non-preferred locations. This presaccadic enhancement was observed across all 8 locations, as indicated by the greater overall decoding accuracy in SVMensemble during saccade preparation than visual encoding (Δdecoding accuracyensemble = 0.09 ± 0.03, P = 0.008; Fig. 2A). Importantly, this presaccadic population benefit was not equally strong across all target locations: the benefit was small for the units’ preferred location (Δdecoding accuracypref = 0.02 ± 0.03; P = 0.711), and much larger for locations far from the preferred locations (Δdecoding accuracynonpref = 0.12 ± 0.03, P = 0.008; Fig. 2B).
Figure 2.
Presaccadic expansion relies on the population-level representation of space. (A) Plot shows the decoding accuracy of the SVM classifier for various locations relative to the preferred location for individual (circles) and ensemble (stars) of units during visual encoding (Enc) and saccade preparation (Sac). The decoding accuracy of the ensemble of units for non-preferred locations remarkably increased from Enc to Sac. (B) The change in decoding accuracy between visual encoding and saccade preparation for individual units and the ensemble of units as a function of target locations. Larger improvements are visible for non-preferred locations for ensembles but not for individual units. (C) A small number of the most informative units account for the majority of decoding accuracy for ensembles. Decoding accuracy is greater during saccade preparation than visual encoding across a range of ensemble sizes. Plot shows the decoding accuracy of the ensemble of neurons as a function of the number of neurons used for the SVM classifier, separately for visual encoding (Enc) and saccade preparation (Sac) epochs. The error bars represent s.e.m.
Similar results were observed when we used the activity of single neurons (i.e., single-units) for sessions in which more than 2 single neurons could be isolated. More specifically, the changes in the decoding accuracy for the preferred and non-preferred locations using individual neurons’ activity were equal to 0.0352 ± 0.0265 (P = 0.20) and 0.0353 ± 0.0081 (P < 10−3), respectively. In contrast, the changes in the decoding accuracy for the preferred and non-preferred locations using the ensembles of single neuron activity were equal to 0.05 ± 0.04 (P = 0.60) and 0.10 ± 0.03 (P = 0.01), respectively.
To examine whether the encoding expansion during saccade preparation was a population phenomenon, we sorted the simultaneously recorded units in each session based on their MI (spatial discriminability), and made a set of neural ensembles by subsequently adding new units (with decreasing MI). Using this approach, we computed the overall decoding accuracy as a function of the number of units in different epochs of the experiment and estimated that about 4 units are enough to explain 75% of the ultimate classifier performance during both visual encoding and saccade preparation (Fig. 2C). More specifically, the number of sufficient units for ensemble encoding during visual and saccade epochs were equal to 4.44 ± 0.84 and 3.82 ± 0.67, respectively (errors based on bootstrapping; see Materials and Methods).
Characteristics of the Observed Presaccadic Expansion
We used the same method for computing the decoding accuracy in individual neurons and in ensembles of neurons (i.e., SVM classifier), in order to be able to compare the magnitude of the encoding expansion in individual neurons and ensembles on the same scale. However, it is possible that the observed encoding expansion was due to an overall smaller decoding accuracy for the non-preferred locations, or due to saturation of accuracy for the preferred location. In order to exclude these possibilities, we also examined the relative changes in the decoding accuracy by dividing the difference in the decoding accuracies by their sum ((a − b)/(a + b)). Using this relative measure, we observed a qualitatively similar encoding expansion. More specifically, the relative changes in the decoding accuracy for the preferred and non-preferred locations using individual units activity were equal to 0.0136 ± 0.0212 (P = 0.6) and 0.0932 ± 0.0153 (P < 10−3), respectively. In contrast, the relative changes in the decoding accuracy for the preferred and non-preferred location using the ensemble of individual units (considering both single- and multiunits) were equal to 0.01 ± 0.03 (P = 0.7) and 0.14 ± 0.04 (P = 0.01), respectively. Moreover, the decoding accuracy at 45 and −45 degrees, which were considered as part of the preferred locations, were just below the accuracy at 0 degree but sill showed a strong presaccadic enhancement. These results illustrate that the observed encoding expansion is not due to a smaller decoding accuracy for the non-preferred location or saturation of decoding accuracy for the preferred locations.
To control for the possibility that the encoding expansion was driven by a few units with high firing rates, we evaluated the decoding performance using normalized responses. We normalized the responses of each neuron by subtracting the mean and dividing by the SD of responses to train stimuli (z-score normalization). We found a similar encoding expansion using the normalized response (Δdecoding accuracypref = 0.04 ± 0.04, P = 0.4; Δdecoding accuracynonpref = 0.11 ± 0.03, P = 0.015), indicating that this effect was not solely dependent on high firing-rate units.
Comparing the firing rates between the Enc and Sac epochs, we found a small but significant increase in single-unit responses during saccade preparation (Enc = 62.07 ± 3.68 Hz; Sac = 68.01 ± 3.8 Hz; 2-sided signrank test, P < 10−3). Therefore, we performed an additional analysis to ensure that this increase in neural responses did not cause the observed encoding expansion. We identified units with no significant change in firing rate between Enc and Sac (using a paired t-test, P > 0.05; average number of units with no change in firing rate = 15.9 ± 2.63) and computed the decoding accuracy using the activity of these units individually and based on their ensembles in a given session. We found presaccadic expansion even for such firing-rate-matched units, similar to that observed in all units. More specifically, there was a small change in the decoding accuracy between Enc and Sac for the preferred locations (Δdecoding accuracyindividual = 0.0512 ± 0.0208, P = 0.0175; Δdecoding accuracyensemble = 0.02 ± 0.04, P = 0.7869). The change in the decoding accuracy between Enc and Sac for the non-preferred locations was smaller for individual units but larger for ensembles (Δdecoding accuracyindividual = 0.0237 ± 0.0062, P < 10−3, Δdecoding accuracyensemble = 0.08 ± 0.02, P = 0.0046). Together, these results show that an increase in the firing rate between the 2 epochs was not the main cause of the observed encoding expansion.
We also used an entirely different type of classifier in order to measure the differential increase in decoding accuracy during Sac compared with Enc. More specifically, we trained a multiclass naive Bayes with Normal (Gaussian) distribution to measure decoding of 8 locations using single-unit and ensemble of single-unit activity. Again, although we did not observe a significant change in the decoding accuracy for individual units (Δdecoding accuracypref = 0.0208 ± 0.0959, P = 0.9; Δdecoding accuracynonpref = 0.0134 ± 0.0463, P = 0.9), the decoding accuracy for the ensemble of units strongly increased for the non-preferred location (Δdecoding accuracypref = 0.01 ± 0.04, P = 0.7; Δdecoding accuracynonpref = 0.12 ± 0.04, P = 0.015).
Moreover, to ensure that there was no over-fitting and the latent structure in the data truly affected the decoding accuracy, we also calculated the empirical chance level by randomly permuting the label of stimuli in both the individual units and ensembles of units and running the SVM classifier on the permuted data. As expected, the classifier performance decreased to a chance level of 0.125 (single-units: Enc = 0.1249 ± 0.0004, P = 0.0573; Sac = 00.1246 ± 0.0004, P = 0.0479; ensemble of units: Enc = 0.125 ± 0.0017, P = 0.967; Sac = 0.127 ± 0.0022, P = 0.4204).
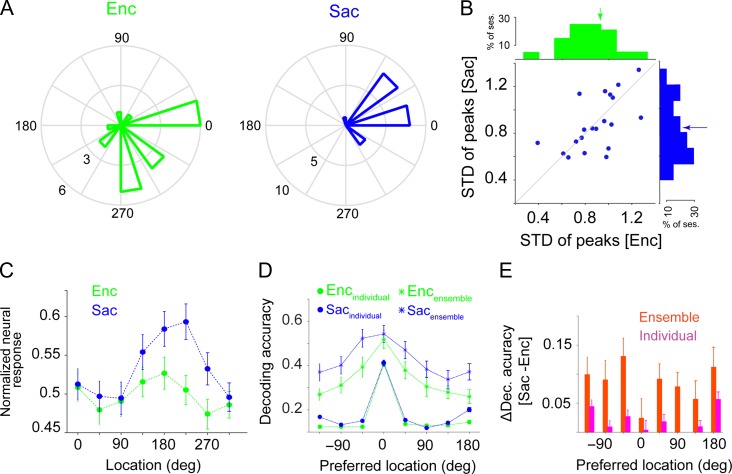
A possible explanation for the observed presaccadic expansion could be that the range of tuning preferences was larger during saccade preparation, or that the recorded neurons differentially changed their preferred locations between visual encoding and saccade preparation such that more neurons encoded non-preferred locations in the later epoch. We used several analyses to show that these factors did not influence our results. First, we computed the tuning similarity in each session of the experiment based on the variance of the preferred locations of all neurons in a given session during Enc and Sac (Fig. 3C). Interestingly, we found no evidence for a change in tuning similarity between Enc and Sac (Enc: 0.89 ± 0.05; Sac: 0.88 ± 0.05; (Sac-Enc): −0.01 ± 0.04; 2-sided signrank test, P = 0.941). We also computed the IQR for the preferred locations of all neurons in a given session during Enc and Sac (see Materials and Methods). The IQR was larger during Enc than Sac for most sessions (17 out of 20), the opposite of the pattern that could undermine our main findings (Enc: 83.81 ± 6.8; Sac: 72 ± 5.06; Sac-Enc: −11.81 ± 7.89; 2-sided signrank test, P = 0.191). Similarly, the average actual tuning preferences of all neurons was wider during Enc than Sac (width of Gaussian fit was equal to 2.31 ± 0.05 and 2.09 ± 0.05 for Enc and Sac, respectively, P < 10−3; Fig. 3D). Together, these results provide no evidence for broader tuning preferences during Sac compared to Enc (if anything we observed the opposite), illustrating that changes in the range of location preferences could not explain the observed broadening of the decoding accuracy during saccade preparation.
Figure 3.
The presaccadic expansion is not due to different ranges of tuning preferences or changes in the preferred location of neurons between visual encoding (Enc) and saccade preparation (Sac). (A) Distribution of the preferred locations (peak of the tuning curve) of individual neurons for one example session. (B) Plot shows the standard deviation of the preferred locations for all neurons in a given session during Sac vs. Enc. Upper and right-hand plots show the histograms of the standard deviation of the preferred locations during each epoch. There was no significant difference in the range of tuning preferences between Enc and Sac. (C) Normalized response of 188 FEF neurons (single-units) to targets presented at different angles relative to the neuron’s preferred location during Enc and Sac. The x-axis shows the actual angular position of the target. The error bars represent s.e.m. (D) Encoding expansion in ensembles of units with less than 90 degrees change in the preferred location. Plot shows the decoding accuracy of the SVM classifier for various locations for individual units (circles) and ensembles (stars) of units which have less than 90 degrees change in their preferred location between Enc and Sac, during the Enc (green) and Sac (blue) epochs. (E) The change in decoding accuracy in (D) between visual encoding and saccade preparation for individual units (pink) and the ensembles of units (red) as a function of target locations.
Examining changes in the preferred location of individual neurons, we found that about 33% of individual units shift their preferred locations by more than 90 degrees between visual encoding and saccade preparation. To test whether such shifts in location preference underlie the presaccadic expansion, we repeated our analyses using ensembles composed only of single-units with less than a 90 degree shift in their preferred location between Enc and Sac (no change and ± 45 deg; 48% of individual units). For these ensembles, we found an encoding expansion similar to that observed for ensembles using all recorded units (Fig. 3E,F). That is, we observed a much larger increase in the decoding accuracy for the non-preferred locations in the ensembles of units (Δdecoding accuracypref = 0.02 ± 0.03; P = 0.494, Δdecoding accuracynonpref = 0.09 ± 0.03, P = 0.004) than in individual units (Δdecoding accuracypref = 0.004 ± 0.0166, P = 0.977; Δdecoding accuracynonpref = 0.0367 ± 0.0049, P < 10−3). Thus the expansion in ensemble encoding did not depend upon individual units with large shifts in tuning preferences.
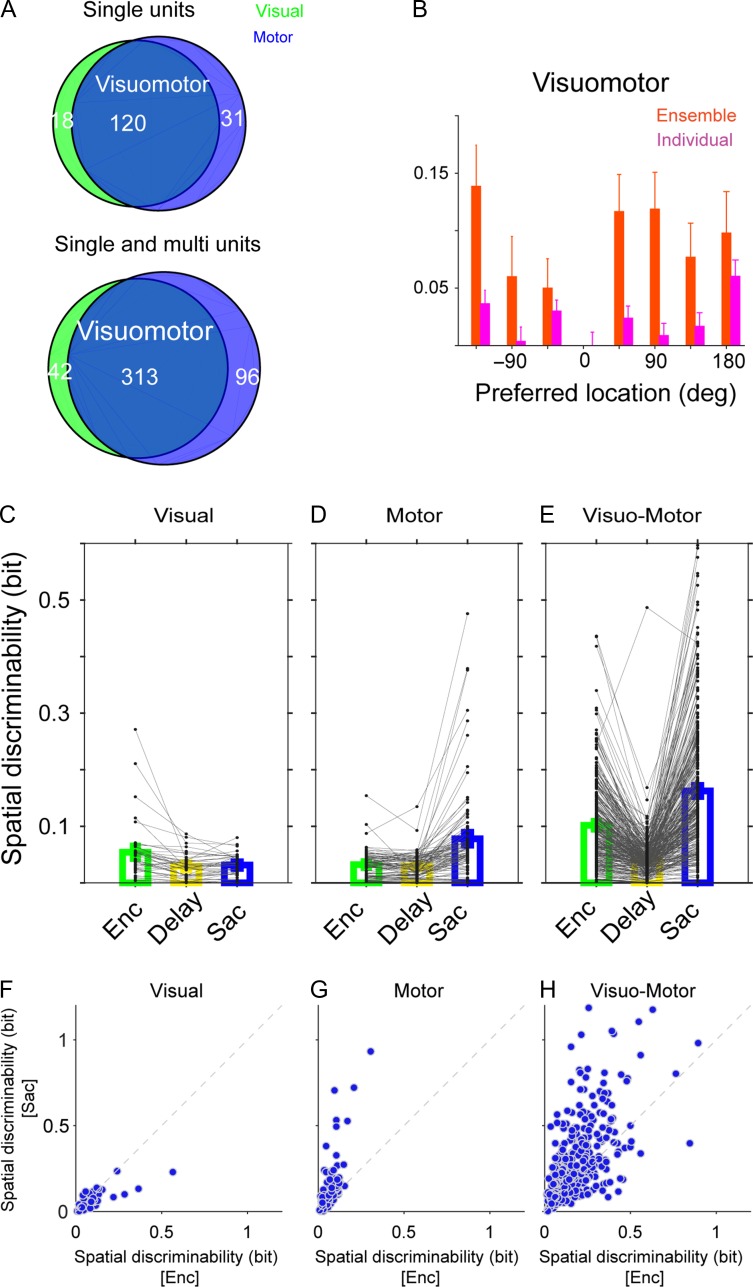
Finally, we performed a few additional analyses to rule out the possibility that the observed encoding expansion is merely due to engagement of neurons with certain types of selectivity during different task epochs (e.g., visual neurons during visual encoding and motor neurons during saccade preparation), or due to a disproportional contribution of neurons that became selective only later in the trial (i.e., motor neurons). We divided units into 3 distinct groups (visual-only, motor-only, and visuomotor) based on the MI of the units during different task epochs (see Materials and Methods) and computed changes in the decoding accuracy of the SVM classifier for each group (Fig. 4). The decoding accuracy could only be computed reliably for the visuomotor units, which were the majority of the recorded units (313 out of 451 single- and multiunits). For these units, changes in the decoding accuracy were: Δdecoding accuracypref = −0.05 ± 0.03, P = 0.1; Δdecoding accuracynonpref = 0.1 ± 0.03, P=0.005, which were very similar to the results for all neurons (Fig. 4B).
Figure 4.
Encoding expansion is present across cell types. (A) The Venn diagrams show the number of units with visual activity, motor activity, or both across all experiments. (B) Changes in the decoding accuracy between Enc and Sac for individual visuomotor units and the ensembles of visuomotor units as a function of target locations. Visuomotor units exhibited an encoding expansion similar to that seen for all units. (C–E) Plots show MI values of different types of neurons during the 3 epochs of the experiment in visual-only (C), motor-only (D), and visuomotor units (E). (F–H) Plots show MI values during saccade versus encoding in the same 3 types of neurons. Most neurons were visuomotor and these neurons increased their selectivity between visual encoding and saccade preparation.
To examine how the information content of different types of units changed over time, we also computed the MI for each type during the 3 task epochs (Fig. 4C–E). As expected, visual-only and motor-only neurons reached their maximum MI during the visual and saccade epochs, respectively. For visuomotor neurons, the MI decreased from the encoding to the delay epoch but then increased during the saccade epoch. Moreover, there was no evidence that neurons that were less selective (small MI) during the visual encoding epoch increased their selectivity prior to the saccade more strongly than other neurons, except for motor-only neurons, which by definition are selective only during saccade preparation (Fig. 4F–H). We found similar results using both the equal-sample and bias-corrected MI values (Supplementary Figs 2 and 3). Overall, these results indicate that the observed encoding expansion is not due to particular contributions of visual or motor neurons during different task epochs, instead relying mainly on visuomotor neurons that were selective during both epochs.
Altogether, our results revealed a selective increase in the information content of neural ensembles prior to saccadic target selection. This enhancement of the neural code was mainly observed at the population level and could not be explained by selective changes in the activity of individual neurons between visual encoding and saccade preparation.
Presaccadic Expansion is a Population Phenomenon and Not Due to the Ceiling Effect
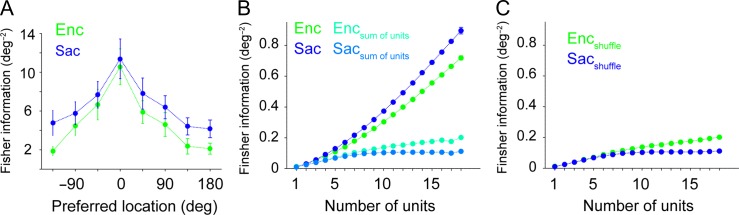
We found that during saccade preparation, the ability of ensembles of neurons to represent target locations selectively expanded beyond that of single neurons. Specifically, locations poorly encoded by the activity of single neurons (non-preferred locations) could be more accurately discriminated using population activity during Sac than Enc. These results were obtained using a decoding method (SVM) that is subject to the ceiling effect. That is, although the maximum value of decoding accuracy is 1, the decoding at the preferred location could be close the maximum performance of the linear SVM classifier for the neural ensembles. To ensure that the lack of increase in decoding performance at the preferred locations was not due to the ceiling effect and that encoding expansion was indeed a population phenomenon, we used the FI, which has no upper bound (see Materials and Methods). To test that the FI exhibits encoding expansion measured via the decoding performance, we calculated the change in the FI between visual encoding and saccade preparation separately for preferred and non-preferred locations, and found a robust encoding expansion at the population level (Fig. 5A; ΔFIpref = 0.8206 ± 1.991, P = 0.7; ΔFInonpref = 2.332 ± 0.7113, P = 0.003).
Figure 5.
Presaccadic expansion based on the Fisher information. (A) Plot shows the Fisher information for various locations relative to the preferred location for ensemble of units during visual encoding (Enc) and saccade preparation (Sac). The error bars represent s.e.m. (B) Plotted is the Fisher information for the locations in simultaneously recorded units that were poorly encoded during both Enc and Sac, as a function of the number of units used for computing the Fisher information in ensembles. The sum of the Fisher information in individual units is also plotted separately for Enc and Sac. (C) Plotted is the Fisher information for shuffled ensembles separately for Enc and Sac for the same locations as in (B). Overall, the sum of FI for individual units were very similar to the shuffled FI and much smaller than the FI for the ensembles, indicating that the interaction between neurons that poorly encode information contributes to the information at the population level strongly.
We then used the FI to determine locations in simultaneously recorded units that were poorly encoded by individual units during both Enc and Sac, i.e., locations at which the average FI in Enc and Sac and the change in the FI from Enc to Sac were among the first quantile. The response of individual units at these locations were then used to construct a set of neural ensembles by subsequently adding new units and computing the FI as a function of the number of units (NU) in different epochs of the experiment (Fig. 5B,C). We found that the FI for this set of ensembles monotonically increased with a larger NU and this increase was larger for Sac than Enc (e.g., FI for NU = 15: Encpopulation = 0.5555 ± 0.0016, Sacpopulation = 0.6895 ± 0.0025; Fig. 5B). In contrast, the sum of FI for individual units in the same set of neurons was much smaller, only moderately increased with adding more units, and was larger for Enc than Sac (e.g., FI for NU = 15: Encsum of units = 0.1763 ± 0.0007, Sacsum of units = 0.1061 ± 0.001; Fig. 5B). These results show that even for locations poorly encoded by individual neurons and with no presaccadic increase in the FI (i.e., non-informative individual units), the increase in the information content of the ensembles was much larger than that of individual units.
To examine the contribution of this inter-neuronal correlations to increases in the FI of the population of non-informative units, we also estimated the FI in the shuffled ensembles (see Materials and Methods). The FI of the shuffled ensembles showed a statistically significant decrease in the spatial information relative to the intact ensembles, and moreover, the FI decreased after shuffling more strongly for Sac than Enc (e.g., for NU = 15, ∆Enc (intact—shuffled) = 0.3793 ± 0.0019, P < 10−3; ∆Sac(intact—shuffled) = 0.5834 ± 0.003, P < 10−3; Fig. 5C). Together, these results illustrate that the observed encoding expansion is a population phenomenon that mainly relies on how non-informative neurons interact with each other.
Next, to further address the relationship between changes in inter-neuronal correlations and encoding expansion in all locations, we made all possible of pair of neuron-locations and studied the effect of changes in noise and signal correlations for preferred and non-preferred locations on spatial information coded in individual and pairs of neurons.
Changes in Inter-Neuronal Correlations Contribute to Encoding Expansion During Saccade Preparation
As mentioned earlier, a reduction in noise correlations between neurons has been proposed as a mechanism to enhance population-level information (Zohary et al. 1994; Shadlen and Newsome 1998; Nirenberg and Latham 2003; Averbeck et al. 2006; Cohen and Maunsell 2009). Hence, we examined the effects of inter-neuronal correlations at the level of pairs of neurons (n = 1165) (see Materials and Methods) in order to address the contribution of correlated neural activity to the enhanced spatial representation prior to saccades.
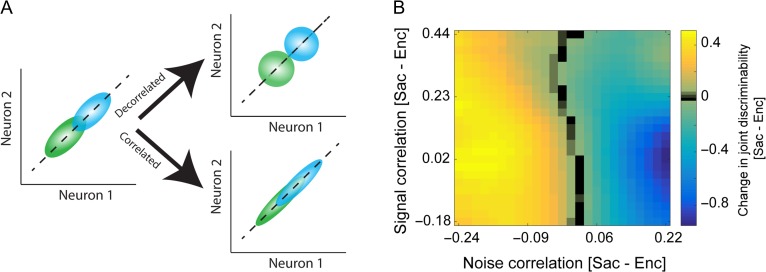
For each neuron-condition pair, the “raw” correlation coefficient between mean responses of a pair of simultaneously recorded neurons across trials captures the overall correlation between responses to 2 separate locations. This correlation can be decomposed into 2 components: 1) the signal correlation (SC), reflecting the degree to which 2 neurons exhibit similar responses to different stimuli or target locations; and 2) the noise correlation (NC), measuring shared variability unrelated to the target location (Cohen and Kohn 2011). Here we defined the SC as the correlation coefficient between the mean responses of a pair of neurons to a given pair of target locations after randomly shuffling the trial number for the responses of the 2 neurons for that pair of target locations (Fig. 6A). The noise correlation is computed by subtracting the signal correlation from the raw correlation (Pachitariu et al. 2015; Tremblay et al. 2015). This method of calculating noise correlation has several advantages. First, it properly takes into account both signal and noise correlation and can be applied to a minimum number of conditions (2 locations in our data) to compute the signal correlation. Second, this method allows the investigation of changes in noise correlation for specific values of signal correlation or change in signal correlation. Note that for each pair of neurons, the order of locations was assigned according to the decoding tuning curves of the ensemble made by single-units in a given session (see Materials and Methods). By transforming the problem of analyzing population-level correlated activity to correlation between pairs of neurons for 2 target locations (~32 400 neuron-condition pairs), we were able to precisely study the contribution of noise and signal correlations to encoding expansion during saccade preparation.
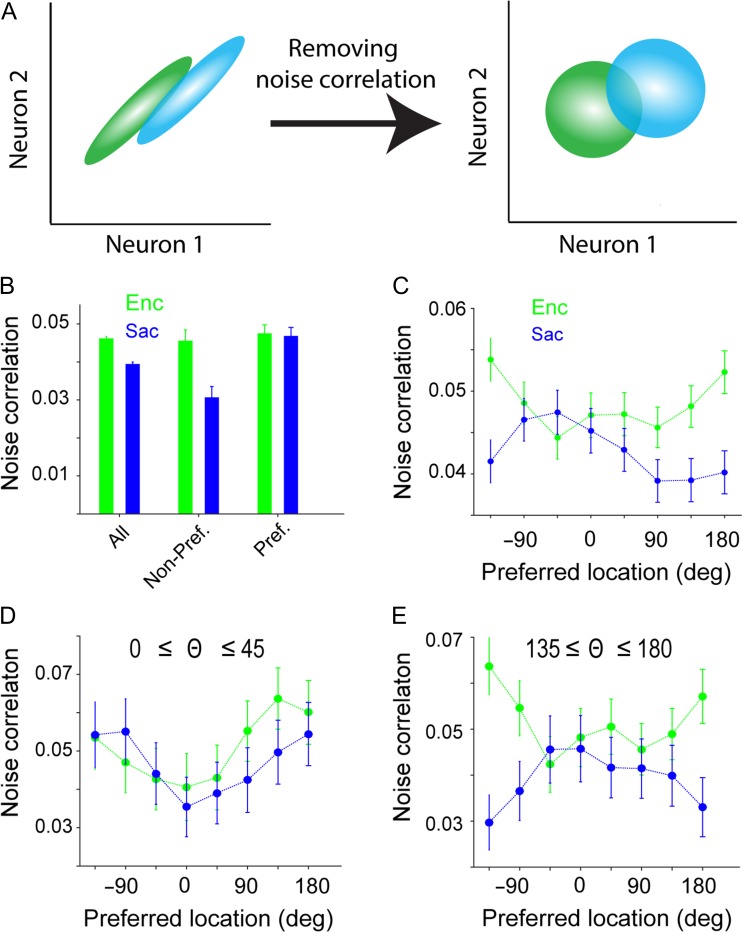
Figure 6.
Differential changes in noise correlation for the preferred and non-preferred locations, between visual encoding and saccade preparation. (A) Schematic of the computations of signal and noise correlations. The signal correlation was computed after shuffling the order of repeated trials within each condition (right panel). The noise correlation was then calculated by subtracting the signal correlation from the total correlation (i.e., correlation coefficient without shuffling). (B) Average noise correlation across all locations and separately for the preferred and non-preferred locations during visual encoding (Enc, green) and saccade preparation (Sac, blue). Noise correlation was reduced during Sac, but this effect was driven by a reduction in noise correlation at the non-preferred locations. (C) Selective reduction in noise correlation for the non-preferred locations during saccade preparation. Plot shows the noise correlation as a function of the target location for the pairs of simultaneously recorded neurons relative to the preferred location of their ensemble (noise correlation tuning curve; see Methods), separately for visual encoding (green) and saccade preparation (blue). The error bars represent s.e.m. (D,E) The selective change in noise correlation was mainly present in pairs of neurons with dissimilar preferred locations. Plots show the tuning curve of noise correlation for pairs of neurons with small (D) or large (E) differences in preferred locations.
We found a higher SC during saccade preparation than visual encoding (SCEnc = 0.0164 ± 0.0005, SCSac = 0.0447 ± 0.0008, P < 10−3). This greater correlation in the spatial tuning of FEF neurons during saccade preparation was consistent with the enhanced response magnitude (Fig. 1C) and spatial discriminability (Fig. 2A) observed during this epoch. In contrast to SC, the NC was reduced in the presaccadic period (NCEnc = 0.046 ± 0.0007, NCSac = 0.039 ± 0.0007, P < 10−3; Fig. 6B). Interestingly, the presaccadic reduction in NC was prominent for pairs of non-preferred locations (>90 deg) compared to preferred locations (ΔNCnonpref = −0.0152 ± 0.0029, ΔNCpref = −0.0007 ± 0.0025, P < 10−3; Fig. 6B). In contrast, increases in signal correlation were not different for preferred and non-preferred locations (ΔSCnonpref = 0.0104 ± 0.0012, ΔSCpref = 0.0139 ± 0.0021, P = 0.376). To precisely measure the modulation of noise correlations during Sac compared to Enc, we assessed the spatial tuning of noise correlations across these epochs. For locations far from the preferred location, NC changed strongly during Sac compared to Enc epoch (Fig. 6C). Interestingly, the selective change in noise correlations was mainly present in pairs of neurons with dissimilar preferred locations (Fig. 6D,E). This differential change in noise correlation (from visual encoding to saccade preparation) across space was consistent with the observed population-level advantage for the processing of non-preferred locations. We also confirmed that this differential decrease in noise correlation was present for all neuron types (data not shown) similar to the presaccadic expansion of the population code measured by the SVM.
Because we calculated noise correlations by subtracting signal correlation from the total correlation, there should be little or no additive bias in the noise correlation due to a higher firing rate. As a result, the measured noise correlation is immune to the effect of firing rate on noise correlation (Cohen and Kohn 2011). Nevertheless, we also controlled for any potential effect of firing rate by restricting our analyses to pairs of neurons with no significant change (increase or decrease) in the firing rates between Enc and Sac (23% of pairs). We found a higher SC during Sac than Enc (SCEnc = 0.0169 ± 0.001; SCSac = 0.0348 ± 0.0014; P < 10−3) but the increases in SC were not different between the preferred and non-preferred locations (ΔSCnonpref = 0.0092 ± 0.0018, ΔSCpref = 0.0083 ± 0.0041, P = 0.290). In contrast, there was a larger reduction of noise correlation in the non-preferred compared to the preferred location in these firing-rate-matched pairs (ΔNCnonpref = −0.0119 ± 0.005, ΔNCpref = 0.0024 ± 0.0053, P = 0.018).
Because signal and noise correlations are defined based on the activity of pairs of neurons and not the whole ensemble, computing their contributions to the observed encoding expansion requires measuring the information content of pairs of neurons as well. We measured the information content of a given pair of neurons by the ability of this pair to discriminate a pair of locations (“joint” discriminability) using the LDA (see Materials and Methods and Fig. 7A). Briefly, the LDA characterizes the optimal vector for linear discrimination between 2 conditions (locations) based on the neural response. We then projected the population response during each trial onto this optimal weight vector, which yields a scalar value. Finally, we computed “joint discriminability” as the MI between the projections of the neural response and the target locations. The LDA enabled us to measure the contributions of changes in NC and SC to the enhancement of the neural representation. Moreover, using the LDA as a supervised dimension reduction method, we were able to compute and estimate the MI of a pair of neurons in one dimension. Consistent with the SVM results, joint discriminability was enhanced during saccade preparation compared to visual encoding (Enc = 0.1572 ± 0.0009, Sac = 0.2274 ± 0.0013, P < 10−3). Moreover, similar to the SVM results (Fig. 2A), non-preferred locations showed greater presaccadic improvements in discriminability than preferred locations (Δjoint discriminabilitynonpref = 0.0281 ± 0.0027, Δjoint discriminabilitypref = 0.0105 ± 0.0031, P < 10−3; Fig. 7B). Qualitatively similar results were obtained for all neuron types (data not shown).
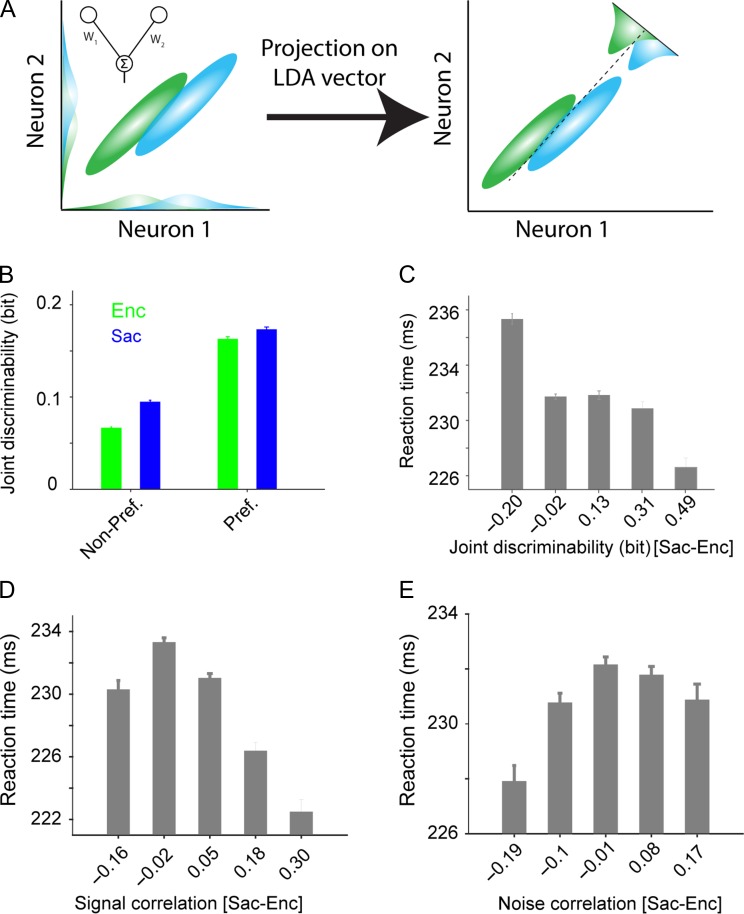
Figure 7.
The information content of pairs of neurons (joint discriminability) changes more for non-preferred locations, and this change correlates with behavior. (A) Schematic of the linear discriminant analysis (LDA) used for computing joint discriminability. Ellipses represent the variability of neural population response in 2 conditions (green and blue). The LDA weight vector for the pair of neurons (solid line in the left panel) is the optimum weight vector for population decoding, and is equal to a linear combination of the 2 neurons that maximally separates neural responses in the 2 conditions. The dashed line (right panel) corresponds to the best criterion to discriminate responses to the 2 conditions (i.e., the LDA line) (B) Plot shows the joint discriminability, measured separately for preferred and non-preferred locations during visual encoding (green) and saccade preparation (blue). Non-preferred locations showed a larger improvement in joint discriminability from visual encoding to saccade preparation. The error bars represent s.e.m. (C) Across trials, faster reaction times corresponded with greater improvements in joint discriminability from visual encoding to saccade preparation. Plot shows the average RT for groups of trials with a specific amount of change in joint discriminability. (D) The same as in C but for changes in signal correlation (D) and noise correlation (E). Presaccadic increases in signal and noise correlations corresponded to faster and slower RT, respectively.
Considering the similarities between the changes in joint discriminability and decoding performance, we next tested whether the greater improvement in joint discriminability for non-preferred vs. preferred locations reflects the encoding expansion measured by the SVM. To do so, we computed the correlation between the encoding expansion index using the SVM and a similar index based on joint discriminability after subtracting a baseline related to the information content of individual units (see Materials and Methods). The expansion indices computed by discriminability (joint and isolated) were averaged across all pairs in a given session to obtain one value for each session. We found a significant correlation between the encoding expansion index based on the SVM and the one based on discriminability, demonstrating that joint discriminability reflects encoding expansion (Spearman correlation, r = 0.53, P = 0.025). We used a non-parametric correlation to deal with the small sample size and possible outliers. Overall, the analyses based on pairwise measures of information confirmed the presaccadic encoding expansion, which was originally revealed by the decoding analysis, and demonstrated that this expansion is detectable in the activity of as few as 2 neurons.
Finally, unlike the encoding expansion measured with an SVM, joint discriminability measures the information content of a pair of neurons on a trial-by-trial basis, and thus can be used to look for behavioral correlates of changes in the information content between visual encoding and saccade preparation. By binning trials based on the change in joint discriminability from visual encoding to saccade preparation, we found that greater changes in joint discriminability were associated with faster reaction times (Fig. 7C). More specifically, there was ~5% difference between the average reaction time when the change in joint discriminability was negative vs. positive (235.32 ± 0.39 vs. 224.60 ± 0.68 ms, P < 10−3), showing that changes in joint discriminability reflected the behavior. We found consistent results when considering changes in signal and noise correlations between Enc and Sac. More specifically, presaccadic increases in signal and noise correlations resulted in faster and slower RT, respectively (Fig. 7D,E). Together, our results suggest a larger contribution of changes in signal and noise correlations to response time than to the accuracy of saccade endpoints.
Changes in Noise Correlation Contribute to Presaccadic Expansion Independent of Signal Correlation
Having established that changes in joint discriminability reflect the encoding expansion, we next examined the relationship between the signal correlation, noise correlation, and joint discriminability for the same pairs of neurons during visual encoding and saccade preparation. This analysis allowed us to study the contribution of signal and noise correlations to encoding expansion.
To do so, we first partitioned our dataset according to the sign of signal and noise correlations in each pair. Interestingly, we found that pairs of neurons with a positive SC were 3 times more likely to have a positive NC (Fig. 8A). Moreover, pairs with positive signal and noise correlations comprised about 45% of the dataset. Finally, presaccadic expansion based on joint discriminability was at least 2 times greater in these pairs than in those pairs with one or more negative correlation values (Fig. 8A). By examining the relationship between signal correlation and joint discriminability during visual encoding for pairs of neuron with positive signal and noise correlations, we found that a higher signal correlation was associated with greater discriminability (Fig. 8B). However, by separating the population based on whether noise correlation decreased or increased during the presaccadic period (comprising 76% and 24% of population, respectively), we found that for a given level of SC the joint discriminability depended upon the change in noise correlation, such that a decrease in noise correlation improved joint discriminability. Furthermore, for neuron pairs with no significant change in SC between Enc and Sac, the change in noise correlation still determined the change in joint discriminability (Fig. 8C); this result indicates that a change in noise correlation is sufficient to drive an encoding expansion during saccade preparation. As a further control, we verified that the isolated discriminability (which excludes the contribution of NC yet incorporates each unit’s spatial sensitivity) stayed the same between neurons for which NC decreased during saccadic preparation and those for which NC increased (Fig. 8D).
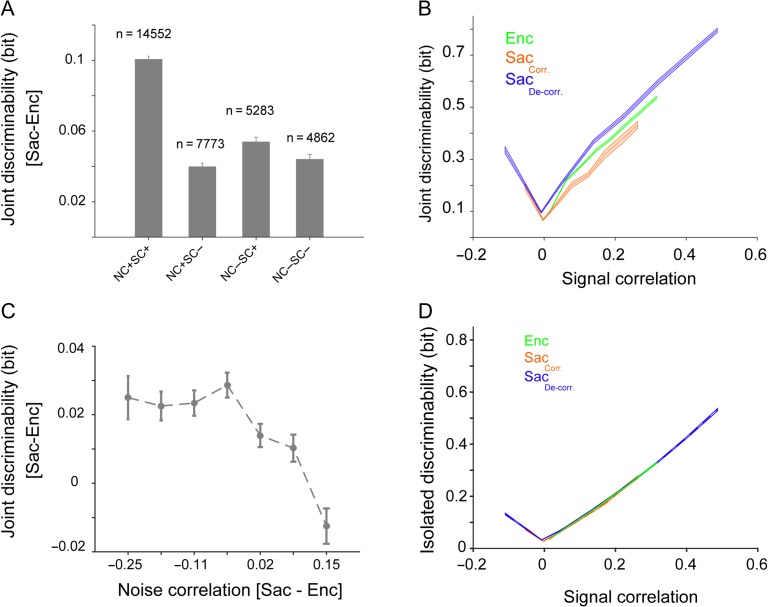
Figure 8.
Changes in noise correlation contribute to presaccadic expansion independent of signal correlation. (A) Neuron pairs with positive signal and noise correlations comprised about half of the population, and exhibited a change in joint discriminability twice that of other pairs of neurons. Plot shows the change in joint discriminability from visual encoding to saccade preparation for various groups of pairs, sorted based on the sign of the signal and noise correlations for the neuron-condition pair. The number of neuron-condition pairs in each group is shown above each bar. (B) Joint discriminability depends upon both signal and noise correlation. Plot shows joint discriminability as a function of signal correlation computed separately for neuron-location pairs during visual encoding (Enc, green) and during saccade preparation (Sac). The latter is plotted for pairs of neurons that showed a large (>0.1) reduction (blue) or increase (red) in noise correlation from visual encoding to saccade preparation. For a given value of signal correlation, the joint discriminability of neurons that became decorrelated was larger than those which became more correlated during saccade preparation. (C) Plot shows the change in joint discriminability for pairs of neurons that show a negligible change in SC between visual encoding and saccade preparation (ΔSC < 0.05, n = 6419), illustrating the direct contribution of NC changes to joint discriminability. Improved joint discriminability during saccade preparation compared to visual encoding is most prominent when NC is reduced in saccade preparation relative to visual encoding in the same pair. (D) Plot shows isolated discriminability as a function of signal correlation computed separately for neuron-location pairs during visual encoding (green) and during saccade preparation. The latter is plotted for pairs of neurons that showed a large (>0.1) reduction (blue) or increase (red) in noise correlation from visual encoding to saccade preparation. The shaded area represents s.e.m.
These results suggest that the change in NC drives the presaccadic expansion and thus, we next estimated the extent to which the reduction in NC was employed for presaccadic expansion. To do so, we applied a shuffling procedure to eliminate the temporal structure in simultaneously recorded ensemble activity, and measured the decoding accuracy using the SVM on this shuffled data. More specifically, we shuffled the identity of trials belonging to the same target location for each single neuron to eliminate noise correlations while preserving single-unit tuning and signal correlations (Tremblay et al. 2015). The SVM classifier performance on the shuffled ensembles (those with more than 2 single-units) revealed a statistically significant increase in the decoding accuracy for the non-preferred (4 ± 2%, P = 0.043) but not the preferred locations (1 ± 2%, P = 0.56) during saccade preparation. During visual encoding, however, shuffling similarly increased the decoding accuracy for both the preferred and non-preferred locations (non-preferred: 5 ± 1% P = 0.005; preferred: 6 ± 2% P = 0.005). These results indicate that existing noise correlations are reducing the ensemble decoding performance, and that further reductions in NC could increase the encoding expansion during saccade preparation.
It has been argued that a reduction in the mean pairwise noise correlation or the removal of an ensemble noise correlation does not improve coding ability per se (Averbeck et al. 2006; Moreno-Bote et al. 2014). Instead, coding ability can be improved by a reduction in noise correlation only if the signal and noise correlations are orthogonal to each other. Such a scenario is depicted in Figure 9A where a decrease in the noise correlation between 2 neurons (decorrelated case) produces a reduction in the overlap of the distributions of the neural responses to the 2 stimuli, corresponding to improved discrimination between the 2 locations. In contrast, an increase in correlation between the 2 neurons (correlated case) creates more overlap between the neural responses to the 2 stimuli, indicating a drop in discriminability. This condition is an example of information-limiting correlation (Moreno-Bote et al. 2014). In contrast, the noise correlation in the locations poorly encoded during both Enc and Sac is an example of information-enhancing correlation because removing this correlation can decrease information (Fig. 5). Therefore the amount of information encoded at the level of single-units is one of the main factors that can predict how the inter-neuronal variability affects information coding in prefrontal cortex. In contrast, when all locations with a wide range of information content were pooled (as in location-neuron pairs structure and LDA analyses), the information-limiting correlation dominates the spatial encoding of prefrontal cortex.
Figure 9.
Presaccadic change in joint discriminability as a function of changes in SC and NC. (A) Effects of changes in inter-neuronal correlations on the discriminability of paired neural responses. Plot shows an idealized response of 2 neurons with positive signal and noise correlations to the target at 2 different locations (green and blue), and ellipses represent the variability of the neural response. (B) Change in joint discriminability was explained by a reduction in noise correlation when the change in signal correlation was taken into account. The change in joint discriminability (separately z-scored across the same change of signal correlation, each row) is plotted as a function of the changes in signal and noise correlations.
To examine the interaction between the influence of signal and noise correlations on coding ability, we quantified the presaccadic change in joint discriminability as a function of changes in SC and NC (for the pairs of neurons with positive SC and NC; Fig 9A). We found that prior to a saccade, joint discriminability increased as NC decreased for any amount of change in SC (Fig. 9B). This result not only illustrates that decorrelation (i.e., a reduction in noise correlation) increases the information content of pairs of neurons (as a proxy for ensembles), but also indicates that detecting such an effect requires controlling for the magnitude of the change in SC. The latter is important because as shown in Fig. 7B, an increase in SC alone can increase joint discriminability.
Discussion
An ensemble of neurons may contribute to various cognitive functions. This requires the neural representation in the ensemble to be dynamically adjusted according to the task at hand. It is unclear, however, whether this dynamic adjustment relies on changes in the activity of individual neurons, in the interaction between neurons, or both. Here, we report that ensembles of FEF neurons dynamically adjust their representation of space as monkeys moved from visual encoding to saccade preparation. We found that during saccade preparation, ensembles of neurons enhance their representation of parts of the visual space poorly encoded by individual neurons. This novel phenomenon, which we refer to as the presaccadic encoding expansion, was not present in the single-cell responses but could be observed in the ensemble of simultaneously recorded neurons (using SVM and the FI) or even when we examined the interaction between only 2 neurons (using joint discriminability). In addition, we found that this encoding expansion was accompanied by selective changes in the noise correlation for non-preferred locations only, indicating the importance of inter-neuronal interactions between neurons selective for different parts of space. Altogether, our findings suggest that cognitive states modify the information content of prefrontal ensemble activity more easily than that of single-cell activity because of the many components that contribute to the population code. For example, the complex manifold of population neural activity could change greatly if the activity of a few neurons is slightly altered by cognitive states.
Our results dovetail with recent findings showing the importance of population-level representations for various cognitive functions, and demonstrate that neural ensembles can utilize the information content of non-selective neurons, which is not detectable at the level of individual neurons, to improve encoding (Hung 2005; Cohen and Maunsell 2010; Zhang et al. 2011; Rigotti et al. 2013; Leavitt et al. 2017; Parthasarathy et al. 2017). The enhanced population-level representation for parts of space poorly encoded by individual neurons indicates that this representation is particularly useful for improving encoding when signal improvement through single-cell mechanisms, such as gain modulation, is limited. A qualitatively similar presaccadic increase in the decoding accuracy of ensembles of lateral prefrontal neurons has been recently reported using a demanding change-detection task (Tremblay et al. 2015). Although it is unclear whether the observed increase was different for preferred and non-preferred locations, the similarities between the results of this and our studies indicate the importance of population-level representations for different cognitive functions. Moreover, this study measured the effect of noise correlation on population encoding and found that removing noise correlations slightly (~6%) increased decoding accuracy for the cue and attention location but not for the saccade. Similarly, we observed a small (~4%) but significant change in the decoding performance of the shuffled and intact ensembles. The shuffling process eliminates noise correlations while preserving other information such as single-unit tuning and signal correlations. These may suggest that the information content of neural ensembles is mainly determined by inter-neuronal correlations other than noise correlation. Nevertheless, the LDA approach, which allowed us to examine changes in the population-level information while controlling for changes in signal correlation, revealed the contribution of noise correlation to the information content of neural ensembles.
In a recent study, Leavitt and colleagues (Leavitt et al. 2017) explored the role of correlation in encoding information for working memory by ensembles of prefrontal neurons. They found that depending on the size and composition of the ensemble, removing the correlation structure could increase or decrease the information content of the ensemble. Moreover, even neurons with poor working-memory selectivity could enhance coding fidelity of neural ensemble through influencing the structure of spike count correlations. Similarly, we found that the changes in noise correlations that result in an enhanced representation of space are stronger for parts of space not well-encoded by individual neurons (i.e., changes in noise correlations are spatially selective). A recent study has suggested that the magnitude of pairwise correlations could put an upper bound on the dimensionality of neural ensembles (Mazzucato et al. 2016). Therefore, a reduction in noise correlation could potentially increase the dimensionality of the population neural representation as well. Considering that changes in signal correlation also influence the population code, our results suggest factors such as modulation by an external source or network states (e.g., excitation-inhibition balance), and changes in interactions between neurons in the same ensemble could all contribute to presaccadic expansion in the population of FEF neurons.
Here we used 2 different decoding methods (SVM and LDA) to assess the information content of the population response. Importantly, both outcome measures (decoding accuracy based on the SVM and joint discriminability based on the LDA) captured changes in the representation of targets between visual encoding and saccade preparation. Two recent studies have utilized decoding methods to extract spatial information from populations of neurons in lateral intraparietal cortex (LIP) and FEF during the memory-guided saccade task (Graf and Andersen 2014; Sajad et al. 2016). Using these methods, Sajad and colleagues (2016) could identify aspects of the ensemble neural response that predict the error in saccade endpoints, whereas Graf and Andersen (2014) constructed a brain-machine interface. In our study, however, only joint discriminability allowed measurement of the information content of pairs of neurons, for which signal and noise correlations could be computed as well. Using this method, we could isolate the effect of changes in inter-neuronal correlations and found that presaccadic changes in noise correlation enhance joint discriminability. Our results based on both the SVM and LDA revealed a presaccadic expansion of the population code, with population-level benefits at the non-preferred locations that can be attributed to both to the population representation and changes in noise correlation between neurons. Using the SVM and LDA, however, we were able to illustrate the contributions of population neural representation and changes in noise correlations within the same study.
Our observations are also consistent with studies demonstrating the effect of stimulus-dependent noise correlations on neural coding (Panzeri, Treves, et al. 1999; Shamir and Sompolinsky 2004). For example, by separating the MI into firing-rate and correlation components Panzeri and colleagues (Panzeri, Schultz, et al. 1999; Panzeri, Treves, et al. 1999; Pola et al. 2003) showed that the stimulus-dependent noise correlation can marginally enhance MI and neural coding in the population. In another study, Franke and colleagues measured noise correlation in pairs of simultaneously recorded retinal cells as a function of the direction of motion in the stimulus in order to address the effect of stimulus-dependent structure on the improvement of visual coding (Franke et al. 2016). Nevertheless, none of these studies has compared correlation across different cognitive states, whereas we were able to link the stimulus-dependent noise correlation to the selective changes in spatial representation between visual encoding and saccade preparation.
Recent empirical evidence suggests that the trial-by-trial variability and noise correlations of purely sensory areas (Ponce-Alvarez et al. 2013; Franke et al. 2016) are tuned to the features of stimuli. For example, it has been showed that tuned noise correlations of MT neurons arise from a network effect and is not a side-product of nonlinear dependence on the firing rate (Ponce-Alvarez et al. 2013). Similarly, our study illustrates that the dynamics of structured variability in prefrontal neurons impacts the efficiency of population codes, specifically for the stimuli which are weekly encoded (by both individual neurons and the population) during visual representation.
Correlations between neurons are an important factor affecting the amount of information in a neuronal population (Panzeri, Schultz, et al. 1999; Petersen et al. 2001). A recent study has suggested that features of neural activity which have an intersection between sensory and choice information are those that drive the behavior (Panzeri et al. 2017). Here, we show that selective changes in the inter-neuronal variability change the coding ability of the FEF ensembles during 2 cognitive states (visual encoding and saccade preparation). Increasing the information content of neural ensembles for parts of space not well-encoded by individual neurons allows different ensembles to have a good amount of information about the upcoming saccade. This phenomenon does not increase the precision of the saccade –perhaps because the precision of saccadic landing points is primarily determined by neurons whose preferred location matches the target location. However, it can improve the response time, potentially by reducing the “conflict” between possible saccade locations based on the activity of different neural ensembles. Together these suggest that inter-neuronal variability could contribute to the intersections of spatiotemporal features of population activity, and thus can be used for perception and representation of higher cognitive functions.
Finally, we find that during saccade preparation, the FEF’s representation of space undergoes an expansion at the level of the population code, showing another example of how a population of neurons can be more informative than sum of the individual neurons. Our findings illustrate the ability of prefrontal neural ensembles to recruit individual neurons to encode a larger part of space, and to exploit population neural representations and changes in inter-neuronal relationships for improving the encoding capacity of the whole population according to cognitive states.
Supplementary Material
Notes
We thank Bard Duchaine and Matt van der Meer for helpful comments and Kelsey Clark for helpful comments and edits on the manuscript. This work was supported by NSF EPSCoR (Award #1632738) to AS and BN, and NSF BCS143221, and NEI R01EY026924 to BN. Conflict of interest: None declared.
Supplementary Material
Supplementary material is available at Cerebral Cortex online.
References
- Abbott LF, Dayan P. 1999. The effect of correlated variability on the accuracy of a population code. Neural Comput. 11:91–101. [DOI] [PubMed] [Google Scholar]
- Adibi M, McDonald JS, Clifford CWG, Arabzadeh E. 2014. Population decoding in rat barrel cortex: optimizing the linear readout of correlated population responses. PLoS Comput Biol. 10:e1003415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asaad WF, Santhanam N, McClellan S, Freedman DJ. 2013. High-performance execution of psychophysical tasks with complex visual stimuli in MATLAB. J Neurophysiol. 109:249–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, Pouget A. 2006. Neural correlations, population coding and computation. Nat Rev Neurosci. 7:358–366. [DOI] [PubMed] [Google Scholar]
- Barnett AH, Magland JF, Greengard LF. 2016. Validation of neural spike sorting algorithms without ground-truth information. J Neurosci Methods. 264:65–77. [DOI] [PubMed] [Google Scholar]
- Britten KH, Newsome WT, Shadlen MN, Celebrini S, Movshon JA. 1996. A relationship between behavioral choice and the visual responses of neurons in macaque MT. Vis Neurosci. 13:87–100. [DOI] [PubMed] [Google Scholar]
- Britten KH, Shadlen MN, Newsome WT, Movshon JA. 1992. The analysis of visual motion: a comparison of neuronal and psychophysical performance. J Neurosci. 12:4745–4765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruce CJ, Goldberg ME. 1985. Primate frontal eye fields. I. Single neurons discharging before saccades. J Neurophysiol. 53:603–635. [DOI] [PubMed] [Google Scholar]
- Bruce CJ, Goldberg ME, Bushnell MC, Stanton GB. 1985. Primate frontal eye fields. II. Physiological and anatomical correlates of electrically evoked eye movements. J Neurophysiol. 54:714–734. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, Shenoy KV. 2012. Neural population dynamics during reaching. Nature. 487:51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Kohn A. 2011. Measuring and interpreting neuronal correlations. Nat Neurosci. 14:811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Maunsell JHR. 2009. Attention improves performance primarily by reducing interneuronal correlations. Nat Neurosci. 12:1594–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Maunsell JHR. 2010. A neuronal population measure of attention predicts behavioral performance on individual trials. J Neurosci. 30:15241–15253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Newsome WT. 2009. Contest-dependent changes in functional circuitry in MT. Neuron. 60:162–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortes C, Vapnik V. 1995. Support-vector networks. Mach Learn. 20:273–297. [Google Scholar]
- Cunningham JP, Byron MY. 2014. Dimensionality reduction for large-scale neural recordings. Nat Neurosci. 17:1500–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG. 2012. Pattern classification. Hoboken, NJ: John Wiley & Sons. [Google Scholar]
- Franke F, Fiscella M, Sevelev M, Roska B, Hierlemann A, da Silveira RA. 2016. Structures of neural correlation and how they favor coding. Neuron. 89:409–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graf ABA, Andersen RA. 2014. Brain–machine interface for eye movements. Proc Natl Acad Sci. 111:17630–17635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutnisky DA, Dragoi V. 2008. Adaptive coding of visual information in neural populations. Nature. 452:220–224. [DOI] [PubMed] [Google Scholar]
- Hsu C-W, Lin C-J. 2002. A comparison of methods for multiclass support vector machines. IEEE Trans Neural Netw. 13:415–425. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. 1959. Receptive fields of single neurones in the cat’s striate cortex. J Physiol. 148:574–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. 1968. Receptive fields and functional architecture of monkey striate cortex. J Physiol. 195:215–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hung CP. 2005. Fast readout of object identity from macaque inferior temporal cortex. Science. 310(80):863–866. [DOI] [PubMed] [Google Scholar]
- Johan AK, Suykens JV. 1998. Least squares support vector machine classifiers. Neural Process Lett. 9:293–300. [Google Scholar]
- Kanitscheider I, Coen-Cagli R, Kohn A, Pouget A. 2015. Measuring Fisher information accurately in correlated neural populations. PLoS Comput Biol. 11:e1004218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leavitt ML, Pieper F, Sachs AJ, Martinez-Trujillo JC. 2017. Correlated variability modifies working memory fidelity in primate prefrontal neuronal ensembles. Proc Natl Acad Sci. 114:E2494–E2503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mante V, Sussillo D, Shenoy KV, Newsome WT. 2013. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature. 503:78–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzucato L, Fontanini A, La Camera G. 2016. Stimuli reduce the dimensionality of cortical activity. Front Syst Neurosci. 10:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merrikhi Y, Clark K, Albarran E, Parsa M, Zirnsak M, Moore T, Noudoost B. 2017. Spatial working memory alters the efficacy of input to visual cortex. Nat Commun. 8:15041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg K a., Reynolds JH. 2009. Spatial attention decorrelates intrinsic activity fluctuations in Macaque Area V4. Neuron. 63:879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morcos AS, Harvey CD. 2016. History-dependent variability in population dynamics during evidence accumulation in cortex. Nat Neurosci. 19:1672–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno-Bote R, Beck J, Kanitscheider I, Pitkow X, Latham P, Pouget A. 2014. Information-limiting correlations. Nat Neurosci. 17:1410–1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nirenberg S, Latham PE. 2003. Decoding neuronal spike trains: how important are correlations? Proc Natl Acad Sci. 100:7348–7353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pachitariu M, Lyamzin DR, Sahani M, Lesica NA. 2015. State-dependent population coding in primary auditory cortex. J Neurosci. 35:2058–2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panzeri S, Harvey CD, Piasini E, Latham PE, Fellin T. 2017. Cracking the neural code for sensory perception by combining statistics, intervention, and behavior. Neuron. 93:491–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panzeri S, Schultz SR, Treves A, Rolls ET. 1999. a. Correlations and the encoding of information in the nervous system. Proc Biol Sci. 266:1001–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panzeri S, Treves A. 1996. Analytical estimates of limited sampling biases in different information measures. Netw Comput neural Syst. 7:87–107. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Treves A, Schultz S, Rolls ET. 1999. b. On decoding the responses of a population of neurons from short time windows. Neural Comput. 11:1553–1577. [DOI] [PubMed] [Google Scholar]
- Parthasarathy A, Herikstad R, Bong JH, Medina FS, Libedinsky C, Yen S-C. 2017. Mixed selectivity morphs population codes in prefrontal cortex. Nat Neurosci. 20:1770–1779. [DOI] [PubMed] [Google Scholar]
- Petersen RS, Panzeri S, Diamond ME. 2001. Population coding of stimulus location in rat somatosensory cortex. Neuron. 32:503–514. [DOI] [PubMed] [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, Simoncelli EP. 2008. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature. 454:995–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pola G, Thiele A, Hoffmann KP, Panzeri S. 2003. An exact method to quantify the information transmitted by different mechanisms of correlational coding. Network-Computation Neural Syst. 14:35–60. [DOI] [PubMed] [Google Scholar]
- Ponce-Alvarez A, Thiele A, Albright TD, Stoner GR, Deco G. 2013. Stimulus-dependent variability and noise correlations in cortical MT neurons. Proc Natl Acad Sci. 110:13162–13167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiroga RQ, Reddy L, Kreiman G, Koch C, Fried I. 2005. Invariant visual representation by single neurons in the human brain. Nature. 435:1102–1107. [DOI] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang X-J, Daw ND, Miller EK, Fusi S. 2013. The importance of mixed selectivity in complex cognitive tasks. Nature. 497:585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sajad A, Sadeh M, Yan X, Wang H, Crawford JD. 2016. Transition from target to gaze coding in primate frontal eye field during memory delay and memory–motor transformation. eNeuro. 3:e0040-16:1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seriès P, Latham PE, Pouget A. 2004. Tuning curve sharpening for orientation selectivity: coding efficiency and the impact of correlations. Nat Neurosci. 7:1129–1135. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Britten KH, Newsome WT, Movshon JA. 1996. A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J Neurosci. 16:1486–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. 1998. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 18:3870–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shamir M, Sompolinsky H. 2004. Nonlinear population codes. Neural Comput. 16:1105–1136. [DOI] [PubMed] [Google Scholar]
- Shannon C. 1948. A mathematical theory of communication. Bell Syst Tech J. 27:379–423. [Google Scholar]
- Shoham S, Fellows MR, Normann RA. 2003. Robust, automatic spike sorting using mixtures of multivariate t-distributions. J Neurosci Methods. 127:111–122. [DOI] [PubMed] [Google Scholar]
- Sundberg KA, Mitchell JF, Reynolds JH. 2009. Spatial attention modulates center-surround interactions in macaque visual area v4. Neuron. 61:952–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay S, Pieper F, Sachs A, Martinez-Trujillo J. 2015. Attentional filtering of visual information by neuronal ensembles in the primate lateral prefrontal cortex. Neuron. 85:202–215. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Meyers EM, Bichot NP, Serre T, Poggio TA, Desimone R. 2011. Object decoding with attention in inferior temporal cortex. Proc Natl Acad Sci. 108:8850–8855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT. 1994. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 370:140–143. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.