MatrixEpistasis: ultrafast, exhaustive epistasis scan for quantitative traits with covariate adjustment

Abstract

Motivation

For many traits, causal loci uncovered by genetic mapping studies explain only a minority of the heritable contribution to trait variation. Multiple explanations for this ‘missing heritability’ have been proposed. Single nucleotide polymorphism (SNP)–SNP interaction (epistasis), as one of the compelling models, has been widely studied. However, the genome-wide scan of epistasis, especially for quantitative traits, poses huge computational challenges. Moreover, covariate adjustment is largely ignored in epistasis analysis due to the massive extra computational undertaking.

Results

In the current study, we found striking differences among epistasis models using both simulation data and real biological data, suggesting that not only can covariate adjustment remove confounding bias, it can also improve power. Furthermore, we derived mathematical formulas, which enable the exhaustive epistasis scan together with full covariate adjustment to be expressed in terms of large matrix operation, therefore substantially improving the computational efficiency (∼10⁴× faster than existing methods). We call the new method MatrixEpistasis. With MatrixEpistasis, we re-analyze a large real yeast dataset comprising 11 623 SNPs, 1008 segregants and 46 quantitative traits with covariates fully adjusted and detect thousands of novel putative epistasis with P-values < 1.48e-10.

Availability and implementation

The method is implemented in R and available at https://github.com/fanglab/MatrixEpistasis.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

For many traits, including susceptibility to common diseases in humans, causal loci uncovered by genetic mapping studies explain only a minority of the heritable contribution to trait variation. Multiple explanations for this ‘missing heritability’ have been proposed. One of the proposals highlights the fact that non-additive interactions among loci (called epistasis) may inflate heritability measures (Zuk et al., 2012). There is growing evidence supporting the important role of epistasis in the etiology of complex traits: studies employing model organisms such as Drosophilla melanogaster and Saccharomyces cerevisiae have suggested that epistasis occurs frequently and, in some cases, produce effects as large as the main effects at the individual loci (Brem et al., 2005; Brem and Kruglyak, 2005; Mackay, 2001; Storey et al., 2005). An exhaustive pairwise scan of genome-wide SNPs poses computational challenges due to the sheer size of the combinatorial space (Marchini et al., 2005). When searching for independent additive effects, each SNP is tested for association with the phenotype, but in order to most powerfully identify epistatic effects, the search must be increased to two dimensions (Evans et al., 2006; Marchini et al., 2005), testing each SNP against all other SNPs. For example, a 10⁶ SNP chip would require 10⁶×10⁶/2 ≈ 5 × 10¹¹ independent tests, which is a massive computational undertaking.

Furthermore, when studying epistasis, it is critical to adjust covariates, e.g. batch effects, population stratification, age and gender. Combarros et al. pointed out that failure to consider covariates might result in lack of replication of epistasis (Combarros et al., 2009). With covariate adjustment, an epistasis scan, however, would become even more computationally intensive. There can potentially be dozens of covariates, especially when using dummy variables (Pindyck and Rubinfeld, 1998) to represent categorical variables such as batch effect and geographic location. Thus, accounting for covariates would result in tens of fold increases in computational burden to the already computationally intensive original epistasis search.

Some methods have been proposed for rapid epistasis searching by restricting the analysis to a small subset of candidate markers, those identified through single-locus analysis or those of biological interest (Emily et al., 2009), or by only checking for interactions between SNPs that are physically close to one another (Slavin et al., 2011). Others like EPIBLASTER (Kam-Thong et al., 2011) and SHIsisEPI (Hu et al., 2010) make use of such specialized hardware as multiple graphical processing units (GPUs) to accelerate the computation. These strategies can be applied together with regression models (Marchini et al., 2005), manipulating contingency tables (Wan et al., 2010; Zhang et al., 2010) or searching for a linkage disequilibrium (LD) contrast between cases and controls (Brinza et al., 2010; Prabhu and Pe'er, 2012).

However, these methods still have limitation. First, most methods do not adjust covariates, with only several (Arkin et al., 2014; Hemani et al., 2011) attempting a partial adjustment for covariates. For instance, epiGPU (Hemani et al., 2011) regresses away the covariates from the phenotype but ignores the confounding information that is still implicated in the genotype and their interaction. Second, most of epistasis tools (Gui et al., 2010; Wei et al., 2014) are designed for case-control studies, whereas the available software for quantitative studies is quite limited. Testing for quantitative associations can be more challenging than with case-control studies, as methods utilizing contingency tables, LD-contrast or binary operations are usually inapplicable. Methods tailored for case-control studies can be applied on quantitative traits after dichotomizing the phenotype (Bhattacharya et al., 2011); however, the statistical test is different than the original, resulting in a loss of power that would be difficult to quantify. Third, it is known that reductionist, candidate SNP-based approaches can miss many real interactions (Culverhouse et al., 2002; Evans et al., 2006) and fail to provide novel biological insights in an unbiased manner. Fourth, brute-force approaches that rely on hardware for speedup may also scale poorly as datasets increase in size and interaction tests increase in complexity.

In this paper, we first demonstrate the difference between a few epistasis models: non-, incomplete- and complete-covariate adjustment models, using both simulation data and mathematical derivation. This analysis suggests that complete covariate adjustment cannot only remove the bias from confounding factors but also improves the power for epistasis detection. Furthermore, we present an ultrafast exhaustive epistasis scan tool, MatrixEpistasis, that uses large matrix operations for full covariate adjustment, which substantially improved the computational efficiency (∼10⁴× faster than the others) and also scales well with the number of covariates. MatrixEpistasis is built on a full regression model, so that it can work for quantitative trait, discrete genotype and continuous imputed genotype data. Due to excellent time-efficiency of MatrixEpistasis, we re-analyze a large real yeast dataset comprising 11 623 SNPs, 1008 segregants and 46 quantitative traits with covariates fully adjusted. We demonstrated the difference of epistasis between models with and without covariate adjustment, reinforcing the importance of covariate adjustment for epistasis detection.

2 Materials and methods

Let a vector $p\in R^n$ be quantitative phenotypic values of all n individuals. Let a matrix $G_{n\mathbf{x}m}$ be genotypic values at m polymorphic loci, where each SNP can take on either discrete values or continuous values from imputation. Let a matrix $C_{n\mathbf{x}l}$ be covariate values for l covariates, e.g. age, gender or population stratification.

Epistasis is a phenomenon where the effect of one genetic variant is masked or modified by other genetic variants. From a statistical point of view, the quantitative genetic concept of epistasis is often defined as the departure from additive effects in a linear model (Fisher, 1919). Many regression-based methods have been developed to detect epistasis (Cordell, 2009; Purcell et al., 2007). The commonly used approach is to model a quantitative phenotype as a linear function of the relevant predictor variables:

$$p=\alpha +{\beta }_1{G}_{\cdot s}+{\beta }_2{G}_{\cdot t}+{\beta }_3{G}_{\cdot s}{G}_{\cdot t}+{\displaystyle \sum {}_v}{\gamma }_v{C}_{\cdot v}+\epsilon ,\text{\hspace{0.17em}where} {\epsilon }_{~}N(0,{\xi }^2)$$

where $\alpha$ is the overall mean of the quantitative phenotype, ${\beta }_1$/${\beta }_2$, ${\beta }_3$ and ${\gamma }_v$ are, respectively, the regression coefficients for the main genetic additive effect, interaction effect and covariates, and $\epsilon$ is a normal variable with zero mean and ${\xi }^2$ variance. In this model, the regression coefficient ${\beta }_3$ gives the size of the effect that the interaction term is having on the phenotype with both main genetic additive effects and covariates adjusted, and therefore, tests of interaction correspond to testing whether the regression coefficient ${\beta }_3$ equals zero or not, i.e. the hypotheses $H_0:{\beta }_3=0$ and $H_1:{\beta }_3\ne 0$. However, in addition to ${\beta }_3$, the conventional algorithm calculates all other variables $\alpha$, ${\beta }_1$, ${\beta }_2$, ${\gamma }_{\mathrm{1..}v}$ and $\epsilon$. This is followed by calculation of P-values based on specific test statistics, which can be also computationally intensive. Differing from the conventional way, MatrixEpistasis only calculates ${\beta }_3$ and scans exhaustively all pairwise genetic interactions, with only the significant ones figured out.

Next, we show how the regression model can be solved progressively. Let $\overline{X}$, $\sigma \left(X\right)$ and $X^{\prime }=\left(X-\overline{X}\right)/\sigma \left(X\right)$ denote the mean, standard deviation and standardized values of variable X. We start from the simple linear regression model, which only includes the interaction term.

Model 1: $p=\beta G_{\cdot s}{G}_{\cdot t}+\epsilon$

For the simple linear regression, the common test statistics, t, F, R² and LR, are equivalent and can be expressed as functions of Pearson correlation:

$$\begin{array}{l}r=\text{cor}\left(G_{\cdot s}{G}_{\cdot t},p\right)\\ =\frac{{\sum }_{i=1}^n\left(G_{is}{G}_{it}-\overline{G_{\cdot s}{G}_{\cdot t}}\right)\left(p_i-\overline{p}\right)}{\sqrt{{\sum }_{i=1}^n{\left(G_{is}{G}_{it}-\overline{G_{\cdot s}{G}_{\cdot t}}\right)}^2{\sum }_{i=1}^n{\left(p_i-\overline{p}\right)}^2}}\end{array}$$

Therefore, we used the Pearson correlation as the test statistic. In order to simplify the calculation of the sample correlation, we standardize the phenotype to have zero mean and unit standard deviation. The equation is rewritten as:

$$\text{cor}\left(G_{\cdot s}{G}_{\cdot t},p\right)=\frac{{\sum }_{i=1}^n{G}_{is}{G}_{it}{p}_i^{\prime }}{\left(n-1\right)\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)}$$ (1)

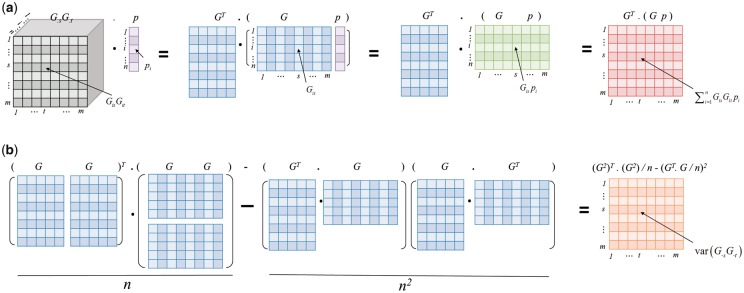
The numerator is the inner product between the SNP interaction and phenotype, motivating us to use the matrix inner product to calculate. The intuitive idea is to first calculate the interaction between two SNPs, and next, calculate the inner product between SNP interaction and phenotype. However, the inner products between all SNP interactions (Fig. 1a, large three-dimensional matrix in grey) and one single phenotype vector (Fig. 1a, purple vector) cannot be further improved using matrix operation. Instead, they can be equivalently expressed in terms of the multiplication between two two-dimensional matrices (Fig. 1a, blue and green matrices), which can be calculated very fast using matrix operation.

Fig. 1.

Pearson correlation between SNP interaction and phenotype can be expressed in term of large matrix operation. (a) Calculation of inner product between SNP interaction and phenotype, i.e. ${\sum }_{i=1}^n{G}_{is}{G}_{it}{p}_i$ and (b) variance of SNP interaction, i.e. $\mathrm{var}(G_{\cdot s}{G}_{\cdot t})$ using matrix operation. The numbers of SNPs and samples are m and n. The grey matrix (mxmxn) represents interactions of all pairwise SNPs; the purple vector (mx1) represents the quantitative trait; the blue matrix (mxn) represents the individual-level genotype; the green matrix represents the product between genotype and quantitative trait; the red matrix (nxn) represents the inner product between SNP interaction and quantitative trait, and the orange matrix (nxn) represents the variance of interactions of all pairwise SNPs. The operation $A\cdot B$ represents the inner product of two matrices A and B, and the operation AB represents the product

On the other hand, the denominator is the standard deviation of SNP interaction term. According to the equation:

$\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)=\sqrt{E[{(G_{\cdot s}{G}_{\cdot t})}^2]-[E(G_{\cdot s}{G}_{\cdot t}){]}^2}=\sqrt{{\left(G_{nxm}^2\right)}^T\cdot G_{nxm}^2/n-{\left(G_{nxm}^T\cdot G_{nxm}/n\right)}^2},$it can be also expressed easily in terms of matrix operation (Fig. 1b).

Model 2: $p={\beta }_0+{\beta }_1{G}_{\cdot s}+{\beta }_2{G}_{\cdot t}+{\beta }_3{G}_{\cdot s}{G}_{\cdot t}+\epsilon$

For this multiple regression model, the partial correlation between SNP–SNP interaction and phenotype conditional on two SNPs, i.e. $p\text{cor}\left(G_{\cdot s}{G}_{\cdot t},p|G_{\cdot s},G_{\cdot t}\right)$ can be used as the test statistic to rank the significance of regression coefficient ${\beta }_3$. By definition, the partial correlation is the Pearson correlation between residuals of SNP–SNP interaction and residuals of phenotype with two SNP additive effects regressed away. It can be also calculated using the iterative equation:

$$p\text{cor}\left(X,Y|Z\right)=\frac{\text{cor}\left(X,Y\right)-\text{cor}\left(X,Z\right)\text{cor}\left(Z,Y\right)}{\sqrt{1-\text{cor}{\left(X,Y\right)}^2}\sqrt{1-\text{cor}{\left(Y,Z\right)}^2}}$$

We show the detailed iterative steps as follows. First, we calculated the Pearson correlations using the following equations:

$$\text{cor}\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot t}\right)=\frac{{\sum }_{i=1}^n{G}_{is}{G}_{it}{G^{\prime }}_{it}}{\left(n-1\right)\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)}$$ (2)

$$\text{cor}\left(G_{\cdot s},p\right)=\frac{{\sum }_{i=1}^n{G^{\prime }}_{is}{p^{\prime }}_i}{n-1}$$ (3)

$$\text{cor}\left(G_{\cdot s},G_{\cdot t}\right)=\frac{{\sum }_{i=1}^n{G^{\prime }}_{is}{G^{\prime }}_{it}}{n-1}$$ (4)

By introducing the Pearson correlations (1)–(4) into the iterative equation, we obtain the partial correlations:

$$\text{pcor}\left(G_{\cdot s}{G}_{\cdot t},p|G_{\cdot s}\right)=\frac{\text{cor}\left(G_{\cdot s}{G}_{\cdot t},p\right)-\text{cor}\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot s}\right)\text{cor}\left(G_{\cdot s},p\right)}{\sqrt{1-\text{cor}{\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot s}\right)}^2}\sqrt{1-\text{cor}{\left(G_{\cdot s},p\right)}^2}}$$ (5)

$$\text{pcor}\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot t}|G_{\cdot s}\right)=\frac{\text{cor}\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot t}\right)-\text{cor}\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot s}\right)\text{cor}\left(G_{\cdot s},G_{\cdot t}\right)}{\sqrt{1-\text{cor}{\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot s}\right)}^2}\sqrt{1-\text{cor}{\left(G_{\cdot s},G_{\cdot t}\right)}^2}}$$ (6)

$$\text{pcor}\left(G_{\cdot t},p|G_{\cdot s}\right)=\frac{\text{cor}\left(G_{\cdot t},p\right)-\text{cor}\left(G_{\cdot s},p\right)\text{cor}\left(G_{\cdot s},G_{\cdot t}\right)}{\sqrt{1-\text{cor}{\left(G_{\cdot s},p\right)}^2}\sqrt{1-\text{cor}{\left(G_{\cdot s},G_{\cdot t}\right)}^2}}$$ (7)

By introducing the partial correlations (5)–(7) into the iterative equation again, we finally obtain

$$\begin{array}{l}\text{pcor}\left(G_{\cdot s}{G}_{\cdot t},p|G_{\cdot s},G_{\cdot t}\right)\\ =\frac{\text{pcor}\left(G_{\cdot s}{G}_{\cdot t},p|G_{\cdot s}\right)-\text{pcor}\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot t}|G_{\cdot s}\right)\text{pcor}\left(G_{\cdot t},p|G_{\cdot s}\right)}{\sqrt{1-\text{pcor}{\left(G_{\cdot s}{G}_{\cdot t},G_{\cdot t}|G_{\cdot s}\right)}^2}\sqrt{1-\text{pcor}{\left(G_{\cdot t},p|G_{\cdot s}\right)}^2}}\end{array}$$ (8)

Model 3:$p=\alpha +{\beta }_1{G}_{\cdot s}+{\beta }_2{G}_{\cdot t}+{\beta }_3{G}_{\cdot s}{G}_{\cdot t}+{\displaystyle \sum {}_v{\gamma }_v{C}_{.v}}+\epsilon$

In addition to additive and interactive effects, the model 3 also considers covariates. For fast computation, it can be reduced to testing of the model 2 for the residuals of $G_{\cdot s}{G}_{\cdot t}$, $G_{\cdot s}$, $G_{\cdot t}$ and p with all covariates $C$ regressed away. For example, we used the regression model: $G_{\cdot s}{G}_{\cdot t}={\lambda }_0+{\displaystyle \sum {}_v{\lambda }_v{C}_{.v}}+GG{\text{res}}_{\cdot st}$ to get the residual of G._sG._t, denoted as GGres._st There are multiple parameters in such regression model, including ${\lambda }_0$ and ${\lambda }_{\mathrm{1..}l}$, but we only need the residuals and do not care the exact values of those parameters. So, we orthonornalize the set of covariates in an inner product space using such methods as principal component analysis, so that we can independently solve the regression coefficient for each resulting orthonormalized covariate. Let $C\prime$ be the orthonormalized covariate matrix. The new equations are (9)–(11), where the regression coefficients are expressed in terms of Pearson correlations, which can be solved independently and fast using equations (1) and (3)

$$p=\overline{p}+{\displaystyle \sum {}_v{\lambda }_v{C}^{\prime }{}_{\cdot v}}+pres,\text{\hspace{0.17em}where\hspace{0.17em}}{\lambda }_v=\sigma \left(p\right)cor(p,C^{\prime }{}_v).$$ (9)

$$G_{\cdot t}=\overline{G_{\cdot t}}+{\displaystyle \sum {}_v}{\lambda }_{tv}{C}^{\prime }{}_{\cdot v}+G\mathrm{res}{\hspace{0.5em}}_{\cdot t},\text{\hspace{0.17em}where\hspace{0.17em}}{\lambda }_{tv}=\sigma \left(G_{\cdot t}\right)cor(G_{\cdot t},C^{\prime }{}_{\cdot v})$$ (10)

$$G_{\cdot s}{G}_{\cdot t}=\overline{G_{\cdot s}{G}_{\cdot t}}+{\displaystyle \sum {}_v}{\lambda }_{stv}{C}_{.v}^{\prime }+GG\mathrm{re}{\mathrm{s}}_{\cdot st},\text{\hspace{0.17em}where\hspace{0.17em}}{\lambda }_{stv}=\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)cor(G_{\cdot s}{G}_{\cdot t},C_{.v}^{\prime })$$ (11)

It does not increase much complexity to calculate the residuals Gres and pres, however, it would be very time-consuming to calculate the residuals for all interaction terms, $GG{\text{res}}_{\cdot \mathrm{st}}$. Fortunately, the orthonornalization of covariates also enables us not to calculate $GG{\text{res}}_{\cdot st}$. By replacing the variables G._sG._t and p by their residuals, the Equation (1) becomes

$$\text{cor}\left(GG{\text{res}}_{\cdot st},\text{pres}\right)=\frac{{\displaystyle \sum {}_{i}GG{\text{res}}_{ist}{\text{pres}\prime }_i}}{\left(n-1\right)\sigma \left(GG{\text{res}}_{\cdot ts}\right)}$$

On the one hand, since $\sum {C^{\prime }}_{iv}{\text{pres}\prime }_i=0$ and $\mathrm{mean}\left(\text{pres}\prime \right)=0$, the numerator becomes:

$$\begin{array}{l}{\displaystyle \sum {}_{i}GG{\text{res}}_{ist}{\text{pres}\prime }_i}\\ ={\displaystyle \sum {}_i}\left(G_{is}{G}_{it}-\overline{G_{\cdot s}{G}_{\cdot t}}-{\displaystyle \sum {}_v\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\text{cor}\left(G_{\cdot s}{G}_{\cdot t},C_{\cdot v}\right){C^{\prime }}_{iv}}\right){\text{pres}\prime }_i\\ ={\displaystyle {\sum }_i{G}_{is}{G}_{it}{\text{pres}\prime }_i}-\overline{G_{\cdot s}{G}_{\cdot t}}{\displaystyle {\sum }_i{\text{pres}\prime }_i}-{\displaystyle \sum {}_v\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\text{cor}\left(G_{\cdot s}{G}_{\cdot t},C_{\cdot v}\right)}\times {\displaystyle {\sum }_i{C^{\prime }}_{iv}{\text{pres}\prime }_i}\\ ={\displaystyle {\sum }_i{G}_{is}{G}_{it}{\text{pres}\prime }_i}\end{array}$$

On the other hand, since $\mathrm{var}\left(x+y\right)=\mathrm{var}\left(x\right)+\mathrm{var}\left(y\right)+2\mathrm{cov}\left(x,y\right)$, cov(x, y + z)=cov(x, y) + cov(x, z), $\mathrm{var}\left({C^{\prime }}_{\cdot v}\right)=1$ and ${\mathrm{cov}}_{w\ne z}\left({C^{\prime }}_{\cdot w},{C^{\prime }}_{\cdot z}\right)=0$ (orthonormalized), we obtain the equation for the denominator:

$$\begin{array}{l}\mathrm{var}\left(GG{\text{res}}_{\cdot ts}\right)\\ =\mathrm{var}\left(G_{is}{G}_{it}-\overline{G_{\cdot s}{G}_{\cdot t}}-{\displaystyle \sum {}_v\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\text{cor}\left(G_{\cdot s}{G}_{\cdot t},C_{\cdot v}\right){C^{\prime }}_{\cdot v}}\right)\\ =\mathrm{var}\left(G_{is}{G}_{it}-\overline{G_{\cdot s}{G}_{\cdot t}}\right)+\mathrm{var}\left({\displaystyle \sum {}_v\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\text{cor}\left(G_{\cdot s}{G}_{\cdot t},C_{\cdot v}\right){C^{\prime }}_{\cdot v}}\right)\\ \begin{array}{ll}& \end{array}-2\mathrm{cov}\left(G_{is}{G}_{it}-\overline{G_{\cdot s}{G}_{\cdot t}},{\displaystyle \sum {}_v\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\text{cor}\left(G_{\cdot s}{G}_{\cdot t},C_{\cdot v}\right){C^{\prime }}_{\cdot v}}\right)\\ =\mathrm{var}\left(G_{\cdot s}{G}_{\cdot t}-\overline{G_{\cdot s}{G}_{\cdot t}}\right)+{\displaystyle \sum {}_v\mathrm{var}\left(\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\text{cor}\left(G_{\cdot s}{G}_{\cdot t},C_{\cdot v}\right){C^{\prime }}_{\cdot v}\right)}\\ \begin{array}{ll}& \end{array}+2{\displaystyle \sum {}_{w>z}\mathrm{cov}(\sigma (G_{\cdot s}{G}_{\cdot t})\text{cor}(G_{\cdot s}{G}_{\cdot t},C_{\cdot w}){C^{\prime }}_{\cdot w},\sigma (G_{\cdot s}{G}_{\cdot t})\times \text{cor}(G_{\cdot s}{G}_{\cdot t},C_{\cdot z}){C^{\prime }}_{\cdot z})}\\ \begin{array}{ll}& \end{array}-2\mathrm{cov}\left(G_{is}{G}_{it}-\overline{G_{\cdot s}{G}_{\cdot t}},{\displaystyle \sum {}_v\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\text{cor}\left(G_{\cdot s}{G}_{\cdot t},C_{\cdot v}\right){C^{\prime }}_{\cdot v}}\right)\\ =\mathrm{var}\left(G_{\cdot s}{G}_{\cdot t}\right)+\mathrm{var}\left(G_{\cdot s}{G}_{\cdot t}\right)\mathrm{var}\left({C^{\prime }}_{\cdot v}\right){\displaystyle \sum {}_v\text{cor}{\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)}^2}\\ \begin{array}{ll}& \end{array}-2\sigma \left(G_{\cdot s}{G}_{\cdot t}\right){\displaystyle \sum {}_v\text{cor}\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)}\mathrm{cov}\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)\\ =\mathrm{var}\left(G_{\cdot s}{G}_{\cdot t}\right)+\mathrm{var}\left(G_{\cdot s}{G}_{\cdot t}\right){\displaystyle \sum {}_v\text{cor}{\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)}^2}\\ \begin{array}{ll}& \end{array}-2\sigma \left(G_{\cdot s}{G}_{\cdot t}\right){\displaystyle \sum {}_v\text{cor}\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)}\text{\hspace{0.17em}cor}\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\\ =\mathrm{var}\left(G_{\cdot s}{G}_{\cdot t}\right)\left(1-{\displaystyle \sum {}_v\text{cor}{\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)}^2}\right)\end{array}$$

Taken collectively, we obtain that

$$\text{cor}\left(GG{\text{res}}_{\cdot st},\text{pres}\right)=\frac{{\displaystyle \sum {}_i{G}_{is}{G}_{it}{\text{pres}\prime }_i}}{\left(n-1\right)\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\sqrt{1-{\displaystyle \sum {}_v\text{cor}{\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)}^2}}}$$ (12)

The above equation suggests that we do not need to calculate residuals for interaction terms, i.e. Equation (11).

Similar to Equations (2)–(4), we can derive Equations (13)–(15):

$$\text{cor}\left(GG{\text{res}}_{\cdot st},G{\text{res}}_{\cdot s}\right)=\frac{{\displaystyle \sum {}_i{G}_{is}{G}_{it}G{\text{res}\prime }_{is}}}{\left(n-1\right)\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)\sqrt{1-{\displaystyle \sum {}_v\text{cor}{\left(G_{\cdot s}{G}_{\cdot t},{C^{\prime }}_{\cdot v}\right)}^2}}}$$ (13)

$$\text{cor}\left(G{\text{res}}_{\cdot s},\text{pres}\right)=\frac{{\displaystyle \sum {}_i{G^{\prime }}_{is}{\text{pres}\prime }_i}}{\left(n-1\right)\sqrt{1-{\displaystyle \sum {}_{v}cor{\left(G_{\cdot s},{C^{\prime }}_{\cdot v}\right)}^2}}}$$ (14)

$$\text{cor}\left(G{\text{res}}_{\cdot s},G{\text{res}}_{\cdot t}\right)=\frac{{\displaystyle \sum {}_{i}G{\text{res}\prime }_{is}G{\text{res}\prime }_{it}}}{n-1}$$ (15)

Next, replace Equations (1)–(4) by Equations (12)–(15) in Equations (5)–(8), then we can obtain $p\text{cor}\left(GG{\text{res}}_{\cdot st},\text{pres}|G{\text{res}}_{\cdot s},G{\text{res}}_{\cdot t}\right)$, which is equivalent to $p\text{cor}\left(G_{\cdot s}{G}_{\cdot t},p|G_{\cdot s},G_{\cdot t},C\right)$, i.e. the partial correlation between SNP–SNP interaction and phenotype conditional on SNP additive effects and covariates. It has the consistent P-value with ${\beta }_3$ in the multiple regression model 3 (Supplementary Fig. S1).

To summarize the main idea of MatrixEpistasis model 3, it regresses the covariates against all the related variables including the phenotype, main effects and interaction effects [(Equations (9)–(11)]. Then in the rest of the calculations, in each regression model for a pair of SNPs, the original data will not be subjected to another least-square estimation. Instead, a simple multiplication (the inner product) will estimate the partial correlations. That is why the presented method is ultrafast.

2.1 Matrix operation

The above equation can be divided into terms ${\sum }_{i=1}^n{G}_{is}{G}_{it}{G^{\prime }}_{it}$, ${\sum }_{i=1}^n{G}_{is}{G}_{it}{p^{\prime }}_i$, ${\sum }_{i=1}^n{G}_{is}{G}_{it}{C^{\prime }}_{iv}$, ${\sum }_{i=1}^n{G^{\prime }}_{is}{G^{\prime }}_{it}$, ${\sum }_{i=1}^n{G}_{is}{p^{\prime }}_i$, ${\sum }_{i=1}^n{G}_{is}{C^{\prime }}_{iv}$ and $\sigma \left(G_{\cdot s}{G}_{\cdot t}\right)$, all of which can be expressed in terms of four types of matrix operations.

Product:

$$X_{nxm}{Y}_{nxm}=\left\{X{Y}_{nxm}|X{Y}_{st}=X_{st}{Y}_{st}\right\}$$

Inner product:

$$X_{nxm}^T\cdot Y_{nxm}=\left\{X{Y}_{mxm}|X{Y}_{st}={\sum }_{i=1}^n{X}_{is}{Y}_{it}\right\}$$

(e.g. ${\sum }_{i=1}^n{G^{\prime }}_{is}{G^{\prime }}_{it}$, ${\sum }_{i=1}^n{G}_{is}{p^{\prime }}_i$ and ${\sum }_{i=1}^n{G}_{is}{C^{\prime }}_{iv}$)

Combination of product and inner product (Fig. 1a):

$$X_{nxm}^T\cdot \left(X_{nxm}{Y}_{nxm}\right)=\left\{XX{Y}_{mxm}|XX{Y}_{st}={\sum }_{i=1}^n{X}_{is}{X}_{it}{Y}_{it}\right\}$$

(e.g. ${\sum }_{i=1}^n{G}_{is}{G}_{it}{G^{\prime }}_{it}$, ${\sum }_{i=1}^n{G}_{is}{G}_{it}{p^{\prime }}_i$ and ${\sum }_{i=1}^n{G}_{is}{G}_{it}{C^{\prime }}_{iv}$)

Variance matrix (Fig. 1b):

$$\begin{array}{l}\sigma (G_{\cdot s}{G}_{\cdot t})=\sqrt{E[{(G_{\cdot s}{G}_{\cdot t})}^2]-[E(G_{\cdot s}{G}_{\cdot t}){]}^2}\\ =\sqrt{{\left(G_{nxm}^2\right)}^T\cdot G_{nxm}^2/n-{\left(G_{nxm}^T\cdot G_{nxm}/n\right)}^2}\end{array}$$

2.2 Hypothesis test

For the linear regression model, the common test statistics, t, F, R² and LR, are equivalent and can be expressed as functions in terms of the sample correlation (Pearson correlation or partial correlation) r. We chose the t-statistic as the test statistic for the linear regression model and threshold it in search for significant SNP–SNP interactions.

$$t=\sqrt{n-2}\frac{r}{\sqrt{1-r^2}}$$

The degree freedoms are (m-2) for model 1, (m-4) for model 2 and (m-l-4) for model 3, where m and l are the numbers of samples and covariates, respectively.

3 Results

3.1 The inferred epistasis from different models is largely inconsistent

The full regression model LR1 (Table 1), taking into account all additive effects, interactive effects and covariates has been considered as standard to model epistasis for quantitative traits with covariates adjusted. To lower computational complexity, various reduced models (Table 1), however, are also used to approximate the full model LR1 (Arkin et al., 2014; Crawford et al., 2016; Hemani et al., 2011). Specially, LR2 considers neither additive effect nor covariates; LR3 considers additive effect but not covariates; and LR4-6 incompletely adjusts covariates by regressing away covariates from additive effects (LR4), trait (LR5) and both (LR6), respectively. These models are frequently used, but their difference in power is poorly understood. Here, we compared these models by applying them to simulated data from a real yeast genotype and quantitative trait dataset. First, a quantitative trait, Maltose, was used, and 200 SNPs, which significantly contribute to the trait by interacting with other SNPs, were randomly selected. Next, to simulate covariates with both additive and interactive effects, we used principal component analysis to extract the top five principal components from 200 SNPs and the top five principal components from the residuals of 20 100 (200 × 199/2 + 100) pairwise SNP interactions with additive effects of two SNPs regressed away. Finally, different models were applied to the simulated dataset. The upper triangle in Figure 2 demonstrates the dramatic difference between models. The models LR2-3, which do not adjust covariates, dramatically overestimate the epistasis effect as compared to LR1, suggesting that the estimation of epistasis might be largely biased by the failure to consider covariates. In contrast, when compared to LR1, the reduced models LR4-6, which incompletely deal with covariates, significantly underestimate the epistasis effect, suggesting that incomplete adjustment of covariates largely reduces the power to detect epistasis. Moreover, LR3 shows better power than LR2, revealing the benefits of considering the additive effects of two SNPs. This comparison also shows the striking inconsistencies between incomplete models themselves. Furthermore, to ensure that the type-I error is under control, we run the simulation to estimate the empirical P-values. We shuffled the phenotype data to build a simulated phenotype and recalculated the epistasis P-values. The permutation was repeated so as to construct a background P-value distribution of no real signals, and next, assessed the frequency of obtaining the genuine signal. Figure 2 (lower triangle) shows that the comparison between different regression models using the empirical approaches is consistent with that using the original P-values. Taken together, our comparisons indicated that complete adjustment of covariates not only removes the bias from confounding factors but also improves the power when studying epistasis, providing a general guideline for the selection of epistasis models.

Table 1.

The list of regression models used to model gene–gene interaction for quantitative traits

Models	Equations
LR1	$p=\alpha +{\beta }_1{G}_{\cdot s}+{\beta }_2{G}_{\cdot t}+{\beta }_3{G}_{\cdot s}{G}_{\cdot t}+{\displaystyle \sum {}_v{\gamma }_v{C}_{.v}+\epsilon }$
LR2	$p=\beta G_{\cdot s}{G}_{\cdot t}+\epsilon$
LR3	$p={\beta }_0+{\beta }_1{G}_{\cdot s}+{\beta }_2{G}_{\cdot t}+{\beta }_3{G}_{\cdot s}{G}_{\cdot t}+\epsilon$
LR4	$p=\alpha +{\beta }_{1}G{\text{res}}_{\cdot s}+{\beta }_{2}G{\text{res}}_{\cdot t}+{\beta }_{3}G{\text{res}}_{\cdot s}G{\text{res}}_{\cdot t}+\epsilon$
LR5	$\text{pres}=\alpha +{\beta }_1{G}_{\cdot s}+{\beta }_2{G}_{\cdot t}+{\beta }_3{G}_{\cdot s}{G}_{\cdot t}+\epsilon$
LR6	$\text{pres}=\alpha +{\beta }_{1}G{\text{res}}_{\cdot s}+{\beta }_{2}G{\text{res}}_{\cdot t}+{\beta }_{3}G{\text{res}}_{\cdot s}G{\text{res}}_{\cdot t}+\epsilon$ where $G{\text{res}}_{\cdot t}=G_{\cdot t}-\overline{G_{\cdot t}}-{\displaystyle \sum {}_v{\gamma }_v{C}_{.v}}$ and $\text{pres}=p-\overline{p}-{\displaystyle \sum {}_v{\gamma }_{v}C{.}_v}$

Fig. 2.

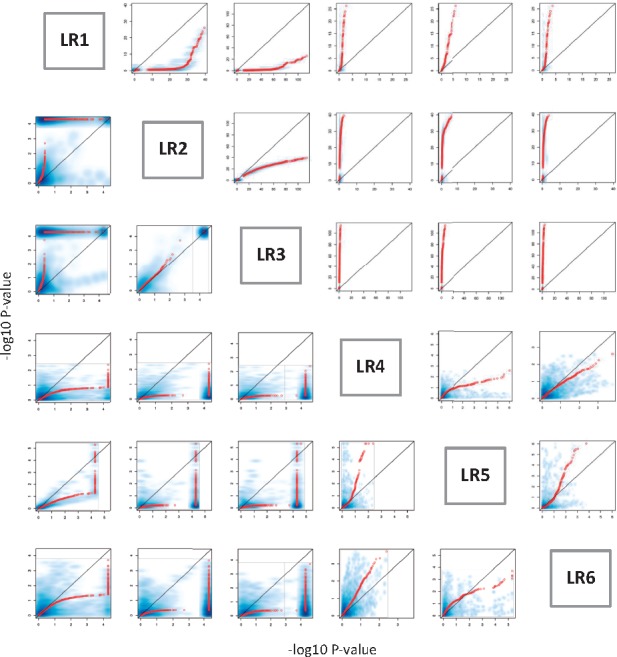
The comparison between different epistasis models using simulation dataset. The x and y axes represent –log10 P-value of the interaction term from a pair of models. The red dot is the QQplot and the blue shadow is a smoothed density representation of the scatterplot between two models. The upper triangle represents the QQplot of original P-values, and the lower triangle represents the QQplot of empirical P-values

3.2 Excellent time efficiency of MatrixEpistasis for epistasis scan with covariate adjustment

Although we demonstrated the critical role of covariate adjustment when studying epistasis, it dramatically increases the computational burden for the epistasis search. To address this, we proposed a novel ultrafast method using matrix operations, MatrixEpistasis (detail in Section 2), that exhaustively scans all pairwise genetic interactions. Its excellent time-efficiency is achieved by the following innovations: (i) it ranks the regression coefficients of the epistasis model using partial correlations, which are not subjected to least-square estimation; (ii) it expresses the calculation of all partial correlations in terms of large matrix inner products (notably, no matrix inverse), avoiding separately calculating each epistasis model; (iii) out of all regression coefficients (including two additive terms, one interaction term and multiple covariate terms), MatrixEpistasis only calculates the test statistic for the interaction term, largely alleviating the computational complexity; (iv) the resulting test statistics from MatrixEpistasis are comparable, so that MatrixEpistasis can calculate P-values only for those exceeding the required significance level, therefore discarding a large number of incomplete Beta or Gamma functions.

To demonstrate the computational efficiency of MatrixEpistasis, we compared it with other tools. Since few tools were proposed to adjust covariates for epistasis of quantitative traits, we compared with two: Combined Analysis of Pleiotropy and Epistasis (CAPE) (Tyler et al., 2013) and Contrived Acronym of Software for SNP Interactions (CASSI) (Howey), both of which can detect epistasis for quantitative trait and also adjust covariates. We did not compare with tools that use sub-sampling or hardware to promote computational efficiency. First, we compared the power between those three methods: MatrixEpistasis, CASSI and CAPE. Not only did we calculate the original P-values of epistasis, but we also estimate the empirical P-values to adjust the type I error. Supplementary Figure S2 showed that all of three methods have the same power with and without covariates adjusted. This is because CASSI and CAPE also use the interaction regression model with covariates fully adjusted. Next, to compare the running time, we applied these methods to a simulated dataset comprised of 10 000 SNPs, 1000 samples and 1 quantitative trait. All methods were tested without parallel computation on a Linux server with 1.8 GHz cores and 256 GB memory. As shown in Table 2, when considering no covariates, CAPE took ∼4.2 days, CASSI took 2.3 h, whereas MatrixEpistasis took only 56 s. This suggests that MatrixEpistasis already builds an excellent foundation for the further covariate adjustment. Next, we compared the running time of different methods with covariate adjustment. When 10 covariates were included, MatrixEpistasis took only 97 s, while CAPE and CASSI took 7.5 and 1.3 days, respectively. Furthermore, we progressively increased covariates and found that the running time of MatrixEpistasis scaled well with the number of covariates: each increase of 10 covariates resulted in a ∼30 s increase in running time. With 40 covariates, MatrixEpistasis took only 202 s, while CAPE and CASSI took much longer time (22.7  and 19 days, respectively) and the running time of these tools did not scale linearly with the number of covariates.

Table 2.

Comparison of running time on 10 000 SNPs

Methods	Samples	Covariates	Running time
CAPE	1000	0	4.2 days
CAPE	1000	10	7.5 days
CAPE	1000	20	10.3 days
CAPE	1000	30	16.6 days
CAPE	1000	40	22.7 days
CASSI	1000	0	2.3 h
CASSI	1000	10	1.3 days
CASSI	1000	20	8 days
CASSI	1000	30	10.8 days
CASSI	1000	40	19 days
MatrixEpi model 1	1000	0	11 s
MatrixEpi model 2	1000	0	28 s
MatrixEpi model 3	1000	0	56 s
MatrixEpi model 3	1000	10	97 s
MatrixEpi model 3	1000	20	134 s
MatrixEpi model 3	1000	30	166 s
MatrixEpi model 3	1000	40	202 s
MatrixEpi model 3	2000	0	70 s
MatrixEpi model 3	3000	0	82 s
MatrixEpi model 3	4000	0	94 s

In addition to the number of covariates, we also tested how MatrixEpistasis scaled with the number of samples. Different number of samples (1000, 2000, 3000 and 4000) were simulated and tested. As shown in Table 2, MatrixEpistasis also scaled well with the number of samples, and took only 94 s for 4000 samples. To compare the running time, we tested these methods using only one core, whereas MatrixEpistasis is very easy to conduct in parallel. Users can simply split the genotype data into chunks and run different chunks in parallel to further improve the time efficiency.

The genotype is often large, which requires large memory to run MatrixEpistasis. Motivated by this, we also investigated how much memory the MatrixEpistasis demands. The simulation analyses were performed on different numbers of SNPs (5000, 10 000 and 15 000), samples (1000, 2000, 3000 and 4000) and covariates (0, 10, 20, 30 and 40). The bsub was used to submit jobs to Load Sharing Facility (LSF) and estimate the memory used (Table 3). As expected, the required memory increases with the elevated number of SNPs, however, increasing the samples and covariates almost do not influence the memory. It suggests that the number of SNPs is the critical factor for the memory. To avoid excessive memory demand, users are suggested to split the data matrices in chunks up to 10 000 SNPs and run the pairwise chunks separately.

Table 3.

The computer memory used for running MatrixEpistasis model 3

SNPs	Samples	Covariates	Average memory (GB)	Maximum memory (GB)
5000	1000	0	1.0	3.4
10 000	1000	0	3.9	11.7
15 000	1000	0	9.1	29.2
10 000	1000	10	5.5	13.5
10 000	1000	20	5.7	13.5
10 000	1000	30	5.8	13.5
10 000	1000	40	5.8	13.5
10 000	2000	0	4.0	13.3
10 000	3000	0	4.2	13.5
10 000	4000	0	4.6	13.5

3.3 Covariates adjustment reveals different epistasis interactions in yeast

Using MatrixEpistasis, we can efficiently interrogate large cohorts to explore the difference of epistasis between models with and without covariate adjustment. Here, we use a real yeast genotype and phenotype dataset (Bloom et al., 2013). This is a large cohort of cross between two yeast strains, which comprises 11 623 SNPs, 1008 segregants and 46 quantitative traits, aiming to explore the source of missing heritability. Researchers have used this data to show that genetic interaction can account for traits varying from near zero to approximately 50%, significantly advancing our understanding of the role of gene–gene interactions in the missing heritability. However, certain traits are highly correlated with each other (Supplementary Fig. S3), raising the possibility that epistasis interaction may contribute to one trait by impacting another trait. In order to capture only the direct impact of epistasis, we studied epistasis on one trait with all the other traits as covariates. First, we use MatrixEpistasis model 2 (no covariate adjustment) to do exhaustive epistasis searches for all 46 quantitative traits (on average, 78 s). Consistent with the previous work (Bloom et al., 2013), MatrixEpistasis found epistasis for multiple traits (Fig. 3a), to some extent validating the effectiveness of our method. We detected 147 genetic interactions for formamide, 1611 for indoleacetic acid, 3798 for magnesium sulfate, 7893 for maltose, 28 for 4-hydroxybenzaldehyde and 377 for YPD: 37 C (Bonferroni corrected P < 0.01). Notably, to more comprehensively capture epistasis, we kept all SNPs in our analysis without linkage distinguishable (LD) pruning, so the number of detected genetic interactions may be larger than that reported in the previous work. Next, in order to study the direct impact of an epistatic interaction on one trait, we run MatrixEpistasis model 3 (with covariate adjustment) to investigate epistasis for each trait with all the other traits as covariates (on average, 289 s). As shown in Figure 3b, we also found epistatic interactions for multiple traits, but very interestingly, they are quite different from those without covariate adjustment. For formamide, indoleacetic acid and YPD: 37 C, we found less epistasis with covariate adjustment (0, 9 and 204) than those without covariate adjustment (147, 1611 and 377). In contrast, for galactose, magnesium sulfate, maltose, 4-hydroxybenzaldehyde and YPD, we found more significant epistasis with covariate adjustment (1386, 5035, 8628, 1369 and 26), compared to those without covariate adjustment (0, 3798, 7893, 28, 0). These facts confirm the difference between models with and without covariate adjustment, reinforcing its important role during epistasis analysis.

Fig. 3.

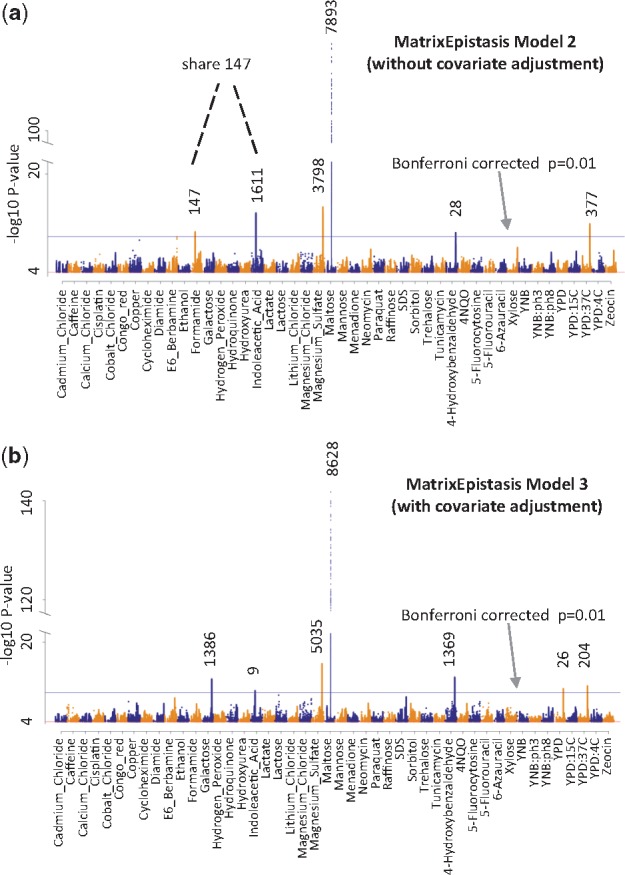
Manhattan plots of MatrixEpistasis model 2 without covariate adjustment (top panel) and MatrixEpistasis model 3 with covariate adjustment (bottom panel). The x axis represents 46 quantitative traits and the y-axis represents –log10 P-value of the interaction term. The horizontal line shows the genome-wide significance level (1.48e-10)

4 Discussion

This paper first demonstrated the difference between epistasis models using a simulated dataset and confirmed it using a large real yeast dataset, suggesting that the adjustment of covariates cannot only remove confounding effects but also improve the power for the epistasis detection. Furthermore, we proposed a novel method in terms of large matrix operation, called MatrixEpistasis, which enables the ultrafast exhaustive epistasis scan together with full covariate adjustment. It substantially improved the computational efficiency (∼10⁴× faster than the others). To deeper understand the underlying rationale, we will discuss, from a simple mathematical perspective, the difference between non-covariate-adjustment (LR2-3), incomplete-covariate-adjustment (LR4-6) and complete-covariate-adjustment epistasis regression models (LR1). Actually, the hypothesis test statistics, which evaluate the significance of regression coefficients for interaction terms in three regression models, can be also ranked by Pearson correlation, semi-partial correlation and partial correlation, respectively (Johnson and Wichern, 2014; Stevens, 2012; Whittaker, 2009). Thus, we can find clues about the model differences via three such correlations. Figure 4 shows the iterative formula and Venn-diagram of explained variance for three correlations. On the one hand, as shown in the iterative formula, the partial correlation (similar to full-covariate adjustment interaction regression model, e.g. LR1) is the same with the semi-partial correlation (similar to incomplete-covariate adjustment interaction regression model, e.g. LR4) except only one item in the denominator: $\sqrt{1-r_{YZ}^2}$ (Fig. 4). Such an item is always less than one, rendering the partial correlation between SNP-SNP interaction and phenotype conditional on covariates always greater than the semi-partial correlation between SNP-SNP interaction and phenotype. This explains why the LR1 model often has greater power than LR4 model. On the other hand, the explained variance (Fig. 4) indicated that the difference between Pearson correlation and partial correlation are the items: mc and nb, i.e. the odds ratio between b/c and m/n determines the difference. In another word, when fixing m and n (i.e. fixing SNP–SNP interaction and phenotype), if covariates are more correlated with phenotype than with the interaction term, then the detected epistasis effect becomes more significant after adjusting covariates than before and vice versa.

Fig. 4.

Different perspectives to explain the Pearson correlation, partial correlation and semi-partial correlation

For our simulated data, the LR2 model underestimates the significance compared to the LR3 model, because the additive effects are more correlated with the traits than the interaction term, while the LR3 model overestimates the significance compared to the LR1 model, because in addition to additive effect, the covariates in the LR1 model are simulated to also have quadratic effects, which are more correlated with interaction term than the trait. Similarly, we can also use the iterative formula and the explained variance to compare other models. Thus, this analysis provides a theoretical way to better understand the underlying rationale of difference by different epistasis detection models. Furthermore, to address the computational challenge of covariate adjustment for epistasis, we proposed the ultrafast method, MatrixEpistasis. Our tests show that MatrixEpistasis is ∼10⁴ times faster than the existing quantitative epistasis software without relying on any speedup from special hardware. Moreover, the running time of MatrixEpistasis only doubles with every 20 covariates that are added to the model. Such performance is achieved by expressing the most computationally intensive part of the algorithm in terms of large matrix operations. We believe that MatrixEpistasis will serve as a foundational tool for studying SNP–SNP or gene–gene epistasis. The tool MatrixEqtl (Shabalin, 2012), which also utilizes matrix operations for significant speedups, has been widely used to study the association between genotype and gene expression. We expect that MatrixEpistasis, as an orthogonal and complementary tool, will also lead to a rich set of applications and offer deeper understanding in epistasis, pleiotropy of epistasis, pheWAS (Bush et al., 2016) and many other fields.