Significance
Current efforts aimed at constructing complex supramolecular structures often suffer from low yields or require long assembly protocols. We address these problems by demonstrating a facile strategy for optimizing the nucleation step of a multicomponent self-assembly reaction. By tracking the formation of multisubunit clusters in situ, our experiments show that modifying the critical nucleus required to initiate structure growth can broaden the range of conditions over which self-assembly occurs and, consequently, can dramatically improve the final yield of correctly formed structures. Since varying the design of only a small portion of the target structure optimizes its yield, this strategy provides a practical route to improve the speed and accuracy of self-assembly in biomolecular, colloidal, and nanoparticle systems.
Keywords: self-assembly, coarse-grained simulation, DNA nanotechnology, nucleation, dynamic light scattering
Abstract
To optimize a self-assembly reaction, it is essential to understand the factors that govern its pathway. Here, we examine the influence of nucleation pathways in a model system for addressable, multicomponent self-assembly based on a prototypical “DNA-brick” structure. By combining temperature-dependent dynamic light scattering and atomic force microscopy with coarse-grained simulations, we show how subtle changes in the nucleation pathway profoundly affect the yield of the correctly formed structures. In particular, we can increase the range of conditions over which self-assembly occurs by using stable multisubunit clusters that lower the nucleation barrier for assembling subunits in the interior of the structure. Consequently, modifying only a small portion of a structure is sufficient to optimize its assembly. Due to the generality of our coarse-grained model and the excellent agreement that we find with our experimental results, the design principles reported here are likely to apply generically to addressable, multicomponent self-assembly.
Increasingly complex structures can now be created by self-assembly (1, 2), from nanostructures with tailored physicochemical properties, such as photonic crystals (3, 4), to quasicrystals (5–7). In the limit where every subunit in a target structure is unique and bonds strongly with specific partners, such self-assembled structures are said to be “addressable.” Thus far, this degree of specificity has been demonstrated most impressively by experiments on “DNA bricks” (8, 9), in which portions of single-stranded DNA molecules are designed to hybridize uniquely with complementary sequences on strands that occupy neighboring positions in the target structure. Modular nanostructures comprising thousands of distinct strands can be formed in this way, and because the location of each molecule in the target structure is precisely known, these structures can be functionalized at a nanometer length scale.
In addition to providing control over the geometry of the target structure, the use of addressable building blocks makes it possible to exert greater control over the mechanism of self-assembly (10). Because each interaction between subunits can be individually tuned, addressable structures provide a useful platform for exploring the determinants of self-assembly pathways more generally (11). Considerable progress has been made in this direction using computer simulations (12–22) and statistical mechanics (23–25) to study coarse-grained models of addressable systems. In particular, coarse-grained modeling has predicted that nucleation barriers are likely to play a particularly important role in addressable self-assembly, since in their absence, the large number of building blocks with similar bonding strengths can instead lead to widespread kinetic trapping and aggregation (14, 23, 24). These models have further shown that addressable systems often have highly nonclassical nucleation barriers and well-defined critical nuclei (19, 23, 24). [The term “nucleation” in the context of DNA self-assembly is occasionally used to refer to the initial thermodynamically disfavored formation of a few base pairs of a double strand, which is then followed by zipping (26); we use the term in the more traditional sense to mean the formation of a small portion of the target structure, which leads to structure assembly.] However, the microscopic nature of a self-assembly process is challenging to study experimentally. While it is possible to characterize structures by stopping the reaction at a specific point along an annealing ramp (27, 28) for subsequent imaging (29, 30), such approaches cannot be performed in situ and may thus perturb the self-assembly process. Furthermore, any assembled structures must first be isolated before carrying out more detailed analyses, for example by using next-generation sequencing to examine defects in DNA nanostructures (31). On the other hand, established in situ methods can provide information on the kinetics of self-assembly, but only by probing the interactions between pairs of subunits (26, 27, 32–34). As a result, these interactions must then be extrapolated to describe the assembly of the complete structure.
In this work, we demonstrate that dynamic light scattering (DLS) can be used to track the collective assembly of addressable structures in greater detail. Unlike alternative in situ techniques, DLS provides a sensitive means of probing the complete distribution of multistrand cluster sizes throughout the course of the annealing protocol. Consequently, by applying DLS to DNA-brick self-assembly and validating these results using atomic force microscopy (AFM), we are able to analyze the nucleation process as a function of temperature and assembly time. Combining these results with extensive simulations, we show that it is possible to control the nucleation behavior rationally, with dramatic consequences for the yield of assembled structures. In particular, we demonstrate that the self-assembly mechanism can be optimized by altering the connections among a specific subset of subunits, which modifies the free-energy barrier for structure nucleation. The simplicity of our coarse-grained model suggests that these design principles are transferable to any multicomponent system where the interactions between subunits can be programmed.
Results
Minor Changes in Nanostructure Design Strongly Affect the Yield and Quality of Self-Assembly.
As a model system, we examined the self-assembly of a 16-helix DNA cuboid. Following the canonical “DNA-brick” design (8), the fundamental building blocks of this structure are 32-nt “scaffold” bricks. Each brick comprises four 8-bp domains that hybridize to connect adjacent helices (Fig. 1A). The cross-section was chosen to ensure that bricks on opposite sides of the structure do not interact directly (Fig. 1B), while the high aspect ratio (4 helices 4 helices 256 bases) facilitates the identification of well-formed structures via AFM imaging.
Fig. 1.
(A) The bonding pattern between two DNA bricks in a strand and a cylindrical representation. Each molecule is partitioned into four domains (indicated by boxes), while the neighboring bricks are bonded through one pair of domains only (green box). The cylindrical representation shows the same 8-bp hybridization. (B) A schematic illustration of our target structure, highlighting the locations of the “edge” and “face” boundary bricks. (C) A schematic of the boundary brick setup. The noninteracting DNA sequence at one of the outer surfaces of the target structure is removed and the remainder of that brick is fused with the adjacent brick, resulting in the formation of a 48-nt boundary brick.
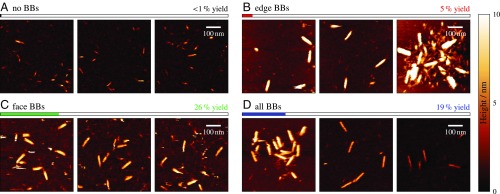
To study the factors affecting the self-assembly yield, we designed variants of this cuboid by increasing the lengths of a small number of complementary domains. This was achieved by varying the numbers and types of 48-nt “boundary bricks” (BBs) at the exterior surfaces of the structure (Fig. 1C and SI Appendix, Fig. S1). In addition to a cuboid composed entirely of scaffold bricks (“no BBs”), where the 16-bp half-bricks at the exterior of the structure were left unconjugated, we designed variants with BBs forming the corner helices (“edge BBs”), connecting pairs of helices on the faces of the cuboid (“face BBs”), or both (“all BBs”). All variants of the cuboid structure self-assembled to some degree over the course of a 66-h linear annealing ramp (SI Appendix, section 1.1). However, AFM imaging (SI Appendix, section 1.2) revealed striking differences in the quality of the assembled structures (Fig. 2). The all-BB, face-BB, and edge-BB designs resulted in the assembly of many copies of structures with the expected aspect ratio, while designs without BBs yielded a negligible number of such structures (SI Appendix, section 1.3 and Fig. S2).
Fig. 2.
(A–D) AFM images taken at the conclusion of a 66-h annealing protocol for each of the four 86-nm–long cuboid designs. No purification was performed on these samples so that incompletely assembled structures can clearly be seen. Typical yields, relative to the total quantity of DNA strands in solution, were estimated via gel electrophoresis and are shown for each system. For the edge-BB system in particular, multistructure aggregates (shown in B, Right) are commonly observed.
Tracking Structure Assembly via DLS.
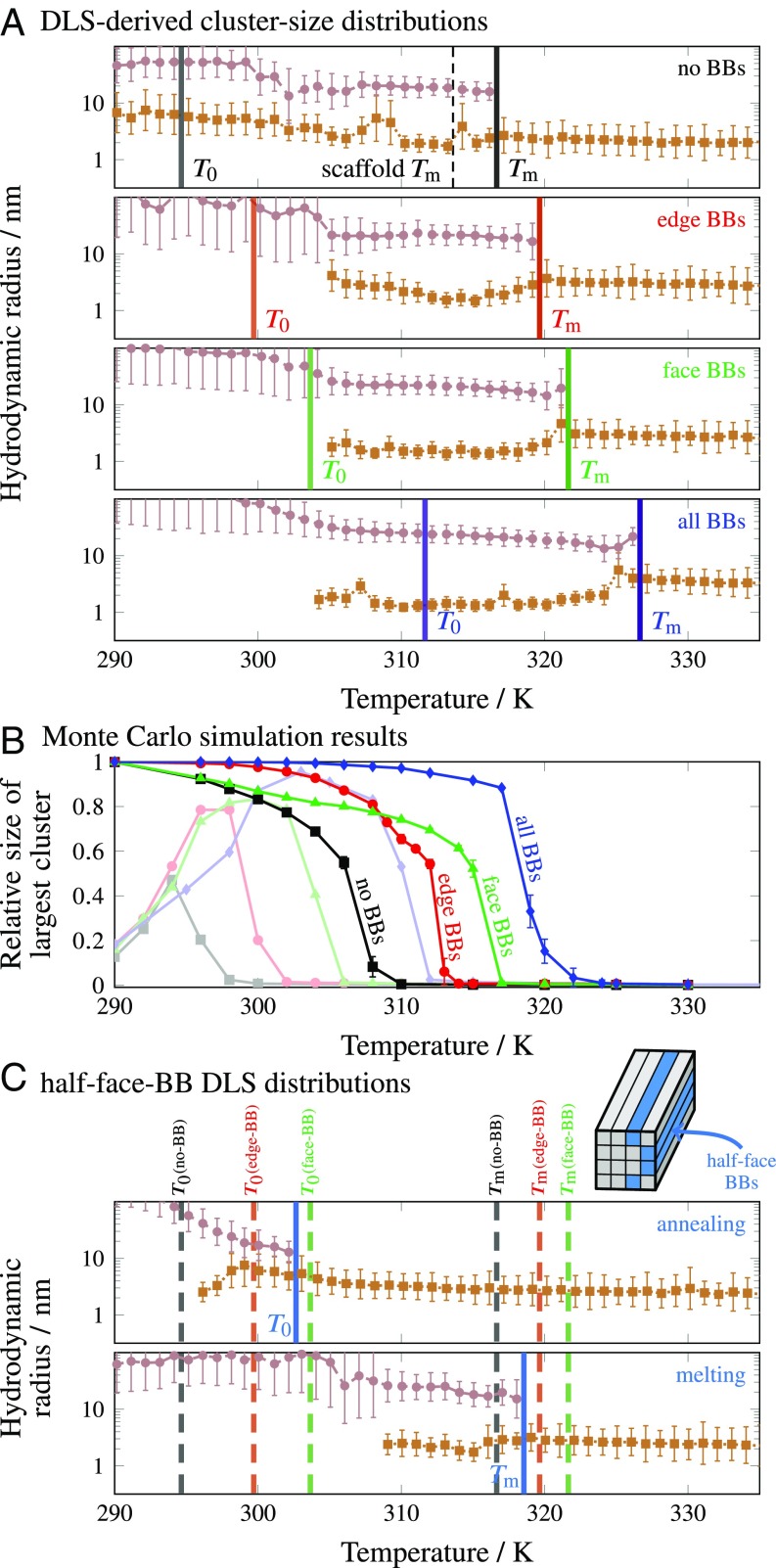
To obtain information on the self-assembly process, we used DLS to probe the size of structures as a function of temperature during the annealing ramp. These measurements provide insight into the growth of clusters of hybridized strands without requiring the introduction of intercalating dyes or other additives that might alter structure assembly. Because submicrometer-sized particles scatter visible light in the Rayleigh limit, where the scattering intensity scales as the sixth power of the particle size, DLS is also highly sensitive to small populations of large clusters. These features of DLS therefore allowed us to detect the initial formation of the target cuboids during the annealing protocol without perturbing the assembly process.
At each temperature step, we obtained the autocorrelation function from a time series of light-scattering intensity measurements to extract a distribution of decay rates. Given the low concentration of macromolecules in our experiments ( by volume), we assumed that the free diffusion of particles in the suspension was not affected by hydrodynamic interactions, so that the decay rates could be related to the translational diffusion coefficients of independent multistrand clusters (35). For ease of interpretation, we present these distributions in terms of the hydrodynamic radius of a spherical particle with an equivalent diffusion coefficient. Since determining the decay rate distribution from the autocorrelation function requires additional assumptions on the smoothness of the cluster-size distribution, we used multiple regularization methods to verify the robustness of our results (SI Appendix, section 1.4 and Fig. S3).
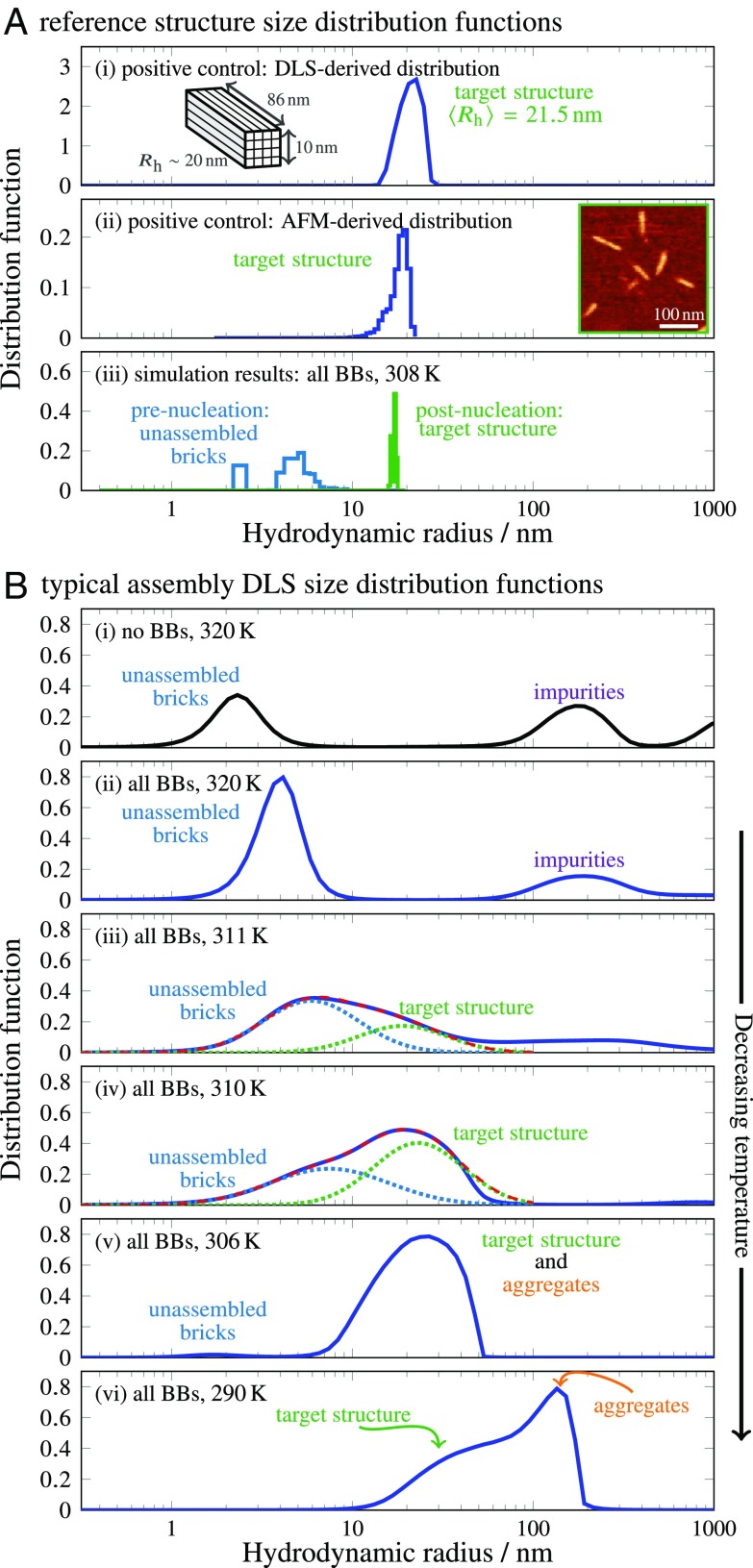
We first determined the reference cluster-size distribution for a purified sample of assembled all-BB cuboids (Fig. 3 A, i). This distribution is peaked at a hydrodynamic radius of 21.5 nm, which matches the expected size of a fully assembled cuboid ( 20 nm; Materials and Methods). This distribution also agrees with the ideal distribution calculated from AFM images of purified all-BB cuboids (Fig. 3 A, ii), in which all imaged particles were treated as rigid cylinders (Materials and Methods). The broadening of the reference distribution relative to this ideal distribution is likely due to the effects of particle anisotropy on light scattering, which we have not attempted to account for here.
Fig. 3.
(A) Reference intensity-weighted size distribution functions for a purified all-BB sample, determined by DLS (A, i) and calculated from AFM images (A, ii) and Monte Carlo simulations (A, iii). In A, i and A, ii, Insets show the dimensions of the target structure and a representative AFM image. In A, iii, the blue curves indicate the metastable cluster-size distribution before nucleation, while the green curves show the equilibrated distribution after the target structure has assembled. The gap between the monomer and dimers in the prenucleation distribution is an artifact of the lattice simulations. (B) Representative intensity-weighted distribution functions at decreasing temperatures. At high temperatures (B, i and B, ii), the no-BB distribution indicates unhybridized scaffold strands, while the all-BB distribution is dominated by small clusters of BBs, as seen in the prenucleation Monte Carlo simulations. At intermediate temperatures (B, iii and B, iv), the distribution can be fitted to a sum of two Gaussians (red dashes), which correspond to the unassembled (blue dots) and target-structure (green dots) populations, respectively. At lower temperatures (B, v and B, vi), a small population of larger aggregates skews the intensity-weighted distribution, but the contribution from the target structure can still be seen in B, vi.
We next used lattice Monte Carlo simulations of an established coarse-grained model (14) to calculate ideal cluster-distribution functions of the all-BB system, equilibrated both before and after nucleation of the target structure (Fig. 3 A, iii and Materials and Methods). Consistent with prior simulations (14, 23, 24), we found that intermediate cluster sizes, with between 8 nm and 15 nm, are unstable. Consequently, the size distribution is either peaked near 5 nm, corresponding to small clusters of primarily BBs, or 18 nm, corresponding to a mostly complete target structure. Because these simulations consider a single copy of the target structure, the system can be in only one state at a time; however, in a larger system with many copies of each brick, the assembly of a fraction of all structures would result in a bimodal cluster-size distribution. The simulation results therefore suggest that the distribution can be used to resolve the target structure during an assembly experiment. We note that the discretization of small cluster sizes in the unassembled population is an artifact of the lattice model and is not expected to be seen in experiments.
Typical size-distribution functions determined by DLS similarly show that is a suitable order parameter for identifying complete structures (Fig. 3B). At high temperatures (Fig. 3 B, i and ii), before nucleation occurs, we observed a single peak (ignoring high–molecular-weight impurities) corresponding to individual strands and small clusters. In particular, in the no-BB system, the peak matches the expected size of a flexible 32-nt strand, 2.7 nm. Then, upon decreasing the temperature, a new population suddenly appeared at 20 nm. As expected from our simulation results, the cluster-size distributions at these intermediate temperatures are well described by bimodal fits to a linear combination of Gaussian functions (Fig. 3 B, iii and iv). In particular, the means of the Gaussian fits coincide with the reference unassembled and target-structure distributions; however, the fitted populations are considerably broader than the reference distributions. This is likely a consequence of the conservative regularization method used in the analysis of the autocorrelation data, which tends to smooth the resulting distributions, as well as heterogeneity due to incomplete assembly. To confirm our interpretation of the bimodal cluster-size distributions, we discuss a complementary validation strategy based on an analysis of AFM images below and in SI Appendix.
At lower temperatures (Fig. 3 B, v and vi), particles with effective hydrodynamic radii larger than 40 nm begin to contribute to the distribution. This shift toward larger is likely due to the formation of aggregates of fully or partially assembled structures. However, we emphasize that because of the sixth-power dependence of the light-scattering intensity on the particle size, only a small fraction of aggregated structures are needed to skew the cluster-size distribution substantially. For the same reason, the large- impurities present at higher temperatures (Fig. 3 B, i and ii) are extremely rare. Nevertheless, despite the tendency of the structure and aggregate peaks to merge due to our conservative choice of regularization method, the population of target structures can still be identified from the shoulder of the cluster-size distribution at 290 K (Fig. 3 B, vi).
Evidence for Nucleation and Growth.
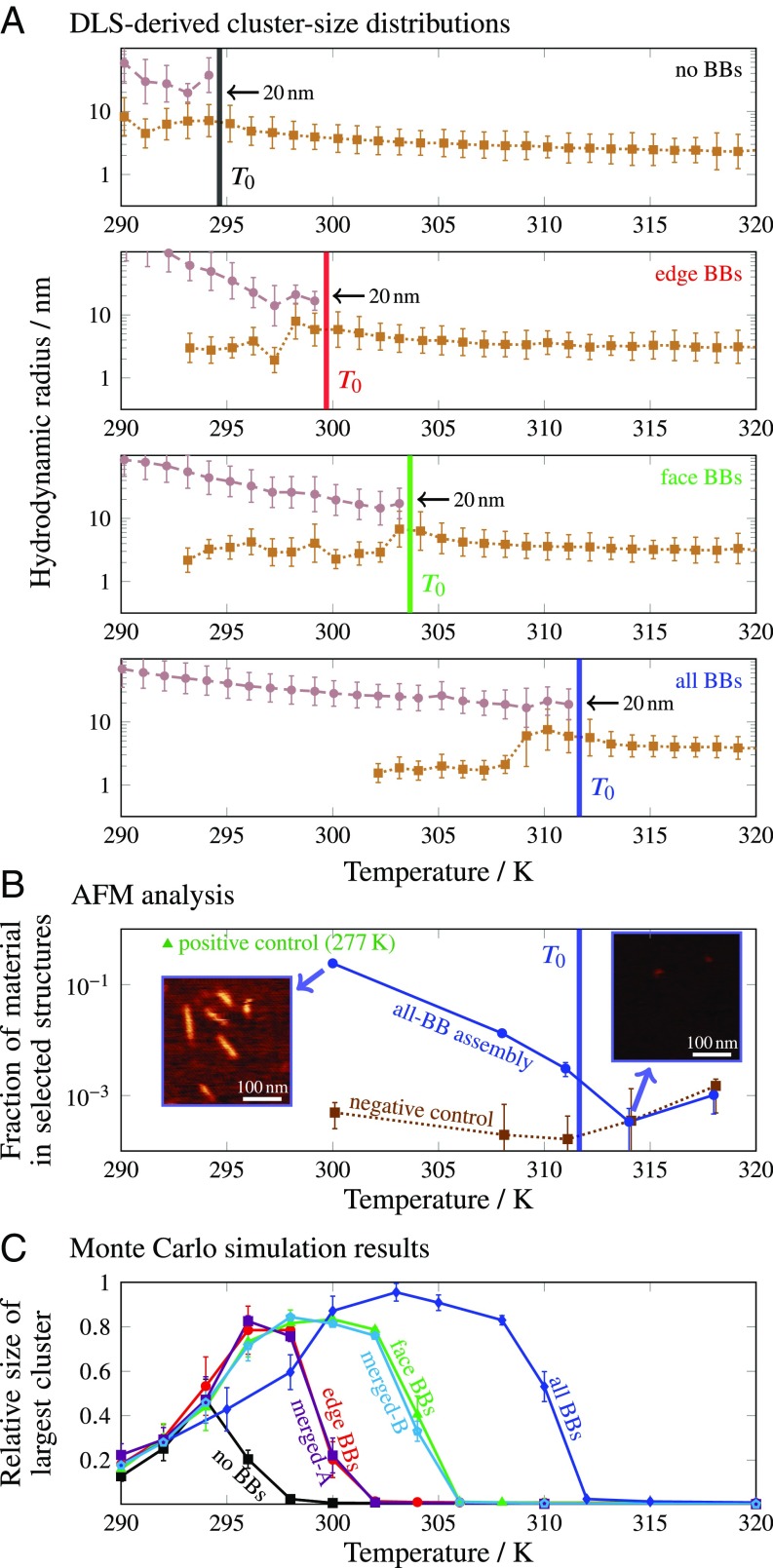
For each structure variant, we determined both the cluster-size distribution via DLS and the extent of subunit hybridization via fluorescence measurements (SI Appendix, section 2) as a function of temperature over the course of a 15.2-h linear annealing protocol. We observed prominent peaks in the fluorescence response of systems containing BBs at high temperatures (). This behavior could be attributed to the formation of stable high-temperature dimers, in which the elongated boundary bricks (Fig. 1C) stably hybridize to other bricks in continuous 16- or 24-bp domains (SI Appendix, Fig. S4). However, in DLS experiments, we did not observe any substantial change in the overall scattering intensity at temperatures above 315 K (SI Appendix, Fig. S5), implying that the assembly of complete structures does not take place at these temperatures. Nevertheless, DLS did resolve differences in the unassembled populations. At temperatures where only a single peak was present (excluding contributions from any impurities in the system), we found that the mean hydrodynamic radius of the no-BB system increased from to upon cooling, reflecting an increasing fraction of scaffold-strand dimers (Fig. 4A). Similarly, the single-peak in systems with BBs increased from nm to upon cooling, consistent with the presence of larger preformed BB dimers.
Fig. 4.
(A) Unimodal and bimodal cluster-size distributions determined via DLS following a 15.2-h annealing protocol. Points and error bars show the mean hydrodynamic radii and standard deviations, respectively, of the Gaussian fits to the unassembled and target-structure populations (compare Fig. 3 B, iii and iv) at each temperature. For each system, indicates the temperature at which the higher- population first appears during the annealing protocol. (B) The volume fraction comprising target cuboids, relative to the total volume of material, determined from AFM analysis of the all-BB system. All samples were rapidly quenched for imaging from the indicated temperatures. The target-structure volume fractions of the positive-control all-BB sample (green triangle) and nonhybridizing oligonucleotides (negative control, dotted line) were calculated in the same way, and the error bars show the estimated SE based on Poisson statistics. Insets show representative portions of the raw AFM images. (C) The size of the largest correctly bonded cluster from Monte Carlo simulations. Each data point corresponds to the average of 10 independent simulations in the long time limit, once nucleation has occurred, with error bars showing the SD. The “merged” curves refer to fixed-edge dimers, as discussed in the text and SI Appendix, Fig. S1.
In each system, we observed the sudden appearance of a second peak in the cluster-size distribution at a temperature (Fig. 4A). This feature appeared at the same temperature in multiple annealing runs for each system, with the exception of the no-BB structure, where varied by across three runs. As in the example distributions shown in Fig. 3 B, iii and iv, the mean hydrodynamic radius of this population, determined by fitting a linear combination of Gaussian functions, coincided with the expected size of the target structure in all systems. Because of the comparable scattering intensities of the two populations at , we ascribed this second peak to the scattering of a relatively small number of essentially complete target structures. The target-structure remained nearly constant for at least 3 K below in all systems before increasing above 20 nm, most likely due to aggregation as discussed above. By contrast, the fluorescence response (SI Appendix, Fig. S4) did not provide definitive insights into the assembly of the complete structure for any cuboid variant.
Our experiments indicate that the target structures do not grow gradually as a function of temperature. Instead, DLS reveals that the transition from having all unassembled subunits to having some complete structures occurs discontinuously. The unassembled population remains easily detectable over a temperature range of ∼10 K below for each structure, indicating that not all subunits are incorporated into complete structures at . For the no-BB, edge-BB, and face-BB systems, the mean of this population is comparable to the mean of unassembled strands above . By contrast, the mean of this population decreased in the all-BB system near 308 K, suggesting that only scaffold strands remained unassociated with target structures or aggregates below this temperature.
To validate further our interpretation of the cluster-size distributions obtained from DLS, we performed a complementary analysis based on AFM imaging of the all-BB system at selected temperatures. Using AFM images of quenched and immobilized samples, we estimated the fraction of the total volume of imaged particles comprising target structures. We first determined appropriate criteria, using the areas and aspect ratios of imaged particles, for identifying correctly assembled cuboids in images of a purified sample (SI Appendix, Fig. S6). We then applied these criteria to estimate the target-structure volume fraction as a function of the temperature from which the sample was quenched (Fig. 4B and SI Appendix, Fig. S7). Because the rapid quenching involved in the preparation of the samples likely affects the particle-size distribution and AFM does not reliably distinguish single-stranded DNA from the background, this method cannot be used to assess the volume fraction of assembled structures quantitatively. In addition, image analysis inevitably identifies some false target structures. However, by comparing the calculated volume fractions with a negative control of ∼200 nonhybridizing, similar-length oligonucleotides, which accounts for sample-preparation and imaging artifacts, we verified that the target structures are indeed present at temperatures below, but not above, . The low estimated volume fraction (∼0.3%) just below is also consistent with the roughly equal areas of the intensity-weighted unassembled and target-structure populations seen in DLS (Fig. 3 B, iii and iv), demonstrating the sensitivity of DLS to small populations of large clusters. This analysis therefore corroborates our primary conclusions from the DLS experiments and supports our interpretation of the population. The remainder of our study is based on DLS data, since this technique can be performed in situ without perturbing the assembly process.
Comparison with Coarse-Grained Monte Carlo Simulations.
To observe the self-assembly process in greater detail, we simulated the assembly of a coarse-grained DNA-brick model using Monte Carlo dynamics at constant temperature (14). Previous studies (14, 24) of this model have found that self-assembly proceeds via nucleation and growth, whereby clusters that are intermediate between unassembled strands and nearly complete target structures are thermodynamically unstable. In particular, the nucleation step, which requires the formation of a critical multistrand cluster, is a thermally activated rare event and thus determines the highest temperature at which self-assembly can occur. Therefore, following an approach established for simulating structures with BBs (20), we studied the nucleation of cuboid designs analogous to those used in our DLS experiments, using a single copy of the target structure and hybridization parameters chosen to mimic the experimental conditions (Materials and Methods).
Remarkably, we found that for each cuboid variant, the highest temperature at which nucleation occurs in our simulations is in nearly quantitative agreement with the temperature at which the population first appears in the DLS experiments. This can be seen by comparing the temperature at which the average cluster size sharply increases in Fig. 4C with the corresponding in Fig. 4A. It is important to note that, unlike in the experiments, all simulations were initialized from an unassembled solution with the total experimental monomer concentration at each temperature. The simulated trajectories should thus be compared only with the initial formation of target structures near during the annealing ramp, after which monomer depletion must be taken into account. In simulations initiated at lower temperatures, kinetic trapping arising from subunit misbonding tends to inhibit structure nucleation, as evidenced by the decreased average cluster sizes at temperatures below (Fig. 4C). In contrast with the variations in nucleation behavior, the effects of misbonding are essentially independent of the structure design in our simulations.
Preformed Clusters Modify Nucleation Barriers.
Based on the evidence of high-temperature hybridization (SI Appendix, section 2), we hypothesized that the presence of preformed clusters involving BBs might play a key role in determining nucleation behavior. Similar behavior is exhibited in our simulations, where BB dimers form nearly completely before structure nucleation (SI Appendix, Fig. S8). We further tested this idea by running simulations in which BB dimers were merged into permanently bonded units, mimicking the result of high-temperature hybridization in the experimental system. To this end, simulations with merged edge BBs (“merged-A”; SI Appendix, Fig. S1) confirmed that nucleation in this system is analogous to the edge-BB structure (Fig. 4C).
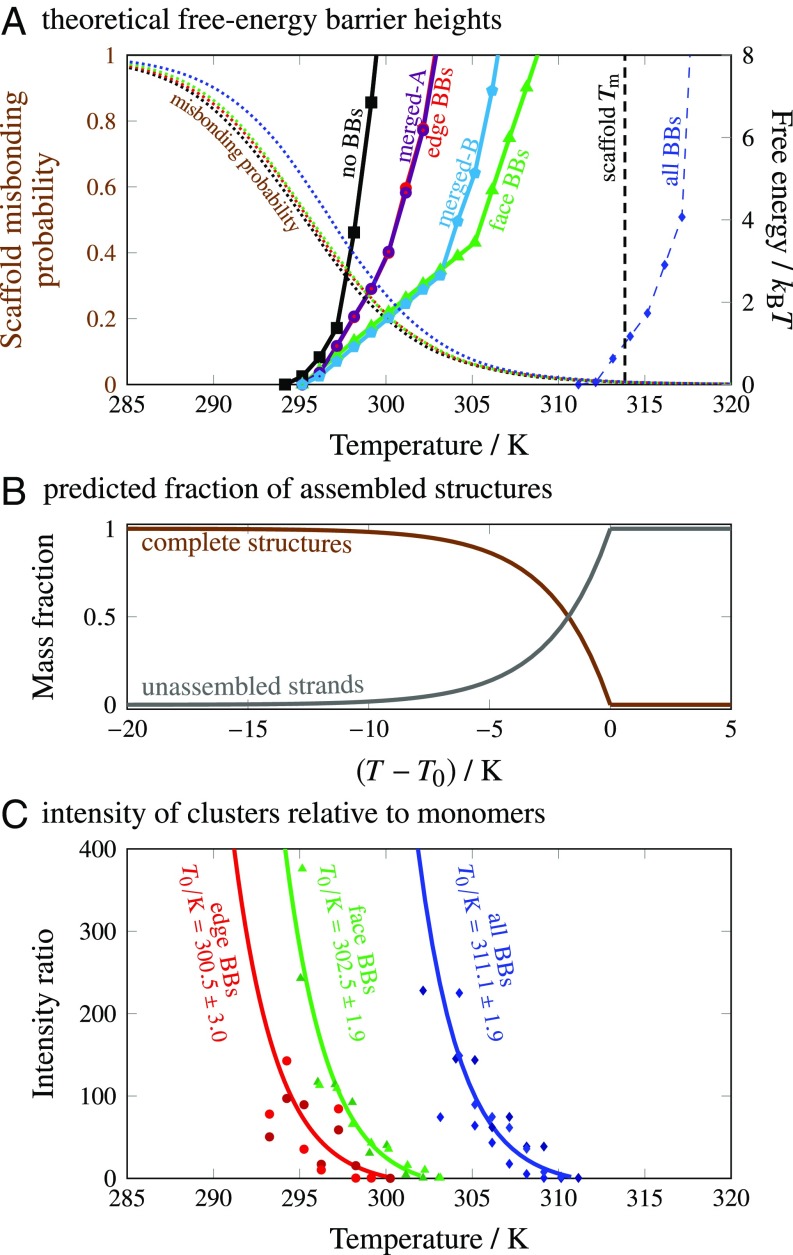
This hypothesis is supported by free-energy calculations using a discrete combinatorial model (23–25), in which each distinct subunit type is represented as a node in an abstract graph that describes the connectivity of the target structure. Assuming that all 16- and 24-bp domains hybridize completely at high temperatures, we merged the corresponding pairs of subunits to account for changes in the local subunit connectivity due to the incorporation of each type of BB. We then used this model to calculate the free-energy barrier to nucleation by further assuming that the number of subunits in a partially assembled cluster is a good reaction coordinate (Materials and Methods). These free-energy calculations predict that the heights of the nucleation barriers, and thus the logarithms of the nucleation rates, vary rapidly with temperature (Fig. 5A). Furthermore, the relative ordering of the nucleation-barrier curves for the no-BB, edge-BB, and face-BB systems is consistent with the DLS and simulation results, indicating that merging subunits via high-temperature hybridization is sufficient to modify the nucleation behavior. For comparison, we show the predicted melting temperature below which the scaffold-strand core of the cuboid is thermodynamically stable; the model predicts that successful nucleation always requires that the system be supersaturated by lowering the temperature below the scaffold-strand . We also show that the effects of strand misbonding are captured by a simple estimate of the probability of pairwise misinteractions (Materials and Methods). As in our simulations, the misbonding probabilities are nearly independent of BB incorporation.
Fig. 5.
(A) The height of the nucleation barrier, at the initial free-strand concentration, as a function of temperature from theoretical calculations. The all-BB barrier refers to the nucleation of a network of BBs, as discussed in the main text. We also show the predicted scaffold melting temperature, , and the median probability that a scaffold strand forms at least one misinteraction in the absence of successful nucleation. (B) The predicted evolution of the unassembled-strand and complete-structure populations over the course of a nucleation-limited annealing protocol, determined from the nucleation-barrier calculations (SI Appendix, section 3). (C) The ratio of the experimentally determined intensities of the two populations as a function of temperature, alongside an exponential fit for each system, with (SI Appendix, section 3). Points are shown for multiple annealing runs.
Interestingly, we found that the assembly of the all-BB structure follows a three-step mechanism that is not well described by a one-dimensional free-energy landscape. In this system, pairs of preformed multimers can hybridize with one another via multiple 8-bp domains. Consequently, bonding networks that are dominated by BBs begin to form at temperatures where all single 8-bp hybridizations are unstable, leading to extensive BB bonding and large cluster-size fluctuations in simulations above 310 K (SI Appendix, Fig. S8). Our simulations show that the nucleation of the interior of the structure then occurs in a separate assembly step, at temperatures slightly below the predicted scaffold-strand melting temperature, . Because the theoretical results assume a one-dimensional order parameter, we show only the predicted free-energy barrier that pertains to the formation of an initial network of BBs in the all-BB system in Fig. 5A.
Nucleation Strongly Affects Self-Assembly Yield.
Because our free-energy calculations predict that the height of the nucleation barrier also depends strongly on the subunit concentration, the nucleation rate is expected to decrease with monomer depletion (10). The changing concentration of unassembled subunits is therefore predicted to result in the continued production of complete structures at temperatures below in an annealing ramp where nucleation is rate limiting (Fig. 5B and SI Appendix, section 3). This prediction takes into account the temperature scaling derived from the calculated nucleation barriers and the temperature dependence of the hybridization free energies (SI Appendix, Fig. S9), assuming perfect stoichiometry and zero aggregation. To test this prediction, we integrated the experimentally determined total scattering intensity associated with each peak in the cluster-size distribution and, assuming that this intensity is proportional to the number density, determined the ratio of large- to small- populations. The trends shown in Fig. 5C for the edge-BB, face-BB, and all-BB structures follow the predictions of our free-energy calculations, as the intensity ratios are consistent with the functional form and temperature scaling shown in Fig. 5B. Since there must be some leftover subunits due to imperfect stoichiometry (measured to be ∼ 10%), we did not expect the unassembled population to decay to zero in the experimental system. However, the associated intensity did not attain a constant level before the small- peak fell below the detection range of the instrumentation.
These observed variations in nucleation behavior therefore provide a likely explanation for the extreme differences in yields among our structural variants and the similarity between the ranking of the final yields and the order of the initial assembly transitions. At any given temperature, only a fraction of the potential structures ultimately form because nucleation slows as large clusters are produced; consequently, decreasing the temperature by an annealing protocol is necessary to continue driving nucleation of additional structures. However, our simulations and no-BB DLS measurements indicate that misbonding dominates below 295 K. Structure designs that nucleate at higher temperatures thus benefit from a broader temperature range over which nucleation can occur.
Nucleation Behavior and Kinetic Stability Can Be Independently Tuned.
The differences among our cuboid variants do not affect the thermodynamic properties of the scaffold strands, which compose the bulk of the structure. However, incorporating BBs can, in principle, increase the kinetic stability of assembled structures. To examine this effect, we reversed the temperature ramp and used DLS to track the melting of assembled structures. We observed the complete melting of all structures in solution, as evidenced by the disappearance of the population, at considerably higher temperatures than in the assembly transitions (Fig. 6A). The complete melting transitions, , of the cuboid variants occurred in the reverse order of the assembly transitions, , indicating that a strong bonding network of BBs provides a kinetic barrier to disassembly. However, the differences in melting temperatures were generally smaller for structures that nucleate at lower temperatures, suggesting that the BBs affect disassembly to a lesser extent than they affect nucleation.
Fig. 6.
(A) Cluster-size distributions determined from DLS melting experiments (compare with Fig. 4A). The temperatures at which all structures have melted, , are compared with the initial assembly temperatures, . The no-BB structures melt completely at a temperature close to the predicted scaffold-strand (dashed line). (B) The hysteresis in the size of the structure as a function of temperature can be seen by comparing the long–time-limit average cluster sizes in simulations initialized from preassembled structures (solid lines) and from an unassembled solution (faded lines from Fig. 4C). In C, we show the annealing (Top) and melting (Bottom) cluster-size distributions for a half–face-BB system. Inset shows a schematic illustration of the BB locations. The temperatures and for the no-BB, edge-BB, and face-BB systems are shown by dashed vertical lines for comparison. Importantly, the order in which the half–face-BB and edge-BB structures nucleate is different from the order in which they melt.
Melting simulations of fully formed structures show similar trends (Fig. 6B). Analysis of the simulation trajectories reveals that scaffold bricks at the edges of the no-BB and face-BB structures disassemble first. The face-BB structures therefore lose bricks at lower temperatures than the edge-BB structures, although the face BBs provide a larger barrier to complete disassembly. Disassembly occurs most abruptly in the case of the all-BB structures, with bricks initially dissociating from the unprotected ends of the structure. Consistent with the assembly simulations, the all-BB structures disassemble via a three-step disassembly mechanism, in which large networks of BB dimers persist for a few degrees above the apparent melting temperature (Fig. 6B).
To distinguish between the effects of nucleation and kinetic stability, we designed the “half–face-BB” cuboid shown schematically in Fig. 6C. By incorporating face BBs on only one half of the structure, we predicted that we would see improved nucleation behavior, as with the full face-BB structure, but reduced kinetic stability. DLS confirmed that this structure initially nucleates at a temperature close to the face-BB (Fig. 6C), in agreement with our simulations and free-energy calculations (SI Appendix, Fig. S10). The assembly yield (SI Appendix, Fig. S11) is dramatically improved relative to that of the no-BB structure, but is less than that of the face-BB structure, presumably because one half of the cuboid is not protected by BBs and is thus more susceptible to aggregation from low-temperature misbonding.
Importantly, DLS reveals that the half–face-BB structure melts before the edge-BB structure does, implying that the lack of BB protection on one face facilitates disassembly of the complete structure. Comparing the half–face-BB and no-BB systems, which have similar melting temperatures, highlights the crucial role of enhanced nucleation, as opposed to increased stability, in improving the yield. More generally, this example demonstrates that the nucleation behavior and thermal stability of DNA-brick nanostructures can be independently tuned.
Nucleation Pathways Are Determined by the Connectivity of Preformed Clusters.
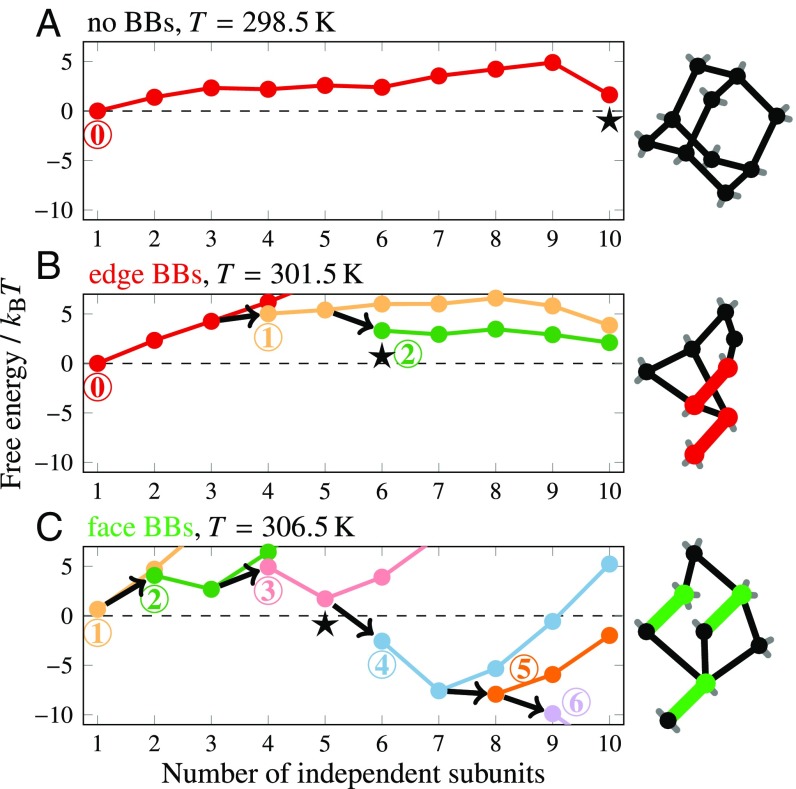
To identify the microscopic origin of the differences in nucleation behavior, we calculated minimum-free-energy pathways using our theoretical model (Fig. 7). For each structure, we determined the free energy as a function of the number of independent subunits and the number of preformed dimers at a temperature where the nucleation barrier is ∼, which is comparable to the barrier height at which nucleation was observed in previous simulations of this model (14, 24). The typical order in which dimers and scaffold strands are incorporated into a growing cluster is indicated by the minimum-free-energy nucleation pathways in Fig. 7 and illustrated in SI Appendix, Figs. S13–S15. Importantly, these calculations allow us to identify typical postcritical nuclei, the smallest multistrand clusters that are more likely to grow via strand addition than to dissociate and whose formation is thus the rate-limiting step on each predicted nucleation pathway. The topologies of these clusters are shown in Fig. 7; however, because there are many topologically equivalent clusters within each structure, with unique sequences for the hybridized segments, there are numerous postcritical nuclei comprising distinct strands with slightly different free energies.
Fig. 7.
(A–C, Left) The free energy as a function of cluster size and composition from theoretical calculations, showing that the minimum-free-energy self-assembly pathway depends on the presence of preformed multimers. The number of preformed multimers within each cluster is indicated by the circled numbers and the corresponding colors. Clusters on the minimum-free-energy pathway grow by incorporating one independent subunit at a time, which may be either a single scaffold brick (following a colored line) or a preformed multimer (following an arrow). For ease of comparison, each free-energy landscape is shown at a temperature at which the nucleation barrier is ∼. The postcritical nuclei, which coincide with the first subunit addition after the highest point on the minimum-free-energy path, are indicated by stars. (A–C, Right) Schematic diagrams of representative postcritical nuclei, with preformed multimers indicated by colored lines. For a comparison with simulation trajectories, see SI Appendix, Fig. S12; representative pathways are also illustrated in SI Appendix, Figs. S13–S15.
These landscapes reveal crucial differences between the edge-BB and face-BB structures, which contain the same number of 48-nt BBs, and point to the key role of the connections between the preformed dimers and interior scaffold strands. Topologically, this difference arises from the fact that face-BB dimers contain segments that directly connect to the fully interior scaffold strands, whereas the edge-BB dimers are only indirectly connected to these “core” strands (SI Appendix, Fig. S1). Because each subunit addition results in a loss of translational entropy, the free energy on a nucleation pathway decreases only when multiple 8-bp bonds are formed with a single subunit addition, resulting in a topologically closed cycle. In the absence of BBs, our previous work has shown that the postcritical nucleus at typical nucleation temperatures is a tricyclic cluster comprising 12 8-bp bonds and 10 subunits (23). Yet by incorporating preformed dimers, fewer independent subunits are needed to reach a postcritical nucleus. The 8-bp bonds can thus be weaker, leading to an elevated nucleation temperature. Despite the fact that the edge-BB and face-BB dimers have the same number of 8-nt domains for binding to other subunits, the topologies of the minimum-free-energy clusters in these structures are different: The edge-BB structures require 6 subunits, including two BB dimers, to form a postcritical bicyclic cluster (Fig. 7B), while face-BB structures only require 5 subunits, including three dimers (Fig. 7C). Consistent with the predicted pathways, simulation trajectories show that BB dimers comprise a larger fraction of the postcritical clusters in the face-BB structure than in the edge-BB structure (SI Appendix, Fig. S12). We can also exclude the concentration of preformed dimers as the determining factor by comparing the half–face-BB and edge-BB structures, as these systems contain the same number of preformed dimers but nucleate at significantly different temperatures.
Based on these findings, we hypothesized that by changing the local connectivity of the edge BBs, we might be able to reproduce the enhanced nucleation behavior of the face-BB structure. To test this hypothesis directly, we ran simulations of the edge-BB system in which we explicitly merged each edge dimer with one of its neighboring scaffold strands in the target structure. The only difference between this structure (“merged-B”; SI Appendix, Fig. S1) and a normal edge-BB dimer is that this additional connection to the interior scaffold strands, which would otherwise need to form spontaneously during the nucleation process and thus entail a loss of translational entropy, has been fixed in place. This modification leads to postcritical nuclei that comprise five independent subunits, resulting in assembly behavior that is nearly analogous to that of the face-BB structure (Figs. 4C and 5A). Thus, although this particular modification would be difficult to achieve experimentally using DNA bricks, our simulations and theory show that the addition of a single connection to the interior of the structure can alter the nucleation behavior significantly.
Design Rules for Enhanced Nucleation.
Based on our experimental, simulation, and theoretical findings, we propose four design rules for enhancing the nucleation behavior and assembly yield in addressable systems:
-
i)
The key determinant of the structure yield is the separation between the initial nucleation and misbonding temperatures. While the misbonding temperature is set by the pairwise interactions and the subunit concentrations, the nucleation temperature can be tuned through rational structure design. By contrast, changes to the subunit interactions that uniformly affect both correct and incorrect bonds are unlikely to improve the yield.
-
ii)
Altering the “valency” of specific subunits to create multistep pathways, for example by forming BB dimers at high temperatures, is a viable strategy for controlling nucleation, because it can change the number of independent subunits in the critical nucleus. On the other hand, tuning individual bond strengths is a less effective strategy for selecting a specific nucleation pathway, since the number of parallel pathways grows superextensively with the size of the target structure.
-
iii)
Controlling the topology of the critical nuclei is crucial. It may not be optimal simply to add high-valency subunits, as in the case of the edge BBs. Instead, efficient nucleation requires that the critical nuclei contain many stabilizing bonds but few subunits, favoring the formation of free-energy–reducing topological cycles earlier in the nucleation pathway. This is achieved in the case of the face-BB and merged-B structures by maximizing the number of bonds between the preformed dimers and the interior scaffold bricks.
-
iv)
Only a small portion of a structure needs to be optimized to achieve enhanced nucleation behavior. For example, comparison of the half–face-BB and no-BB systems shows that modifying fewer than 20% of the subunits drastically raises the initial nucleation temperature and markedly improves the yield.
Discussion
By combining dynamic light scattering with a coarse-grained theoretical model, we have shown that the ultimate yield of correctly assembled structures is largely determined by the nucleation pathway. As a specific example, we have investigated the role of nucleation kinetics in addressable self-assembly by modifying the bonding characteristics of specific subunits at the boundaries of a DNA-brick nanostructure. We have shown that the location and design of the altered subunits determine the free-energy landscape for self-assembly and control the temperature at which nucleation first becomes feasible. Moreover, the nearly quantitative agreement between the predictions of a coarse-grained model and our experimental results allows us to rationalize these striking effects on the self-assembly behavior.
Taken together, our experiments and modeling establish practical design principles for improving the self-assembly of addressable nanostructures. In a typical annealing protocol, structures have a limited time and temperature window in which to form: At high temperatures, a large free-energy barrier inhibits nucleation, while at low temperatures, self-assembly is limited by kinetic arrest. The key to successful self-assembly is to increase the width of the temperature window over which nucleation can occur, thereby maximizing the thermodynamic segregation between the critical nucleation step and detrimental misbonding. This can be achieved by stabilizing the critical nuclei, which allows self-assembly to proceed when the subunit interactions are still relatively weak. To demonstrate this principle with DNA bricks, we have shown that the increased valency of BB dimers, which assemble at temperatures much higher than those at which nucleation can occur, lowers the free-energy barrier to nucleation by decreasing the entropic cost of forming a critical number of stabilizing bonds. However, this strategy works only if the high-valency subunits are optimally connected to the remainder of the structure, as evidenced by the difference in nucleation behavior between the edge-BB and face-BB structures. More generally, our results show that it is possible to use a relatively small number of high-valency subunits to design the nucleation pathway rationally and suggest that this approach is not necessarily limited to manipulating bricks at the boundaries of a structure.
Our experiments provide an explicit characterization of 3D structure nucleation in the context of addressable self-assembly. This advance has been enabled by our use of DLS, which allows us to probe multistrand structure growth, as opposed to the fraction of intersubunit bonds that are formed at a given temperature. This distinction is particularly evident in the system evaluated here, where the initial nucleation temperature does not necessarily correlate with the maximal increase in DNA base pairing. Furthermore, the cluster-size distributions that we obtain from DLS resolve the populations of unincorporated bricks, complete structures, and aggregates, making it possible to track the evolution of these species throughout the course of an annealing protocol. Together with the complementary AFM-based validation, these measurements provide experimental evidence that DNA bricks self-assemble via a nucleation-and-growth mechanism and reveal the relationship between the design of addressable structures and their nucleation kinetics.
The excellent agreement between the predictions of our theoretical model and our experimental results demonstrates that our coarse-grained approach captures the fundamental physics of addressable self-assembly. This agreement gives us confidence that our theory and simulations can be used to guide rational design strategies for complex self-assembly, not only in the context of DNA bricks specifically, but—precisely because of the generality of the models used—also for optimizing addressable systems more broadly. We anticipate that the principles established here will therefore guide efforts to design the nucleation behavior of colloidal systems such as supramolecular and nanoparticle lattices (36–38), protein nanostructures (39), and DNA-origami–based systems with programmable interactions (40). For example, analogous prenucleation clusters could be constructed by forming high-temperature bonds between caged nanoparticles (41) or by directly introducing a small population of dumbbell-like subunits. Alternatively, the connectivity of specific subunits could be altered by changing the arrangement of directional patches on colloidal particles (42). As we have demonstrated here, successful implementation will require knowledge of the effects of such modifications on the critical nucleus for structure assembly, which dictates the optimal design strategy for any specific system.
Materials and Methods
In SI Appendix, we describe how we chose the DNA sequences for the strands for each system studied. We also provide complete details of the annealing protocols, the conditions used in AFM and gel electrophoresis, and the protocols used when obtaining fluorescence and light-scattering data in SI Appendix, Extended Methods. Supporting data are available at the University of Cambridge Data Repository, https://www.data.cam.ac.uk/repository (doi: 10.17863/CAM.22991).
Structure Annealing.
Structures were assembled using a strand concentration of 153 nM per sequence in a buffer of 15 mM MgCl2, 0.5 mM EDTA, and 5 mM Tris, pH 8. Strands in the reaction mixture were denatured at 90 °C for 10 min and then gradually cooled via either (i) a 15.2-h protocol (reciprocal cooling rate 12 min ·K−1) or (ii) a 66-h protocol (reciprocal cooling rate 52 min ·K−1).
AFM.
Samples from annealing protocol ii were immobilized for 10 on poly-l-ornithine–coated mica discs and imaged in liquid in intermittent contact mode, using a BioLever Mini cantilever and JPK Nanowizard 3 AFM.
Agarose Gel Electrophoresis.
Structures were analyzed via gel electrophoresis on a gel made from 2 wt% agarose in and 10 mM MgCl2. Electrophoresis was performed at 80 V and 4 °C for 2 h. The gel was poststained with ethidium bromide and the yield was estimated using GelBandFitter software (43).
Fluorescence Annealing.
Annealing protocol i was used for fluorescence annealing experiments with 10 nM SYBR green I solution (44) added to the reaction mixture. The fluorescence signal was measured as a function of temperature with an ABI Prism 7900HT-Fast Real Time PCR system at 488 nm.
Static and DLS.
Using annealing protocol i, light-scattering measurements were performed in the last 2 min of each temperature step. Light scattering of 20-L samples was measured using a Malvern Zetasizer NanoZSP apparatus at an angle of 173°. For DLS, the intensity autocorrelation function was computed from 12 measurements at 10-s intervals. Cluster-size distributions were determined from these data, using multiple regularization methods (45) to verify their robustness (SI Appendix, Fig. S3).
Reference Hydrodynamic Radius Calculations.
The hydrodynamic radius of a freely jointed chain is (46), where is the number of segments and is the length of a segment. To estimate the hydrodynamic radius for single-stranded DNA, we used a typical Kuhn length of and length per DNA base of (47). A 32-nt scaffold brick comprises Kuhn segments and hence ; for a 48-nt boundary brick, . Since the quantities and used here do not correspond to the temperatures and salt concentrations used in our experiments, these calculations provide us only with rough estimates of the magnitudes of for unhybridized strands.
For cylindrical structures, the translational diffusion coefficient is (48)
| [1] |
where is the Boltzmann constant, is the absolute temperature, is the viscosity of the medium, is the cylinder length, is the cylinder diameter, and is an end-effect correction given by . Assuming that the hydrodynamics of a cylinder are well approximated by a sphere with hydrodynamic radius , we can equate this diffusion coefficient to that of a sphere using the Stokes–Einstein–Smoluchowski equation,
| [2] |
leading to an approximate hydrodynamic radius of
| [3] |
Assuming a typical interhelical spacing of (49), our target structure can be treated as a cylinder with circumscribed diameter and length , resulting in an expected hydrodynamic radius of .
Image Analysis.
Particle identification in AFM images was done by applying the threshold function of Gwyddion version 2.5.0 (50). The reference distribution shown in Fig. 3 A, ii was calculated using the lengths, , and aspect ratios, , where is the projected area, of the particles assuming the cylindrical formula given above; particles with a minimum width greater than 25 nm, which correspond to overlapping structures, were excluded from this calculation. To compute the distribution function, particles were weighted by , and the distribution was normalized.
To calculate the fraction of correctly assembled structures in an AFM image, we selected all particles that satisfied constraints on both the projected area, , and the circularity, . These limits were chosen based on the distribution of imaged particles in the purified all-BB system (SI Appendix, Fig. S6). All particles were weighted by their volumes, as determined by the Laplacian background basis feature of Gwyddion, to assess the total fraction of the material contained in the selected particles. To reduce background noise, we also required that the area of the selected particles measured at half the particle height be at least and the average height be at least 2 nm. Standard errors were assigned to the yields by assuming a Poisson distribution based on the calculated yield and the absolute number of selected particles.
Monte Carlo Simulations.
We performed lattice Metropolis Monte Carlo simulations of DNA brick self-assembly, using a coarse-grained potential and dynamics that preserve the cluster-size dependence of the diffusion rates (14, 18, 20). Every DNA brick was represented as a “patchy particle” with four patches corresponding to its four domains, each of which was assigned a specific unique sequence, chosen randomly but with the constraint that patches that are bonded in the target structure have complementary DNA sequences. The interaction energies correspond to the hybridization free energies of these sequences obtained from the SantaLucia parameterization (51). When computing these hybridization free energies, we used a salt correction (52) corresponding to salt concentrations of and . In the simulations reported here, we used a system of 550 bricks in a box with lattice parameter , where is the shortest possible distance between any two particles. Assuming typical brick dimensions of (8, 19), this setup corresponds to a concentration of 153 nM. We accounted for BBs by imposing rigid bonds between dimers (or, in certain cases, larger multimers) of these patchy particles that would be merged into a single BB in experiment (20). Particles connected in this way remain at a fixed distance and dihedral angle to one another throughout the simulation. Noninteracting patches on the outside of the target structure were assigned poly-T sequences. We estimated a Kirkwood-like (53) hydrodynamic radius of each cluster by computing
| [4] |
where is the number of particles in the cluster, indicates a summation over every pair of particles and in the cluster, and is the distance between them on the lattice, using the typical brick dimensions given above to determine that for the lattice unit of length. The monomer is set to 2.7 nm, while the addition of in Eq. 4 crudely accounts for the dangling ends of monomers at one of the bases of the structure, which are not otherwise accounted for in the coarse-grained model. Eq. 4 thus predicts that a scaffold brick dimer will have a hydrodynamic radius of .
Free-Energy Calculations.
All free-energy calculations were carried out using the abstract-graph model described in ref. 23. The free energy of a particular cluster , comprising a set of subunits , is
| [5] |
where is the number of subunits in the cluster, indicates the set of strands that are neighbors of strand in the target structure, and the dimensionless bond strengths are . We determined for each pair of complementary sequences in the experimental systems using the SantaLucia parameterization described above. Each subunit, with concentration , was assumed to have rotational degrees of freedom, and each single bond was assumed to have dihedral degrees of freedom; these values were chosen to match the Monte Carlo simulations. refers to the number of “bridges” in the graph (23). The cluster free energy as a function of the number of correctly bonded subunits is
| [6] |
where is the indicator function. was calculated using the efficient Monte Carlo approach described in ref. 23. Similarly, in Fig. 7A, the cluster free energy was calculated as a function of the total number of subunits and the number of preformed dimers.
The melting temperature of an infinite lattice of scaffold strands with coordination number was estimated based on the mean of the 8-bp scaffold-strand hybridization free energies by solving the equation
| [7] |
Misbonding Calculations.
We used a two-state model (i.e., bonded or not bonded) to calculate the probability that a strand forms at least one misinteraction, assuming that no domains are correctly hybridized. We found the longest complementary subsequence for each pair of strands and that are not neighbors in the target structure and calculated the associated hybridization free energy, . [In cases where there are multiple complementary subsequences of the same length for a given pair of strands, we calculated the Boltzmann-weighted sum, .] We then computed the probability that a strand forms a misinteraction, ,
| [8] |
| [9] |
When computing the probability of scaffold-strand misbonding, the index represents a scaffold strand, while the index runs over all strands in the system. This approximate approach captures the competition between designed and incorrect bonding seen in the Monte Carlo simulations (Fig. 4C) remarkably well.
Supplementary Material
Acknowledgments
We thank Daan Frenkel for helpful discussions. This work was supported by the Engineering and Physical Sciences Research Council (Program Grant EP/I001352/1), the European Regional Development Fund (100185665), Fraunhofer Attract Funding (601683), and the National Institutes of Health (Grant F32GM116231).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. A.Z.P. is a guest editor invited by the Editorial Board.
Data deposition: Numerical data plotted in this paper’s figures and the underlying raw experimental data are deposited in the University of Cambridge Data Repository, https://www.data.cam.ac.uk/repository (doi: 10.17863/CAM.22991).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1806010115/-/DCSupplemental.
References
- 1.Whitelam S, Jack RL. The statistical mechanics of dynamic pathways to self-assembly. Annu Rev Phys Chem. 2015;66:143–163. doi: 10.1146/annurev-physchem-040214-121215. [DOI] [PubMed] [Google Scholar]
- 2.Frenkel D. Order through entropy. Nat Mater. 2015;14:9–12. doi: 10.1038/nmat4178. [DOI] [PubMed] [Google Scholar]
- 3.Zhang J, Sun Z, Yang B. Self-assembly of photonic crystals from polymer colloids. Curr Opin Colloid Interface Sci. 2009;14:103–114. [Google Scholar]
- 4.Sowade E, Blaudeck T, Baumann RR. Self-assembly of spherical colloidal photonic crystals inside inkjet-printed droplets. Cryst Growth Des. 2016;16:1017–1026. [Google Scholar]
- 5.Urgel JI, et al. Quasicrystallinity expressed in two-dimensional coordination networks. Nat Chem. 2016;8:657–662. doi: 10.1038/nchem.2507. [DOI] [PubMed] [Google Scholar]
- 6.Reinhardt A, Schreck JS, Romano F, Doye JPK. Self-assembly of two-dimensional binary quasicrystals: A possible route to a DNA quasicrystal. J Phys Condens Matter. 2017;29:014006. doi: 10.1088/0953-8984/29/1/014006. [DOI] [PubMed] [Google Scholar]
- 7.Damasceno PF, Glotzer SC, Engel M. Non-close-packed three-dimensional quasicrystals. J Phys Condens Matter. 2017;29:234005. doi: 10.1088/1361-648X/aa6cc1. [DOI] [PubMed] [Google Scholar]
- 8.Ke Y, Ong LL, Shih WM, Yin P. Three-dimensional structures self-assembled from DNA bricks. Science. 2012;338:1177–1183. doi: 10.1126/science.1227268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ong LL, et al. Programmable self-assembly of three-dimensional nanostructures from 10,000 unique components. Nature. 2017;552:72–77. doi: 10.1038/nature24648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jacobs WM, Frenkel D. Self-assembly of structures with addressable complexity. J Am Chem Soc. 2016;138:2457–2467. doi: 10.1021/jacs.5b11918. [DOI] [PubMed] [Google Scholar]
- 11.Cademartiri L, Bishop KJM. Programmable self-assembly. Nat Mater. 2015;14:2–9. doi: 10.1038/nmat4184. [DOI] [PubMed] [Google Scholar]
- 12.Schulman R, Winfree E. Programmable control of nucleation for algorithmic self-assembly. SIAM J Comput. 2010;39:1581–1616. [Google Scholar]
- 13.Zenk J, Schulman R. An assembly funnel makes biomolecular complex assembly efficient. PLoS One. 2014;9:e111233. doi: 10.1371/journal.pone.0111233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Reinhardt A, Frenkel D. Numerical evidence for nucleated self-assembly of DNA brick structures. Phys Rev Lett. 2014;112:238103. doi: 10.1103/PhysRevLett.112.238103. [DOI] [PubMed] [Google Scholar]
- 15.Zeravcic Z, Manoharan VN, Brenner MP. Size limits of self-assembled colloidal structures made using specific interactions. Proc Natl Acad Sci USA. 2014;111:15918–15923. doi: 10.1073/pnas.1411765111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Madge J, Miller MA. Design strategies for self-assembly of discrete targets. J Chem Phys. 2015;143:044905. doi: 10.1063/1.4927671. [DOI] [PubMed] [Google Scholar]
- 17.Madge J, Miller MA. Optimising minimal building blocks for addressable self-assembly. Soft Matter. 2017;13:7780–7792. doi: 10.1039/c7sm01646h. [DOI] [PubMed] [Google Scholar]
- 18.Reinhardt A, Ho CP, Frenkel D. Effects of co-ordination number on the nucleation behaviour in many-component self-assembly. Faraday Discuss. 2016;186:215–228. doi: 10.1039/c5fd00135h. [DOI] [PubMed] [Google Scholar]
- 19.Reinhardt A, Frenkel D. DNA brick self-assembly with an off-lattice potential. Soft Matter. 2016;12:6253–6260. doi: 10.1039/c6sm01031h. [DOI] [PubMed] [Google Scholar]
- 20.Wayment-Steele HK, Frenkel D, Reinhardt A. Investigating the role of boundary bricks in DNA brick self-assembly. Soft Matter. 2017;13:1670–1680. doi: 10.1039/c6sm02719a. [DOI] [PubMed] [Google Scholar]
- 21.Wales DJ. Atomic clusters with addressable complexity. J Chem Phys. 2017;146:054306. doi: 10.1063/1.4974838. [DOI] [PubMed] [Google Scholar]
- 22.Fonseca P, et al. Multi-scale coarse-graining for the study of assembly pathways in DNA-brick self-assembly. J Chem Phys. 2018;148:134910. doi: 10.1063/1.5019344. [DOI] [PubMed] [Google Scholar]
- 23.Jacobs WM, Reinhardt A, Frenkel D. Communication: Theoretical prediction of free-energy landscapes for complex self-assembly. J Chem Phys. 2015;142:021101. doi: 10.1063/1.4905670. [DOI] [PubMed] [Google Scholar]
- 24.Jacobs WM, Reinhardt A, Frenkel D. Rational design of self-assembly pathways for complex multicomponent structures. Proc Natl Acad Sci USA. 2015;112:6313–6318. doi: 10.1073/pnas.1502210112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jacobs WM, Frenkel D. Self-assembly protocol design for periodic multicomponent structures. Soft Matter. 2015;11:8930–8938. doi: 10.1039/c5sm01841b. [DOI] [PubMed] [Google Scholar]
- 26.Pinheiro AV, Nangreave J, Jiang S, Yan H, Liu Y. Steric crowding and the kinetics of DNA hybridization within a DNA nanostructure system. ACS Nano. 2012;6:5521–5530. doi: 10.1021/nn301448y. [DOI] [PubMed] [Google Scholar]
- 27.Sobczak JPJ, Martin TG, Gerling T, Dietz H. Rapid folding of DNA into nanoscale shapes at constant temperature. Science. 2012;338:1458–1461. doi: 10.1126/science.1229919. [DOI] [PubMed] [Google Scholar]
- 28.Majikes JM, Nash JA, LaBean TH. Search for effective chemical quenching to arrest molecular assembly and directly monitor DNA nanostructure formation. Nanoscale. 2017;9:1637–1644. doi: 10.1039/c6nr08433h. [DOI] [PubMed] [Google Scholar]
- 29.Song J, et al. Direct visualization of transient thermal response of a DNA origami. J Am Chem Soc. 2012;134:9844–9847. doi: 10.1021/ja3017939. [DOI] [PubMed] [Google Scholar]
- 30.Kato T, Goodman RP, Erben CM, Turberfield AJ, Namba K. High-resolution structural analysis of a DNA nanostructure by cryoEM. Nano Lett. 2009;9:2747–2750. doi: 10.1021/nl901265n. [DOI] [PubMed] [Google Scholar]
- 31.Myhrvold C, et al. Barcode extension for analysis and reconstruction of structures. Nat Commun. 2017;8:14698. doi: 10.1038/ncomms14698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wei X, Nangreave J, Jiang S, Yan H, Liu Y. Mapping the thermal behavior of DNA origami nanostructures. J Am Chem Soc. 2013;135:6165–6176. doi: 10.1021/ja4000728. [DOI] [PubMed] [Google Scholar]
- 33.Jiang S, Hong F, Hu H, Yan H, Liu Y. Understanding the elementary steps in DNA tile-based self-assembly. ACS Nano. 2017;11:9370–9381. doi: 10.1021/acsnano.7b04845. [DOI] [PubMed] [Google Scholar]
- 34.Wei X, Nangreave J, Liu Y. Uncovering the self-assembly of DNA nanostructures by thermodynamics and kinetics. Acc Chem Res. 2014;47:1861–1870. doi: 10.1021/ar5000665. [DOI] [PubMed] [Google Scholar]
- 35.Berne BJ, Pecora R. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics. Wiley; London: 1976. [Google Scholar]
- 36.Macfarlane RJ, et al. Nanoparticle superlattice engineering with DNA. Science. 2011;334:204–208. doi: 10.1126/science.1210493. [DOI] [PubMed] [Google Scholar]
- 37.Huang M, et al. Selective assemblies of giant tetrahedra via precisely controlled positional interactions. Science. 2015;348:424–428. doi: 10.1126/science.aaa2421. [DOI] [PubMed] [Google Scholar]
- 38.Lin H, et al. Clathrate colloidal crystals. Science. 2017;355:931–935. doi: 10.1126/science.aal3919. [DOI] [PubMed] [Google Scholar]
- 39.Bale JB, et al. Accurate design of megadalton-scale two-component icosahedral protein complexes. Science. 2016;353:389–394. doi: 10.1126/science.aaf8818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gerling T, Wagenbauer KF, Neuner AM, Dietz H. Dynamic DNA devices and assemblies formed by shape-complementary, non-base pairing 3D components. Science. 2015;347:1446–1452. doi: 10.1126/science.aaa5372. [DOI] [PubMed] [Google Scholar]
- 41.Liu W, et al. Diamond family of nanoparticle superlattices. Science. 2016;351:582–586. doi: 10.1126/science.aad2080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang Y, et al. Colloids with valence and specific directional bonding. Nature. 2012;491:51–55. doi: 10.1038/nature11564. [DOI] [PubMed] [Google Scholar]
- 43.Mitov MI, Greaser ML, Campbell KS. GelBandFitter–A computer program for analysis of closely spaced electrophoretic and immunoblotted bands. Electrophoresis. 2009;30:848–851. doi: 10.1002/elps.200800583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zipper H, Brunner H, Bernhagen J, Vitzthum F. Investigations on DNA intercalation and surface binding by SYBR Green I, its structure determination and methodological implications. Nucleic Acids Res. 2004;32:e103. doi: 10.1093/nar/gnh101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hansen S. DLSanalysis.org: A web interface for analysis of dynamic light scattering data. Eur Biophys J. 2018;47:179–184. doi: 10.1007/s00249-017-1232-8. [DOI] [PubMed] [Google Scholar]
- 46.Teraoka I. Polymer Solutions: An Introduction to Physical Properties. Wiley; New York: 2002. [Google Scholar]
- 47.Chi Q, Wang G, Jiang J. The persistence length and length per base of single-stranded DNA obtained from fluorescence correlation spectroscopy measurements using mean field theory. Physica A. 2013;392:1072–1079. [Google Scholar]
- 48.García de la Torre J, Bloomfield VA. Hydrodynamic properties of complex, rigid, biological macromolecules: Theory and applications. Q Rev Biophys. 1981;14:81–139. doi: 10.1017/s0033583500002080. [DOI] [PubMed] [Google Scholar]
- 49.Fischer S, et al. Shape and interhelical spacing of DNA origami nanostructures studied by small-angle X-ray scattering. Nano Lett. 2016;16:4282–4287. doi: 10.1021/acs.nanolett.6b01335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Nečas D, Klapetek P. Gwyddion: An open-source software for SPM data analysis. Cent Eur J Phys. 2012;10:181–188. [Google Scholar]
- 51.SantaLucia J, Jr, Hicks D. The thermodynamics of DNA structural motifs. Annu Rev Biophys Biomol Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 52.Koehler RT, Peyret N. Thermodynamic properties of DNA sequences: Characteristic values for the human genome. Bioinformatics. 2005;21:3333–3339. doi: 10.1093/bioinformatics/bti530. [DOI] [PubMed] [Google Scholar]
- 53.Kirkwood JG. The general theory of irreversible processes in solutions of macromolecules. J Polym Sci. 1954;12:1–14. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.