Significance
Here we show a unique, natural method for microscale jetting of fluid made possible by the tuning of material properties from which the jets emanate. The composite, layered construction of the citrus exocarp allows for the buildup of fluid pressure in citrus oil gland reservoirs and their subsequent explosive rupture. Citrus jetting has not been documented in literature, and its purpose is unknown. This method for microscale fluid dispersal requires no auxiliary equipment and may open avenues for new methods of medicine and chemical delivery. We show how jet kinematics are related to substrate properties and reservoir shape.
Keywords: natural fluid dispersal, biomaterial failure, pressure-vessel rupture, Newtonian jet instability, droplet velocity
Abstract
The rupture of oil gland reservoirs housed near the outer surface of the citrus exocarp is a common experience to the discerning citrus consumer and bartenders the world over. These reservoirs often rupture outwardly in response to bending the peel, which compresses the soft material surrounding the reservoirs, the albedo, increasing fluid pressure in the reservoir. Ultimately, fluid pressure exceeds the failure strength of the outermost membrane, the flavedo. The ensuing high-velocity discharge of oil and exhaustive emptying of oil gland reservoirs creates a method for jetting small quantities of the aromatic oil. We compare this jetting behavior across five citrus hybrids through high-speed videography. The jetting oil undergoes an extreme acceleration to reach velocities in excess of 10 m/s. Through material characterization and finite element simulations, we rationalize the combination of tuned material properties and geometries enabling the internal reservoir pressures that produce explosive dispersal, finding the composite structure of the citrus peel is critical for microjet production.
Liquid microjets have been of interest to the engineering community for their use in inkjet printers (1, 2), drug delivery (3, 4), microfabrication (5, 6), and chemical synthesis (7). Microjet technologies have been made possible by careful control of piezoelectric drivers, microfabrication of precision nozzles, and tuned fluid properties (8–10). It is critical to control the breakup distance of these jets so the drops they produce find the intended location. Technologies that produce microjets require precision-machined parts, pumps, and electronic controls, which carry a large cost and complexity.
While studies of synthetic microjet production and use abound, few studies have considered microjets in nature, which may provide alternative methods for robust jet production through the clever choice of material and geometry and without cumbersome supporting systems. Examples of microjets in nature include spitting termites of the subfamily Nasutitermitinae, which spit a viscous salivary toxin in defense of invertebrate attackers (11, 12), and spitting spiders, Scytodes thoracica, emit venomous silk from vibrating fangs to snare prey (13). Outside the realm of arthropods, jetting in nature is commonplace and includes urination in mammals (14), spitting of venomous snakes (15), and squirting cucumbers (16), but these examples do not approach the microscale.
More common to the human experience is the peeling of a citrus fruit, which produces a strong citrus aroma and wet fingers. Upon careful observation, the peeler can witness ephemeral atomization of oils contained in the peel. A widespread technique for giving flavor and aroma to cocktails is the inclusion of a twisted orange peel. Twisting the peel releases the oils beneath the flavedo accenting the beverage. Despite its commonality, the mechanics of fluid projection have not been previously studied.
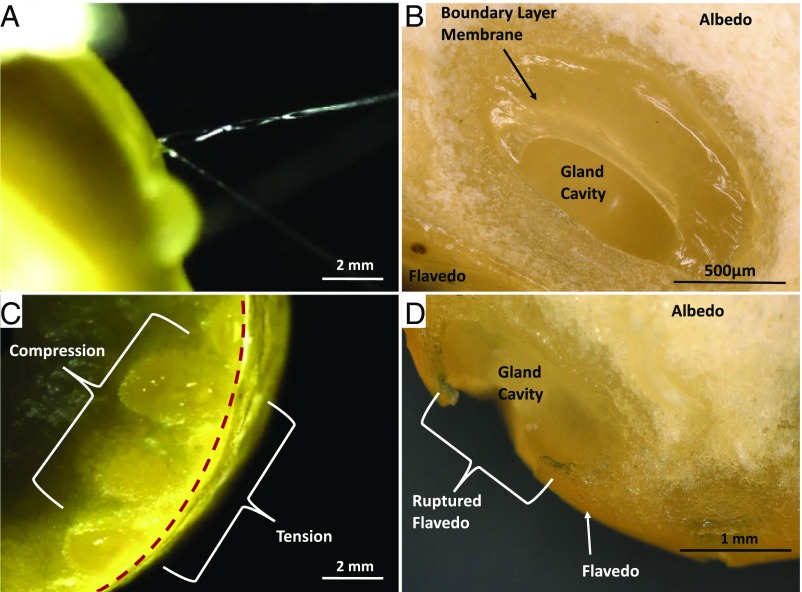
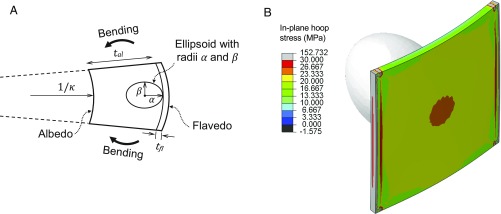
In this study, we show that in response to external bending deformation, oil gland reservoirs housed underneath the outer surface of citrus exocarps may rupture, producing high-speed microjets, by an exhaustive emptying of the fruit’s aromatic volatile oil, as seen in Fig. 1. These free jets are best witnessed after a fruit is peeled and by bending the peel such that the flavedo, or rind, faces outward (Figs. 1 and 2A). Oil reservoirs reside in the mesocarp, or albedo, a compressible foam-like layer commonly known as the “pith” that fills the space between the fruit locules and the thinner, stiffer flavedo (17). The flavedo caps the reservoirs and shields the fruit from the environment. Gland placement within the peel and relative size can be seen in Fig. 2 B and C. The spaces between glands house stomata, the fruits’ gas exchange pores (18) that measure 20 m in diameter. A layer of glossy boundary cells separates the oil in the reservoirs from the absorbent albedo and is clearly seen in Fig. 2B (19), where the window into the reservoir is a fortuitous result of cutting. Ruptured reservoirs result from pressurizing the oil through externally applied forces. When its failure stress is reached, the flavedo cracks, allowing the pressurized oil to escape and the albedo to expand into the vacated space, deforming the reservoir, as seen in Fig. 2D.
Fig. 1.
Image of oil jets issuing from subsurface oil glands in the highly bent peel of a navel orange. The highly unstable jets issue at velocities that produce motion blur in the photo, giving the appearance of jet stability over longer distances.
Fig. 2.
Microscopic images of (A) oil ejection from oil gland reservoir through the flavedo, (B) a cross-sectional view of a singular oil gland with boundary layer membrane partially intact, (C) a group of unbroken oil glands subjected to external bending, and (D) a cross-sectional view of an oil gland after rupture. The gland in D appears slightly collapsed due to ingress of the albedo toward the flavedo during rupture.
It is believed all fruits in the citrus family have been developed by cross-breeding three core fruits in the last 1,000 y: the mandarin orange, pummelo, and citron (20). All citrus fruits tested in this study exhibited oil-jetting behavior, but despite this shared characteristic, there remains no determinate evolutionary function of the oil and no mention of oil atomization in the literature to the authors’ knowledge. The volatile oils may be an attractant to pollinators (21) but are toxic to many arthropods (22–24). Citrus oils are known to be phytotoxic (25) and antimicrobial (26) and so potentially able to protect the fruit and seeds from infection and select predation. Citrus fruits experiencing blunt impact often suffer internal reservoir rupture leading to spoiled fruit as adjacent cells burst in contact with oil (27). Commercially, citrus oils are extracted for their aroma (28), flavoring food (29), and cleaning products (30).
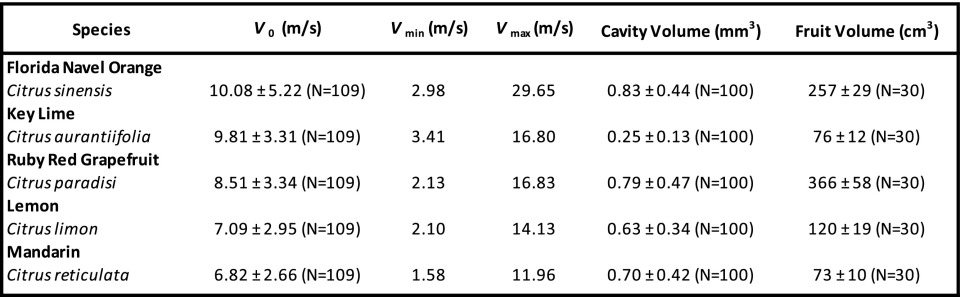
We hypothesize citrus fruit jetting is made possible by the composite peel structure housing the oil reservoirs—namely, a soft reservoir boundary capped by a stiffer film. To test this hypothesis, we purchase, peel, squeeze, and film the jetting of oil from five Citrus (C) species readily available in most markets (Movie S1). These species, listed in Table 1, have a range of sizes and show large variability in bulk fruit and reservoir volume within a species. We find no dependence of reservoir volume with fruit volume (SI Appendix, Fig. S1). Although comparative experiments are performed, we focus much of our effort on one fruit, the Florida navel orange, Citrus sinensis. We buy cold-pressed, commercially available orange oil for rheological measurement and find it has a density g/mL (n = 10), dynamic viscosity cP (n = 12), and surface tension dynes/cm (n = 5).
Table 1.
Citrus hybrid species used in this study and associated measurements. Velocity measurements were taken within the first 2 wk of purchase
 |
In this study, we investigate the jetting mechanism exhibited by Citrus fruits to rapidly disperse essential oils. Examples of these citrus jets can be seen in Fig. 1 and Movie S1. We begin Results with a description of the jets including kinematics and size and proceed by calculating the approximate pressures driving the jet from analytical modeling approaches. Next, we investigate the material properties of the exocarp and show that the contrasting nature of materials comprising the exocarp is critical for high-speed jet production. Experimentally garnered material properties are used in a finite element (FE) model to verify the analytical approaches and explore material property impact on bursting pressure. Lastly, in Discussion, we discuss the implications of our work.
Results
Rupture Process.
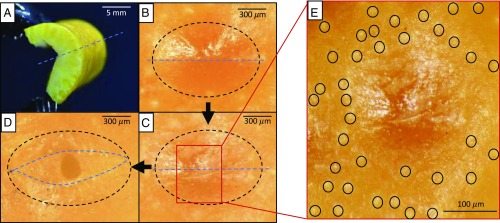
The process leading to reservoir rupture begins by establishing a strain gradient through a cross-section of a citrus peel, as seen in Fig. 2C. Physically, the gradient is established by bending a section of peel through a large angle of deflection, as seen with the Florida navel orange in Fig. 3A and Movie S2. Bending increases stresses in the flavedo, with the most perceptible increase in the direction normal to the dashed blue line drawn in Fig. 3 A–D. The surface of a gland, as seen looking down onto a flavedo, can be seen in Fig. 3 B–D and outlined by a dashed black ellipse. As the magnitude of bending increases, a failure precursor wrinkle forms on the flavedo surface atop the oil reservoir, as seen in Fig. 3 C and E. Further bending induces the failure seen in Fig. 3D, unveiling a channel to the gland reservoir. A higher resolution photograph of flavedo failure at jetting can be found in SI Appendix, Fig. S2. The crack in Fig. 3D begins atop the reservoir and is arrested by stomata surrounding the gland. Stomata are outlined in Fig. 3E and are small, nearly circular voids in the flavedo.
Fig. 3.
The process of glandular rupture. The process begins with bending a peel (A). From an external view of the flavedo, the unstressed gland in B is stressed to eminent failure in C and to failure in D, which shows the channel leading to the oil reservoir. A zoom box of a crack forming prior to failure is shown in E. Black dashes outline gland extents beneath the flavedo, and the blue dashed lines represent the line normal to externally applied stress.
Citrus Jet Kinematics.
Through high-speed videography at fps, we film and track microjet expulsion from the five species of citrus hybrids listed in Table 1. Jets were produced by squeezing the exocarp of peeled fruits with fixed pliers. The sequence of jetting lasts about 0.5 s, where some jets finish before others begin. Digital tracking and measurement allows for characterization of initial jet velocity, temporal velocity decay of ejected jet fronts, and diameters of intact and broken jets.
We measure jet exit velocities across all hybrids within 2 wk of purchase, finding a singular minimum of 1.58 m/s (mandarin) and singular maximum of 29.65 m/s (orange), with an average m/s (n = 545) across all species. The average, SD, minimum, and maximum for each hybrid is presented in Table 1. We find average for a citrus species to be independent of reservoir and total fruit volume (SI Appendix, Fig. S1).
Florida navel oranges serve as the model organism to characterize jetting kinematics because of their attainability. A typical jetting event by a navel orange is seen in Fig. 1. Jet diameters are measured to be m (n = 10), using three individual oranges. We note that diameter measurements were taken as if jets had circular cross-sections, which is a simplification, as discussed in SI Appendix. These measured jets have a corresponding range of , indicating laminar flow.
Following emergence from a reservoir at , jets rapidly break up into streams of droplets, losing all streamline velocity in less than 100 ms. We discuss jet instability in SI Appendix. The temporal decay of for a spherical droplet neglecting body forces can be expressed (31) as
| [1] |
where is the droplet mass, is the droplet diameter, cP is the dynamic viscosity of air, and is the drag factor. Clift and Gauvin (32) provide an expression for valid for subcritical , where kg/m3 is the density of air.
| [2] |
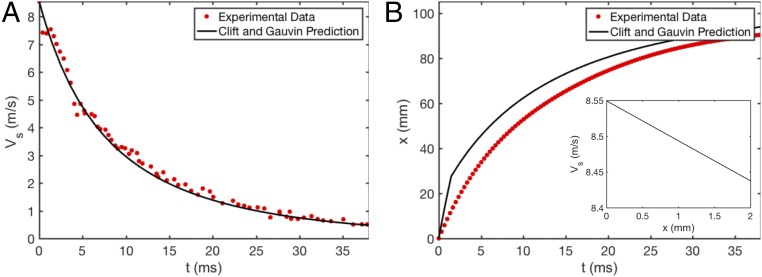
Integration of Eq. 1 produces a curve for that captures the deceleration of droplets, as seen in Fig. 4A. Matching this model to experimental data are highly sensitive to the measurement of , which is difficult at this scale and velocity; pixelation, image blur, and glare artifacts disrupt droplet outline clarity. For the droplet tracked in Fig. 4 A and B, we measure a droplet on-screen to have m, whereas the model suggests the droplet has m. More generally, we measure orange jet droplets to have an average diameter m (n = 50). Additional sources of model departure may include droplet elongation while in flight and nonuniform shape as the droplets oscillate after breakup. We predict droplet evaporation does not significantly impact droplet kinematics. From a quiescent pool, we measure the evaporative flux of oil to be mgmincm2 (n = 5, 74○F, 52% relative humidity). While moving droplets will evaporate more quickly, an evaporative flux 10× that measured for a quiescent pool yields a droplet volume change of for a 100 m diameter droplet over a 100 ms flight.
Fig. 4.
Temporal tracks of (A) droplet velocity and (B) position show droplet deceleration is rapid after expulsion from the gland.
The model of temporal velocity decay in Eq. 1 also provides insight into the change in jet size due to deceleration preceding breakup. While it is not possible to discern the exact breakup distance for these small jets, we do observe discrete droplets 2 mm from the flavedo surface (Movie S3). In Fig. 4B, Inset, we plot the predicted velocity of a jet over the short distance relevant to breakup. Over 2 mm from emergence, the jet with m/s loses 1% of its initial velocity, translating into an increase of diameter near 1 m.
Jet velocities will deviate from those observed when jets fire out of the plane of observation of the camera. This deviation is quantifiable such that the actual velocity , where is the angle of deviation from the viewing plane. We average five frames to quantify but combat error in velocity measurements by constraining tracking to jets that remain in focus for at least 40 frames (10 ms) for the focal depth of our lens mm. A jet with m/s will have an average velocity m/s over the time of interest ms according to Eqs. 1 and 2 and could have a maximum velocity measurement deviation , where . For m/s, . The slowest recorded jet is at m/s, .
Bursting Pressure.
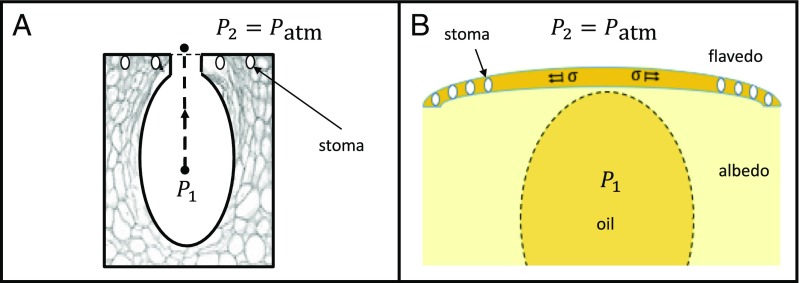
We assume changes in pressure within the reservoir are negligible from the instant of flavedo rupture to the emergence of fluid into the atmosphere, which occurs over a period not observable with our camera at 16,000 fps, less than 63 s. We consider a streamline from the gland reservoir center to the exocarp orifice, as seen in Fig. 5A. The differential pressure between points 1 and 2 along the streamline can be expressed by a balance of static and dynamic pressures, neglecting body forces,
| [3] |
where is atmospheric pressure, is oil velocity at rest in the reservoir, is the oil velocity at bursting, and is the excess pressure drop—namely, the viscous loss imposed by flow constriction through a microscale orifice. Hasegawa et al. (33) provided experimental data for pressure drop through orifices of comparable size and for . We infer that at , which is independent of orifice geometry at that scale. From Eq. 3 we calculate a gauge pressure for reservoir bursting kPa psi, for m/s, as measured 1 d after purchase.
Fig. 5.
Schematics of oil gland reservoirs corresponding to two methods for calculating internal bursting pressure: (A) total pressure of flowing oil and (B) hoop stress.
By measuring material properties of the flavedo, we may alternatively estimate from the hoop stress, which predicts the static fluid pressure at the moment of bursting without considering fluid flow,
| [4] |
where is the critical stress to propagate a material flaw dictated by Griffith’s theory (34), is flavedo thickness, and is the radius of curvature of the flavedo cap at rupture. We find m (n = 10) for navel orange flavedos and measure the radius curvature mm upon bulk jetting inception, as seen in Fig. 5B. Using tensile test data, we determine a range of critical stresses MPa (n = 3) for oranges tested 1 d following purchase. Further discussion of the material properties of peels and the use of Griffith’s theory is given in Relation of Jet Velocity to Flavedo Failure, and validation of hoop stress assumptions is given in Exocarp Bending Simulation. The range in values of , , and yields kPa psi, which is in reasonable agreement with the value of predicted by Eq. 3. Due to this agreement, we infer the hoop stress in the flavedo is very close to the hoop stress in the wall of the reservoir—the flavedo is extremely thin. We are unable to measure hoop stress in the reservoir walls directly due to inability to measure in the boundary layer membrane (Fig. 2B).
Relation of Jet Velocity to Flavedo Failure.
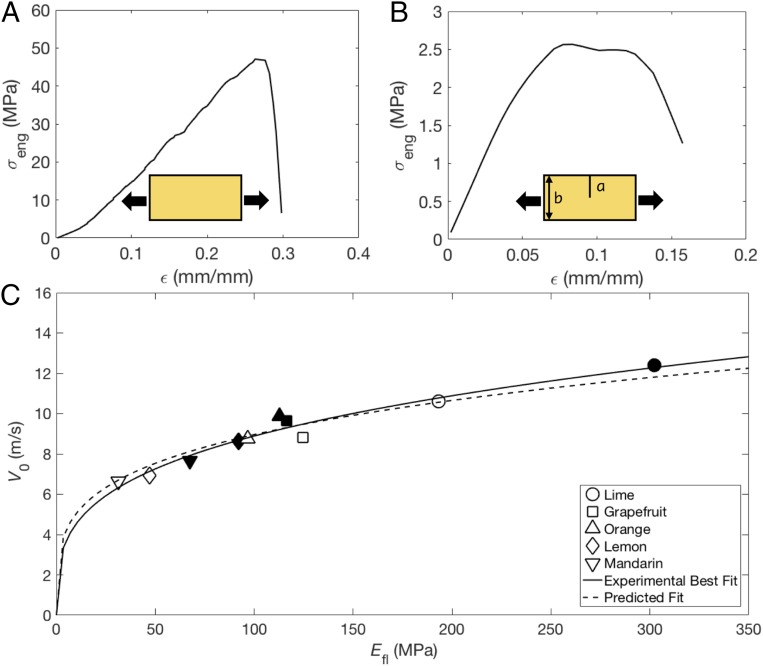
We hypothesize that high-speed jetting requires a soft, compressible base layer and a stronger, stiffer external covering that withstands the buildup of fluid pressure in the reservoir and fails abruptly. To test our hypothesis, we seek a relation between jetting velocity and flavedo stiffness, . We begin by mechanically separating flavedo from albedo to perform independent tensile tests, in contrast to previous studies that considered material properties of an intact peel (35, 36). We find the albedo layer, averaging kPa across all test species, two orders of magnitude less stiff than the flavedo layer, whose average stiffness at small strain ranges from MPa, reported in Table 2 and Fig. 6 for each species. A typical stress–strain curve for an orange flavedo is seen in Fig. 6A and shows failure at engineering stress MPa at large engineering strain . On average, orange flavedos exhibited MPa for those tested 1 and 8 d following purchase and experienced complete failure around MPa, which is comparable to the strength of acrylonitrile butadiene styrene (ABS).
Table 2.
Stiffness and velocity values for all species tested at various times past purchase
 |
Fig. 6.
Material characterization in citrus flavedo. (A) Stress–strain curve for determining flavedo stiffness in an orange, with schematic of test specimen shown in Inset. (B) Stress–strain curve for crack propagation stress , with schematic of test specimen shown in Inset. (C) The relation between jet exit velocity (n = 9 for each point) and (n = 5 for each point) for fruits measured 1 d (filled symbols) and 8 d (open symbols) after purchase to quantify the effects of ripeness on jetting velocities and flavedo properties.
In Rupture Process, we describe that cracks in the flavedo begin atop the reservoir and are arrested by stomata surrounding the gland. Over the region of interest, the 100 m opening through which a jet emanates (Fig. 3D), failure of the flavedo resembles the propagation of a flaw under remote tensile stress. Based on the flavedo’s response under tension, as seen in Fig. 6 A and B, we treat the flavedo as linearly elastic just before failure and apply Griffith’s theory (37–39) to form a scaling relation between flavedo stiffness and fluid jet velocity.
Before presentation of the scaling model derived from Griffith’s theory, we address the impact of curvature on the validity of its use. Curvature induces coupling between bending and extension, which can result in deviation from the ideal flat material geometries used in traditional Griffith theory (40). However, for curved sheets with low radii of curvature, deviation from ideal behavior is negligible. Folias (1970) (40) derived a scaling law to compare the ratio of near crack tip stresses in curved and flat sheets, and , respectively. The ratio is for , where , m is half the flaw length, and is the sheet thickness. We set Poisson’s ratio as done by previous works (41, 42) on comparable materials. When applied to citrus flavedos, we find , indicating little influence of curvature on elastic behavior. Our use of as the length of the material flaw from which flavedo cracks begin is discussed in Exocarp Bending Simulation.
Griffith’s (37–39) theory predicts the critical stress needed to propagate a material flaw in the flavedo and is expressed as
| [5] |
We address the variables in Eq. 5 as dependent or independent of .
The strain energy release rate is related to fracture toughness and elastic modulus as (39)
| [6] |
where
| [7] |
is the stress intensity factor (39), accurate to within 0.5% for any . The value of across the range of fruits used in the study is found by performing tensile fracture tests on peel samples measuring 20 mm × 45 mm with precut “cracks” of length , where is the width of the test sample (Fig. 6B, Inset). A typical stress–strain curve for crack propagation tensile tests is shown in Fig. 6B. We note the critical stress MPa occurs at a moderate strain and is much less than the failure stress witnessed for uncut tensile samples. For oranges, MPa (n = 3), which dictates the value of and, according to Eq. 3 is related to . From Eqs. 6 and 7 we find kPam across all species and find no clear trend between and (SI Appendix, Fig. S3). We thus fix as constant for our scaling argument.
We consider characteristic flaw length in unbroken peels to be the size of the jet opening and is fixed as constant for all species for our analysis. Therefore, from Eq. 5 the scaling relation may be written, , and from Eq. 3, we find . For the problem at hand, remains constant and is omitted from subsequent scaling relations. Likewise, we see no trend in from one fruit to another but find it is dependent on albedo thickness , which is highly variable from one specimen to another and across individual fruits. We discuss the impact of variation in in Discussion. Accordingly, Eq. 4 provides the relation . Combining these relations yields the prediction
| [8] |
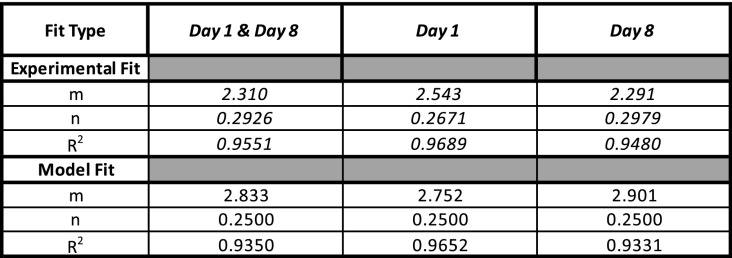
We plot against , in Fig. 6, and report the associated values in Table 2. The effect of fruit aging is quantified by testing subsets of individual fruit specimens on 1, 8, and 15 d following purchase, such that these fruits produce both tensile test samples and velocity measurements. Data for days 1 and 8 are plotted in Fig. 6, while data for day 15 are plotted only in SI Appendix, Fig. S4C; signs of rot and excessive levels of material degradation are present 2 wk after purchase. We fit Eq. 8 to the combined data with .
A power law best fit of the combined day 1 and 8 data yields
| [9] |
Thus, among these species, we observe a clear dependency of jet velocity on flavedo stiffness. Generally, the flavedos stiffen and jets attain higher velocities with age. It is noteworthy that the predicted exponent (0.25) is within the 95% confidence intervals of our experimental best fit (0.29), indicating excellent agreement between the predicted exponent and the measured one. We attribute this small discrepancy, which scales as , to simplifications in our model, most likely regarding variation in peel properties across species and some nonlinear effects, discussed in Discussion. We report prefactors, exponents, and coefficients of determination for the aforementioned fits of the form in Table 3. Days 1, 8, and 15 are all fit with Eqs. 8 and 9 separately in SI Appendix, Fig. S4 and include SD bounds.
Table 3.
Fitting parameter data corresponding to the curves in Fig. 6 and SI Appendix, Fig. S4 of the form
 |
Exocarp Bending Simulation.
A notable material property contrast between albedo and flavedo layers is elastic modulus. FE simulations allow us to test a range of moduli and reservoir geometry to determine their impact on . Additionally, FE modeling provides a view of the pressure distribution in the volume surrounding the reservoirs and across the flavedo surface. We model a unit of peel comprised of mm-thick albedo containing a single oil gland reservoir covered by m of flavedo, as seen in Fig. 7. We assume the entire peel geometry can be reconstructed by tessellating this representative volume element (RVE). The remote bending load on the peel (Fig. 3A) is transferred to the RVE by rotations on either side of the unit cell as denoted in Fig. 7A. Oil in the reservoir is modeled as static, incompressible, and not subject to body forces. The reservoir geometry is made to mimic that observed in peel cross-sections, an ellipsoid with longitudinal radius and transverse radius . Ratios are chosen such that the volume of the reservoirs remain a constant 1 mm3.
Fig. 7.
Finite element simulations are performed by considering (A) a unit cell undergoing rotation at the boundaries, which show (B) in-plane hoop stress to be approximately uniform in tension with a local maximum at the center. This region of greater stress is most likely to fail first, which is supported by experiments. The white ellipsoid is the gland beneath the flavedo.
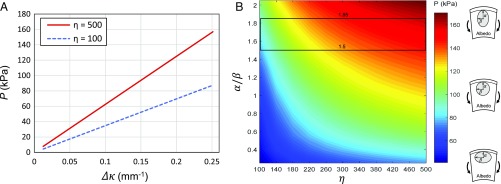
We set the values of and according to ranges in experimental data and fix Poisson’s ratio at 0.49 and 0.25, respectively, as done by previous works (41, 42) on analogous materials. For all simulated moduli and fluctuations in peel bending curvature , in-plane hoop stress contours across the flavedo indicate higher stress atop the oil reservoir, shown in Fig. 7B, supporting the previous calculation of by a hoop stress model in Eq. 4 and our choice of . Here, corresponds to a round and unperturbed fruit with mm. We plot oil gland reservoir pressure as a function of bending severity, as is increased from mm−1, as seen in Fig. 8A. The dotted lines show increasing for greater curvature using range of material stiffness ratio (dashed line) and 500 (solid line) and . Greater discrepancies in stiffness produce greater reservoir pressures. Pressures in the range of kPa are in good agreement with the estimate for fluid pressure given by Eq. 3, 111 kPa, and the range predicted by Eq. 4, kPa.
Fig. 8.
Pressure in oil gland reservoir simulated by varying (A) change in curvature for fixed and (B) gland eccentricity and material stiffness ratio . The box in B bounds experimental values of .
By fixing (mm−1), a highly bent peel, we can perform a parametric FE simulation to understand the influence of reservoir shape () and on . The phase plot in Fig. 8B shows that for , remains low, even for large values of . Pressures are highest for vertically lobed reservoirs, such that . Like Fig. 8A, the plot in Fig. 8B shows that contrasting flavedo and albedo stiffness is likewise critical to the generation of high fluid pressure and will elevate fluid pressure when is slightly adverse. Experimentally observed ranges for are bounded by the black box in Fig. 8B.
Discussion
Our study elucidates the mechanisms underlying the high-speed microjets emitted from the exocarps of citrus fruit. The velocity of these jets is a result of quickly releasing internal oil gland reservoir gauge pressures in the approximate range of kPa. The buildup and release of pressure is made possible by the composite nature of the citrus peel—namely, a thick, compressible albedo that houses reservoirs and is capped by a thin, stiff flavedo. In general, fruit aging causes flavedo modulus to increase and produce greater jetting velocities. A greater understanding of this system may lead to technologies that mimic the bursting of oil reservoirs to disperse or aerosolize small amounts of fluid and new tools to characterize fruit.
The choice of applying Griffith’s criteria in Relation of Jet Velocity to Flavedo Failure requires simplifying assumptions. Using uniaxial tensile test data, we find the flavedo is a nonlinear, stiffening material before failure, with a small strain elastic modulus, MPa. While this is contrary to Griffith’s theory of fracture (37–39), the flavedo does not exhibit pronounced ductile behavior. The reason for brittle behavior following stiffening is unclear but could be a result of little resistance to crack growth (flat R-curve) (34) offered by loosely held polymeric chains. This justifies the use of a single fracture toughness parameter for the current study. In recent past, a computational study using atomistic simulations captured strain-stiffening and hyperelastic behavior on crack propagation, and found significant influence of hyperelastic behavior on the crack tip dynamics, but the fundamental scaling law that we have used, , was found to be valid (43). For hyperelastic strain-stiffening materials (such as neo-Hookean or exponential hardening), recent work (44) has shown that energy release rate remains very close to linear elastic fracture mechanics (LEFM) values for moderate values of and moderate stress tri-axiality. According to Fig. 6C, the fruits most critical to curve fitting lie the furthest from the origin. And so for limes, . The authors (44) found the agreement even better if the stiffening is exponential in nature. We are thus justified in basing our scaling analysis on LEFM in this study.
This study highlights that citrus jet velocity is a function of flavedos’ fracture toughness, most clearly demonstrated by Eq. 4. Therefore, peeling citrus does not require careful extraction of the albedo, nor does natural variation in albedo thickness across the fruit impact local jet velocities. However, the curvature of the peel during jetting is strongly dependent on albedo girth. The line in Fig. 8A will decrease in slope with decreasing albedo thickness, therefore requiring higher values of to achieve a critical bursting pressure.
The size of citrus oil reservoirs and the velocity of oil ejection result in large accelerations by jetting fluid. Liquid at rest in the pockets is accelerated to velocities in excess of 10 m/s over the distance of 1 mm. Assuming the fluid is incompressible and acceleration is constant, parcels of fluid in the reservoir will experience 5,100 gravities () of acceleration before exit, which is comparable to the acceleration of a bullet leaving a rifle. In nature, this acceleration is outdone only be the mantis shrimp (45) (Stomatopoda) at over 10,000 and Dung Cannon fungus (46) (Pilobolus crystallinus) at 180,000 but is perhaps unmatched in the plant kingdom. A notable contender in the plant kingdom is the bunchberry dogwood flower, which launches stamen at 2,400 as pedals open at 2,200 (47).
Our results and FE investigations predict reservoir fluid pressures in agreement with Eqs. 3 and 4, but it would appear citrus fruits achieve suboptimal configuration from the standpoint of achieving even higher pressures by not maximizing . However, note that the top right corner of the phase plot would represent much stiffer flavedos. This material synthesis is likely limited due to the biological origin of the material. Therefore, the system leverages reservoir geometry for enhanced performance (high ), indicating the observed values of . Such is a recurring theme in many biological systems where the limitations of material properties are overcome by geometry or topology of the structure (48–60). In contrast, an outer layer with very low strength would not withstand the stresses associated with pressure rise in the small reservoirs and would thus rupture at lower pressures and produce slower yet more stable jets.
Methods
High-Speed Image Analysis and Microscopy.
All Citrus fruits used in experiments were obtained from local groceries. Once peeled, specimens were used within 15 min to preserve material properties. Oil jets were filmed with Photron Mini UX100 and AX100 cameras at 4,000 to 16,000 fps, depending on the scale and phenomenon of interest. Jets were initiated by placing peels between stationary pliers. Jet velocity, diameter, and breakup distance were measured digitally using Open Source Physics Tracker software. Pores from which jets issue were imaged pre- and postjetting with a Keyence VHX-900 digital microscope with built-in area and dimension measurement capability.
Material Property Measurements.
Tensile testing is performed with a MTS Tytron 250, using a 50 N load cell, and pulled at a rate of 0.3 mm/s. We prepare tensile test samples by mechanically separating flavedo and albedo with a sharp blade immediately after peeling. Samples of flavedo and albedo are cut into rectangular sections 12 mm (polar) × 25 mm (equitorial). Flavedo samples to measure strain energy release rate are cut into rectangular sections 25 mm (polar) × 50 mm (equitorial) and given a mm manufactured flaw in the form of a thin cut orthogonal to the direction of applied loading. Such flaws lie within of the width of the sample.
FE Simulations.
To simulate the bending of a citrus peel and measure the pressure field surrounding an oil reservoir, we perform an analysis with ABAQUS (Dassault Systèmes) general static step, using an RVE with rotational boundary conditions at the side walls. To avoid rigid body motion, we fix one node of this unit cell on the middle symmetric plane and mesh with quadratic tetrahedron elements (C3D10) around reservoir geometry and quadratic hexagonal elements (C3D20) in other regions. A linear elastic material model was used for all simulations, and gland fluid was modeled as incompressible.
Oil Gland Reservoir and Fruit Volume Measurements.
We image orange peel cross-sections with a Nikon D850 SLR camera and digitally trace the outer boundaries of gland reservoirs in images. We assume reservoirs are symmetric about the jetting axis and use MATLAB to perform shell integration volume calculations for the coordinates of reservoir boundaries captured in photos. Whole fruit volume measurements were taken by recording the fluid displaced during complete submersion.
Supplementary Material
Acknowledgments
We thank Dr. David Hu of Georgia Tech for the initial idea to explore citrus jets; undergraduate researchers Alex Olvera, Richard Galasso, Yva Luc, and Nicolas Gonzalez for experimental contributions; Dr. Quan-Fang Chen for access to his laboratory MTS Tytron 250; and the University of Central Florida for the funding of this research.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1720809115/-/DCSupplemental.
References
- 1.Furlani E. Temporal instability of viscous liquid microjets with spatially varying surface tension. J Phys A Math Gen. 2004;38:263–276. [Google Scholar]
- 2.Furlani EP, Price BG, Hawkins G, Lopez AG. 2006 Thermally induced marangoni instability of liquid microjets with application to continuous inkjet printing. Proceedings NSTI Nanotechnology Conference. Available at https://nsti.org/publications/Nanotech/2006/pdf/802.pdf. Accessed July 16, 2017.
- 3.Menezes V, Kumar S, Takayama K. Shock wave driven liquid microjets for drug delivery. J Appl Phys. 2009;106:086102. [Google Scholar]
- 4.Tagawa Y, Oudalov N, El Ghalbzouri A, Sun C, Lohse D. Needle-free injection into skin and soft matter with highly focused microjets. Lab Chip. 2013;13:1357–1363. doi: 10.1039/c2lc41204g. [DOI] [PubMed] [Google Scholar]
- 5.Carter JC, et al. Fabricating optical fiber imaging sensors using inkjet printing technology: A ph sensor proof-of-concept. Biosens Bioelectron. 2006;21:1359–1364. doi: 10.1016/j.bios.2005.06.006. [DOI] [PubMed] [Google Scholar]
- 6.MacFarlane D, et al. Microjet fabrication of microlens arrays. IEEE Photonics Technol Lett. 1994;6:1112–1114. [Google Scholar]
- 7.Zhang Y-P, Lee S-H, Reddy KR, Gopalan AI, Lee K-P. Synthesis and characterization of core-shell SiO2 nanoparticles/poly (3-aminophenylboronic acid) composites. J Appl Polym Sci. 2007;104:2743–2750. [Google Scholar]
- 8.Arora A, et al. Needle-free delivery of macromolecules across the skin by nanoliter-volume pulsed microjets. Proc Natl Acad Sci USA. 2007;104:4255–4260. doi: 10.1073/pnas.0700182104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yuan S, Zhou Z, Wang G. Experimental research on piezoelectric array microjet. Sens Actuators A. 2003;108:182–186. [Google Scholar]
- 10.Yuan S, Zhou Z, Wang G, Liu C. MEMS-based piezoelectric array microjet. Microelectron Eng. 2003;66:767–772. [Google Scholar]
- 11.Prestwich G. Defense mechanisms of termites. Annu Rev Entomol. 1984;29:201–232. [Google Scholar]
- 12.de Mello AP, Azevedo NR, da Silva AMB, Gusmão MAB. Chemical composition and variability of the defensive secretion in nasutitermes corniger (Motschulsky, 1885) in urban area in the Brazilian semiarid region. Entomotropica. 2016;31:82–90. [Google Scholar]
- 13.Suter R, Stratton G. Predation by spitting spiders: Elaborate venom gland, intricate delivery system. In: Nentwig W, editor. Spider Ecophysiology. Springer; Heidelberg: 2013. pp. 241–251. [Google Scholar]
- 14.Yang PJ, Pham J, Choo J, Hu DL. Duration of urination does not change with body size. Proc Natl Acad Sci USA. 2014;111:11932–11937. doi: 10.1073/pnas.1402289111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Triep M, et al. 3D flow in the venom channel of a spitting cobra: Do the ridges in the fangs act as fluid guide vanes? PLoS One. 2013;8:e61548. doi: 10.1371/journal.pone.0061548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Farahani YF, Amin G, Sardari S, Ostad N. Effect of ecballium elaterium fruit on Candida albicans, Aspergillus fumigatus and Escherchia coli. Int J Biol Res. 2016;4:44–45. [Google Scholar]
- 17.Ladanyia M, Ladaniya M. Citrus Fruit: Biology, Technology and Evaluation. Academic; Oxford: 2010. [Google Scholar]
- 18.Ben-Yehoshua S, Burg SP, Young R. Resistance of citrus fruit to mass transport of water vapor and other gases. Plant Physiol. 1985;79:1048–1053. doi: 10.1104/pp.79.4.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bennici A, Tani C. Anatomical and ultrastructural study of the secretory cavity development of citrus sinensis and citrus limon: Evaluation of schizolysigenous ontogeny. Flora-Morphol Distrib Funct Ecol Plants. 2004;199:464–475. [Google Scholar]
- 20.Velasco R, Licciardello C. A genealogy of the citrus family: Clarification of the genetic relationships among species opens new possibilities for enhancing citrus diversity and disease resistance. Nat Biotechnol. 2014;32:640–643. doi: 10.1038/nbt.2954. [DOI] [PubMed] [Google Scholar]
- 21.Maffei ME, Gertsch J, Appendino G. Plant volatiles: Production, function and pharmacology. Nat Prod Rep. 2011;28:1359–1380. doi: 10.1039/c1np00021g. [DOI] [PubMed] [Google Scholar]
- 22.Koul O, Walia S, Dhaliwal G. Essential oils as green pesticides: Potential and constraints. Biopesticides Int. 2008;4:63–84. [Google Scholar]
- 23.Nannapaneni R, et al. Antimicrobial activity of commercial citrus-based natural extracts against Escherichia coli O157: H7 isolates and mutant strains. Foodborne Pathog Dis. 2008;5:695–699. doi: 10.1089/fpd.2008.0124. [DOI] [PubMed] [Google Scholar]
- 24.Weldon PJ, et al. Anointing chemicals and hematophagous arthropods: Responses by ticks and mosquitoes to citrus (Rutceae) peel exudates and monoterpene components. J Chem Ecol. 2011;37:348–359. doi: 10.1007/s10886-011-9922-7. [DOI] [PubMed] [Google Scholar]
- 25.Underhill SJ, McLauchlan RL, Dahler JM, Bertram J. Flavedo and albedo changes in ‘Eureka’ lemons caused by static compression and impact loading. J Texture Stud. 1998;29:437–452. [Google Scholar]
- 26.Kirbaşlar FG, Tavman A, Dülger B, Türker G. Antimicrobial activity of Turkish citrus peel oils. Pakistan J Bot. 2009;41:3207–3212. [Google Scholar]
- 27.Knight TG, Klieber A, Sedgley M. Structural basis of the rind disorder oleocellosis in Washington navel orange (Citrus sinensis L. Osbeck) Ann Bot. 2002;90:765–773. doi: 10.1093/aob/mcf258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Matura M, et al. Oxidized citrus oil (r-limonene): A frequent skin sensitizer in Europe. J Am Acad Dermatol. 2002;47:709–714. doi: 10.1067/mjd.2002.124817. [DOI] [PubMed] [Google Scholar]
- 29.Fisher K, Phillips C. Potential antimicrobial uses of essential oils in food: Is citrus the answer? Trends Food Sci Technol. 2008;19:156–164. [Google Scholar]
- 30.Nazaroff WW, Weschler CJ. Cleaning products and air fresheners: Exposure to primary and secondary air pollutants. Atmos Environ. 2004;38:2841–2865. [Google Scholar]
- 31.Mashayek A, Ashgriz N. Dynamics of liquid droplets. In: Mashayek A, Ashgriz N, editors. Handbook of Atomization and Sprays. Springer; Boston: 2011. pp. 97–123. [Google Scholar]
- 32.Clift R, Gauvin W. Motion of entrained particles in gas streams. Can J Chem Eng. 1971;49:439–448. [Google Scholar]
- 33.Hasegawa T, Suganuma M, Watanabe H. Anomaly of excess pressure drops of the flow through very small orifices. Phys Fluids. 1997;9:1–3. [Google Scholar]
- 34.Anderson TL. Fracture Mechanics: Fundamentals and Applications. CRC Press; Boca Raton, FL: 2017. [Google Scholar]
- 35.Fidelibus M, Teixeira A, Davies F. Mechanical properties of orange peel and fruit treated pre–harvest with gibberellic acid. Trans ASAE. 2002;45:1057–1062. [Google Scholar]
- 36.Singh KK, Reddy BS. Post-harvest physico-mechanical properties of orange peel and fruit. J Food Eng. 2006;73:112–120. [Google Scholar]
- 37.Griffith A. VI. The phenomena of rupture and flow in solids. Philos Trans R Soc A. 1921;221:163–198. [Google Scholar]
- 38.Irwin GR. Analysis of stresses and strains near the end of a crack traversing a plate. J Appl Mech. 1957;E24:351–369. [Google Scholar]
- 39.Tada H, Paris PC, Irwin GR. The Stress Analysis of Cracks Handbook. Del Research Corporation; London: 1973. [Google Scholar]
- 40.Folias ES. On the theory of fracture of curved sheets. Eng Fract Mech. 1970;2:151–164. [Google Scholar]
- 41.Holzapfel AG. Nonlinear Solid Mechanics II. John Wiley & Sons, Inc.; Hoboken, NJ: 2000. [Google Scholar]
- 42.Jiménez N, Picó R, Redondo J, Camarena F, Roig B. FDTD techniques applied to acoustic propagation in vegetable tissue: The elastodynamic behavior of the orange fruit. In: Burgess M, Davey J, Don C, McMinn T, editors. Proceedings of the 20th International Congress on Acoustics. International Congress on Acoustics; Sydney: 2010. pp. 616–621. [Google Scholar]
- 43.Buehler MJ, Abraham FF, Gao H. Hyperelasticity governs dynamic fracture at a critical length scale. Nature. 2003;426:141–146. doi: 10.1038/nature02096. [DOI] [PubMed] [Google Scholar]
- 44.Liu T, Long R, Hui C-Y. The energy release rate of a pressurized crack in soft elastic materials: Effects of surface tension and large deformation. Soft Matter. 2014;10:7723–7729. doi: 10.1039/c4sm01129e. [DOI] [PubMed] [Google Scholar]
- 45.Patek S, Caldwell R. Extreme impact and cavitation forces of a biological hammer: Strike forces of the peacock mantis shrimp odontodactylus scyllarus. J Exp Biol. 2005;208:3655–3664. doi: 10.1242/jeb.01831. [DOI] [PubMed] [Google Scholar]
- 46.Yafetto L, et al. The fastest flights in nature: High-speed spore discharge mechanisms among fungi. PLoS One. 2008;3:e3237. doi: 10.1371/journal.pone.0003237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Edwards J, Whitaker D, Klionsky S, Laskowski MJ. Botany: A record-breaking pollen catapult. Nature. 2005;435:164–164. doi: 10.1038/435164a. [DOI] [PubMed] [Google Scholar]
- 48.Rho J-Y, Kuhn-Spearing L, Zioupos P. Mechanical properties and the hierarchical structure of bone. Med Eng Phys. 1998;20:92–102. doi: 10.1016/s1350-4533(98)00007-1. [DOI] [PubMed] [Google Scholar]
- 49.Barthelat F, Tang H, Zavattieri P, Li C-M, Espinosa H. On the mechanics of mother-of-pearl: A key feature in the material hierarchical structure. J Mech Phys Solids. 2007;55:306–337. [Google Scholar]
- 50.Cranford SW, Buehler MJ. Biomateriomics. Vol 165 Springer Science & Business Media; Heidelberg: 2012. [Google Scholar]
- 51.Ashby M, Gibson L, Wegst U, Olive R. The mechanical properties of natural materials. I. Material property charts. Proc R Soc A. 1995;450:123–140. [Google Scholar]
- 52.Chen IH, Yang W, Meyers MA. Leatherback sea turtle shell: A tough and flexible biological design. Acta Biomater. 2015;28:2–12. doi: 10.1016/j.actbio.2015.09.023. [DOI] [PubMed] [Google Scholar]
- 53.Raabe D, Sachs C, Romano P. The crustacean exoskeleton as an example of a structurally and mechanically graded biological nanocomposite material. Acta Mater. 2005;53:4281–4292. [Google Scholar]
- 54.Ghosh R, Ebrahimi H, Vaziri A. Contact kinematics of biomimetic scales. Appl Phys Lett. 2014;105:233701. [Google Scholar]
- 55.Liu G, Ghosh R, Mousanezhad D, Vaziri A, Nayeb-Hashemi H. Thermal conductivity of biomimetic leaf composite. J Compos Mater. 2017:002199831773331. [Google Scholar]
- 56.Porter MM, Adriaens D, Hatton RL, Meyers MA, McKittrick J. Why the seahorse tail is square. Science. 2015;349:aaa6683. doi: 10.1126/science.aaa6683. [DOI] [PubMed] [Google Scholar]
- 57.Zhang Y, Yao H, Ortiz C, Xu J, Dao M. Bio-inspired interfacial strengthening strategy through geometrically interlocking designs. J Mech Behav Biomed Mater. 2012;15:70–77. doi: 10.1016/j.jmbbm.2012.07.006. [DOI] [PubMed] [Google Scholar]
- 58.Wegst UG, Bai H, Saiz E, Tomsia AP, Ritchie RO. Bioinspired structural materials. Nat Mater. 2015;14:23–36. doi: 10.1038/nmat4089. [DOI] [PubMed] [Google Scholar]
- 59.Fu Y, Tippets CA, Donev EU, Lopez R. Structural colors: From natural to artificial systems. Wiley Interdiscip Rev Nanomed Nanobiotechnol. 2016;8:758–775. doi: 10.1002/wnan.1396. [DOI] [PubMed] [Google Scholar]
- 60.Marvi H, Hu DL. Friction enhancement in concertina locomotion of snakes. J R Soc Interface. 2012;9:3067–3080. doi: 10.1098/rsif.2012.0132. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.