Significance
In 1952, Alan Turing proposed that biological morphogenesis could arise from a dynamical process in reaction systems with a rapidly diffusing inhibitor and a slowly diffusing activator. Turing’s conditions are disappointingly hard to achieve in nature, but recent stochastic extension of the theory predicts pattern formation without such strong conditions. We have forward-engineered bacterial populations with signaling molecules that form a stochastic activator–inhibitor system that does not satisfy the classic Turing conditions but exhibits disordered patterns with a defined length scale and spatial correlations that agree quantitatively with stochastic Turing theory. Our results suggest that Turing-type mechanisms, driven by gene expression or other source of stochasticity, may underlie a much broader range of patterns in nature than currently thought.
Keywords: Turing patterns, biofilm, synthetic biology, signaling molecules, stochastic gene expression
Abstract
The origin of biological morphology and form is one of the deepest problems in science, underlying our understanding of development and the functioning of living systems. In 1952, Alan Turing showed that chemical morphogenesis could arise from a linear instability of a spatially uniform state, giving rise to periodic pattern formation in reaction–diffusion systems but only those with a rapidly diffusing inhibitor and a slowly diffusing activator. These conditions are disappointingly hard to achieve in nature, and the role of Turing instabilities in biological pattern formation has been called into question. Recently, the theory was extended to include noisy activator–inhibitor birth and death processes. Surprisingly, this stochastic Turing theory predicts the existence of patterns over a wide range of parameters, in particular with no severe requirement on the ratio of activator–inhibitor diffusion coefficients. To explore whether this mechanism is viable in practice, we have genetically engineered a synthetic bacterial population in which the signaling molecules form a stochastic activator–inhibitor system. The synthetic pattern-forming gene circuit destabilizes an initially homogenous lawn of genetically engineered bacteria, producing disordered patterns with tunable features on a spatial scale much larger than that of a single cell. Spatial correlations of the experimental patterns agree quantitatively with the signature predicted by theory. These results show that Turing-type pattern-forming mechanisms, if driven by stochasticity, can potentially underlie a broad range of biological patterns. These findings provide the groundwork for a unified picture of biological morphogenesis, arising from a combination of stochastic gene expression and dynamical instabilities.
A central question in biological systems, particularly in developmental biology, is how patterns emerge from an initially homogeneous state (1). In his seminal 1952 paper “The chemical basis of morphogenesis,” Alan Turing showed, through linear stability analysis, that stationary, periodic patterns can emerge from an initially uniform state in reaction–diffusion systems where an inhibitor morphogen diffuses sufficiently faster than an activator morphogen (2). However, the requirements for realizing robust pattern formation according to Turing’s mechanism are prohibitively difficult to realize in nature. Although Turing patterns were observed in a chemical system in 1990 (3), the general role of Turing instabilities in biological pattern formation has been called into question, despite a few rare examples (ref. 4 and references therein).
Recently, Turing’s theory was extended to include intrinsic noise arising from activator and inhibitor birth and death processes (5–8). According to the resulting stochastic Turing theory, demographic noise can induce persistent spatial pattern formation over a wide range of parameters, in particular, removing the requirement for the ratio of inhibitor–activator diffusion coefficients to be large. Moreover, stochastic Turing theory shows that the extreme sensitivity of pattern-forming systems to intrinsic noise stems from a giant amplification resulting from the nonorthogonality of eigenvectors of the linear stability operator about the spatially uniform steady state (8). This amplification means that the magnitude of spatial patterns arising from intrinsic noise is not limited by the noise amplitude itself, as one might have thought naively. These developments imply that intrinsic noise can drive large-amplitude stochastic Turing patterns for a much wider range of parameters than the classical, deterministic Turing theory. In particular, it is often the case in nature that the activator and inhibitor molecules do not have widely differing diffusion coefficients; nevertheless, stochastic Turing theory predicts that, even in this case, pattern formation can occur at a characteristic wavelength that has the same functional dependence on parameters as in the deterministic theory.
To explore how global spatial patterns emerge from local interactions in isogenic cell populations, we present here a synthetic bacterial population with collective interactions that can be controlled and well-characterized (an introduction to this perspective is in ref. 9), where patterning is driven by activator–inhibitor diffusion across an initially homogeneous lawn of cells. Synthetic systems can be forward-engineered to include relatively simple circuits that are loosely coupled to the larger natural system into which they are embedded. This makes it easier to design and control the molecular underpinnings of the biological pattern phenomenon (10) and even front propagation phenomena (11). Previous pattern formation efforts in synthetic biology have focused on oscillations in time (12) or required either an initial template (13) or an expanding population of cells (14), neither of which show a Turing mechanism.
Experimental Results
Synthetic Biology of a Bacterial Community.
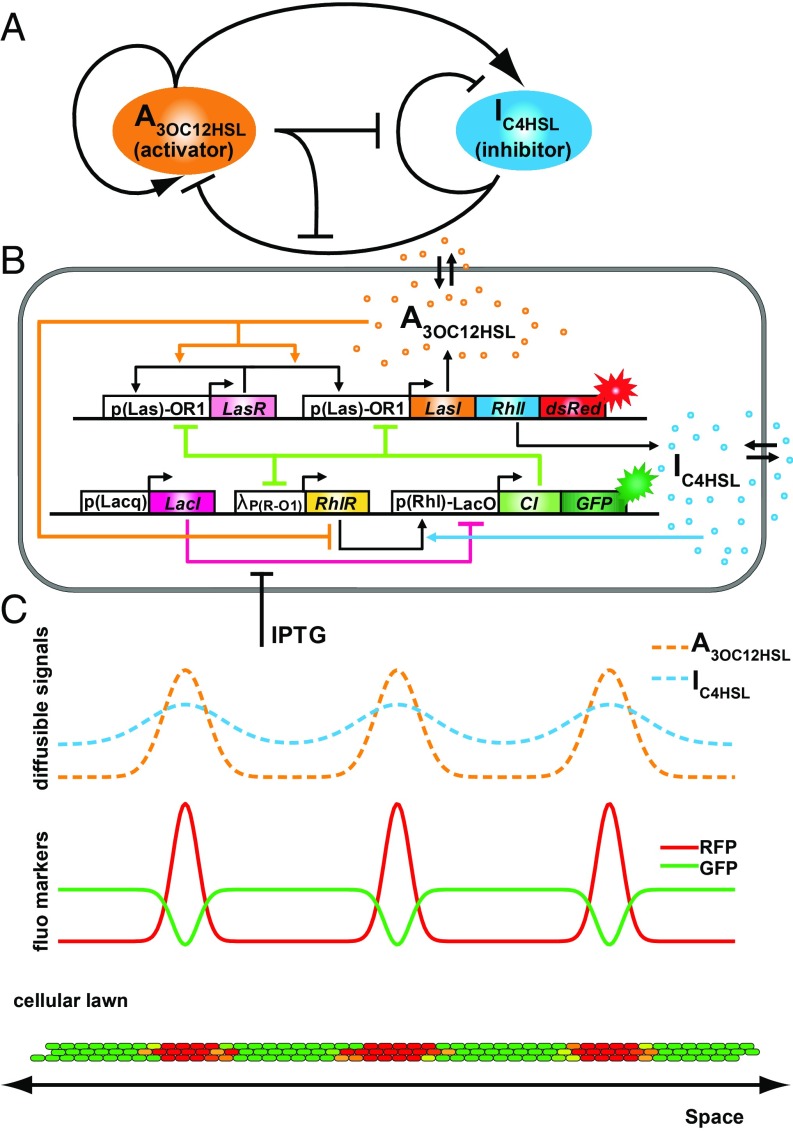
In our synthetic gene network design, which was guided by computational modeling (SI Appendix, section 1), we used two artificial diffusible morphogens: the small molecule N-(3-oxododecanoyl) homoserine lactone, denoted here as A, and the small molecule N-butanoyl-l-homoserine lactone, denoted here as I, from the Pseudomonas aeruginosa las and rhl quorum sensing pathways, respectively, in P. aeruginosa (15). A serves as an activator of both its own synthesis and that of I, while I serves as an inhibitor of both signals (Fig. 1 A and B and SI Appendix, section 1). A activates its own synthesis and synthesis of I by binding regulatory protein LasR to form a complex that activates the hybrid promoter . This promoter regulates expression of LasI, an A synthase, and RhlI, an I synthase. To increase the sensitivity of A self-activation, LasR is regulated by a second copy of . I inhibits synthesis of A and itself by forming a complex with the regulatory protein RhlR. This complex activates expression of lambda repressor CI, which in turn, represses transcription of LasI, RhlI, LasR, and RhlR. Pattern formation in our system can be modulated by altering the concentration of isopropyl -d-1-thiogalactopyranoside (IPTG), a small molecule inducer that binds LacI and alleviates repression of . GFP and red fluorescent protein (RFP) are expressed from the rhl and las hybrid promoters, respectively, to aid in experimental observation (SI Appendix, section 2).
Fig. 1.
Design of a synthetic multicellular system for emergent pattern formation. (A) Abstractly, the system consists of two signaling species A and I. A is an activator catalyzing synthesis of both species, while I is an inhibitor repressing their synthesis, with additional repression by A via competitive binding. (B) Genetic circuit implementation. Promoter regions are indicated by white boxes, while protein coding sequences are indicated by colored boxes. IPTG is an external inducer modulating system dynamics. (C, Top) Illustration of signaling species concentrations in 1D space. The dashed orange and blue lines correspond to A and I, respectively. (C, Middle) Spatial profiles of reporter proteins. RFP expression (red line) correlates with A concentrations, while GFP expression (green line) roughly mirrors RFP expression. (C, Bottom) A vertical slice of cell lawn. Cells express fluorescence proteins according to the profiles above and produce a global multicellular pattern.
In our experimental setup, the A activator diffuses more slowly than the I inhibitor (SI Appendix, section 3). The estimated diffusion coefficient for A is 83 /s, and for I, it is 1,810 /s. The experimentally determined ratio of diffusion rates in our system of 21.6 is much higher than the value of 1.5 predicted by Wilke–Chang correlation in water (16), likely due to partitioning of A in the cell membrane, which slows its diffusion from cell to cell (17). The slower diffusion rate of A coupled with positive feedback regulating its synthesis allows A to aggregate in local domains, leading to formation of visible red fluorescent spots (cellular lawn illustration is shown in Fig. 1C). Within these red domains, both A and I are found in high concentrations, but because A competitively binds RhlR (SI Appendix, section 4 and Fig. S8), GFP is attenuated (18). The faster diffusion rate of I allows it to diffuse into regions outside of the red fluorescent domains. Here, I is free to bind RhlR, activating GFP expression. Collectively, these processes lead to green regions between red spots.
Experimental Patterns and Controls.
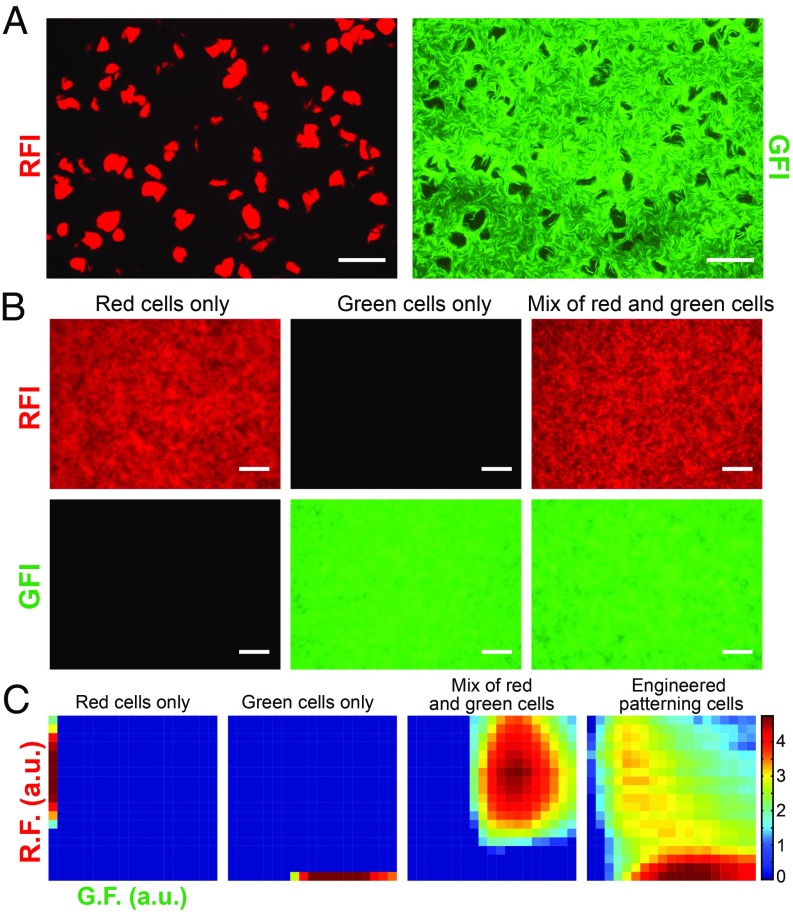
To study pattern-forming behavior, engineered cells are first cultured in liquid media, and then, they are concentrated and plated on a petri dish to form an initially homogeneous “lawn” of cells (Materials and Methods). After plating, the petri dish is incubated for 24 h at 30 °C, and microscope fluorescence images are captured as needed. Before the self-activation of the A synthase positive feedback loop, the cell lawn exhibits no fluorescence. However, over time, red fluorescent spots emerge with sizes much larger than that of a single cell (10–1,000×). Simultaneously, green fluorescence develops in a pattern with dark voids positioned precisely in the locations of the intense red fluorescence (Fig. 2A). Time series microscopy reveals that patterns begin to emerge after approximately 16 h (SI Appendix, Fig. S12).
Fig. 2.
Experimental observations of emergent pattern formation measured by green fluorescence intensity (GFI) and red fluorescence intensity (RFI). (A) Representative microscope images (based on six technical replicates) of a typical field of view showing a fluorescent pattern formed by an initially homogeneous isogenic lawn of cells harboring the Turing circuit with no IPTG. Spots and voids appear in the red fluorescence (RF) and green fluorescence (GF) channels, respectively. (Scale bar: 100 μm.) (B) Microscope images of cell lawns with constitutive expression of fluorescent proteins. (Left) Cells expressing RFP, (Center) cells expressing GFP, and (Right) mixed population of red and green cells. (C) Fluorescence density plots computed from the images above (from left to right: red, green, red/green, and Turing). Color intensity is in log scale [arbitrary units (a.u.)].
In control experiments, we show that our patterns are not simply a result of the outward growth of clusters of differentially colored cells (Fig. 2 B and C and SI Appendix, section 5). Also, by performing an experiment with cells that harbor independent bistable green/red toggle switches, we test whether observable patterns would emerge if individual cells autonomously made cell fate decisions at some point after plating (SI Appendix, section 5). The fluorescence fields after 24 h of incubation at 30 °C in both control experiments are uniform, showing no emergence of patterns.
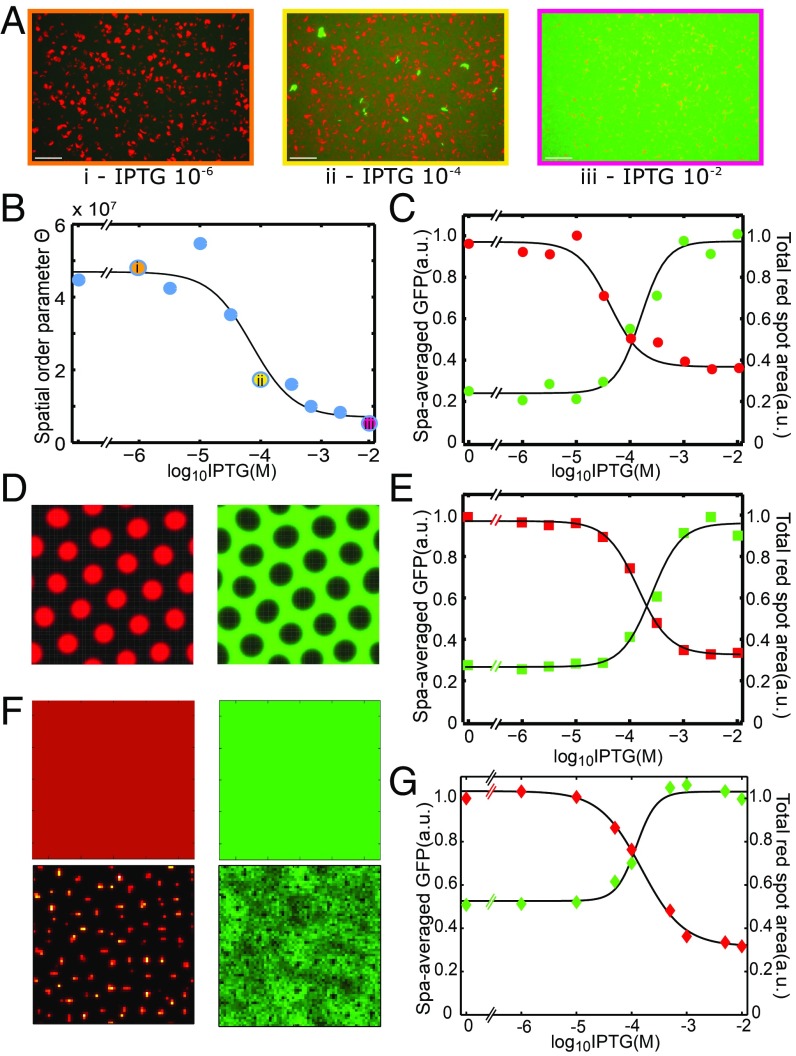
Next, we examine how changes in the strengths of localized interactions lead to different global outcomes in our pattern-forming gene circuit. In our system, IPTG can be used to modulate the inhibitory efficiency of I in individual cells by affecting CI expression from . Specifically, IPTG relieves LacI repression of CI and GFP reporter. The increased range of CI ultimately increases inhibition of both morphogens, which is expected to decrease activator spot sizes, while causing the field of CI and GFP reporter to be more strongly expressed. Our data show that mean GFP levels increase sigmoidally with inducer concentration, while the overall area of red spots decreases (Fig. 3 A and C). In addition to offering further support that our gene circuit gives rise to emergent patterns, these results show how pattern formation characteristics can potentially be tuned to fit future application needs.
Fig. 3.
Mathematical modeling and correlation between pattern modulation experiments and simulations. (A) Experimental results for IPTG modulation of pattern formation with microscopy images corresponding to specific IPTG concentrations in B. The same display mappings were used for all images in A. (B) Collectivity, metric parameter is influenced by IPTG modulation. (C) Pattern statistics over IPTG modulation for experimental results. (D) Pattern obtained from simulating a deterministic reaction–diffusion model with . (E) Pattern statistics over IPTG modulation for deterministic modeling. (F) Patterns obtained from simulating our deterministic model (Upper) and stochastic spatiotemporal model (Lower) at the measured diffusion ratio of . (G) Pattern statistics over IPTG modulation for stochastic modeling. a.u., arbitrary unit.
Theoretical Results
Having established that our system forms emergent patterns, we proceeded to study the mechanisms driving these patterns. We formulated deterministic and stochastic models and analyzed our data to assess agreement with the theory of stochastic Turing patterns.
Deterministic Model.
We first developed a detailed deterministic reaction–diffusion model (SI Appendix, section 7). The model explicitly describes chemical reactions for the LasI and RhlI synthases, regulatory protein CI, and synthesis and diffusion of the morphogens A and I. As the overall system involves a large number of reactions with rate constants that span multiple timescales, we made two commonly used simplifying assumptions. First, we assume that operator states of a promoter fluctuate much faster than protein degradation rates. Second, we assume that mRNA half-life is much shorter than protein half-life. These assumptions allow us to eliminate operator fluctuation and mRNA kinetics and model the system at the communication signals and protein levels as follows:
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
where and are the concentrations of the two diffusible morphogens A and I, respectively; and are the concentrations of corresponding acyl homoserine lactone (AHL) synthases, respectively; and refers to CI.
We model the hybrid promoters using the following Hill functions:
| [6] |
| [7] |
where and are the production rates of the promoters and , respectively; and are the LasR-A complex and the RhlR-I complex, respectively; and is the concentration of unbound LacI protein. We use the definitions
| [8] |
| [9] |
| [10] |
where is the IPTG concentration and and are the regulatory proteins LasR and RhlR, respectively:
| [11] |
| [12] |
A summary of the variables used in our model is available in SI Appendix, Table S5, and definitions of the rate constants are in SI Appendix, Tables S6 and S7. Hill functions used in this model have a shared form of , where and correspond to the input and output of the function, respectively; is the dissociation constant; is the Hill coefficient; and is the fold change of on full induction by .
We initially ran simulations of this model using a high diffusion rate ratio () of 100. These simulations yield patterns of red spots and green voids (Fig. 3D), suggesting that the underlying dynamics of our system are Turing-like, with the potential for Turing instabilities. Deterministic simulations of IPTG modulations also correlate well with the trends of the experimental results (Fig. 3E and SI Appendix, section 6).
While the overall behavior of our system is reminiscent of classical Turing patterns (19), there are key differences. In particular, when we ran simulations at the measured diffusion rate ratio of , patterns did not arise (Fig. 3F). For some two-node implementations of Turing systems, this rate would be sufficient for pattern formation (20). In addition, certain networks with more nodes can allow small or even equal morphogen diffusion rate ratios to generate Turing instabilities (21). However, a practical biological implementation imposes certain dynamics, such as delays associated with protein production, that can strongly impact pattern formation (22, 23). Indeed, our deterministic modeling results suggest that the ratio of diffusion constants for the activator and inhibitor in our system is either barely within the range required for a Turing instability or even outside the range, depending on the precise medium in which signal diffusion is measured (SI Appendix, section 7). In addition, whereas in the deterministic simulation, spots are identical and evenly distributed, those in the experimental systems vary in size, shape, fluorescence intensity, and the intervals between them.
Stochastic Model.
The deterministic modeling results indicate that our system may be beyond the regime where classical Turing patterns are formed but still within the regime where stochastic Turing patterns occur (5–8). Indeed, gene expression in microbes is inherently noisy due to the small volume of cells and the fact that many reactants are present in low numbers, suggesting that stochastic Turing patterns could be present in our system (24).
Noise in stochastic Turing patterns expands the range of parameters in which patterns form, in contrast to the usual expectation that noise serves as a destabilizing agent. The patterns observed in stochastic Turing systems correspond to the slowest decaying mode of the fluctuations. Similar noise stabilization phenomena can be observed in other systems that are out of equilibrium. For example, in predator–prey systems, fluctuations can drive temporal oscillations of populations (25, 26). Noise-driven stabilization has also been recently discovered in the clustering of molecules on biological membranes (27, 28) and in models that exhibit Turing-like pattern formation (7). In particular, whereas spatial symmetry breaking and pattern formation via the original Turing design require two morphogens with diffusion rates that differ by a large factor on the order of 10 or 100 (1), the requirements to form stochastic Turing patterns are less stringent. For example, in a pattern-forming plankton–herbivore ecosystem, the noise associated with discrete random birth and death processes reduces the required ratio of diffusion constants for pattern formation from a threshold of 27.8 for normal Turing patterns to a threshold of 2.48 for stochastic Turing patterns (5–8).
To determine whether noise in the chemical reactions underlying gene expression and morphogen diffusion in our system can cause the emergence of patterns over a wider range of parameters than a deterministic model, we constructed a stochastic spatiotemporal model using the same biochemical reactions, diffusion, and rate constants used in our deterministic model (SI Appendix, section 8). This model captures stochastic effects in the production and degradation of the proteins and morphogens in our system but approximates diffusion as deterministic. Simulations of the stochastic model generically produce patterns with large variability in spot size, shape, intensity, and intervals, which are similar to the patterns observed in our experiments and different from those predicted for the deterministic model (Fig. 3F). We have compared the experimental patterns with stochastic simulations in both real space and in 2D Fourier transform (2DFT) space (SI Appendix, section 8). Neither the experimental 2DFT nor the simulated 2DFT contain pronounced peaks that would be present in a deterministic honeycomb Turing pattern. Moreover, as the IPTG concentration is increased, both experimental and simulated patterns become more regular (Fig. 3G).
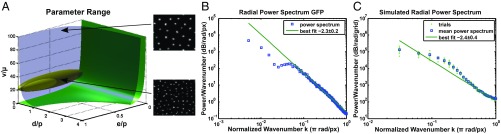
To further test the hypothesis that we are observing stochastic Turing patterns, we measured the power spectrum for both of our fluorescent reporters. Theory predicts that the power spectrum will have a power law tail as a function of wavenumber, , for large wavenumbers, with an exponent characteristic of the noise source (7, 25). The exponent values are −2 and −4 for stochastic Turing patterns and deterministic Turing patterns with additive noise, respectively, and can be interpreted simply as follows. The −2 arises, because at small frequency or wavenumber, the random variable (i.e., concentration) is simply diffusing and therefore, follows the behavior of a random walk, which has a power spectrum that exhibits a −2 power law. The −4 arises, because for a system that is executing deterministic damped periodic motion but driven by additive white noise, the response of the random variable is a Lorentzian, with an asymptotic behavior for the power spectrum that exhibits a −4 exponent.
For the GFP channel, we observe a power law tail with an exponent of (Fig. 4B and SI Appendix, section 9A). For the RFP channel, we also observe a power law tail with an exponent of (SI Appendix, section 9A). To better understand the implications of these tails, we examined our detailed stochastic model of the genetic systems and also developed a reduced stochastic model that explicitly includes only the morphogens (SI Appendix, section 9B). Both models predict that our experimental parameters will produce a stochastic pattern with a power law tail of for both the activator and the inhibitor at asymptotically large wavenumbers (Fig 4C and SI Appendix, section 9C). However, in the range of parameters likely to correspond to the experiments (Fig. 4A and SI Appendix, section 9C), the detailed stochastic model predicts that the exponent of the power law tail for the activator will be over a large range of intermediate wavenumbers before it eventually undergoes a cross-over to a power law with an exponent at high wavenumbers (SI Appendix, Fig. S24). This behavior once again agrees with our experimental data and supports our identification of stochastic Turing patterns. In summary, spectral analysis of the patterns of activator and inhibitor is consistent with a model in which fluctuations in the amount of signaling morphogens drive stochastic Turing patterns.
Fig. 4.
Spectral analysis and parameter analysis. (A) Pattern-forming regimes in parameter space and estimated parameters for our system. Parameters above the green surface of neutral stochastic stability can form stochastic patterns, and parameters above the blue surface of deterministic neutral stability can form deterministic Turing patterns. The ratio of the diffusion coefficients /, the ratio of degradation rate to production rate , and the ratio of production rates are estimated for our system by the yellow ellipsoid. The parameters for our system are mostly in the regime where stochastic patterns form and outside the region where deterministic Turing patterns form. Example stochastic simulations are shown for parameters drawn from a deterministic parameter region with (Upper Right) and a stochastic region with (Lower Right). (B) Radial power spectrum of green fluorescence and best fit power law tail with an exponent of . (C) Radial power spectrum for eight trials of our stochastic simulation, their mean, and the best fit power law tail.
Our analysis of the stochastic Turing model predicts that stochastic patterns form over a wide range of parameters (SI Appendix, section 8). Indeed, our stochastic model predicts that stochastic Turing patterns are possible at the measured ratio of diffusion rates for A and I (Figs. 3F and 4A). In addition, to determine the sensitivity of the stochastic model to the parameters chosen, we individually varied parameters from 0.5× their nominal value to 1.5× their nominal value while keeping all other parameters fixed at their best estimated value. For each set of parameters, we calculate the analytical power spectrum and the eigenvalues of the Jacobian (linear stability matrix) of the stochastic model evaluated at a fixed point found numerically. Based on this analysis (SI Appendix, section 8), we classify each set of parameters as producing an unstable homogeneous state at wavenumber , a stable homogeneous state, a stochastic Turing pattern, or a deterministic Turing pattern. Specifically, we classify a set of parameters as producing a pattern if they produce a peak in the calculated power spectrum at a nonzero wavenumber. To distinguish between stochastic Turing patterns and deterministic Turing patterns, we examine the eigenvalues of the corresponding Jacobian. If the real part of all of the eigenvalues is negative for all wavenumbers, then the pattern must be due to stochasticity. If there is any range of wavenumbers that have corresponding positive real parts of their eigenvalues, then the pattern is produced by the traditional Turing mechanism. The results of this analysis are shown in SI Appendix, Fig. S22 and illustrate the significant ranges for each parameter that can lead to stochastic Turing patterns. Indeed, the estimated parameter values yield stochastic Turing patterns and variation of , , and IPTG, and several other parameters never produce deterministic patterns; therefore, our results are very insensitive to estimation error of these important parameters. Overall, varying the parameters one at a time, of the values yield stochastic Turing patterns.
To quantify the way in which stochasticity enlarges the pattern-forming regime of parameter space, we simultaneously varied all model parameters and performed the classification used above. Specifically, we used Latin hypercube sampling to randomly generate 500 parameter sets, where all of the parameters were allowed to vary between 0.5× and 1.5× their nominal value. For this analysis, we found that of parameters produced unstable fixed points, produced stable homogeneous states, produced stochastic Turing patterns, and produced Turing patterns. Thus, over this arbitrarily large range of parameters, pattern formation occurs only of the time in the absence of stochasticity but of the time when stochasticity is included. By including stochasticity, the range in which patterns can form has been increased by .
Discussion
Alternative Hypotheses.
Now, we consider alternative hypotheses to our claim that the theory of stochastic Turing patterns explains our experimental observations. We consider the duration and dynamics of our pattern formation experiments. One may expect to observe early events in Turing pattern formation, such as splitting of clusters or increases in intercluster distances. These processes may be, in fact, be taking place but may be difficult to observe due to weak reporter expression in the earlier stages. In addition, we must consider the limited duration of our experiments and the possibility that, theoretically, longer observations may result in different patterns if nonlinear processes eventually began to dominate dynamics. Indeed, we do not feed fresh nutrients to sustain the system for extremely long durations. However, as confirmed by analysis of the dynamics in SI Appendix, Fig. S12, cluster size growth and spacing between clusters appear to be stabilizing toward the end of the experiment. In addition, domains are neither created nor destroyed in the later time periods. Essentially, it appears that the patterns are close to stabilizing within the 32-h observation period.
Another alternative hypothesis is that cell growth dynamics primarily drive the observed pattern formation. Our control experiments with mixtures of red and green cell populations (SI Appendix, Fig. S9) along with our bistable switch control (SI Appendix, Fig. S10) suggest that cell growth does not explain our patterns. Moreover, our ability to tune pattern characteristics offers support for the fact that our patterns are not a simple consequence of natural biofilm growth morphologies but rather, are driven by our genetic circuit. However, growth may indeed impact regularity and may likely explain the fact that our experimental patterns are less regular than those observed in our stochastic models (Fig. 3F). Indeed, future experiments to show different classes of patterns (e.g., labyrinth patterns) would offer further support, but collectively, our experiments strongly support our hypothesis that a Turing mechanism driven by our genetic circuit explains our observed patterns.
Summary of Evidence for Stochastic Turing Patterns.
We summarize our evidence for showing stochastic Turing patterns and not showing amplification of random noise as follows. Our control experiments with mixtures of red and green cells (Fig. 2B and SI Appendix, Fig. S9) along with a bistable switch (SI Appendix, Fig. S10) did not produce the patterns that we observe with our genetic circuit (Fig. 2A). Our ability to tune pattern characteristics offers further support that pattern formation is driven by our genetic circuit. In addition to our experimental controls, we identify patterns in the stochastic model but not in the deterministic model of our system for the experimentally observed ratio of diffusion rates (Fig. 3F). These model patterns resemble the experimentally observed patterns in real space, exhibit no peaks in the 2DFT (SI Appendix, Figs. S13 and S20), and recapitulate the observed trend with IPTG variation. Analyses of our experimental data are also in accord with the theory of stochastic Turing patterns. The exponents in the tails of the experimental radial power spectra agree with theoretical predictions (Fig. 4B and SI Appendix, Fig. S13). In addition, although spatial regularity is weak, we observe a radial spectral peak for our experimental patterns (Fig. 4B and SI Appendix, Fig. S13), indicating a characteristic length scale. Furthermore, exploration of the large parameter space of the stochastic model indicates that the experimental parameters are most likely to be in the regime where only stochastic patterns can form (SI Appendix, section 8). Collectively, this body of evidence suggests that our experiments indeed exhibit stochastic Turing pattern formation.
Materials and Methods
Strains and Conditions.
Our patterning system was constructed using two plasmids that correspond to the upper and lower portions of the circuit diagram in Fig. 1B: pFNK512 and pFNK806 in Fig. 2A and pFNK512 and pFNK804lacOlacI in Fig. 3. The two-color bistable toggle switch plasmid pTOG-1 was constructed from plasmid pIKE-107. All plasmids were constructed using standard cloning and DNA recombination techniques. Plasmid construction details are described here and in SI Appendix, section 2. Escherichia coli strain MG1655 was used for all experiments.
Code Availability.
Custom code used in this manuscript is currently available at https://www.dropbox.com/sh/di3hbaaubx5qd0q/AADpSOMfJtm_F_lEDRFoch0sa?dl=0.
Experimental Procedure.
Cells harboring appropriate plasmids were initially grown in LB liquid media with corresponding antibiotics at 30 °C until OD at 600 nm was reached . Cells were then concentrated and resuspended in M9 media with appropriate antibiotics (29); 0.5 mL of concentrated cell solutions () were poured onto a 2% M9 agar plate (-mm petri dish) to form a cellular lawn. Plates were incubated at C, and fluorescence images were captured periodically. To examine the single-cell fluorescence evolution of toggle switch cell populations, we performed flow cytometry at the beginning of the experiment (0 h) and the end of the experiment (24 h).
Data Analysis.
Fluorescence density plots, power spectrum of green fluorescence, averaged green fluorescence, total area of red spots, collectivity metric, and Moran’s I were all computed by analyzing the experimental time-lapse microscopy data with custom Matlab software.
Mathematical Modeling.
The patterning system was simulated by numerically integrating differential equations using in house-developed C software. We also developed stochastic spatiotemporal models using a hybrid stochastic simulation algorithm (30). SI Appendix has details about the models and the simulation environments.
Note Added in Proof.
After the completion and acceptance of this work, an independent observation of stochastic Turing patterns in the cyanobacteria colonies of Anabaena sp. was reported (31).
Supplementary Material
Acknowledgments
We thank D. Volfson and T. Danino for help in mathematical modeling and E. Andriananto for help in plasmid construction. We also thank R. Mehreja and J. Ku for help in creation of the RhlR mutant. We thank members of the laboratory of R.W., especially N. Davidsohn, J. Sun, S. Gupta, M. Chen, C. Grecu, L. Wroblewska, and Y. Li, for discussions. This work was supported by the NIH and National Science Foundation Grants CCF-1521925 and CNS-1446474. D.K. acknowledges support from the Independent Research and Development Program of the Johns Hopkins University Applied Physics Laboratory. K.M.M. acknowledges partial support from the Center for the Physics of Living Cells through National Science Foundation Physics Frontiers Center Program PHY 1430124.
Footnotes
The authors declare no conflict of interest.
Data deposition: The DNA sequences of plasmids reported in this paper have been deposited in the GenBank database (accession nos. MH300673–MH300677).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1720770115/-/DCSupplemental.
References
- 1.Gierer A, Meinhardt H. A theory of biological pattern formation. Biol Cybern. 1972;12:30–39. doi: 10.1007/BF00289234. [DOI] [PubMed] [Google Scholar]
- 2.Turing A. The chemical basis of morphogenesis. Philos Trans R Soc Lond Ser B Biol Sci. 1952;237:37–72. doi: 10.1098/rstb.2014.0218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Castets V, Dulos E, Boissonade J, De Kepper P. Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern. Phys Rev Lett. 1990;64:2953–2956. doi: 10.1103/PhysRevLett.64.2953. [DOI] [PubMed] [Google Scholar]
- 4.Raspopovic J, Marcon L, Russo L, Sharpe J. Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients. Science. 2014;345:566–570. doi: 10.1126/science.1252960. [DOI] [PubMed] [Google Scholar]
- 5.Butler T, Goldenfeld N. Robust ecological pattern formation induced by demographic noise. Phys Rev E. 2009;80:030902. doi: 10.1103/PhysRevE.80.030902. [DOI] [PubMed] [Google Scholar]
- 6.Biancalani T, Fanelli D, Di Patti F. Stochastic turing patterns in the brusselator model. Phys Rev E. 2010;81:046215. doi: 10.1103/PhysRevE.81.046215. [DOI] [PubMed] [Google Scholar]
- 7.Butler T, Goldenfeld N. Fluctuation-driven turing patterns. Phys Rev E. 2011;84:011112. doi: 10.1103/PhysRevE.84.011112. [DOI] [PubMed] [Google Scholar]
- 8.Biancalani T, Jafarpour F, Goldenfeld N. Giant amplification of noise in fluctuation-induced pattern formation. Phys Rev Lett. 2017;118:018101. doi: 10.1103/PhysRevLett.118.018101. [DOI] [PubMed] [Google Scholar]
- 9.Scholes NS, Isalan M. A three-step framework for programming pattern formation. Curr Opin Chem Biol. 2017;40:1–7. doi: 10.1016/j.cbpa.2017.04.008. [DOI] [PubMed] [Google Scholar]
- 10.Andrianantoandro E, Basu S, Karig D, Weiss R. Synthetic biology: New engineering rules for an emerging discipline. Mol Syst Biol. 2006;2:0028. doi: 10.1038/msb4100073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tayar AM, Karzbrun E, Noireaux V, Bar-Ziv RH. Propagating gene expression fronts in a one-dimensional coupled system of artificial cells. Nat Phys. 2015;11:1037–1041. [Google Scholar]
- 12.Stricker J, et al. A fast, robust and tunable synthetic gene oscillator. Nature. 2008;456:516–519. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fernandez-Rodriguez J, Moser F, Song M, Voigt CA. Engineering RGB color vision into Escherichia coli. Nat Chem Biol. 2017;13:706–708. doi: 10.1038/nchembio.2390. [DOI] [PubMed] [Google Scholar]
- 14.Liu C, et al. Sequential establishment of stripe patterns in an expanding cell population. Science. 2011;334:238–241. doi: 10.1126/science.1209042. [DOI] [PubMed] [Google Scholar]
- 15.Pesci E, Iglewski B. The chain of command in Pseudomonas quorum sensing. Trends Microbiol. 1997;5:132–134. doi: 10.1016/S0966-842X(97)01008-1. [DOI] [PubMed] [Google Scholar]
- 16.Stewart P. Diffusion in biofilms. J Bacteriol. 2003;185:1485–1491. doi: 10.1128/JB.185.5.1485-1491.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pearson J, Van Delden C, Iglewski B. Active efflux and diffusion are involved in transport of Pseudomonas aeruginosa cell-to-cell signals. J Bacteriol. 1999;181:1203–1210. doi: 10.1128/jb.181.4.1203-1210.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pesci E, Pearson J, Seed P, Iglewski B. Regulation of las and rhl quorum sensing in Pseudomonas aeruginosa. J Bacteriol. 1997;179:3127–3132. doi: 10.1128/jb.179.10.3127-3132.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kondo S, Miura T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science. 2010;329:1616–1620. doi: 10.1126/science.1179047. [DOI] [PubMed] [Google Scholar]
- 20.Hagberg A, Meron E. Pattern formation in non-gradient reaction-diffusion systems: The effects of front bifurcations. Nonlinearity. 1994;7:805–835. [Google Scholar]
- 21.Marcon L, Diego X, Sharpe J, Müller P. High-throughput mathematical analysis identifies turing networks for patterning with equally diffusing signals. eLife. 2016;5:e14022. doi: 10.7554/eLife.14022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gaffney EA, Monk NAM. Gene expression time delays and Turing pattern formation systems. Bull Math Biol. 2006;68:99–130. doi: 10.1007/s11538-006-9066-z. [DOI] [PubMed] [Google Scholar]
- 23.Seirin Lee S, Gaffney EA, Monk NAM. The influence of gene expression time delays on Gierer–Meinhardt pattern formation systems. Bull Math Biol. 2010;72:2139–2160. doi: 10.1007/s11538-010-9532-5. [DOI] [PubMed] [Google Scholar]
- 24.Kærn M, Elston TC, Blake WJ, Collins JJ. Stochasticity in gene expression: From theories to phenotypes. Nat Rev Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 25.McKane AJ, Newman TJ. Predator-prey cycles from resonant amplification of demographic stochasticity. Phys Rev Lett. 2005;94:218102. doi: 10.1103/PhysRevLett.94.218102. [DOI] [PubMed] [Google Scholar]
- 26.Howard M, Rutenberg AD. Pattern formation inside bacteria: Fluctuations due to the low copy number of proteins. Phys Rev Lett. 2003;90:128102. doi: 10.1103/PhysRevLett.90.128102. [DOI] [PubMed] [Google Scholar]
- 27.Wehrens M, ten Wolde PR, Mugler A. Positive feedback can lead to dynamic nanometer-scale clustering on cell membranes. J Chem Phys. 2014;141:205102. doi: 10.1063/1.4901888. [DOI] [PubMed] [Google Scholar]
- 28.Altschuler SJ, Angenent SB, Wang Y, Wu LF. On the spontaneous emergence of cell polarity. Nature. 2008;454:886–889. doi: 10.1038/nature07119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Brenner K, Karig D, Weiss R, Arnold F. Engineered bidirectional communication mediates a consensus in a microbial biofilm consortium. Proc Natl Acad Sci USA. 2007;104:17300–17304. doi: 10.1073/pnas.0704256104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rossinelli D, Bayati B, Koumoutsakos P. Accelerated stochastic and hybrid methods for spatial simulations of reaction–diffusion systems. Chem Phys Lett. 2008;451:136–140. [Google Scholar]
- 31.Di Patti F, et al. Robust stochastic Turing patterns in the development of a one-dimensional cyanobacterial organism. PLoS Biol. 2018;16:e2004877. doi: 10.1371/journal.pbio.2004877. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.