Squeezing and stick–slip friction behaviors of lubricants in boundary lubrication

Significance

Lubricant films under extreme confinement at nanometer scales play a crucial role in lubrication engineering. Improved understanding of squeezing and friction behaviors of such ultrathin films can lead to strategies for preventing surface failure and efficient national energy usage. Through computer simulations we show that lubricant films under compression can solidify below some critical monolayers distance. Under sliding friction these solidified films exhibit stick–slip friction in which the slip occurs at solid–lubricant interfaces. However, dilation of the lubricant during slips (a signature of shear melting) is never observed, which is consistent with other experimental findings. These insights, with strong support from surface force balance experiments, may open the way to improved lubricant design.

Abstract

The fundamental questions of how lubricant molecules organize into a layered structure under nanometers confinement and what is the interplay between layering and friction are still not well answered in the field of nanotribology. While the phase transition of lubricants during a squeeze-out process under compression is a long-standing controversial debate (i.e., liquid-like to solid-like phase transition versus amorphous glass-like transition), recent different interpretations to the stick–slip friction of lubricants in boundary lubrication present new challenges in this field. We carry out molecular dynamics simulations of a model lubricant film (cyclohexane) confined between molecularly smooth surfaces (mica)––a prototypical model system studied in surface force apparatus or surface force balance experiments. Through fully atomistic simulations, we find that repulsive force between two solid surfaces starts at about seven lubricant layers (n = 7) and the lubricant film undergoes a sudden liquid-like to solid-like phase transition at n < 6 monolayers thickness. Shear of solidified lubricant films at three- or four-monolayer thickness results in stick–slip friction. The sliding friction simulation shows that instead of shear melting of the film during the slip of the surface, boundary slips at solid–lubricant interfaces happen, while the solidified structure of the lubricant film is well maintained during repeated stick–slip friction cycles. Moreover, no dilation of the lubricant film during the slip is observed, which is surprisingly consistent with recent surface force balance experimental measurements.

For a long time the structural and shear behaviors of simple nonpolar lubricants confined between two solid surfaces have been a controversial debate in the surface force apparatus or surface force balance experiments (1–4). Recent upsurge in this debate concerns whether lubricants fluidize in stick–slip boundary lubrication and whether the dilatency associated with lubricant fluidization could be a criterion for judging the changes in molecular reorganization (5–8). To summarize, we have two questions that need to be answered:

• i)Under normal compression between two molecularly smooth surfaces, how does a nonpolar lubricant film proceed in a thinning or squeeze-out process? And, what is the molecular packing structure of the film during this process? In other words, does the lubricant film undergo a liquid-like to solid-like phase transition (2, 3) or a glass-like transition (4)?
• ii)For a stick–slip friction in boundary lubrication, what happens to the confined lubricant film during the slip when the shear stress exceeds the yield point? Over the past decades, shear melting (9–11) of the confined film during the slip is a common idea in stick–slip friction. During the slip, most of the stored elastic energy in the solidified film is dissipated (10). At the end of the slip the film solidifies again, whereupon the stick–slip cycle repeats itself until the driving block completely stops. What is lacking so far is that one cannot directly observe shear melting in surface force experiments. An indirect way of predicting the absence of shear melting was through the observation of zero dilation of the moving surface during a slip (within a resolution of 0.1 nm) (5). Computational simulation studies using a simple Lennard-Jones (LJ) model fluid (12–14) showed strong evidence of interlayer slips and boundary slips, instead of shear melting. These theoretical studies provide at least some alternate mechanisms of stick–slip friction in boundary lubrication. A challenging issue, however, has been raised recently which states that dilatency alone, whether it exists or not, cannot be a sufficient criterion for concluding the changes in molecular reorganization (6). This is because interlayer slips or boundary slips without shear melting may also result in dilations of lubricant films (1, 6). Moreover, even in a liquid state, dilatency of a nanoconfined lubricant may exist due to the variation of energy dissipation along the film thickness (15).

Here, we perform fully atomistic molecular dynamics (MD) simulations to understand the detailed structural changes and dynamics of a lubricant film during the normal compression and stick–slip motion in boundary lubrication, a critical issue in the field of nanotribology. Given the well-developed computational model of cyclohexane (16), for which the force–distance profile and stick–slip friction of the lubricant were measured in surface force experiments (3, 17–20), the present study focuses on the MD simulation of cyclohexane confined between two molecularly smooth mica surfaces (Materials and Methods). This model lubricant shows the very similar normal compression and shear responses as the OMCTS (octamethylcyclotetrasiloxane) lubricant, a more often used model lubricant in surface force experiments. However, force-field parameters for OMCTS are still in the developmental stage (21, 22).

Results and Discussion

We confine a film of cyclohexane between molecularly smooth mica surfaces in a liquid–vapor molecular dynamics (LVMD) ensemble (Materials and Methods) (14). Cyclohexane lubricant, similar to OMCTS, is known to have very similar force oscillations starting at n = 6 or 7 molecular layers (3), and subsequent sliding of the confining mica surfaces when a shear force is applied leads to a stick–slip motion (17).

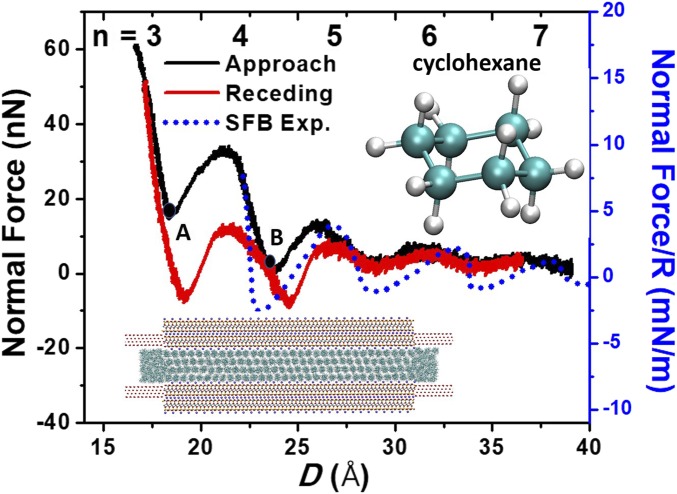
Initially, we use the LVMD simulation to study the normal force oscillations of cyclohexane confined between two mica surfaces. To mimic the surface force balance experiments, we apply a driving spring to the top mica surface and slowly compress the spring to allow the lubricant film to be freely squeezed out (Materials and Methods). Fig. 1 shows the force profiles during the normal approach and receding between mica surfaces. The oscillatory force profile signifies a layered structure formed in cyclohexane between the confining mica surfaces. On approach, the force oscillates between maxima and minima with increasingly pronounced repulsive force peaks as the gap distance (D) is decreased. As can be seen in the figure, repulsive normal force starts at about seven cyclohexane layers (n = 7), corresponding to a film thickness of 3.75 nm or about seven molecular diameters of cyclohexane molecules. The period of force oscillation corresponds to the molecular diameter of 0.55 nm. Remarkably, the positions of force peaks during normal approach are largely consistent with the surface force balance force measurement for cyclohexane (3), while the receding force peak at n = 4 layers has a slight outward shift compared with the experimental results. A detailed MD simulation analysis demonstrates that the layering transition for n < 6 layered film is an abrupt, liquid-like to solid-like phase transition (see Movie S1 for n = 5 → 4 layer transition), consistent with other simulation result for the same liquid film (23, 24). A snapshot of the solidified crystalline structure of cyclohexane film at n = 4 layers is shown in Fig. 1, Lower Inset.

Fig. 1.

Normal forces vs. surface separation (D) between two mica surfaces across cyclohexane during approach and receding. (Inset) Solid-like crystalline structure of cyclohexane film at n = 4 layers. The surface force balance (SFB) experimental results are shown by a dotted trending line for comparison, which was obtained from normal approach and receding force measurements (3). Points A and B on the force-distance profile correspond to normal forces for sliding friction simulations at n = 3 and n = 4 layers.

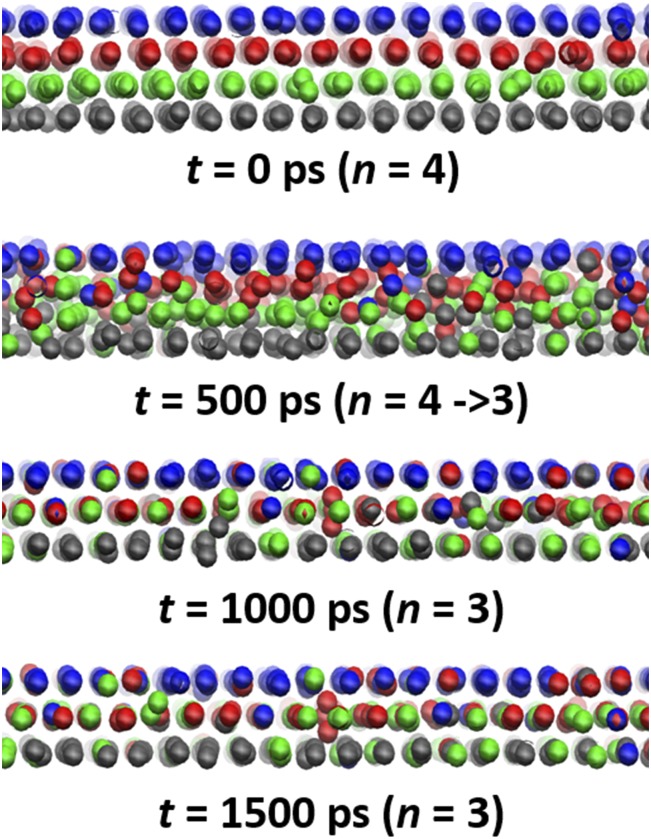
To further understand how the solidified cyclohexane film undergoes layering transition during normal compression, in Fig. 2 we show the detailed snapshots (a)–(d) of configuration changes of the molecular film during the n = 4 → 3 layering transition. Here, cyclohexane molecules are represented by center-of-mass points, with each monolayer molecules colored differently in the n = 4 film before the transition. As the unstable transition begins, we find that the confined molecules start to undergo local permeations during the layering transition, while cyclohexane molecules far from the central region are pushed away from the contact region. This squeeze-out mechanism is fundamentally different from the common idea of layer-by-layer collective squeeze-out mechanism (25, 26), but consistent with a recent surface force experimental study on the layering transition of OMCTS (27), in which the propagation of the squeeze-out front was attributed to the molecular permeation, rather than the large-scale coherent flow of monolayer sliding. This squeeze-out front was also observed in previous computational simulations of LJ model fluids (28). In Fig. 2, the last snapshot clearly shows that the final equilibrium structure of the cyclohexane film at n = 3 layers contains cyclohexane molecules from the original four-monolayer film before the layering transition, supporting the local permeation mechanism of the layering transition.

Fig. 2.

Dynamic progression of the squeeze-out of cyclohexane molecules in the confined region. Molecules in the initial monolayers of n = 4 film are colored differently.

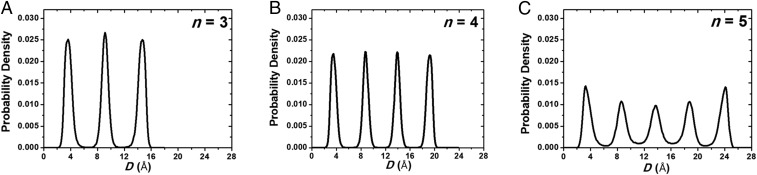
To investigate the structural and dynamic properties of cyclohexane under different confinements between mica surfaces, we carried out MD equilibrium simulations for n = 3, 4, and 5 monolayers for at least 4 ns. We calculated molecular density distributions across cyclohexane films, as well as molecular diffusion coefficients and rotational correlation functions. Fig. 3 shows the equilibrium density distributions of cyclohexane across the film thickness. Overall, the magnitudes of density peaks are gradually decreased from n = 3 to n = 5 layers, especially in the middle region in n = 5 film due to more defects formed in the solid-like crystalline film. For molecular diffusion coefficients (D_mol) of cyclohexane in different layered films (Materials and Methods), our simulation results showed that the diffusion coefficients in n = 3–5 layered films are 0.15, 0.38, and 5.7 × 10⁻¹⁰ m²/s, respectively. The bulk diffusion coefficients from our simulation and experiment (30) are 17.3 and 14.5 × 10⁻¹⁰ m²/s, separately. Evidently, in the solid-like films such as n = 3 and 4 layers, the diffusion coefficient of cyclohexane is decreased by roughly two orders of magnitude compared with the bulk values. This is very surprising because it was suggested that the effective viscosity of lubricant during the liquid-like to solid-like phase transition could be increased by seven orders of magnitude (3) (equivalent to the decrease in diffusion of lubricant molecules by the same orders of magnitude). The reason for this inconsistency, as we explained in our early studies, is due to the significant vacancy diffusion in crystalline solidified films (29).

Fig. 3.

Density distributions of cyclohexane across solidified films of (A) n = 3, (B) n = 4, and (C) n = 5.

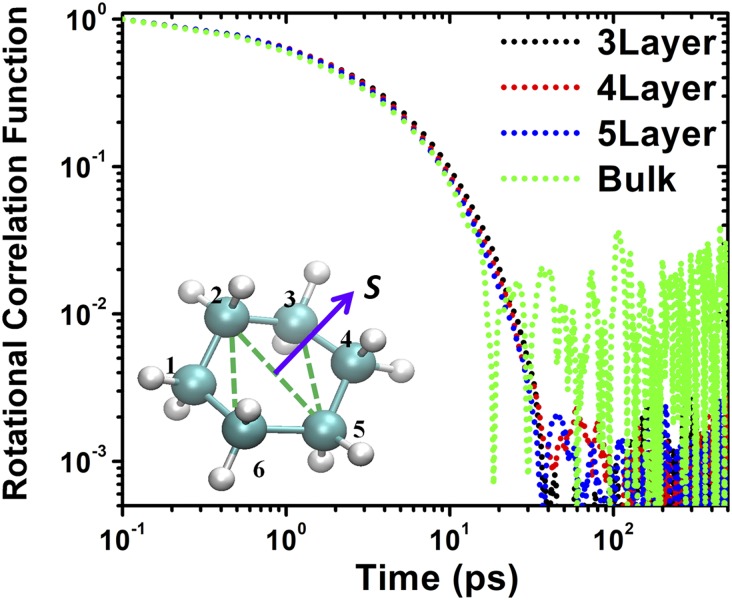
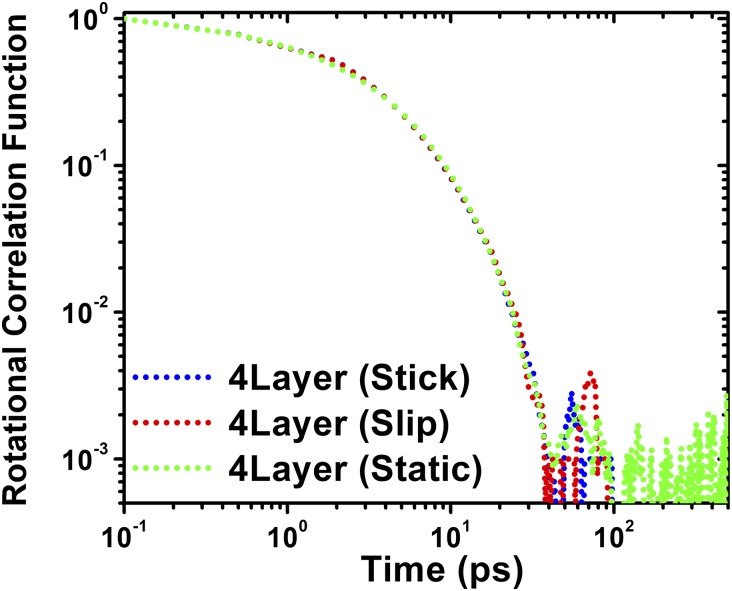
We now consider the rotational dynamic behavior of individual molecules of cyclohexane under nanoconfinement, which is an important measure of relaxation times for such lubricant molecules under different degrees of confinements. We calculate the time variation of the rotational autocorrelation function of the normal vector S perpendicular to the cyclohexane frame, as shown in the Fig. 4, Inset (Materials and Methods). In contrast to the slowing down of diffusion in the molecular film, Fig. 4 shows that the decays of the rotational autocorrelation functions of cyclohexane in different solidified films (n = 3–5 layers) are almost the same as in the bulk fluid. This unexpected result shows that while nonpolar lubricants such as cyclohexane undergo liquid-like to solid-like phase transition under nanoconfinement, this extreme confinement has almost no effect on the internal rotational dynamics of individual molecules. Detailed MD animations of individual cyclohexane molecules in n = 3 solidified film and in the bulk lubricant (Movies S2 and S3) within a time period of 100 ps are provided in SI Appendix.

Fig. 4.

Time variations of rotational autocorrelation functions of cyclohexane molecules in different solidified films and in the bulk lubricant. (Inset) Normal vector S perpendicular to the molecular frame of cyclohexane.

The sliding friction simulation is performed by pulling the top mica surface with a lateral spring (k_y) along the y direction, while holding the normal spring (k_z) in a compressive state (Materials and Methods). We first investigate the sliding friction of n = 3 layers. The normal force during friction is kept at about 16 nN, corresponding to point A in Fig. 1. Fig. 5A shows the stick–slip friction force versus the pulling distance of the spring at a driving speed v = 1m/s. This driving speed is below the critical velocity (v_c) for stick–slip friction happening (31) and is also much slower than the typical sliding speed used in MD simulations of LJ lubricants in Couette flow (on the order of 10∼100 m/s) (11, 32). Given the fact that v = 1 m/s is still at least six orders of magnitude higher than that used in surface force balance experiments while the lateral length scale of the present MD simulation system is at least three orders of magnitude smaller than that of the contact area in surface force balances (3, 17), we point out that the physics of stick–slip friction revealed in MD simulations should be the same as in the surface force experiments. The elegance of the small quantity of lubricant material studied in the MD simulation is its fast relaxation toward equilibrium, allowing the nanoconfined system to respond much faster than the motion of the top mica plate (15). Consequently, the stick–slip dynamics in MD simulations could proceed in a much shorter time scale with a very high driving speed.

Fig. 5.

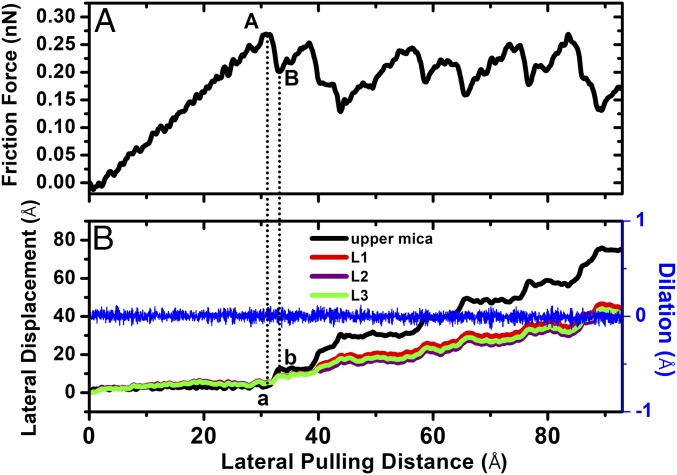
Solidified cyclohexane film (n = 3): (A) Stick–slip friction force versus the lateral pulling distance of the top mica surface. (B) Variations of the lateral displacements of the top mica surface and the three monolayers of the cyclohexane film, as well as the dilation of cyclohexane film, versus the lateral pulling distance of the top mica surface during the stick–slip motion. In A, point A corresponds to the maximum static friction force (about 0.26 nN) before the first slip, and point B corresponds to the friction force at the end of the slip. This slip corresponds to a displacement jump of the top mica surface from point a to b in B.

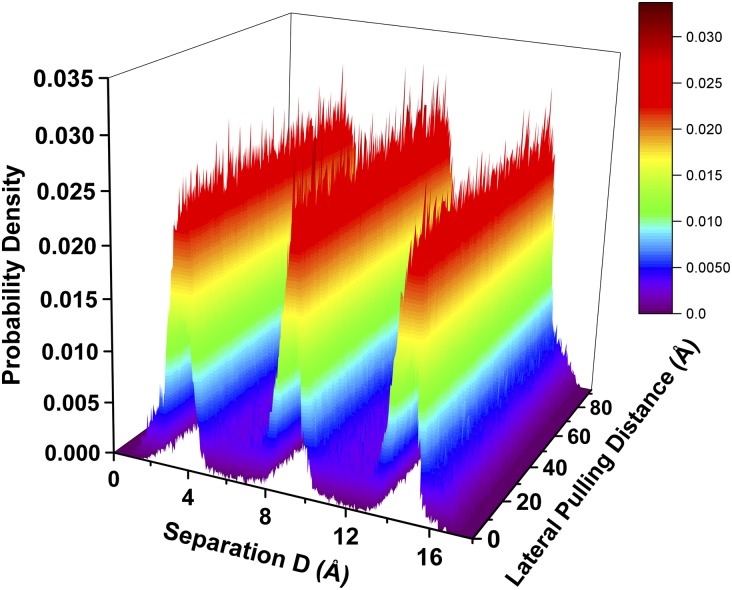
Fig. 5A shows that, initially, as the tension in the spring increases, the static friction force rises linearly. When the maximum static friction force of about 0.26 nN is reached (point A in Fig. 5A), subsequent slip of the top mica surface proceeds until it completely stops for the next stick–slip cycle (point B in Fig. 5A). This slip corresponds to a displacement jump of the upper mica surface by about 1.0 nm (from point a to b in Fig. 5B). We find that, instead of the shear melting of the film, the solidified structure of cyclohexane film is well maintained during the slip. This can be seen in Fig. 6, in which the density peaks of the three monolayers of cyclohexane film keep constant along the stick–slip pathway. Unlike the interlayer slips and wall slips during the stick–slip friction of nonpolar argon film (14), here we find that the slips essentially take place at the mica–cyclohexane interfaces, because all of the three monolayers of cyclohexane undergo the same amount of displacement jumps during the slips (Fig. 5B). Such wall slips at both upper and lower solid–lubricant boundaries are seen in the subsequent stick–slip motions and the difference between the displacement of the top mica surface and the cyclohexane film (as well as between the cyclohexane film and the lower fixed mica surface), becomes increasingly large as the lateral pulling distance increases. These slips result in sharp drops in friction force before a new stick–slip cycle begins. Most notably, we monitor the fluctuation of mica gap distance during the sliding motion of the top mica surface. As shown in Fig. 5B, we do not find any dilation of the cyclohexane film during the stick–slip motion. This result is surprisingly consistent with recent surface force balance experimental findings for the stick–slip friction of lubricant in boundary lubrication (5).

Fig. 6.

Density distributions of the n = 3 cyclohexane film along the stick–slip pathway as a function of lateral pulling distance.

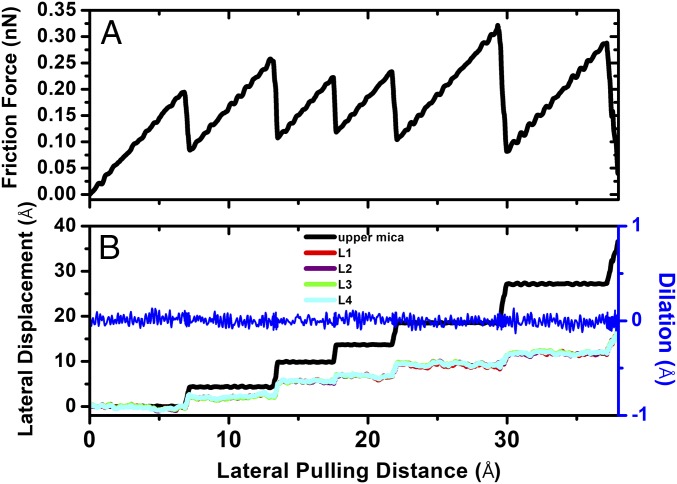
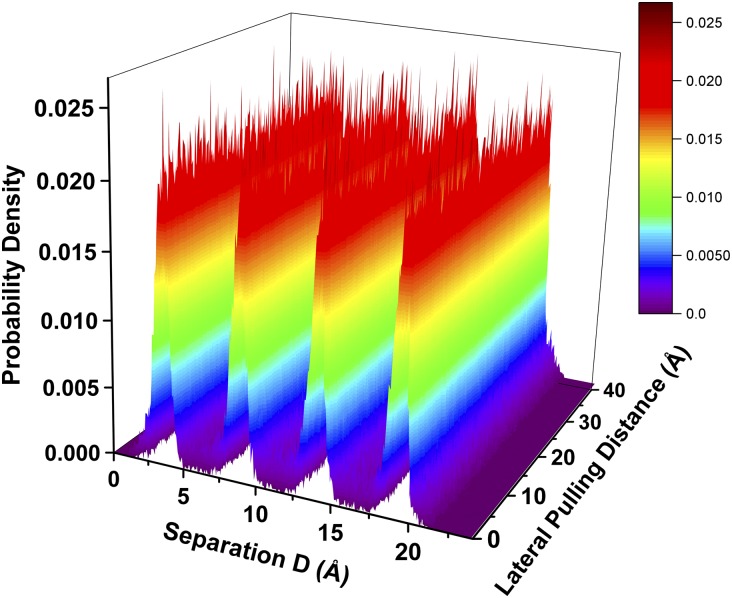
We have also carried out sliding friction simulations for n = 4 layers of cyclohexane film. In this case, the normal force during friction is kept at about 2 nN, corresponding to point B in Fig. 1. Since the maximum static friction force or yield point of a solidified lubricant film is decreased by approximately one order of magnitude as the film thickness is increased from n to n + 1 layers (20), and also because of the very small contact area in MD simulations compared with the very large contact area in surface force balance experiments, we find that shear forces for the n = 4 film are indistinguishable from the thermal noise of force fluctuations. For this reason, we adopt a different approach to simulate stick–slip friction for n = 4 layers. Here, while we use the same lateral spring to drive the top mica surface along the sliding direction at v = 0.2 m/s (compared with v = 1 m/s for n = 3 film), we also use a much harder spring (k_hard = 70 N/m) to drag the top mica surface against the sliding direction, which is equivalent to increasing the static friction force before the slip. At the point where the static friction force is large enough, we release the hard spring and allow the top mica surface to slide until it completely stops. At this point the hard spring is applied again and the system will then be in the next stick stage with continuous extension of the soft spring, until the static friction force is increased significantly before the next slip. Fig. 7 shows variations of the stick–slip friction force (Fig. 7A), the lateral displacements of the top mica surface, and the four monolayers of the cyclohexane film, as well as the dilation of the top mica surface (Fig. 7B), versus the lateral pulling distance of the driving spring. We find that slip events of the top mica surface usually take 200–300-ps time period, equivalent to a very small pulling distance of 0.4–0.6 Å by the soft driving spring. All of the findings found in the case of n = 4 layers are similar to those for n = 3 layers. We find that, during the slip, the crystalline structure of the solidified cyclohexane film is well maintained, as shown by the constant density peaks of the four monolayers shown in Fig. 8. Moreover, there is no dilation of the film during the stick–slip motion of the top mica surface (Fig. 7B).

Fig. 7.

Solidified cyclohexane film (n = 4): (A) Stick–slip friction force versus the lateral pulling distance of the top mica surface. (B) Variations of the lateral displacements of the top mica surface and the four monolayers of the cyclohexane film, as well as the dilation of cyclohexane film, versus the lateral pulling distance of the top mica surface during the stick–slip motion.

Fig. 8.

Density distributions of the n = 4 cyclohexane film along the stick–slip pathway as a function of the lateral pulling distance.

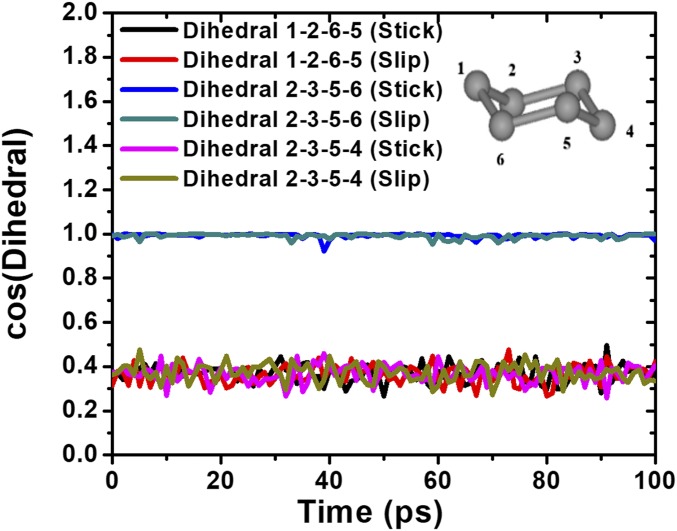
An interesting question concerns whether the rotational dynamics of cyclohexane molecules during the slip stage will be different from the stick stage. In Fig. 9 we show the rotational autocorrelation functions of the normal vector S of cyclohexane molecules during the stick and slip stages versus time in n = 4 solidified film, and compare the results with that of the n = 4 film under equilibrium compression state (Fig. 4). By all means, the stick–slip friction has no effect on the internal rotational dynamics of cyclohexane molecules. Moreover, we are concerned about whether the chair shape of cyclohexane molecules (the most stable conformation at room temperature; Materials and Methods and Fig. 10, Inset) will be maintained during the stick–slip motion, an interesting question of “molecular rigidity” of this kind of molecule. We calculate the cosine values of three different dihedral angles of the molecular frame. As shown in Fig. 10, these cosine values fluctuate around 0.368 and 1.0, respectively, during the time period of 100 ps in either stick or slip stage. They correspond to 68.4° and 0° dihedral angles of the cyclohexane molecule in its free-standing state (16). Apparently, cyclohexane molecules in a solidified film are quite rigid under extreme nanoconfinement, and even keep this property during the stick–slip friction in boundary lubrication.

Fig. 9.

Time variations of rotational autocorrelation functions of cyclohexane molecules in n = 4 film during stick and slip stages. For comparison, the rotational autocorrelation function of the n = 4 film under equilibrium compression state (Fig. 4) is also shown in the figure.

Fig. 10.

Time variations of cosine values of the three dihedral angles of cyclohexane in n = 4 solidified film during stick and slip stages. (Inset) Chair shape of cyclohexane with each bead representing a CH₂ group.

In summary, the present MD simulation studies of cyclohexane films confined between molecularly smooth mica surfaces reveal the following insights into the layering transition and stick–slip friction observed in surface force balance experiments: (i) the confinement-induced layering transition is an abrupt liquid-like to solid-like phase transition; (ii) the layering transition of a nanoconfined cyclohexane film is through a local permeation process, rather than by the layer-by-layer squeeze out mechanism; (iii) the slowing down of molecular diffusion of cyclohexane under nanoconfinement is at most by two orders of magnitude due to the vacancy diffusion in solidified films. However, confinement has no effect on the internal rotational dynamics of cyclohexane molecules; (iv) stick–slip friction happens at mica–lubricant interfaces and the solidified cyclohexane film is well maintained; (v) no dilations of the lubricant film are observed during the slip; and (vi) stick–slip friction has no effect on the internal rotational dynamics of cyclohexane molecules and the molecular rigidity of cyclohexane under extreme nanoconfinement or during stick–slip friction is preserved.

Materials and Methods

Cyclohexane Model.

Cyclohexane (C₆H₁₂) is a nonpolar alkane lubricant that has essentially four different conformations, i.e., chair, half-chair, boat, and twist boat. The most stable conformation is the chair shape (Fig. 10, Inset), followed by the second stable conformation of twist boat, with an energy barrier of 8.53 kcal/mol (16). At room temperature of 298 K, this energy barrier is much higher than kT (∼0.6 kcal/mol). Therefore, the conformation of cyclohexane molecules used in surface force experiments (3, 17–20) should be of a chair shape. We use the OPLS-AA (Optimized Potentials for Liquid Simulations All-Atom) force field (16) for organic hydrocarbon molecules with partial charges on H and C atoms. In OPLS-AA, cyclohexane is among those organic molecules and peptides which are included for fitting force-field parameters, thus there is no issue of potential transferability. For the torsional parameters of cyclohexane molecule, the updated version (33) is adopted, which was proved to be more consistent with experimental data.

Mica Surface.

Muscovite mica [chemical formula K₂Al₄(Al,Si₃)₂O₂₀(OH)₄] is widely used as a molecularly smooth surface in surface force balance experiments. We use the CLAYFF force field (34) to describe atomic interactions in mica. To reduce the computational cost, the top mica sheet is treated as a rigid body and the bottom mica sheet is fixed in the simulation box.

Cyclohexane–Mica Interactions.

Atomic interactions between cyclohexane and mica surfaces include: (i) electrostatic interactions between the charged particles in mica surface and the partial charges on C and H in cyclohexane molecules, and (ii) the LJ interactions between atoms in cyclohexane and mica surfaces. It was believed that the cyclohexane–mica attractive interactions are largely contributed from their electrostatic interactions (23), in which the partial charges are already determined from the OPLS-AA for cyclohexane and the CLAYFF for mica force fields. The atomic LJ interaction parameters between cyclohexane and mica are obtained by using the standard Lorentz–Berthelot combining rules (35). Using these force-field parameters in MD simulations, we compare our results with the previous work (23, 24) with slightly different force-field parameters and conclude the same liquid-to-solid phase transition for cyclohexane under nanoconfinements.

LVMD Simulation.

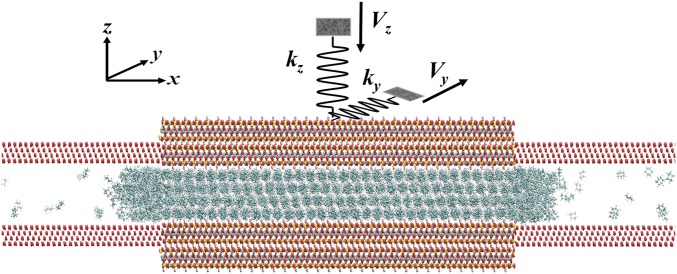
As described in our previous studies (14, 28), we use an LVMD ensemble to allow cyclohexane film to be freely squeezed out during normal compression. This is made possible by extending the mica slit pore with frictionless walls along the squeeze-out direction. The sketch of this LVMD ensemble is shown by Fig. 11. Since the normal and shear forces in the surface force balance experiments are measured through the bending of normal and lateral springs, a driven dynamics model of spring-block system with force constants (k_x, k_y, k_z) should be included. Here, we select k_x = 150 N/m (not shown in Fig. 11), k_y = 0.1 N/m, and k_z = 150 N/m. For the lateral friction simulation, sliding of the top mica surface is along the y direction with a periodic boundary condition applied in this dimension. The molecular system includes a cyclohexane droplet containing 2,512 cyclohexane molecules. The top and bottom mica surfaces are two-layer mica sheets with each mica surface having 32 × 12 × 2 unit cells, containing 64,512 atoms in total. Additional extended frictionless walls are made of 27,648 LJ particles. The dimensions of mica surfaces in the three dimensions are 16.61 × 10.82 × 2 nm. Considering the frictionless LJ walls, the total length of the simulation box in the x direction is 41.5 nm. Simulations are performed using the LAMMPS computational package (36). The time step is 1.0 fs in MD simulation and the temperature of the molecular system is controlled at 298 K by a Nosé–Hoover thermostat (37, 38). A cutoff distance of 11.0 Å is used for the LJ interactions, while the long-range electrostatic interactions for atoms in both mica surfaces and cyclohexane film are computed by the particle–particle particle–mesh method (39).

Fig. 11.

Sketch of the LVMD simulation ensemble.

Calculation of Molecular Diffusion of Cyclohexane.

The translational motion of cyclohexane molecules can be well described by the self-diffusion coefficient, D_mol, determined by the Einstein relation (35): $\langle |r\left(t\right)-r\left(0\right){|}^2\rangle =2d{D}_{mol}t$, where r(t) is the position of the center of mass of cyclohexane molecules at time t, d is the dimensionality of the space in which the molecular diffusion is considered. Here, d = 2 because we only consider the diffusion in the lateral dimensions. The mean-square displacement <|r(t) − r(0)|²> of individual molecules is calculated over all of the cyclohexane molecules in the confined film in the mica slit pore and the time origin average is also taken into account.

Calculations of Rotational Autocorrelation Function of Cyclohexane.

The internal rotational dynamics of cyclohexane molecules can be described by the autocorrelation function decay of normal vector S, defined by the first rank Legendre polynomial, viz., $P_{1,S}\left(t\right)=\langle S\left(t\right)\cdot S\left(0\right)\rangle =\langle \cos \left({\theta }_S\left(t\right)\right)\rangle$, where θ_S(t) is the angle between the vector S at time t₀ = 0 and that at time t₀ + t. The time average runs over all of the cyclohexane molecules in the confined film in the mica slit pore and the time origin average is also taken into account.