Physics considerations in MV-CBCT multi-layer imager design

Abstract

Megavoltage (MV) cone-beam computed tomography (CBCT) using an electronic portal imaging (EPID) offers advantageous features, including 3D mapping, treatment beam registration, high-z artifact suppression, and direct radiation dose calculation. Adoption has been slowed by image quality limitations and concerns about imaging dose. Developments in imager design, including pixelated scintillators, structured phosphors, inexpensive scintillation materials, and multi-layer imager (MLI) architecture have been explored to improve EPID image quality and reduce imaging dose. The present study employs a hybrid Monte Carlo and linear systems model to determine the effect of detector design elements, such as multi-layer architecture and scintillation materials. We follow metrics of image quality including modulation transfer function (MTF) and noise power spectrum (NPS) from projection images to 3D reconstructions to in-plane slices and apply a task based figure-of-merit, the ideal observer signal-to-noise ratio (d′) to determine the effect of detector design on object detectability. Generally, detectability was limited by detector noise performance. Deploying an MLI imager with a single scintillation material for all layers yields improvement in noise performance and d′ linear with the number of layers. In general, improving x-ray absorption using thicker scintillators results in improved DQE(0). However, if light yield is low, performance will be affected by electronic noise at relatively high doses, resulting in rapid image quality degradation. Maximizing image quality in a heterogenous MLI detector (i.e. multiple different scintillation materials) is most affected by limiting total noise. However, while a second-order effect, maximizing total spatial resolution of the MLI detector is a balance between the intensity contribution of each layer against its individual MTF. So, while a thinner scintillator may yield a maximal individual-layer MTF, its quantum efficiency will be relatively low in comparison to a thicker scintillator and thus, intensity contribution may be insufficient to noticeably improve the total detector MTF.

I. Introduction

Megavoltage (MV) cone-beam computed tomography (CBCT) using an electronic portal imaging device (EPID) provides a number of advantageous features in the radiation therapy clinical workflow including 3D mapping and registration using the treatment beam, high-z material artifact suppression, adjustment for patient and tumor anatomical changes, quality-assessment (QA) in pre- and in-treatment contexts (Mijnheer et al., 2013; Celi et al., 2016; Grzadziel et al., 2007), as well as techniques such as dose-guided radiation therapy (DGRT). However, adoption is often limited by the relatively poor image quality and the high dose that current state-of-the-art detectors require. The inherent physical contrast compared with kV counterparts is low, and the MV energies also provide low quantum detective efficiency (QDE), manifesting ultimately as low detective quantum efficiencies (DQE) (Myronakis et al., 2017; Hu et al., 2017b). Recently, a great deal of work has been devoted to the improvement of EPID technology. Studies exploring concepts including multi-layer imager (MLI) architectures (Myronakis et al., 2017; Rottmann et al., 2016a; Hu et al., 2017b), pixelated scintillators (Star-Lack et al., 2015), structured phosphors (Zhao et al., 2004), and novel scintillation materials (Rottmann et al., 2016b) have each shown the potential to substantially improve MV QDE and DQE. Specifically, MLI architectures have been shown to improve DQE(0) by a factor of the number of stacked layers (Hu et al., 2017b), specifically up to approximately 8% for 4-layer imagers with gadolinium oxysulfide (GOS) scintillators (Rottmann et al., 2016a).

The present study uses a hybridized Monte Carlo (Myronakis et al., 2017) and linear systems approach (Hu et al., 2017b) to analyze the potential benefits to MV-CBCT of deploying MLI EPID construction, where four layers, each composed of a conversion-scintillator-readout complex, are stacked. We explore the passage of the frequency domain metrics modulation transfer function (MTF) and noise power spectrum (NPS) from 2D projection space to 3D volumes, quantifying the improvement over currently available single layer imagers (SLI) in MV-CBCT image quality that MLI EPIDs may affect. Further, the ideal observer signal-to-noise ratio (SNR), known as the detectability index (d′) (Gang et al., 2011; Hu et al., 2017a; Hu and Zhao, 2011, 2014; Ikejimba et al., 2014; Richard and Siewerdsen, 2007; Richard and Siewerdsen, 2008b; Vennart, 1997; Hu et al., 2017b) is used as a figure-of-merit in order to precisely quantify task-specific improvements for the detection of clinically relevant targets, such as fiducial markers, tumor masses, and anatomical structures (e.g. the spine) and the improvement in dose savings afforded by the MLI detector. Specifically, the effects of MLI architecture and scintillation material are studied.

II. Theory/Methods

To analyze the effect of detector design on projection image quality and MV-CBCT image quality for both reconstructed volumes (3D) and in-plane slices (IP), a hybrid Monte Carlo simulation and parallel cascaded linear systems modeling approach was devised. Subsequently, modeling of 3D reconstruction was based on the application of the central slice theorem (Gang et al., 2011; Hu et al., 2008; Hu and Zhao, 2011; Richard and Siewerdsen, 2008a; Richard et al., 2008; Siewerdsen et al., 2002; Tward and Siewerdsen, 2008; Tward et al., 2008; Zhao and Zhao, 2008), simulating analytical reconstruction algorithms such as filtered backprojection (FBP).

II.A. Developing projection images

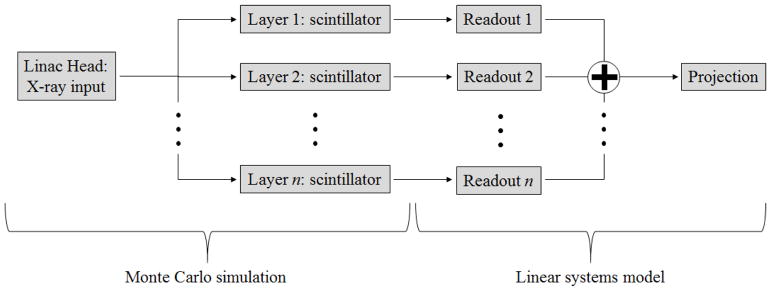
In the present study, the detector transfer functions: modulation transfer function (MTF) and noise power spectrum (NPS); are followed through each stage of the imaging chain. Transfer functions from projection images of an arbitrary MLI detector were modeled based on a hybrid methodology, combining a validated Monte Carlo simulation (MCS) with linear systems theory as seen in Fig. 1.

Fig 1.

Flow chart of the hybrid model for projection images.

II.A.1. Monte Carlo simulation

The Monte Carlo simulation (MCS) is based on Geant4 Application for Tomographic Emission (GATE) and has been validated for flat-panel detection of clinical MV beams in previous work (Myronakis et al 2017). Specifically, scintillation, Mie scattering and optical absorption were included in the simulation. Optical surfaces were simulated using the UNIFIED model. The top surface of the scintillator layer was placed in contact with a white PET layer. The PET-scintillator boundary was specified as a polished Lambertian surface with 96% reflectivity (specified by manufacturer). The modeled LKH-5 scintillator was simulated with a refractive index of 1.58, absorption length of 160 nm and full absorption at an emission wavelength at 545 nm. Scintillation yield was 400 or 600 optical photons per absorbed x-ray photon for LKH-5 and GOS detectors, respectively: one tenth of the actual values for LKH-5 and 1/100 for GOS. Scintillation yield was modeled at reduced values compared to the actual material properties to reduce simulation time and computational resources (Star-Lack et al., 2014). All parameters were acquired through private communications with the manufacturer. It should be noted that LKH-5 is an experimental scintillation material and some properties may be subject to change.

The MLI detector in total is simulated as a parallel cascade, where each layer was modeled using the MCS as an individual single-layer imager (SLI). Each imager included a parallel cascade of a copper conversion plate with 1 mm thickness, a scintillation material and a 0.7 mm silicon dioxide (SiO₂) component to account for the physical properties of the amorphous silicon (a-Si) thin-film transistor (TFT) readout. Both SLI and MLI included a lead-alloy back-plate with 3 mm thickness to prevent back-scattered radiation, which was also modeled. MTF and normalized quantum NPS (qNNPS) were simulated for 6 MV exposures. The beam spectrum was provided by Varian and implemented in the MC model.

II.A.2. Multi-layer model: parallel linear systems

As shown in Fig. 1, projection MTF and NPS for the MLI is the combined result from each individually simulated MCS detector from II.A.1. The MTF and NPS for each MCS detector layer simulation was modified by the aperture function of a square readout, modeling the sampling effect of the TFT array. This is equivalent to multiplication with a sinc function and sinc² function, respectively. The transfer functions of the MLI are calculated by modeling the detector as a parallel cascade, where each SLI layer contributes to the total NPS according to (Richard and Siewerdsen, 2007; Richard and Siewerdsen, 2008a, b; Richard et al., 2005; Richard et al., 2008):

$$S_{\mathit{MLI}}(f_x,f_y)=\sum _{n=1}^N{S}_{\mathit{SLI},n}(f_x,f_y),$$ (1)

where S denotes the NPS along the lateral (x−) and the superior-inferior (y−) directions, and n is the layer number of the MLI, with n = 1 being the top layer of the detector and n = N (where N is typically 4) the bottom. The total MTF may be calculated as (Richard and Siewerdsen, 2008a; Richard et al., 2008):

$$T_{\mathit{MLI}}(f_x,f_y)=\left|\frac{{\displaystyle \sum _{n=1}^N}{k}_n{T}_{\mathit{SLI},n}(f_x,f_y)}{{\displaystyle \sum _{n=1}^N}{k}_n}\right|,$$ (2)

Where T is the MTF (including the aperture function from TFT readout) and k denotes the intensity contribution of an individual SLI layer, which is a linear function of the total number of generated optical photons.

II.B. Modeling CBCT reconstruction

The analysis of CBCT reconstruction is based on a linear-systems analysis using analytical algorithms; i.e. filtered backprojection (FBP). Similar models have been employed for planar imaging (Cunningham et al., 2002; Hu and Zhao, 2014; Richard and Siewerdsen, 2008a; Richard et al., 2005) and other forms of 3D imaging, including kV-CBCT (Gang et al., 2011; Gang et al., 2010; Tward and Siewerdsen, 2008; Tward et al., 2008) as well as partially-3D modalities such as digital tomosynthesis (DTS) (Dahlman et al., 2011; Fredenberg et al., 2010; Hu et al., 2008; Hu and Zhao, 2011; Ikejimba et al., 2014; Zhao and Zhao, 2008; Zhao et al., 2009). In short, measurements of 3D resolution and noise may be derived from planar measurements or models of projection space MTF and NPS. The 3D model was developed based on a system with the same geometry as a Varian TrueBeam linear accelerator (linac) operating at 6 MV, with a source-to-axis distance (SAD) and a source-to-imager distance (SID) of 100 and 150 cm, respectively.

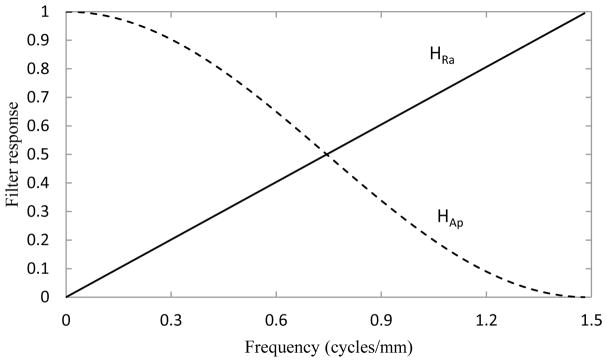
First, projection MTF and NPS are modified by reconstruction filters, including the ramp filter (H_Ra), and apodization filter (H_Ap), plotted in Fig. 2. The ramp filter is calculated by:

$${\mathrm{H}}_{\text{Ra}}=\frac{\left|f_x\right|}{f_{Ny}},$$ (3)

where f is the spatial frequency, which may be defined in the lateral (x−), cranial-caudal (y−), and posterior-anterior (z−) directions, and f_Ny is the Nyquist frequency, calculated as 1/(2m_x), where m_x defines the voxel width in the x-direction. The apodization filter is defined by:

$${\mathrm{H}}_{\text{Ap}}=\frac{1}{2}\left(1+cos(2\pi f_x{m}_x)\right).$$ (4)

Fig. 2.

Reconstruction filters used in the modeled reconstruction algorithm including ramp filter (H_Ra – solid line) and apodization filter (H_Ap – dashed line).

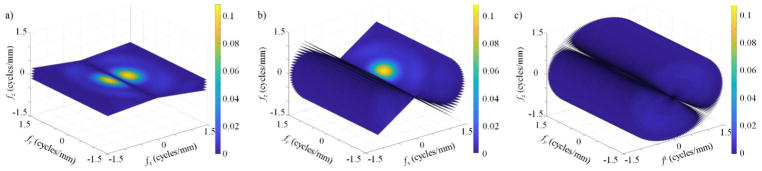
An illustration of the 2D-to-3D conversion is shown in Fig. 3, the mathematical specifics of which have been published previously (Tward and Siewerdsen, 2008; Zhao and Zhao, 2008). Briefly, the response from a projection image at some angle with respect to gravity is mapped along that same angle with respect to the detector plane (i.e. orthogonal to the acquisition angle). As the total scan angle approaches 180 degrees, complete angular sampling is achieved. Increasing the number of views improves sampling of frequency space.

Fig. 3.

Visualization of the conversion from 2D projection images to 3D reconstructions. Modeled conditions include an 18 degree scan with 5 views (a); a 90 degree scan with 25 views (b); and a complete, 180 degree scan with 100 views (c).

In the present study, an acquisition of 400 views over 180 degrees of equiangular projections was analyzed. The MLI was compared to a currently available SLI detector with respect to projection-space, 3D and in-plane NPS and MTF as well as low-dose performance, accounting for electronic noise.

II.C. Ideal observer SNR: d′

We evaluate MV-CBCT performance by employing the detectability index, d′ (Vennart, 1997). d′ is a single figure-of-merit, assessing the ability of the imaging system to accomplish a specific task based on standard metrics of image quality. The present work, being primarily interested in system-level performance, employs an ideal observer formulation of d′ according to (Vennart, 1997; Gang et al., 2011; Hu et al., 2017a; Hu and Zhao, 2011, 2014; Ikejimba et al., 2016; Hu et al., 2017b):

$$\begin{gathered} {d^{\prime }}_{3D}=\sqrt{\int \int \int {\mathit{SNR}}_{3D}^2(f_x,f_y,f_z)d{f}_{x}d{f}_{y}d{f}_z} \\ {d^{\prime }}_{IP}=\sqrt{\int \int {\mathit{SNR}}_{IP}^2(f_x,f_z)d{f}_{x}d{f}_z}, \end{gathered}$$ (5)

where 3D and IP designate entire 3D volumes or reconstructed (in-plane) axial slices, as CBCT images are typically viewed. SNR² is calculated for each frequency according to:

$$\begin{gathered} {\mathit{SNR}}_{3D}^2(f_x,f_y,f_z)=\frac{{[K_c\left|\mathit{task}(f_x,f_y,f_z)\right|T(f_x,f_y,f_z)]}^2}{S(f_x,f_y,f_z)} \\ {\mathit{SNR}}_{IP}^2(f_x,f_z)=\frac{{[\int K_c\left|\mathit{task}(f_x,f_y,f_z)\right|T(f_x,f_y,f_z)d{f}_y]}^2}{\int S(f_x,f_y,f_z)d{f}_y}, \end{gathered}$$ (6)

where T and S denote MTF and NPS, respectively, and task and K_c define the imaging task formulated in the frequency domain and its contrast. In the present study, where image contrast is not affected by the changing studied parameters, K_c is set equal to 1.

It should be noted that the calculation of IP MTF and NPS is simply the summation of the analogous 3D response function in the direction perpendicular to the slice-of-interest.

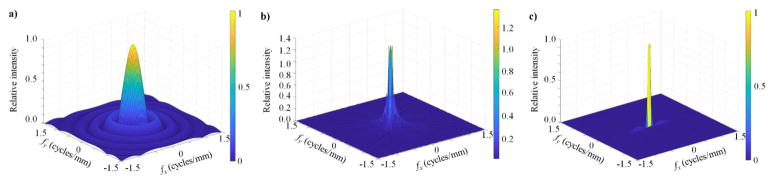
The imaging tasks analyzed were chosen to mimic clinically relevant features (Fig. 4). Fiducial markers and tumors are modeled as spherical objects with radii (r) of 3 and 30 mm at the treatment isocenter. Spherical tasks have object spectra in the frequency domain defined according to (Desponds et al., 1991):

$${\mathit{task}}_{\mathit{Spk}}(f_x,f_y,f_z)=\frac{2r}{2\sqrt{f_x^2+f_y^2+f_z^2}}{J}_1(2\pi r\sqrt{f_x^2+f_y^2+f_z^2}),$$ (7)

where J₁ is the first-order Bessel function of the first kind. Further, the spine is modeled as a 100×4.5 cm cylinder aligned along the y-axis according to (Desponds et al., 1991):

$${\mathit{task}}_{\mathit{Cyl}}(f_x,f_y,f_z)=\frac{2rL}{2\sqrt{f_x^2+f_z^2}}{J}_1(2\pi r\sqrt{f_x^2+f_z^2})\frac{sin(L{f}_y)}{L{f}_y},$$ (8)

where L denotes the cylinder length.

Fig. 4.

2D object spectra for a modeled fiducial marker (2 mm sphere - a), a tumor (30 mm sphere - b), and the spine (1000×45 mm cylinder - c) oriented along the y-axis. Each presented plot is a representative of the axial plane of each 3D object spectra.

This methodology was applied to determine the effect of A) stacking imager layers as in the MLI detector; B) comparing the effects of different scintillation materials on an SLI; and C) designing a heterogeneous MLI, employing multiple scintillation materials.

II.D. Detector configurations

To determine the physical effects of exploring several detector parameters on imaging performance, the model was implemented in several configurations. In the present manuscript, the effects of multi-layer imaging and scintillation material are explored.

II.D.1. Multi-layer, single material imagers

The effect of employing MLI structure as opposed to the typical SLI design for GOS EPIDs was studied. The SLI design was based on a Varian AS-1200 where the GOS thickness (N_GOS) was approximately 290 μm. The modeled MLI detector is based on the prototype imager, which is installed with 430 μm of GOS in each layer.

II.D.2. Single-layer, single material imagers: comparing scintillators

To determine how scintillation material affects CBCT performance we first consider SLI architecture. In this case, based again on the AS-1200 configuration, we consider two scintillators: 290 μm GOS, and 12 mm of LKH-5 segmented scintillating glass. Each reflective segment was 1.51 mm in pitch. LKH-5 was chosen for comparison due to its potential as a commercial scintillation material. It is relatively inexpensive, compared to other solutions, while providing an improvement in DQE(0) of up to approximately 8–11% (Rottmann et al., 2016b).

II.D.3. Multi-layer, multi-material imagers

To determine the effect of multiple scintillation materials in a single MLI detector, we consider a two-layer imager, where one layer consists of LKH-5 (for high-sensitivity) and one layer of GOS (for improved resolution). Both scintillation material thickness and pixel pitch of the GOS layer were considered. Eqs. (1) and (2) were applied to produce projection space NPS and MTF quantities, where the weighting function k for a typical 290 μm GOS layer was 3.59e⁴ and 1.13e³ for the prototype LKH-5 scintillator.

III. Results

III.A. Effect of MLI architecture

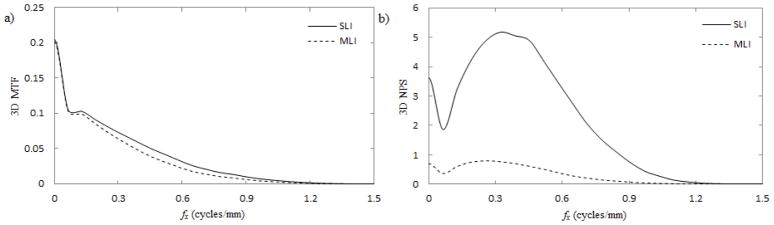
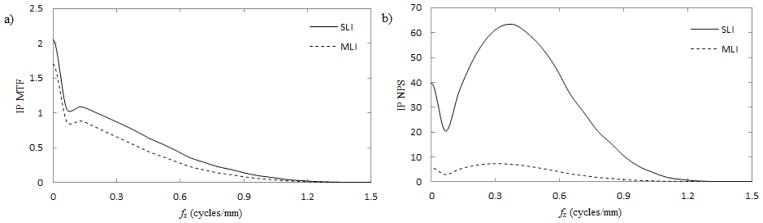
The 3D performance of reconstructed images (i.e. over the entire reconstructed volume) is compared for SLI and MLI imagers in Fig. 5. The in-plane (IP) performance (i.e. any arbitrary axial slice of the 3D reconstruction) is compared in Fig. 6. Losses up to approximately 20% are observed in both 3D and IP MTF. In both 3D and IP NPS, the MLI exhibits a roughly 4–5 fold reduction at all frequencies.

Fig. 5.

The 3D MTF (a) and NPS (b) using SLI (solid lines) and MLI (dashed lines) detectors.

Fig. 6.

The IP MTF (a) and NPS (b) along the f_x-direction using SLI (solid lines) and MLI (dashed lines) detectors. IP response functions were calculated as described in section II.c.

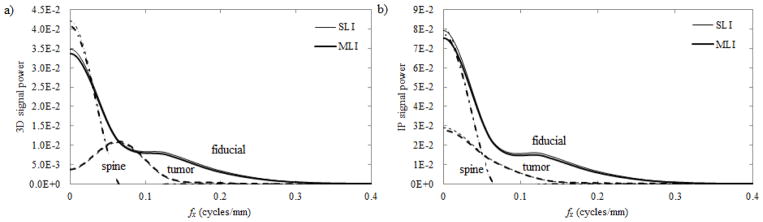
A comparison of the 3D (a) and IP (b) signal power, which is calculated as the numerator in Eq. (6) is plotted in Fig. 7. Although small losses in the MTF are observed in Figs. 5(a) and 6(a) for the MLI, they are sufficiently small and of relatively high frequency that they result in only a small reduction of signal power at maximum (~3%).

Fig. 7.

The 3D (a) and IP (b) signal power as a function of f_x for a variety of imaging tasks including fiducial markers (solid lines); 3 cm tumors (dashed lines); and the spine (dash-dotted lines). Signal power was measured for both SLI (thin lines) and MLI (thick lines) detectors.

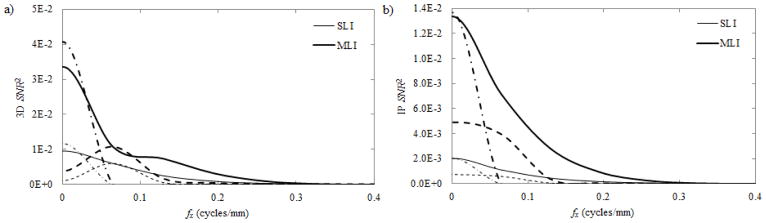
Fig. 8 shows the 3D (a) and IP (b) SNR² as a function of frequency as calculated in Eq. (6). At all frequencies for all objects, the MLI provides an improvement of SNR² 3–5 times better than the SLI detector. Improvements in d′, as evaluated by Eq. (5) are tabulated in Table. 1.

Fig. 8.

The 3D (a) and IP (b) SNR² as a function of f_x for the studied imaging tasks: fiducial markers (solid lines); 3 cm tumors (dashed lines); and the spine (dash-dotted lines). Both SLI (thin lines) and MLI (thick lines) detectors were analyzed.

Table I.

Relative detection task performance, normalized to SLI performance

	3D	IP
Fiducial (2 mm sphere)	1.60	2.57
Tumor (30 mm sphere)	1.40	2.59
Spine (1000×45 mm cylinder)	1.87	2.59

III.B. Mixing scintillator materials

III.B.1. Choosing scintillator materials

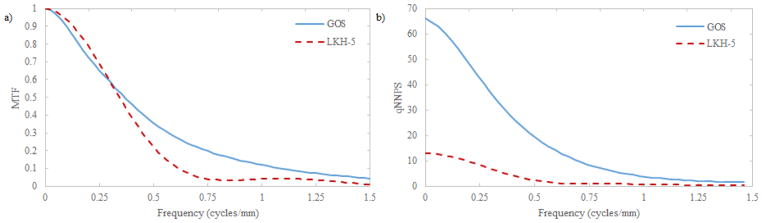
The modeled LKH-5 scintillator, as seen in Fig. 9(a) exhibits a degraded MTF above approximately 0.35 cycles/mm. However, due to its thick scintillator, the qNNPS is almost 5 times lower than the GOS counterpart at all frequencies.

Fig. 9.

A comparison of modeled projection space MTF (a) and qNNPS (b) for GOS and LKH-5 scintillation materials.

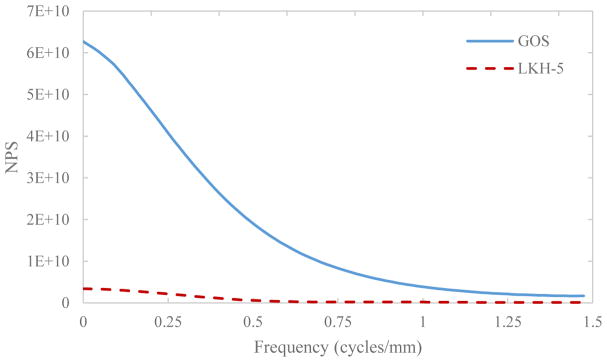
Un-normalized NPS is linear as a function of dose as well as scintillator light yield. As shown in Fig. 10, the NPS for LKH-5 at 1.5 MU is roughly 20 times lower at zero frequency than for GOS.

Fig. 10.

Plot of the NPS for a simulated 1.5 MU exposure for GOS (solid line) and LKH-5 (dashed line).

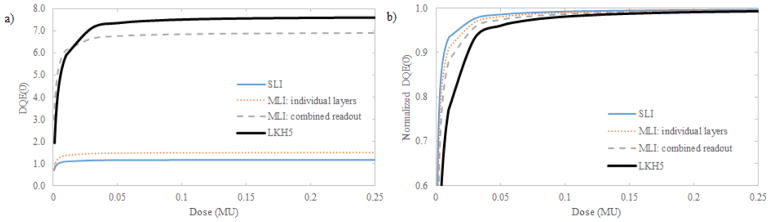
Shown in Fig. 11 is the projection DQE(0) (a) and normalized DQE(0) (b) for a GOS SLI (thin, solid line), individual layers of the MLI (dotted line), the four-layer readout of the MLI (dashed line), and an LKH-5 SLI (thick, solid line). The normalization term was the DQE(0) for a quantum noise limited dose (2.0 MU). As seen in Fig. 11(a), employing MLI architecture or use of the LKH-5 scintillation glass improves DQE(0) by a factor of approximately 4 at quantum noise limited doses. As seen in Fig. 11(b), the DQE(0) of the LKH-5 detector degrades more quickly with decreasing dose than any of the GOS detectors, reaching 96% at approximately 0.05 MU versus less than 0.03 MU for the SLI GOS detectors. Additionally, employing MLI design results in more severe relative degradation of DQE(0) at all doses than any individual MLI layer or the GOS SLI detector. In both MLI and LKH-5 cases, as seen in Fig. 11(a), DQE(0) exceeds that of the standard SLI detector at all studied doses.

Fig. 11.

Plot of the projection DQE(0) (a) and DQE(0) normalized to the quantity at a quantum noise limited exposure (2.0 MU) as a function of dose (in MU).

III.B.2. Effect of multi-layer, multi-material EPIDs

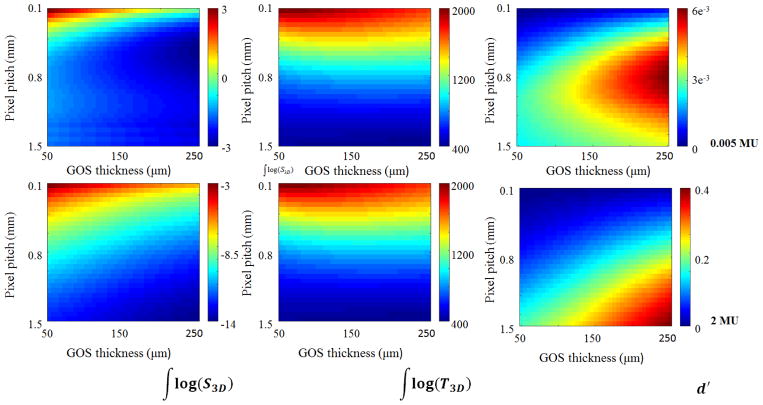
Plotted in Fig. 12 are the logarithm of the total NPS (left column); the total MTF (center column); and d′_IP (right column) as a function of the GOS layer pixel width and scintillator thickness, considering 0.005 MU/projection (top row) and 2 MU/projection exposures (bottom row). In all cases, increasing GOS thickness and pixel width resulted in reduced NPS. While decreasing pixel pitch generally improved MTF, a width between 0.2 mm and 1 mm yielded an optimum value for intermediate thicknesses of GOS. Although reducing noise generally resulted in improvement of d′, at 0.005 MU/projection for GOS thicknesses above 0.200 mm, a pixel pitch between 0.9 and 1.4 produced an optimal result.

Fig. 12.

Comparison of the log of the total NPS (left column), the total MTF (center column), and d′ (right column) for in-plane images of a 0.66 mm spherical object at isocenter imaged at 0.005 MU per projection (top row) and 2 MU per projection (bottom row).

IV. Discussion

IV.A. Effect of MLI architecture

As is seen in Figs. 5(a) and 6(a) the thicker per-layer scintillator of the MLI degrades the MTF at the middle and high frequencies, which is the result of increased optical photon spread. With even thicker scintillators, the expectation would be further MTF degradation. However, despite these losses in spatial resolution, signal power (Fig. 7) and subsequently SNR² (Fig. 8) and d′ are relatively unaffected. This is explained by the fact that losses in MTF are appreciated primarily above 0.25 cycles/mm. The objects modeled, as seen in Figs. 4 and 7, retain most of their spectral power below this frequency. Further, the degradation of the MTF of the thicker layer represents only about 20% at maximum for the IP case. Ultimately, the effect of NPS improvement provided by the MLI configuration is the limiting factor in d′ and SNR². Despite these small losses in signal power from the additional thickness of the prototype detector, improvements in 3D and IP image quality are factors of approximately 1.5 and 2.6, respectively. Greater improvements in IP images in comparison to 3D volumes may be explained by the integration of both signal power and NPS step over f_y prior to division, yielding SNR.

IV.B.1. Adoption of scintillation materials for MV-CBCT

LKH-5, an inexpensive glass scintillator, exhibits a zero-frequency qNNPS roughly 5 times lower than a 290 μm GOS layer (Fig 9b). Although the MTF is degraded above 0.3 cycles/mm due to the 12 mm scintillator thickness, the improved quantum efficiency improves DQE(0) in concurrence with the improvement in qNNPS. While DQE(0) gains are attractive for many imaging applications, it is not the only factor to consider for MV-CBCT. It should be noted that a major limitation of adoption of MV-CBCT is the relatively high imaging dose. While improved DQE will allow lower doses to be implemented while operating above quantum-noise limited doses, division of the total exposure over 400+ views for CBCT requires concurrent analysis of the electronic noise and NPS. NPS, whose quantity is linear with respect to both dose and optical photon yield of the scintillation material, is much lower for LKH-5 than GOS as seen in Fig. 10. This is because the light yield for LKH-5 is much lower than that of GOS. Total NPS of the detector is the sum of the NPS from the scintillation material and that of the TFT array. qNNPS and NNPS are defined as the quotient of the NPS and q (the number of absorbed x-ray photons) and q², respectively; reducing light yield as in the case of LKH-5 will result in a greater effect of additive noise due to detector electronics in comparison with the 290 μm GOS scintillator. This results in the quicker degradation of DQE(0) for LKH-5 exhibited in Fig. 11. So, while improved detector DQE(0) may be beneficial for most imaging applications, particularly when operated at quantum noise limited doses, some consideration to light yield and electronic noise must be made for the design of an MV-CBCT detector.

IV.B.2. Multi-layer, multi-material EPIDs

The results presented in Fig. 12 show that in general, d′ is limited by the total noise of the detector, even considering a very small, spherical object. When detector dimensions are held constant, decreasing pixel pitch results in additional electrical components, increasing electronic noise. Conversely, increasing GOS thickness improves x-ray quanta absorption, decreasing total noise. Although largely a secondary effect, MTF may be maximized at some intermediate GOS thickness as seen in Fig. 12. This is because as per Eq. (2), the final MTF of the detector is the weighted average of the MTF of the LKH-5 layer and the GOS layer, where each scintillator’s contribution is scaled by its relative intensity. Thus, some balance must be struck between a) signal output, which scales with x-ray absorption, which is related to scintillator thickness; and b) maximizing the MTF of the material. At 0.005 MU/projection (top row of Fig. 12) an optimization effect for pixel pitch may be observed between 100 and 250 μm of GOS. This is caused by two factors: 1) the detector is no longer necessarily operating under quantum noise limited conditions; 2) implementation of the reconstruction filters. In the model, the Nyquist frequency was defined as the minimum Nyquist frequency of the MLI detector. So, when the pixel pitch for the LKH-5 layer is smaller than that of the GOS layer, the Nyquist frequency is defined by the pixel pitch of the GOS layer. This results in the relative amplification of low and middle frequency noise by the ramp filter, which eventually offsets improvements in image noise, achieved by reduction of electronic noise and by increasing scintillator thickness. In low dose operation, implementation of reconstruction algorithms may be an important consideration in developing an appropriate detector.

V. Conclusion

We have presented a framework for the analysis and design of multi-layer imagers (MLIs) as well as some physical compromises and concepts for which these EPIDs may be designed and optimized for MV-CBCT imaging. We have shown that in general, MLI design improves detectability through the reduction of noise and that while high-DQE scintillation materials are preferable, some consideration to electronic noise and light yield must be made. Further, we have demonstrated the design considerations when using multiple scintillation materials in a single MLI design and that although MTF may be maximized by following these guidelines, detectability remains largely driven by improvements in noise performance.