Abstract
A cancer of unknown primary (CUP) is a metastatic cancer for which standard diagnostic tests fail to identify the location of the primary tumor. CUPs account for 3–5% of cancer cases. Using molecular data to determine the location of the primary tumor in such cases can help doctors make the right treatment choice and thus improve the clinical outcome. In this paper, we present a new method for predicting the location of the primary tumor using gene expression data: locating cancers of unknown primary (LoCUP). The method models the data as a mixture of normal and tumor cells and thus allows correct classification even in impure samples, where the tumor biopsy is contaminated by a large fraction of normal cells. We find that our method provides a significant increase in classification accuracy (95.8% over 90.8%) on simulated low-purity metastatic samples and shows potential on a small dataset of real metastasis samples with known origin.
Keywords: cancer of unknown origin, classification, transcriptomics, precision medicine
1. Introduction
Cancers are named based on their primary location (the type of tissue where the cancer originated). A lung cancer that has metastasized (spread) to the liver will for example still be defined as a lung cancer and not a liver cancer. In 3–5% of cancer cases doctors only find a metastasis but fail to locate the original tumor; these are called cancers of unknown primary (CUP) [1]. The standard treatment is different for different types of cancer and CUP cases are thus generally harder to treat and consequently have significantly worse prognosis compared to the average cancer patient. Finding the source of malignancy, i.e. the location of the primary tumor, is crucial for improving the treatment of CUP patients. Pathologic evaluation of a biopsy usually includes immunohistochemical (IHC) testing that in some cases can help identify the tissue of origin, but often these tests cannot give a definitive answer. As a result there is a growing interest in using genomic or proteomic molecular data from the biopsy to identify the location of the primary tumor. Several kinds of molecular data from the metastasis such as gene expression [1], methylation [2], miRNA expression [3] or somatic mutations [4] have been shown to be informative about the tissue of origin. Additionally, a FDA-approved test for CUP classification also exists [2]. In this paper, we present a novel method for predicting the location of the primary tumor using gene expression data.
Inherent to the diagnosis, it is impossible to collect samples of the primary tumor from CUP patients and thus no dataset of metastasis and primary tumor samples from CUP patients exists. Instead CUP classification methods have to use data from patients with known primary tumors as training data. Optimally, the training data would come from metastases collected from patients with a known primary tumor, but almost all publicly available data comes from biopsies of primary tumors. For this reason, we use publicly available primary tumor RNA-seq data generated by the TCGA Research Network (http://cancergenome.nih.gov/) as training data.
A problem that can lead to classification errors when predicting the tissue type of a tumor is that biopsies are not pure, but a mixture of tumor tissue and adjacent normal tissue. This is particularly a problem for biopsies from metastases since the surrounding tissue will be of a different tissue type. It is thus very relevant to develop a CUP classification method that is robust to sample impurity. Our method, locating cancers of unknown primary (LoCUP), takes sample purity into account by [1] modelling the mixture of normal and tumor cells directly, [2] employing an empirical prior on sample purity during training, and [3] exploiting that the normal tissue component of the metastatic sample is known when predicting on a metastatic sample. This provides substantial improvements in classification accuracy on impure samples. To our knowledge, LoCUP is the first method to model tumor purity during CUP classification. It is however not the first method to incorporate tumor purity in the analysis of gene expression data. Several methods [5], [6], [7] have been developed that address the closely related problem of deconvolution of a mixed sample into its constituent tumor and normal part. Such deconvolution methods can improve the accuracy of differential expression studies and lead to more accurate biomarkers but they are not directly applicable to the problem of CUP classification.
We compare our method to the classifier used clinically at Department of Molecular Medicine (MOMA), Aarhus University Hospital, Denmark, a multinomial logistic regression classifier with ridge penalty (MLRR) which does not take purity of the samples into account. To the best of our knowledge, this classifier is the only existing solution for CUP samples. Both classifiers are evaluated in three stages. First, classification accuracy is determined when predicting the tissue of origin of primary tumor samples. Second, classification accuracy is determined when predicting on simulated metastatic samples. Third, we evaluate the classifier on a small dataset of real metastatic samples with known primary.
2. Implementation
The input to our method is a m×n matrix where entry i, j is the gene expression of gene j in tissue sample i. A sample xi comes from either a primary tumor (T) or normal, healthy tissue (N) adjacent to a primary tumor denoted by zi∈{T, N}. The tissue type of the each sample is denoted yi∈{1,…,K}.
The gene expression levels of a tumor sample are assumed to be a mixture of two normal distributions. One distribution represents the normal tissue from which the sample is collected and the other distribution represents the tumor of origin. The degree of mixing of the two distributions is determined by a sample-specific mixing coefficient 0≤αi≤1, which has a tissue-dependent beta-distributed prior with shape parameters β1k and β2k which are assumed to be known (see Section 2.1). We illustrate the idea behind the model in Figure 1. The likelihood splits up into tissue-specific likelihoods, i.e.:
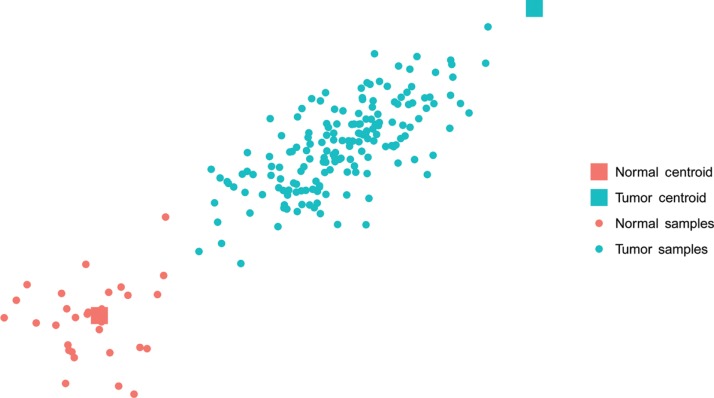
Figure 1:
Example of the model in a 2-dimensional space using simulated data. The normal tissue samples belong to an ordinary normal distribution with “Normal Centroid” as mean. The tumor samples produce an elongated shape because impurity drags them towards the normal tissue centroid.
for k=1,…,K where are the centroids of normal and tumor tissue respectively from tissue type k. The variance of the normal distribution is fixed within each tissue type. We obtain a pseudo-likelihood by multiplying the likelihood with a ridge regularization term of
where we determine λ through grid search. We maximize each tissue-specific pseudo-likelihood independently to get estimates of for k=1,…,K. That is the “training” of the model.
To train the model standard gradient ascend can be applied. However, for efficiency reasons we maximize the pseudo-likelihood by alternating between analytically maximizing the likelihood for with fixed αi’s, and numerically optimizing α until convergence.
To predict the tumor tissue type of a given metastatic sample our classifier takes the metastatic sample, x, and the tissue type of the metastatic-adjacent tissue, y. We classify to the best explaining tumor centroid using the Euclidean distance.
2.1. Estimation of Parameters for Beta Priors
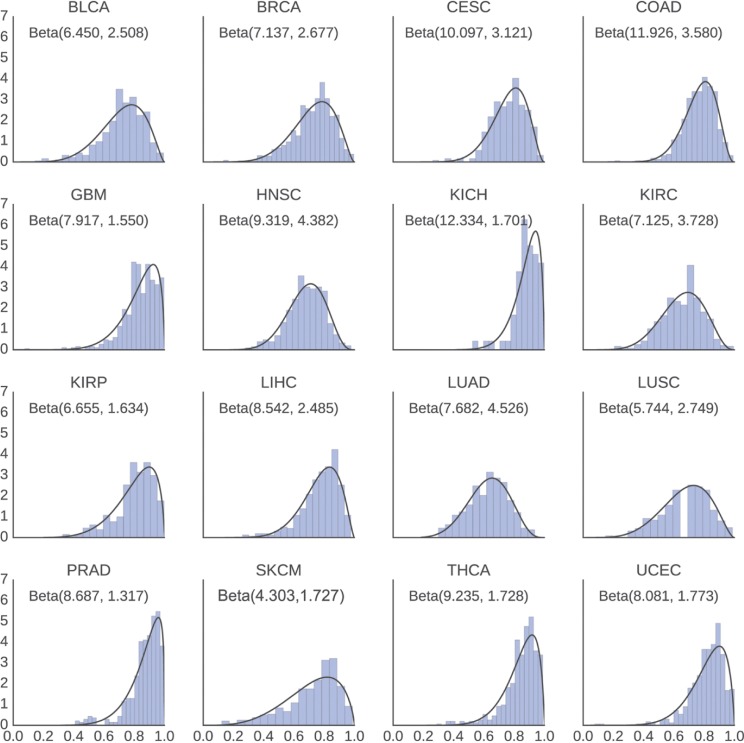
Shape parameters β1k and β2k for the empirical beta priors were estimated from data published in [8] by fitting a beta distribution to the consensus measurement of purity estimations (abbreviated CPE in [8]) for each disease. Histograms of the estimated purities and the fitted distributions can be seen in Figure 2.
Figure 2:
Distribution of estimated purities and the fitted beta distributions. Estimated shape parameters are shown as Beta (β1k, β2k). We observe that a beta distribution is a good fit for the tumor purity estimates.
2.2. Preprocessing
Before training and prediction, the data is [1] scaled to zero mean and unit variance, and [2] the number of dimensions is reduced. We performed a grid search with both principal component analysis (PCA) and linear discriminant analysis (LDA) to determine the most suitable method for dimensionality reduction. The best method and number of components for each type of experiment (see Section 3) is listed in Table 1. Our experiments without scaling and dimensionality reduction resulted in a significantly lower accuracy for both of the tested methods.
Table 1:
Results for the primary (P) and simulated (S) experiments for both methods.
| Accuracy (%) |
Best parameters |
|||||
|---|---|---|---|---|---|---|
| Method | CV | Validation | Dimensionality reduction | Number of components | Regularization factor | |
| P | LoCUP | 94.9 | 95.2 | LDA | 221 | 819.2 |
| MLRR | 96.4 | 97.2 | LDA | 15 | 0.05 | |
| S | LoCUP | 96.3 | 95.5 | LDA | 55 | 102.4 |
| MLRR | 91.1 | 90.8 | LDA | 105 | 0.1 | |
The best parameters were found through a grid search for each experiment and method. On simulated metastatic data, our method clearly outperforms the MLRR method. Note that we in some cases obtain a higher accuracy on the validation data since more training data is available.
3. Application
To investigate the performance of our method we performed a series of experiments on primary tumors, and simulated and true metastatic samples. In this section, we will give an overview of the datasets used and the experimental setup. Source code for the LoCUP classifier and data files used in the analysis are available by request to the corresponding author.
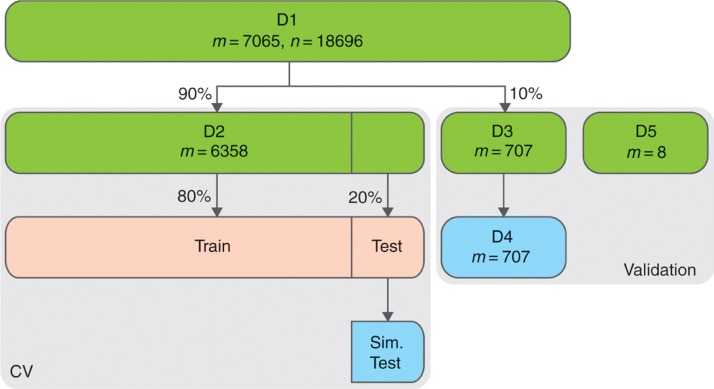
Gene expression data covering K = 16 diseases was collected from The Cancer Genome Atlas (TCGA) (m = 7065, n = 18,696 after removing genes that were expressed in less than 75% of samples). Approximately 10% of the samples are normal tissue. Note that this dataset does not contain any metastatic or CUP samples. We will denote this dataset D1. The dataset was split into a cross-validation (CV) (m = 6358, denoted D2) and validation set (m = 707, denoted D3) in a stratified manner such that each set contains approximately the same number of tissue types and tumor/normal samples. A fourth dataset, D4, was simulated from the validation set by mixing tumor and normal samples (m = 707) from D3. To simulate a metastatic sample, a tumor xT and a normal xN sample is sampled with replacement. The mixed sample is then computed as αxT + (1 − α)xN where α is sampled from the prior distribution for the tissue type of xT. The simulated data maintains the distribution of tissue types of the original data.
Additionally, a dataset, denoted D5, consisting of eight metastatic samples (all with colon primary, ⅛ metastasized to liver, ⅞ metastasized to lung) was obtained from the Department of Molecular Medicine, Aarhus University Hospital, Denmark. This data was processed via a replica of the pipeline used by TCGA. Note that this dataset does not include any normal tissue samples and only contains metastatic samples with known prior. The relationship between these datasets is illustrated in Figure 3.
Figure 3:
Relationship between the datasets used for test (grid search and cross-validation) and validation. Simulated datasets are shown in blue. Datasets derived during cross-validation (only a single fold is shown) are shown in red.
A grid search with 5-fold cross-validation on D2 was performed to optimize the hyper parameters of each method and the preprocessing pipeline. For each set of parameters, two experiments were performed for each fold of the cross-validation. First, to estimate the best parameters of each method on the task of predicting the tissue type of a tumor/normal sample, the method was trained on the training data and predictions were made on the test data. This experiment is denoted P (primary). Second, to estimate the best parameters of each method on the task of predicting the primary tumor component of a metastatic (mixed) sample, each method was trained on the training data and the test data was then used to simulate metastatic samples on which predictions were made. This experiment is denoted S (simulated).
Finally, each method was trained on D2 with the best parameters obtained from the grid search was used to predict on D3 to assess the prediction accuracy on primary tumor samples, D4 to assess the prediction accuracy on simulated metastatic samples, and D5 to assess the prediction accuracy on real metastatic samples.
4. Discussion
We performed three experiments to validate the performance of the classifiers. Firstly, the performance of the classifiers on the problem of tissue prediction. That is, the samples that are predicted on may be either tumor or normal and we simply wish to predict the tissue type. The classifiers were trained on D2 and predictions were made on D3. Our method obtains an accuracy of 95.32% while MLRR obtains an accuracy of 97.2%. This is to be expected since we in this experiment do not take advantage of the ability of our method to handle mixtures of tumor and normal tissue. Secondly, we assessed the performance of the classifiers on simulated mixed samples by training on D2 and predicting on D4. Our method obtains an accuracy of 95.5%, compared to 90.8% for MLRR. Our method thus provides a substantial increase in prediction accuracy. The results are summarized in Table 1.
Thirdly, we were able to collect a small dataset (D5) of metastatic samples with known primary. While this dataset is too small to conclude any improvement in prediction accuracy, it provides an extra layer of validation and suggests that our method predicts as well or better than the MLRR method on real samples. While the two classifiers agree in most cases, we observe a single sample where our method correctly predicts COAD while the MLRR method predicts LUAD (see Table 2).
Table 2:
Prediction on dataset of real metastatic samples with known primary tumor (D5).
| # | Prediction |
True |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| LoCUP |
MLRR |
Est. α | Normal | Tumor | |||||
| 1st | 2nd | 3rd | 1st | 2nd | 3rd | ||||
| 1 | KIRC | KICH | KIRP | KIRC | CESC | LUSC | 0.99 | LIHC | COAD |
| 2 | COAD | LIHC | CESC | LUAD | COAD | CESC | 0.50 | LUAD | COAD |
| 3 | LIHC | COAD | UCEC | LIHC | COAD | CESC | 0.39 | LIHC | COAD |
| 4 | COAD | CESC | BLCA | COAD | LIHC | CESC | 0.53 | LIHC | COAD |
| 5 | LIHC | SKCM | BLCA | LIHC | CESC | BLCA | 0.99 | LIHC | COAD |
| 6 | COAD | CESC | BRCA | COAD | CESC | BRCA | 0.96 | LIHC | COAD |
| 7 | COAD | CESC | BLCA | COAD | LIHC | CESC | 0.50 | LIHC | COAD |
| 8 | COAD | CESC | UCEC | COAD | KIRC | CESC | 0.82 | LIHC | COAD |
Our method correctly predicts five of eight samples while MLRR correctly predicts four of eight samples. Sample 2 is correctly predicted by LoCUP, while MLRR predicts LUAD. Note that the second-best scoring LoCUP prediction for sample 3 is also correct. However, MLRR also predicts correctly on sample 2 and 3 when considering the second-best prediction. Sample 1 may be a polluted or mislabeled sample.
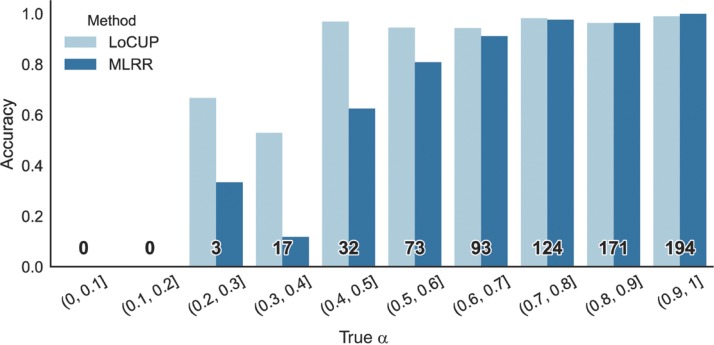
To further validate that our method improves classification on impure tumor samples we plotted the prediction accuracy on the simulated data (D4) binned by the true (simulated) value of αi. See Figure 4. The plot clearly illustrates that our method has a higher accuracy on samples of low to mid-range αi, i.e. a higher accuracy on impure samples.
Figure 4:
Accuracy for the LoCUP and MLRR methods binned by the true α of the simulated samples in D4. The number of samples in each bin is shown in bold. Our method outperforms MLRR on samples where α∈(0, 2, 0.7), that is low-purity samples.
In conclusion, we have developed a method for prediction of the tumor of origin of metastatic samples by modelling a metastatic sample as a mixture of the tumor of origin and the adjacent normal tissue of the metastasis. We have shown that our method outperforms the classification method used at Department of Molecular Medicine (MOMA), Aarhus University Hospital, Denmark for clinical diagnostics (see Table 1) on simulated metastatic samples, with a clear improvement on very impure samples (see Figure 4). We have further validated our method on a small dataset of real metastatic samples (see Table 2) and obtained a small improvement. The method models metastatic samples as a mixture between normal and tumor cells, but in some cases tumor purity can also be affected by tumor-infiltrating leukocytes [7]. A possible future improvement of the method would thus be to investigate this phenomenon and possibly improve the classification by adding leukocytes as a third component to the mixture.
Acknowledgments
The results presented here are in part based upon data generated by the TCGA Research Network: http://cancergenome.nih.gov/. We wish to thank Jacob Malte Jensen and Palle Villesen for useful discussions.
Conflict of interest statement:
Authors state no conflict of interest. All authors have read the journal’s Publication ethics and publication malpractice statement available at the journal’s website and hereby confirm that they comply with all its parts applicable to the present scientific work.
References
- [1].Vikeså J, Møller AK, Kaczkowski B, Borup R, Winther O, Henao R. et al. Cancers of unknown primary origin (CUP) are characterized by chromosomal instability (CIN) compared to metastasis of known origin. BMC Cancer. 2015;15:151. doi: 10.1186/s12885-015-1128-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Moran S, Martínez-Cardús A, Sayols S, Musulén E, Balañá C, Estival-Gonzalez A. et al. Epigenetic profiling to classify cancer of unknown primary: a multicentre, retrospective analysis. Lancet Oncol. 2016;17:1386–95. doi: 10.1016/S1470-2045(16)30297-2. [DOI] [PubMed] [Google Scholar]
- [3].Ferracin M, Pedriali M, Veronese A, Zagatti B, Gafà R, Magri E. et al. MicroRNA profiling for the identification of cancers with unknown primary tissue-of-origin. J Pathol. 2011;225:43–53. doi: 10.1002/path.2915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Marquard AM, Birkbak NJ, Thomas CE, Favero F, Krzystanek M, Lefebvre C. et al. TumorTracer: a method to identify the tissue of origin from the somatic mutations of a tumor specimen. BMC Med Genom. 2015;8:58. doi: 10.1186/s12920-015-0130-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Wang N, Gong T, Clarke R, Chen L, Shih IM, Zhang Z. et al. UNDO: a Bioconductor R package for unsupervised deconvolution of mixed gene expressions in tumor samples. Bioinformatics. 2015;31:137–9. doi: 10.1093/bioinformatics/btu607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Ahn J, Yuan Y, Parmigiani G, Suraokar MB, Diao L, Wistuba II. et al. DeMix: deconvolution for mixed cancer transcriptomes using raw measured data. Bioinformatics. 2013;29:1865–71. doi: 10.1093/bioinformatics/btt301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Anghel CV, Quon G, Haider S, Nguyen F, Deshwar AG, Morris QD. et al. ISOpureR: an R implementation of a computational purification algorithm of mixed tumour profiles. BMC Bioinformat. 2015;16:156. doi: 10.1186/s12859-015-0597-x. Available from: [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Aran D, Sirota M, Butte AJ. Systematic pan-cancer analysis of tumour purity. Nat Commun. 2015;6:8971. doi: 10.1038/ncomms9971. [DOI] [PMC free article] [PubMed] [Google Scholar]