Abstract
Nonlinear protein binding is traditionally thought of as an increasing fraction unbound with increasing total drug concentration. In the past several years, research into the protein binding of several tetracyclines has shown that an unexpected and counterintuitive phenomenon has been observed. Specifically, that of decreasing unbound drug fraction with increasing total concentrations of drug over certain concentration ranges. While several studies of tigecycline have shown the importance calcium and its chelation may play in the protein-drug interaction, the potential clinical implications and relevance have not been explored. Here we define typical and atypical nonlinear protein binding, overview protein binding theory, and discuss theoretical implications on pharmacokinetics. Using tigecycline as an example, in silico simulations and calculations show how when atypical nonlinear protein binding is not accounted for free drug exposure and drug tissue penetration may be overestimated. It is important to revisit the impacts of nonlinearity in protein binding on clinical pharmacokinetics and pharmacodynamics, and ultimately, clinical efficacy. While this phenomenon could potentially warrant clinical dose adjustment for certain compounds, it also presents a potential opportunity to exploit underlying mechanisms to develop new therapies and better understand molecular interactions of xenobiotics within the physiological system.
Keywords: protein binding, clinical pharmacokinetics, nonlinear pharmacokinetics
1. Introduction
For nearly a century, the protein binding of drugs has been depicted by a simple saturable binding of drug to protein binding sites. Very often, due to the large binding capacities of proteins or low binding affinities of drugs for proteins, saturation does not occur clinically and the unbound drug fraction is therefore independent of its total concentration. This is referred to as linear protein binding. Saturation of proteins results in concentration dependency and can occur and have clinical relevance for some drugs in general, or in specific clinical scenarios or populations. Until recently the saturation behavior was the only nonlinear phenomenon widely known. The recent development of several tetracycline derivatives (i.e. tigecycline, eravacycline) has revealed atypical nonlinear protein binding i.e. the counterintuitive trend of increased binding to protein as total drug concentrations increase1–4. Implications of atypical nonlinear protein binding on clinical efficacy or safety were not assessed.
This review aims to describe the concepts surrounding protein binding, while giving a more in depth view into nonlinear protein binding than presented previously. The theoretical pharmacokinetic (PK) impacts of nonlinear protein binding including typical and atypical will be discussed. And finally, tigecycline is used as an example to explore potential effects of atypical nonlinear plasma protein binding on clinical PK.
2. Basics of Protein Binding
2.1. A BRIEF HISTORY
The techniques by which protein binding of drugs are characterized were first developed in the early 1900s5. The idea of blood as transport organ was described by Bennhold in the late 1930s5. Langmuir’s isotherm established the chemical interaction basis for these protein-drug interactions, which is still used today6. Over the years there has been intense discussion regarding the clinical significance of protein binding and corresponding alterations7–9. One could argue that for the majority of drugs, alterations in PK caused by changes in protein binding are clinically insignificant9. Even if true only for a particular population, it should be part of the clinical reasoning to consider the effects of altered drug-protein binding in different disease states, age groups, acute inflammatory conditions, and polypharmacy.
If the efficacy of a drug is known to be potentially impacted by changes in plasma protein binding, investigation of such potential alterations should be performed. Protein binding is an important consideration in drug design, discovery and development 10. Protein binding is evaluated in in vitro and in vivo pre-clinical settings and ideally is used to predict unbound (active) concentrations in clinical studies, allowing for lead optimization10. Protein binding may be determined in clinical samples, but this is not always the case. Often protein binding values from previous in vitro determination in human plasma are used to estimate binding of clinical samples. For accurate extrapolation or prediction of free clinical drug exposure, differences in interspecies physiological, metabolic, and elimination processes should be considered.. Furthermore, any expected pharmacodynamic effect, be it drug efficacy or toxicity, should be predicted based on free exposure. Given the increased use of pharmacometrics to predict clinical dosing, mathematical models may be developed to predict the effects of such alterations in a clinical setting. In the future, clinical models may be developed and implemented at the bedside to deliver optimized therapy to patients for drugs requiring adjustment in the presence of more complex PK phenomena, such as nonlinear protein binding.
2.2. THEORY OF NONLINEAR PROTEIN BINDING
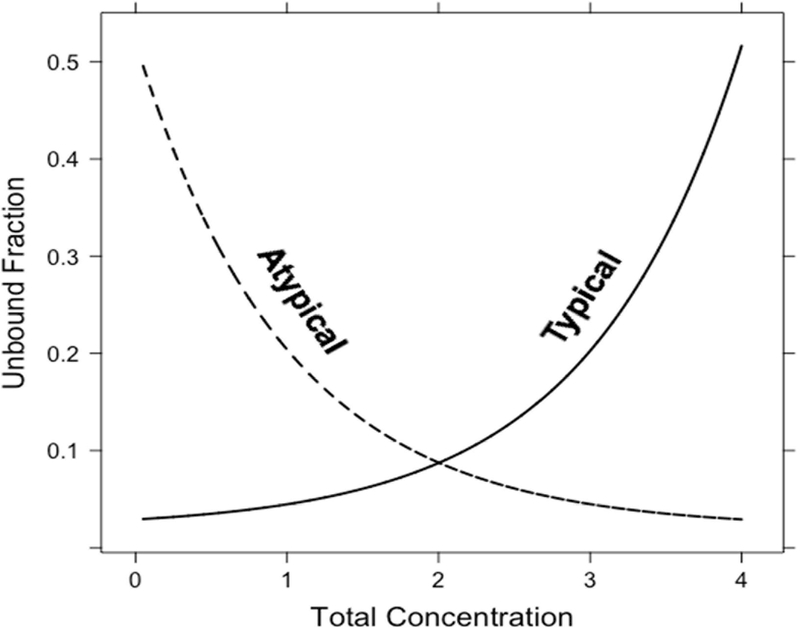
The expected binding behavior for almost all drugs is that the fraction unbound (fu) is constant over a concentration range (i.e. linear protein binding) until a point at which protein binding sites begin to be saturated, leading to increasing unbound fraction with increasing total concentrations, typically referred to as nonlinear protein binding. This behavior is described as part of the Langmuir model5,6 (illustrated in Equation 1 and Figure 1), where Amax is the maximum binding capacity for substrate, Kd is the dissociation constant, Cu is the unbound drug concentration, and Cb is the bound drug concentration.
Figure 1: Illustration of different types of nonlinear protein binding.
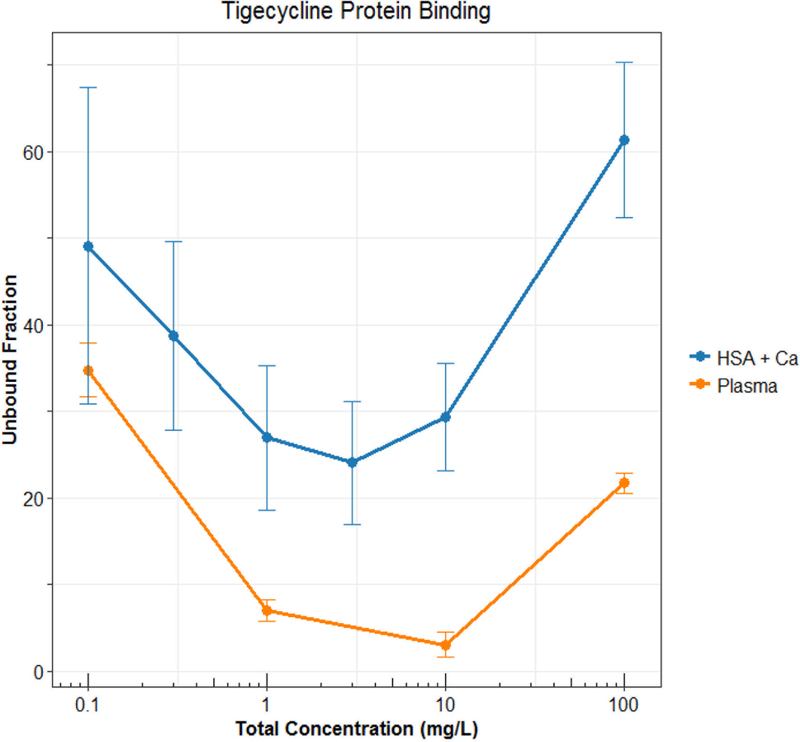
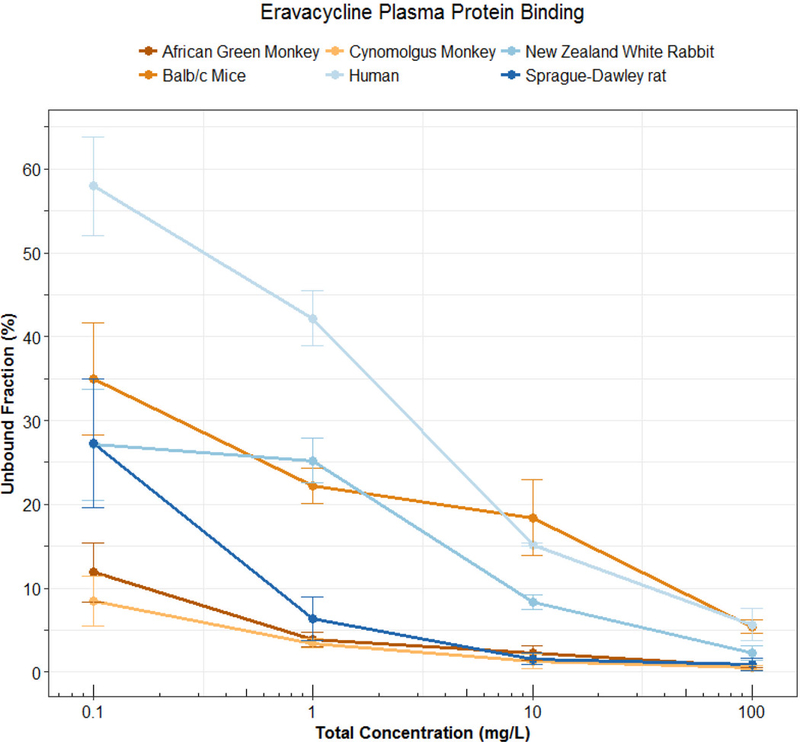
Technically speaking, nonlinear protein binding is defined as any pattern of protein binding which is not linear (or at a concentration range at which the fu is not constant). Until recently, nonlinear behaviors other than the Langmuir model had not been well described. During the development of tigecycline, a unique protein binding behavior was observed and not pursued further until recent investigations linked the nature of the behavior to divalent metal ion chelation1,11,12. Other tetracyclines (i.e. eravacycline2,13, TP-2714, minocycline and doxycycline3) have displayed similar behavior, but further mechanistic investigations have not been performed. The nonlinear protein binding of tigecycline has been described as “U-shaped” with a counterintuitive decrease in fu with increasing total concentrations and an eventual return to the appearance of the more typical saturation behavior (Figure 2). The evidence of increasing binding with increasing total concentrations of eravacycline in several species is shown in Figure 3. Similar trends have been observed for minocycline, doxycycline, and TP-271.
Figure 2: Observed “U-shaped” protein binding behavior of tigecycline (Mean±SD). Data from Mukker et al.24 and Dorn et al.12 HSA: human serum albumin.
Figure 3: Protein binding (Mean±SD) of eravacycline in pooled plasma of 6 different species. Data previously presented by Singh et al.2.
Any behavior deviating from a typical Langmuir, saturation-related, nonlinear behavior, has been defined as “atypical nonlinear protein binding”11, while the former will be referred to as “typical nonlinear protein binding”. These definitions have been listed in Table 1 for quick reference and clarity.
Table 1: Pertinent definitions and examples of different binding phenomenon.
| Term | Definition | Examples |
|---|---|---|
| Clinical concentration range |
A concentration range which is clinically observable or expected for a given regimen |
When X mg of drug A is given to a patient of interest, observable in vivo concentrations range from 0 to XX mg/L at the site where protein binding is being assessed (typically, the plasma) |
| Linear protein binding | - fu remains constant over a clinical concentration range |
- Most drugs |
| Nonlinear protein binding |
- fu does not remain constant over a clinical concentration range |
|
| Typical Nonlinear protein binding |
- A subclassification of nonlinear binding - Protein is saturated and fu increases with total concentration (Langmuir model) - Often what is being referred as “nonlinear protein binding” or “concentration-dependent protein binding” |
- Most drugs exhibit this behavior at some concentration range (may or may not be clinical) - disopyramide41 - ceftriaxone42 - valproic acid43 - eplerenone44 - linagliptan45 - trandolaprilat46 - prednisolone47 |
| Atypical Nonlinear protein binding |
- A subclassification of nonlinear binding - Any nonlinear behavior which does not follow typical saturation/Langmuir model |
- doxycycline3 - minocycline3 - tigecycline1,12,24 - eravacycline2,13 - TP-2714 |
2.3. FACTORS IMPACTING PLASMA PROTEIN BINDING DETERMINATION
Various methods for plasma protein binding determination are available, including equilibrium dialysis, ultrafiltration, ultracentrifugation, charcoal adsorption, chromatographic methods, and solid phase microextraction. Table 2 briefly describes advantages and disadvantages of commonly used protein binding methods. Equilibrium dialysis is often considered the gold standard but the ease of use and fast processing makes other methods like ultrafiltration attractive in many settings14. Protein binding should be determined under appropriate physiological conditions, over a clinically meaningful concentration range15, and with great methodological care for experimental factors such as pH15, buffers15 and solvents used, device16, temperature16, animal species17, protein concentration15, proteins or endogenous substances present15, and sample volume. Regardless of the method used, each method has its own caveats and considerations that have been reviewed and investigated extensively elsewhere14.
Table 2: Summary of advantages and disadvantages of commonly used protein binding determination methods.10,
| Method | Advantages | Disadvantages |
|---|---|---|
| Equilibrium dialysis | - High throughput - Relatively straight forward method - Reliable results, gold standard |
- Experiment duration (drug stability) - Less physiological - Technical concerns (volume shifts) |
| Ultrafiltration | - High throughput - Rapid - Relatively straight forward method - Ease of use |
- Technical considerations (binding to membrane, leakage, volume shifts) |
| Ultracentrifugation | - Simple - No membrane-related technicalities |
- Low throughput - May overestimate binding - Not favorable for large molecules |
| Microdialysis | - Can use in nearly any tissue of interest - Versatile - Can use in vivo - No concern of volume shifts - Ease of continuous sampling |
- Semi-invasive - Low throughput - Technically more complex (binding to membrane/tubing, equilibration and assay development) |
| Charcoal adsorption | - No membrane adsorption concerns - Good for drugs bound to lipoproteins - Characterize full binding profile |
- Binding underestimation - Extensive sampling |
| Chromatographic methods |
- Accurate - Fewer practical considerations (binding to membrane, volume gradients, membrane leakage) - Rapid - Small sample volume needed |
- Less physiological - More complex development and execution - Low sensitivity |
| Solid phase microextraction |
- Simple - High throughput - Highly sensitive |
- Experiment duration - Technically sensitive |
3.0 Theoretical Implications and Examples
3.1 THEORETICAL IMPLICATIONS
The impacts of changing fu in linear scenarios have been previously discussed18. In summary, any changes in protein binding may affect the clearance (CL) and/or volume of distribution (Vd) of a drug, which may or may not significantly impact PK parameters (i.e. half-life, and free and total steady state, minimum and maximum concentrations), PK in the tissues of interest, or bioavailability. These changes may be significant based on route of administration (oral versus parenteral), low versus high extraction, and original tissue distribution (or the magnitude of Vd). Given that changes may affect elimination processes, for orally administered drugs subject to first pass metabolism, bioavailability may be impacted for high extraction drugs but not for low extraction drugs. Conversely total clearance would be significantly affected for low extraction drugs for either route of administration. In the case of drugs with low Vd, changing fu may not significantly impact Vd, while for high Vd, changes in fu are more likely to impact distribution. Changes in Vd also depend on tissue binding relative to changes in plasma protein binding.
3.1.1 Typical Nonlinear
Similar to linear protein binding, effects of changing protein binding can be anticipated based on Vd, extraction ratio, and administration route. Given the time- and concentration-dependent nature of changing PK parameters in the presence of nonlinear binding, predicting PK is complicated. As concentration-time profiles may not explain much about changes in distribution, it is important to assess the implications of these alterations at clinically relevant doses/concentrations and be aware of underlying mechanisms. Several simulation and modelling exercises have been performed to investigate the effects of nonlinear binding behavior on clinical PK.
Martin evaluated dissociation constants (Kd) a main driver of the potential for albumin saturation stating that Kd less than 1×10−4 was conducive with potential saturation especially at higher doses19. He noted that calculating elimination rate constants (ke) from apparently linear total concentration-time curves would underestimate elimination19,20. More drug is present in plasma as concentrations decline due to a decrease in saturation of proteins and decrease in fu. As time goes on, this decline in fu leads to a continued decrease in ke and an increase in half life (t1/2). ke as related to free drug concentration over time remains linear. Given the expected increase in protein saturation at high doses, ke at high concentrations is especially underestimated, while at later time points, when concentrations are lower and saturation decreases, ke is overestimated. Log(concentration)-time nonlinearities may be mistaken for slower elimination at higher doses, rather than nonlinear protein binding.
øie and colleagues recognized that earlier simulations assumed linear tissue binding and thus explored saturable plasma and/or tissue binding in a one compartment model after intravenous (IV) administration for drugs with various intrinsic clearance (CLint) and Vd values21. Their model also assumed binding in the extracellular space when saturable plasma protein binding was present and therefore defined tissue binding as that intracellular binding. Table 3 summarizes their simulated results for eight scenarios: Typical nonlinear plasma protein binding with low or high Vd, and low or high CLint, linear plasma protein binding with typical nonlinear tissue binding, with low or high CLint, and finally, typical nonlinear plasma and tissue protein binding, with low or high CLint. After a single IV administration, when typical nonlinear binding was present in either plasma or tissues, as expected, unbound fraction in plasma and/or tissue (fuP and fuT) decreased with total concentration. Decreases in fuP results in decreased Vd over time, while decreases in fuT led to increased Vd over time. When both fuP and fuT change (in the case of typical nonlinear binding in plasma and tissue), Vd may increase, decrease or remain similar, depending on the relative magnitude of the unbound fraction changes. In these simulations, fuP and fuT changed proportionally and the subsequent changes in ke, t1/2, and PK profiles reflected no change in Vd. As per theory, only changes in fuP affect low extraction (low CLint) drugs, while high extraction drugs are unaffected. In the case of low Vd and low extraction with typical nonlinear plasma binding only, since the Vd decreases with concentration, the concavity of the log-concentration time curve is less striking. For high Vd, low extraction drugs with only saturable plasma binding, the approximate changes in Vd and CL were similar, leading to no apparent change in ke. This is interesting as the log-total concentration versus time curve exhibits convexity, which would lead one to assume nonlinear elimination. By examining the log-free concentration versus time profile, linear elimination is revealed. While these explorations by øie and colleagues did not address all possible scenarios, especially those where simultaneous changes are not proportional, they serve as a good starting point for predicting expected alterations in PK resulting from changes in fuP and fuT under various PK scenarios. It should not go without emphasis that without considering saturable binding these curves may be misinterpreted as nonlinearities in drug metabolism or multiple compartmental distribution.
Table 3: Simulated PK changes caused by nonlinear plasma and tissue protein binding.
| Change with Time | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| fuP | fuT | CLint | Vd | fuP | fuT | Vd | CL | ke | t1/2 | Cp | Cu |
| Typical Nonlinear |
Linear | Low | Low | ↓ | - | ↓ | ↓ | ↓* | ↑* | Concave* | Concave* |
| High | ↓ | - | ↓ | ↓ | -* | -* | Convex* | Linear* | |||
| High | Low | ↓ | - | ↓ | - | ↑ | ↓ | Convex | Sigmoidal | ||
| High | ↓ | - | ↓ | - | ↑ | ↓ | Convex | Convex | |||
| Linear | Typical Nonlinear |
Low | - | - | ↓ | ↑ | - | ↓ | ↑ | Concave | Concave |
| High | - | - | ↓ | ↑ | - | ↓ | ↑ | Concave | Concave | ||
| Typical Nonlinear |
Low | - | ↓ | ↓ | -* | ↓ | ↓* | ↑* | Concave* | Concave* | |
| High | - | ↓ | ↓ | -* | - | -* | -* | Linear* | Sigmoidal* | ||
*During the simulations of øie and colleagues21 changes in influential parameters impacted subsequent parameters differently depending on the relative changes in other parameters. For those with an asterisks, simulated results are listed but theoretically under different conditions the results may differ.
McNamara and colleagues concurred with øie and colleagues model and derived new Vd terms to describe the changing PK terms and applied this to ceftriaxone22,23. They assumed no intracellular/tissue binding given the properties of ceftriaxone and included typical nonlinear binding of proteins in the extracellular space based on the expected concentration of albumin in the interstitium as compared to plasma. In their simulations they observed concave concentration-time profiles for ceftriaxone at higher doses.
3.1.2 Atypical Nonlinear
With these models of typical nonlinear protein binding, one could predict PK alterations for atypical nonlinear protein binding. The complexity arises from when the drug potentially reverses back to the typical nonlinear phenomenon at higher concentrations, which is the case for tigecycline. In these situations, use of pharmacometric modelling to simulate complex changes, is a better approach.
Currently the only class of drugs which appears to have atypical nonlinear PPB is the tetracyclines. While it is important to note that this behavior has not been observed or characterized for all tetracyclines, it has been recently well-described for minocycline3, doxycycline3, tigecycline12,24 , eravacycline2,13, and TP-2714. Of note, the plasma protein binding of omadacycline, a new tetracycline derivative in clinical development, was found to be linear over the investigated concentration range25. This may be due to the overall lower binding of omadacycline (21.3%25) as compared to other tetracyclines exhibiting atypical nonlinear binding (73–93%26). Clinical PK effects of these atypical phenomena have not been studied in clinical trials or modeled with the changing fu in mind. One study has investigated the use of the fu in clinical breakpoint determination for tigecycline27, which has also been adopted by others for eravacycline28. There is a clear gap in work examining the expected PK alterations due to increase binding with total concentration.
3.2 POTENTIAL IMPLICATIONS ON TIGECYCLINE
3.2.1 Pharmacokinetic Effects
Current pharmacokinetic models do no account for the atypical nonlinear protein binding of tigecycline29–32, eravacycline33, doxycycline34 or minocycline35. Based on what we know from drugs with typical nonlinear protein binding, the free drug will follow linear PK, while total drug will have nonlinear PK. Since most population PK models assume linear processes, the modelling of potentially nonlinear processes using linear models may mischaracterize the existing nonlinearity as additional compartments or multiple elimination processes36. Use of these models in predictions may lead to error in PK profiles and expected exposures. Our group modified a population PK model of tigecycline in healthy volunteers29 to incorporate nonlinear protein binding based on a previously developed model27. Fourteen-day dosage regimens were simulated in NONMEM (Version 7.3) for linear and nonlinear scenarios for doses ranging from 25 to 200 mg every 12 hours. As shown in Figure 4, CL and Vd varied widely for nonlinear binding as compared to linear binding scenarios with predicted CL of 4.98–26.5 L versus 16.8 L/h and predicted Vd of 14.8–48 L versus 27.8 L for nonlinear versus linear binding, respectively. The resulting fluctuation in t1/2 was less substantial. This change could be naively overlooked as parameter variability. Simulated total exposures (AUC) were higher for the nonlinear scenario (up to 202% of linear binding) and free exposures (fAUC) were up to 30% lower for higher doses (Figure 5). Trends were maintained when CLint or tissue binding were changed. Overall, these simulations suggest that at higher doses free drug exposure may be overestimated by current models when atypical nonlinear binding is unaccounted for, which could lead to subtherapeutic dosing and possibly clinical failure. In addition, PK variability across doses may result from nonlinear binding.
Figure 4: Effects of changing plasma protein binding on different PK parameters over a total concentration range with atypical (blue) and linear (orange) plasma protein binding.
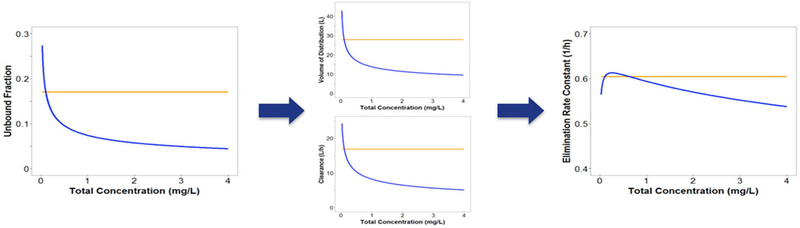
Figure 5: Cumulative total and free exposure (CAUC and fCAUC) for each dosing regimen under atypical (blue) and linear (orange) plasma protein binding scenarios.
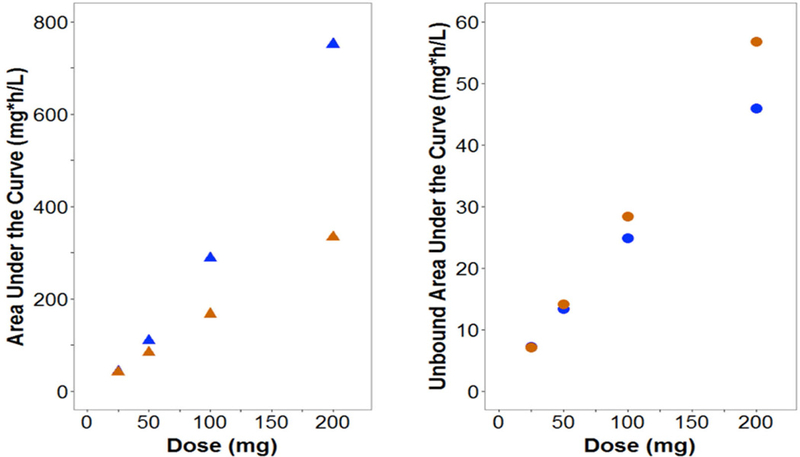
This analysis has some limitations that should be noted: Lacking the original data, a new model was not constructed, instead original model parameters were used as reference points in implementing alterations. There is little known about the tissue binding and nonlinear binding was only incorporated into the central compartment, a point also brought up by øie and colleagues21. With this these simulations should only be regarded as hypothesis generating and as motivation to examine free exposure of tigecycline at the site of action (infected tissue) to truly understand and develop an accurate model of the active concentration-time profiles.
3.2.2 Calculating Penetration
When determining pharmacological activity, free concentrations at the site of action need to be considered. Often predicted plasma concentrations are extrapolated to the tissues with the use of penetration ratios (i.e. AUCtissue:AUCplasma). In our analysis of free tigecycline penetration, we found that penetration ratios may also be overestimated if linear binding is assumed. Two studies37,38, examining the penetration of tigecycline into ELF fluid utilized quantified total plasma concentrations. If the fAUC in plasma or serum are calculated by simply multiplying AUC by a constant fu of 0.21, then the ratio of fAUCELF to fAUCcentral were 5.04 and 7.94 for each study. If the clinical protein binding model developed by Bulik and colleagues39 is used to calculate free concentrations and subsequently fAUCs, the resulting penetration ratios are much lower (1.86 and 2.32). In a subcutaneous microdialysis study39, fAUCtissue:fAUCplasma ratios were 0.99 and 1.00 in the thigh and wound, respectively, closer to these values than those calculated based on linear binding.
The gross overestimation of drug penetration calculated based on linear binding for drugs exhibiting atypical nonlinear binding could lead to overestimation of pharmacodynamic effects and subsequent underdosing. In the case of tigecycline, inadequate treatment of an infection could lead to prolonged and progressive illness, the need for intubation, additional antibiotics, or surgical intervention, or death. Subtherapeutic concentrations from underdosing may also result in increased antibiotic resistance, eventually leading to further development of superbugs against which few antibiotics are effective.
4 Conclusion
Assessment of protein binding in determining pharmacologically active drug concentrations at the site of action is critical in drug development and clinical practice. The PK effects of linear and typical nonlinear binding have been well studied for a variety of compounds. Given the discovery of the novel atypical nonlinear phenomenon, it is important to revisit the impacts of nonlinearity in protein binding on clinical pharmacokinetics and pharmacodynamics, and ultimately, clinical efficacy. The presented analyses using tigecycline as an example to demonstrate the need for further studies into this phenomenon, its underlying mechanism and impact on dosing across patient populations. The discovery of the atypical protein binding phenomenon also presents the promise of potential opportunity to exploit underlying mechanisms to develop new therapies and better understand molecular interactions of xenobiotics within the physiological system.
Acknowledgements
Funding: This work supported in part by the NIH/NCATS Clinical and Translational Science Award to the University of Florida UL1 TR000064. The sponsor had no involvement in study design, data collection, analysis or interpretation, or in the writing or decision to submit the published work.
While R.S.P.S. is a current employee of Pfizer and may hold stock.
A.N.D. would like to thank the American Foundation for Pharmaceutical Education for their support through their Pre-Doctoral Fellowship in Pharmaceutical Sciences.
The authors would like to acknowledge Johannes Kast and Uwe Liebchen for their contributions to the clinical simulation example and Daniel Baecker, Kristen Kollecas, and Eleni Tagari for their assistance with literature review.
The eravacycline protein binding data was presented at the 2013 Interscience Conference on Antimicrobials Agents and Chemotherapy (ICAAC) in Denver, CO2. The clinical simulation examples were presented at the American College of Clinical Pharmacology (ACCP) 2016 Annual Meeting in Bethesda, MD40.
References:
- 1.Muralidharan G, Micalizzi M, Speth J, Raible D, Troy S. Pharmacokinetics of tigecycline after single and multiple doses in healthy subjects. Antimicrob Agents Chemother. 2005;49(1):220–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Singh R, Falcao N, Sutcliffe J, Derendorf H. Plasma protein binding of eravacycline in mouse, rat, rabbit, cynomolgus monkey, African green monkey and human using microdialysis. In: Interscience Conference on Antimicrobial Agents and Chemotherapy 2013:A-015. [Google Scholar]
- 3.Zhou J, Tran BT, Tam VH. The complexity of minocycline serum protein binding. J Antimicrob Chemother 2017:39–41. [DOI] [PubMed] [Google Scholar]
- 4.Murphy TM, Weiss WJ, Pulse M, Sutcliffe JA, Grossman TH. Pharmacodynamic Evaluation of TP-271, a novel Fluorocycline, in a Neutropenic Murine Lung Model Infected with Streptococcus pneumoniae. In: Interscience Conference on Antimicrobial Agents and Chemotherapy Washington, DC; 2014:F-1601. [Google Scholar]
- 5.Goldstein A The interactions of drugs and plasma proteins. J Pharmacol Exp Ther 1949;95 Pt. 2(4):102–165. [PubMed] [Google Scholar]
- 6.Langmuir I The constitution and fundamental properties of solids and liquids. Part I. Solids. J Am Chem Soc 1916;38:2221–2295. [Google Scholar]
- 7.Zeitlinger MA, Derendorf H, Mouton JW, et al. Protein binding: do we ever learn? Antimicrob Agents Chemother 2011;55(7):3067–3074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Heuberger J, Schmidt S, Derendorf H. When is protein binding important? J Pharm Sci 2013;102(9):3458–3467. [DOI] [PubMed] [Google Scholar]
- 9.Benet LZ, Hoener B. Changes in plasma protein binding have little clinical relevance. Clin Pharmacol Ther 2002;71(3):115–121. [DOI] [PubMed] [Google Scholar]
- 10.Bohnert T, Gan L- S. Plasma protein binding: from discovery to development. J Pharm Sci 2013;102(9):2953–2994. [DOI] [PubMed] [Google Scholar]
- 11.Singh RSP, Mukker JK, Deitchman AN, Drescher SK, Derendorf H. Role of Divalent Metal Ions in Atypical Nonlinear Plasma Protein Binding Behavior of Tigecycline. J Pharm Sci 2016;105(11):3409–3414. [DOI] [PubMed] [Google Scholar]
- 12.Dorn C, Kratzer A, Liebchen U, et al. Impact of experimental variables on the protein binding of tigecycline in human plasma as determined by ultrafiltration. J Pharm Sci September 2017. [DOI] [PubMed] [Google Scholar]
- 13.Thabit AK, Monogue ML, Nicolau DP. Eravacycline Pharmacokinetics and Challenges in Defining Humanized Exposure In Vivo. Antimicrob Agents Chemother 2016;60(8):5072–5075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang F, Xue J, Shao J, Jia L. Compilation of 222 drugs’ plasma protein binding data and guidance for study designs. Drug Discov Today 2012;17(9–10):475–485. [DOI] [PubMed] [Google Scholar]
- 15.Koch-Weser J, Sellers EM. Binding of drugs to serum albumin (first of two parts). N Engl J Med 1976;294(6):311–316. [DOI] [PubMed] [Google Scholar]
- 16.Kratzer A, Liebchen U, Schleibinger M, Kees MG, Kees F. Determination of free vancomycin, ceftriaxone, cefazolin and ertapenem in plasma by ultrafiltration: impact of experimental conditions. J Chromatogr B Analyt Technol Biomed Life Sci 2014;961:97–102. [DOI] [PubMed] [Google Scholar]
- 17.Colclough N, Ruston L, Wood JM, MacFaul PA. Species differences in drug plasma protein binding. Med Chem Commun 2014;5(7):963–967. [Google Scholar]
- 18.Schmidt S, Gonzalez D, Derendorf H. Significance of protein binding in pharmacokinetics and pharmacodynamics. J Pharm Sci 2010;99(3):1107–1122. [DOI] [PubMed] [Google Scholar]
- 19.Martin BK. Potential effect of the plasma on drug distribution. Nature 1965;207(994):274–276. [DOI] [PubMed] [Google Scholar]
- 20.Martin BK. Kinetics of elimination of drugs possessing high affinity for the plasma proteins. Nature 1965;207(5000):959–960. [DOI] [PubMed] [Google Scholar]
- 21.øie S, Guentert TW, Tozer TN. Effect of saturable binding on the pharmacokinetics of drugs: a simulation. J Pharm Pharmacol 1980;32(7):471–477. [DOI] [PubMed] [Google Scholar]
- 22.McNamara PJ, Gibaldi M, Stoeckel K. Volume of distribution terms for a drug (ceftriaxone) exhibiting concentration-dependent protein binding. I. Theoretical considerations. Eur J Clin Pharmacol 1983;25(3):399–405. [DOI] [PubMed] [Google Scholar]
- 23.McNamara PJ, Gibaldi M, Stoeckel K. Volume of distribution terms for a drug (ceftriaxone) exhibiting concentration-dependent protein binding. II. Physiological significance. Eur J Clin Pharmacol 1983;25(3):407–412. [DOI] [PubMed] [Google Scholar]
- 24.Mukker JK, Singh RP, Derendorf H. Determination of atypical nonlinear plasma-protein-binding behavior of tigecycline using an in vitro microdialysis technique. J Pharm Sci 2014;103(3):1013–1019. [DOI] [PubMed] [Google Scholar]
- 25.Villano SJ, Tzanis E, Tanaka SK. In Vitro Protein Binding With Omadacycline, A First In Class Aminomethylcycline Antibiotic. In ASM Microbe ; 2016:Poster M-518. [Google Scholar]
- 26.Agwuh KN, MacGowan A. Pharmacokinetics and pharmacodynamics of the tetracyclines including glycylcyclines. J Antimicrob Chemother 2006;58(2):256–265. [DOI] [PubMed] [Google Scholar]
- 27.Singh RSP, Mukker JK, Drescher SK, Deitchman AN, Derendorf H. A need to revisit clinical breakpoints of tigecycline: effect of atypical non-linear plasma protein binding. Int J Antimicrob Agents 2017;49(4):449–455. [DOI] [PubMed] [Google Scholar]
- 28.Zhao M, Lepak AJ, Marchillo K, VanHecker J, Andes DR. In Vivo Pharmacodynamic Target Assessment of Eravacycline against Escherichia coli in a Murine Thigh Infection Model. Antimicrob Agents Chemother 2017;61(7):AAC.00250–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Van Wart SA, Cirincione BB, Ludwig EA, Meagher AK, Korth-Bradley JM, Owen JS. Population pharmacokinetics of tigecycline in healthy volunteers. J Clin Pharmacol 2007;47(6):727–737. [DOI] [PubMed] [Google Scholar]
- 30.Van Wart SA, Owen JS, Ludwig EA, Meagher AK, Korth-Bradley JM, Cirincione BB. Population pharmacokinetics of tigecycline in patients with complicated intra-abdominal or skin and skin structure infections. Antimicrob Agents Chemother 2006;50(11):3701–3707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rubino CM, Ma L, Bhavnani SM, et al. Evaluation of tigecycline penetration into colon wall tissue and epithelial lining fluid using a population pharmacokinetic model and Monte Carlo simulation. Antimicrob Agents Chemother 2007;51(11):4085–4089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ramirez J, Dartois N, Gandjini H, Yan JL, Korth-Bradley J, McGovern PC. Randomized phase 2 trial to evaluate the clinical efficacy of two high-dosage tigecycline regimens versus imipenemcilastatin for treatment of hospital-acquired pneumonia. Antimicrob Agents Chemother 2013;57(4):1756–1762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhanel GG, Cheung D, Adam H, et al. Review of Eravacycline, a Novel Fluorocycline Antibacterial Agent. Drugs 2016;76(5):567–588. [DOI] [PubMed] [Google Scholar]
- 34.Hopkins AM, Wojciechowski J, Abuhelwa AY, Mudge S, Upton RN, Foster DJR. Population Pharmacokinetic Model of Doxycycline Plasma Concentrations Using Pooled Study Data. Antimicrob Agents Chemother 2017;61 (3). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhou J, Ledesma KR, Chang K- T, Abodakpi H, Gao S, Tam VH. Pharmacokinetics and Pharmacodynamics of Minocycline against Acinetobacter baumannii in a Neutropenic Murine Pneumonia Model. Antimicrob Agents Chemother 2017;61 (5):1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.McNamara PJ, Slattery JT, Gibaldi M, Levy G. Accumulation kinetics of drugs with nonlinear plasma protein and tissue binding characteristics. J Pharmacokinet Biopharm 2015;7(4):397–405. [DOI] [PubMed] [Google Scholar]
- 37.Conte JE, Golden JA, Kelly MG, Zurlinden E. Steady-state serum and intrapulmonary pharmacokinetics and pharmacodynamics of tigecycline. Int J Antimicrob Agents 2005;25(6):523–529. [DOI] [PubMed] [Google Scholar]
- 38.Gotfried MH, Horn K, Garrity-Ryan L, et al. Comparison of Omadacycline and Tigecycline Pharmacokinetics in the Plasma, Epithelial Lining Fluid, and Alveolar Cells in Healthy Adult Subjects. Antimicrob Agents Chemother 2017;(July):AAC.01135–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bulik CC, Wiskirchen DE, Shepard A, Sutherland C a, Kuti JL, Nicolau DP. Tissue penetration and pharmacokinetics of tigecycline in diabetic patients with chronic wound infections described by using in vivo microdialysis. Antimicrob Agents Chemother 2010;54(12):5209–5213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Deitchman AN, Singh RS, Kast J, Liebchen U, Derendorf H. Potential Implications of Atypical Nonlinear Plasma Protein Binding on Tigecycline Clinical Pharmacokinetics. Clin Pharmacol Drug Dev 2016;5(S1):10. [Google Scholar]
- 41.Lima JJ, Boudoulas H, Blanford M. Concentration-dependence of disopyramide binding to plasma protein and its influence on kinetics and dynamics. J Pharmacol Exp Ther 1981. ;219(3):741–747. [PubMed] [Google Scholar]
- 42.Stoeckel K, Koup JR. Pharmacokinetics of ceftriaxone in patients with renal and liver insufficiency and correlations with a physiologic nonlinear protein binding model. Am J Med 1984;77(4C):26–32. [PubMed] [Google Scholar]
- 43.Cloyd JC, Dutta S, Cao G, et al. Valproate unbound fraction and distribution volume following rapid infusions in patients with epilepsy. Epilepsy Res 2003;53(1–2):19–27. [DOI] [PubMed] [Google Scholar]
- 44.Mori Y, Chiba K, Takahashi H, Ogata H. A population approach to eplerenone pharmacokinetics and saturable protein binding. Drug Metab Pharmacokinet 2010;25(6):551–559. [DOI] [PubMed] [Google Scholar]
- 45.Graefe-Mody U, Retlich S, Friedrich C. Clinical pharmacokinetics and pharmacodynamics of linagliptin. Clin Pharmacokinet 2012;51(7):411–427. [DOI] [PubMed] [Google Scholar]
- 46.Epic Pharma LLC. TRANDOLAPRIL- trandolapril tablets tablet [package insert] 2017. https://dailymed.nlm.nih.gov/dailymed/drugInfo.cfm?setid=10f25119-9970-46fe-bf36-6fec6064895b.
- 47.Xu J, Winkler J, Derendorf H. A pharmacokinetic/pharmacodynamic approach to predict total prednisolone concentrations in human plasma. J Pharmacokinet Pharmacodyn 2007;34(3):355–372. [DOI] [PubMed] [Google Scholar]