Optimized computer-aided segmentation and 3D reconstruction using intracoronary optical coherence tomography

Abstract

We present a novel and time-efficient method for intracoronary lumen detection which produces three-dimensional (3D) coronary arteries using Optical Coherence Tomographic (OCT) images. OCT images are acquired for multiple patients and longitudinal cross-section (LOCS) images are reconstructed using different acquisition angles. The lumen contours for each LOCS image are extracted and translated to 2D cross-sectional images. Using two angiographic projections the centerline of the coronary vessel is reconstructed in 3D and the detected 2D contours are transformed to 3D and placed perpendicular to the centerline. To validate the proposed method, 613 manual annotations from medical experts were used as gold standard. The 2D detected contours were compared to the annotated contours and the 3D reconstructed models produced using the detected contours were compared to the models produced by the annotated contours. Wall shear stress (WSS), as dominant hemodynamics factor, was calculated using computational fluid dynamics and 844 consecutive 2-mm segments of the 3D models were extracted and compared to each other. High Pearson’s correlation coefficients were obtained for the lumen area (r=0.98) and local WSS (r=0.97) measurements, while no significant bias with good limits of agreement was shown in the Bland-Altman analysis. The overlapping and non-overlapping areas ratio between experts’ annotations and presented method was 0.92 and 0.14, respectively. The proposed computer-aided lumen extraction and 3D vessel reconstruction method is fast, accurate and likely to assist in a number of research and clinical applications.

I. Introduction

Coronary angiography is the conventional method for assessing artery wall morphology [1], it produces two-dimensional (2D) images which depict the arterial lumen and is widely used by the physicians. However, it offers unreliable or no information about the arterial wall structure (i.e. thickness and plaque) [2]. In contrast, optical coherence tomography (OCT) [3], [4] is an invasive imaging modality which provides high resolution cross sectional images of the arterial wall morphology with utmost resolution. OCT uses light to capture micrometer-resolution allowing vessel visualization in high analysis: lateral and axial resolution: 20–90 μm and 12–18 μm, respectively [5]. This unique imaging resolution has made OCT the method of choice in accessing high risk lesions in coronary arteries, i.e. high-risk plaque characteristics [6] and in performing accurate lumen measurements [7]. OCT is ideally used to depict and quantify the composition of the superficial atherosclerotic plaques as its limited tissue penetration restricts deeper imaging (maximum depth: 1.5–2.0 mm) [8]. Although recent attempts were made to detect the media-adventitia border [9], this structure is rarely detectable by OCT and the entire plaque cannot be defined. Moreover, OCT does not provide information regarding the curvature of the vessel. Therefore several 3D coronary reconstruction methods have been developed which combine angiography and intravascular imaging [10]–[14]

Extraction of a 3D centerline path is the foundation of all 3D OCT reconstruction methods [11] differing primarily in the computer-aided lumen detection [10]–[14] that they use. Lumen detection methods are time consuming, limiting the use of 3D modeling when fast and accurate diagnoses are required, and while assumptions of circularity allow rapid analysis non-realistic models are produced. Traditionally, OCT lumen detection [15], [16] was performed manually which is a time consuming process and sensitive to intra- and inter-observer variability. These drawbacks led to the implementation of automated and semi-automated methodologies detecting only the lumen border of the vessel [17]–[21] or detecting the lumen border and estimating the plaque area of the vessel [22]. The first lumen detection methodologies were presented by Tanimoto et al. [17] and Sihan et al. [18]. They applied edge detection algorithms to automatically segment the lumen border by processing two dimensional (2D) cross sectional DICOM OCT images. Their methods had excellent agreement when compared to commercially available software (CURAD vessel analysis, CURAD BV, Wijk bij Duurstede, The Netherlands). In a similar attempt Tsantis et al. [19] used 2D cross sectional DICOM OCT images to segment the lumen border and to detect stent struts, and were as accurate and robust as manual segmentation performed by experts. Ughi et al. [20] and Ahn et al. [21] segmented the lumen border by processing the A-lines of the OCT equipment (2D OCT in polar coordinates) to detect stent struts as well as manual annotation by experts. Using the same data input Athanasiou et al. [22] detected the lumen borders and estimated plaque area.

These methods can sufficiently detect the OCT lumen border in 2D OCT images, yet none of the methods can be applied in real time and none of them can take into consideration the vessels’ spatial continuity when detecting the lumen border; they can only make border approximation in segments having branches by using the lumen of the preceding and succeeding frame. Lost therefore is the contiguity between numerous consecutive contour segments in a sequence of several branched frames. The spatial coherence of the lumen cannot be fully represented by 2D-cross sectional OCT images or by using only the preceding and succeeding frame; the lumen border in several sequential frames having side branches is not visible and often disrupted by several artifacts. Therefore, the literature methods cannot sufficiently estimate all the branches in the arterial segments. Furthermore, the spatial continuity in 2D-cross sectional OCT images can be interrupted by several artifacts, such as those generated by residual blood inside the lumen area or tip of the catheter [23]. When residual blood is present in the OCT image most of the algorithms recognize as lumen border the residual blood and produce erroneous lumen results. The inaccurate lumen detection results are transferred to the 3D geometry of the coronary artery as errors are constantly propagated in multi-steps methodologies [24]. To overcome these drawbacks the lumen area must be detected by a faster and more anatomically correct intracoronary illustration which will represent the sequential area of the OCT pullback.

We present a novel method for fast and reliable border detection and 3D reconstruction using OCT images. The method uses as input 2D cross sectional OCT images, produces longitudinal cross-section (LOCS) images of the artery at different angles, which represent more accurately the sequential area of the OCT pullback, and detects the lumen using the LOCS. The lumen contours are extracted for each 2D cross-sectional image, are placed onto a 3D path and produce 3D coronary models.

II. Materials and Methods

A. Image acquisition

OCT acquires individual reflected A-lines representing the optical energy as a function of time [25]. Each A-line of the same arteria segment is sequentially stored in a 2D matrix (I_matrix) with each line corresponding to an acquisition angle of the optical probe. The 2D matrix is the representation of the 2D cross section image in polar coordinates I(r, θ), with r representing the range dimension and θ the acquisition angle, which are then converted to Cartesian coordinates (I(i, j)) with i = rcosθ and j = rsinθ and stored (Fig. 1a, b).

Fig. 1.

(a) The polar 2D data grayscale image (A-lines image), (b) its corresponding Cartesian 2D cross-sectional image, (c) the cross-section lines of the four different angles (0°, 45°, 90° and 135°) in the 2D data grayscale image and (d) its corresponding 2D cross-sectional image.

The Longitudinal cross sectional (LOCS) images represent the traverse sections of the vessel and are constructed from 2D OCT cross-sectional images (Cartesian). The pixels that correspond to the cross-section lines of four different angles (0°, 45°, 90° and 135°, Fig. 1c, d) for each 2D image were sequentially stored and reconfigured to construct the LOCS image. For the N 2D images of the OCT pullback, with each image having dimensions of L × L, four different LOCS images are constructed having dimensions N × L (Fig. 2).

Fig. 2.

The four constructed LOCS images one for each angle: 0°, 45°, 90° and 135° (grayscale images) using all the 2D cross-sectional images (colored images-top).

B. Lumen detection

Detection of the borders of the LOCS images enable identification of the lumen which is further augmented by a smoothing filter [26] applied to the LOCS images and then by using K-means algorithm [27].

B.1 Bilateral filtering

Bilateral [26] non-linear filters are, like Gaussian filters, smoothing but, use of pixel differences in intensity preserves edges and reduces image noise. The intensity values of each pixel of the image is replaced by a weighted average of the intensities values from the neighborhood pixels, similar to Gaussian convolutions. The key idea of bilateral filtering is that it focuses not only on geographic proximity but intensity representation – i.e. a pixel should not only be a neighbor of the central pixel in a kernel that represents a local intensity, but should have similar intensity to be able to influence the value of the central pixel.

The bilateral filter is defined as:

$$I^{\prime }(x)=\frac{1}{W_p}{\sum }_{x_i\in W}I(x_i)f_r(\Vert I(x_i)-I(x)\Vert )g_s(\Vert x_i-x\Vert ),$$ (1)

where W_p is the normalization factor:

$$W_p={\sum }_{x_i\in W}{f}_r(\Vert I(x_i)-I(x)\Vert )g_s(\Vert x_i-x\Vert ),$$ (2)

I′ is the filtered image, I is the initial image, x are the coordinates of the central pixel that its value is replaced and W is the window mask (neighborhood of the central pixel). Parameters f_r and g_s are the range Gaussian kernel for smoothing differences in intensities and the spatial Gaussian kernel for smoothing differences in coordinates.

B.2 K-means algorithm

K-means [27] is an unsupervised learning algorithm able to solve a clustering problem [28]. The algorithm follows a simple procedure to classify the given data to a fixed a priori clusters k. K-means aims to partition a given a set of M observations {x₁, x₂, …, X_M}, into a fixed number of k clusters S = (S₁, S₂, …, S_k) and minimizes the within cluster sum of squares:

$$\underset{S}{\mathit{arg}\mathit{min}}{\sum }_{h=1}^k{\sum }_{x_h\in S_k}{\Vert x_h-{\mu }_{\kappa }\Vert }^2,$$ (3)

where μ_κ is the mean of points in S_k.

We examined cases of two to four clusters and concluded that two clusters are sufficient to differentiate the vessel from lumen/background pixels with precision.

B.3 Lumen representation

Once the K-means algorithm is applied to the four LOCS images the lumen border of the LOCS ( $I_{\mathit{LOCS}}^{\theta }$) images is detected. For each $I_{\mathit{LOCS}}^{\theta }$ image we scan the middle row of the image, defining and connecting the non-zero pixels in the row which is half of a length of the $I_{\mathit{LOCS}}^{\theta }$ to the left and then to the right (Fig. 3).

Fig. 3.

The lumen detection in a LOCS image: (a) initial LOCS image, (b) filtered LOCS image, (c) segmented using K-means LOCS image showing the scan direction for the detection of non-zero pixels and (d) the connected nonzero pixels which represent the LOCS lumen borders.

After detecting the lumen in the four LOCS images the detected lumen points are translated to their corresponding points in the 2D cross sectional images. The final lumen is detected for each 2D cross sectional image by iterating on the number of N images. For each of the four LOCS images with dimensions N × L, we find the two border points of the specific row and place the point of the detected borders onto the 2D OCT image with dimensions L × L (Fig. 4-a, b). The result of the algorithm is a 2D OCT image including 8 points which represent the points of the lumen border (Fig. 4-b). To detect all the points of the lumen border a cubic spline function is applied to these points (Fig. 4-c). A B-spline curve [29] is a parametric curve defined as a linear combination of V control points with U knots:

$$b(U)={\sum }_{a=1}^{\lambda }{D}_{\alpha ,p}(U)V_a,$$ (4)

where:

Fig. 4.

(a) The four different LOCS images, their corresponding detected lumen borders (white) and the n (n ∈ [0 N]) row of the LOCS images corresponding to the n frame of the OCT pullback and to one of the four angles (0°-yellow row, 45°-green row, 90°-red row and 135°-white row). (b) The n^th 2D OCT image having 8 points which correspond to n^th the row of each LOCS image. (c) The cubic spline function applied to the 8 points representing the lumen border of the 2D OCT image.

p: is the degree of the B-spline, D_a,p: is the basic B-spline function defined by the Cox-de Boor recursion formula:

$$D_{\alpha ,0}(U)=\{\begin{array}{cc}1& if{U}_a\le U\le U_{a+1}\\ 0& \mathit{otherwise}\end{array},\text{when}p=0$$ (5)

and:

$$D_{\alpha ,p}(U)=\frac{U-U_a}{U_{a+p}-U_a}{D}_{\alpha ,p-1}(U)+\frac{U_{a+p+1}-U}{U_{a+p+1}-U_{a+1}}{D}_{\alpha +1,p-1}(U),\text{when}p>0.$$ (6)

C. 3D reconstruction

To reconstruct the arteries we used a previously developed method [11] and extracted the vessel 3D centerline using two different angiographic projections. The centroid of each lumen border was calculated and the 2D lumen borders were placed perpendicular to the 3D path. The centroid C(C_i, C_j) of each lumen border having l number of pixels, is defined as:

$$C_i=\frac{1}{6A}{\sum }_{q=1}^{l-1}(i_q+i_{q+1})(i_q{j}_{q+1}-i_{q+1}{j}_q),$$ (7)

$$C_j=\frac{1}{6A}{\sum }_{q=1}^{l-1}(i_q+i_{q+1})(i_q{j}_{q+1}-i_{q+1}{j}_q),$$ (8)

where A is the lumen area defined as:

$$A=\frac{1}{2}{\sum }_{q=1}^{l-1}(i_q{j}_{q+1}-i_{q+1}{j}_q).$$ (9)

Their relative axial displacement and the absolute orientation of the first OCT frame were estimated by using the side branches of the artery [11]. M (M ≠ even) equidistant points of each of the N contours are extracted clock wisely and a triangulation approach is implemented to construct the mesh surfaces of the 3D lumen. The M contours points (inner/outer of two sequential frames are connected to construct a triangle mesh.

III. Dataset

For the current study we analyzed clinical data from 11 patients who underwent optical coherence tomography (OCT) and interventional X-ray (angiography) for the treatment of coronary artery disease. All images were acquired by a commercial Fourier Domain OCT system (C7-XRTM OCT Intravascular Imaging System, St. Jude Medical, St. Paul, Minnesota) and by a commercial interventional X-ray system (Philips Medical Systems, Amsterdam, Netherlands) at Heart Institute of University of São Paulo (São Paulo, Brazil). Intracoronary nitroglycerine was initially administrated and the OCT catheter (C7 Dragonfly, St. Jude Medical, St. Paul, Minnesota) was advanced through a “0.014”guidewire to the distal target vessel. OCT images were acquired using a pullback speed of 20 mm/s during intra-coronary blood displacement by a contrast media injection (Iodixanol 320, Visipaque^™, GE Health Care, Ireland) through the guiding catheter. All images were digitally stored for offline evaluation and subsequent stent and vessel analysis. 613 images were extracted randomly from 11 OCT pullbacks (one for each patient) and contours were annotated manually by expert clinicians blinded to patient information excluding images having artifacts as saturation, foldover and pixel proximity [23]. The distal marks of the catheter were visible only on 6 of the 11 angiographic pairs of images, and these were used to reconstruct the 3D arterial models.

IV. Results

2D lumen detection

To examine the method’s degree of correlation with experts lumen annotations we computed Pearson’s correlation coefficients between the method’s results and the experts annotations, performed Bland-Altman analysis and calculated the positive predictive value (PPV). As true positive values (TP) we denote the common area detected by the method and annotated by the experts. As false positive (FP) values we refer to the area detected by the method and not by the experts and as false negative (FN) the area annotated by the expert and not detected by the method. Additionally, the ratio of overlapping and non-overlapping areas between the method and experts annotations was computed. The ratio of overlapping areas (sensitivity) was defined as:

$$R_{\mathit{over}}=\frac{TP}{TP+FN},$$ (10)

and of non-overlapping areas as:

$$R_{\mathit{nover}}=\frac{FN+FP}{TP+FN}.$$ (11)

There was an excellent correlation between the areas detected by the method and annotated by experts (R²=0.96) (Fig. 5). Pearson’s correlation coefficient was 0.95, R_over (sensitivity) and R_nover values were 0.92 and 0.14, respectively (Table 1). The reported high correlation coefficients demonstrate that the proposed method can detect the same lumen area with experts while the high R_over (0.92) confirms that the lumen area is detected on the same location with the annotated lumen area. However an important finding is the low R_n–over (0.14) which indicates that our method does not overestimate the detected lumen; an overestimation (FP > FN) of the detected lumen can give high R_over and high R_n–over. Having low R_nover and high R_over indicates that the detected lumen borders have the similar perimeter and shape to the annotated borders.

Fig. 5.

(a) Correlation plot and (b) Bland-Altman plots for the lumen areas estimated by our method and experts annotations.

TABLE I.

Validation results summary and comparison with the literature ^a

		N	r	R2	Rover	Rnover	PPV
Proposed method	2D (area)	613	0.98	0.96	0.92	0.14	0.93
	3D (WSS)	844	0.97	0.95	-	-	-
	3D (HD)	Average maximum:0.38 mm ± 0.19
		Average mean: 0.053 mm ± 0.19
		Average RMS: 0.073 ± 0.27
	Time complexity: ~ 120 seconds/OCT pullback
Previous method [22]	2D (area)	613	0.93	0.96	0.91	0.14	0.93
	3D (WSS)	844	0.84	0.71	-	-	-
	3D (HD)	Average maximum:0.51 mm ± 0.25
		Average mean: 0.087 mm ± 0.13
		Average RMS: 0.13 ± 0.84
	Time complexity: ~ 1080 seconds/OCT pullback

^aHD: Hausdorff Distance, N: number of samples, r: Pearson’s Correlation, R²: Determination coefficient, R_over: Overlapping area, R_nover: Non-overlapping area, PPV: Positive predictive value.

3D reconstruction

To examine the accuracy of the method in constructing 3D models the volume and the Hausdorff Distance (HD) of the arteries produced using the lumen borders detected by the proposed method (method model) were compared to the ones annotated by the experts (experts model) (Fig. 6). The measured volume of the method’s models is similar to the experts’ models, while the maximum, mean and root mean square (RMS) HD specify that the produced 3D models are practically matching (Table 1).

Fig. 6.

Volume comparison of the 3D arteries produced using expert annotations and algorithm’s lumen detection.

To further examine the usability of the method’s model, blood flow simulations were performed in all models and the wall shear stresses (WSS) were calculated and compared. Steady incompressible blood flow was simulated solving the Navier-Stokes equations in a coupled finite volume Solver (ANSYS CFX, Canonsburg, PA, USA). The shear-thinning behavior of blood was considered modeling it as a non-Newtonian fluid with density of 1060 kg/m³ and shear dependent dynamic viscosity following the Carreau model [30], [31]:

$$\frac{\mu -{\mu }_{\infty }}{{\mu }_O-{\mu }_{\infty }}={[1+{(\lambda ·\stackrel{.}{\gamma })}^2]}^{(n-1)/2},$$ (12)

where γ̇ is the shear rate, μ_O = 0.25 kg/m.s and μ_∞ = 0.0035 kg/m.s are the blood viscosities at infinite and zero shear rates, and λ = 25 s and n =0.25 values are Carreau parameters [32]. Volumetric flow rate at the inlet was set to 0.95 mL/s [33] while the outlet boundary was extended (to minimize the numerical noise of boundary condition) and set to zero pressure. Sensitivity analysis was performed on the boundary conditions by considering ±10 % and ±20 % change in the inlet mass flow and showed no significant change in the acquired results. After mesh independency was ensured, the numerical equations were solved on appropriately-fine grid till the residuals of variables were reduced bellow 10⁻⁷ of their initial values and mass balance was monitored in parallel.

To apply a direct quantitative comparison between the WSS calculated in the two models, perpendicular planes (segments) where created for all the models. Each 3D reconstructed coronary artery was divided into consecutive 0.2-mm segments [13] along the 3D luminal centerline, and the average local WSS was assessed. A total of 844 segments were available for analysis and resulted to an excellent correlation between the WSS calculated by the method’s and experts’ models (R²=0.95). The overall similarity in the WSS distribution between the pair of models (method-experts) (Fig. 7, Fig. 8) emphasizes that the presented method permits accurate evaluation of local WSS distribution and patient’s hemodynamics in general.

Fig. 7.

(a) Correlation plot and (b) Bland-Altman plots for the wall shear stress estimated by our method and experts.

Fig. 8.

Representative three-dimensional (3D) reconstructed models using the annotated (middle) and the proposed method detected lumen contours (right). The models are color-coded by wall shear stress (WSS) values (left).

Application

To assess and visualize the detected lumen borders and 3D reconstruct the arteries, an in-house tool was developed using MATLAB (r2016a, The MathWorks Inc., Natick, MA). C++ code was implemented and executed using Matlab’s MEX libraries to speed up the proposed method. The time complexity of the proposed methodology for detecting the lumen borders in an OCT pullback (270 frames) is ~ 120 seconds using a core i7 desktop computer with 64 GB of RAM. This time can be reduced even more if the LOCS images are constructed during the pullback acquisition in the catheterization lab. To assess, reconstruct and visualize the 3D centerline, we used a previously developed tool using C# [34]. The reconstruction process after selecting the two angiograms is ~ 60 seconds.

To assess the ability of the proposed method to overcome the literature limitations we implemented the lumen detection method of the literature which reported the highest sensitivity (0.99) [22]. This method [22] was applied to our dataset using the same desktop computer. Using the literature [22] method the reported time complexity for an OCT pullback (270 frames) is ~ 1080 seconds while the following scores were reported: sensitivity 0.91, PPV=0.93, non-overlapping area: 0.14, r=0.95, and R²=0.9. Although the 2D results are comparable with our method (Table 1) there are significant larger differences in the lumen areas (Fig. 9) which are propagated into the 3D reconstruction step and create defective 3D coronary models and incorrect WSS values (Table 1, Fig. 10).

Fig. 9.

Histogram with a Gaussian fit for the difference in lumen areas between the annotations - proposed method (green) and the annotations - literature [22] method (blue).

Fig. 10.

Ability of the proposed method on correcting existing methods drawbacks: three-dimensional (3D) reconstructed model using (a) the annotated, (b) the proposed method, and (c) the literature method [22] lumen contours highlighted with red color on the OCT images. The literature method [22] fails to detect the lumen contour in areas having artifacts (d): the presented OCT image (a, b, c: top and d) has residual blood inside the catheter tip and the lumen area.

V. Discussion

In this work, we present a computer-aided luminal border detection and 3D reconstruction method for the analysis of the OCT lumen borders in 2D and 3D mode. OCT images are acquired and the LOCS images are reconstructed using different acquisition angles. The lumen contours for each LOCS image are extracted and translated to 2D cross-sectional images. Using two angiographic projections the centerline of the coronary vessel is 3D reconstructed [11] and the detected 2D contours are transformed in 3D and placed perpendicular to the centerline. Finally the 3D contours are connected together and form the 3D arterial surface. The presented method rapidly and accurately detects the lumen in all OCT images, provides a realistic representation of the 3D complex anatomy of coronary arteries, and enables the use of the derived 3D models for blood flow simulation and wall shear stress (WSS) computation.

Although several lumen detection [17]–[22] and 3D reconstruction [10]–[12], [35], [36] methods exist, none of them is able to create fast and realistic coronary models. Using the traditional lumen detection methods, the lumen border is detected individually for each frame resulting to several limitations: increased computational time, unreliable lumen detection in side branches and irrelevant detection in frames having artifacts. On the contrary the presented method, overcomes these drawbacks by detecting the lumen faster and more anatomically correct with respect to vessel’s spatial continuity. The extended validation of the presented method shows that it can be used to assess the coronary morphology in 2D and 3D (lumen area: r=0.98, Fig. 6) and to enable the functional assessment of the coronary vasculature (WSS: r=0.97). The 3D coronary models are widely used to investigate the role of hemodynamic factors in predicting clinical events in patients with coronary artery disease [37], [38]. Using the proposed method, the produced 3D coronary models provide reliable coronary representation and luminal size measurements while they permit accurate evaluation of the local WSS distribution to identify areas exposed to a proatherogenic environment, i.e. low WSS values.

Lumen correlation reported between the areas detected by the method and annotated by the experts (lumen area: R²=0.96, r= 0.98, R_over =0.92 and R_n–over 0.14) makes the method able to perform accurate lumen measurements. The fast (120 sec) processing of the OCT pullback is of utmost importance as the method can potentially be used during real-time OCT acquisition in catheterization laboratories. Beyond the lumen detection, the proposed method enables fast and accurate (WSS: R²=0.95, r= 0.97) 3D coronary representation, overcoming the limitations of the current 3D reconstruction methods: increased computational time [10]–[12] and use of circular contour [35], [36] instead of the lumen contour. Furthermore, the proposed method can be used in OCT based studies focusing in hemodynamic factors [1], as our findings support the application of the method for calculating the local WSS in coronary arteries. However, further validation in a large amount of dataset is needed, before this methodology can have applications in a clinical setting. It should be noted that for the present study none of the frames were manually corrected, which in clinical practice is always happening; experts tend to apply minor changes in the lumen detection algorithms to improve the accuracy of their measurements. Nevertheless, the comparison results of the proposed method show that any required changes are the minimum that can be done compared to the literature methods. Finally, a potential integration of our methodology with the OCT equipment is likely to increase the applicability of the lumen detection method and further decrease the computational time. Likewise, the integration of the X-ray system with the method will provide sort time 3D models in the catheterization lab providing valuable information to the clinicians.

VI. Conclusions

The current report, presents a novel computer-aided OCT lumen extraction and 3D reconstruction method. Going beyond the current literature limitations the proposed method rapidly and accurately detects the lumen borders within the spatial continuum, and provides a realistic representation of the 3D complex anatomy of the coronary arteries. The head-to-head comparison of the method 3D coronary models with the respective experts’ 3D models of the same arteries for WSS assessment demonstrates that the method results in accurate calculations of the WSS distribution. Finally, the reduced computational time makes the method potentially applicable in both research and clinical arena to provide further insight into the pathophysiological processes of atherosclerosis.

Fig. 11.

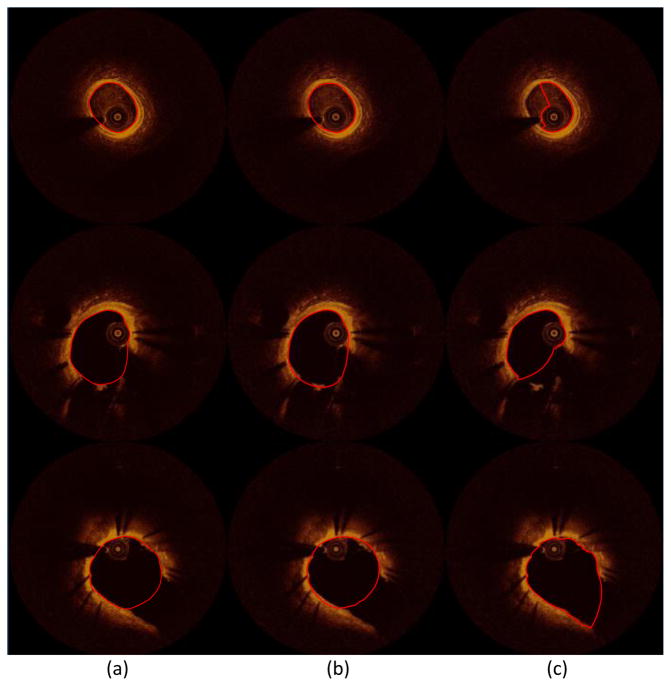
Application examples of the proposed method and literature method showing the ability of our method in detecting more accurately the lumen border in segments having branches (middle and bottom image sets) and residual blood artifacts (top image set): (a) annotated images, (b) the result of the proposed method, and (c) the result of the literature’s method [22]. The lumen contours are highlighted with red.

Biographies

Lambros Athanasiou was born in Ioannina, Greece, in 1985. He received his diploma degree from the Department of Information and Communication Systems Engineering, University of the Aegean, Greece, in 2009 and the PhD degree from the Department of Materials Science and Engineering, University of Ioannina, Greece, in 2015. Dr. Athanasiou is currently working as a Postdoctoral Research Fellow at the Institute for Medical Engineering & Science, Massachusetts Institute of Technology, Cambridge, MA, USA. His research interests include medical image processing, biomedical engineering, decision support and medical expert systems.

Farhad Rikhtegar Nezami, is currently affiliated as a postdoctoral associate in Harvard-MIT biomedical engineering lab. He has got his PhD in Mechanical engineering from ETH Zurich, where he conducted research on hemodynamics and drug transport in stented coronary arteries. He completed his masters at Sharif University of Technology in Tehran. Dr Rikhtegar’s research interests revolve around mechanistic understanding of human pathophysiology, successful translation of preclinical experiments to clinical practices, design and optimization of medical devices with utmost systematic biocompatibility and developing engineering platforms to drive progress from the laboratory bench and computational toolkits to the patient’s bedside.

Micheli Zanotti Galon is an interventional cardiologist from the Heart Institute (InCor) of São Paulo University Medical School, Brazil. She received her M.D. degree from the Federal University of Espírito Santo, Brazil and she is board certified in Brazil for internal medicine, general cardiology and interventional cardiology. She is currently a PhD research fellow of São Paulo University Medical School, Brazil. Her research interests include invasive and non-invasive imaging of coronary arteries, preclinical and clinical research of novel interventional device therapies and atherosclerotic vascular disease.

Dr. Celso Lopes was born in Brazil in 1981. He received his MD degree (Magna Cum Laude) from Federal University of Ceara, Brazil in 2004. He completed residency in Internal Medicine and fellowships in Cardiovascular Disease and Interventional Cardiology at the University of Sao Paulo, Brazil in 2005–11. Dr Lopes held a Postdoctoral Fellow position at the Institute for Medical Engineering & Science, Massachusetts Institute of Technology in 2013–14. Currently he works as director of the interventional cardiology center at Monte Klinikum Hospital, Fortaleza, Brazil. His research interests include medical devices, intravascular imaging, percutaneous coronary interventions, and structural heart disease.

Dr. Pedro Lemos, is a staff physician in the Department of Interventional Cardiology at the Heart Institute (InCor) of the University of Sao Paulo Medical School, Sao Paulo, Brazil. He received his medical degree from the University of Brasilia and his clinical training in internal medicine, general cardiology, and interventional cardiology at the University of Sao Paulo, in Brazil. He served as a fellow at the Erasmus Medical Center – University of Rotterdam, The Netherlands, where he received his PhD degree in 2004. Dr. Lemos is currently the head of the Interventional Cardiology Department at the University of Sao Paulo, Brazil. He has published over 150 peer-reviewed journals, mainly focused on catheter-based diagnostic and therapeutic methods for cardiovascular diseases. Dr. Lemos has been frequently invited to present his clinical and pre-clinical works at medical symposia and conferences in Latin America, Japan, Europe, India and the USA.

Jose M de la Torre Hernandez, MD, PhD, FESC, is an interventional cardiologist, head of the CV interventional dpt. in the Hospital Universitario Marques de Valdecilla, in Santander, Spain. He is member of the scientific committee of the Spanish Society of Cardiology and is fellow of the European Society of Cardiology. Associate director of the Trans Catheter Therapeutics Meeting in US. Faculty of ESC, PCR, ACC and TCT meetings. Coordinator of the ESTROFA, XIMA and LITRO study groups. He is currently visiting scientist at Harvard-MIT biomedical engineering center. His research interests include intravascular imaging, coronary artery disease and drug eluting stents.

Eyal Ben-Assa, is an interventional cardiologist from the Tel Aviv Medical Center, Israel. He received his M.D. and B.Sc. degree’s from the Hebrew University of Jerusalem and holds a clinical instructor appointment at the Sackler Faculty of Medicine, Tel Aviv University, Israel. He is board certified in Israel for both internal medicine and general cardiology. He has completed 2 years of post-doctoral research at the Institute for Medical Engineering & Science, Massachusetts Institute of Technology, Cambridge, MA, USA. Currently he is an interventional cardiology fellow at Massachusetts General Hospital, Boston, MA, USA. His main research interest includes analyzing advance hemodynamic parameters in structural heart disease, intra-cardiac flow dynamics, coronary imaging and physiology assessment.

Elazer R. Edelman, MIT Cabot Professor of Health Sciences and Technology, and Harvard Medical School Professor of Medicine, is a cardiac care unit cardiologist at Brigham and Women’s Hospital and director of MIT’s Biomedical Engineering Center. His research melds clinical and medical training, integrating biological and engineering sciences to understand tissue repair and device optimization.