Safety margins in robotic bone milling: from registration uncertainty to statistically safe surgeries

Abstract

Background

When robots mill bone near critical structures, safety margins are used to reduce the risk of accidental damage due to inaccurate registration. These margins are typically set heuristically with uniform thickness, which does not reflect the anisotropy and spatial variance of registration error.

Methods

A method is described to generate spatially varying safety margins around vital anatomy using statistical models of registration uncertainty. Numerical simulations are used to determine the margin geometry that matches a safety threshold specified by the surgeon.

Results

The algorithm was applied to CT scans of five temporal bones in the context of mastoidectomy, a common bone milling procedure in ear surgery that must approach vital nerves. Safety margins were generated that satisfied the specified safety levels in every case.

Conclusions

Patient safety in image-guided surgery can be increased by incorporating statistical models of registration uncertainty in the generation of safety margins around vital anatomy.

1 |. INTRODUCTION

Bone milling was one of the first applications considered in surgical robotics^1-3 due to the similarity to computer-assisted manufacturing processes. Examples of systems that have been commercialized and used clinically include the ROBODOC (Curexo, Inc., Seoul, South Korea), RIO Robotic Arm Interactive (Mako Surgical Inc., Ft Lauderdale, FL, USA), and the computer assisted surgical planning and robotics (CASPAR) system (URS Ortho GMBH & Co. KG, Rastatt, Germany). These platforms are examples of two different ways that robotic bone milling can be accomplished. ROBODOC is a fully autonomous system that plans the cutting burr’s path preoperatively before it is carried out. In contrast, RIO is a cooperatively controlled robotic arm that uses preoperative planning to enforce ‘no fly zones’ called virtual fixtures or active constraints,^4,5 ensuring that the surgeon removes only the desired volume, while leaving the surgeon in control of the exact path the robot traverses. Both approaches rely on accurate registration between the pre-operative images and the patient in the operating room. Any errors in registration make it so that locations in the surgeon’s preoperative plan, which is made in CT image space, will not perfectly align with corresponding locations in the patient.

As imaging resolution and registration techniques have improved, it has become possible to apply robotic bone drilling and milling to applications that require higher accuracy than the orthopedic surgeries addressed by the commercial systems mentioned above. Skull base surgeries are particularly well suited for the use of image-guidance and robotics because of their high accuracy requirements and the frequency with which the procedures are performed and this has motivated several research groups to pursue such solutions.^6-15 One example procedure, is mastoidectomy, i.e. bone removal in the mastoid portion of the temporal bone, to gain access to the underlying anatomy of the ear. Mastoidectomy is performed approximately 120 000 times annually in the United States alone (extrapolating the results of French et al.¹⁶ to the current population and to include both inpatient and out-patient procedures). It is performed as a preliminary step in more complex procedures of the middle and inner ear and to remove abnormal bone tissue arising from mastoiditis, cholesteatoma or other diseases. Critical structures are present within or near the surgical field during mastoidectomy that must be preserved during milling, including the facial nerve (damage causes facial paralysis), the chorda tympani (damage causes impaired sense of taste), the sigmoid sinus (damage causes bleeding), and the internal auditory canal (contains the auditory, vestibular, and facial nerves which may be irreparably damaged leading to hearing loss, balance disorders, and/or facial paralysis). Avoiding damage to these critical structures is challenging. The surgeon must first locate them using visual and tactile feedback while milling nearby bone then carefully remove the necessary bone.

An example of a complex otologic procedure that requires a mastoidectomy is acoustic neuroma tumor removal surgery. Acoustic neuromas, more properly called vestibular schwannomas, are benign tumors which arise within or in close proximity to the internal auditory canal. While benign, their growth causes local compressive damage including hearing loss, balance disturbances, facial paralysis, and - in rare cases when they grow to large sizes - death from intracranial complications (e.g. intracranial bleeding, compression of the brainstem suppressing respiratory drive). Treatment options include radiation therapy and surgical removal, with the most common surgical approach being a translabyrinthine approach which consists of a mastoidectomy followed by deeper bone milling to remove the labyrinth, including the semicircular canals, allowing access to the internal auditory canal. Figure 1 shows a preoperative segmentation of a translabyrinthine approach with critical structures annotated. The translabyrinthine approach is a strong candidate for image-guided robotic assistance for two reasons. First, from a surgical perspective, mastoidectomy and labyrinthectomy involve bulk removal of bone and are currently done by a human surgeon over several hours to reach the internal auditory canal following which the surgeon must change tasks to delicately handle exposed neural tissue in removing the tumor. Second, from a technological standpoint, since the anatomy is rigid and thus does not deform relative to the pre-operative image, a robot that is guided by a path planned in a preoperative image could be programmed to remove the necessary bone while avoiding the critical anatomy.

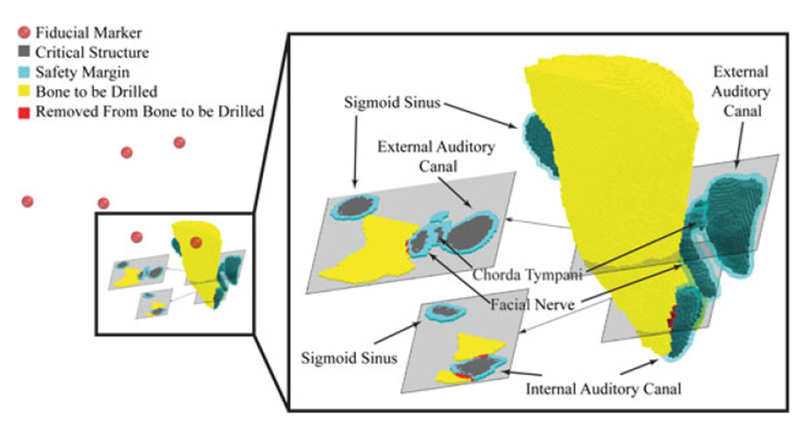
FIGURE 1.

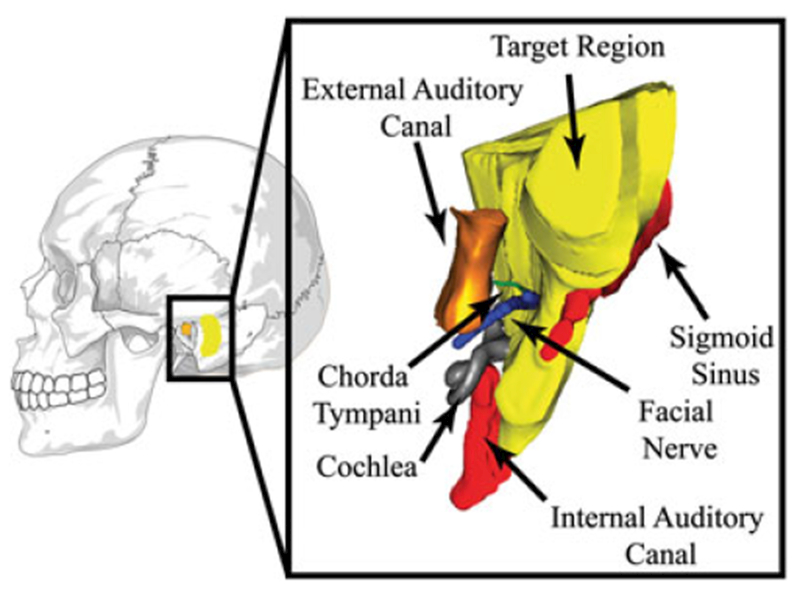
Mastoidectomy involves removal of the bone volume highlighted in yellow. Several critical structures lie near the volume to be milled, including the facial nerve, chorda tympani, internal auditory canal, sigmoid sinus, etc. Damage to these critical structures causes complications for the patient. Note: the segmentation on the right has been rotated for ease of visualization

This paper focuses on improving safety in robotic bone milling for otologic surgery with a specific emphasis on mastoidectomy and acoustic neuroma tumor removal surgery. No method currently exists to provide statistical confidence that the inevitable small registration errors will not lead to accidental damage to critical structures. Thus, the purpose of this work is to describe an algorithm that can provide such statistical confidence for systems that make use of point-based registration. The algorithm provides this confidence by establishing safety margins of bone around each critical structure that will not be targeted in the planned path. With a stiff robot and tool, milling up to the boundary of these safety margins will enable the cutting burr to come as close to the critical structure as possible, based on registration error statistics and a surgeon-specified safety level for each structure. For example, the surgeon might wish to be 99.9% sure that the system does not accidentally contact the facial nerve. These safety levels are ensured by choosing an appropriately sized and shaped safety margin, which is determined using numerical simulation and target registration error (TRE) theory.¹⁷ Separate safety margins are obtained for each critical structure so that individual safety levels can be specified.

Examples of prior work that are most similar to that presented here are that of Haidegger et al.,¹⁸ and Noble et al..¹⁹ Haidegger et al. estimated the instantaneous level of danger to critical structures for an optically tracked tool.¹⁸ In contrast, in this paper we seek a global approach that analyzes the entire procedure before any milling commences. Noble et al. estimated the danger to critical structures posed by a linear drill path for minimally invasive cochlea access.¹⁹ Here, we generalize to nonlinear tool paths. A preliminary version of this work was presented in Siebold et al..²⁰ The present work encompasses those results, which have not previously been published in archival form, and also extends them by providing a more accurate approach to collision detection and a more extensive numerical evaluation that includes simulations on five cadaver specimens, additional critical structures to avoid, and a comparison with constant thickness safety margins.

2 |. MATERIALS AND METHODS

The workflow for robotic mastoidectomy previously developed by our research group²¹ constitutes the general framework of this study. Briefly, the target volume is defined by the surgeon in a preoperative computed tomography (CT) scan and then used to generate a milling path for the robot. In the operating room, the pre-operative plan is registered to the patient using point-based registration of bone-implanted fiducial markers that are localized in an intra-operative CT scan. Our goal is to calculate safety margins around vital patient anatomy to limit the risk of accidental collisions with the robotic milling tool caused by registration error. Critical structures involved in a typical mastoidectomy procedure include the facial nerve, the chorda tympani, the sigmoid sinus and, the internal auditory canal. Safety margins will be iteratively grown around these structures to define a region in which the robot will not be allowed to operate (Figure 2).

FIGURE 2.

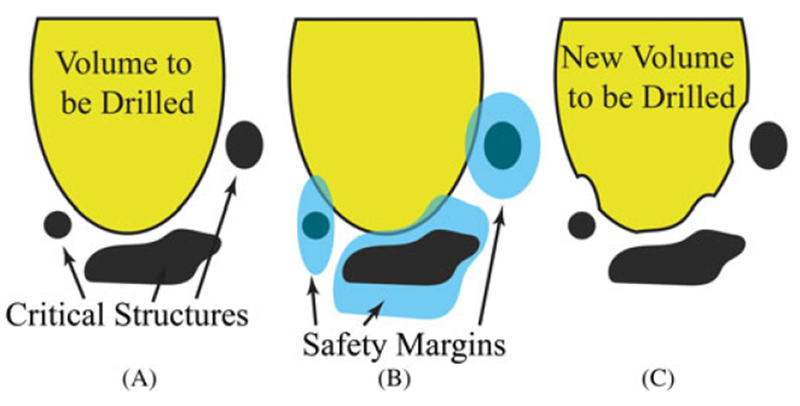
(A) An illustration of a segmented volume, with critical structures and a volume to be milled. (B) The same volume superimposed with safety margins. (C) The final result after the intersection of the safety margins and the volume to be milled has been removed from the volume to be milled. This reduced volume to be milled may now be milled with statistical assurance that the protected structures are safe from registration error

2.1 |. Algorithm overview

The proposed algorithm takes as input a three-dimensional voxelized representation of the patient’s anatomy wherein critical structures have been segmented. An example is shown in Figure 1. For each critical structure, individual spatially varying safety margins of minimal volume are determined using the four-step iterative process illustrated in Figure 3. The safety margin is initialized to include zero voxels, and is progressively expanded by including voxels that surround the critical structure. In the first step of the algorithm, we simulate a high number of imperfect registrations between the preoperative plan and the patient’s anatomy in the operating room. These simulations are used to determine the ‘overall damage risk’ which is defined as the risk of accidental overlap between the structure we want to preserve and the voxels that surround the critical structure which, if milled, would cause damage to the critical structure. Registrations are simulated by generating fiducial locations from repeated sampling of the distribution of fiducial localization error (FLE), which is a property of the imaging system and fiducial markers. If the overall damage risk does not meet the tolerance level specified by the surgeon, the safety margin is grown by including neighboring voxels. Priority is given to those voxels that, if reached during the milling procedure, would pose a higher threat to the critical structure. Such a threat is quantified using a metric called ‘point damage risk’. This process is iterated until the overall damage risk falls below the threshold specified by the surgeon. Table 1 contains a glossary of frequently used terms.

FIGURE 3.

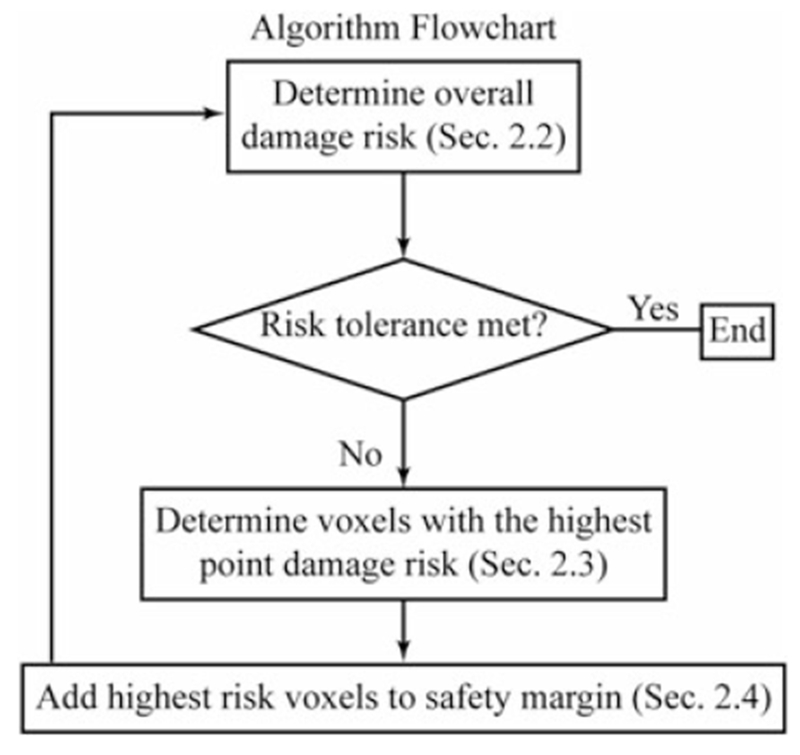
A flow chart is shown outlining the method employed to generate the safety margins surrounding the critical structures

TABLE 1.

Glossary of terms that are frequently used in this paper

Term	Definition
Image space	The coordinate system associated with the preoperative scan
Physical space	The coordinate system associated with patient in the operating room
Fiducial localization error (FLE)	Positional error in the fiducial markers’ locations caused by the inability to consistently determine their locations in both the physical and image spaces.
Target registration error (TRE)	The difference in the positions of an arbitrary point (not a fiducial location) in physical space and image space after registration.
Critical structure	An anatomical structure in the patient that is also represented by a set of voxels in a medical image.
Safety margin	A set of voxels surrounding the critical structure. This set is enlarged iteratively until the specified value of the overall damage risk is reached.
Overall damage risk	The probability that the critical structure in the patient will be damaged if all voxels surrounding the union of the critical structure and the safety margin were to be milled.
Neighboring voxels	Voxels that share at least one common vertex. Each voxel has 26 neighbors.
Analyzed shell	Voxels that share a voxel vertex with the union of the critical structure and the safety margin.
Point damage risk	The probability that the critical structure in the patient will be damaged if an individual voxel neighboring the union of the critical structure and the safety margin were to be milled. This value is calculated for each voxel in the analyzed shell.
Transfer percentage	The percentage of the analyzed shell that is transferred into the safety margin during a given iteration.

2.2 |. Overall damage risk

The overall damage risk is determined via numerical simulation. To perform this simulation, covariance matrices are estimated to describe the FLE distributions for each of the fiducial markers used during registration. These error distributions are then sampled to simulate imperfect fiducial locations that are used in a rigid registration to obtain a transformation from image space to physical space. This transformation is used to transform the voxels exterior to the safety margin from image space to physical space, where a check is performed for overlap with the critical structure. Note that because of the computational intensity of this approach, we only consider those voxels directly neighboring the outer boundary of the safety margin (voxels are considered as neighboring if they share a vertex, and as a result each voxel has 26 neighbors). This outer shell of voxels is called the ‘analyzed shell’ and is updated as the safety margin is ‘grown’ through algorithm iterations.

The overlap check is performed by discretizing faces of the voxels on the interior of the analyzed shell into a set of points (voxel corners). If, after registration, any point from this set lies within the critical structure, a collision has occurred. Figure 4 shows an example of such a registration. In Figure 4A, the true critical structure is black and the safety margin is cyan. Figure 4B shows the set of points associated with the interior faces of the voxels in the analyzed shell. Figure 4C shows a 3D rendering and a 2D slice taken from the rendering of Figure 4A and B registered together. Here, the green points are on the face of the analyzed shell and are external to the critical structure. The red points are on the face of the analyzed shell and are within the critical structure after registration. This simulation is repeated N_r (typically thousands) times. N_r is chosen by running the algorithm on a sample scan many times for various N_r values and recording the resulting damage probabilities. An acceptable N_r value is found when the variation of the trials falls below a given threshold (i.e. a value is selected that yields consistent results but is not overly computationally intensive). The overall damage risk is finally calculated as the fraction of those registrations containing overlap between the critical structure and the analyzed shell.

FIGURE 4.

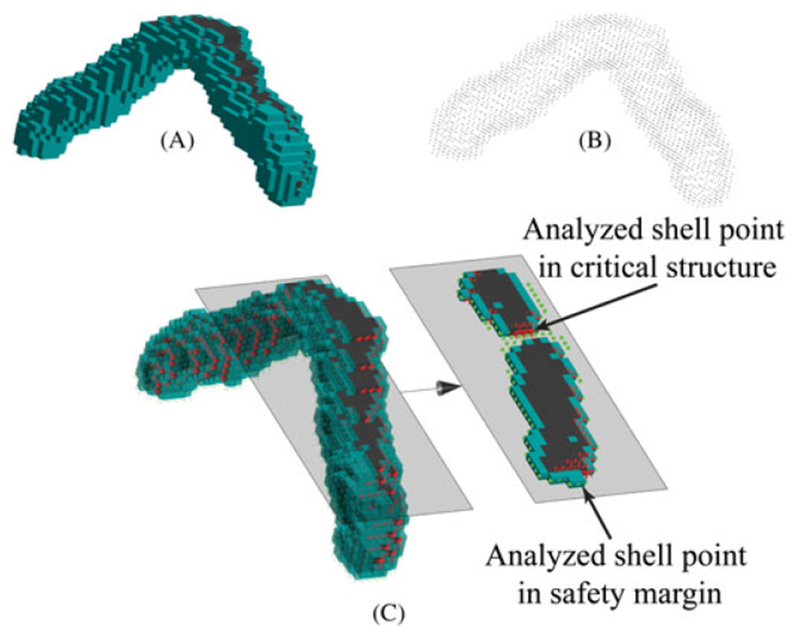
The effect of simulated registration error. A, The true location of the critical structure (black) and the safety margin (cyan) in physical space. B, A set of points located on the faces of the analyzed shell voxels that are neighbors of either critical structure or safety margin in image space. C, Superposition of A and B, after they have been registered together. The error in registration from image space to physical space is due to fiducial localization error (FLE) that is added to the true fiducial positions in both spaces before registration. Red stars represent points on the analyzed shell that lie within the critical structure, and green dots represent points on the analyzed shell that are external to the critical structure. Computing many such simulated registrations and tabulating the fraction of registrations that contain at least one red point yields the ‘overall damage risk’

2.3 |. Point damage risk

If the overall damage risk is above the safety level originally specified by the surgeon, additional voxels will be included in the safety margin. One simple approach would be to include the voxels closest to the critical structure. However, because of the anisotropic nature of the target registration error (TRE) this would produce a sub-optimal safety margin, i.e. a margin with uniform thickness but highly varying risk at the margin boundary. Here we use a different approach, in which each voxel is individually evaluated based on the probability that, after registration, the critical structure would be damaged if the voxel was targeted by the robotic mill. This probability is the ‘point damage risk’.

Given the FLE covariances described in the section ‘Overall damage risk’, we use the approach of Danilchenko and Fitzpatrick to determine the covariance of the TRE distribution at any point.¹⁷ This covariance can be used to determine point damage risk. We determine this risk by considering the smallest Mahalanobis distance between the point under consideration and a set of points on the surface of the critical structure. Mahalanobis distance is a multidimensional generalization of the standard deviation and can be related to Euclidean distance by applying a ‘whitening transformation’ (so-called because of an analogy with ‘white’ noise in visible images), which is an affine transformation dependent on the TRE covariance matrix. The TRE distribution in the whitened space is isotropic so the Mahalanobis distance and Euclidean distances are equivalent. The probability that the point under consideration actually (due to registration error) lies outside an ellipsoid defined by a constant Mahalanobis distance (illustrated as an ellipse in Figure 5C) can be calculated by evaluating a three-degree-of-freedom Chi-squared cumulative distribution function at the Mahalanobis distance squared. This computation yields the probability that despite registration error the point will remain within the ellipse in any direction, not necessarily the direction that would cause damage to the critical structure. Thus, the complement of this probability is a conservative estimate of the point damage risk. Note that because of the anisotropic nature of the TRE distribution, the point damage risk of the point under consideration in Figure 5 is higher than we would have assumed looking at only the Euclidean distance (red line in Figure 5B).

FIGURE 5.

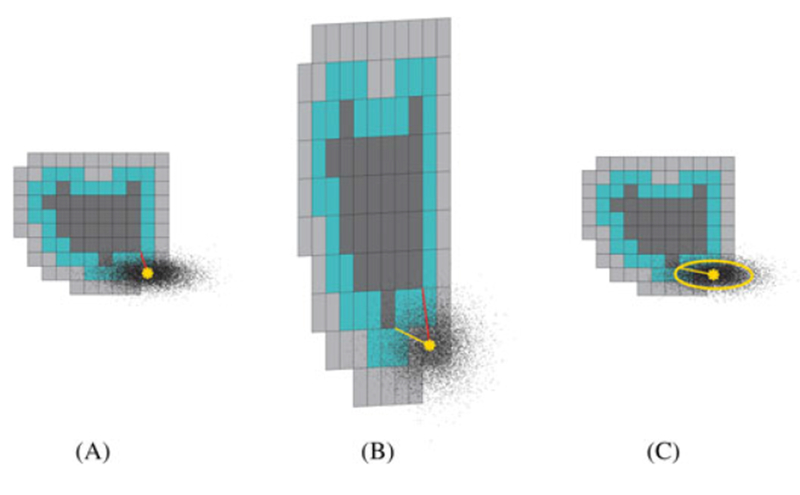
An illustration of the Mahalanobis distance calculation. A, A critical structure (black), safety margin (cyan), and analyzed shell (gray) are shown. The risk to the critical structure of milling a specific point (yellow star) is examined. The shortest distance between it and the critical structure is shown in red. B, ‘Whitened’ space, formed by applying the whitening transformation. The shortest distance is shown in yellow. C, In the whitened space, the probability that the point is within the yellow ellipse is easily obtained. The complement of this probability is a conservative estimate of the probability that the registration error could cause the center of a mill bit at the center of the circle to fall within the critical structure

As explained above, the point damage risk is inversely related to the shortest Mahalanobis distance between the point and the critical structure. This distance is calculated for each voxel in the analyzed shell and is used to rank the voxels based on their point damage risk. A visualization of the risk level of the voxels within an analyzed shell surrounding a critical structure and its safety margin is shown in Figure 6.

FIGURE 6.

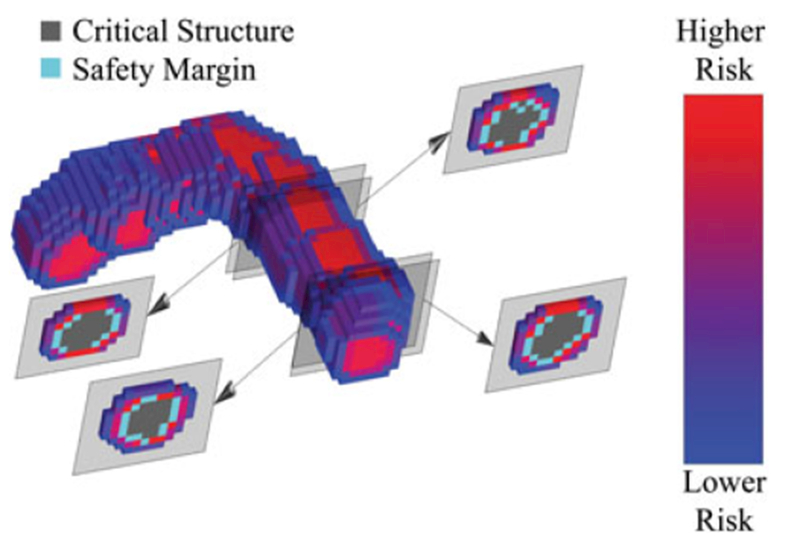
All the voxels surrounding a portion of a critical structure and its safety margin are shown. These voxels are color coded by the relative risk posed by each voxel to the critical structure in the patient, if that voxel location were to be milled. Several 2D cross-sections of the region of interest can be seen on either side of the 3D rendering

It is important to note that even though these individual probability estimates are conservative, they will not lead to an oversized safety margin because the overall damage risk, calculated via the simulation method described in the section ‘Overall damage risk’, is the final arbiter on how many voxels are included.

2.4 |. Growing the safety margin

The safety margin is expanded by transferring a percentage of the voxels in the analyzed shell associated with high risk to the critical structure (as identified in the section ‘Point damage risk’) into the current safety margin. This transfer is repeated as illustrated in Figure 7. The percentage of high-risk voxels moved into the safety margin at each iteration (transfer rate) is the key parameter of this process: a low transfer rate results in a high number of algorithm iterations, thereby increasing computation time; by contrast, a high transfer rate ensures quick convergence of the algorithm, but may result in unnecessarily thick margins. To address this tradeoff, we adapt the transfer rate as the algorithm progresses: it is initially set to a fixed value and then linearly decreases as the overall damage risk approaches the value specified by the surgeon (as illustrated in Figure 8). We note that the final result will always be conservative, since, while it is possible for slightly too many voxels to be transferred through this process, it is not possible for too few to be transferred to match the surgeon’s desired safety threshold. We will show in numerical simulations in the ‘Results’ section that the overshoot is small, when using the transfer percentage function illustrated in Figure 8.

FIGURE 7.

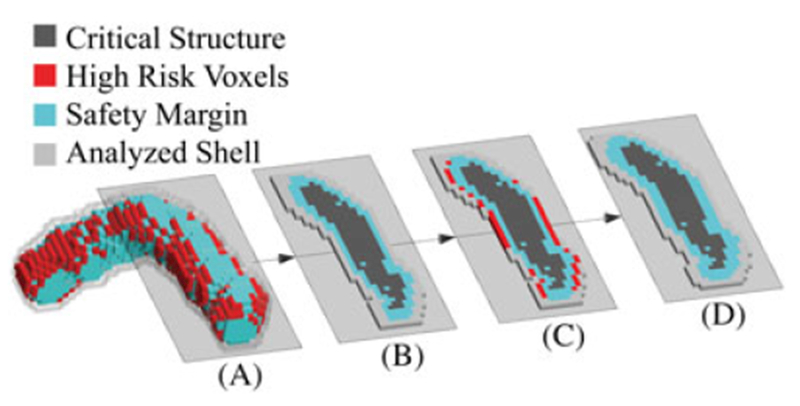
One iteration in the process of growing a safety margin around a critical structure is shown. The 2D slices are taken from the indicated plane of the 3D rendering A. B, 2D slice at the beginning of the iteration. C, High-risk voxels in red surrounding the critical structure + current safety margin. D, The high-risk voxels have been transferred to the safety margin, and the analyzed shell surrounding the union of the critical structure + safety margin has been updated. This result is the start of the next iteration

FIGURE 8.

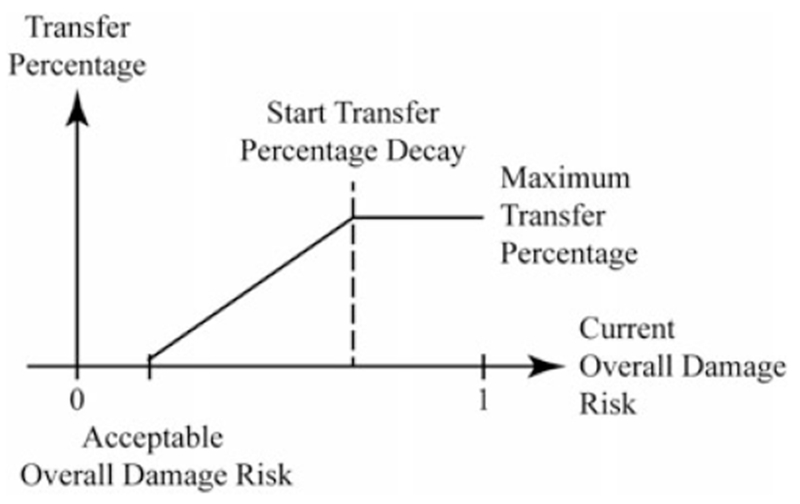
The linear interpolation by which transfer percentage is reduced is illustrated. Note that the overall damage risk is being reduced each time the algorithm iterates; therefore, the current overall damage risk moves from right to left along the figure’s horizontal axis

3 |. RESULTS

3.1 |. Experiments

We evaluated our algorithm by applying it to the preoperative planning of mastoidectomy. The facial nerve, chorda tympani, internal auditory canal, external auditory canal, and the sigmoid sinus are the critical structures for which we generate safety margins in this example. We applied the procedure summarized in Figure 3 to five cadaver specimens. The scans were obtained using a xCAT ENT portable CT scanner (Xoran Technologies, Ann Arbor, MI, USA) whose voxel is a 0.4 mm cube with a scan volume of 640 × 640 × 355 voxels. For comparison, a second set of scans was created by upsampling each of our five scans such that the voxels became 0.2 mm cubes. The volume of bone to be removed, the internal auditory canal, and the sigmoid sinus were manually segmented, and the chorda tympani, facial nerve, and external auditory canal were automatically segmented via methods described by Noble et al..²² A configuration of six bone-implanted fiducials unique to each specimen was located roughly 20 mm above the volume of bone to be removed (Figure 9). These fiducials were localized in the image,²³ and also serve as the attachment points for the robot to the patient.^12,21 Fiducial localization errors were generated for our computer simulations by selecting error displacements from true fiducial positions from an isotropic distribution. The distribution was normal with zero mean and standard deviation equal to $0.176∕\sqrt{3}=0.1016\mathrm{mm}$, which produces a root-mean-square three-dimensional error length, FLE, of 0.176 mm. This value is the average of the results of a detailed analysis of FLE for several scanners and localization methods.²⁴ The localization error was also ‘homogeneous’, meaning that the same distribution was used for each fiducial. For each registration in the section ‘Overall damage risk’ a random value was selected from this distribution for each component of each fiducial in each space. The 3D renderings of the initial segmentations can be seen in Figure 9. The parameters associated with two of our critical structures and their acceptable overall damage risks were taken from Noble et al.,¹⁹ as follows: facial nerve =0.001, and the external auditory canal =0.05. For the other structures, the acceptable overall damage risks were chosen with input from a surgeon as follows: chorda tympani =0.05, internal auditory canal =0.01, and the sigmoid sinus =0.01. We determined via simulation that the number of simulated registrations, N_r, required in order for these probabilities to be achieved to three decimal places was N_r = 25 000. The initial transfer percentage (Figure 8) was 20%. The overall damage risk threshold values after which the transfer percentage begins to decay (Figure 8) were 0.3 for the facial nerve, 0.4 for the chorda tympani, 0.5 for the internal auditory canal, 1.0 for the sigmoid sinus, and 0.5 for the external auditory canal. To further validate the final safety margins generated by the algorithm, we generated a shell of voxels that shared voxel faces with the union of the final safety margin and the critical structure. We recorded the average and standard deviation of the minimum Mahalanobis distances between the centers of the voxels in this final shell and the same set of discretized points on exterior of the critical structure we used in the section ‘Point damage risk’. The algorithm was also run with the Mahalanobis distance in the point damage risk calculation, replaced with a Euclidean distance. This caused the algorithm to generate safety margins that were uniformly distributed around their respective critical structures. These uniformly thick safety margins are then compared with the spatially varying safety margins developed by our algorithm.

FIGURE 9.

A cadaver scan is shown with six fiducial locations (red spheres), target region, critical structures, and the safety margins that our algorithm generated. After the removal of the intersection of the safety margins and the target region, the resulting reduced target region can be milled with statistical assurance of safety from registration error

3.2 |. Results

The results for each specimen can be found in Table 2. Figure 9 shows Scan 4 before the algorithm is applied (solid black critical structures), and after the TRE safety margins have been generated (transparent cyan safety margins). The simulation was written in MATLAB (with the Mahalanobis Distance calculation in a. mex file) and the workload was distributed in parallel among six CPUs using MATLAB’s parallel loop processing facility. The simulations were run on a Dell Precision 5810 with a six-core 3.5 GHz Intel Xenon processor and 16 GB of ram.

TABLE 2.

The results (with 95% confidence intervals) from running the TRE compensation algorithm on five cadaver scans

	Voxel size 0.43 mm3 Spatially varying safety margins	Voxel size 0.43 mm3 Uniformly thick safety margins	Voxel size 0.23 mm3 Spatially varying safety margins	Voxel size 0.23 mm3 Uniformly thick safety margins
Facial nerve
Volume of safety margin (mm3)	229.13±19.55	262.46±21.45	140.18±24.53	162.66±15.25
Final overall damage risk (acceptable =0.001)	6.56E-04±3.81E-04	4.64E-04±4.06E-04	6.88E-04±4.88E-04	6.16E-04±2.99E-04
Average mahalanobis distance from final shell voxels to critical structure	7.70±0.49	8.95±0.55	5.59±0.82	6.71±0.48
Standard deviation of mahalanobis distances from final shell voxels to critical structure	1.07±0.14	2.40±0.24	0.52±0.04	1.77±0.18
Chorda tympani
Volume of safety margin (mm3)	69.17±9.87	47.80±7.21	24.94±2.20	26.71±3.53
Final overall damage risk (acceptable =0.05)	0.0105±0.0269	0.0068±0.0119	0.0486±0.0019	0.0368±0.0131
Average mahalanobis distance from final shell voxels to critical structure	7.77±0.61	6.52±0.28	4.32±0.09	4.89±0.12
Standard deviation of mahalanobis distances from final shell voxels to critical structure	1.17±0.20	1.94±0.41	0.51±0.11	1.42±0.24
Internal auditory canal
Volume of safety margin (mm3)	227.39±56.00	222.96±55.25	142.39±26.46	158.28±27.24
Final overall damage risk (acceptable = 0.01)	0.0012±0.0014	0.0059±0.0053	0.0078±0.0054	0.0071±0.005
Average mahalanobis distance from final shell voxels to critical structure	7.34±0.19	7.57±1.55	4.84±0.48	5.57±0.59
Standard deviation of mahalanobis distances from final shell voxels to critical structure	1.15±0.15	1.93±0.57	0.55±0.13	1.32±0.35
Sigmoid sinus
Volume of safety margin (mm3)	646.57±184.37	661.26±265.14	470.96±154.14	514.44±174.98
Final overall damage risk (acceptable = 0.01)	0.0024±0.0043	0.0051±0.0054	0.0075±0.0052	0.0034±0.0038
Average mahalanobis distance from final shell voxels to critical structure	7.35±0.19	7.56±1.29	5.24±0.67	5.76±0.38
Standard deviation of mahalanobis distances from final shell voxels to critical structure	1.03±0.09	1.73±0.45	0.56±0.05	1.04±0.14
External auditory canal
Volume of safety margin (mm3)	426.98±65.60	347.70±39.15	241.88±29.13	262.82±17.77
Final overall damage risk (acceptable =0.05)	0.0203±0.0283	0.0105±0.0162	0.0477±0.0022	0.0407±0.0064
Average mahalanobis distance from final shell voxels to critical structure	7.39±0.46	6.56±0.49	4.44±0.30	4.99±0.20
Standard deviation of mahalanobis distances from final shell voxels to critical structure	1.16±0.18	1.93±0.66	0.51±0.12	1.22±0.17
Time (m)	3.85±1.79	14.87±11.46	108.70±40.76	137.49±82.23

4 |. DISCUSSION

These results indicate that using the method described in this paper, critical structures may now be given statistical safety guarantees with respect to registration uncertainty throughout robotic bone milling. This work is the first to generate safety margins that compensate for registration error by preserving critical structures (e.g. vasculature, nerves, etc.) to a specified safety level throughout the duration of a robotic surgical procedure. The safety methods were selected based on estimated complication rates in the conventional approaches as well as prior work in planning image-guided otologic surgery near vital anatomy. However, it is important to note that the values can be selected by the surgeon according to a variety of factors, including weighing the importance of the structure with the importance of removing nearby bone.

Every application of the algorithm was successful in that for each structure in each cadaver scan the acceptable overall damage risk values were satisfied. The similarity of the final overall damage risk values to their predefined acceptable values demonstrates the effectiveness of varying the analyzed shell transfer percentage. The calculation of instantaneous tool damage probabilities is an important first step toward increasing patient safety, as so aptly pointed out by Haidegger et al..¹⁸ However, we note that the average point damage risks of the shell of voxels that share at least one face with the union of the final safety margin and critical structure are on the order of 10⁻⁷ or smaller. This value is several orders of magnitude smaller than any of our final overall damage probabilities. Such a large disparity indicates that determining the safety of a critical structure based solely on instantaneous tool damage probabilities may greatly underestimate the danger presented to the critical structure. This observation under-scores the need to generate damage probabilities for the entire path traversed by the cutting burr, rather than relying on damage probability estimates that account only for the burr’s instantaneous positions. The final overall damage risks of the upsampled regions are much closer to the acceptable overall damage risks. The standard deviation of the Mahalanobis distances from the final shell voxels to the critical structure from the upsampled scans are smaller than those calculated for the original scans. These observations imply that the higher resolution of the upsampled volumes enables the shape of the optimal safety margins to be more closely approximated than they are in the original scans. The significantly smaller standard deviations of the Mahalanobis distances in the spatially varying safety margins coupled with their smaller safety margin volumes implies that the spatially varying safety margins are more optimally shaped than the safety margins of uniform thickness. Therefore, upsampling the input medical scan is an effective method to improve the volumetric efficiency of the safety margins generated by this algorithm.

In this work, the guarantees are based on the assumption that rigid point-based registration is the sole source of error. While this assumption is imperfect, other error sources whose statistics are known could be incorporated as well. These sources could include robot-specific physical errors such as calibration errors, joint positioning errors, system compliance, etc. Initial work toward modeling and incorporating these additional system errors into the safety margin algorithm is presented in Dillon et al..²⁵ The relative contribution of registration and other error sources is specific to a given system. Like registration error, other system error sources are typically spatially varying and anisotropic; thus, simulations like those described in this paper are necessary to account for patient-specific conditions related to each error source. Note that all of these errors represent positional uncertainty and potential damage to the underlying structure via direct contact with the cutting burr. Damage to sensitive anatomy such as nerves can also occur as a result of excessive heat.²⁶ In mastoidectomy, the open cavity can be irrigated throughout the procedure, minimizing the risk of thermal damage. However, in other procedures, such as minimally invasive drilling for cochlear implantation, irrigation is difficult and thermal damage to nerves needs to be considered. In this case, the heat rise can be modeled in a manner similar to that of Feldmann et al.²⁷ and included in the generation of safety margins.

While we have demonstrated the use of this algorithm on a system for robotic mastoidectomy previously developed in our lab (Figure 10H), there are several other robotic systems designed for skull base surgery that could benefit from this approach as well. Examples include freestanding or table mounted systems that optically track either the entire procedure or a tool that is used to register the patient to the robot (Figure 10A–E)^6-9,11 and bone-attached robots (Figure 10 F–H).^10,12,21 These systems are designed to perform skull base bone milling for otologic surgery (Figure 10A,B,D,H) and neurosurgery (Figure 10C), and linear drilling for minimally invasive cochlear implantation (Figure 10E–G). The accuracy and technical requirements of skull base bone milling and minimally-invasive cochlear implantation are similar since both involve removing bone in close proximity to critical structures to provide access to anatomy deep beneath the surface of the skull. These requirements suggest that any of these systems would benefit from the application of the algorithm presented in this work. All that is required to use the algorithm is segmentations of the vital anatomy in the medical image, knowledge of the locations of the fiducial markers relative to the anatomy, and estimates of the FLE, which can be used to generated estimates of registration error distributions near the anatomy. FLE of a given marker imaged with a particular scanner can be determined experimentally using geometric precise phantoms.^24,28

FIGURE 10.

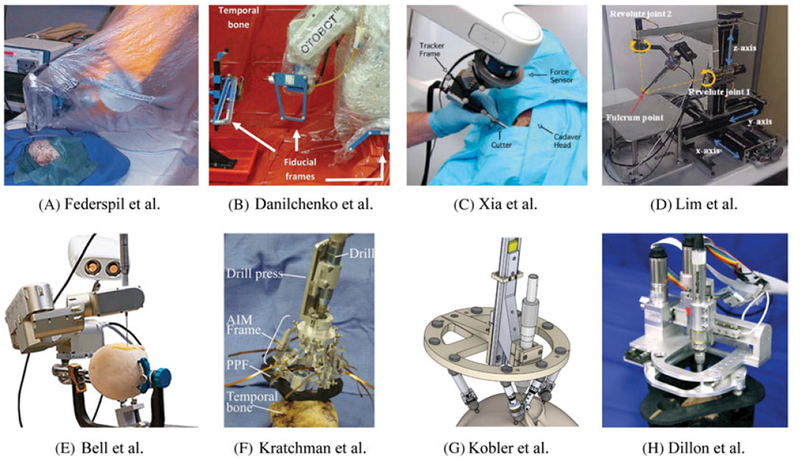
Several robotic systems developed for skull base surgery. Systems (a)-(d) are free standing robots used to mill portions of the skull base under guidance of an external tracking system. Systems (a) and (b) are autonomous robots while systems (c) and (d) are cooperatively controlled by the surgeon. Systems (e)-(g) are robots that drill a tunnel through the mastoid for minimally invasive cochlear implantation. System (e) mounts to the patient’s bed and is guided by an external tracking system while systems (f) and (g) are attached directly to the patient. Finally, system (h) is a bone-attached milling robot for mastoidectomy. All of these systems served as inspiration for the present work

In addition, the algorithm described in this paper has the potential to be applied to other surgical procedures substantially different from those we have discussed. The algorithm can be applied to any procedure that is reliant on a registration method whose TRE may be estimated statistically, and it provides a way to convert surgeon-specified safety thresholds into non-uniform margin thicknesses that provide a statistical assurance of safety. For example, in the placement of a deep-brain stimulation electrode, registration is typically accomplished via either bone-implanted fiducial markers or surface registration. Our algorithm could be used in this application to ensure the preservation of critical structures such as those listed by Bériault: ‘surface veins, arteries running within the sulci, ventricles, critical motor and sensory cortices, and deep nuclei such as the caudate nucleus’.²⁹ Thermal ablation of cancerous tumors, and needle placement for biopsy are also procedures that might benefit from this algorithm. It is also possible that this algorithm will enable the aforementioned procedures to be targeted in a safer manner by methods utilizing non-linear trajectories such as steerable needles. By developing this algorithm for generally shaped regions of interest, we have replaced safety margins based only on intuition with a statistically sound approach that has the potential to increase the safety in a broad range of surgeries.