Producing genome structure populations with the dynamic and automated PGS software

Abstract

Hi-C technologies are widely used to investigate the spatial organization of genomes. Because genome structures can vary considerably between individual cells of a population, interpreting ensemble-averaged Hi-C data can be challenging, in particular for long-range and inter-chromosomal interactions. We pioneered a probabilistic approach for generating a population of distinct diploid 3D genome structures consistent with all the chromatin-chromatin interaction probabilities from Hi-C experiments. Each structure in the population is a physical model of the genome in 3D. Analysis of these models yields new insights into the causes and the functional properties of the genome’s organization in space and time. We provide a user- friendly software package, called PGS, which runs on local machines (for toy runs) and high- performance computing platforms. PGS takes a genome-wide Hi-C contact frequency matrix along with information about genome segmentation and produces an ensemble of 3D genome structures entirely consistent with the input. The software automatically generates an analysis report, and provides tools to extract and analyze the 3D coordinates of specific domains. Basic Linux command line knowledge is sufficient for using this software. A typical running time of the pipeline is about 3 days with 300 cores on a computer cluster to generate a population of 1,000 diploid genome structures at TAD level resolution.

INTRODUCTION

The question of how a genome is intricately packed inside the nucleus has sparked a burgeoning field of study. Advanced Hi-C techniques are generating rich datasets of the contact frequencies between chromosome regions, which are extremely valuable for investigating the spatial organization of the genome^1–9. Reconstructing the genome in 3D is an appealing approach to understanding the relationship between genome structure and function. However, the 3D organization of the genome varies greatly between cells^{9– 13}. This variability poses a great challenge to interpreting ensemble Hi-C contact frequencies, which are averaged across an ensemble of cells. Long-range and inter-chromosomal interactions, which have low frequencies to begin with, are particularly difficult to integrate into consistent 3D models^8,14–20. To address this challenge, we recently introduced the concept of population-based genome structure modeling. This probabilistic approach deconvolves the ensemble Hi-C data and generates an ensemble of distinct diploid 3D genome structures that is fully consistent with the input dataset of chromatin-chromatin interactions. Hence, our method explicitly models the variability of 3D genome structures across cells^8,19. Moreover, because the generated population contains many different structural states, mutually exclusive interactions (often low-frequency, long-range interactions) can be accommodated by incorporating these in different structures. As a result, almost all observed chromatin interactions can be considered and alternative chromatin structural states can be analyzed in detail²⁰. Our method is sufficiently flexible to integrate additional experimental information (e.g. Lamina DamID²¹) and model the genome at various levels of resolution.

Data-driven genome modeling approaches can be divided into three categories: i) consensus methods, ii) resampling methods, and iii) population-based deconvolution method²² (see a comparison in Table 1). Consensus methods generate a single structure from ensemble Hi-C data^23,24 by relating contact frequencies with spatial distances, which are then used to generate a single 3D structure by optimizing a scoring function^3,23–26, a likelihood function through Bayesian inference²⁷, or solving a generalized linear model²⁸. These methods are conceptually simple and computationally time efficient. However, by generating a single 3D model they cannot simultaneously reproduce all the contacts present in the Hi-C experiment, nor can they represent the considerable structural variability of genome structures between cells, which calls into question that a single-structure approach can fairly represent the complexity of genome structures. In contrast, resampling methods, such as TADbit²⁹ and MCMC5C³⁰ optimize many structures from the same scoring function to consider aspects of genome structure variability. TADbit performs many independent optimizations starting from random configurations using IMP^31,32, while MCMC5C calculates an ensemble by assuming independency after large numbers of iterations in Markov chain Monte Carlo sampling³⁰. Both methods mainly focus on 5C (Chromosome Conformation Capture Carbon Copy)³³ data, which typically span several hundred kilo bases. Resampling is also applied by other methods like InfMod3Dgen³⁴ and non-distance based methods like MOGEN^35,36, and Chrom3D³⁷. Gehlen et al. and Meluzzi et al. built polymer models at ~4kb resolution using a resampling strategy^16,38. Common to all resampling methods is that usually the same input dataset is applied to all structures of the ensemble, which can include conflicting data from mutually exclusive chromatin conformations. This may lead to inconsistencies between data and models (i.e., restraints violations) when the complete data is considered simultaneously in a single structure.

Table 1. Comparison of data-driven 3D genome modeling methods.

Representation (column 5) refers to the structural representation of the genome. All genome structure models are coarse grain models, which represent chromatin in a simplified way, e.g. beads on string or connected points. ‘Spheres’ indicates that the chromatin region is represented as a sphere with an excluded volume, which is either explicitly or implicitly considered during sampling. For ‘point’ representations, usually no excluded volume is considered. ‘Polymer’ representations are more physical fiber models where stretching and bending energies are included into the objective function. Model type (last column) refers to a strategy used during the sampling. A consensus model strategy usually generates a single average model. Resampling methods usually acknowledge the structural variability by generating a number of independent replica optimization using the same input data for each model. ‘Population’ refers to a population-based deconvolution strategy, which attempts to de-convolve the ensemble Hi-C data into a population of individual structures. The PGS method has been improved since our first version in 2011 in terms of the deconvolution techniques, chromatin resolution, and the IMP version implemented.

Method	Year	Available online	Chromatin resolution	Representation	Sampling method	Distance/ contact based	Diploid Genome	Genome coverage	Species	Model type
Duan et al.3	2010	No	10kb	Spheres	Interior-point gradient-based method	Distance	No	Whole Genome	Budding Yeast	Consensus
BACH27	2013	Yes	TAD	Points	Gibbs sampler with hybrid MC and adaptive rejection	Distance	No	All chromosomes	Mouse	Consensus
AutoChrom3D23	2013	Yes	8kb	Points	Nonlinear constrained	Distance	No	500–800kb	Human	Consensus
ChromSDE24	2013	Yes	40kb–1Mb	Points	Semidefinite programming	Distance	No	Chromosome 13	Mouse, Human	Consensus
PASTIS25	2014	Yes	100kb–1Mb	Points	Interior point filter algorithm	Distance	No	All chromosomes	Mouse	Consensus
ShRec3D26	2014	Yes	3kb–150kb	Points	Shortest path reconstruction	Distance	No	30Mb, Chromosome 1	Human	Consensus
HSA28	2016	Yes	25kb–1Mb	Points	Hamiltonian dynamics with simulated annealing	Distance	No	All chromosomes	Human	Consensus
3D-GENOME44	2016	Web server	hierarchical	Polymer	Monte Carlo simulated annealing	Distance	No	All chromosomes	Human	Consensus
MCMC5C30	2011	Yes	Fragment (5C) 1Mb(HiC)	Points	MCMC sampling using Metropolis-Hastings algorithm	Distance	No	142kb(5C) 88.4Mb(Chr14, HiC)	Human	Resampling
TADbit29	2012	Yes	Fragment (5C)	Spheres	Monte Carlo sampling and Simulated Annealing with Metropolis scheme	Distance	No	500kb(5C)	Human	Resampling
Junier et al.14	2012	No	30nm fiber	Polymer	Monte-Carlo algorithm with Metropolis	Contact	No	1.2Mb (chr11)	Human	Resampling
Gehlen et al. 38	2012	No	3.9kb	Polymer	Molecular dynamics	Contact	No	Whole Genome	Budding Yeast	Resampling
Meluzzi and Arya16	2013	No	3–6kb	Polymer	Brownian dynamics	Contact	No	135–270kb	Pseudo	Resampling
Trieu and Cheng35	2014	No	200kb–1Mb	Points	Gradient descent	Contact	No	All chromosomes	Human	Resampling
InfMod3DGen34	2015	Yes	Fragment	Polymer	Gradient ascent	Distance	No	All chromosomes	Yeast	Resampling
MOGEN36	2016	Yes	1Mb	Points	Gradient ascent optimization	Contact	No	Whole Genome	Human	Resampling
Chrom3D37	2017	Yes	TAD	Spheres	Monte Carlo optimization	Contact	Yes	Whole genome	Human	Resampling
Kalhor et al.8	2012	No	1–4Mb	Spheres	Simulated Annealing/Molecular dynamics	Contact	Yes	Whole genome	Human	Population
Giorgetti et al.17	2014	No	3kb	Spheres	Iterative Monte Carlo scheme	Contact	No	780kb	Human	Population
MiChroM18,45	2015	No	40kb–50kb	Polymer	Molecular dynamics	Contact	No	All chromosomes	Mouse	Population
PGS (ours)19	2017	Yes	TAD	Spheres	Simulated Annealing/Molecular dynamics	Contact	Yes	Whole genome	Human	Population

In contrast to resampling methods, population-based deconvolution approaches deconvolve ensemble Hi-C data into a population of individual structures. These structures reproduce ensemble Hi-C data by distributing chromatin contacts across all structures of the population^8,17,18, rather than imposing the same data set on each structure individually. As a result, structures can be in different conformational states, which could contain chromatin contacts that would otherwise be mutually exclusive when imposed on the same structure. They can typically reproduce almost all the contacts from Hi-C experiments without generating unphysical structures from imposing conflicting data in a structure. Previously, we developed one of the first population-based deconvolution methods for modeling diploid genomes from Hi-C data⁸. Another approach, developed by Giorgetti et al., uses an iterative Monte Carlo scheme to generate a population of chromatin loci spanning 780 kb¹⁷. Zhang et al. uses the maximum entropy principle and molecular dynamics to model mouse chromosomes¹⁸. However, software packages of population-based deconvolution methods have not been openly available and neither of them can currently be used to interpret Hi-C data on a diploid whole genome scale.

In this paper, we provide the protocol to run our software pipeline, named PGS (Population-based Genome Structure), which has been substantially improved from the earlier version. Briefly, we employ a structure-based deconvolution of Hi-C data and optimize a population of distinct diploid 3D genome structures by maximizing the likelihood of observing the Hi-C data. Because there is no closed form solution, we employ an iterative and step-wise restraint optimization procedure. Each iteration involves two steps: constraint assignment (termed the A-step) and optimizing the structure population with a combination of the simulated annealing and conjugate gradient methods^31,39,40 (termed the M-step). We increase the optimization hardness in a step-wise manner by gradually adding more contact constraints during the iterative optimization process (Fig. 1). Importantly, by embedding an ensemble of genome structures in 3D space as part of the optimization process, the method can detect which chromatin contacts are likely to co-occur in individual cells. Hence, the population represents a deconvolution of the Hi-C data into individual structures and domain contacts; it is the best approximation to the underlying true population of genome structures in the Hi-C experiment, given the available data and assumptions. Because our approach considers the stochastic nature of chromosome conformations it allows analysis of alternate chromatin structural states²⁰. Our expectation-maximization (EM) modeling framework is extendable for integration of other data sources, for example combining Hi-C with Lamina DamID data²¹. The chromatin domain contacts of the structure population as a whole are statistically highly consistent with the Hi-C data.

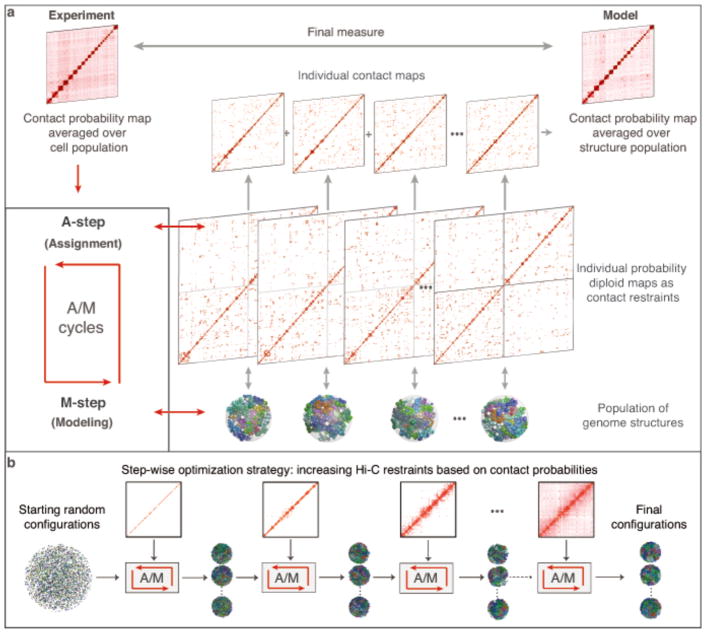
Figure 1.

Schematic of the PGS algorithm that deconvolves ensemble-averaged Hi-C data into a population of distinct diploid 3D genome structures. (Reprinted with permission from Tjong et al. 2016⁷) (a) The iterative scheme involves constraint assignments (A-step) and dynamic optimization of the structures (M-step). The new structures are used as feedback for the next A-step. (b) Constraints are added to the model gradually by decreasing a contact probability threshold.

Our PGS modeling package takes two inputs: an experimental Hi-C contact frequency map, and a segmentation of the genome sequence into chromatin domains (e.g., Topological Associated Domains, henceforth TADs) (Fig. 2). PGS generates a population of 3D genome structures where each domain is represented as a sphere, and the distribution of physical contacts between domain spheres across the population reproduces the Hi-C experiment. The software automatically generates an analysis of the structure population, including a description of the model quality based on its contact probability agreement with experiments and various structural genome features, including the radial nuclear positions of individual chromatin domains. The software also comes with a set of additional tools to facilitate user customized analysis, such as a tool for exporting PDB structures for visualization. The individual genome structures also contain a wealth of information and can be used to detect higher-order structural patterns of chromatin regions (as described in Ref.8). As gold standard assessment, it is necessary to compare defined structural features from the structure population with independent experiments not included as input information when generating the models, for example, such information may be distances between specific loci from 3D FISH experiments¹⁹, contact frequencies between chromatin and the nuclear envelope from lamina DamID experiments²¹ or spatial features extracted from soft X-ray tomography experiments¹⁹.

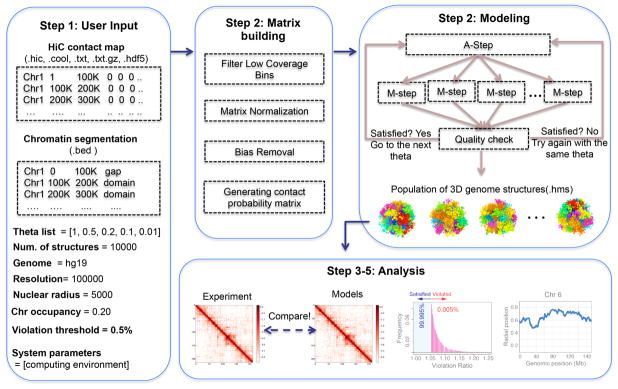
Figure 2.

PGS software workflows. Building the input matrix, modeling and optimizing structure population with A/M cycles, and basic analysis from the final structure population.

Limitations of PGS

The major drawback of PGS is the intense computational resources required by the pipeline as it relies on optimizing a large number of genome structures (typically 1,000–10,000 structures). Depending on the computational resources, this requirement may practically limit the model resolution for calculating entire diploid genome structures of mammalian cells to ~50 to ~100kb resolution. For parallel computing, PGS currently supports only the Sun Grid Engine (SGE) and Portable Batch System (PBS) workload managers, e.g. Torgue. Other workload managers and cloud computing is not support yet. Also, Python 3 is not supported at this moment.

Software design and implementation

The PGS package generates a large number of genome structures, which constitute an optimized structure population consistent with the input data. The complexity of this computational problem originates also from the large scale of the input data (high-resolution, genome-wide Hi-C contact frequencies), which must be processed to generate constraints on the structure population. To meet this computational challenge, PGS has been designed to run in a high-performance computing (HPC) environment, such as Sun grid engine (SGE) or Torque. We have also designed PGS to work on a laptop or personal computer, but this application should only be used to generate a small population of structures (around 100 for testing purposes). PGS is implemented as a single Python software package for ease of installation and use. We wrapped the source code in pyflow (https://github.com/Illumina/pyflow), a lightweight parallel task engine developed by Illumina, which runs the whole complex simulation process through a single command without any intermediate human intervention. Note that while the original pyflow library only supports local computers and SGEs, we developed a modified version of pyflow, called pyflow-alabmod (https://github.com/shanjunUSC/pyflow-alabmod) allowing PGS to run in a HPC environment with PBS (Portable Batch System) script. In addition to PGS, users must install the independent modeling software IMP (version 2.4 or above), which can be downloaded from https://integrativemodeling.org/. Users should also install Python 2 (version 2.7 or higher) and its libraries, including numpy, matplotlib, pandas, h5py, seaborn, and scipy (web addresses indicated in the Materials section). To provide flexibility, we divided the whole workflow into three independent, consecutive stages (Fig. 2):

1. Producing a domain-domain contact probability matrix from the input Hi-C data. (Step 2, matrix building)

2. Generating the optimized structure population. (Step 2, modeling step)

3. Producing a basic analysis summary for the resulting structure population. (Step 3–5)

Users who already have a domain-domain contact probability matrix can skip Step 2, matrix building via the graphical user interface (GUI) (Fig. 3a) by selecting TAD-TAD Prob option. By default, PGS takes a raw (Hi-C) contact matrix as the input (Fig. 3b). In any case, even if the user skips this matrix building step, they must provide a text file containing the chromosome segmentations (i.e., the domain or TAD definitions; Fig. 3c). The required file formats are described in the Materials section.

Figure 3.

PGS setup. (a) GUI to help users generate configuration files. (b) An example showing the format of an acceptable contact frequency matrix file. (c) An example showing the format of an acceptable TAD file.

PGS comes with a GUI to help new users generate the input configuration file (a json file). For an experienced user, it is straightforward to directly modify the input configuration file. This file contains the location of the raw Hi-C matrix file, the location of the chromatin segmentation or TAD definition file, modeling parameters, and system parameters. The first component normalizes the raw Hi-C contact map using KR-normalization^41,42 and generates a TAD-level contact probability matrix. The second component generates an optimized population of a given number of genome structures through the iterative A-step and M-step cycles. The third component produces a report on the quality of the optimization, as well as basic structural analyses such as contact frequency heat maps and the average nuclear radial position of each TAD (Fig. 4).

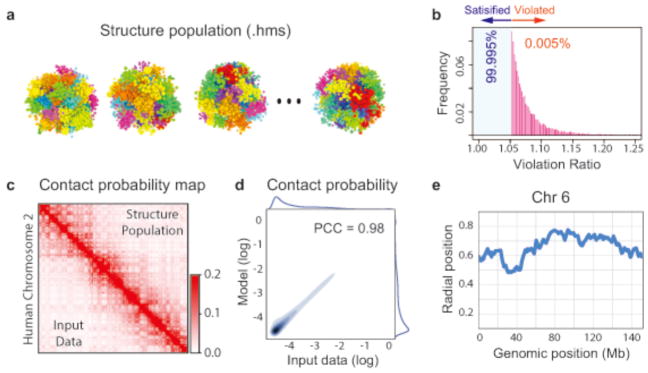
Figure 4.

Examples of PGS outputs. (a) Structure population as hms files. (b) Histogram of violated constraints. The maximum number of violated restraints is defined in the “violation cutoff” configuration setting (see Step 1). (c) Comparison of contact probabilities for chromosome 2 between the input data from Hi-C experiment and the genome structure population. Input data are shown in the lower triangular of the matrix and the contact probabilities from the final structure population are show in the upper triangular of matrix. The color scheme is from white (0) to red (0.2). (d) Density scatter plots comparing all pairwise domain contact probabilities from the structure population and the input Hi-C data. The Pearson’s correlation coefficient (PCC) of the comparison is indicated. Histograms of the contact probabilities are shown along the sides of the plot.(e) The average radial position of domains along a chromosome. PGS generates this plots for every chromosome.

MATERIALS

Equipment

• A workstation with Linux or Mac OS X system, or HPC cluster with 2Gb of RAM per computing node.

• PGS (https://www.github.com/alberlab/PGS).

• CRITICAL PGS is a Python 2.7 package which runs on Linux and Mac OS X systems.

• Python 2.7 (http://www.python.org/)

• Numpy 1.12.0(http://www.numpy.org/)

• Scipy 0.18.1 (http://www.scipy.org/)

• Matplotlib 2.0.0 (http://matplotlib.org/)

• Pandas 0.19.2 (http://pandas.pydata.org/)

• H5py 2.6.0 (http://www.h5py.org/)

• Seaborn 0.7.1 (http://seaborn.pydata.org/)

• IMP (Integrative Modeling Package) version 2.4 or later (https://integrativemodeling.org/)

• JavaSE version 6 or later (https://www.java.com/) if the user want to use graphic user interface (GUI)

• Input files (see Box 1)

Box 1. Input files for PGS.

Prepare the experimental data. Depending on options chosen by the user during configuration, PGS can take different kinds of input files.

Option 1 (raw + TAD definition). The user provides a raw contact frequency matrix (uniformly binned) and TAD index information. PGS generates a TAD-TAD contact probability matrix from the raw data and automatically proceeds to the modeling component. This option requires two input files:

• File 1: Genome-wide chromatin-chromatin interaction matrix, where each of the N rows describes one bin of the Hi-C data. This text file can be gzip or bzip compressed. It is formatted as follow (see Fig. 3b).

  • No header

  • Column 1: chromosome name (e.g. Chr1, Chr2, …, ChrX)

  • Column 2: start genomic position of the Hi-C bin (0-based)

  • Column 3: end genomic position of the Hi-C bin (1-based)

  • Columns 4 to N+3: contact vector of the bin with all other bins (i.e. contact matrix) (integers)

  There is also a wide range of existing storing methods for sharing Hi-C data. In addition to the raw dense matrix storing method we also provide support for *.hic (https://github.com/theaidenlab/juicer/wiki/Data)⁴³ and *.cool (https://github.com/mirnylab/cooler) data files. With the correct file extensions, data in these formats can be directly processed by PGS.

• File 2: Chromosome segmentation file, where each row defines one topological associated domain (Fig. 3c). This text file has the BED file format:

  • No header

  • Column 1: chromosome name (e.g. Chr1, Chr2, …, ChrX)

  • Column 2: start genomic positions of TAD (0-based)

  • Column 3: end genomic positions of TAD (1-based)

  • Column 4: flag for the kind of TAD (“domain”, “gap”, “CEN”)

Option 2 (TAD-TAD probabilities + TAD information). In this case, the user has already prepared a TAD-TAD contact probability matrix and must also provide the TAD definitions in a file. The two input files have the same formats as files 1 and 2 in Option 1. The bins in the first file represent TADs and the matrix elements must be probability values between 0 and 1.

Option 3 (hdf5 prob). The user provides a TAD-TAD contact probability matrix that was generated by PGS. This option is useful for producing independent structure populations from a different random initialization of the structures, or for testing different model parameters using the same input data.

Equipment setup

Installation of PGS

We recommend following the installation instructions from our online documentation (http://pgs.readthedocs.io/en/latest/quickstart.html). The easiest way to install PGS is to use a conda package manager. Both Anaconda (https://www.continuum.io/downloads) and the minimal package Miniconda (http://conda.pydata.org/miniconda.html) are suitable for managing all the required packages, including IMP. Once the PGS package has been downloaded along with all the dependencies mentioned above, set up the package using the following command.

$ python setup.py install

The script “ setup.py” is located in the PGS directory. To confirm that PGS is installed properly, users can execute the following shell commands.

$ cd test
$ sh runPgs_workflow_test.sh

This process should take less than two minutes on any current computing workstation. Users are encouraged to run “ runPgs_workflow_test.sh” and “ runPgs_probMat_run_test.sh” bash scripts located in test directory to test if the installation is successful.

PROCEDURE

Generate the configuration file and execution script. Timing: less than 10 minutes

• 1Use the graphical user interface (GUI) called PGS-Helper (requires Java) to generate the configuration file and execution script (option A). More experienced users can modify the prepared configuration file and execution script directly (option B). 11

A. Using PGS-Helper (if Java is installed)

1. Open PGS-Helper by running the following command:

   $ java –jar PGSHelper.jar
   

   The command will display the PGS GUI (Fig. 3a) prompting the user to enter the needed information. In Table 2 we describe the fields displayed in the GUI. Most of the fields are pre-populated, so the user can just review and modify them if necessary. There are 4 blank fields that the user must complete, i.e. ‘Working Directory”, “PGS Source Directory” and “Raw Matrix(txt)” and “TAD file (.bed)” in the Input section of the GUI. ?Troubleshooting

2. Click the “Generate” button at the bottom. The user then can review the usage in the bottom box, and confirm to generate the configuration ( input_config.json) and executable files ( runPGS.sh).

Table 2. PGS-Helper GUI fields.

PGS-Helper is a GUI to simplify the input parameter generation for end users. The GUI has 6 fields (Figure 3a). Field by field explanations of PGS-Helper GUI is shown in each row. Bold italic words refer to the corresponding input box in each field. Prepopulated default values are also given in brackets.

Field 1: Working directory	This is the directory where the output of the GUI (the executable script runPGS.sh and the configuration file input_config.json), the log files (pyflow.data directory), and the results of the 3D genome modeling will be stored.
Field 2: PGS Source directory	This is the PGS installation directory, which contains pgs.py
Field 3: Input	Select one of the three options to specify which types of input files are to be used (see Equipment for details), and specify the file locations. Genome. The current version of PGS supports recent human and mouse genomes: hg19, hg38, mm9, and mm10. PGS automatically generates the diploid autosome and X chromosome representations. Resolution. The bin resolution (integer number of base pairs) of the raw Hi-C matrix.
Field 4: Modeling Parameters	Num of structures. The number of structures in the population to optimize (default = 1,000). We recommend increasing this value to at least 10,000 for a final sampling). Violation cutoff. The maximum proportion of violated constraints. A smaller value will generally result in better agreement with the input data (default = 0.05). Theta list. A decreasing series of values in the range 1 ≤ theta < 0. Each theta is a contact probability threshold, determining which contacts are used in the optimization. PGS progresses through all the values in this list, gradually including more and more Hi-C contacts in the optimization (default = 1, 0.2, 0.1, 0.05, 0.02, 0.01). Max iteration. The maximum number of A/M cycles for each value of theta (default = 10). Nucleus Radius. The radius of the nucleus in nanometers. A typical human nucleus has a radius of 5000 nm (default = 5000). Genome occupancy. The ratio between the genome-wide chromosomal volume and the total volume of the nucleus (default= 0.2).
Field 5: System Parameters	Default core. The default number of computing cores to use for each job. Light jobs, such as the modeling step (M-step), do not require more than one CPU (default = 1). Default mem MB. The memory limit for each job in megabytes (default = 1,500). Max core. The maximum number of computing cores to allocate for a heavy job, such as building the matrix or calculating pairwise distance distributions (default = 8). Max mem MB. The memory allocation limit for a heavy job (default = 64,000 MB).
Field 6: Command setup	Run mode. The user’s computing platform. This can be local (e.g. a personal workstation), SGE (Sun Grid Engine), or Torque. Core limit. Specify the maximum number of cores to allocate. (This setting is valid for all three run modes. In local mode, set this value to the cores of the computer.) Mem limit. Specify the limit of total memory usage in MB. Optional argument list. Additional unix-style command line arguments (user specific) for all job submissions. The GUI provides a template allowing the user to recognize and supply missing values (e.g. in [‘-q’,‘[qname]’,‘- l’, ‘walltime=hh:mm:ss’] replace qname with the user’s HPC queue name, and hh:mm:ss with hours:minutes:seconds.).

B. Check and modify the configuration and executable files directly

1. In case users do not have Java installed to run the PGS Helper program, the package also provides examples to set the parameters in a text file. Open the configuration file “ input_config.json” (Box 2) and “ runPGS.sh” (Box 3) in the pgs/test directory, and modify them as needed.

Box 2. Editing Guideline for input_config.json.

This is an example of input_config.json file. Each parameter is explained in brackets. Refer to Table 2 for more detailed information for each parameter. There are also examples in pgs/test directory, which can be easily modified.

 {“source_dir” : “[Directory name where pgs socurce is]”,
  “input” : {
     “contact_map_file_hdf5” : “[Contact map file]”,
       “TAD_file” : “[ TAD file, .bed format]”
       “resolution” : “[Resolution of input contact_map_file] e,g. 100000”
       “genome” : “[Genome version], e.g. hg19”
     },
  “output_dir” : “[Output Directory to store the results], e.g.
$PROJECT_DIR/result”,
 “modeling_parameters” : {
     “theta_list” : [Theta list] e.g, [“1”, “0.2”, “0.1”,”0.05”,”0.02”,”0.01”],
      “num_of_structures” : [Number of structure to generate] e.g. 10000,
       “max_iter_per_theta” : [Max Iterations per job] e.g. 10,
       “violation_cutoff” : [Violation Cutoff ] e.g. 0.005
       “chr_occupancy” : [Chromosome Occupancy ] e.g. 0.2
       “nucleus_radius” : [Nucleus Radius ] e.g. 5000.0
    },
   “system” : {
        “max_core” : [Maximum number of cores in a single node], e.g. 8,
        “max_memMB” : [Maximum size of mem(MB) in a single node] e.g. 64000,
        “default_core” : [Default number of cores], e.g. 1,
        “default_memMB” : [Default size of mem(MB)] e.g. 1500
    }
}

Box 3. Editing Guideline for runPGS.sh.

This is an example of runPGS.sh file. This is a bash command line file with only one simple command. Please replace parameters starting with the dollar sign ‘$’ with the actual directory name. Please also modify parameters after double dash flags. There are also examples in the pgs/test directory, which can be easily modified.

python $PGS_DIRECTORY/pgs.py
--input_config $PROJECT_DIR/input_config.json
--run_mode [running platform]
--nCores 300
--memMb 800000
--pyflow_dir $PROJECT_DIR
--schedulerArgList [“-q”,”[qname]”,”-l”,”walltime=100:00:00”]

Run PGS. Timing: 3d to 2 weeks, depending on parameters

• 2After the configuration file and execution script are generated, execute PGS with the following command.

  $ sh runPgs.sh
  

  This step consists of 2 parts: matrix building and modeling. These two parts are consecutively executed automatically.

  The matrix building step is a general preprocessing of Hi-C contacts. The purpose of this step is to convert the raw Hi-C count matrix to a probability matrix. The details of this procedure can be found in the Supplementary Data.

  The modeling step is also fully automatic. Structure populations (Fig. 4a) will be generated and stored in structure directory (See anticipated results for more information)

  CRITICAL STEP If an unexpected error occurs during the run, a simple restart of the step will usually fix the problem.

  ?Troubleshooting

Analysis. Timing: ~1h

• 3Analyse the data using the tools offered in the PGS package (details can be found at http://pgs.readthedocs.io/en/latest/tools.html) or by customizing tools using alab API (http://pgs.readthedocs.io/en/latest/alabapi.html).

  To extract the 3D coordinates of the genome, run the following commands in Python:

  import alab
  hmsfile = ‘result/structure/copy0.hms
  problvl = ‘0.01a’
  hms = alab.modelstructures(hmsfile, [problvl])
  TADidx = hms.idx #TADs information
  xyz = hms[0].xyz #diploid set of coordinates
  

  This stores the coordinates in xyz for analysis. The TAD information with genomic location is stored in the TADidx variable. In the following we provide some other usage of coordinates.

• 4Make the contact probability map by running the following commands in Python:

  import alab
  hmsfiledir = ‘result/structure’
  problvl = ‘0.01a’
  nstruct = 1000
  summary = alab.structuresummary(hmsfiledir, problvl, nstruct)
  m = summary.getContactMap()
  m.plot(‘heatmap.png’,format=’png’,clip_max=1)
  m.makeIntraMatrix(‘chr1’).plot(‘chr1_heatmap.pdf’,format=’pdf’,clip_max=1) 
  

  This will create the probability maps in the result/report/heatmap and result/report/intraMatrix folders.

• 5(OPTIONAL) Some users might wish to get the coordinates and radii in a Protein Data Bank (PDB) format, e.g. for visualization purposes. Transfer the coordinates to PDB format with the scripts in the tool/ directory by running the following shell command under $PROJECT_DIR/:

  $ tools/hms_export.py result/structure/copy0.hms 0.01b copy0.pdb
  

TROUBLESHOOTING

Troubleshooting advice can be found in Table 3.

Table 3.

Troubleshooting

Step	Problem	Possible reason	Solution
1	Java is installed, but the GUI of PGS Helper does not appear	X11 for graphical display is not turned on	Log in again to your HPC with the “ssh – X” option
2	The terminal where PGS was executed closed, so the PGS process was stopped	Accidentally closed, system shut-down, or broken node.	Rerun PGS, using the same command as before
2	PGS stops with [ERROR] messages containing “… failed sub-workflow classname: ‘BuildTADMapFlow’ …” and “IndexError: … is out of bounds …”	The resolution is set incorrectly, or the input matrix format is wrong.	Fix the resolution parameter in input- config.json, and check the input file format.
2	PGS stops with [ERROR] messages containing “… failed sub-workflow classname: ‘BuildTADMapFlow’ …”, “… using non-integer …”, and “originHist = …”	The raw input matrix contains a non- integer	Check and fix the matrix
2	PGS stops while running the A/M- cycles	Computing cluster problems	Try to request more than 10 GB memory for the main PGS program

TIMING

Step 1: The configuration of PGS should take only about 1 minute.

We have designed PGS to automatically and dynamically run a series of processes or steps. If there are failures on a running job, for example because a node is down, the network is busy, or there is a disk I/O failure, PGS tries to resubmit the failed job two more times before aborting.

Step 2: The total run time for PGS can vary widely depending on available computing resources, data size, and modeling complexity. The first task is to build the input matrix, which takes about 1 minute or less for input options 2 and 3. If the user selects input option 1, this task takes from several minutes to several hours depending on the size of the matrix (Box 1) For instance, it takes about one minute to process a 2 Mb resolution Hi- C matrix, but 14 hours to build the ~2300x2300 contact probability matrix from a 100kb resolution Hi-C matrix (these times are on a single ~2.8 GHz CPU). The second task is to optimize the structure population by running A/M cycles (iterations of the A-step and M-step). This process starts immediately after the input matrix is generated, with PGS submitting many simultaneous jobs on a computing cluster. The typical time required to finish one M-step optimization for a single genome structure with ~2x2300 TAD domains is about 45~90 minutes (at ~1 Mb resolution). If the user asked for a population of 2,000 structures, and allocates 500 CPUs to the task, then PGS will run the first 500 jobs simultaneously. The remaining 1500 jobs are queued and sent one by one to CPUs on the cluster as they become available. PGS waits until the M-step is complete for all structures before it submits the A-step jobs. In this example, the A-step calculation takes about 5–30 minutes. Thus, a single A/M cycle for a population of 2000 structures at ~1 Mb resolution could take about 3 hours. The length of the theta list and number of iterations per theta value will also affect the timing, as multipliers of the A/M cycle time. The expected total time is about equal to the number of theta parameters plus 5 to 10 (based on our experience) times the A/M cycle time. Since PGS decides on the fly (based on the violation cutoff parameter) whether to continue iterating the A/M cycle or move to the next theta level, we cannot provide a more accurate prediction of the timing. The run time also depends on the quality of the data set. Noisy or inconsistent data are likely to produce artifacts that are hard to optimize and hence require more A/M cycles.

Step 3–5: The actual time for follow up analysis can vary considerably. Extracting model coordinates and exporting to a PDB file for visualization takes less than a second for one particular structure (Step 3 and Step 5). However, looping through all the structures in a population will consume time up to hours. Generating a contact matrix (Step 4) usually takes ~1 hour for genomes with TAD sizes around 1Mb. However, this time will also scale up by O(n²) where n is the number of TADs in the genome.

ANTICIPATED RESULTS

The main output of PGS is a structure population. All results are stored under the resultdirectory. In this version, PGS writes to four subdirectories:

• probMat: contains the input contact probability matrix (in hdf5 binary format) if option 1 or 2 is selected (See Software design and implementation section).

• actDist: contains intermediate files generated by the A-step, which are used in the subsequent M-step.

• structure: contains the genome structure information during optimization, saved in hdf5 binary files (with .hms file extension). One file corresponds to one structure, and contains a history of optimization snapshots for the different theta parameters. The smallest theta, with the last iteration step (alphabetically ordered, i.e. the last snapshot) is the final model. We refer to the whole set of final models as the structure population (Fig 4a). Users then read TAD coordinates from these structure files and perform further analysis that relates to their research. We have provided a library of tools on the PGS public repository to help users easily analyze the structure population (for further details, refer to the PGS documentation page at http://pgs.readthedocs.io/en/latest/tools.html).

• report: contains some basic analysis, e.g. heat maps of contact probability matrices, radial positions of TADs, and the quality of optimization (Figs. 4b–e). PGS writes the average nuclear radial position for every TAD in the file radialPlot_summary.txt. Users can also find a summary of the violation portion that reflects the overall quality agreement between experiment data (input of PGS) and the structure population (output of PGS).