Abstract
In the last decade, detailed hemodynamic analysis of blood flow in pathological segments close to aneurysm and stenosis has provided physicians with invaluable information about the local flow patterns leading to vascular disease. However, these diseases have both local and global effects on the circulation of the blood within the cerebral tree. The aim of this paper is to demonstrate the importance of extending subject-specific hemodynamic simulations to the large-scale cerebral arterial tree with hundreds of bifurcations and vessels, as well as evaluate hemodynamic risk factors and waveform shape characteristics throughout the cerebral arterial trees. Angioarchitecture and in vivo blood flow measurement were acquired from healthy subjects and in cases with symptomatic intracranial aneurysm and stenosis. A global map of cerebral arterial blood flow distribution revealed regions of low to high hemodynamic risk that may significantly contribute to the development of intracranial aneurysms or atherosclerosis. Comparison of pre- and post-intervention of pathological cases further show large angular phase shift (~33.8°), and an augmentation of the peak-diastolic velocity. Hemodynamic indexes of waveform analysis revealed on average a 16.35% reduction in the pulsatility index after treatment from lesion site to downstream distal vessels. The lesion regions not only affect blood flow streamlines of the proximal sites, but also generate pulse wave shift and disturbed flow in downstream vessels. This network effect necessitates the use of large-scale simulation to visualize both local and global effects of pathological lesions.
Keywords: Patient-specific, parametric hexahedral mesh, near-wall disturbed flow, pulsatility index, stenosis, aneurysm
Graphical Abstract
Introduction
Quantitative magnetic resonance angiography (qMRA) is a commonly used non-invasive imaging modality to quantify blood flow in the cerebral arteries. However, it is limited to large cerebral arteries [1] and cannot reliably measure slow flow in small arteries. Moreover, qMRA does not provide enough spatial and, more importantly, temporal resolution to assess near-wall hemodynamic factors that are critical in understanding of cerebrovascular disease (CVD). Near-wall hemodynamic factors include wall shear stress (WSS), time-averaged WSS (TAWSS), oscillatory shear index (OSI), relative residence time (RRT). The importance of disturbed flow and WSS vector directional changes [2–4] in CVD have been shown in the vascular tree. OSI has been correlated with plaque formation [5,6] and high TAWSS initiates cerebral aneurysm formation [7]. The occurrence of atherosclerosis-prone regions strongly correlates with low TAWSS and high OSI (i.e. high RRT) [8,9]. A clinical study by Kawaguchi et al. [10] demonstrated that there were distinctive flow patterns in the ruptured versus unruptured blebs and that the WSS was significantly lower in the ruptured aneurysm. Animal and clinical studies have shown that sustainable secondary flow can significantly reduce the likelihood of thrombosis formation inside vascular grafts [11,12]. Since none of these clinical parameters can be measured directly, we propose to complement in vivo blood flow measurements by performing subject-specific CFD computations on a large cerebral arterial tree to assess hemodynamic risks.
Accurate cerebral arterial tree modelling requires precise subject-specific reconstruction of the cerebral vasculature, which exhibits significant geometrical variations between individuals. Even small variations in vascular topology can potentially create large effects on WSS and its derivatives [13]. For example, the circle of Willis (CoW) is an important pathway in maintaining and distributing cerebral blood supply. Its ability to redistribute blood depends highly on its morphology, as well as the presence and the shape of the communicating arteries. The effect of anatomical variation of the CoW on CVDs has been thoroughly studied [14–16]. A close correlation between low distribution capacity of the CoW and an increased risk of stroke has been reported [17,18]. Beyond the CoW, the pial arterial networks which extend to the main vascular territories vary widely between individuals. Small changes in resistance and configuration of these vascular territories give rise to different levels of collateral blood supply, which is responsible for vascular reserve. In order to address individual anatomical variations, we propose to automatically generate subject-specific models of the large-scale vascular trees from medical images.
Numerous studies have been devoted to performing CFD hemodynamic analysis, where detailed 3D simulations were performed mostly on a few branches or short segments. Here, we propose the extension of excellent prior work [19–23] to the large portion of the 3D cerebral arterial tree to enable near-wall hemodynamic analysis. The ability of multi-scale algorithms to resolve important biophysical processes of cerebral circulation has been addressed previously [24–30]. However, previous global simulations were mostly performed on simplified flow network with 1D plug flow assumptions [31–34]. Our global approach has the advantage of assessing near-wall hemodynamic analysis for a large portion of the arterial tree with the inclusion of downstream vessels where undesired hemodynamics changes could occur far away from the site of intervention. For example, delayed ipsilateral parenchymal hemorrhage (DIPH) was reported in arteries far downstream of the site of flow diversion deployment [35–38]. Assessment of changes in cerebral circulation for a large cerebral arterial tree would shed light on the pathophysiology of the unexplained DIPH [39]. The possibility of remote and delayed hemorrhage caused by endovascular intervention underscores the need for assessing hemodynamic changes not just on a local scale, but throughout a large portion of the cerebrovascular tree.
Since high-risk hemodynamic parameters cannot be measured directly, we propose to augment the value of in vivo flow measurements with subject-specific CFD analysis to infer hemodynamic risk factors. In this paper, we will assess risks regions throughout the large-scale cerebral circulation for six healthy and two illustrative cases with cerebrovascular before and after endovascular treatment.
Methods
Time-of-flight (TOF) and phase contrast magnetic resonance angiography (PC-MRA) were used to measure blood flow and source imaging data were input for anatomical reconstructions of six healthy volunteers and two pathological cases, one with intracranial aneurysms and the other with a stenosis. A vesselness enhancement filter [40] was applied to enhance the contrast of cerebral angioarchitecture [41] down to pial arteries (400 μm). After image filtering, information on the vessel centerline and radius of the vascular network were extracted. We then applied an automatic parametric meshing technique to generate flow-aligned subject-specific hexahedral meshes of the arterial trees[42,43]. Regional in vivo volumetric cerebral blood flows were measured at major arteries in the Circle of Willis. Three-dimensional dynamic CFD analysis was performed to calculate blood flow and hemodynamic risk factors in the cerebral arterial tree for the healthy and illustrative pathological cases.
Image acquisition and enhancement
Six healthy human subjects with no known cerebrovascular diseases and two illustrative pathological cases (intracranial stenosis and aneurysms) were recruited and underwent MR imaging studies on a General Electric 3T MR750 scanner using a 32-channel phased array coil. Magnetic resonance angiography (MRA) were acquired for healthy volunteers (five men and one woman between 25 to 31 years old) with the following parameters: repetition time = 26 ms, echo time = 3.4 ms, flip angle = 18°, matrix size = 512×512×408, voxel size = 0.39×0.39×0.3 mm3, acceleration factor = 2, number of slab = 4, magnetization transfer = on, and scan time of 30 min. In addition, three-dimensional digital subtraction angiography (DSA) data set for the two illustrative pathological cases were collected to enhance the image reconstruction.
The first illustrative pathological case was a 74-year-old female who had a large aneurysm involving the right posterior inferior cerebellar artery (PICA), who was treated with aneurysm clipping. The second illustrative pathological case was a 59-year-old male diagnosed with a severe left middle cerebral artery stenosis, who was treated with angioplasty.
Time-dependent blood flow data were obtained using TOF angiography and anatomical information was acquired with PC-MRA. For the illustrative cases with stenosis/aneurysm, the same flow data was acquired twice: one pre-intervention (PRI), and second post-intervention (PSI). Finally, raw TOF and Magnetic Resonance Angiography (MRA) images were passed to a vessel enhancement filter to successfully identify and segment small pial arteries. We used our in-house developed vesselness filter to enhance the contrast of the arterial tree in MRA images [40,41,44]. The scan parameters of TOF and PC-MRA are documented in Appendix 1, Table A1. MRA and DSA were acquired under Institute Review Board approval at the University of Illinois at Chicago.
Large-scale parametric mesh generation
We used a parametric structured mesh generation method described previously [42,43]. In brief, geometrical descriptors such as centerline and radii were extracted using the Vascular Modelling Toolkit (VMTK) software [45]. A Bezier spline approximation was used to delineate vascular centerlines. To complete the vascular network reconstruction, structured hexahedral meshes were parameterized along the vascular segments in radial, cross-sectional and longitudinal directions, as shown in Figure 1A. For each branch, the number of longitudinal subdivisions was chosen based on the local curvature and vessel diameter. Statistics of the reconstructed cerebral arterial trees with parametric meshing technique for six volunteers are summarized in Table 1.
FIGURE 1.
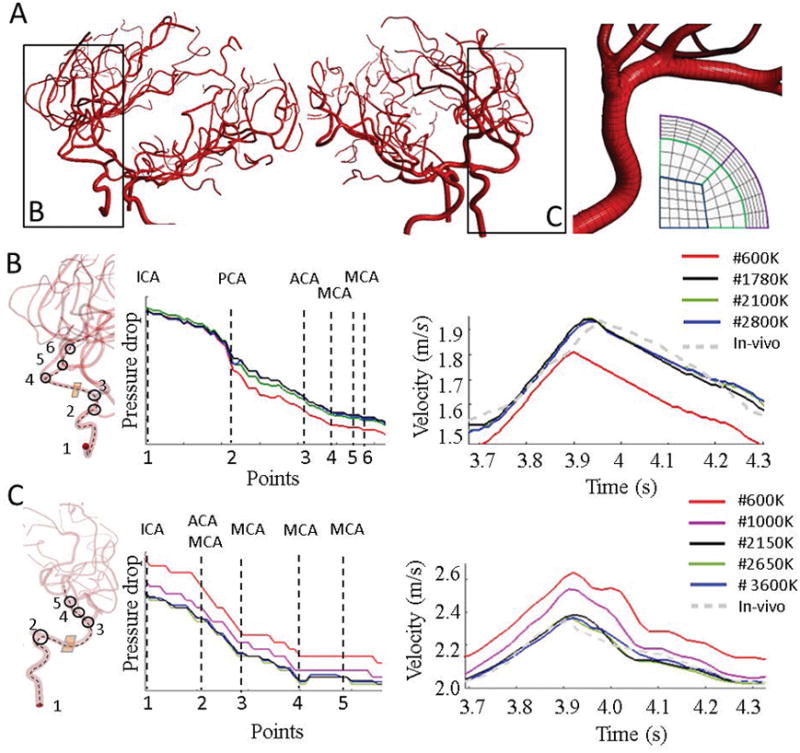
Mesh independence test for parametric structured meshes in two subject-specific cerebral arterial trees. (A) Parametric mesh of two subjects. Longitudinal and cross-sectional mesh density can be adjusted to control mesh resolution. Here, refinement was optimally performed based on the local diameter and centerline curvature. (B) Mesh independence for Subject I. A centerline from RICA to RMCA passing through six main bifurcations was used to compare pressure values computed with different mesh element numbers. For each mesh, time-dependent velocity profiles for a plane marked in orange was also plotted. Meshes with fewer cross-sectional element (black) slowly approached stable results shown for high-resolution models (green and blue) thus demonstrating mesh independence. (C) Mesh independence for subject II. Pressure trajectories for different resolution were plotted along large sections of the centerline spanning the LICA to LMCA branches. In addition, average velocity magnitude profiles are shown for a location at the entrance of the LMCA for different mesh resolution. Pressure and velocity results for green and blue are virtually identical with 2650K and 3600K elements. By varying cross-sectional density, mesh-independent results were achieved with a 2150K mesh. These results demonstrate the achievement of mesh independence with parametric meshing technique.
TABLE 1.
Statistics of reconstructed, mesh generation and simulation cerebral arterial trees with parametric meshing technique for six volunteers.
| Subjects | #Points | #Branches | #Bifurcations | Blood volume (ml) | #Elements | Meshing time (min) | CPU timeTc (min) |
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
| I | 15688 | 133 | 68 | 4.01 | 1783K | 15.6 | 78 |
| II | 22502 | 294 | 100 | 4.28 | 2158K | 18.4 | 86 |
| III | 17436 | 175 | 89 | 5.36 | 1876K | 16.8 | 103 |
| IV | 24485 | 309 | 122 | 4.75 | 2115K | 19.6 | 89 |
| V | 20477 | 247 | 99 | 4.76 | 1918K | 17.5 | 72 |
| VI | 19203 | 206 | 93 | 4.70 | 1897K | 17.4 | 82 |
|
|
|
|
|
|
|
|
|
| Mean | 19965 | 227 | 95 | 4.64 | 1958K | 17.6 | 85 |
Tc: Total CPU time for simulation of one cardiac cycle.
We also applied our parametric meshing method for two illustrative cases with vascular diseases: an MCA stenosis lesion case and a large saccular aneurysm involving the right posterior inferior cerebellar artery (PICA). The stenosed region was readily meshed using parametric meshing. For aneurysm case, we used hybrid meshing to combine the advantage of highly dense mesh refinement in the aneurysm with economic reconstruction of the disease-free portion of the cerebral circulation. We used an unstructured meshing approach specifically for the outpouching of the aneurysm, [1,2,24,46]. To create a seamless connection between the aneurysm and the parametric arterial tree, an axial cross-section containing surface and interior points were deployed as seed points for initiating unstructured mesh generation of the aneurysm. This task was supported by ICEM CFD mesh editing tools (e.g. merge-nodes, split-edges). The unstructured aneurysm mesh was connected at the proximal and the distal end to the parametric mesh of the remaining disease-free portion of the arterial tree. Hybrid meshing enabled use of a flexible mesh for the irregular pathology, combined with economic reconstruction of the normal portion of the patients’ cerebral circulation.
Subject-specific blood flow measurement
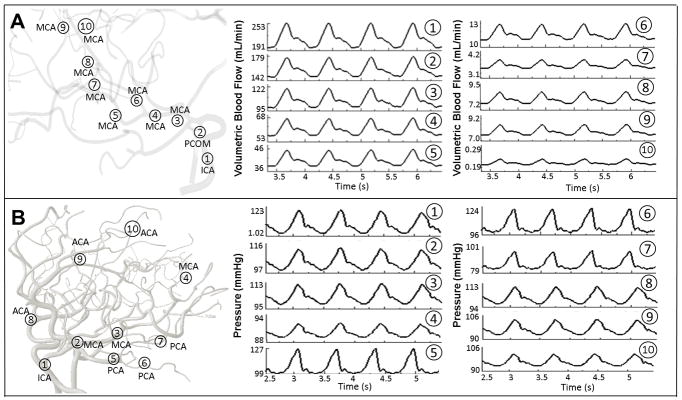
Two imaging protocols, TOF and PC-MRA were used for acquiring anatomical and dynamic information to quantify volumetric pulsatile blood flow. These images were processed using a commercial flow analysis software, NOVA (Vassol Inc, River Forest, IL) [47]. Blood flow was measured from incoming flow to CoW including the left and right internal carotid arteries (LICA and RICA) and basilar artery (BA); in addition, arteries leaving the CoW include the anterior cerebral arteries (LACA and RACA), middle cerebral arteries (LMCA and RMCA) and the left and the right posterior cerebral arteries (LPCA and RPCA). Total scan time for each subject was 50–60 minutes. Acquired volumetric blood flow measurements for three healthy volunteers are depicted in Figure 2 and summarized in Table 2.
FIGURE 2.

Comparison of regional blood flow measurement and subject-specific simulation using PC-MRA flow measurements. Three examples of in vivo measurements are shown in the first row. The color-coded slice plane is perpendicular to the longitudinal axis of a vessel segment showing where the measurement was made in the main cerebral arteries. The solid color-coded curves are measured blood flow and gray dotted profiles are the simulated blood flow in the main arteries of the cerebral arterial tree.
TABLE 2.
Comparison of volumetric blood flow rate acquired by PC-MRA (NOVA protocol) and CFD simulation results in cerebral arteries.
| Average flow rate [mL/min] | Subject I | Subject II | Subject III | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|||||||
| NOVA | CFD | % Diff | NOVA | CFD | % Diff | NOVA | CFD | % Diff | |
|
|
|
|
|
||||||
| RACA | 60.11 | 59.80 | 0.52 | 60.80 | 61.80 | 1.64 | 92.20 | 92.50 | 0.32 |
| RMCA | 103.4 | 105.0 | 1.55 | 165.7 | 168.9 | 1.93 | 118.5 | 114.9 | 3.03 |
| RPCA | 63.10 | 62.90 | 0.32 | 68.80 | 69.60 | 1.16 | 60.90 | 57.60 | 5.41 |
| LACA | 47.40 | 49.20 | 3.79 | 61.90 | 62.40 | 0.81 | 63.70 | 62.90 | 1.25 |
| LMCA | 103.1 | 102.3 | 0.78 | 172.6 | 171.4 | 0.69 | 124.9 | 132.7 | 6.24 |
| LPCA | 61.10 | 62.90 | 2.95 | 95.10 | 89.00 | 6.41 | 63.700 | 62.96 | 1.16 |
|
|
|
|
|
||||||
| Avg. Frequency | 1.330 | 1.35 | - | 1.470 | 1.460 | - | 1.550 | 1.520 | - |
|
|
|
|
|
||||||
| Avg. Amplitude | 15.09 | 15.9 | - | 20.02 | 21.31 | - | 18.69 | 21.50 | - |
LICA/RICA: left and right internal carotid arteries. BA: Basilar artery. LACA/RACA: left and right anterior cerebral arteries.
LMCA/RMCA: left and right middle cerebral arteries. LPCA/RPCA: left and right posterior cerebral arteries.
Hemodynamic simulation and anatomical labeling
Transient hemodynamic simulations were carried out using ANSYS Fluent 18.0 (ANSYS Inc., Canonsburg, PA) with a second-order upwind scheme using the parallel 14-core processor on dual 2.4 GHz Xenon CPUs. Blood rheology is modelled as a viscous, incompressible, single phase Newtonian fluid with a density of 1055 kg/m3 and dynamic viscosity of 4.265 × 10−3 Pa.s. The vessel walls were assumed rigid with no-slip boundary condition. Convergence criterion of the simulation was set to 10−6 for residual error of continuity within each time step of 0.1 msec. The required CPU time for each cardiac cycle for each subject is listed in Table 1. The simulation results were reported after multiple cardiac cycles to eliminate initial transients. Streamlines and hemodynamic variables were computed using CFD-Post 18.0 and MATLAB R2016b.
We first classified the vessels based on their anatomical territories. The inflow arteries include left and right internal carotid arteries (LICA and RICA) as well as either basilar artery (BA) or both right and left vertebral arteries (RVA and LVA). Outflow vessels were categorized based on their feeding anatomical regions in six groups of the left and right middle cerebral arteries (LMCA, RMCA), posterior cerebral arteries (LPCA, RPCA) and anterior cerebral arteries (LACA, RACA).
Blood flow measurements obtained from the NOVA scans at the RICA, LICA, as well as BA (or RVA, LVA) served to set pulsatile inlet boundary conditions for our simulations. For all outlets, outflow pressure boundary conditions were assigned so as to match the volumetric flow rates from in vivo measurements at LMCA, RMCA, LPCA, RPCA, LACA, RACA vessels [40] as shown in Figure 2. Dynamic pressure boundary conditions were set for the six outflow territories including (LACA. RACA. LMCA, RMCA, LPCA, RPCA outlets) were inferred by an optimization problem described in Appendix 2. A similar optimization-based technique was described here [48].
We used a Fourier series approximation to set velocity boundary conditions at the inlet of the basilar and carotid arteries, which were implemented in ANSYS Fluent with user-defined functions (UDF).
The same procedure was used for each of the healthy and illustrative pathological cases with stenosis and aneurysm, each with their specific anatomical vascular trees, and intracranial flow measurements as an input and output for the CFD analysis. The Fourier series approximation to set velocity boundary conditions at the inlet of the basilar (or vertebral arteries) and carotid arteries is given in Eq. (1).
| (1) |
Here k stands for the different inlet vessels, including RICA, LICA as well as BA (or RVA and LVA ). a0,an and bn are the coefficients of the trigonometric Fourier series. N is the total number of the harmonics in the Fourier series. ω, T and t are the fundamental frequency, period and time domain of the flow profile, respectively.
Near-wall hemodynamic risk factors
In this section, we will first introduce a suitable set of near-wall hemodynamic factors chosen for this study. Based on these parameters, we will quantify hemodynamic risks and classify the regions into normal, low-risk and high-risk regions. Our choice is justified because changes in static or dynamic WSS have been implicated in cerebrovascular pathologies [49]. The temporal distribution of WSS and associated biomechanical stresses in the vessel walls were quantified by TAWSS and OSI. TAWSS was calculated by integration of the WSS magnitude at each node over one cardiac cycle, Eq. (2). OSI is a nondimensional parameter quantifying the direction of WSS fluctuations during one cardiac cycle, Eq. (3) [5,50]. The residence time of particles near the wall is proportional to a combination of TAWSS and OSI Eq. (4) [51].
| (2) |
| (3) |
| (4) |
is the magnitude of instantaneous WSS vectors (N/m2) and τ (sec) is the duration of a cardiac cycle. Regions with high OSI are predisposed to endothelial dysfunction, showing the high risk of local thrombosis and plaque formation [5,52,53]. WSS ranging between 1.0 to 7.0 Pa in the arterial network is considered normal in human arteries [54–56]. The physiological level of OSI to maintain normal endothelial function has been reported to be under 0.2 [57,58]. On the other hand, low TAWSS values (less than 0.4 Pa), [56] and high RRT (higher than 10 m2/N) [59,60] are known to promote atherosclerosis. OSI greater than 0.3 have been also shown to promote atherogenesis [50]. Considerably, we summarized the literature results into three regions of normal, low-risk and high-risk regions in Table 3. These classifications were used to categorize the level of hemodynamic risk in healthy and pathological cases.
TABLE 3.
Problematic reported ranges of near-wall hemodynamic parameters (RRT, OSI, and TAWSS). Normal zone as well as low- to high-risk zones are defined based on literature reports.
| Parameter | Normal range [54–58] | Low-risk range | High-risk range[56,59,60] |
|---|---|---|---|
|
|
|
|
|
| TAWSS [Pa] | 1.0 to 7.0 | 0.4 to 1.0 | ≤0.4 |
| OSI | ≤0.2 | 0.2 to 0.3 | ≥0.3 |
| RRT [m2/N] | - | <10 | ≥10 |
TAWSS: time-averaged wall shear stress; OSI: oscillatory shear index; RRT: relative residence time.
Results
Mesh generation for cerebrovascular tree
We first report on the anatomical consistency of the reconstructed vascular trees. For each of the six healthy subjects, the large cerebral arterial tree was reconstructed with an average of 227±68 vessel segments and 95±17 bifurcations. Statistical information about reconstructed arterial trees, computational meshes, CPU time for mesh generation and simulation for all volunteers are listed in Table 1. The CoW topologies show substantial subject-specific anatomical variations are depicted in Figure 3A. For example, Subject I and III are missing left posterior communicating artery (PCOM). In Subject II, A1 segment of the right anterior cerebral artery and right PCOM are absent. Subject IV has an absent left PCOM and the ACA has an azygos origin that forms a common trunk and splits distally into two segments. Subject V has both right and left PCOM absent. Subject VI possesses a complete CoW. The CPU time for vascular network segmentation and parametric mesh generation of the cerebrovascular tree takes less than 17 minutes on single-core processor of 2.4 GHz Xenon CPUs. The total number of required mesh cells after mesh-independence tests are listed in Table 1 and shown in Figure 1B–C.
FIGURE 3.
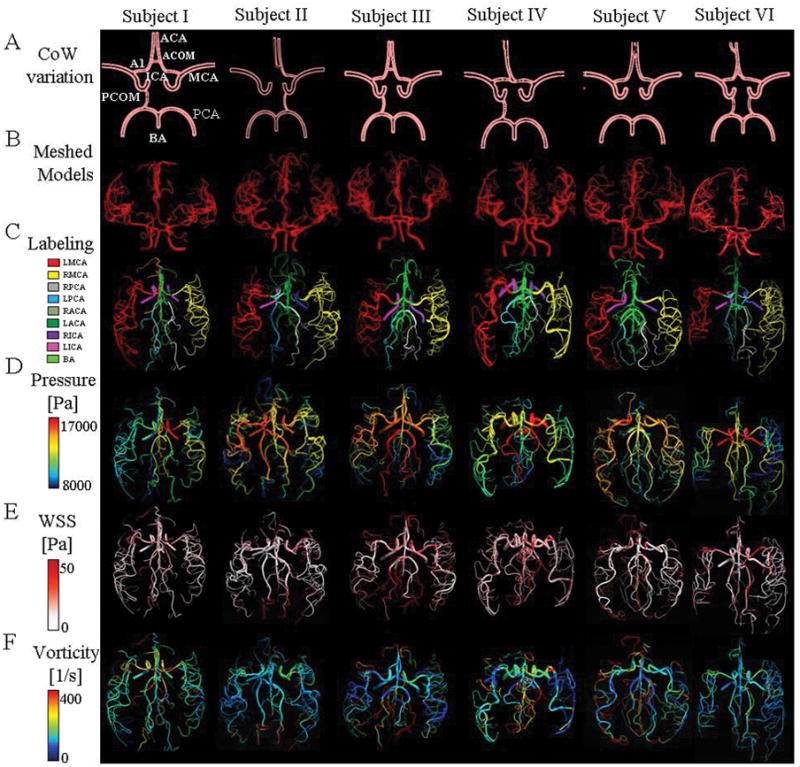
Cerebrovascular tree reconstructions (A–B), labeling (C), and simulation (D–F) for six healthy subjects. Each column represents different subject. (A) Schematic frontal views of anatomical variation of Circle of Willis. Absence of Left PCOM in Subject I. Subject II: Absence of A1 segment and right PCOM. In Subject III: Absence of Left PCOM. Subject IV Absence of left PCOM and presence of Azygos ACA present. Subject V: Absence of both PCOMs. Finally, a complete CoW in Subject VI. (B) An anterior view of parametric mesh of the subject-specific cerebral arterial trees. (C) Atlas of cerebral arterial tree. Cerebral arterial trees were labeled in their corresponding anatomical regions of LMCA, RMCA, LPCA, RPCA, LACA, RACA and BA. (D) Predicted pressure field at systole obtained by 3D CFD simulation for the entire cerebrovascular tree. Higher blood pressure in ICAs and BA, which gradually decreased towards the smaller outlet vessels. (E) Computed WSS on the arterial wall at peak-systole. (F) Visualization of blood flow vorticity magnitude in arterial trees to show the presence of secondary flow patterns at peak-systole.
Subject-specific blood flow simulation
PC-MRA blood flow measurements in the main arterial territories (RMCA, LMCA, RACA, LACA, RPCA and LPCA) for six healthy and two illustrative stenosis/aneurysm cases (pre- and post-intervention) were acquired. In-vivo PC-MRA flow results were compared with CFD predictions. Figure 2 illustrates color-coded slice planes perpendicular to the main flow direction, and plots dynamically measured and computed volumetric flow rates in the main cerebral arteries for the first three subjects with average volumetric flow error of 2.27±0.64%. The deviations between measurements and simulations for territories are summarized in Table 2. The blood flow analysis also includes average volumetric blood flow, frequency, and amplitude.
Hemodynamic analysis of low- to high-risk regions
Here we illustrate quantification of near wall hemodynamic risks as outlined in the method section and classify the regions into normal, low-risk and high-risk sites in Table 3. The large-scale analysis enables detection of lesion-prone sites through the wide portion of the cerebral arterial tree.
Low-risk regions
We first visualize the low-risk hemodynamic sites in healthy and stenosis/aneurysm cases. Only relative high RRT regions were illustrated in Figure 4. However, these locations had a low-risk range of OSI and TAWSS (data not shown). Figures 4A and 4B exhibit the location of relative higher RRT in the outer and inner walls of the carotid siphon of subject II, and subject IV, respectively. Low-risk sites were also found on a curved vessel following the aneurysm lesion in PRI as shown in Figure 4C. Figures 4D and 4F show the relatively high level of RRT mostly at the side of the daughter branches at the bifurcations of subject III and subject VI, respectively. In subject I and subject III (data not shown), nearly perpendicular bifurcations such as the junction of PCOM and PCA or basilar tip were also found to have relatively high RRT as shown in Figure 4G. Distal vessels of MCA in the stenosis cases were detected as risky regions while after angioplasty, no sign of low-risk was visualized in regions downstream of the MCA as shown in Figures 4H–I.
FIGURE 4.
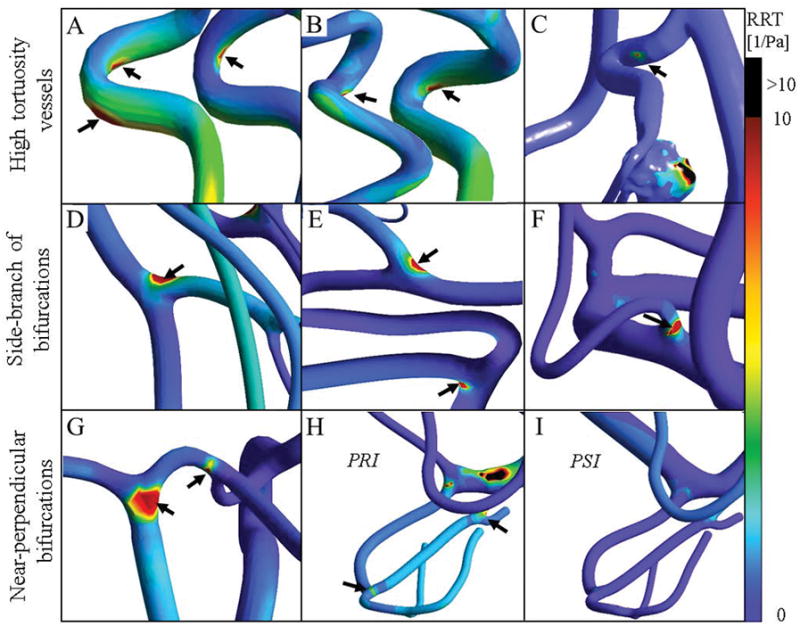
Assessment of hemodynamic low-risk regions in healthy and pathological cases. Black arrows indicate low-risk regions with a high relative residence time (RRT). These locations also exhibited low-risk range of OSI and TAWSS (data not shown). (A–B) Internal carotid arteries with high tortuosity exhibit hemodynamic risky regions mostly in the inner curve of the carotid siphon of subject II, and subject IV. (C) The downstream artery of the aneurysm exhibits a low-risk area at the point of high curvature. (D–F) High RRT regions were observed at bifurcations with daughter branches of different diameter ratios in subject III and subject VI. (G) The walls of thinner side branches are more prone to atherosclerosis as indicated by the hemodynamic parameters. In subject I, low-risk regions were found to be located at near perpendicular-bifurcations such as the junction of PCOM and PCA and the basilar tip. High-velocity blood flow impinges on the opposite arterial wall in near perpendicular bifurcations. (H) High-velocity blood flow jets generate risky areas in the downstream vessels in stenosis case (PRI). (I) Risky regions in the patient shown in panel H were remedied after treatment (PSI).
High-risk regions
Figure 5 exhibits the reconstructed arterial tree and high-risk disturbed flow locations before and after aneurysm clipping. Figure 5B illustrates the inflow jet stream into the aneurysm sac on different planes oriented perpendicularly and horizontally to the aneurysm ostium before treatment. High-risk prolonged RRT sites were located on a bleb close to the separation of the inflow streamline in the aneurysm sac (Figure 5C). The WSS vector plots captured during the different cycled phase of peak-systole, mid-diastole and end-diastole (Figure 5D).
FIGURE 5.
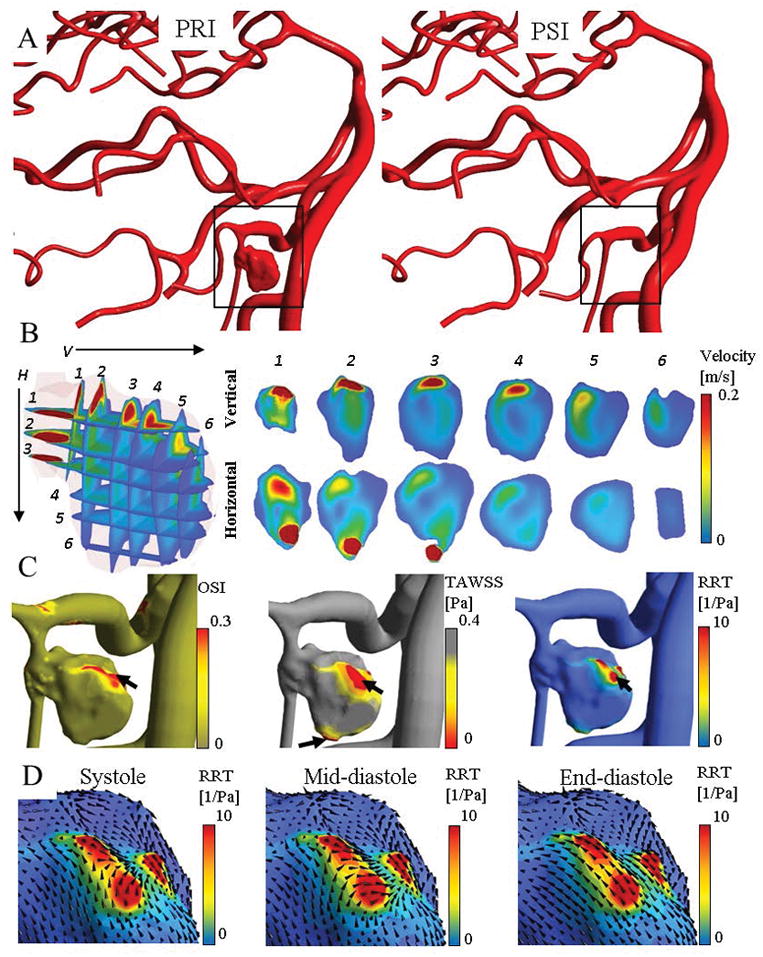
Disturbed flow quantification and high-risk region detection for a patient with a large saccular aneurysm on the PICA. Panel (A) visualizes the reconstructed model before and after aneurysm clipping at peak-systole. (B) Several horizontal and vertical planes to the aneurysm neck were used to visualize the pattern of inflow into the aneurysm sac. (C) The area of prolonged RRT (arrow) was found on a bleb of the aneurysm close to the stagnation of inflow jet. The WSS vector plots captured during different cycled time revealed that the WSS vector arrangement highly changed in diastole phase.
Figure 6 visualizes the high-risk sites with disturbed flow locations in a stenotic patient in PRI and PSI. Before the intervention, flow separation and recirculation occurred in the post-stenotic region leading to elevated RRT sites (Figure 6A). High-risk regions were mostly present in the post-stenotic zones but also further downstream in distal vessels as shown in Figure 6B. These regions were monitored and compared in the post-treatment model, which can be considered as high risk for developing atherosclerosis. After angioplasty, hemodynamic analysis for blood circulation after angiography showed the normalization of the high RRT segments both proximal and distal to the stenosis as shown in Figure 6C. Post-treatment, there was a 36% drop in blood flow within the anterior cerebral artery (ACA); and a 76% increase in flow within the MCA stenosis. Similarly, there was a 53% reduction in the mean velocity within the angioplasty segment. The flow decrease within the ACA post angioplasty may be an indicator of a reduced demand from collateral pial vessels following the restoration of MCA flow after the successful intervention. Normalized WSS vectors are depicted at the different phases of the cardiac cycle as shown in Figure 6D. Most WSS vector changes occurred between mid- to end-diastolic phase of the cardiac cycle.
FIGURE 6.
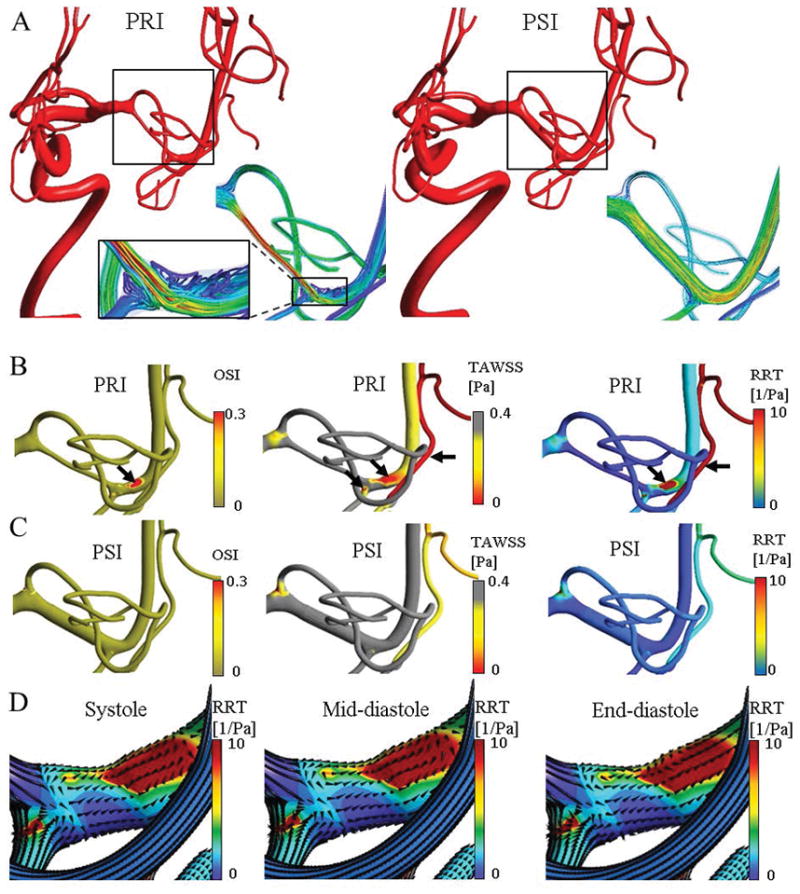
Disturbed flow quantification and high-risk region detection for an illustrative case in a patient with MCA stenosis. Panel (A) illustrates the reconstructed model with high-density blood flow streamline in pre-intervention (PRI) and post-intervention (PSI) at peak-systole. In PRI, the magnified view visualized the disturbed flow circulation at post stenosis region. (B) Disturbed flow generated regions with relative high OSI and low TAWSS, i.e. high RRT. Note that the scale is inverted for TAWSS to highlight the risky regions. Black arrows indicates the high-risk locations at post-stenosis and distal down-stream vessel. (C) After angioplasty, it showed the normalization of the high RRT segments both proximal and distal to the stenosis (red RTT zones). Panel (D) visualize the normalized wall shear stress vectors on disturbed flow regions in systole, mid-diastole, and end-diastole. Most changes are between mid to end-diastole.
Hemodynamic indices for waveform analysis
We observed pressure and flow rate attenuation of the blood flow pulsatility along the paths from the ICA to distal pial arteries in the MCA and PCA and ACA territories as shown in Figure A1, Appendix 3. The waveform shapes are depicted from lesion site to downstream distal vessels in Figure 7 for pathological cases. We also calculated the hemodynamic indexes for waveform analysis using pulsatility index (PI), resistance index (RI), systole to diastole ratio (S/D) of the velocity profile, and phase shift degree at post-lesion regions using Eqs. (7–10).
FIGURE 7.
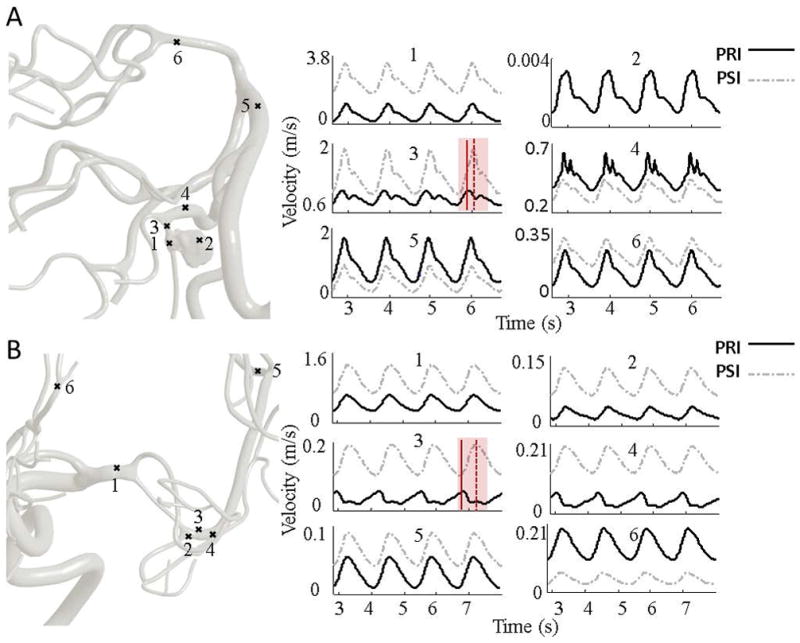
Computed blood flow velocity for the MCA stenosis illustrative case in pre- and post-intervention (PRI and PSI). Panel (A) visualizes dynamic velocity profiles at different locations starting from the proximal to distal vessels. The transparent red area highlights the largest phase lag. In aneurysm case, a very low velocity of stagnated flow was recorded close to high RRT at point 2. In the post-aneurysm region, points 3 and 4, there was a phase lag and an augmentation of the secondary peak compared to the PSI. The angular phase shift between PRI and PSI are 38.82° and 10.58° at points 3 and 4, respectively. Panel (B) visualized the dynamic velocity profile at pre-stenosis, 1, post-stenosis, 2–4, downstream MCA vessel, 5 and downstream ACA territory, 6 of the stenosis patient in pre-intervention (PRI) and post-intervention (PSI). Red solid and dotted line represent the maximum systolic velocity at PRI and PSI, respectively. The phase shift between the PRI and PSI in poststenotic region (points 3 and 4) are 106.05° and 78.14°, respectively. The global blood flow analysis revealed a phase lag of 11.16° in distal MCA vessels (point 5).
| (7) |
| (8) |
| (9) |
| (10) |
Where, VS and VD are peak-systolic and end-diastolic velocity, respectively. VTA is the time-averaged velocity over one cardiac cycle. Δϕ is the phase shift in degrees; Δt is the time difference between pre- and post-intervention velocity wave peaks; T is the wave period in seconds. Note that the wave periods were the same between the PRI and PSI stage.
Hemodynamic indexes for waveform analysis are summarized in Table 4 for post-lesion regions. PI, RI and S/D increased in the post-lesion downstream flows and were normalized after the intervention.
TABLE 4.
Hemodynamic indexes for waveform analysis at post-lesion regions of aneurysm (Case I) and stenosis (Case II). A comparison between PRI and PSI.
| Case Number | Point Location | Pulsatility Index | Resistance Index | S/D Ratio | Phase Shift | ||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
||||||
| PRI | PSI | PRI | PSI | PRI | PSI | Δt | Δϕ | ||
|
|
|
|
|
|
|||||
| Case I | #1 | 1.82 | 0.69 | 0.84 | 0.49 | 6.36 | 1.95 | 0.03 | 10.58 |
| Case I | #3 | 0.34 | 0.68 | 0.29 | 0.48 | 1.40 | 1.93 | 0.11 | 38.82 |
| Case I | #4 | 0.59 | 0.47 | 0.43 | 0.37 | 1.75 | 1.59 | 0.03 | 10.58 |
| Case I | #5 | 0.97 | 0.89 | 0.61 | 0.58 | 2.59 | 2.37 | 0.02 | 8.47 |
| Case II | #2 | 1.06 | 0.64 | 0.67 | 0.47 | 3.03 | 1.90 | 0.02 | 6.95 |
| Case II | #3 | 0.65 | 0.53 | 0.45 | 0.41 | 1.84 | 1.71 | 0.38 | 106.05 |
| Case II | #4 | 1.18 | 0.50 | 0.66 | 0.39 | 2.94 | 1.66 | 0.28 | 78.14 |
| Case II | #5 | 0.56 | 0.42 | 0.43 | 0.34 | 1.76 | 1.53 | 0.04 | 11.16 |
PRI: Pre-intervention, PSI: Post-intervention. Δϕ: Phase shift in degrees. Δt: Time difference between PSI and PRI velocity wave peaks. S/D: systolic/diastolic ratio
In the post-aneurysm region, there was a phase lag and an augmentation of peak-diastolic velocity (also known as secondary peak or notching) in the pre-intervention model as shown in Figure 7A. The angular phase shift between PRI and PSI were 38.82° and 10.58° at points #3 and #4, respectively.
In Figure 7B, phase shifts of 106.05° and 78.14° were calculated in the elevated RRT region at the proximal post-stenotic region. An angular phase difference of 11.16° was found in distal MCA vessels. Consequently, the lesion region not only affects the proximal sites (ex. post-stenotic region), but also potentially generate pulse wave delay in downstream vessels.
Discussion
We deployed an image-based workflow specifically tailored for large-scale blood flow computations in subject-specific cerebral arterial trees. Predicted CFD flows were compared to in vivo qMRA measurements. Overall agreement between measured flow and 3D dynamic CFD simulations was favorable with total average percentage flow difference of 2.27±0.64%. Flow measurements in combination with the computational analysis allow us to visualize the near-wall hemodynamic map throughout the cerebral arterial tree to better detect potential low- to high-risk sites. Global maps of hemodynamic risk parameters derived from in vivo measurements in combination with tree-wide CFD simulations provide unique observations about the hemodynamic status that no current imaging technique is capable of measuring directly.
Global maps of low- to high-risk hemodynamic analysis
Two illustrative cases of intracranial stenosis and aneurysm were chosen because the mechanism for the development of aneurysms or stenosis is affected by the local hemodynamic factors. In addition, once aneurysms or stenoses have formed, the pathology may cause further changes to local and more significantly to the global blood flow distribution pattens. Adverse distal effects such as remote ipsilateral hemorrhage [61] may be detected and pinpointed with the proposed global hemodynamic analysis. The proposed parametric structured meshing technique extends rigorous CFD analysis from a single site to large portions of the cerebrovascular network.
Low-risk regions were found to be located at bifurcations with perpendicular branches (T-shape) such as at the junction of PCOM and PCA and the basilar tip. At these bifurcations, the high-velocity blood flow impinges at the apex causing perpendicular forces on the arterial wall. Additionally, regions with relatively low WSS and high OSI were observed at bifurcations with daughter branches of largely different diameter ratios. The smaller side-wall branches are consequently more prone to atherosclerosis as indicated by the hemodynamic parameters. Moreover, internal carotid arteries with high tortuosity exhibit an area of locally elevated residence time, mostly on the inner curve of the carotid siphon due to the predominant helical flow in curved vessels rather than the parabolic velocity profiles that occur in straight vascular segments [62]. In the stenosis/aneurysm, disturbed laminar blood flow after stenosis and aneurysm generate low-risk sites in distal disease-free vessels as potential future problem areas.
The simulation of the large-scale cerebral arterial tree helped identify and localize high-risk regions of disturbed flow in the pathological cases. The area of prolonged RRT was found on a bleb of the aneurysm close to the stagnation of the inflow jet. There were slow-velocity streamlines at 0.62 mm beneath the wall with elevated RRT.
Our hemodynamic analysis was able to pinpoint potential problem spots in pathological cases. In the stenosis case, elevated levels of pre-operative RRT and TAWSS both upstream and downstream from the MCA stenosis were detected. Without the intervention (angioplasty), this MCA stenosis could eventually initiate stenoses in other sites. After angioplasty, normalization occurred in high RRT segments both proximal and distal to the stenosis. The visualization of normalized WSS vectors showed that the directional changes were mainly between mid- to end-diastole.
Blood flow waveform
We predicted velocity fields from inlets down to the small distal vessels in both normal as well as malformed vascular segments. Post-intervention, flow pulsatility was attenuated far downstream of the lesion sites, as is desirable. Waveform indexes such as PI, RI and S/D ratio reduced by 16.3%, 11.52%, and 18.86%, respectively. Large angular phase difference was found between pre- and post-intervention flow profiles in downstream flow field following vascular lesions. The angular shift ranged from 106.87° in proximal to 7.06° in distal vessels from the malformed vessels. We also visualized the augmentation of peak-diastolic flow waveform downstream of the diseased vessels. Since in vivo MRA blood flow acquisition is not simultaneous, such phase shift differences cannot be studied with current in vivo blood flow measurements. Large-scale CFD analysis is capable of supplying critical temporal and spatial hemodynamic information throughout a large portion of the cerebral arterial tree that cannot be measured by imaging technologies.
Many researchers showed that hemodynamic parameter changes are highly associated with geometric features rather than physiological variations of the flow rate, blood pressure, and wave shapes [62]. Additionally, it has been reported that the augmented diastolic-peak of velocity correlates with age and is significantly higher in the blood flow waveforms of old adults [63,64] leading to microvascular damage and impaired function [65]. However, it is unclear if lesion-induced phase lag and waveform dynamic changes encourage endovascular lesions in distal vessels. For example, specific shear stress frequencies may correlate with inflammatory response in the endothelium [66]. We believe that the blood flow waveform is significant; because near-wall hemodynamic analysis and WSS components are directly affected by blood flow patterns of each cardiac cycle. A future study should evaluate the effect of post-lesion waveform changes on downstream distal vessels and quantify the physiological relevance of the waveform to endovascular diseases.
Same day clinical screening modality
The CPU time for mesh generation is on average 17.6±1.24 min, simulation of one cardiac cycle requires 85±9.7 min for each subject. Anatomic reconstruction with parametric meshing cuts processing cut the processing time for both mesh generation and simulation, thus eliminating current bottlenecks so that large-scale hemodynamic analysis can be realized on the same day. In the future, availability of automated (same day) simulations code will provide surgeons with indicators for potential benefits and risks associated with endovascular procedures for individual patients. Tighter integration of imaging, endovascular interventions, and rigorous hemodynamic analysis will also eliminate barriers between surgeons and biomedical device designers aiming at better outcomes for cerebrovascular diseases.
The significance of large-scale versus truncated simulations
Multiple assumptions are commonly introduced to approximate physiological outflow boundary conditions [24,67–69] when in vivo flow measurements in small and very numerous branches of arterial trees are unavailable. However, boundary conditions can greatly affect the wave profile in the downstream arteries [70]. A comparative study of large-scale simulation of the arterial tree with a shorter truncated version showed that the predicted hemodynamic risk factors changed significantly between the full and the truncated version. Specifically, Appendix 4 shows the difference between RRT distribution map between large-scale and a truncated vascular model with the same velocity inlet boundary condition. Although the qualitative features are relatively unchanged, detailed analysis showed substantial differences in RRT values. Therefore, hemodynamic risk analysis should be performed on larger portions of the arterial tree to reduce the effect of uncertain boundary conditions.
Limitation and future work
In the current model, we employed a rigid wall assumption for all simulation. Even though the deformations are small [71], wall deformations may significantly impact pressure attenuation, blood flow waveform and stress distribution in vessel walls. An extension to deformable vessels is a logical next step, which will benefit from the parametric structured meshes, because the wall geometry can easily be generated by extending the radial surface mesh to the desired wall thickness. However, reliable mechanical properties and vessel thickness measurements of all arterial blood vessels are necessary before attempting more rigorous 3D fluid-structure interaction (FSI) simulations for large sections of the cerebral vasculature. In addition, near-wall hemodynamic risk analysis can be extended to more WSS components such as Lagrangian processing of the WSS vector field [3,72].
Another future improvement concerns the use of non-Newtonian blood flow rheology [73]. This step would be critical for blood vessels less than 100 μm in diameter. In this study, we did not use complex rheology models because all arterial branches had diameters of D>400μm due to the limited MRA resolution.
Future work should address the multi-scale arterial to venous system simulation with consideration of vein walls compliance. Another possible future step is to integrate rigorous 3D CFD arterial tree simulations with lower order microcirculatory closures [26,71,72].
Conclusion
Global maps of hemodynamic risk parameters derived from in vivo measurements in combination with tree-wide CFD simulations provide unique global observations about the hemodynamic status that no current imaging technique is capable to visualize directly. The large-scale subject-specific hemodynamic analysis is a promising next step for quantifying the surgical outcomes. This proposed method can be used to highlight the potential hemodynamic risks that might lead to aneurysm formation or increase the risk of aneurysm rupture, as well as understanding of the hemodynamic risks for atherosclerosis. Tree-wide simulation is expected to serve as a basis to predict changes to the large-scale flow redistribution after the endovascular intervention. To achieve this long-term goal, the global flow distribution model presented here may serve as a starting point. Automation of image segmentation, parametric meshing and efficient CFD segmentation with structured grid may pave the way for same-day CFD hemodynamic risk analysis.
Acknowledgments
The authors would like to acknowledge partial support of this project by NSF grant of CBET-1301198 and NIH-1R21NS099896. No conflicts of interest were posed in the conduct of this research.
Appendix 1
TABLE A1.
Scan parameters of time-of-flight (TOF) and phase contrast MRA (PC-MRA) flow measurement for investigated subjects.
| Scan parameters | TOF | PC-MRA (NOVA protocol) |
|---|---|---|
|
|
|
|
| Number of excitations | 1 | 2 |
| Temporal resolution (ms) | 26 | 10.9 |
| Echo Time | 3.4 | 4.2 |
| Flip angle (deg) | 18° | 25° |
| Acceleration factor | 2 | - |
| Number of slabs | 4 | - |
| Magnetization transfer | on | - |
| Matrix size | 512 × 512 × 408 | - |
| Voxel size (mm) | 0.39 × 0.39 | - |
| Slice Thickness (mm) | 0.6 | - |
| Slice Spacing | 0.3 | 5 |
| Echo Train Length | 1 | 1 |
| Pixel Spacing | 0.3906 | 0.625 |
| Cardiac Number of Images | - | 12 |
| Velocity Encoding (VENC) | - | 1000 |
| Acquisition time (s) | 18000 | - |
Appendix 2
Large-scale blood flow simulations required suitable boundary condition selections. Here we describe a procedure to obtain optimal choices for terminal outflow pressures consistent with given blood flow measurements. The desired pressures are calculated optimally by minimizing the difference between measured flows f̂(t) and simulated flow f(t) at six regions of interest (LMCA, RMCA, LPCA, RPCA, LACA, RACA). Clearly, rigorous optimization would imply full scale 3D dynamic fluid flow inversion, which is impractical. Instead, the inversion problem was solved using a 1D network model composed of cylindrical tubes. This surrogate network was used to determine simultaneously the set of “optimal” boundary pressures that best fit the measured flows. Pressures are determined by solving the optimization problem in system Eq. (A1).
| (A1) |
Here, f̂(t) and f(t) are the measured and the predicted flow, respectively. p(t) is the predicted pressure. The symmetric matrix A contains the flow resistances, Z1 is the network nodal matrix and Z2 is the flow incidence matrix of the vascular network.
Optimal pressure boundaries can be determined for averaged flow rates (steady-state flow) or extended to time-dependent signals by repeatedly solving the optimization problem for each frequency of a suitable Fourier decomposed version of the measurement signal. The proposed optimization problem implies an assumption about territorial blood flow distribution in terminal nodes. Here we assumed that terminal branches discharge blood flow volume in proportion to their cross-sectional area. Note that at least one inlet pressure needs to be selected to calibrate the absolute pressure level (Here, we chose LICA/RICA). Hence, absolute pressure levels cannot be inferred from flow measurements alone. These boundary signals were used in the 3D CFD simulation. If desired, the initial boundary pressure choices obtained by optimization of the 1D network can be finely adjusted in dynamic 3D CFD simulations to sharpen the alignment between measured and simulated flows.
Appendix 3
FIGURE A.1.
Computed flow and pressure of cerebral arterial tree. (A) The map of dynamic flow rates shows attenuation of the blood flow pulsatility from ICA to the arteries in MCA territory down to distal pial arteries for Subject I. (B) Pressure profile plotted from left ICA down to distal arteries in left MCA, PCA, and ACA, for Subject III.
Appendix 4. A case study to compare large-scale with small-scale simulations
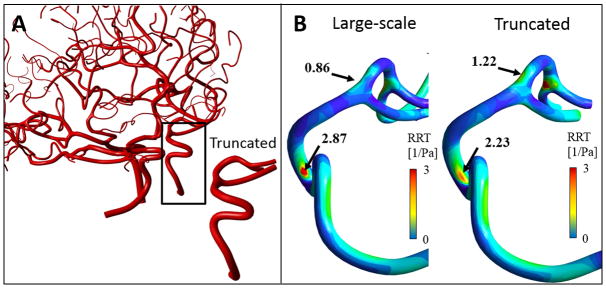
To examine the effect of domain size on the hemodynamic risk factors, we created a small section of Subject II covering only a section of the RICA to RMCA. Both the full and the trimmed simulations used exactly the same inlet velocity profile to eliminate the effect of inlet boundary condition [75]. We imposed the boundary condition to the truncated locations as computed by large-scale model. The truncated model is exactly obtained from large-scale vascular tree to ensure the equality of surface and volumetric meshes with the full model. The trimmed model was not geometrically extended to highlight the effect of full versus trimmed models.
Note that even though the “correct” average pressure dynamics was input, the cross-sectional pressure distribution was not imposed exactly for every point, thus only the spatial average determined the truncated simulation. As a result, RRT maps and the maxima for the full large-scale and truncated vascular model depicted in Figure A2, show substantial differences (specifically, elevated RRT in the MCA segment in the full model=0.86, truncated model max=1.22). These differences illustrate that small-scale simulation leads to risk factors prediction that can differ significantly from results determined by a large tree-wide simulation.
FIGURE A.2.
Hemodynamic risk-factor analysis of large-scale and truncated cerebrovascular tree. (A) A small section of Subject II’s cerebroarterial tree with five segments from the RICA to RMCA was truncated. Dynamic pressure profile was extracted from the large-scale model at three outlets and was used them as pressure boundary condition for the truncated model. (B) Distribution of relative residual time (RRT) of the truncated and large-scale vascular tree were different. The major different regions with the elevated RRT values are shown with black arrows. Predicted RRT map varied widely between small and large-scale models despite “correct” pressure outlet.
References
- 1.Cebral J, Mut F, Sforza D, et al. Clinical Application of Image-Based CFD for Cerebral Aneurysms. International journal for numerical methods in biomedical engineering. 2011;27(7):977–992. doi: 10.1002/cnm.1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Arzani A, Shadden SC. Characterizations and Correlations of Wall Shear Stress in Aneurysmal Flow. Journal of Biomechanical Engineering. 2015;138(1) doi: 10.1115/1.4032056. 014503/1-014503/10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shadden SC, Arzani A. Lagrangian postprocessing of computational hemodynamics. Annals of Biomedical Engineering. 2015;43(1):41–58. doi: 10.1007/s10439-014-1070-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gallo D, Steinman DA, Morbiducci U. An insight into the mechanistic role of the common carotid artery on the hemodynamics at the carotid bifurcation. Annals of Biomedical Engineering. 2015;43(1):68–81. doi: 10.1007/s10439-014-1119-0. [DOI] [PubMed] [Google Scholar]
- 5.Ku DN, Giddens DP, Zarins CK, Glagov S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis (Dallas, Tex) 1985;5(3):293–302. doi: 10.1161/01.atv.5.3.293. [DOI] [PubMed] [Google Scholar]
- 6.Rikhtegar F, Knight JA, Olgac U, et al. Choosing the optimal wall shear parameter for the prediction of plaque location-A patient-specific computational study in human left coronary arteries. Atherosclerosis. 2012;221(2):432–437. doi: 10.1016/j.atherosclerosis.2012.01.018. [DOI] [PubMed] [Google Scholar]
- 7.Dolan JM, Kolega J, Meng H. High wall shear stress and spatial gradients in vascular pathology: a review. Annals of Biomedical Engineering. 2013;41(7):1411–1427. doi: 10.1007/s10439-012-0695-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Buchanan JR, Kleinstreuer C, Hyun S, Truskey GA. Hemodynamics simulation and identification of susceptible sites of atherosclerotic lesion formation in a model abdominal aorta. Journal of Biomechanics. 2003;36(8):1185–1196. doi: 10.1016/s0021-9290(03)00088-5. [DOI] [PubMed] [Google Scholar]
- 9.Buchanan JR, Kleinstreuer C, Truskey GA, Lei M. Relation between non-uniform hemodynamics and sites of altered permeability and lesion growth at the rabbit aorto-celiac junction. Atherosclerosis. 1999;143(1):27–40. doi: 10.1016/s0021-9150(98)00264-0. [DOI] [PubMed] [Google Scholar]
- 10.Kawaguchi T, Nishimura S, Kanamori M, et al. Distinctive flow pattern of wall shear stress and oscillatory shear index: similarity and dissimilarity in ruptured and unruptured cerebral aneurysm blebs. Journal of Neurosurgery. 2012;117(4):774–780. doi: 10.3171/2012.7.JNS111991. [DOI] [PubMed] [Google Scholar]
- 11.Caro CG, Cheshire NJ, Watkins N. Preliminary comparative study of small amplitude helical and conventional ePTFE arteriovenous shunts in pigs. Journal of the Royal Society Interface. 2005;2(3):261–266. doi: 10.1098/rsif.2005.0044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huijbregts HJTaM, Blankestijn PJ, Caro CG, et al. A helical PTFE arteriovenous access graft to swirl flow across the distal anastomosis: results of a preliminary clinical study. European Journal of Vascular and Endovascular Surgery: The Official Journal of the European Society for Vascular Surgery. 2007;33(4):472–475. doi: 10.1016/j.ejvs.2006.10.028. [DOI] [PubMed] [Google Scholar]
- 13.Peiffer V, Sherwin SJ, Weinberg PD. Does low and oscillatory wall shear stress correlate spatially with early atherosclerosis? A systematic review Cardiovascular Research. 2013;99(2):242–250. doi: 10.1093/cvr/cvt044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liang F, Fukasaku K, Liu H, Takagi S. A computational model study of the influence of the anatomy of the circle of willis on cerebral hyperperfusion following carotid artery surgery. Biomedical Engineering Online. 2011;10:84. doi: 10.1186/1475-925X-10-84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Huang PG, Muller LO. Simulation of one-dimensional blood flow in networks of human vessels using a novel TVD scheme. International Journal for Numerical Methods in Biomedical Engineering. 2015;31(5):e02701. doi: 10.1002/cnm.2701. [DOI] [PubMed] [Google Scholar]
- 16.Liang F, Liu X, Yamaguchi R, Liu H. Sensitivity of flow patterns in aneurysms on the anterior communicating artery to anatomic variations of the cerebral arterial network. Journal of Biomechanics. 2016;49(15):3731–3740. doi: 10.1016/j.jbiomech.2016.09.031. [DOI] [PubMed] [Google Scholar]
- 17.Maaly MA, Ismail AA. Three dimensional magnetic resonance angiography of the circle of Willis: Anatomical variations in general Egyptian population. The Egyptian Journal of Radiology and Nuclear Medicine. 2011;42(3–4):405–412. doi: 10.1016/j.ejrnm.2011.09.001. [DOI] [Google Scholar]
- 18.Alastruey J, Parker KH, Peiró J, Byrd SM, Sherwin SJ. Modelling the circle of Willis to assess the effects of anatomical variations and occlusions on cerebral flows. Journal of Biomechanics. 2007;40(8):1794–1805. doi: 10.1016/j.jbiomech.2006.07.008. [DOI] [PubMed] [Google Scholar]
- 19.Marshall I, Zhao S, Papathanasopoulou P, Hoskins P, Xu Y. MRI and CFD studies of pulsatile flow in healthy and stenosed carotid bifurcation models. Journal of Biomechanics. 2004;37(5):679–687. doi: 10.1016/j.jbiomech.2003.09.032. [DOI] [PubMed] [Google Scholar]
- 20.Papathanasopoulou P, Zhao S, Köhler U, et al. MRI measurement of time-resolved wall shear stress vectors in a carotid bifurcation model, and comparison with CFD predictions. Journal of magnetic resonance imaging: JMRI. 2003;17(2):153–162. doi: 10.1002/jmri.10243. [DOI] [PubMed] [Google Scholar]
- 21.Steinman DA, Thomas JB, Ladak HM, Milner JS, Rutt BK, Spence JD. Reconstruction of carotid bifurcation hemodynamics and wall thickness using computational fluid dynamics and MRI. Magnetic Resonance in Medicine. 2002;47(1):149–159. doi: 10.1002/mrm.10025. [DOI] [PubMed] [Google Scholar]
- 22.Stroud JS, Berger SA, Saloner D. Numerical analysis of flow through a severely stenotic carotid artery bifurcation. Journal of Biomechanical Engineering. 2002;124(1):9–20. doi: 10.1115/1.1427042. [DOI] [PubMed] [Google Scholar]
- 23.Moore JA, Steinman DA, Ethier CR. Computational blood flow modelling: errors associated with reconstructing finite element models from magnetic resonance images. Journal of Biomechanics. 1998;31(2):179–184. doi: 10.1016/s0021-9290(97)00125-5. [DOI] [PubMed] [Google Scholar]
- 24.Grinberg L, Anor T, Madsen J, Yakhot A, Karniadakis G. Large-Scale Simulation of the Human Arterial Tree. Clinical and Experimental Pharmacology and Physiology. 2009;36(2):194–205. doi: 10.1111/j.1440-1681.2008.05010.x. [DOI] [PubMed] [Google Scholar]
- 25.Grinberg L, Cheever E, Anor T, Madsen JR, Karniadakis GE. Modeling Blood Flow Circulation in Intracranial Arterial Networks: A Comparative 3D/1D Simulation Study. Annals of Biomedical Engineering. 2010;39(1):297–309. doi: 10.1007/s10439-010-0132-1. [DOI] [PubMed] [Google Scholar]
- 26.Perdikaris P, Grinberg L, Karniadakis GE. Multiscale modeling and simulation of brain blood flow. Physics of Fluids. 2016;28(2) doi: 10.1063/1.4941315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Formaggia L, Nobile F, Quarteroni A, Veneziani A. Multiscale modelling of the circulatory system: a preliminary analysis. Computing and Visualization in Science. 1999;2(2–3):75–83. doi: 10.1007/s007910050030. [DOI] [Google Scholar]
- 28.Passerini T, Luca M, de Formaggia L, Quarteroni A, Veneziani A. A 3D/1D geometrical multiscale model of cerebral vasculature. Journal of Engineering Mathematics. 2009;64(4):319. doi: 10.1007/s10665-009-9281-3. [DOI] [Google Scholar]
- 29.Liang F, Oshima M, Huang H, Liu H, Takagi S. Numerical Study of Cerebroarterial Hemodynamic Changes Following Carotid Artery Operation: A Comparison Between Multiscale Modeling and Stand-Alone Three-Dimensional Modeling. Journal of Biomechanical Engineering. 2015;137(10):101011. doi: 10.1115/1.4031457. [DOI] [PubMed] [Google Scholar]
- 30.Liang F, Takagi S, Himeno R, Liu H. Multi-scale modeling of the human cardiovascular system with applications to aortic valvular and arterial stenoses. Medical & Biological Engineering & Computing. 2009;47(7):743–755. doi: 10.1007/s11517-009-0449-9. [DOI] [PubMed] [Google Scholar]
- 31.Müller LO, Toro EF. A global multiscale mathematical model for the human circulation with emphasis on the venous system. International Journal for Numerical Methods in Biomedical Engineering. 2014;30(7):681–725. doi: 10.1002/cnm.2622. [DOI] [PubMed] [Google Scholar]
- 32.Müller LO, Toro EF. Enhanced global mathematical model for studying cerebral venous blood flow. Journal of Biomechanics. 2014;47(13):3361–3372. doi: 10.1016/j.jbiomech.2014.08.005. [DOI] [PubMed] [Google Scholar]
- 33.Blanco PJ, Watanabe SM, Passos MARF, Lemos PA, Feijóo RA. An Anatomically Detailed Arterial Network Model for One-Dimensional Computational Hemodynamics. IEEE Transactions on Biomedical Engineering. 2015;62(2):736–753. doi: 10.1109/TBME.2014.2364522. [DOI] [PubMed] [Google Scholar]
- 34.Blanco PJ, Watanabe SM, Dari EA, Passos MARF, Feijóo RA. Blood flow distribution in an anatomically detailed arterial network model: criteria and algorithms. Biomechanics and Modeling in Mechanobiology. 2014;13(6):1303–1330. doi: 10.1007/s10237-014-0574-8. [DOI] [PubMed] [Google Scholar]
- 35.Cruz JP, Chow M, O’Kelly C, et al. Delayed Ipsilateral Parenchymal Hemorrhage Following Flow Diversion for the Treatment of Anterior Circulation Aneurysms. American Journal of Neuroradiology. 2012;33(4):603–608. doi: 10.3174/ajnr.A3065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wermer MJH, Greebe P, Algra A, Rinkel GJE. Incidence of Recurrent Subarachnoid Hemorrhage After Clipping for Ruptured Intracranial Aneurysms. Stroke. 2005;36(11):2394–2399. doi: 10.1161/01.STR.0000185686.28035.d2. [DOI] [PubMed] [Google Scholar]
- 37.Amini A, Osborn AG, McCall TD, Couldwell WT. Remote Cerebellar Hemorrhage. American Journal of Neuroradiology. 2006;27(2):387–390. [PMC free article] [PubMed] [Google Scholar]
- 38.Mitha AP, Mynard JP, Storwick JA, Shivji ZI, Wong JH, Morrish W. Can the Windkessel Hypothesis Explain Delayed Intraparenchymal Haemorrhage After Flow Diversion? A Case Report and Model-Based Analysis of Possible Mechanisms Heart, Lung & Circulation. 2015;24(8):824–830. doi: 10.1016/j.hlc.2015.02.001. [DOI] [PubMed] [Google Scholar]
- 39.Levitt MR, McGah PM, Aliseda A, et al. Cerebral aneurysms treated with flow-diverting stents: Computational models using intravascular blood flow measurements. AJNR American journal of neuroradiology. 2014;35(1):143–148. doi: 10.3174/ajnr.A3624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hsu C-Y, Schneller B, Alaraj A, Flannery M, Zhou XJ, Linninger A. Automatic recognition of subject-specific cerebrovascular trees. Magnetic Resonance in Medicine. 2017;77(1):398–410. doi: 10.1002/mrm.26087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hsu C-Y, Ghaffari M, Alaraj A, Flannery M, Zhou XJ, Linninger A. Gap-free segmentation of vascular networks with automatic image processing pipeline. Computers in Biology and Medicine. 2017;82:29–39. doi: 10.1016/j.compbiomed.2017.01.012. [DOI] [PubMed] [Google Scholar]
- 42.Ghaffari M, Hsu C-Y, Linninger AA. Automatic reconstruction and generation of structured hexahedral mesh for non-planar bifurcations in vascular network. Comput Aided Chem Eng. 2015 [Google Scholar]
- 43.Ghaffari M, Tangen K, Alaraj A, Du X, Charbel FT, Linninger AA. Large-scale subject-specific cerebral arterial tree modeling using automated parametric mesh generation for blood flow simulation. Computers in Biology and Medicine. 2017;91:353–365. doi: 10.1016/j.compbiomed.2017.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hsu C-Y, Schneller B, Ghaffari M, Alaraj A, Linninger A. Medical Image Processing for Fully Integrated Subject Specific Whole Brain Mesh Generation. Technologies. 2015;3(2):126–141. doi: 10.3390/technologies3020126. [DOI] [Google Scholar]
- 45.Antiga L, Piccinelli M, Botti L, Ene-Iordache B, Remuzzi A, Steinman DA. An image-based modeling framework for patient-specific computational hemodynamics. Medical & Biological Engineering & Computing. 2008;46(11):1097–1112. doi: 10.1007/s11517-008-0420-1. [DOI] [PubMed] [Google Scholar]
- 46.Sankaran S, Moghadam ME, Kahn AM, Tseng EE, Guccione JM, Marsden AL. Patient-Specific Multiscale Modeling of Blood Flow for Coronary Artery Bypass Graft Surgery. Annals of Biomedical Engineering. 2012;40(10):2228–2242. doi: 10.1007/s10439-012-0579-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Antiga L, Ene-iordache B, Remuzzi A. Centerline Computation and Geometric Analysis of Branching Tubular Surfaces with Application to Blood Vessel Modeling. Proceedings of the 11th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision; Plzen, Czech Republic. 2003; pp. 11–18. [Google Scholar]
- 48.Adib MAHM, Ii S, Watanabe Y, Wada S. Minimizing the blood velocity differences between phase-contrast magnetic resonance imaging and computational fluid dynamics simulation in cerebral arteries and aneurysms. Medical & Biological Engineering & Computing. 2017;55(9):1605–1619. doi: 10.1007/s11517-017-1617-y. [DOI] [PubMed] [Google Scholar]
- 49.Takeuchi S, Karino T. Flow patterns and distributions of fluid velocity and wall shear stress in the human internal carotid and middle cerebral arteries. World Neurosurgery. 2010;73(3):174–185. doi: 10.1016/j.surneu.2009.03.030. discussion e27. [DOI] [PubMed] [Google Scholar]
- 50.He X, Ku DN. Pulsatile flow in the human left coronary artery bifurcation: average conditions. Journal of Biomechanical Engineering. 1996;118(1):74–82. doi: 10.1115/1.2795948. [DOI] [PubMed] [Google Scholar]
- 51.Himburg HA, Grzybowski DM, Hazel AL, LaMack JA, Li X-M, Friedman MH. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. American Journal of Physiology Heart and Circulatory Physiology. 2004;286(5):H1916–1922. doi: 10.1152/ajpheart.00897.2003. [DOI] [PubMed] [Google Scholar]
- 52.Wootton DM, Ku DN. Fluid mechanics of vascular systems, diseases, and thrombosis. Annual Review of Biomedical Engineering. 1999;1:299–329. doi: 10.1146/annurev.bioeng.1.1.299. [DOI] [PubMed] [Google Scholar]
- 53.Davies PF. Hemodynamic shear stress and the endothelium in cardiovascular pathophysiology. Nature Clinical Practice Cardiovascular Medicine. 2009;6(1):16–26. doi: 10.1038/ncpcardio1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Meng H, Wang Z, Hoi Y, et al. Complex Hemodynamics at the Apex of an Arterial Bifurcation Induces Vascular Remodeling Resembling Cerebral Aneurysm Initiation. Stroke. 2007;38(6):1924–1931. doi: 10.1161/STROKEAHA.106.481234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zeng Z, Kallmes DF, Durka MJ, et al. Sensitivity of CFD Based Hemodynamic Results in Rabbit Aneurysm Models to Idealizations in Surrounding Vasculature. Journal of biomechanical engineering. 2010;132(9):091009. doi: 10.1115/1.4001311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Malek AM, Alper SL, Izumo S. Hemodynamic Shear Stress and Its Role in Atherosclerosis. JAMA. 1999;282(21):2035–2042. doi: 10.1001/jama.282.21.2035. [DOI] [PubMed] [Google Scholar]
- 57.Glor FP, Ariff B, Hughes AD, et al. Image-based carotid flow reconstruction: a comparison between MRI and ultrasound. Physiological Measurement. 2004;25(6):1495–1509. doi: 10.1088/0967-3334/25/6/014. [DOI] [PubMed] [Google Scholar]
- 58.Glor FP, Long Q, Hughes AD, et al. Reproducibility Study of Magnetic Resonance Image-Based Computational Fluid Dynamics Prediction of Carotid Bifurcation Flow. Annals of Biomedical Engineering. 2003;31(2):142–151. doi: 10.1114/1.1537694. [DOI] [PubMed] [Google Scholar]
- 59.Morbiducci U, Gallo D, Ponzini R, et al. Quantitative Analysis of Bulk Flow in Image-Based Hemodynamic Models of the Carotid Bifurcation: The Influence of Outflow Conditions as Test Case. Annals of Biomedical Engineering. 2010;38(12):3688–3705. doi: 10.1007/s10439-010-0102-7. [DOI] [PubMed] [Google Scholar]
- 60.Lee S-W, Antiga L, Steinman DA. Correlations Among Indicators of Disturbed Flow at the Normal Carotid Bifurcation. Journal of Biomechanical Engineering. 2009;131(6):061013–061013. doi: 10.1115/1.3127252. [DOI] [PubMed] [Google Scholar]
- 61.Shakur SF, Aletich VA, Amin-Hanjani S, Hussein AE, Charbel FT, Alaraj A. Quantitative assessment of parent vessel and distal intracranial hemodynamics following pipeline flow diversion. Interventional Neuroradiology. 2016 doi: 10.1177/1591019916668842. 1591019916668842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Cebral JR, Castro MA, Appanaboyina S, Putman CM, Millan D, Frangi AF. Efficient pipeline for image-based patient-specific analysis of cerebral aneurysm hemodynamics: technique and sensitivity. IEEE Transactions on Medical Imaging. 2005;24(4):457–467. doi: 10.1109/TMI.2005.844159. [DOI] [PubMed] [Google Scholar]
- 63.Hoi Y, Wasserman BA, Xie YJ, et al. Characterization of volumetric flow rate waveforms at the carotid bifurcations of older adults. Physiological Measurement. 2010;31(3):291–302. doi: 10.1088/0967-3334/31/3/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.O’Rourke MF, Safar ME. Relationship between aortic stiffening and microvascular disease in brain and kidney: cause and logic of therapy. Hypertension (Dallas, Tex: 1979) 2005;46(1):200–204. doi: 10.1161/01.HYP.0000168052.00426.65. [DOI] [PubMed] [Google Scholar]
- 65.Mitchell GF, van Buchem MA, Sigurdsson S, et al. Arterial stiffness, pressure and flow pulsatility and brain structure and function: the Age, Gene/Environment Susceptibility--Reykjavik study. Brain: A Journal of Neurology. 2011;134(Pt 11):3398–3407. doi: 10.1093/brain/awr253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Himburg HA, Dowd SE, Friedman MH. Frequency-dependent response of the vascular endothelium to pulsatile shear stress. American Journal of Physiology - Heart and Circulatory Physiology. 2007;293(1):H645–H653. doi: 10.1152/ajpheart.01087.2006. [DOI] [PubMed] [Google Scholar]
- 67.Mut F, Ruijters D, Babic D, Bleise C, Lylyk P, Cebral JR. Effects of changing physiologic conditions on the in vivo quantification of hemodynamic variables in cerebral aneurysms treated with flow diverting devices. International Journal for Numerical Methods in Biomedical Engineering. 2014;30(1):135–142. doi: 10.1002/cnm.2594. [DOI] [PubMed] [Google Scholar]
- 68.Vignon-Clementel IE, Alberto Figueroa C, Jansen KE, Taylor CA. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Computer Methods in Applied Mechanics and Engineering. 2006;195(29–32):3776–3796. doi: 10.1016/j.cma.2005.04.014. [DOI] [Google Scholar]
- 69.Spilker RL, Feinstein JA, Parker DW, Reddy VM, Taylor CA. Morphometry-Based Impedance Boundary Conditions for Patient-Specific Modeling of Blood Flow in Pulmonary Arteries. Annals of Biomedical Engineering. 2007;35(4):546–559. doi: 10.1007/s10439-006-9240-3. [DOI] [PubMed] [Google Scholar]
- 70.Olufsen MS. Structured tree outflow condition for blood flow in larger systemic arteries. American Journal of Physiology - Heart and Circulatory Physiology. 1999;276(1):H257–H268. doi: 10.1152/ajpheart.1999.276.1.H257. [DOI] [PubMed] [Google Scholar]
- 71.Valencia A, Ledermann D, Rivera R, Bravo E, Galvez M. Blood flow dynamics and fluid–structure interaction in patient-specific bifurcating cerebral aneurysms. International Journal for Numerical Methods in Fluids. 2008;58(10):1081–1100. doi: 10.1002/fld.1786. [DOI] [Google Scholar]
- 72.Arzani A, Gambaruto AM, Chen G, Shadden SC. Wall shear stress exposure time: a Lagrangian measure of near-wall stagnation and concentration in cardiovascular flows. Biomechanics and Modeling in Mechanobiology. 2017;16(3):787–803. doi: 10.1007/s10237-016-0853-7. [DOI] [PubMed] [Google Scholar]
- 73.Gould IG, Linninger AA. Hematocrit distribution and tissue oxygenation in large microcirculatory networks. Microcirculation (New York, NY: 1994) 2015;22(1):1–18. doi: 10.1111/micc.12156. [DOI] [PubMed] [Google Scholar]
- 74.Linninger AA, Gould IG, Marinnan T, Hsu C-Y, Chojecki M, Alaraj A. Cerebral microcirculation and oxygen tension in the human secondary cortex. Annals of Biomedical Engineering. 2013;41(11):2264–2284. doi: 10.1007/s10439-013-0828-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Xiang J, Siddiqui AH, Meng H. The effect of inlet waveforms on computational hemodynamics of patient-specific intracranial aneurysms. Journal of Biomechanics. 2014;47(16):3882–3890. doi: 10.1016/j.jbiomech.2014.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]