Abstract
Objective
Recent reports indicate that making better assumptions about the user’s intended movement can improve decoder calibration for intracortical brain-computer interfaces. Several methods now exist for estimating user intent, including an optimal feedback control model, a piecewise-linear feedback control model, ReFIT, and other heuristics. Which of these methods yields the best decoding performance?
Methods
Using data from the BrainGate2 pilot clinical trial, we measured how a steady-state velocity Kalman filter decoder was affected by the choice of intention estimation method. We examined three separate components of the Kalman filter: dimensionality reduction, temporal smoothing, and output gain (speed scaling).
Results
The decoder’s dimensionality reduction properties were largely unaffected by the intention estimation method (the unsmoothed velocity vectors differed by <5% in terms of how accurately they pointed at the target and how their speeds decreased near the target). In contrast, the smoothing and gain properties of the decoder were greatly affected (> 50% difference in average values). Surprisingly, simulation results show that these differences in gain and smoothing values were largely arbitrary, as all methods failed to optimize the gain and smoothing values to match the task parameters.
Conclusion
Our results show that, gain and smoothing differences aside, current intention estimation methods yield nearly equivalent decoders and that simple models of user intent, such as a position error vector (target position minus cursor position), perform comparably to more elaborate models. Our results also highlight that current calibration methods yield arbitrary differences in gain and smoothing properties that can confound decoder comparisons.
Index Terms: brain-machine interface, brain-computer interface, motor cortex
I. Introduction
Standard decoding approaches for intracortical BCIs (iBCIs) require a calibration step that tunes the decoder’s parameters to match the user’s unique neural signals, which vary from person to person and from day to day within the same user [1]–[5]. Decoders can either be calibrated in “open-loop”, where neural activity is recorded while the user watches, imagines, or attempts to make a series of cued movements, or in “closed-loop”, where neural activity is recorded while the user actively controls the movement using the brain-computer interface [6]–[10], [3], [4], [11], [12]. In either case, decoders are typically calibrated using statistical data fitting approaches that tune the decoder to predict a time series of movement parameters (e.g. intended arm velocities) given a time series of recorded neural activity [13], [6], [14]–[19], [1], [2], [20], [11].
Recent reports indicate that closed-loop calibration can improve performance relative to open-loop calibration alone, since the user’s neural activity is different during active control of the iBCI [17], [8], [3], [9]–[11]. In some contexts, closed-loop calibration may also enable seamless refinement of the decoder during normal use without requiring the user to pause for an explicit calibration routine [4]. Although closed-loop calibration is now standard [1], [7], [2], [9], [10], [4], [3], [21], [11], it adds the complexity of having to estimate the user’s intended movements during active control of the iBCI.
One simple method of estimating user intent during closed-loop control is to use the output of the original decoder that was active during the calibration dataset. If the decoder is working well enough, this approach yields a rough estimate of the user’s intended movement that contains some amount of decoding error. That decoding error may impair the calibration process by forcing the newly calibrated decoder to reproduce the decoding error in addition to the user’s intended movement. Recent work on the “recalibrated feedback intention-trained Kalman filter” (called ReFIT-KF) has demonstrated that using the originally decoded velocity vectors for calibration does not perform as well as modifying them to point straight at the target and setting them equal to zero when the cursor is on top of the target [8], [3], [10]. Rotating and zeroing the decoded velocity is based on the assumption that the user’s intended movement direction is always straight towards the target and that the person does not intend to move the cursor whenever it is overlapping the target.
While the ReFIT intention estimation method has been shown to yield a better decoder than using decoded velocity directly [8], [10], it is not well known how ReFIT performs relative to other methods that also improve upon using the originally decoded velocity to estimate intent. One alternative method represents the user’s intent with a unit vector that points straight from the cursor to the target, but only during presumed “ballistic” time periods, when the cursor is at least a certain distance away from the target [1], [4], [9]. A different heuristic, originally used in an early iBCI study 15 years ago [6], uses data from the entire trajectory and represents the user’s intent with a “position error” vector pointing from the cursor towards the target with a magnitude equal to the distance between them.
Instead of heuristic rules, a different approach to intention estimation is to use a more complete feedback control model to infer the user’s intended motor command. One recent study employed an optimal feedback control model based on the linear-quadratic-Gaussian framework [11]. The model was used to generate an optimal control policy whose output was taken to be the user’s intention (they called this approach “instant-OFC”). Recently, we proposed a non-linear feedback control model (called PLM for “piecewise-linear model”) that can be fit to any user’s unique feedback control policy in a data-driven manner [22]. We showed that the PLM modeled the user’s motor command (neural population activity) and simulated cursor movements more accurately than other intention estimation methods, including the optimal feedback control model. The PLM can take into account the effect of visual feedback delay on the user’s motor command, and can also describe how the intended motor command may sometimes point away from the target in order to compensate for the cursor’s momentum [22].
Though a variety of promising intention estimation methods now exist, there are few studies comparing the effect of these methods on decoder calibration directly against one another. We know of only two studies that compare the ReFIT method to using the originally decoded velocity for calibration [8], [10] and a more recent study comparing the performance of decoders calibrated with an optimal feedback control model to those calibrated with ReFIT [11]. Here, we aim to more fully quantify the effect of different intention estimation methods on decoder properties by comparing several previously proposed intention estimation methods to one another. We were motivated partly by the desire to come to a consensus on a standard method, and partly by the possibility that the PLM’s improved ability to model and describe the user’s feedback control policy would translate into a significant improvement in decoder calibration. Note that while our previous work demonstrates that the PLM is more accurate for modeling the user’s neural activity [22], it is not known whether this improved accuracy will translate into a noticeable improvement in decoder performance when the PLM is used for decoder calibration.
We tested each calibration method using one type of decoder that is commonly used for continuous neural control in the human iBCI literature: a steady-state velocity Kalman filter [15], [1], [23], [7], [9], [24], [4], [3], [12]. The steady-state Kalman filter is composed of a linear dimensionality reduction step combined with exponential smoothing, a common framework used in many other iBCI studies; as such, the results obtained here should also be applicable to other continuous velocity decoders [6], [16], [2], [11].
To more fully understand how the decoder was affected by each intention estimation method, we separated the steady-state Kalman filter into three components: dimensionality reduction (mapping the high-dimensional neural features to a two-dimensional vector that controls the cursor velocity), temporal smoothing of the decoded velocity, and overall gain (speed scaling). We performed offline analyses on datasets of closed-loop 2D cursor control from three participants in the BrainGate2 clinical trial to determine how the intention estimation method affects each of these three components. We complemented these core results with online performance comparisons and computer simulations.
Our main finding is that the choice of intention estimation method had only a small effect on the decoder’s dimensionality reduction property, but had a large effect on its gain and smoothing properties. In other words, regardless of the assumptions made about the user’s intended movement, the decoded velocities were essentially the same set of vectors but with different amounts of scaling and smoothing applied. While large, this difference in gain and smoothing properties was mostly arbitrary, with different intention estimation methods tending to bias the gain and smoothing values up or down on average. Using simulation, we show that all intention estimation methods are almost completely unable to optimize the gain and smoothing parameters to match the task demands (e.g. no method could produce lower gains when calibrated on datasets with smaller targets).
II. Methods
A. Study Permissions and Participants
Permission for these studies was granted by the US Food and Drug Administration (Investigational Device Exemption #G090003) and the Institutional Review Boards of University Hospitals Cleveland Medical Center (04-12-17), Stanford University (20804), Partners Healthcare/Massachusetts General Hospital (2011P001036), Providence VA Medical Center (2011-009), and Brown University (0809992560). All participants were enrolled in a pilot clinical trial of the BrainGate Neural Interface System (http://www.clinicaltrials.gov/ct2/show/NCT00912041). Informed consent, including consent to publish, was obtained in writing from the participants prior to their enrollment in the study.
This study includes data from four participants (identified as T6-T9) with chronic tetraplegia who received intracortical implants as part of the BrainGate2 pilot clinical trial. Participants were implanted with one (T6) or two (T7, T8, T9) 96 channel intracortical microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT) in the hand area of dominant motor cortex (1.0-mm electrode length for T6, 1.5-mm length for T7, T8 and T9). At the time of the study, participant T6 was a 52-year-old woman with tetraplegia due to ALS. Participant T7 was a 59-year-old man with tetraplegia due to ALS. Participant T8 was a 53-year-old man with tetraplegia due to high cervical spinal cord injury (C4, ASIA-A). Participant T9 was a 52-year-old man with tetraplegia due to ALS. More details about participants and surgical procedures can be found in [15], [25], [3].
B. Offline Datasets
For offline analysis, we used 13 center-out-back datasets that have been previously reported [22]. In these sessions, participants T6, T7 and T8 used a steady-state velocity Kalman filter to move a neural cursor to acquire targets on a 2D computer screen by dwelling on them. During these sessions, a different set of gain and smoothing parameters was imposed for each 4-5 minute block of recording, yielding a rich dataset of cursor movements made under a variety of decoder dynamics. During each block, targets appeared alternately in either the center of the workspace or in one of eight radially spaced outer locations. In addition to these 13 original datasets, we analyzed datasets from 2 additional sessions that further explored the effect of smoothing on online performance, yielding a total of 15 sessions. Each session used for offline analysis is detailed in Supplemental Section 1.
C. Online Performance Comparison Datasets
We collected 4 additional datasets with participants T8 and T9 (2 sessions each) to compare the online, closed-loop performance of steady-state, velocity Kalman filters calibrated with three different intention estimation methods: ReFIT, Unit Vector, and PLM (these methods are described in a separate section below). For these sessions (detailed in Supplemental Section 1), data were collected in sets of 3 blocks, each lasting 4 minutes. In each block, the participant completed a center-out-back target acquisition task using a decoder calibrated with one of the three intention estimation methods. After each set of 3 blocks, one of those 3 blocks was pseudo-randomly chosen and used to calibrate three new decoders. These new decoders were then used for the next set of comparison blocks (tested in a pseudo-random order).
This experimental design aimed to reduce variance and increase the number of independent estimates of decoder performance. Building all three decoders on the same set of data substantially reduced variability in performance due to variations in data quality caused by changes in neural signal quality across blocks. Additionally, rebuilding the decoders anew after every block set enabled us to independently evaluate decoder calibration quality multiple times in a session.
To calibrate the first set of decoders, we collected a single open-loop block at the beginning of the session that we used to calibrate an initial decoder (using the “UnitVector” method). The participant then completed a preliminary closed-loop block using that initial decoder. This preliminary closed-loop block provided calibration data for the first set of decoder comparison blocks.
Participants acquired targets by holding the cursor in unbroken contact with the target region for 0.75 seconds. A trial was considered unsuccessful and the cursor was reset to the target position if a maximum movement time of 8 seconds was exceeded. After a target was acquired, another target appeared immediately afterwards. Additional details are listed in Supplemental Section 1.
D. Decoder Calibration
To calibrate Kalman filter decoders for offline analysis and online use, we used the MATLAB 2014b function “kalman” which solves the discrete-time algebraic Riccati equation to yield a steady-state Kalman filter. The neural features used for decoding were threshold crossing rates and spike-band spectral power (250-5000 Hz) in 20 ms time bins for each electrode, extracted as in [22]. The features were z-scored before being passed through the decoder.
The state transition model that describes how velocity changes from time step to time step is:
| (1) |
| (2) |
where is the velocity vector at time step t, A is the 2 × 2 state transition matrix, and is the process noise. Each time step is 20 ms long. The measurement equation, which relates the neural features to the velocity, is:
| (3) |
| (4) |
where ft is an N × 1 neural feature vector, H is the N × 2 neural encoding model, qt is a neural noise vector, and Q is the N × N neural noise covariance matrix.
We estimated A using least squares regression to minimize , where M is the number of samples available for fitting in the calibration dataset. After estimating A, we estimated W using the sample covariance of the residuals , where and are a 2 × (M−1) matrices of velocity vectors, with containing velocity vectors delayed by one sample relative to .
Similarly, we estimated H using least squares regression to minimize , where is the neural feature vector, and is the “calibration” vector given by the intention estimation method (which may represent intended velocity, a feedback control vector, etc.). After estimating H, we estimated Q using the sample covariance of the residuals , where is a 2 × M matrix of calibration vectors, is an N × M matrix of neural feature vectors.
Solving the algebraic Riccati equation yields the Kalman gain matrix K, which updates the decoded velocity at each time step as follows:
| (5) |
E. Decoder Reparameterization
Using the methods in [22], [26], we reparameterized the Kalman filter’s update equation (eq. 5) to explicitly separate its dimensionality reduction step from its temporal smoothing dynamics and overall gain (speed scaling). This allowed us to isolate and analyze each component to determine how it was affected by the intention estimation method. The reparameterized update equation takes the form:
| (6) |
where α is a scalar value between 0 and 1 that defines the amount of temporal smoothing (and was typically greater than 0.8), β is a scalar value greater than 0 that defines the gain, and D is a 2 × N matrix that performs the dimensionality reduction (mapping high dimensional neural features to the two dimensional velocity space). Given any steady-state velocity Kalman filter, α, β and D can be computed to describe it.
We computed α using the following approximation that relates in the Kalman update equation to α in the reparameterized equation:
| (7) |
where and is a value close to zero (<0.01 for our datasets). Then we computed β and D using the equation that relates K in the Kalman update equation to in the reparameterized equation. To ensure that β alone defined the gain, we normalized D so that, on average, D produced velocity vectors with a magnitude of 1 when the user is far from the target. Note that this normalization only controls the overall scale of D, and does not restrict it to only decoding unit vectors.
To normalize D, we projected the unsmoothed, decoded velocity vectors onto a unit vector pointing straight from the cursor to the target when the cursor was far from the target (> 80% of the center-out distance). We then set β equal to the average magnitude of the projections and divided by β to yield . Note that projection is a necessary step and that averaging the magnitudes before projecting yields a biased estimate (see Supplemental Section 2 for more details). When D is normalized in this way, β alone parameterizes the maximum speed of the cursor by defining the cursor’s “terminal velocity”, or the speed that the cursor would approach if the user pointed the Dft vector in the same direction forever and at maximum magnitude. We report decoder gain as this maximum speed.
F. Intention Estimation Methods
The intention estimation methods we studied are defined in Table 1 and illustrated in Figure 1. Of special note is the optimal feedback control (OFC) model that was proposed in [11]. We found that the version of the model that performed the best in that study (called “instant-OFC”) yielded calibration vectors and decoder performance results that were very similar to the position error method (correlation > 0.998 between the calibration vectors generated by the two methods across all blocks). As such, we labeled the results for the position error method as “PE/OFC”, grouping these two methods together for succinctness (but see Supplemental Section 3 for the results of each method reported separately and for a computational explanation of the similarity).
TABLE I.
Intention Estimation Methods
| Method | Implementation | Motivation |
|---|---|---|
| Piecewise Linear Model (PLM) | The calibration vector is equal to the feedback control vector, as estimated using the piecewise linear model proposed in [22] (and described in detail in the Methods). | This model accounts for visual feedback delay and nonlinearities in the user’s control policy, and can describe how the intended motor command may even point away from the target to offset the cursor’s momentum. It outperformed other methods at describing the user’s neural population activity and simulating trajectories in prior work [22]. |
| Position Error (PE/OFC) | The calibration vector is equal to the target position (g) minus the cursor position (p): |
This method was first used 15 years ago [6]. It can be interpreted as a linear approximation of the user’s feedback control policy. |
| Instant-OFC (PE/OFC) | The calibration vector is described by a linear feedback control policy [11]: The L matrix is solved for using the infinite-horizon, discrete-time LQG framework and takes the form: |
This feedback control model of user intent was recently reported to outperform the ReFIT intention estimation method when used to calibrate a point process filter [11]. The way L is determined, the velocity-related component lv is small by design [11] and hence this method performed very similarly to the position error method. We therefore grouped it together by labeling position error results as “PE/OFC” (but see Supplemental Section 3 for the results reported separately). |
| Unit Vector (UnitVec) | The calibration vector is equal to a unit vector pointing from the cursor (p) to the target (g): When this method was used in previous studies, time steps where the cursor was near the target and/or time steps occurring a certain time after target appearance were intentionally excluded from calibration [1], [4], [9]. We ran an optimization routine for each block to estimate the optimal window of data to include. |
This method is intended to capture only the initial “ballistic” portion of the movement, when the assumption that the person intends to move the cursor directly to the target at a constant speed is least likely to be violated (e.g. by error correction, attenuation of the magnitude of the motor command near the target, etc.). Estimating the user’s aiming direction is also more accurate when the cursor is far from the target, because small differences in the actual cursor position and the user’s internal estimate of the cursor position do not cause large errors in estimated aiming angle. |
| ReFIT | The calibration vector is equal to the originally decoded velocity, but modified to point towards the target and to be zero when the cursor is on top of the target [3], [8], [10]. | The user intends to move straight towards the target and stop when the cursor overlaps the target. This method has been used to calibrate the ReFIT-KF decoder [8], which currently has the highest-reported bitrates for cursor movements in monkeys [21] and in humans [12]. |
| Raw Decoded Velocity (RawVel) | The calibration vector is equal to the velocity vector originally decoded during the calibration dataset. | This method is included as a control and is expected to perform worse than other methods because the originally decoded velocity contains decoding error. |
Fig. 1.
Illustration of the five intention estimation methods we studied. For this illustration (but not for analysis), the calibration vectors were normalized by dividing by their average magnitude in order to aid visualization by placing them into the same range. (A) The calibration vectors given by each method are plotted in color for one example movement made by participant T8 (the cursor trajectory is drawn in gray). The movement was chosen for illustration to contain some curvature. No vectors are drawn during a brief reaction time interval at the start of the movement. Note that calibration vectors from the UnitVec method are not drawn near the end of the movement, since time steps where the cursor is near the target are intentionally excluded with this method. (B) The angle and magnitude of the calibration vectors are plotted as time series for each method. Time zero corresponds to the end of the reaction time interval and the time series ends when the target is acquired. The angle vs. time curves given by the PE/OFC, UnitVec, and ReFIT were offset for visualization purposes but are identical. The calibration vectors from the ReFIT method jump to zero when the cursor begins overlapping the target.
Also of note is the Unit Vector method [1], [4], [9] which uses snippets of data only from the beginning of the movement, as defined by distance to the target and/or time after movement onset. Since the optimal exclusion criteria may change depending on the participant and the parameters of the task, we added an optimization routine to the Unit Vector calibration process that searched for the best distance threshold for data exclusion using the training data. The optimization routine measured cross-validated decoder performance under each distance threshold (distance from cursor to target < 0%, 10%, …, 70% of the starting target distance) and selected the threshold that yielded the lowest mean angular error in the decoder output for building the final decoder.
G. Piecewise-Linear Feedback Control Model
We used the piecewise-linear model (PLM) of iBCI cursor movements described in [22] in two ways described in detail below: (1) as an intention estimation method for decoder calibration, and (2) to generate simulated datasets of cursor movements (see next section).
The PLM describes the user’s intended motor command as a two-dimensional feedback control vector, ct, that varies as a function of the target position and the user’s internal estimate of cursor position and velocity:
| (8) |
where gt is the target position, is the user’s internal estimate of cursor position, is the user’s internal estimate of cursor velocity, and ftarg and fvel are piecewise-linear, one-dimensional weighting functions that are fit empirically to the data. Intuitively, this equation models ct as the sum of a point-at-target vector (scaled by the function ftarg) and a velocity damping vector (scaled by fvel) that points in the direction of the estimated cursor velocity. Note that, according to the model, the user does not have direct access to the true cursor position and velocity; instead, the user employs an “internal estimate” of cursor position and velocity made from delayed visual feedback and a forward model matched to the decoder dynamics. Thus, the PLM takes into account the effect of the user’s visual feedback delay on ct.
To use the PLM for intention estimation, we first fit the parameters of the PLM (ftarg and fvel) using the decoded population activity, Dft, observed during the calibration dataset. Parameters were fit to minimize . After fitting the model, we used the resultant time series of ct generated by the model as the calibration vectors.
In the original PLM study, movements were simulated entirely in two-dimensional state space and individual neural features were not simulated [22]. To use the PLM to generate simulated datasets that could be used for decoder calibration, we added simulated neural activity to the model. The simulated neural features were linearly tuned to the user’s motor command ct and were drawn from a multivariate normal distribution:
| (9) |
where ft is an N × 1 column vector of simulated neural features, H is an N × 2 matrix of tuning coefficients for each feature, and Q is an N × N covariance matrix. To define the simulated user’s control policy, we set fvel to zero (for simplicity) and took ftarg from the average ftarg curves depicted in [22]. We simulated a visual feedback delay of 300 ms.
H. Simulated Datasets
We used simulation to assess each intention estimation method’s ability to optimize the decoder’s gain and smoothing properties to match the task on which it was calibrated. For each simulated dataset, the neural tuning coefficient matrix H and noise covariance matrix Q were randomly generated. Each entry of H was drawn from a normal distribution with a mean of 0 and standard deviation of 1. Q was a diagonal matrix with each entry on the diagonal equal to 7x−1, where x was drawn from the exponential distribution with λ=0.5. These settings yielded a population-level neural signal quality approximately equal to that of participant T8. To initialize the decoder that was used to simulate the first block of closed-loop control, we first generated simulated open-loop data where the cursor automatically completed a center-out task (following a minimum jerk trajectory lasting 1 s). The corresponding motor commands ct were generated using the PLM.
Simulated neural activity was generated for the open-loop data according to a modified tuning matrix Hol that was equal to H plus a randomly generated context-dependence term for each entry (drawn from a normal distribution with a standard deviation of 0.75). This context-dependence term was included to simulate the known phenomenon that neural activity during open-loop tasks is different than neural activity during closed-loop tasks [23], [8], [9], and caused the closed-loop simulations to begin with a useable but imperfect decoder.
Once the decoder was initialized from open-loop data, we proceeded to simulate blocks of closed-loop movements for 8,000 time steps of data per block (time steps were 20 ms long, yielding 160 seconds of data). After each closed-loop block, the decoder was re-calibrated using data from the previous block. The target acquisition task followed the same center-out-back structure as it did with the participants, with the following parameters: target distance = 14 cm, dwell time = 1 s, maximum movement time = 10 s.
III. Results
A. Offline Analysis of Dimensionality Reduction Properties
We first examined how the outputs of the dimensionality reduction (DR) component of the Kalman filter (i.e. the Dft vectors) were affected by each intention estimation method. To do so, we calibrated Kalman filters offline with each intention estimation method, using data from 15 center-out-back sessions of closed-loop iBCI control from three participants (T6, T7, T8). When assessing the output of the dimensionality reduction step, we used 6-fold cross-validation to generate decoder output for each time step of hold-out data using a decoder that was calibrated using the remaining data.
Fig. 2A illustrates example cursor trajectories from one block with participant T6, and Fig. 2B illustrates the corresponding DR output of decoders calibrated with five different intention estimation methods. The DR output is remarkably similar across methods; both the underlying motor command (a large spike in the negative Y direction) and the noise (high frequency jitter in the time series) is conserved across all five methods. Note that the DR output is considerably noisier than the cursor velocity because it has not yet been smoothed by the Kalman filter’s smoothing dynamics. Note also that the DR output has normalized units (see methods section E for how the DR step was normalized).
Fig. 2.
Differences in the output of the Kalman filter’s dimensionality reduction (DR) step as a function of intention estimation method. (A) Example center-out and return-to-center cursor movements made by T6 (targets are drawn as black circles, movement trajectories as gray lines, and movement end points as black dots). The movement highlighted in red begins in the center of the workspace and proceeds downwards to acquire the bottom target, taking 2.2 seconds in total (including a 1 second dwell time). (B) The normalized DR output (i.e. the Dft vectors) during the movement highlighted in A for Kalman filters calibrated with different intention estimation methods (computed offline in a retrospective analysis). (C) Average correlations between the DR outputs of each Kalman filter (top) and the calibration vectors given by each intention estimation method (bottom) across all datasets (X and Y correlations are averaged together). The DR output is more highly correlated across methods than the calibration vectors themselves. (D) Average magnitude of the DR output (top) and the calibration vectors (bottom) as a function of target distance, after projecting onto a unit vector pointing from the cursor to the target. Block-specific curves were normalized so that their maximum magnitude was equal to 1 before averaging across all blocks. The calibration methods make very different assumptions from each other, but the average output of the decoder is nearly identical across all methods.
Fig. 2C summarizes the average correlations between the DR output of each method across all blocks for each participant. Correlations were generally high (>0.9) with the exception of the RawVel method, which differed more substantially from the other methods. In contrast to the DR output, the calibration vectors given by each intention estimation method were less correlated with each other (Fig. 2C, bottom). This shows that the similarity in DR output was not simply due to a comparable similarity in the calibration vectors. Instead, it suggests that the DR component of the Kalman filter is relatively insensitive to variations in the calibration vectors.
Next, we addressed the question: do the assumptions made about the user’s intent during decoder calibration shape the decoder output to be more like those assumptions? For example, if we assume that the magnitude of the user’s motor command declines linearly as the cursor approaches the target when calibrating the decoder (as assumed by the position error method), does the DR output obtained using that decoder also decline more linearly as the cursor approaches the target? To answer this question, we estimated how the magnitude of the DR output declined as the cursor approached the target for each method. To do so, we projected the DR output at each time step onto a unit vector pointing from the cursor to the target, and then averaged the magnitude of these projections as a function of target distance. The results, shown in Fig. 2D, indicate that the DR output is not substantially affected by the assumptions made during decoder calibration. Each decoder yields output with the same distance vs. magnitude curve regardless of what was assumed about the magnitude profile of the calibration vectors (the bottom row of Fig. 2D shows that many of these assumptions were quite different from each other).
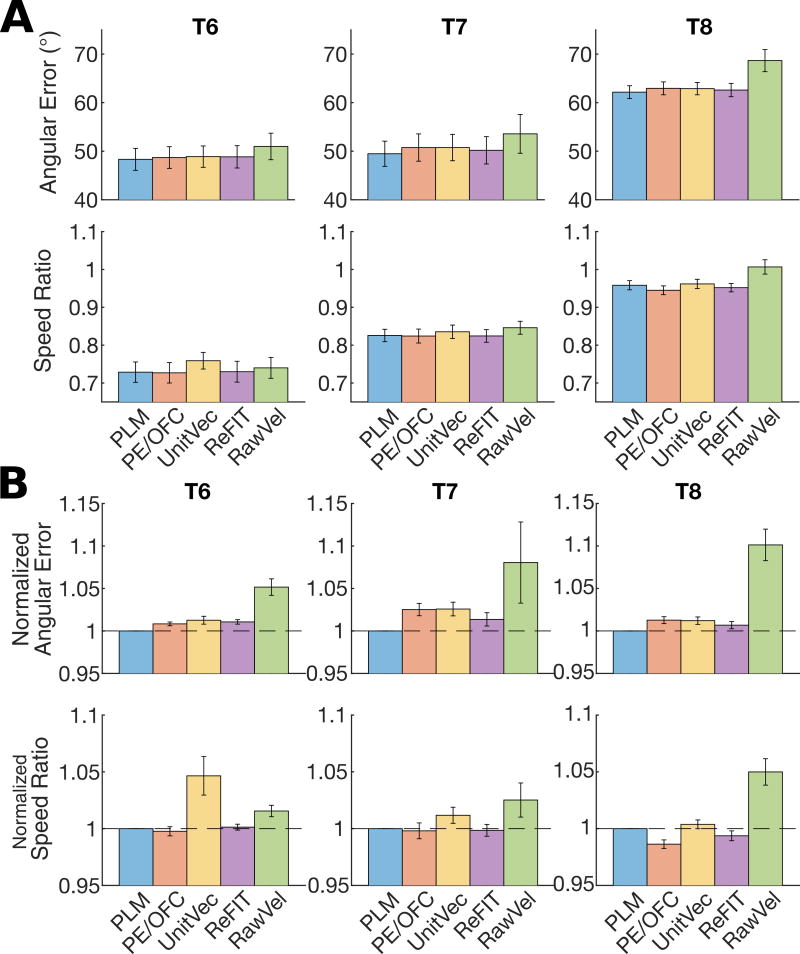
Finally, we analyzed how each intention estimation method affected the accuracy of the DR output using two metrics: angular error and speed ratio (Fig. 3). Angular error was computed assuming that the DR output should point directly at the target, using only time steps when the cursor was not touching the target (when there was a clear angular goal). Although the assumption that the DR output should point at the center of the target may not always be true (e.g. when the user must compensate for the cursor’s “momentum” [22]), we include it because it is a straightforward metric that is commonly used to evaluate decoder performance offline (e.g. [8]). We assessed the accuracy of the DR output magnitude by computing the “speed ratio” of the average DR output magnitude when the cursor was overlapping the target vs. when it was not (as used in [8]). Lower ratios imply a greater ability to decode small speeds when on top of the target and larger speeds when moving towards the target. The results, shown in Fig. 3, indicate that there are only small differences between the intention estimation methods (generally <5% difference in angular error and speed ratio) that are only clearly visible when normalizing within each block before comparing. The RawVel method is an outlier; it is consistently worse than the other methods in both metrics, especially in participant T8, whose neural signals had less movement information than T6 and T7.
Fig. 3.
Accuracy of the dimensionality reduction (DR) step of the Kalman filter as a function of intention estimation method. (A) DR accuracy is quantified by the average angular error of the DR output (absolute angular difference between the DR output and a vector that points straight from the cursor to the target) and by its speed ratio (the ratio of average DR output magnitude when the cursor is overlapping the target vs. when it is not). Lower values are better for both metrics. Bar heights show the mean across all blocks and error bars depict a 95% confidence interval. (B) A normalized version of the plots in A reveals subtle differences between the methods. Values were normalized within each block to the angular error or speed ratio of the PLM before averaging in order to facilitate comparisons across blocks with different noise characteristics. The dashed line is included to facilitate comparison to 1.
B. Online Performance Comparison of Dimensionality Reduction Properties
The offline results in Fig. 3 suggest that the differences in DR accuracy between the intention estimation methods are not large enough to cause substantial differences in online performance (with the exception of RawVel consistently performing significantly worse than the other methods). We confirmed this result online by comparing the closed-loop performance, under both low and high gains, of decoders built with each of three methods (UnitVec, ReFIT, and PLM). We did not have enough session time to test all five methods for an adequate number of trials, so we chose to focus on these three methods. For this comparison, the DR matrix of each decoder was allowed to vary, but the gain and smoothing properties were held constant across decoders. The smoothing parameter α was set to 0.96 and the gain parameter β was set to 8.8 cm/s for low gain blocks and 15.6 cm/s (T8) or 18.4 cm/s (T9) for high gain blocks.
To quantify the movement quality across calibration methods, we computed the mean translation time and dial-in time across all blocks within each condition (Fig. 4A). Translation time was defined as the time between the start of the movement (target appearance) and the first time the cursor touched the target. Dial-in time was defined as the time between when the cursor first touched the target and completion, minus the obligatory dwell time [8]. The mean dial-in times and translation times of the three decoders were very similar (all 95% confidence intervals overlapped) across the number of trials we collected (total of N=2,116 for T8 and N=954 for T9 across all blocks). There were also no substantial differences between the calibration methods in time course or movement accuracy that were consistent across participants and gain conditions (Fig. 4B). The fact that the performance was nearly equivalent across methods even at high gain, when both participants had trouble stopping on the target, indicates that the performance equivalency between methods was not trivially attributable to a performance ceiling effect.
Fig. 4.
Comparison of online performance under each of three intention estimation methods pooled across all low gain (β=8.8 cm/s) and high gain (β=15.6 or 18.4 cm/s) blocks when only the dimensionality reduction component of the decoder is allowed to vary. (A) Average translation time and dial-in time under each intention estimation method and each gain setting for T8 (top) and T9 (bottom). Error bars depict 95% confidence intervals for the mean. (B) Average distance vs. time curves for each intention estimation method and gain for T8 (top) and T9 (bottom). Shaded regions depict 95% confidence intervals. The curves are terminated at each method’s average movement time. Curves that level off above the target acquire edge indicate that the cursor is oscillating around the target instead of stopping precisely within the target region (Supplemental Section 4 shows example trajectories).
C. Offline Analysis of Gain and Smoothing Properties
In contrast to the relatively small differences we found in the DR output, we found that the gain and smoothing properties of the Kalman filter were strongly affected by the intention estimation method (Fig. 5A). However, the effect on gain was largely dominated by incidental differences in the magnitudes of the calibration vectors. For example, when using the unit vector method, all calibration vectors have a magnitude of 1, but when using the position error method their magnitudes range between 0 and the size of the workspace, which can be much larger or smaller than 1 depending on the units used to measure distance. A more meaningful comparison can be made across methods if the magnitudes of the calibration vectors are first standardized across methods, which we accomplished by normalizing by their average magnitudes (Fig. 5B).
Fig. 5.
(A) Average smoothing and gain properties of the Kalman filter for each calibration method. Bar heights show the average gain and smoothing properties across all blocks (with error bars depicting 95% confidence intervals). Substantial variations can be seen between methods; however, differences in gain are largely dominated by incidental differences in how each method determines the overall scale of the calibration vectors. (B) A more meaningful comparison can be made if the calibration vectors are first divided by their average magnitude, putting all methods into the same range. Substantial variations in gain and smoothing can still be seen between methods (e.g. gain differs by 50% between the UnitVec and ReFIT methods, even though the accuracy of their DR output differs by only a few percentage points).
Even when the calibration vectors were normalized, the average gain still varied across intention estimation methods by as much as 50% (e.g. compare UnitVec to ReFIT). Note also that decoders calibrated on data from different participants had different overall levels of gain and smoothing, possibly due to the different amounts of movement information in each participant’s neural signals. Lower neural signal qualities cause the Kalman filter to increase smoothing and decrease gain to minimize prediction error.
What causes the differences in gain and smoothing between methods? Ultimately the Kalman filter dynamics are determined by the state transition and observation models. We looked for differences in these models between methods and found that there was a high correlation between the fit quality (measured by the fraction of variance accounted for) of the state transition model and the amount of smoothing (r > 0.75; see Supplemental Section 5). In other words, intention estimation methods whose calibration vectors were more predictable across time caused the Kalman filter to add more smoothing. However, we found no such clear relationship for gain. This lack of clear relationship could be because the Kalman filter is related to the state and observation models through the algebraic Riccatti equation, which expresses nonlinear interactions between the state and observation models that may not always be straightforward.
D. Optimal Gain and Smoothing Values are Task Specific
Fig. 5 demonstrates that each intention estimation method has a different effect on gain and smoothing. How should these differences affect one’s choice of intention estimation method? When evaluating the DR output step, it is clear that lower angular errors and speed ratios are generally preferable (i.e. would lead to higher quality neural control). However, it is not as clear how to evaluate the relative utility of different gain and smoothing settings, especially given that different gain and smoothing settings might work better in different situations. For example, when precision is required (e.g. the targets are small), lower gains and higher smoothing values are better, while the opposite is true for situations in which speed is more important than precision. To demonstrate this contrast, we asked participant T8 to complete alternating center-out-back blocks of a “hard” task (target radius = 1.75 cm, dwell time = 1 s) and an “easy” task (target radius = 4 cm, dwell time = 0.5 s) using either an “easy-optimized” set of gain and smoothing parameters (β = 16.2 cm/s, α=0.93) or a “hard-optimized” set (β = 6.8 cm/s, α=0.96) (Fig. 6). As predicted, in the hard task, the lower gain and higher smoothing setting worked better by making it easier to hold on the targets, whereas in the easy task, the higher gain and lower smoothing parameters worked better by enabling faster movements.
Fig. 6.
Optimal gain and smoothing parameters depend on the task. Average movement time (the total time taken to acquire a target) and target acquisition success rate are shown for a “hard” and “easy” task while participant T8 used either an easy-optimal decoder (with a higher gain and lower smoothing value) or a hard-optimal decoder (with a lower gain and higher smoothing value). The “optimal” decoder parameters were chosen using the PLM to perform a simulated parameter sweep to minimize average movement time. The hard-optimal decoder enables slower but more accurate movements, which is better when the target radius is small and dwell time is long (“hard” task), but is worse when the radius is large and the dwell time is short (“easy” task). Error bars depict 95% confidence intervals for the mean.
Fig. 6 is consistent with prior work that suggested that the decoder’s gain and smoothing properties control a speed-accuracy tradeoff [26], [27]. For example, in one recent study [26], we demonstrated that translation time and dial-in time trade off as the decoder gain is varied. The movement time equation proposed and validated in [26] describes how the optimal tradeoff point depends on the target radius and distance.
E. Kalman Filter Calibration Fails to Optimize Gain and Smoothing in a Task-Specific Way
The differences in gain and smoothing parameters shown in Fig. 5 could be due to one of the two following causes: (1) each method arbitrarily biases the average gain and smoothing values differently irrespective of the task parameters, and/or (2) each method optimizes the gain and smoothing values in a task-specific way with varying degrees of success. Differences due solely to (1) leave no reason to prefer one intention estimation method over another, since the best gain and smoothing settings depend on the task. Although a certain method may perform best on task A if the gain and smoothing parameters it yields just happen to be optimal for task A, there is no reason it would generalize to a different task B.
On the other hand, in the case of (2), a stronger ability to adapt the gain and smoothing parameters to match the task used to obtain the calibration data would indeed be a valuable characteristic for an intention estimation method to possess. However, we do not necessarily expect (2) to be the case, since the Kalman filter calibration process does not explicitly take into account task parameters (e.g. target radius and dwell time do not enter into the Kalman filter calibration equations at any point).
For completeness, we used computer simulation to test rigorously whether it could be the case that certain intention estimation methods optimize the gain and smoothing parameters for the task used to obtain the calibration data. Simulation allowed us to test this idea in an exhaustive way and under the most favorable conditions where the neural tuning assumptions and movement intentions match the intention estimation method exactly. Simulation also enabled us to know with certainty what the optimal gain and smoothing values are for any particular task and simulated user (via an exhaustive simulated search).
In Fig. 7A, we simulated the closed-loop calibration process for a set of tasks with different target radii, using the PLM to simulate the user (where neural features were linearly tuned to ct). Kalman filters were calibrated with each intention estimation method using an initial open-loop dataset, and were then re-calibrated using data from a closed-loop block collected with the initial open-loop filter. The calibration vectors produced by the PLM, PE/OFC and UnitVec methods were scaled so that their maximum speed was 14 cm/s to give a reasonable range of values for the simulated datasets (ReFIT and RawVel did not require scaling because their magnitudes match the cursor speeds from the calibration dataset, which are already in a reasonable range).
Fig. 7.
A simulation analysis demonstrating that no intention estimation method properly optimizes the gain and smoothing parameters of the Kalman filter to match the task requirements. (A) Re-calibration on a specific task does not yield gain values more optimal for that task. Gain and smoothing values are shown for each calibration method as a function of target radius. Though lower gains and higher smoothing values would be more beneficial for smaller radii, gain stays constant or increases slightly for smaller radii and smoothing only increases slightly. Methods that yield higher overall gain values perform better for larger target radii (shorter movement times) and worse for smaller target radii (longer movement times). (B) Continuing the re-calibration process for more iterations does not cause the gain and smoothing values to converge towards the optimal ones. The result of a continued re-calibration process is shown for a target radius of 1.75.
The results in Fig. 7A indicate that no method is able to adjust the gain and smoothing values correctly to account for the target radius. This is true even for the PLM method, whose assumptions matched the simulated user exactly. In Fig. 7B, we allow the re-calibration process to continue for several more iterations, to test whether eventually, any of the methods optimize the gain and smoothing for the task being used for calibration. Generally, the gain and smoothing values settle to some non-optimal value. Interestingly, for methods that use the originally decoded speeds to set the speed of the calibration vectors (ReFIT and RawVel), the gain actually declines over time and approaches zero. This is probably because the Kalman filter predicts slightly lower speeds on average than the speeds that are present in the calibration vectors (in order to minimize the effect of noise on prediction error).
IV. Discussion
A. Overview
We characterized the effect of five different intention estimation methods on the closed-loop calibration of steady-state velocity Kalman filter decoders. Contrary to our expectations, the accuracy of the Kalman filter’s dimensionality reduction component was largely unaffected by the intention estimation method (Figs. 2–4). The one exception was calibrating using the originally decoded velocity vectors, which caused the resultant decoders to be substantially less accurate than decoders calibrated using the other methods, consistent with prior reports [8], [10]. In contrast, the different intention estimation methods had a large effect on the gain and smoothing properties of the Kalman filter (Fig. 5). Taken together, these results show that regardless of the assumptions that were made about the user’s intended movement during calibration, the decoder output was essentially the same set of vectors but with different amounts of scaling and smoothing applied. We showed that this difference in scaling and smoothing was largely arbitrary, with different methods biasing the mean gain and smoothing values in different ways but failing to optimize them appropriately in a task-specific manner (Fig. 7).
B. Results Contrary to Expectations
Our results were not entirely expected. We demonstrated in an earlier study that the piecewise-linear feedback control model (PLM) described the user’s intent (neural population activity) significantly better than ReFIT and PE/OFC and at more time points than UnitVec [22]. Here, we expected this improved fidelity to translate into a meaningful performance benefit for decoder calibration. Instead, we found that even though the PLM described user intent significantly better (for example, explained on average > 10% more variance in the user’s population activity than PE/OFC [22]), this improvement did not translate into > 10% decoder performance differences when the PLM was used for decoder calibration. Thus, using a more accurate description of the user’s intent when calibrating a decoder does not necessarily translate into higher decoding performance. Furthermore, we found that the average output of the dimensionality reduction step was essentially identical across intention estimation methods despite large differences in their assumptions. For example, assuming a linear decline in speed as the cursor approached the target (as done by the PosErr method) did not cause the decoded speed to decline more linearly.
Spurious differences in gain and smoothing aside, our results indicate that the calibration of Kalman filters is not very sensitive to assumptions about the user’s intent and that even very simple methods are sufficient for high performance (e.g. PosErr). Note that this equivalence between decoders was not the result of online adaptation by the user – it was present for offline results as well (Figs. 2–3). How, then, can we account for prior reports that suggested a more substantial difference between decoders calibrated with different intention estimation methods [8], [10], [11]? These results could be explained by our finding that each intention estimation method biases the gain and smoothing properties of the decoder differently, which in turn could bias the result of an online performance comparison towards whichever method happens to yield better parameters for the specific task used to evaluate performance. However, this difference in performance would not be reflective of any meaningful difference between the methods, because it would not be expected to generalize to tasks with different parameters.
C. Task-Specific Optimization of Gain and Smoothing
The optimal gain and smoothing properties for a steady-state Kalman filter depend on the task parameters (e.g. target radius, dwell time, etc.), as demonstrated in Fig. 6 and implied by previous work [26], [27]. Interestingly, we found that the standard closed-loop recalibration process was almost completely unable to customize the decoder’s gain and smoothing properties to appropriately match the task parameters regardless of what intention estimation method was used (Fig. 7).
If standard methods cannot optimize the decoder dynamics, then what can? A trial and error approach could be used, but would be time consuming, and would have to be redone whenever the task or the quality of the user’s neural signals changed. An alternative approach could be to model the process of closed-loop control so that the online effects of gain and smoothing can be simulated and predicted ahead of time. In theory, the PLM is capable of accurately simulating online performance for a specific user and gain/smoothing parameter set. The results from Fig. 6, in which the PLM was used to find optimal gain and smoothing values for two different tasks, are promising; we are currently exploring this simulation-based approach in greater detail.
D. Extension to Different Decoding Architectures and End Effectors
We found that the Kalman filter’s gain and smoothing properties were very sensitive to the intention estimation method used. Decoders with more general dynamics (e.g. a Wiener filter [13], [28], [29] or a neural network [30]–[33]), might be even more sensitive to the intention estimation method because they are capable of expressing a wider range of filtering properties. Care should be taken to ensure that the effect of the calibration vectors on the decoder dynamics is consistent with what was intended, or to reparametrize the decoder so that the dynamics can be explicitly controlled and matched to the task demands.
Though we found that the Kalman filter’s dimensionality reduction step is relatively insensitive to the intention estimation method, it is possible that this result will not generalize to nonlinear decoders. To understand this, consider that a linear decoder can only decode a linearly distorted (scaled, skewed, or rotated) version of whatever is encoded in the neural activity. For example, suppose that the user’s motor command varies in magnitude throughout a movement but the calibration vectors are all of unit magnitude (which is true for the unit vector method). Then the calibrated decoder, if it is linear, will still decode a command that varies in magnitude, because a linear transformation is not flexible enough to clamp the magnitude at a constant value (as shown in Fig. 2D). A nonlinear decoder, however, may learn to apply a magnitude clamping operation in order to better match the calibration vectors, causing its dimensionality reduction step to be substantially altered.
We constrained the scope of our study to examine only two-dimensional cursor movements. Can one expect similar results for different end effectors, for example a three-dimensional robotic arm [1], [2]? We believe so, as long as a vector pointing from the current effector position to the target effector position remains a reasonable approximation of the user’s feedback control policy for generating motor commands. All calibration methods we tested worked by generating such a point-at-target vector, and the differences between them (e.g. differences in how the magnitude of that vector was determined or small differences in angle) did not seem to have a large effect on the resultant decoder. For situations where a point-at-target vector may be a poor approximation of the user’s intended motor command (for example, when the decoder requires the user to control joint torques instead of velocity [34], [35]), a different intention estimation method may be needed. A feedback control approach could be useful for developing such a method [11], [22].
V. Conclusion
Our results resolve an open question in the literature about the impact of different intention estimation methods on linear decoder properties and performance. We showed that decoders calibrated using simple intention estimation methods (e.g. a position error vector) perform as well as those calibrated using more involved methods, suggesting that further refinement of our ability to estimate the user’s true motor intent may not yield a large decoder performance benefit (at least for 2D Kalman filters). Our results also caution against comparing the online performance of decoders without controlling for the gain and smoothing properties of the candidate decoders (or without separately optimizing them in a task-specific way). If not accounted for, these relatively “superficial” decoder properties can dominate a performance comparison since they have a large effect on online performance [19], [27], [36], [26]. Finally, our simulation results suggest a need for alternative approaches to decoder calibration that can better optimize the decoder dynamics (e.g. gain and smoothing properties), since standard calibration methods seem almost completely unable to optimize them in a way that is sensitive to the task parameters.
Supplementary Material
Acknowledgments
We thank participants T6, T7, T8, T9 and their caregivers and families.
Funding for this work was provided by: NSF GRFP, DGE-0951783; Office of Research and Development, Rehabilitation R&D Service, Department of Veterans Affairs (N9288C, B6453R, A6779I, P1155R); Eunice Kennedy Shriver National Institute of Child Health & Human Development NICHD (R01HD077220), NICHD-NCMRR (N01HD10018), NICHD (N01HD53403); The US National Institutes of Health - National Institute on Deafness and Other Communication Disorders NIDCD (R01DC014034), NIDCD (R01DC009899); MGH-Deane Institute; The Executive Committee on Research (ECOR) of Massachusetts General Hospital; Movement Disorders Foundation; Stanford BioX-NeuroVentures; Larry and Pamela Garlick; Samuel and Betsy Reeves; the Craig H. Neilsen Foundation.
References
- 1.Hochberg LR, et al. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature. 2012 May;485(7398):372–375. doi: 10.1038/nature11076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Collinger JL, et al. High-performance neuroprosthetic control by an individual with tetraplegia. The Lancet. 2013 Feb.381(9866):557–564. doi: 10.1016/S0140-6736(12)61816-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gilja V, et al. Clinical translation of a high-performance neural prosthesis. Nat Med. 2015 Oct.21(10):1142–1145. doi: 10.1038/nm.3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jarosiewicz B, et al. Virtual typing by people with tetraplegia using a self-calibrating intracortical brain-computer interface. Sci Transl Med. 2015 Nov.7(313):313ra179–313ra179. doi: 10.1126/scitranslmed.aac7328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ajiboye AB, et al. Restoration of reaching and grasping movements through brain-controlled muscle stimulation in a person with tetraplegia: a proof-of-concept demonstration. The Lancet. 2017 May;389(10081):1821–1830. doi: 10.1016/S0140-6736(17)30601-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Taylor DM, Tillery SIH, Schwartz AB. Direct Cortical Control of 3D Neuroprosthetic Devices. Science. 2002 Jun.296(5574):1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- 7.Orsborn A, Dangi S, Moorman H, Carmena J. Closed-Loop Decoder Adaptation on Intermediate Time-Scales Facilitates Rapid BMI Performance Improvements Independent of Decoder Initialization Conditions. IEEE Trans Neural Syst Rehabil Eng. 2012 doi: 10.1109/TNSRE.2012.2185066. [DOI] [PubMed] [Google Scholar]
- 8.Gilja V, et al. A high-performance neural prosthesis enabled by control algorithm design. Nat Neurosci. 2012 Dec.15(12):1752–1757. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jarosiewicz B, et al. Advantages of closed-loop calibration in intracortical brain-computer interfaces for people with tetraplegia. J Neural Eng. 2013 Aug.10(4):46012. doi: 10.1088/1741-2560/10/4/046012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fan JM, Nuyujukian P, Kao JC, Chestek CA, Ryu SI, Shenoy KV. Intention estimation in brain-machine interfaces. J Neural Eng. 2014 Feb.11(1):16004. doi: 10.1088/1741-2560/11/1/016004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shanechi MM, Orsborn AL, Carmena JM. Robust Brain-Machine Interface Design Using Optimal Feedback Control Modeling and Adaptive Point Process Filtering. PLoS Comput Biol. 2016;12(4):e1004730. doi: 10.1371/journal.pcbi.1004730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pandarinath C, et al. High performance communication by people with paralysis using an intracortical brain-computer interface. eLife. 2017 doi: 10.7554/eLife.18554. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Brain-machine interface: Instant neural control of a movement signal. Nature. 2002;416(6877):141–142. doi: 10.1038/416141a. [DOI] [PubMed] [Google Scholar]
- 14.Carmena JM, et al. Learning to Control a Brain–Machine Interface for Reaching and Grasping by Primates. PLoS Biol. 2003;1(2):e2. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hochberg LR, et al. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006 Jul.442(7099):164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- 16.Velliste M, Perel S, Spalding MC, Whitford AS, Schwartz AB. Cortical control of a prosthetic arm for self-feeding. Nature. 2008 May;453(7198):1098–1101. doi: 10.1038/nature06996. [DOI] [PubMed] [Google Scholar]
- 17.Chase SM, Schwartz AB, Kass RE. Bias, optimal linear estimation, and the differences between open-loop simulation and closed-loop performance of spiking-based brain-computer interface algorithms. Neural Netw Off J Int Neural Netw Soc. 2009 Nov.22(9):1203–1213. doi: 10.1016/j.neunet.2009.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li Z, O’Doherty JE, Hanson TL, Lebedev MA, Henriquez CS, Nicolelis MAL. Unscented Kalman Filter for Brain-Machine Interfaces. PLoS ONE. 2009 Jul.4(7):e6243. doi: 10.1371/journal.pone.0006243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Koyama S, Chase SM, Whitford AS, Velliste M, Schwartz AB, Kass RE. Comparison of brain-computer interface decoding algorithms in open-loop and closed-loop control. J Comput Neurosci. 2010 Aug.29(1–2):73–87. doi: 10.1007/s10827-009-0196-9. [DOI] [PubMed] [Google Scholar]
- 20.Shanechi MM, Williams ZM, Wornell GW, Hu RC, Powers M, Brown EN. A real-time brain-machine interface combining motor target and trajectory intent using an optimal feedback control design. PloS One. 2013;8(4):e59049. doi: 10.1371/journal.pone.0059049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nuyujukian P, Fan JM, Kao JC, Ryu SI, Shenoy KV. A high-performance keyboard neural prosthesis enabled by task optimization. IEEE Trans Biomed Eng. 2015 Jan.62(1):21–29. doi: 10.1109/TBME.2014.2354697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Willett FR, et al. Feedback control policies employed by people using intracortical brain–computer interfaces. J Neural Eng. 2017 Feb.14(1):16001. doi: 10.1088/1741-2560/14/1/016001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kim S-P, Simeral JD, Hochberg LR, Donoghue JP, Black MJ. Neural control of computer cursor velocity by decoding motor cortical spiking activity in humans with tetraplegia. J Neural Eng. 2008 Dec.5(4):455–476. doi: 10.1088/1741-2560/5/4/010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sadtler PT, et al. Neural constraints on learning. Nature. 2014 Aug.512(7515):423–426. doi: 10.1038/nature13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Simeral JD, Kim S-P, Black MJ, Donoghue JP, Hochberg LR. Neural control of cursor trajectory and click by a human with tetraplegia 1000 days after implant of an intracortical microelectrode array. J Neural Eng. 2011 Apr.8(2):25027. doi: 10.1088/1741-2560/8/2/025027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Willett FR, et al. Signal-independent noise in intracortical brain–computer interfaces causes movement time properties inconsistent with Fitts’ law. J Neural Eng. 2017;14(2):26010. doi: 10.1088/1741-2552/aa5990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gowda S, Orsborn AL, Overduin SA, Moorman HG, Carmena JM. Designing Dynamical Properties of Brain-Machine Interfaces to Optimize Task-Specific Performance. IEEE Trans Neural Syst Rehabil Eng. 2014 Sep.22(5):911–920. doi: 10.1109/TNSRE.2014.2309673. [DOI] [PubMed] [Google Scholar]
- 28.Fagg AH, Ojakangas GW, Miller LE, Hatsopoulos NG. Kinetic Trajectory Decoding Using Motor Cortical Ensembles. IEEE Trans Neural Syst Rehabil Eng. 2009 Oct.17(5):487–496. doi: 10.1109/TNSRE.2009.2029313. [DOI] [PubMed] [Google Scholar]
- 29.Willett FR, Suminski AJ, Fagg AH, Hatsopoulos NG. Improving brain–machine interface performance by decoding intended future movements. J Neural Eng. 2013 Apr.10(2):26011. doi: 10.1088/1741-2560/10/2/026011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Burrow M, Dugger J, Humphrey DR, Reed DJ, Hochberg LR. Cortical Control of a Robot Using a Time-delay Neural Network. in Proceedings of International Conference on Rehabilitation Robotics ICORR. 1997:83–86. [Google Scholar]
- 31.Wessberg J, et al. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000 Nov.408(6810):361–365. doi: 10.1038/35042582. [DOI] [PubMed] [Google Scholar]
- 32.Sussillo D, et al. A recurrent neural network for closed-loop intracortical brain–machine interface decoders. J Neural Eng. 2012 Apr.9(2):26027. doi: 10.1088/1741-2560/9/2/026027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sussillo D, Stavisky SD, Kao JC, Ryu SI, Shenoy KV. Making brain–machine interfaces robust to future neural variability. Nat Commun. 2016 Dec;7 doi: 10.1038/ncomms13749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Suminski AJ, Willett FR, Fagg AH, Bodenhamer M, Hatsopoulos NG. Continuous decoding of intended movements with a hybrid kinetic and kinematic brain machine interface. Conf Proc Annu Int Conf IEEE Eng Med Biol Soc IEEE Eng Med Biol Soc Conf. 2011;2011:5802–5806. doi: 10.1109/IEMBS.2011.6091436. [DOI] [PubMed] [Google Scholar]
- 35.Chhatbar PY, Francis JT. Towards a Naturalistic Brain-Machine Interface: Hybrid Torque and Position Control Allows Generalization to Novel Dynamics. PLoS ONE. 2013 Jan.8(1):e52286. doi: 10.1371/journal.pone.0052286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Marathe AR, Taylor DM. The impact of command signal power distribution, processing delays, and speed scaling on neurally-controlled devices. J Neural Eng. 2015 Aug.12(4):46031. doi: 10.1088/1741-2560/12/4/046031. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.