Abstract
Diffusion microstructural imaging techniques have attracted great interest in the last decade due to their ability to quantify axon diameter and volume fraction in healthy and diseased human white matter. The estimates of compartment size and volume fraction continue to be debated, in part due to the lack of a gold standard for validation and quality control. In this work, we validate diffusion MRI estimates of compartment size and volume fraction using a novel textile axon (“taxon”) phantom constructed from hollow polypropylene yarns with distinct intra- and extra-taxonal compartments to mimic white matter in the brain. We acquired a comprehensive set of diffusion MRI measurements in the phantom using multiple gradient directions, diffusion times and gradient strengths on a human MRI scanner equipped with maximum gradient strength (Gmax) of 300 mT/m. We obtained estimates of compartment size and restricted volume fraction through a straightforward extension of the AxCaliber/ActiveAx frameworks that enables estimation of mean compartment size in fiber bundles of arbitrary orientation. The voxel-wise taxon diameter estimates of 12.2 ± 0.9 µm were close to the manufactured inner diameter of 11.8 ± 1.2 µm with Gmax = 300 mT/m. The estimated restricted volume fraction demonstrated an expected decrease along the length of the fiber bundles in accordance with the known construction of the phantom. When Gmax was restricted to 80 mT/m, the taxon diameter was overestimated, and the estimates for taxon diameter and packing density showed greater uncertainty compared to data with Gmax=300 mT/m. In conclusion, the compartment size and volume fraction estimates resulting from diffusion measurements on a human scanner were validated against ground truth in a phantom mimicking human white matter, providing confidence that this method can yield accurate estimates of parameters in simplified but realistic microstructural environments. Our work also demonstrates the importance of a biologically analogous phantom that can be applied to validate a variety of diffusion microstructural imaging methods in human scanners and be used for standardization of diffusion MRI protocols for neuroimaging research.
Keywords: Diffusion, microstructure, phantom validation, AxCaliber, q-space, Human Connectome Project
Introduction
Diffusion microstructural imaging techniques have attracted great interest in the last decade due to their ability to quantify axon diameter and volume fraction in healthy and diseased human white matter. The estimation of compartment size and packing density by diffusion MRI continues to be debated, in part due to the lack of a gold standard for validation and quality control. The validation of tissue parameter estimates obtained from diffusion MRI is especially timely as model-based diffusion MRI techniques are increasingly adopted for large-scale population studies (Miller et al., 2016) and clinical trials (Mallik et al., 2014; Winston et al., 2014). Comparison of the derived estimates against reference measurements is essential to refining tissue compartment models of the underlying fiber architecture and standardizing diffusion MRI acquisitions for multi-center trials.
Several approaches have been taken to validate the metrics obtained from a variety of diffusion MRI methods ranging from fiber tractography to compartment size mapping, including the use of software phantoms (Balls and Frank, 2009; Close et al., 2009; Hall and Alexander, 2009; Leemans et al., 2005; Tournier et al., 2002), ex vivo samples (Dyrby et al., 2011; Kim et al., 2005; Miller et al., 2012), and physical phantoms (Farrher et al., 2012; Fieremans et al., 2008b; Fillard et al., 2011; Hubbard et al., 2015; Perrin et al., 2005). Software phantoms offer the greatest degree of control regarding the composition of substrates but are limited by assumptions in the process of data synthesis and may lack the realism of physical tissues. Ex vivo samples come from real tissue, provide the realism of tissue complexity and enable long scan times that are not feasible for in vivo experiments, and thus are widely used in validation of biophysical models (Assaf et al., 2008b; Dyrby et al., 2013; Xu et al., 2014; Xu et al., 2016). But the process of fixation alters the physical properties of tissue, to the point that the sample composition may not accurately reflect in vivo properties. Ex vivo tissues are known to undergo alterations that are reflected in diffusion MRI experiments, such as lower diffusivity (McNab et al., 2009; Sun et al., 2005), lower fractional anisotropy (Shepherd et al., 2009a), compartment size changes (Shepherd et al., 2009b), and tissue deformation and shrinkage (Wehrl et al., 2015). Physical phantoms that mimic biological tissues, usually with a simplified representation, can address some of the above limitations. It is clear that physical phantoms cannot replace ex vivo samples in revealing the actual composition of real tissue. Nevertheless, physical phantoms can serve as a bridge between the software phantoms (simulations) and biological tissues and thus remain invaluable for the development and validation of in vivo quantitative diffusion MRI methods, especially if they could be constructed to mimic biological structures and be externally validated with invasive methods such as electron microscopy without the undesirable tissue changes often occurring in ex vivo samples over time.
A number of physical phantoms have been previously described for validating and standardizing diffusion MRI measurements (Bach et al., 2014; Fieremans et al., 2008b; Fillard et al., 2011; Gatidis et al., 2014; Poupon et al., 2008; Pullens et al., 2010; Reischauer et al., 2009). Most of these phantoms are constructed with water between solid filaments and are thus only able to mimic the extra-axonal space. While these phantoms do demonstrate diffusion anisotropy and are useful in validating diffusion tractography methods, they fall short in assessing compartment-specific diffusion models that attempt to obtain information regarding compartment size and relative fractions of intra- and extra-axonal water. More recently, several methods have been proposed to achieve compartment-specific water pools by constructing pores in various types of media. For example, a glass capillary array wafer technique was used to construct regularly spaced pore structures with uniform inner diameters between 5–82 µm (Komlosh et al., 2017; Komlosh et al., 2011; Yanasak and Allison, 2006). The glass capillary array phantoms were used to validate diffusion MRI methods of pore size estimation using single and double pulsed field gradient experiments (Komlosh et al., 2017). Other approaches include creating a “honeycomb” structure inside polymer based materials (Hubbard et al., 2015) and the creation of channels inside silicon-based organic polymers (Ebrahimi et al., 2010). These phantoms show varying degrees of diffusion anisotropy in diffusion tensor imaging experiments, depending on the pore sizes and densities. Porous phantoms are promising in validating estimates of compartment size but lack the extracellular compartment to be truly reflective of extra-axonal hindered diffusion. Recently, a biomimetic phantom constructed of hollow polypropylene filaments filled with water was proposed (Guise et al., 2014; Guise et al., 2016). The hollow fibers separate the water pool inside the filaments from that outside the filaments and more closely mimic intra-axonal and extra-axonal compartments expected in white matter. To our knowledge, the hollow polypropylene yarn phantom provides the closest representation of white matter microstructure among existing phantoms.
Typically, diffusion within white matter in the brain is modeled as a combination of intraaxonal restricted diffusion, extra-axonal hindered diffusion and isotropic free diffusion arising from cerebrospinal fluid (Alexander et al., 2010; Assaf and Basser, 2005; Assaf et al., 2008a; Assaf et al., 2004; Barazany et al., 2009). These approaches include the composite hindered and restricted model of diffusion (CHARMED), which estimated the fraction of restricted and hindered water based on a priori assumptions regarding the underlying distribution of axon diameters in white matter (Assaf and Basser, 2005; Assaf et al., 2004). The AxCaliber approach (Assaf et al., 2008a) expanded upon the CHARMED model (Assaf and Basser, 2005; Assaf et al., 2004) to fit a gamma distribution of axon diameters based on the known orientation of white matter within certain tracts, such as the spinal cord and corpus callosum (Assaf et al., 2008a; Barazany et al., 2009). The ActiveAx technique generalized the original AxCaliber experimental paradigm to obtain a single axon diameter index in fiber bundles of arbitrary orientation using an optimized protocol with only a few shells of varying diffusion-weighting parameters and gradient directions (Alexander et al., 2010). The higher gradient strengths now available on human MRI scanners (Setsompop et al., 2013) have improved the sensitivity of axon diameter mapping methods to smaller diameter axons for in vivo imaging in both healthy subjects (Duval et al., 2015; Dyrby et al., 2013; Huang et al., 2015a; McNab et al., 2013) and disease populations such as patients with multiple sclerosis (Huang et al., 2016). Validation of axon diameter and volume fraction estimates provided by AxCaliber and related techniques on human scanners is a necessary step toward translation of methods targeted at in vivo estimation of axon diameter and density.
In this work, we validate estimates of compartment size and volume fraction using a biomimetic brain phantom constructed from hollow polypropylene yarns with biologically meaningful diameters arrayed in fiber bundles of varying direction and packing density. We acquire a comprehensive set of diffusion MRI measurements in the phantom using multiple gradient directions, diffusion times and gradient strengths on a human MRI scanner equipped with gradient strengths up to 300 mT/m. The compartment size and density were estimated through a straightforward extension of the AxCaliber framework that enables estimation of mean compartment size in fiber bundles of arbitrary orientation, similar in spirit with ActiveAx (Alexander et al., 2010). The estimates of compartment size and packing density are compared against ground truth based on the known construction of the hollow fiber phantom. We have also acquired a comparable dataset with gradient strengths up to 80 mT/m (equivalent to Siemens Prisma capabilities) to explore the impact of gradient strength on the performance of the proposed approach using the same phantom for validation.
Methods
Phantom composition
The current phantom prototype was designed with several modules (i.e., layers) for multiple purposes, including T1, T2 and diffusion calibrations, and the overall packing measures about 20×20×30 cm (Fig. 1A, where only the diffusion layer was illustrated). In the diffusion module, the fiber substrates were constructed from hollow multifilament polypropylene yarns produced by a melt-spinning extrusion technique to generate textile axons (“taxons”) with inner diameter (ID) of 11.8±1.2 µm and outer diameter (OD) of 33.5±2.3 µm (Fig. 1E) (Guise et al., 2016) (Psychology Software Tools, Inc., Sharpsburg, Pennsylvania). The taxons were arranged in parallel and crossing geometries within 3D-printed placeholders mounted in the phantom (Fig. 1A). Parallel fiber bundles were placed within 6 rectangular chambers, which had different dimensions. Each chamber had 4 “steps” of different depths (Fig. 1C) to achieve different fiber packing densities along the length of the fiber bundle (Fig. 1D). The sizes of the 6 chambers (in narrowest dimension) were: 10 mm × 10 mm =100 mm2, 8.9 mm × 8.9 mm = 80 mm2, 7.74 mm × 7.74 mm = 60 mm2, 6.32 mm × 6.32 mm = 40 mm2, 4.47 mm × 4.47 mm = 20 mm2, and 3.16 mm × 3.16 mm = 10 mm2, which were filled with 112640 (100%), 90112 (80%), 67584 (60%), 45056 (40%), 22528 (20%) and 11264 (10%) taxon fibers, respectively, to achieve an identical range of packing densities in each chamber. While there is no theoretical limit in the manufactured size of the chambers, the practical upper limit was 10 mm due to a labor-intensive filling and verification process. Fiber crossings of 90°, 45° and 30° were created by interleaving the polypropylene filaments in separate 3D printed placeholders (Fig. 1F, G).
Revised Figure 1.
Phantom composition. (A) Diagram of the phantom, which measures 24.8 cm from top of the dome to top of the base and 19 cm in diameter. The taxon holder inside the phantom was 3D-printed, and the central piece was outlined in purple with a three-dimensional schematic inset shown in (B). An “axial” cross-section (outlined in red) is shown to reveal the internal structure of the individual chambers. Each chamber has 4 “steps” along the length of the chamber to achieve variable packing densities. A “sagittal” cross section (see plane labeled in black in B) was shown in (C), where taxon fibers ran along the length of the chamber, so that a wider depth in the chamber yielded a lower packing density. (D) Scanning electron micrographs (SEM, obtained with 220× magnification) of the taxon fiber bundles with different packing densities (numbers correspond to the sections of the chamber numbered in C). (E) A zoomed-in view of the SEM showing the size of the taxons (ID 11.8 ± 1.2 µm, OD 33.5±2.3 µm). (F) An overview of the diffusion phantom shown with a GRE image. (G) A colored FA map demonstrating principal diffusion directions. An x-y-z coordinate system is labeled on subfigures to assist in orienting the reader, where x, y, and z correspond to the left, posterior and superior directions, respectively, in the magnet.
The phantom was filled with distilled water by pressure filling. Specifically, the filling was done through a multistage industrial process by the supplying firm Psychology Software Tools Inc. The fibers were put in silicone, and degassed filtered water was applied under high pressure on one end. The other end was immersed in oil. The pressure filling produced micro bubbles that came out of the fibers on the other end. Filling was verified by observing water exiting the taxons via light microscope. Verified fill rates were in the 85–90% range. To maximize stability of the phantom, it was stored on a shelf at room temperature in a vertical standing position.
MRI experiments
All scans were performed on the dedicated high-gradient 3T CONNECTOM MRI system with maximum gradient strength of 300 mT/m using a Siemens product 20-channel head-neck coil. The phantom was placed in the magnet so that the axes of taxon fibers were oriented perpendicular to the static magnetic field (see Fig. 1 and x-y-z coordinate labels). During the experiment, the temperature of the scanning room was kept constant at 25°C. Airflow inside the magnet bore was used throughout the scan.
The imaging protocol was similar to our previous in vivo human study (Huang et al., 2015a), but more comprehensive to take the advantage of being free of time constraints in phantom scanning. For the Gmax=300mT/m dataset, a series of 2-mm isotropic resolution axial diffusion-weighted spin echo echo planar images (EPI) were acquired in the phantom using the following parameters: TR/TE = 4100/110ms, gradient strength Gmax = 300 mT/m, and diffusion gradient pulse duration δ = 8 ms. Given an expected taxon inner diameter of 12 µm, diffusion times of Δ = 20, 30, 40, and 50 ms were sampled, which correspond to mean diffusion displacements of 9–15 µm, respectively, assuming a longitudinal diffusivity of 2.2×10−9 m2/s (see Data Analysis for details on calculation of the longitudinal diffusivity for the phantom used in this study). Data were collected with 256 non-collinear diffusion-encoding gradient directions, which were evenly distributed on a sphere, with 20 interspersed b=0 images. Another dataset with Gmax=80mT/m dataset was acquired in a similar manner for comparison. The voxel size, TR/TE, δ/Δ, and diffusion direction sets were all kept the same, except that the gradient strength sampling was scaled down and capped at Gmax = 80 mT/m. As a result, for each diffusion time in the Gmax=300mT/m dataset, the gradient strength linearly varied from 24 to 290 mT/m to produce b-values ranging between 50 to 18,250 s/mm2, and for the Gmax=80mT/m dataset, the gradient strength ranged from 17 to 80 mT/m with a range of b-values of 50 to 1400 s/mm2 (Table 1). Data were acquired in both anterior to posterior and posterior to anterior phase encoding directions to correct for image distortions due to susceptibility artifact. The total acquisition time was about 38 hours. Other imaging parameters included a field-of-view of 256×256 mm, partial Fourier of 6/8, and receive bandwidth of 1148 Hz/pixel. A regular non-accelerated EPI sequence was used to minimize parallel imaging artifact.
Table 1.
Diffusion-weighting parameters for experimental data
| Gmax = 290 mT/m | |||
|
| |||
| Diffusion times at each q-value (Δ, ms) | Gradient strength (mT/m) | Range of q-value in µm−1 (# of q-values) | Range of b-value (s/mm2) |
|
| |||
| 20 | 25.1 – 290.5 | 0.009 – 0.1 (8) | 50 – 6700 |
| 30 | 28.3 – 289.6 | 0.010 – 0.1 (8) | 100 – 10500 |
| 40 | 24.2 – 290.2 | 0.008 – 0.1 (8) | 100 – 14400 |
| 50 | 26.3 – 290.1 | 0.009 – 0.1 (8) | 150 – 18250 |
|
| |||
| Gmax = 80 mT/m | |||
|
| |||
| Diffusion times at each q-value (Δ, ms) | Gradient strength (mT/m) | Range of q-value in µm−1 (# of q-values) | Range of b-value (s/mm2) |
|
| |||
| 20 | 25.1 – 79.5 | 0.009 – 0.27 (6) | 50 – 500 |
| 30 | 20.0 – 80.1 | 0.007 – 0.27 (7) | 50 – 800 |
| 40 | 17.1 – 80.3 | 0.006 – 0.27 (7) | 50 – 1100 |
| 50 | 21.5 – 80.5 | 0.007 – 0.27 (7) | 100 – 1400 |
In addition, T1 and T2 relaxation times were mapped in the phantom using an inversion recovery spin echo sequence (TR = 9570 ms, TI = 25, 50, 100, 200, 500, 1000, and 2000 ms) and a turbo spin echo sequence (TR = 8 s, TE = 13.2, 26.4, 39.6, 52.8, 66, 79.2, 92.4, 105.6, 118.8, 132, 145.2, and 158.4 ms), respectively. We also acquired a GRE image for “anatomical” structures (Fig. 1F), where TR/TE = 4.5/1.94ms, flip angle = 5°, with an isotropic voxel size of 1 mm.
Simulations
Synthetic MRI data was generated using the Monte Carlo diffusion simulator of Camino (Cook et al., 2006; Hall and Alexander, 2009) for diffusion within impermeable, hexagonal-packed cylinders with uniform diameter ranging from 2–12 µm and a range of intra-axonal volume fractions between 0.1–0.7. Smaller inner diameters were also generated in addition to 12 µm (i.e., the expected taxon inner diameter), to confirm that the imaging protocol could provide sufficient diffusion resolution for the proposed approach to differentiate 12 µm from smaller diameters with reasonable accuracy and precision. Simulations were performed using the same diffusion MRI protocol (Gmax=300mT/m only) that was used for the experiments (see Table 1). 100,000 walkers and 5,000 time steps were used for the simulation. Data with infinite signal-to-noise ratio (SNR) and SNR of 30 were generated based on the estimated temporal SNR of the parallel fiber bundles, which ranged from 30 to 60. For infinite SNR, synthetic data was generated for a single voxel; for SNR of 30, synthetic data was generated for 200 voxels.
Data preprocessing and analysis
The experimental data was preprocessed to correct for distortions due to gradient nonlinearity, susceptibility effects, B0 drift, and eddy currents (Andersson and Sotiropoulos, 2016; Fan et al., 2016; Jenkinson et al., 2012). Due to the length of the phantom scan (about a day), the static magnetic field (B0) drifts due to hardware heating during the scan resulted in small image displacements along the phase encoding direction, which mimicked head motion (Haacke et al., 1999). To address this issue, the first b=0 image of all individual shells (i.e., for each q-value) were concatenated and used for a joint field map estimate using TOPUP (Andersson et al., 2003; Smith et al., 2004), where image displacements due to B0 drift were modeled in the same way as head motion. Eddy current correction was performed using the EDDY (Andersson and Sotiropoulos, 2016) tool in FSL.
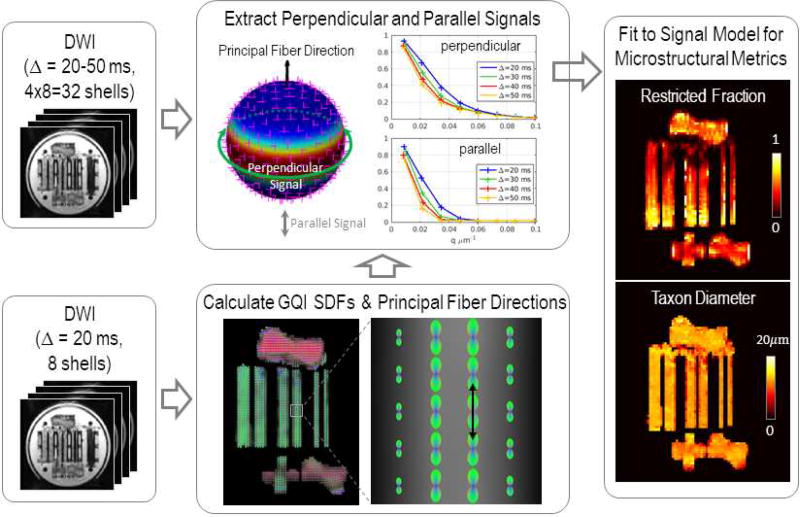
The data analysis steps were illustrated in Fig. 2. Specifically, the generalized q-sampling imaging (Yeh et al., 2010) was used to identify the principal fiber direction in each voxel by searching for the global maximum on the orientation distribution function of diffusing spins, termed the spin distribution function, which was fitted for using the shortest diffusion time dataset (Δ = 20 ms). The b-values ranged from 50 to 6700 s/mm2 for this diffusion time, which were closest in range to the b-values (max. b=5000 s/mm2) used in (Yeh et al., 2010). The average signal perpendicular to the principal fiber direction was then obtained following the procedure described in (Tuch, 2004). The signal was resampled for each diffusion direction and was averaged along the equator about the principal fiber direction to obtain the mean perpendicular signal using a Gaussian weighting function dependent on the distance of each resampling vertex from the equator. Similarly, the parallel signal was obtained by resampling the signal along the principal fiber direction for each shell. The longitudinal diffusivity (Dr) was then calculated by fitting a mono-exponential decay to the parallel signal averaged in a region of interest consisting of 105 voxels inside the parallel fiber bundles, using all shells with a b-value smaller than 1500 s/mm2 in the Gmax = 290mT/m dataset (i.e., b = 50, 100, 150, 300, 500, 700, 800, 850, and 1250 s/mm2).
Figure 2.
Flowchart outlining the analysis stream. Using the diffusion-weighted images (DWI) for the shortest diffusion time (Δ = 20 ms), the spin distribution functions (SDFs) were reconstructed in each voxel using generalized q-sampling imaging (GQI), and the principal fiber directions (black arrow) were calculated for each SDF. Spherical harmonics expansion was performed for each shell of DWI data to determine the average signal perpendicular to (dark green circle) and parallel with (gray arrows) the principal fiber direction (black arrow). A three-compartment model of intra-axonal, extra-axonal, and free water diffusion was fitted to the perpendicular signal to obtain estimates of restricted volume fraction and taxon diameter.
Signal Model and Model Fitting
We sought to obtain estimates of average compartment size and restricted volume fraction from the corrected multi-diffusion time and gradient strength diffusion MRI data by adopting a straightforward analysis method modeled after the AxCaliber and ActiveAx approaches (Alexander et al., 2010; Assaf et al., 2008a). A three-compartment model of intra-taxonal restricted, extra-taxonal hindered, and free diffusion was fitted to the average signal perpendicular to the fibers to obtain estimates of taxon diameter, restricted and free water volume fractions, and hindered diffusivity (Huang et al., 2015b), similar to the approach taken in AxCaliber (Assaf et al., 2008a) but only fitting for a single diameter as in ActiveAx (Alexander et al., 2010). See Appendix A for further details of model description.
Model fitting was performed on a voxel-wise basis using Markov chain Monte Carlo (MCMC) sampling, similar to the approach taken by Alexander et al. (Alexander et al., 2010). MCMC simulations provided samples of the posterior distributions of the model parameters (inner diameter a, restricted volume fraction fr, free water fraction ffw, and hindered diffusivity Dh) given the data. Broad uniform priors with the ranges given in parentheses were used for taxon diameter a (0.1–20 µm), restricted volume fraction fr (0–1), and free water volume fraction ffw (0–1). The restricted diffusion coefficient Dr was set to be the calculated longitudinal diffusivity Dr = 2.2 µm2/ms, and the diffusion coefficient of free water Dfw was assumed to be that at room temperature 25°C (2.3 µm2/ms). A Rician noise model was adopted for parameter estimation as in (Alexander, 2008; Alexander et al., 2010). The total number of 200,000 MCMC samples were calculated for each voxel, which were saved at intervals of 100 iterations after an initial burn-in period of 20,000 iterations (i.e., 1800 samples were saved). The mean and standard deviation of the estimates for axon diameter a, restricted volume fraction fr, and free water volume fraction ffw were then calculated for each voxel by taking the mean and standard deviation over the MCMC samples.
T1 and T2 estimation
T1 and T2 relaxation times were calculated by fitting a mono-exponential decay function to the data in MATLAB using Levenberg-Marquardt nonlinear least squares minimization. The first echo from the spin-echo train was excluded for the T2 calculation, which is a common practice for multiple spin echo acquisitions (Mosher et al., 2010; Smith et al., 2001; Sumpf et al., 2011).
Results
Signal-to-noise ratio and T1 and T2 relaxation times in the phantom
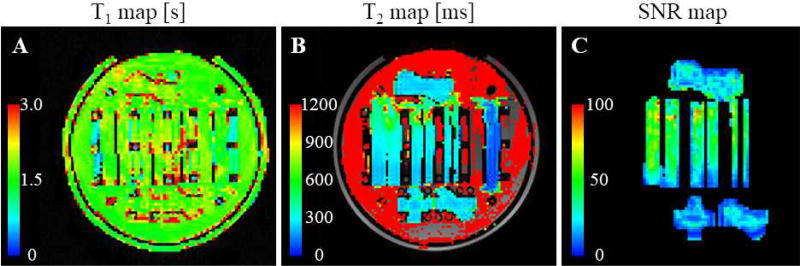
The T1 relaxation time within the parallel fibers was measured to be approximately 1.5 to 2 s (Fig. 3A), which is longer than that of white matter in the brain at 3T (about 1 s) (Stanisz et al., 2005) and shorter than that of free water (about 3 s) (Lin et al., 2001; Lu et al., 2005). The T2 relaxation time was estimated to be about 300 ms in the region of the taxons (Fig. 3B), which is longer than that of white matter (about 70 ms) (Stanisz et al., 2005). The T2 relaxation time of the background water was approximately 2 s, which is consistent with that of bulk water measured in other phantoms (Fieremans et al., 2008a). Temporal SNR estimated using the 80 interleaved b=0 images (in the Gmax=290mT/m dataset) was approximately 50 throughout most of the straight fibers (Fig. 3C), with the most densely packed portions demonstrating lower SNR due to lower water content.
Figure 3.
T1-, T2- and SNR maps. Maps of (A) T1- and (B) T2- relaxation time throughout the phantom, and (C) temporal SNR map on the b=0 images. Note that the T2 time of the background water was approximately 2 s and exceeded the upper limit of the color scale in (B).
Simulations
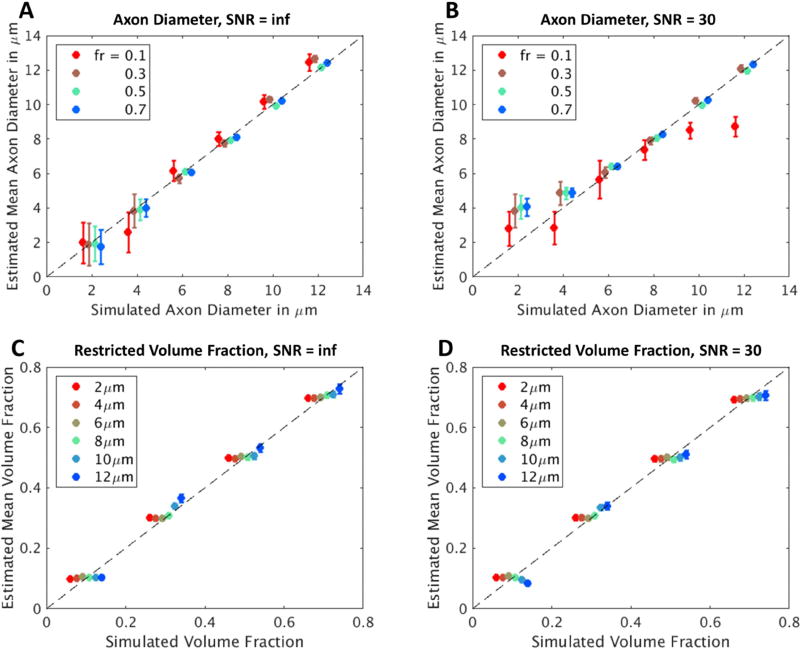
The results of model fitting on the simulation data are summarized in Fig. 4. Overall, our method yielded estimates of compartment size and restricted volume fraction that were consistent with the known simulated values. Specifically, the estimated cylinder diameter showed good agreement with known simulated values in the absence of noise, with a relatively higher uncertainty for small diameters (a = 2 µm) and low restricted volume fraction (fr = 0.1) (Fig. 4A). At SNR = 30, the estimated diameter showed similar trends, except that it tended to be over-estimated for smaller diameters (a ≤ 4 µm), and the fitted values showed greater uncertainty at lower restricted volume fraction (fr = 0.1) (Fig. 4B). The estimated restricted volume fraction showed good agreement with the known values used to generate the simulated data for all diameters, volume fractions and SNR levels tested in the simulations (Fig. 4C, D).
Figure 4.
Estimates of axon diameter and restricted volume fraction plotted against simulated axon diameter and restricted volume fraction, respectively, in synthetic substrates consisting of impermeable cylinders of variable diameter and packing density with (A, C) infinite SNR and (B, D) SNR of 30. For the infinite SNR simulations, the mean and standard deviation across MCMC samples are calculated and reported, while for the SNR=30 simulations, the mean and standard deviation for each metric over all 200 voxels are reported.
Phantom experiments
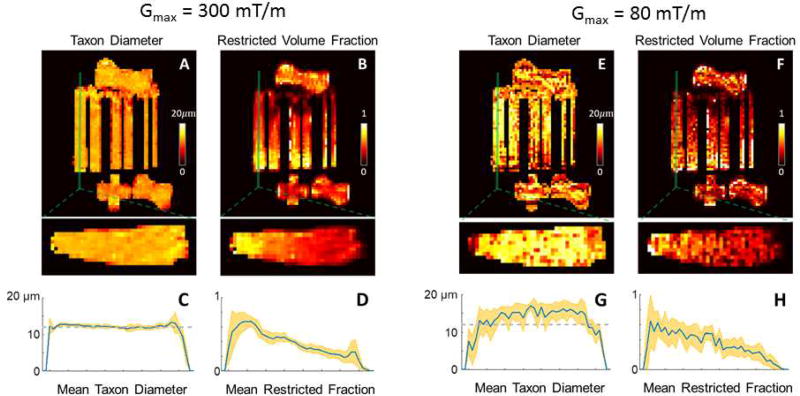
In experiments on the phantom, the estimates of compartment size and restricted volume fraction were largely consistent with the known construction of the phantom for the Gmax=300mT/m dataset (Fig. 5). The diameter estimates were fairly uniform throughout the phantom with a mean value of 12.2 µm and standard deviation of 0.9 µm, which were close to the actual ID of 11.8 µm (Fig. 5A). The estimated restricted volume fraction also showed an expected decrease as the packing density decreased along the length of the fiber bundle. In the Gmax=80mT/m experiments, the axon diameter was overestimated in general, and the fitting results yield much higher uncertainty compared to the Gmax=300mT/m estimates.
Revised Figure 5.
Experimental results from voxel-wise MCMC model fitting using the Gmax=290mT/m and Gmax=80mT/m datasets. Maps of (A,E) textile axon (“taxon”) diameter and (B,F) restricted volume fraction are shown in axial (top) and sagittal (bottom) views, with cross-sectional profiles of (C,G) taxon diameter and (D,H) restricted fraction averaged over the three central sagittal slices of the fiber bundle (inset). The shaded bands in orange indicate the standard deviation within the cross-sectional area at each position along the length of the fiber bundle, and the dashed gray line in (C,G) indicates the known inner diameter of the taxons (11.8 µm) estimated from scanning electron microscopy.
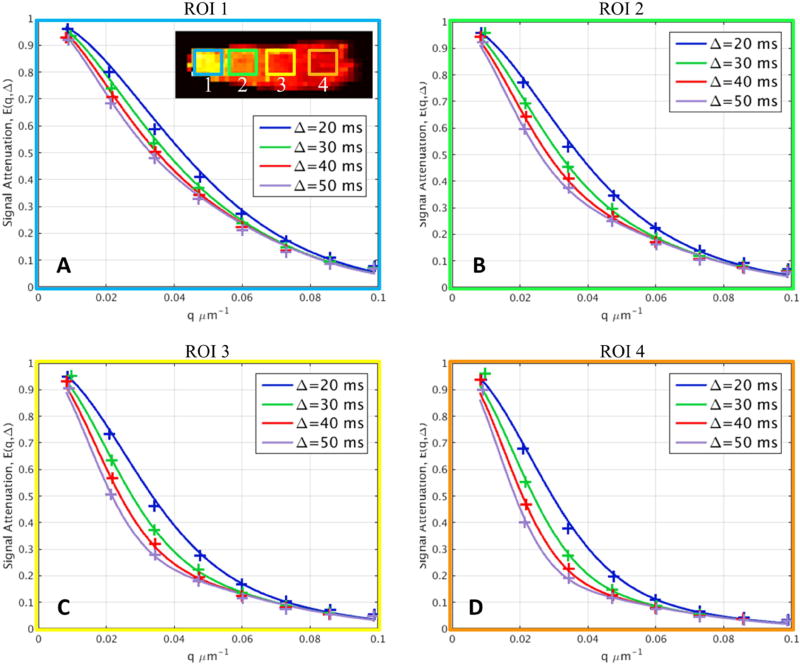
In addition, the signal predicted by the model was compared to the measured signal perpendicular to the primary diffusion direction for different regions of interest representative of each packing density in the Gmax=300mT/m dataset (Fig. 6). There were clear differences in the signal decays for different portions of the phantom corresponding to different packing densities. The signal model was derived for an ideal substrate of impermeable parallel cylinders and was able capture the trends in the experimental data without visible discrepancies between the measured and model-predicted signals, which supports the validity of our approach
Figure 6.
Diffusion signal decays in regions of interest (inset) with different packing densities along the length of the fiber bundle. The measured perpendicular signal was averaged across the three central slices within the ROIs illustrated in (A) and were plotted against q-value. The predicted signals using the three-compartment model were plotted as superimposed curves upon the experimental data points. There is clear difference between different portions of the phantom with different packing densities. The signal model fits the data well, indicating that the signal model used here can capture the trends in the experimental data without visible discrepancies between the measured data and model-predicted signals.
Discussion
In this study, we used a novel biomimetic brain diffusion phantom constructed with hollow polypropylene fibers to validate taxon diameter and density estimates obtained on the 3T CONNECTOM human MRI scanner. We leveraged the 300 mT/m gradient strength on the CONNECTOM scanner and acquired a comprehensive diffusion-weighted MRI dataset that sampled four diffusion times and eight q-values per diffusion time. The results of our fitting show that our approach to compartment size and packing density estimation, which extends the AxCaliber approach to address arbitrary fiber orientations, provides estimates of compartment size and restricted volume fraction that are in good agreement with the known values in this phantom, indicating the validity of the approach.
We intend this phantom dataset to serve as a benchmark for validating other diffusion microstructural imaging methods, such as the White Matter Tract Integrity (WMTI) metrics (Fieremans et al., 2011), CHARMED model (Assaf and Basser, 2005), and Neurite Orientation Dispersion and Density Imaging method (NODDI) (Zhang et al., 2011), among other diffusion microstructural models. Toward this goal, the data reported in this paper have been deposited in the XNAT Central database, https://central.xnat.org/ (project ID: dMRI_Phant_MGH), which is accessible for users to download upon registration and approval of the data usage agreement.
To the best of our knowledge, this is the first validation study of diffusion MRI metrics using a biomimetic phantom that provides diffusion properties analogous to both the intra-axonal and extra-axonal spaces on a human MRI scanner equipped with 300 mT/m gradients. The extra-axonal (Bach et al., 2014; Fieremans et al., 2008b; Fillard et al., 2011; Gatidis et al., 2014; Poupon et al., 2008; Pullens et al., 2010; Reischauer et al., 2009) and intra-axonal (Ebrahimi et al., 2010; Komlosh et al., 2017; Komlosh et al., 2011; Yanasak and Allison, 2006) compartment only phantoms have both been previously reported as promising in validating diffusion models, but none have incorporated both compartments simultaneously. Limitations of the current phantom include the thickness of the polypropylene walls and the relatively large ID (about 12 µm) used in the current prototype of the phantom compared to human axons, which are typically in the range of 0.25–10 µm (Alexander, 2008). Nevertheless, the design of hollow fibers separating the intra-taxonal water pool from the extra-taxonal pool captures the fundamental structure of myelinated axons and emulates the microstructural composition of white matter in the human brain.
The filaments in the taxon phantom were made of polypropylene, which is advantageous for several reasons. For one, the use of polymer fibers facilitates the construction of crossing fiber regions within the phantom, which is more difficult to achieve with materials such as glass. More importantly, synthetic polymers are thought to be one of the best candidate materials for water-filled diffusion phantom construction owing to the smaller susceptibility differences between polymers and water compared to materials such as glass (Fieremans et al., 2008a). The internal field gradients caused by susceptibility differences between water and the fiber material are expected to yield an orientationally dependent signal loss with respect to the static magnetic field B0. Previous work by Fieremans et al. (Fieremans et al., 2008a) has shown that polymer materials (e.g., nylon) have minimal signal loss and B0 dependence to the NMR signal caused by internal gradients. In this study, we were not able to measure the effect of susceptibility gradients properly because the size and shape of the phantom limited its placement in the receiver coil, such that the taxon fibers could only be placed perpendicular to the static magnetic field B0 and not rotated to be more aligned with B0. Further experiments are needed to investigate susceptibility effects once the same taxon diffusion module can be packed into a smaller case. However, due to the use of polypropylene yarns similar to the material used by Fieremans et al., we anticipate minimal signal loss caused by this particular mechanism.
Differences in SNR from data acquired in the phantom compared to the in vivo scenario must be acknowledged. The longer T2 relaxation time measured in the phantom water would lead to a higher SNR in the phantom imaging data compared to in vivo data. At the same time, the lower proton density in physical diffusion phantoms compared to the brain would yield a lower SNR, which would at least partially counterbalance the SNR increase due to longer T2. Differences in SNR would alter the robustness (e.g., variance) of the final fitting results, which should be considered in designing in vivo human experiments if pilot data were collected with physical phantoms.
The simulation results show that the Gmax = 300 mT/m imaging protocol and analysis approach can resolve the compartment size represented in the fiber substrate of this diffusion phantom. Given that the diffusion times accessible on the CONNECTOM scanner with the currently available maximum slew rate of 200 T/m/s are on the order of 10 ms or greater, we would expect to be sensitive to mean diffusion displacements on the order of 6 µm or greater for a longitudinal diffusivity of 2.2×10−9 m2/s. We chose diffusion times of 20–50 ms for our experiments on this phantom to be sensitive to mean squared displacements of 9–15 µm, which encompassed the actual taxon diameter of 12 µm. Our simulations showed that the variance in diameter estimation for 2 µm with infinite SNR and a high packing density (fr = 0.7) was greater than for diameters simulated up to 12 µm (Fig. 4), which confirms that a lower bound to compartment size estimation does exist, and that 2 µm is below this lower bound. This finding is consistent with the projected resolution limit of axon diameter estimation at Gmax = 300 mT/m from prior studies (Dyrby et al., 2013; Nilsson and Alexander, 2012; Nilsson et al., 2017).
In the experiment with Gmax = 300 mT/m, the voxel-wise estimates of taxon ID were fairly uniform between the 6 parallel fiber bundles of different sizes, and the value was close to the known ID of 11.8 µm. The restricted volume fraction estimates demonstrated an expected decrease corresponding to decreasing packing density along the length of the fiber bundle with increasing well size, with the caveat being that the actual restricted volume fraction was difficult to determine. The scanning electron micrographs shown in Fig. 1 appeared to overestimate the actual taxon separation due to splaying of the fibers when they were cut to produce the SEM images, and thus should be interpreted as a conservative representation of intra-taxonal volume fractions. The Gmax=80mT/m results indicate that the axon diameter was overestimated in general, and that the fitting results were less certain compared to the Gmax=300mT/m estimates. Overall, our results with the Gmax=80mT/m dataset as acquired and analyzed here seemed to overestimate the actual taxon diameter, which was expected to be 12 µm, and support the use of high Gmax to improve the contrast and stability of axon diameter estimates, as suggested by Dyrby et al. (2013). There are some drawbacks to the acquisition chosen here for Gmax=80mT/m, in that the protocol was purposely matched to the Gmax=300 mT/m protocol. The matching was done by lowering the maximum available gradient amplitude to 80 mT/m and adjusting protocols to be as close as possible otherwise. This may not necessarily be a generally optimal acquisition scheme for Gmax=80mT/m, i.e., the selection of q-values, diffusion times, and echo time can be further refined. We chose to match the two protocols for a basic illustration of the impact from scaling down the gradient strength, but we cannot simply conclude with this particular dataset that 80 mT/m is not adequate to resolve 12 µm inner diameter if a different model or acquisition strategy is used. Further investigations are needed to characterize the compartment size resolution achievable with different gradient strength, such as those described in Nilsson et al. (2017), which are beyond the scope of the current study.
The signal model used in this study assumed a single fiber bundle comprised of parallel fibers and would not be applicable to crossing fibers, which is a limitation of the current approach. It is an interesting and somewhat surprising finding that the axon diameter estimates in the crossing fiber region is close to the expected 12 µm, while the discrepancies were mainly accommodated by an under-estimated restricted volume fraction. This result can be replicated with simulated data (not shown), and further investigations are needed for a better understanding of the phenomenon. In the meantime, efforts are being made in our group to generalize the current framework to incorporate crossing fibers by following an approach similar to the CHARMED model, where the intra-axonal water is modeled separately for each fiber, the extra-axonal water is modeled jointly by a diffusion tensor model, and the axon diameters and restricted volume fractions are estimated separately for each fiber, noting that the number of model parameters would increase accordingly. In this paper, we chose to use the simplest possible model to explain the diameter estimates in parallel fiber portions of the phantom and anticipate addressing crossing fibers in future work.
The approach proposed in this study to estimate axon diameter is similar in spirit to ActiveAx, but it is important to point out that the two approaches still differ from each other in several aspects. In ActiveAx, all directions were included in the signal model for fitting, whereas our signal model focused on the perpendicular signal component only, which has the highest SNR and highest sensitivity to intra- and extra-taxonal diffusion differences. The ActiveAx signal model assumes tortuosity model for the hindered diffusivity, whereas our signal model fits for hindered diffusivity simultaneously with axon diameter and compartment volume fractions. The ActiveAx imaging protocol samples only 4 “shells” which is a key feature of the optimized protocol, and the gradient duration δ was varied between shells, whereas our imaging protocol was based on the principle of extensive sampling of the available q-space with multiple diffusion times.
A major advantage of this work is the flexible design of the biomimetic brain phantom. In future prototypes, the phantom construction will be refined by including taxons with a range of diameters that are closer in size to actual human axons. In fact, our current manufacturing capabilities have been expanded to construct taxons with inner diameter in the range of 0.3–4 µm. The manufacturing technique has also been modified to limit dispersion of the taxon fibers. Furthermore, future iterations of the phantom could allow for selective filling of the intra- or extra-taxonal compartment with MR-invisible material such as paraffin or deuterated water, which will be beneficial in understanding how each compartment contributes to the overall signal and help in refining models of intra- and extra-axonal diffusion within white matter. It is also worth mentioning that the taxon modules can be equally suitable for preclinical scanners, once they are packed in smaller cases that can fit inside small-bore systems. Another limitation of the current phantom lies in the zero permeability of the taxon membrane, which is an assumption that may not hold in the presence of pathology (Nedjati-Gilani et al., 2017). Further investigations are needed to explore phantom construction methods that incorporate variable membrane permeability as well as validation of methods for measuring permeability. In brief, although the current prototype of the phantom is limited in a number of aspects, a great deal of flexibility exists in tailoring the construction of the taxon-based biomimetic diffusion phantom to facilitate the study of white matter microstructure from multiple perspectives.
In summary, we performed diffusion MRI experiments on a novel biomimetic phantom constructed of hollow polymer fibers on a human MRI scanner equipped with gradient strengths up to 300 mT/m. We comprehensively sampled q-space over a range of diffusion times and gradient strengths to estimate the inner diameter and volume fraction of the taxon fibers. Our results (Gmax = 290 mT/m) showed good agreement with the known construction of the phantom, which provides supportive empirical evidence for the validity of our approach. The study demonstrates the importance of a biologically analogous phantom that can be applied to validate other diffusion microstructural imaging methods and be used for standardization of diffusion MRI protocols for neuroimaging research.
Supplementary Material
Acknowledgments
This work was funded by an NIH Blueprint for Neuroscience Research Grant U01MH093765, as well as NIH funding from NCRRP41EB015896, NIBIBR01EB006847, NIBIBR00EB015445, NINDSK23NS096056, NHLBIR01HL131635, NHLBIR56HL125590 and Instrumentation Grants S10-RR023401, S10-RR023043, and S10-RR019307. Funding support was also received from Chronic Effects of Neurotrauma Consortium/Veterans Affairs Rehabilitation Research & Development project F1880, U.S. Army12342013 (W81XWH-12-2-0139), the American Heart Association Postdoctoral Fellowship Award (17POST33670452), a Radiological Sciences of North America Research Resident Grant and the MGH Executive Committee on Research Fund for Medical Discovery Fellowship Award. The authors thank Dr. Bo Zhao for helpful discussions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander DC. A general framework for experiment design in diffusion MRI and its application in measuring direct tissue-microstructure features. Magn Reson Med. 2008;60:439–448. doi: 10.1002/mrm.21646. [DOI] [PubMed] [Google Scholar]
- Alexander DC, Hubbard PL, Hall MG, Moore EA, Ptito M, Parker GJ, Dyrby TB. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage. 2010;52:1374–1389. doi: 10.1016/j.neuroimage.2010.05.043. [DOI] [PubMed] [Google Scholar]
- Andersson JL, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage. 2003;20:870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- Andersson JL, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage. 2016;125:1063–1078. doi: 10.1016/j.neuroimage.2015.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf Y, Basser PJ. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage. 2005;27:48–58. doi: 10.1016/j.neuroimage.2005.03.042. [DOI] [PubMed] [Google Scholar]
- Assaf Y, Blumenfeld-Katzir T, Yovel Y, Basser PJ. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn Reson Med. 2008a;59:1347–1354. doi: 10.1002/mrm.21577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf Y, Blumenfeld-Katzir T, Yovel Y, Basser PJ. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn Reson Med. 2008b;59:1347–1354. doi: 10.1002/mrm.21577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf Y, Freidlin RZ, Rohde GK, Basser PJ. New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter. Magn Reson Med. 2004;52:965–978. doi: 10.1002/mrm.20274. [DOI] [PubMed] [Google Scholar]
- Bach M, Fritzsche KH, Stieltjes B, Laun FB. Investigation of resolution effects using a specialized diffusion tensor phantom. Magn Reson Med. 2014;71:1108–1116. doi: 10.1002/mrm.24774. [DOI] [PubMed] [Google Scholar]
- Balls GT, Frank LR. A simulation environment for diffusion weighted MR experiments in complex media. Magn Reson Med. 2009;62:771–778. doi: 10.1002/mrm.22033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barazany D, Basser PJ, Assaf Y. In vivo measurement of axon diameter distribution in the corpus callosum of rat brain. Brain. 2009;132:1210–1220. doi: 10.1093/brain/awp042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Close TG, Tournier JD, Calamante F, Johnston LA, Mareels I, Connelly A. A software tool to generate simulated white matter structures for the assessment of fibre-tracking algorithms. Neuroimage. 2009;47:1288–1300. doi: 10.1016/j.neuroimage.2009.03.077. [DOI] [PubMed] [Google Scholar]
- Cook PA, Bai Y, Nedjati-Gilani S, Seunarine K, Hall MG, Parker GJ, Alexander DC. Proc. ISMRM. Seattle: 2006. Camino: Open-Source Diffusion-MRI Reconstruction and Processing; p. 2759. [Google Scholar]
- Duval T, McNab JA, Setsompop K, Witzel T, Schneider T, Huang SY, Keil B, Klawiter EC, Wald LL, Cohen-Adad J. In vivo mapping of human spinal cord microstructure at 300mT/m. Neuroimage. 2015;118:494–507. doi: 10.1016/j.neuroimage.2015.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyrby TB, Baare WF, Alexander DC, Jelsing J, Garde E, Sogaard LV. An ex vivo imaging pipeline for producing high-quality and high-resolution diffusion-weighted imaging datasets. Hum Brain Mapp. 2011;32:544–563. doi: 10.1002/hbm.21043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyrby TB, Sogaard LV, Hall MG, Ptito M, Alexander DC. Contrast and stability of the axon diameter index from microstructure imaging with diffusion MRI. Magn Reson Med. 2013;70:711–721. doi: 10.1002/mrm.24501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebrahimi B, Nejad Davarani SP, Ding G, Jiang Q, Chupp TE. A microfabricated phantom for diffusion tensor imaging. 2010 76261Q-76261Q-76268. [Google Scholar]
- Fan Q, Witzel T, Nummenmaa A, Van Dijk KR, Van Horn JD, Drews MK, Somerville LH, Sheridan MA, Santillana RM, Snyder J, Hedden T, Shaw EE, Hollinshead MO, Renvall V, Zanzonico R, Keil B, Cauley S, Polimeni JR, Tisdall D, Buckner RL, Wedeen VJ, Wald LL, Toga AW, Rosen BR. MGH-USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. Neuroimage. 2016;124:1108–1114. doi: 10.1016/j.neuroimage.2015.08.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farrher E, Kaffanke J, Celik AA, Stocker T, Grinberg F, Shah NJ. Novel multisection design of anisotropic diffusion phantoms. Magn Reson Imaging. 2012;30:518–526. doi: 10.1016/j.mri.2011.12.012. [DOI] [PubMed] [Google Scholar]
- Fieremans E, De Deene Y, Delputte S, Ozdemir MS, Achten E, Lemahieu I. The design of anisotropic diffusion phantoms for the validation of diffusion weighted magnetic resonance imaging. Phys Med Biol. 2008a;53:5405–5419. doi: 10.1088/0031-9155/53/19/009. [DOI] [PubMed] [Google Scholar]
- Fieremans E, De Deene Y, Delputte S, Ozdemir MS, D'Asseler Y, Vlassenbroeck J, Deblaere K, Achten E, Lemahieu I. Simulation and experimental verification of the diffusion in an anisotropic fiber phantom. J Magn Reson. 2008b;190:189–199. doi: 10.1016/j.jmr.2007.10.014. [DOI] [PubMed] [Google Scholar]
- Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage. 2011;58:177–188. doi: 10.1016/j.neuroimage.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fillard P, Descoteaux M, Goh A, Gouttard S, Jeurissen B, Malcolm J, Ramirez-Manzanares A, Reisert M, Sakaie K, Tensaouti F, Yo T, Mangin JF, Poupon C. Quantitative evaluation of 10 tractography algorithms on a realistic diffusion MR phantom. Neuroimage. 2011;56:220–234. doi: 10.1016/j.neuroimage.2011.01.032. [DOI] [PubMed] [Google Scholar]
- Gatidis S, Schmidt H, Martirosian P, Schwenzer NF. Development of an MRI phantom for diffusion-weighted imaging with independent adjustment of apparent diffusion coefficient values and T2 relaxation times. Magn Reson Med. 2014;72:459–463. doi: 10.1002/mrm.24944. [DOI] [PubMed] [Google Scholar]
- Guise C, Fangueiro R, Nobrega JM, Schneider W. Study on fibrous materials for brain phantoms. Stud Health Technol Inform. 2014;207:163–172. [PubMed] [Google Scholar]
- Guise C, Fernandes MM, Nobrega JM, Pathak S, Schneider W, Fangueiro R. Hollow Polypropylene Yarns as a Biomimetic Brain Phantom for the Validation of High-Definition Fiber Tractography Imaging. ACS Appl Mater Interfaces. 2016;8:29960–29967. doi: 10.1021/acsami.6b09809. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Thompson MR, Venkatesan R, Brown RW. Magnetic resonance imaging : physical principles and sequence design. J. Wiley & Sons; New York: 1999. [Google Scholar]
- Hall MG, Alexander DC. Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI. IEEE Trans Med Imaging. 2009;28:1354–1364. doi: 10.1109/TMI.2009.2015756. [DOI] [PubMed] [Google Scholar]
- Huang S, Witzel T, Fan Q, McNab JA, Wald LL, Nummenmaa A. Proc. ISMRM. Toronto, Canada: 2015a. TractCaliber: Axon diameter estimation across white matter tracts in the in vivo human brain using 300 mT/m gradients. [Google Scholar]
- Huang SY, Nummenmaa A, Witzel T, Duval T, Cohen-Adad J, Wald LL, McNab JA. The impact of gradient strength on in vivo diffusion MRI estimates of axon diameter. Neuroimage. 2015b;106:464–472. doi: 10.1016/j.neuroimage.2014.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang SY, Tobyne SM, Nummenmaa A, Witzel T, Wald LL, McNab JA, Klawiter EC. Characterization of Axonal Disease in Patients with Multiple Sclerosis Using High-Gradient-Diffusion MR Imaging. Radiology. 2016;280:244–251. doi: 10.1148/radiol.2016151582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbard PL, Zhou FL, Eichhorn SJ, Parker GJ. Biomimetic phantom for the validation of diffusion magnetic resonance imaging. Magn Reson Med. 2015;73:299–305. doi: 10.1002/mrm.25107. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. FSL. Neuroimage. 2012;62:782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Kim S, Chi-Fishman G, Barnett AS, Pierpaoli C. Dependence on diffusion time of apparent diffusion tensor of ex vivo calf tongue and heart. Magn Reson Med. 2005;54:1387–1396. doi: 10.1002/mrm.20676. [DOI] [PubMed] [Google Scholar]
- Komlosh ME, Benjamini D, Barnett AS, Schram V, Horkay F, Avram AV, Basser PJ. Anisotropic phantom to calibrate high-q diffusion MRI methods. J Magn Reson. 2017;275:19–28. doi: 10.1016/j.jmr.2016.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komlosh ME, Ozarslan E, Lizak MJ, Horkay F, Schram V, Shemesh N, Cohen Y, Basser PJ. Pore diameter mapping using double pulsed-field gradient MRI and its validation using a novel glass capillary array phantom. J Magn Reson. 2011;208:128–135. doi: 10.1016/j.jmr.2010.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leemans A, Sijbers J, Verhoye M, Van der Linden A, Van Dyck D. Mathematical framework for simulating diffusion tensor MR neural fiber bundles. Magn Reson Med. 2005;53:944–953. doi: 10.1002/mrm.20418. [DOI] [PubMed] [Google Scholar]
- Lin C, Bernstein M, Huston J, Fain S. Proc. ISMRM. Glasgow, Scotland, UK: 2001. Measurements of T1 Relaxation times at 3.0T: Implications for clinical MRA; p. 1391. [Google Scholar]
- Lu H, Nagae-Poetscher LM, Golay X, Lin D, Pomper M, van Zijl PC. Routine clinical brain MRI sequences for use at 3.0 Tesla. J Magn Reson Imaging. 2005;22:13–22. doi: 10.1002/jmri.20356. [DOI] [PubMed] [Google Scholar]
- Mallik S, Samson RS, Wheeler-Kingshott CA, Miller DH. Imaging outcomes for trials of remyelination in multiple sclerosis. J Neurol Neurosurg Psychiatry. 2014;85:1396–1404. doi: 10.1136/jnnp-2014-307650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNab JA, Edlow BL, Witzel T, Huang SY, Bhat H, Heberlein K, Feiweier T, Liu K, Keil B, Cohen-Adad J, Tisdall MD, Folkerth RD, Kinney HC, Wald LL. The Human Connectome Project and beyond: initial applications of 300 mT/m gradients. Neuroimage. 2013;80:234–245. doi: 10.1016/j.neuroimage.2013.05.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNab JA, Jbabdi S, Deoni SC, Douaud G, Behrens TE, Miller KL. High resolution diffusion-weighted imaging in fixed human brain using diffusion-weighted steady state free precession. Neuroimage. 2009;46:775–785. doi: 10.1016/j.neuroimage.2009.01.008. [DOI] [PubMed] [Google Scholar]
- Miller KL, Alfaro-Almagro F, Bangerter NK, Thomas DL, Yacoub E, Xu J, Bartsch AJ, Jbabdi S, Sotiropoulos SN, Andersson JL, Griffanti L, Douaud G, Okell TW, Weale P, Dragonu I, Garratt S, Hudson S, Collins R, Jenkinson M, Matthews PM, Smith SM. Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nat Neurosci. 2016;19:1523–1536. doi: 10.1038/nn.4393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KL, McNab JA, Jbabdi S, Douaud G. Diffusion tractography of post-mortem human brains: optimization and comparison of spin echo and steady-state free precession techniques. Neuroimage. 2012;59:2284–2297. doi: 10.1016/j.neuroimage.2011.09.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosher TJ, Liu Y, Torok CM. Functional cartilage MRI T2 mapping: evaluating the effect of age and training on knee cartilage response to running. Osteoarthritis Cartilage. 2010;18:358–364. doi: 10.1016/j.joca.2009.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nedjati-Gilani GL, Schneider T, Hall MG, Cawley N, Hill I, Ciccarelli O, Drobnjak I, Wheeler-Kingshott C, Alexander DC. Machine learning based compartment models with permeability for white matter microstructure imaging. Neuroimage. 2017;150:119–135. doi: 10.1016/j.neuroimage.2017.02.013. [DOI] [PubMed] [Google Scholar]
- Nilsson M, Alexander DC. Investigating tissue microstructure using diffusion MRI: How does the resolution limit of the axon diameter relate to the maximal gradient strength? International Society for Magnetic Resonance in Medicine; Melbourne, Australia: 2012. p. 3567. [Google Scholar]
- Nilsson M, Lasic S, Drobnjak I, Topgaard D, Westin CF. Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion. NMR Biomed. 2017;30 doi: 10.1002/nbm.3711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrin M, Poupon C, Rieul B, Leroux P, Constantinesco A, Mangin JF, Lebihan D. Validation of q-ball imaging with a diffusion fibre-crossing phantom on a clinical scanner. Philos Trans R Soc Lond B Biol Sci. 2005;360:881–891. doi: 10.1098/rstb.2005.1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poupon C, Rieul B, Kezele I, Perrin M, Poupon F, Mangin JF. New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (HARDI) models. Magn Reson Med. 2008;60:1276–1283. doi: 10.1002/mrm.21789. [DOI] [PubMed] [Google Scholar]
- Pullens P, Roebroeck A, Goebel R. Ground truth hardware phantoms for validation of diffusion-weighted MRI applications. J Magn Reson Imaging. 2010;32:482–488. doi: 10.1002/jmri.22243. [DOI] [PubMed] [Google Scholar]
- Reischauer C, Staempfli P, Jaermann T, Boesiger P. Construction of a temperature-controlled diffusion phantom for quality control of diffusion measurements. J Magn Reson Imaging. 2009;29:692–698. doi: 10.1002/jmri.21665. [DOI] [PubMed] [Google Scholar]
- Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage. 2013;80:220–233. doi: 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd TM, Flint JJ, Thelwall PE, Stanisz GJ, Mareci TH, Yachnis AT, Blackband SJ. Postmortem interval alters the water relaxation and diffusion properties of rat nervous tissue--implications for MRI studies of human autopsy samples. Neuroimage. 2009a;44:820–826. doi: 10.1016/j.neuroimage.2008.09.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd TM, Thelwall PE, Stanisz GJ, Blackband SJ. Aldehyde fixative solutions alter the water relaxation and diffusion properties of nervous tissue. Magn Reson Med. 2009b;62:26–34. doi: 10.1002/mrm.21977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith HE, Mosher TJ, Dardzinski BJ, Collins BG, Collins CM, Yang QX, Schmithorst VJ, Smith MB. Spatial variation in cartilage T2 of the knee. J Magn Reson Imaging. 2001;14:50–55. doi: 10.1002/jmri.1150. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med. 2005;54:507–512. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imaging. 2011;34:420–428. doi: 10.1002/jmri.22634. [DOI] [PubMed] [Google Scholar]
- Sun SW, Neil JJ, Liang HF, He YY, Schmidt RE, Hsu CY, Song SK. Formalin fixation alters water diffusion coefficient magnitude but not anisotropy in infarcted brain. Magn Reson Med. 2005;53:1447–1451. doi: 10.1002/mrm.20488. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, King MD, Gadian DG, Connelly A. Limitations and requirements of diffusion tensor fiber tracking: an assessment using simulations. Magn Reson Med. 2002;47:701–708. doi: 10.1002/mrm.10116. [DOI] [PubMed] [Google Scholar]
- Tuch DS. Q-ball imaging. Magn Reson Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- Wehrl HF, Bezrukov I, Wiehr S, Lehnhoff M, Fuchs K, Mannheim JG, Quintanilla-Martinez L, Kohlhofer U, Kneilling M, Pichler BJ, Sauter AW. Assessment of murine brain tissue shrinkage caused by different histological fixatives using magnetic resonance and computed tomography imaging. Histol Histopathol. 2015;30:601–613. doi: 10.14670/HH-30.601. [DOI] [PubMed] [Google Scholar]
- Winston GP, Micallef C, Symms MR, Alexander DC, Duncan JS, Zhang H. Advanced diffusion imaging sequences could aid assessing patients with focal cortical dysplasia and epilepsy. Epilepsy Res. 2014;108:336–339. doi: 10.1016/j.eplepsyres.2013.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Li H, Harkins KD, Jiang X, Xie J, Kang H, Does MD, Gore JC. Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy. Neuroimage. 2014;103:10–19. doi: 10.1016/j.neuroimage.2014.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Li H, Li K, Harkins KD, Jiang X, Xie J, Kang H, Dortch RD, Anderson AW, Does MD, Gore JC. Fast and simplified mapping of mean axon diameter using temporal diffusion spectroscopy. NMR Biomed. 2016;29:400–410. doi: 10.1002/nbm.3484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yanasak N, Allison J. Use of capillaries in the construction of an MRI phantom for the assessment of diffusion tensor imaging: demonstration of performance. Magn Reson Imaging. 2006;24:1349–1361. doi: 10.1016/j.mri.2006.08.001. [DOI] [PubMed] [Google Scholar]
- Yeh FC, Wedeen VJ, Tseng WY. Generalized q-sampling imaging. IEEE Trans Med Imaging. 2010;29:1626–1635. doi: 10.1109/TMI.2010.2045126. [DOI] [PubMed] [Google Scholar]
- Zhang H, Hubbard PL, Parker GJ, Alexander DC. Axon diameter mapping in the presence of orientation dispersion with diffusion MRI. Neuroimage. 2011;56:1301–1315. doi: 10.1016/j.neuroimage.2011.01.084. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.