Adaptive MCMC in Bayesian phylogenetics: an application to analyzing partitioned data in BEAST

Abstract

Motivation

Advances in sequencing technology continue to deliver increasingly large molecular sequence datasets that are often heavily partitioned in order to accurately model the underlying evolutionary processes. In phylogenetic analyses, partitioning strategies involve estimating conditionally independent models of molecular evolution for different genes and different positions within those genes, requiring a large number of evolutionary parameters that have to be estimated, leading to an increased computational burden for such analyses. The past two decades have also seen the rise of multi-core processors, both in the central processing unit (CPU) and Graphics processing unit processor markets, enabling massively parallel computations that are not yet fully exploited by many software packages for multipartite analyses.

Results

We here propose a Markov chain Monte Carlo (MCMC) approach using an adaptive multivariate transition kernel to estimate in parallel a large number of parameters, split across partitioned data, by exploiting multi-core processing. Across several real-world examples, we demonstrate that our approach enables the estimation of these multipartite parameters more efficiently than standard approaches that typically use a mixture of univariate transition kernels. In one case, when estimating the relative rate parameter of the non-coding partition in a heterochronous dataset, MCMC integration efficiency improves by > 14-fold.

Availability and Implementation

Our implementation is part of the BEAST code base, a widely used open source software package to perform Bayesian phylogenetic inference.

Supplementary information

Supplementary data are available at Bioinformatics online.

Introduction

Bayesian inference has become increasingly popular in molecular phylogenetics over the past decades, with Markov chain Monte Carlo (MCMC) integration revolutionizing the field (Yang and Rannala, 1997). The basic idea is to construct a Markov chain that has as its state space the parameters of the statistical model and a stationary target distribution that is the posterior probability distribution of the parameters. Although MCMC has made analysis of many complex models possible, it is not a panacea, as chains can fail to converge to the target distribution for a number of reasons, including poor mechanisms for proposing new states (Huelsenbeck et al., 2001). In addition, the large number of parameters associated with increasing model complexity and the amount of sequence data in modern-day datasets have considerably elevated the computational demands of Bayesian phylogenetic analyses.

It is generally acknowledged that the choice of an effective proposal distribution for the random walk Metropolis algorithm is essential in order to obtain reasonable results in a limited amount of time (Haario et al., 2001). This choice concerns both the size and the spatial orientation of the proposal distribution, which are often very difficult to choose well since the target density is unknown. A possible remedy is provided by adaptive algorithms, which use the history of the chain in order to adequately tune the proposal distribution (Haario et al., 2001). Adaptive MCMC algorithms are typically used to achieve efficient mixing when sampling from complicated high-dimensional distributions, by automatically learning better parameter values of such algorithms while they are running (Roberts and Rosenthal, 2009). Using computer simulations, Roberts and Rosenthal (2009) show that adaptive MCMC performs very well compared to non-adaptive algorithms, even in the case of high dimensions, in terms of MCMC chain mixing.

While Bayesian inference allows for complex evolutionary models to be used in phylogenetic inference, recent advances in sequencing technology are continuously challenging the computational complexity of phylogenetic analyses. The availability of full genome data and the frequent use of data partitioning strategies in Bayesian phylogenetics have resulted in an abundance of parameters that need to be estimated. Large protein-coding datasets have been shown to benefit from being partitioned by gene and by codon position, for both computational reasons and the increases in model fit partitioning strategies have to offer (Baele and Lemey, 2013).

While codon-based models explicitly incorporate information about the genetic code, and as such are arguably among the more biologically realistic models of the evolution of coding sequences, the currently available codon models are not necessarily the best choice for analysing protein-coding datasets. For example, Shapiro et al. (2006) determined the most appropriate model for alignments of 177 RNA virus genes and 106 yeast genes, using 11 substitution models including one codon model and four codon partition (CP) models. Despite the often-claimed biological realism of codon models, the authors found that the majority of analysed gene alignments are best described by CP substitution models that avoid the computational cost of full codon models, rather than by standard nucleotide models. These results make it clear that CP substitution models are not only a computationally realistic alternative to standard models but also may be frequently statistically superior (Shapiro et al., 2006; Baele and Lemey, 2013).

Whether using full codon models or CP models, the number of parameters of a typical Bayesian phylogenetic analysis increases drastically by partitioning strategies, resulting also in a large array of likelihoods that need to be evaluated simultaneously. However, the computational resources available to researchers have also markedly increased, with impressive consistency over a similar time scale to the advances in sequencing technology. One important aspect of this is the ubiquitous availability of multi-processor and multi-core computers, inviting novel parallel algorithms to make efficient use of these machines (Suchard and Rambaut, 2009).

Many Bayesian phylogenetics software packages, such as BEAST (Drummond et al., 2012) and MrBayes (Ronquist et al., 2012), do not fully exploit the inherent parallelism of such multi-core systems when confronted with partitioned data because they typically update one single parameter at a time (a practice called single-component Metropolis-Hastings; Gilks et al., 1996). Under such an update scheme on multi-processor systems, only one of the potentially large collection of (observed) data likelihoods is being modified at any one time, thereby vastly underusing the computational power of such hardware. However, updating all the models’ parameters at once would lead to multiple data likelihoods being modified simultaneously, thereby putting to better use the resources offered by these multi-core systems.

Instead of updating all the parameters one by one, by using low-dimensional or scalar components (Gilks et al., 1996), we propose here to use multivariate components to update blocks of parameters, leading to acceptance or rejection for all of those parameters simultaneously. To accomplish this, we exploit an adaptive MCMC approach based on the study of Roberts and Rosenthal (2009), for which we provide an implementation in the popular open source BEAST software package (Drummond et al., 2012), to simultaneously estimate a large number of partition-specific parameters. In this article, we apply such an adaptable variance multivariate normal (AVMVN) transition kernel to a collection of clock model parameters, speciation model parameters, coalescent model parameters and partition-specific evolutionary model parameters (which include substitution model parameters, varying rates across sites parameters and relative rate parameters). Note that other model parameters, such as for discrete and continuous trait models and sequence error models for example, can also be used with our proposed AVMVN transition kernel. We show that such an AVMVN transition kernel tremendously increases estimation performance over a standard set of single-parameter transition kernels. We also provide a new parallel likelihood implementation in BEAST, to be used with the BEAGLE library (Ayres et al., 2012) and show that this implementation further increases performance.

2 Materials and methods

2.1 Adaptive MCMC

We consider a version of the adaptive Metropolis (AM) algorithm discussed by Haario et al. (2001) and Roberts and Rosenthal (2009) that continuously adapts its d-dimensional proposal distribution to better match the target distribution. The AM algorithm is based on the classical random walk Metropolis algorithm (Metropolis et al., 1953) and an earlier study by Haario et al. (1999) that entertains a Gaussian proposal distribution centred on the chain’s current state and with a covariance calculated from a fixed number of previous states. The AM algorithm generalizes this by computing the covariance of the proposal distribution using all of the previous states. Importantly, this extension does not lead to an increased computational cost since one can apply simple recursion formulae to update the covariances (Haario et al., 2001). An important advantage of the AM algorithm is that it starts using the cumulating information from the beginning of the run, ensuring that the search becomes more effective at an early stage.

Apart from updating the proposal distribution by using currently available knowledge about the target distribution, the construction of the AM algorithm is identical to the usual random walk Metropolis-based chain. Suppose that at iteration $n-1$ we have sampled the states $X_0,X_1,\dots ,X_{n-1}$, where X₀ is the initial state. Fix the real parameter C_d and integer parameter C₀; a candidate point Y is then sampled from the (asymptotically symmetric) normal proposal distribution, given at iteration n by $Q_n(x,·)=N(x,{(C_d)}^2{I}_d/d)$ for $n\le C_0$, while for $n>C_0$

$$Q_n(x,·)=(1-\beta )N(x,{\Sigma }_n/d)+\beta N(x,{(C_d)}^2{I}_d/d),$$ (1)

where Σ_n is the current empirical estimate of the covariance structure of the target distribution based on the run so far, I_d is the d-dimensional identity matrix and β is a small positive constant. The candidate point Y is accepted with probability

$$\alpha (X_{n-1},Y)=\text{min}\hspace{0.17em}\left(1,\frac{\pi (Y)}{\pi (X_{n-1})}\right),$$ (2)

in which case we set $X_n=Y$, and otherwise $X_n=X_{n-1}$, where $\pi (·)$ is the target distribution, the posterior density given the observed data.

Note that the chosen probability for the acceptance resembles the familiar acceptance probability of the Metropolis algorithm. This choice for the acceptance probability is not based on symmetry/reversibility conditions as these cannot be satisfied, given that the corresponding stochastic chain is no longer Markovian (Haario et al., 2001). It is known that adaptive MCMC algorithms will not always preserve stationarity of $\pi (·)$ (Roberts and Rosenthal, 2009). However, having proven the ergodicity of adaptive MCMC under certain conditions (Roberts and Rosenthal, 2007), the authors have also shown that the AM algorithm above will indeed converge to $\pi (·)$ and satisfy the Weak Law of Large Numbers, even though it is not Markovian.

We have implemented the AM algorithm described above in BEAST (Drummond et al., 2012) through the AVMVN transition kernel. While Roberts and Rosenthal (2009) fix C₀ to equal 2d, i.e. two times the dimension of the parameter space being updated by the AM algorithm, phylogenetic models may take a long time to approach their stationary distributions. As a value of 2d is likely to be insufficient to provide adequate performance, we ask BEAST users to specify a value for C₀. Further, Roberts and Rosenthal (2001) show that the proposal $N(x,{(2.38)}^2{\Sigma }_n/d)$ is optimal in a particular large-dimensional context, hence their corresponding proposal to approximate such a scenario. We do not follow this approach because we rely on the automatic tuning approaches present in BEAST (Drummond et al., 2012). We also do not follow the suggestion of fixing C_d to 0.1 (Roberts and Rosenthal, 2009), but instead allow BEAST users to specify this value, with a default of C_d = 1.0. Finally, while Roberts and Rosenthal (2009) assume β to equal 0.05, we here allow users to set this value as well.

In addition to our adaptations of the AM algorithm proposed by Roberts and Rosenthal (2009), we also extend this approach by allowing BEAST users to make use of the following two additional arguments/options. First, we suggest determining the covariance Σ_n by using only an increasing part of the history (Haario et al., 2001), for example by forgetting the first n₀ samples. This is specifically useful if the chain starts far away from the target distribution and collects samples to estimate the variance, which would result in the variance being very large. We offer guidance on setting values for C₀ and n₀ in the Discussion and in the Supplementary Materials. Second, we allow BEAST users to specify an integer $n_1>1$, which results in the covariance being updated every n₁^th step only, but in still using the entire history if one chooses (Haario et al., 2001). Such a subsampling approach results in a decreased learning rate/slower adaptation for the AM algorithm, but may economise on computation time when d is large.

2.2 Transformations

Finally, the AVMVN transition kernel assumes that all d dimensions of its parameters live on the real line, i.e. $x\in {ℝ}^d$. This rarely holds in the phylogenetics problems where parameters are often rates on $[0,\infty )$ or are constrained such that several parameters are non-negative and always sum to a fixed value. To handle these situations, the AVMVN transition kernel may act on appropriate transforms of the parameters that expand their ranges onto the real line. These transforms include the $\mathsf{log}(·)$ and $\mathsf{logit}(·)$ functions for univariate parameters that attain strictly positive values and values between 0 and 1, respectively.

For multivariate parameters $(x_1,\dots ,x_M)$ that are all strictly positive and constrained to sum to a constant $C$, such as the relative rate parameters in a partitioned dataset, we invoke a scaled, multivariate logistic function (Glonek and McCullagh, 1995) from a transformed space $({\tilde{x}}_1,\dots ,{\tilde{x}}_M)\hspace{0.17em}\in \hspace{0.17em}{ℝ}^M$. Specifically, let $L=\sum _j\hspace{0.17em}\text{exp}\hspace{0.17em}({\tilde{x}}_j)$ for $j=1,\dots ,M$, then

$$x_j=\frac{C}{L}\text{exp}\hspace{0.17em}({\tilde{x}}_j).$$ (3)

Notably, the transformed space carries one more degree-of-freedom than the constrained space. To rectify this, we augment the untransformed space with the extra random variable $L$. Since our original target distribution $\pi (·)$ does not depend on $L$, we are free to construct an augmented target distribution as the product of the original and any distribution on $L$ we choose, including a point-mass on a single value, such as $C$.

After transformation, the AVMVN kernel is not necessary symmetric. Minor modifications through a Hastings ratio (Hastings, 1970) become necessary and are straight-forward. For the scaled, multivariate logistic transform, the Hastings ratio for proposing $(y_1,\dots ,y_M)$ given the chain is currently at $(x_1,\dots ,x_M)$ is

$$\prod _j\left(\frac{y_j}{x_j}\right).$$ (4)

2.3 Priors

In a recent study, we have shown the importance of using proper priors (probability distributions that integrate to 1) when performing Bayesian model selection, which also applies when performing Bayesian inference through MCMC (Baele et al., 2013). The frequently used constant function, often inaccurately called a uniform distribution, over an infinite interval is an example of an improper prior; the use of such priors may lead to a posterior distribution that does not exist. We use the following priors in our analyses throughout this article: a pure birth process (Yule, 1924) as the tree prior for the isochronous dataset, with a diffuse normally distributed prior on the log growth rate; an exponential growth coalescent model as the demographic prior for the heterochronous dataset, with a diffuse normally distributed prior on the log population size and a diffuse Laplace prior on the growth rate; a diffuse normally distributed prior on the log transition/transversion parameter of the HKY model; a diffuse Dirichlet prior on the relative rate parameters of the different partitions; an exponential prior on (each of) the rate heterogeneity parameter(s) (Yang, 1996) and a continuous-time Markov chain reference prior on the strict molecular clock rate in the heterochronous dataset (Ferreira and Suchard, 2008).

2.4 Transition kernel weight determination

MCMC sampling in BEAST uses a random-scan of transition kernels, such that each kernel carries a weight that is proportional to its selection probability for use at each chain step. We use the following procedure for determining the weights of the different transition kernels in this article. First, a BEAST XML file for both datasets was generated using BEAUti, i.e. the user interface accompanying BEAST. The weights for the tree transition kernels, i.e. all kernels that operate on the tree topology and/or the node heights, were kept at their default values. The weights for the remaining parameters were slightly adjusted to arrive at a baseline scenario where the effective sample size (ESS; computed using the coda package; Plummer et al., 2006) for all parameters of interest were fairly similar when performing inference using the default transition kernels. For the isochronous carnivores dataset (see Data), this mainly resulted in a reduction of the weight on the transition kernel for the birth rate of the Yule process. For the heterochronous Ebola virus dataset (see Data), only the weights on the shape parameters that describe rate heterogeneity for the different partitions were increased.

We set the weight on each AVMVN transition kernel equal to the sum of the weights of the separate transition kernels on the corresponding parameters. For the carnivores dataset, one transition kernel was constructed, containing all non-tree related parameters. The Ebola virus dataset was tested using two multivariate transition kernels: one for the parameters of the exponential growth coalescent model and another for the remaining parameters. This is motivated by performance considerations, as evaluating coalescent likelihoods is much faster than calculating all the observed data likelihoods.

2.5 Multi-threaded likelihood and load balancing

The development of the BEAGLE library and its corresponding likelihood implementations has resulted in large performance increases of the BEAST package (Suchard and Rambaut, 2009; Ayres et al., 2012). To perform efficient evaluation of a possibly large collection of (observed) data likelihoods simultaneously, we have implemented a new multi-threaded likelihood in BEAST (Drummond et al., 2012) that significantly reduces the existing overhead when few (observed) data likelihoods need to be recalculated.

Given that most high-performance computing machines are equipped with a large number of cores, we also propose an automated load-balancing algorithm, now available in BEAST (Drummond et al., 2012), that determines how many additional data partitions—with associated data likelihoods and shared parameters—need to be created to maximize performance on a given multi-core CPU system. An additional data partition is hence created when this leads to a faster overall likelihood evaluation, by proposing to further split the partition with the largest number of unique site patterns. This load-balancing algorithm is available to BEAST/BEAGLE users through XML specification, with an option to specify the number of likelihood evaluations that will be averaged in determining execution time for each combination of partitions. We provide more detailed information on our load-balancing algorithm in the Supplementary Materials.

2.6 Hardware

All BEAST/BEAGLE calculations were performed on a 24-core (i.e. 2 × 12) Intel Xeon (R) Xeon E5-2680 v3 2.50 GHz system (Haswell microarchitecture) with Infiniband FDR and a 40-core (i.e. 4 × 10) Intel Xeon(R) E7-4870 2.40 GHz system (Westmere-EX microarchitecture). The former has a Quick Path Interconnect (QPI) speed of 9.6 GT/s and a maximum boost frequency of 3.30 GHz and is equipped with DDR4 memory running at 2133 MHz, whereas the latter has a QPI speed of 6.4 GT/s and a maximum boost frequency of 2.80 GHz and is equipped with DDR3 memory running at 1066 MHz.

2.7 Rescaling procedure

For all our computations, we used CPUs with 64-bit (double) precision. However, even at double precision, rounding error can still occur while propagating the partial likelihoods up a large tree (Suchard and Rambaut, 2009). In anticipation of an under- or over-flow occurring when computing the likelihood, we have implemented a rescaling procedure—a minor variation of the existing dynamic (default) rescaling—in BEAST (Drummond et al., 2012) to help avoid roundoff, following the suggestion of Yang (2000). Our rescaling scheme does not compute scaling factors each iteration but keeps the current ones until an under- of over-flow occurs (or every N iterations) because finding appropriate scale factors is much more expensive than actually using them.

2.8 Data

As a first dataset, we analyse the ND5 gene from a collection of 62 mitochondrial genomes from carnivores, previously analysed by Suchard and Rambaut (2009). This dataset contains 1836 nt columns, of which approximately 99% consist of a unique site pattern, and is partitioned according to codon position. As a second dataset, we analyse a full genome Ebola virus dataset, consisting of 633 publicly available genome sampled over the course of the 2013–2016 Ebola virus disease epidemic in West Africa. This dataset contains 18 998 nt columns and is partitioned according to codon position, with one additional partition for the intergenic region (which consists of several non-coding regions interspersed in the genome). For both datasets, we consider the underlying phylogeny to be unknown and estimate the tree topology and branch lengths during our Bayesian inference approach.

3 Results

3.1 Isochronous samples

The 62-taxa carnivores dataset consists of a single gene (ND5) that we partition according to codon position. We assume that each partition evolves at a different relative rate and according to an independent HKY model (Hasegawa et al., 1985), with rate variation among sites in each partition modelled by a discrete gamma distribution with 4 rate categories (Yang, 1996). Together with the Yule process prior (Yule, 1924) on the tree, this amounts to 10 parameters to be estimated in addition to the phylogeny: three transition/transversion ratios (${\kappa }_1,{\kappa }_2,{\kappa }_3$) - $\log$-transformed, three shape parameters to model varying rates across sites (${\alpha }_1,{\alpha }_2,{\alpha }_3$) - $\log$-transformed, three relative rates (${\mu }_1,{\mu }_2,{\mu }_3$) - scaled $\mathrm{logit}$-transformed, and a birth rate ψ - $\log$-transformed - for the Yule process prior.

The default approach in BEAST is to use scale or random walk transition kernels, 1 on each parameter, which we compare here to 1 AVMVN transition kernel that simultaneously proposes new values for all 10 parameters. Weights for the default transition kernels for ${\mu }_1,{\mu }_2,{\mu }_3$ and κ₃ were set at 6 and 3, respectively, with the remaining non-tree transition kernel weights set at 2 (see Materials and methods); weights for the tree transition kernels were kept at their original values at the time of writing (as of BEAST v1.8.4 the default weights for the transition kernels have been changed). This leads to a combined weight of 21 for the AVMVN transition kernel; the tree transition kernels and their weights were kept to their defaults. For the AVMVN transition kernel, C₀ was set to 1.000, with n₀ set at 500, which leads to slightly better performance compared to what we consider to be the default values for datasets with a relatively low amount of parameters ($C_0=5.000$ and $n_0=2.500$).

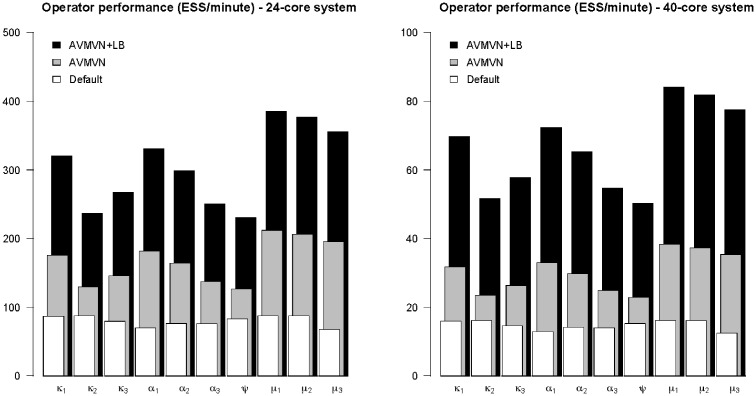
We evaluate the performance of the different sets of transition kernels for the carnivores dataset (Fig. 1) on different multi-core CPU systems across five independent replicates. We measure the performance under both sets of transition kernels by computing the total ESS per minute for all of the parameters of interest. While the more recent Haswell platform has much greater execution speed than the Westmere platform, which can be attributed to its substantially higher memory bandwidth, the observed performance gains are very similar across both platforms. We observe a large but varying increase in performance using our multivariate normal transition kernel, which performs an equal amount of update operations on all parameters, over the default transition kernels. This already illustrates the power of our approach, but the performance of our proposed AVMVN transition kernel can be further increased by using our load-balancing algorithm, which determines the optimal amount of processor cores for the analysis to run on. This algorithm yields a similar performance on both systems, generating on average 5 and 6 additional partitions/threads, on the Haswell and Westmere systems respectively, resulting in runs with a total of 8 and 9 partitions/threads on average.

Fig. 1.

Performance comparison on a single gene carnivores dataset, partitioned according to the codon position, across five replicates measured on 24-core and 40-core Xeon systems. The 24-core CPU system, while equipped with fewer processor cores than the 40-core CPU system, has a faster maximum processor frequency and comes equipped with much faster memory, explaining the difference in performance as measured in ESS per time unit. Mixing of all parameters of interest is compared using the default BEAST transition kernels, our proposed AVMVN transition kernel and our proposed AVMVN transition kernel that takes advantages of our proposed load-balancing approach to further exploit multi-core parallelism (AVMVN + LB). All update schemes assign an equal weight distribution between updating continuous parameters and updating the tree. The AVMVN transition kernel, equipped with our load-balancing approach, yields an increase in performance over the default BEAST transition kernels between 171 and 424%, measured in ESS/minute, on a 24-core CPU system and between 221 and 520%, measured in ESS/minute, on a 40-core CPU system

We observe the lowest performance increase for the birth rate parameter of the Yule process (ψ), indicating that this is the most difficult to estimate efficiently. Mixing may be improved by specifying a separate transition kernel on the birth rate parameter, with its own tuning parameter and possibly an increased weight. However, pursuing this is beyond the scope of our goal to compare the performance of default transition kernels and our multivariate transition kernel.

3.2 Heterochronous samples

The 633-taxa Ebola virus dataset consists of a large coding region, which we partition according to codon position, and a non-coding region. We again assume that each partition evolves according to an HKY model (Hasegawa et al., 1985), impose a discrete gamma distribution with 4 rate categories (Yang, 1996) on each partition, allow the codon positions to evolve at different (relative) rates and assume a strict molecular clock. Together with specifying an exponential growth coalescent prior on the tree, this leads to 15 parameters to be estimated: four transition/transversion ratios (${\kappa }_1,{\kappa }_2,{\kappa }_3,{\kappa }_4$) - $\log$-transformed, four shape parameters to model varying rates across sites (${\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4$) - $\log$-transformed, four relative rates (${\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4$) - scaled $\mathrm{logit}$-transformed, the strict clock rate γ - $\log$-transformed, an effective population size $\varphi$ - $\log$-transformed - and an exponential growth rate ρ in the coalescent prior.

To achieve maximal performance for this dataset, we have used two different AVMVN transition kernels on two disjunct sets of parameters. Weights for the default transition kernels for ${\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4$ were increased to 3, while the other transition kernel weights were kept at their default values, i.e. 3 for the joint update process on ${\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4$, 1 for each of the ${\kappa }_i,i\in 1\dots 4$ and 30 for the clock rate γ, population size $\varphi$ and exponential growth rate ρ in the coalescent prior. Weights for the tree transition kernels were kept at their original values at the time of writing.

Our first AVMVN transition kernel acts on both parameters of the exponential growth coalescent model with a weight of 60, which is the combined weight of the default transition kernels. We are able to increase this kernel’s performance by setting C₀ to 2.000 and $n_0=1.000$, although our proposed default settings (of $C_0=5.000$ and $n_0=2.500$) offered nearly similar performance in terms of ESS per time unit. Our second AVMVN transition kernel acts on the remaining parameters using its default settings (of $C_0=5.000$ and $n_0=2.500$), including the clock rate (of which a proposed change also triggers a full recalculation of all observed data likelihoods), again with a weight set to the sum of the weights of the default transition kernels on these parameters. Using two separate transition kernels is a sensible choice given that the coalescent density evaluation takes only a fraction of the time required to calculate any of the observed data likelihoods. Moreover, this allows assigning different weights to the AVMVN transition kernels and the optimization of a different tuning parameter.

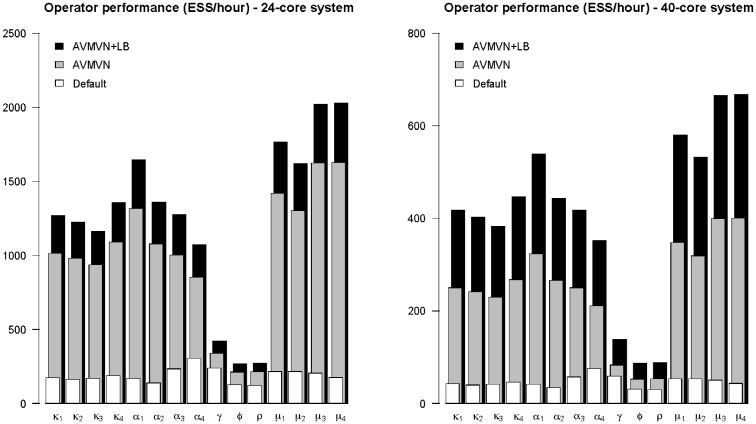
The performance comparison between the transition kernels for the Ebola virus dataset on different CPU server systems across five independent replicates is shown in Figure 2. Because of a much larger dataset size as compared to the carnivores dataset, we measure the performance under both scenarios by computing the total ESS per hour for all of the parameters of interest. The observed performance gains are again similar across both platforms, but larger performance gains are achieved on the 40-core Westmere system compared to the more recent 24-core Haswell platform. The slower execution speed of the former translates into additional partitions/threads being created by the load-balancing algorithm, as information between the threads is exchanged less frequently, allowing for longer periods of time during which the different threads can perform concurrent calculations. The load-balancing algorithm generates on average three additional partitions/threads on top of the four initial partitions/threads on the Haswell system and on average six additional partitions/threads on top of the 4 initial partitions/threads on the Westmere system, which amounts to a total of 7 and 10 partitions/threads on average.

Fig. 2.

Performance comparison on a full genome Ebola virus dataset, partitioned according to the codon position, across five replicates measured on 24-core and 40-core Xeon systems. Mixing of all parameters of interest is compared between the default BEAST transition kernels, the AVMVN transition kernel and the AVMVN transition kernel that takes advantages of a load-balancing approach to further exploit multi-core parallelism (AVMVN + LB). All update schemes assign an equal weight distribution between updating continuous parameters and updating the tree. Relative to the default BEAST transition kernels, the performance of the AVMVN transition kernel, equipped with our load-balancing approach, increases with between 76% and 1057%, measured in ESS/minute, on a 24-core CPU system and between 134 and 1452% (for μ₄, the relative rate of the non-coding partition), measured in ESS/hour, on a 40-core CPU system

Except for those parameters directly related to estimating the coalescent tree, i.e. the clock rate, population size and exponential growth rate, a considerable increase in performance for the AVMVN transition kernels over the default transition kernels can be seen in Figure 2. Whereas we observe a 2- to 3-fold performance increase for the clock rate, population size and exponential growth rate parameters, their performance increase clearly lags behind that of the other parameters. Changing the relative weights of both AVMVN transition kernels does not yield any further performance gains, nor does adjusting the kernels’ settings.

4 Discussion

In this article, we present an adaptation of the adaptive MCMC approach of Roberts and Rosenthal (2009) for use in Bayesian phylogenetics. Using this approach, we show that there is a large potential for performance increase in Bayesian phylogenetic inference, with parameter estimates exhibiting an up to fourteen-fold increase in performance. Additionally, our proposed AVMVN transition kernel is able to operate on a wide variety of model parameters, such as for example substitution model parameters, (molecular) clock model parameters and speciation/coalescent model parameters. Obtaining good mixing for these parameters can be challenging, in particular in the absence of very strong calibrating information (e.g. temporal signal in heterogeneously sampled data), and because they are correlated through the tree height, they can also affect mixing of node height estimates. Our results also uncover other interesting avenues for research into estimating large coalescent trees, as the parameters relating to the tree are more difficult to estimate and are shown to benefit to a lesser extent from our proposed approach. While this may be due to more complicated population dynamics over time than can be represented using an exponential growth coalescent model, as the Ebola virus dataset covers both the growth and the decline phase of the epidemic, novel tree transition kernels that navigate through tree space more efficiently can yield faster convergence and better mixing, particularly when confronted with large topologies (see e.g. Höhna and Drummond, 2012). Further, correlated parameters such as the root height, the clock rate and population size for example may benefit from joint estimation, which could be accommodated by our transition kernel we propose here, but further research is required to evaluate the performance of such parameter mixes in our framework. Nonetheless, the novel parallel likelihood evaluation and load-balancing approach we employ does not depend exclusively on the AVMVN transition kernel and hence can increase overall computational performance when evaluating proposed tree topologies as well.

We have analysed the variance-covariance structure of our proposed AVMVN transition kernels (see Supplementary Materials) and tested many different computational settings. Our tests on the datasets analysed in this article show that a C₀ setting of 5.000, with the first $n_0=2.500$ samples being discarded, typically yields consistent results that offer a large increase in performance over the default transition kernels. For datasets where the parameters easily converge to their posterior distribution, as was the case for the carnivores dataset in this article, further increases in efficiency (of up to 10%, but depending on the parameter) can be achieved by lowering those settings to, for example, $C_0=2.000$, with discarding the first $n_0=1.000$ samples. Datasets that contain parameters that do not converge as easily, such as the molecular clock rate in the Ebola virus dataset in this paper, benefit from increasing the C₀ setting. Coalescent model parameters, such as the population size and the growth rate in the exponential growth model applied to the Ebola virus dataset, on the other hand, also benefit from lowered settings for C₀ and n₀.

We have also tested how our proposed AVMVN transition kernel performs on an example dataset with a much larger number of partitions and corresponding increase in number of parameters (see Supplementary Materials). We extended the isochronous dataset discussed in this article to incorporate eight genes, with each gene being partitioned according to codon position, leading to 24 partitions that were all equipped with a general time-reversible model (Tavaré, 1986), increasing the total number of parameters to 169. We show that our AVMVN transition kernel is able to (drastically) improve ESS values for the vast majority of parameters, but that computational restraints of multi-core CPU systems prevent a sufficiently fast simultaneous evaluation of all the data likelihoods. Further, our tests show that a C₀ setting of 40.000, with the first $n_0=30.000$ samples being discarded, typically yields consistent results that offer a large increase in performance over the default transition kernels. This shows that additional work is needed to express these settings as a function of the number of parameters, and perhaps more importantly, as a function of the information present in each partition. We propose to tentatively set C₀ at 200 times the number of parameters in the (combined) AVMVN transition kernel(s), with n₀ equal to $C_0/2$.

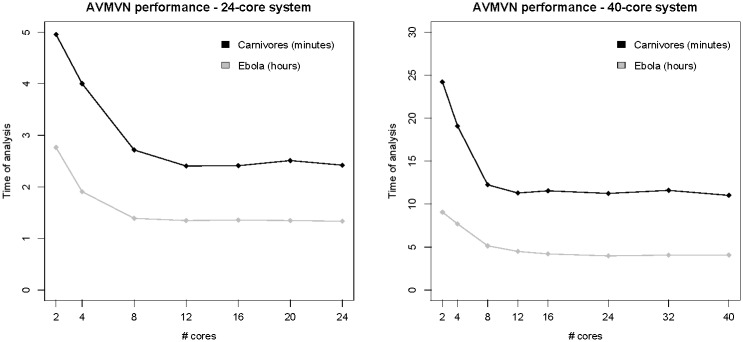
The results we present in this article are obtained using multi-core CPU architectures, which still constitute the vast majority of hardware investments for high-performance computing solutions. In order to improve computational speed, such a solution is however limited and not always cost-effective because of storage issues, cooling requirements and maintenance. Figure 3 examines the optimal number of processor cores that our approach could exploit in order to reach maximal performance. Whereas computational improvements are easy to come by initially, investing in a multi-core CPU setup that involves over 12 cores no longer yields additional performance increases. Further, the memory specifications of such a system may be of critical importance, as the 24-core CPU system we use holds random-access memory (RAM) with twice the speed - and hence a much higher memory bandwidth - compared to the 40-core CPU system. For multi-threaded computations, such as the ones presented here, an increasing core count puts pressure on the cache capacity and memory bandwidth. Increased memory bandwidth is therefore essential to move data from the main memory to the cores fast enough and may be more important than adding additional cores.

Fig. 3.

Performance of the AVMVN transition kernel as a function of the number of cores in a multi-core CPU setup, measured in time to run the analyses performed (in minutes for the carnivores dataset and in hours for the Ebola virus dataset) across five independent replicates. Both CPU systems we evaluate show the same trend, i.e. the run time decreases systematically when additional cores are used, until a saturation point is reached where creating additional partitions no longer increases performance due to an associated increase in overhead

Graphics processing units (GPUs) offer a much less expensive alternative than multi-processor multi-core systems, while being fairly easy to manage as they fit into many desktop computers. At the first release of the BEAGLE library (Ayres et al., 2012), GPUs were still fairly limited in their number of cores and specifically in the amount of on-board memory, leading to computations often being split onto multiple GPUs (Suchard and Rambaut, 2009). GPUs now come equipped with thousands of cores and larger amounts of memory, enabling them to process and evaluate larger datasets such as those generated by next-generation sequencing efforts. Combining our proposed multivariate approach with a GPU’s computing capabilities on datasets containing a large number of partitions hence represents the next step in our development, given that the higher memory bandwidth of GPUs will allow for a larger number of partitions to be evaluated simultaneously.

GPUs can achieve extremely high arithmetic intensity if one can transfer the input data and output results onto and off of the processors quickly. Using CUDA or OpenCL, it becomes possible for software libraries such as BEAGLE to manage concurrency by executing asynchronous commands in streams, sequences of commands that execute in order. Different streams may execute their commands concurrently or out of order with respect to each other. The current BEAGLE implementation (2.1.2) does not allow yet to make use of the concurrency capabilities promised by using these CUDA streams. Allowing for concurrent computation of a much larger collection of partitions/threads in BEAGLE represents an important avenue of further development.

Funding

The research leading to these results has received funding from the European Union Seventh Framework Programme for research, technological development and demonstration under Grant Agreement no. 278433-PREDEMICS. The VIROGENESIS project receives funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 634650. The COMPARE project receives funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 643476. This work is supported by National Science Foundation (NSF) [DMS 1264153 to M.A.S.] and National Institutes of Health [R01 HG006139 to M.A.S.]. G.B. acknowledges the support of a Research Grant of the Research Foundation - Flanders (FWO; Fonds Wetenschappelijk Onderzoek - Vlaanderen). We acknowledge funding of the ‘Bijzonder Onderzoeksfonds', KU Leuven (BOF, No. OT/14/115) and the Research Foundation - Flanders (FWO, G0D5117N & G0B9317N).

Conflict of Interest: none declared.