Abstract
NK-2, derived from a cationic core region of NK-lysin, displays antimicrobial activity toward negatively charged bacterial membranes. We have studied the interaction of NK-2 with various phospholipid membranes, using a variety of experimental techniques, such as, isothermal titration calorimetry (ITC), ζ potential, and dynamic light scattering. As bacteria mimicking membranes, we have chosen large unilamellar vesicles (LUVs) composed of negatively charged phospholipid and neutral phospholipids. ITC and ζ potential results show the stronger binding affinity of NK-2 to negatively charged membranes than to neutral membranes. Saturation of the isotherm, obtained from ITC, at a given lipid to NK-2 ratio, was found to be consistent with the charge compensation, determined from ζ potential. A surface partition model with electrostatic contribution was used to estimate the intrinsic binding constant and other thermodynamical parameters of binding kinetics of NK-2. The size distribution of negatively charged LUV in the presence of NK-2 was found to increase drastically, indicating the presence of large aggregates. Such a large aggregate has not been observed in neutral membranes, which supports the ITC and ζ potential results.
1. Introduction
Antimicrobial peptides (AMPs) are an innate immune response in animal and human body against invading pathogens, such as viruses, fungi, bacteria, etc.1,2 They target the bacterial membrane, especially negatively charged surface, and create defects, such as pores, leading to disruption of the membrane.3 An important property of AMP is the specificity of bacterial targets and excludes the killing of most eukaryotic cells.4 The resistance to conventional antibiotics and the natural cell lytic activity of many AMP and their unique mode of action have led to a new possibility in the development of AMP as human therapeutics.5 Therefore, studies on the interaction of AMP with lipid membranes have drawn a lot of attention due to their potential biomedical applications.1,6−8 Diverse applications of AMP include as anti-infective agents, anticancer agents, drug delivery and nonviral gene transfer.1,9 A major problem that has impeded the development of drug design is the toxicity. NK-2, an AMP, which is nontoxic and nonhemolytic to the human skin cells, can be a potential candidate for designing antibiotics.10
NK-2 is a water soluble linear amphipathic helical peptide.8 It is the highest density region of NK-lysin having cationic charge of +10 at physiological pH. The high positive charges within the NK-2 promote strong binding to the negatively charged membranes.11 The antimicrobial activity of NK-2 toward parasitic membranes involves the interaction with lipids in the membranes. A teleost NK-lysin peptide, NKLP27, is known to induce degradation of bacterial DNA and inhibits bacterial and viral infection.12 There have been a large number of studies of many AMP, using a variety of experimental techniques, such as optical microscopy,13−16 oriented circular dichroism,17 X-ray and neutron scattering,18 isothermal titration calorimetry (ITC),19 and differential scanning calorimetry.20 However, very little is known in the case of NK-2. NK-2 impels significant changes in cellular morphology of human cancer cells and eventually cells lose their cellular integrity until destruction.21 NK-2 intercalates and binds to the negatively charged membranes, such as 1,2-dipalmitoyl-sn-glycero-3-phosphoglycerol (DPPG) and 1,2-dioleoyl-sn-glycero-3-phospho-l-serine (DOPS), but does not interact with the phosphatidylcholine (PC) or sphingomyelin, as revealed by the fluorescence resonance energy transfer21 and ζ potential.22 Conformational changes as well as the orientation of AMP play a vital role in the formation of transmembrane pores.7,21 Previous study of NK-2, dissolved in different aqueous solutions, has shown mainly α-helical conformation in the presence of negatively charged amphiphiles.8 Similar α-helical confirmation in the membrane environment has also been found in other AMP, such as melittin23 and Magainin 2.24 However, NK-2 adopts an unoriented random coil structure in the buffer, including water and in the presence of cationic and neutral amphiphiles below their critical micellar concentration. The conformational transition from random coil to helix arises mainly due to electrostatic interaction of positively charged residues of the peptide with the negatively charged head group of amphiphiles.8 However, penetration of peptides into the hydrophobic core is a result of hydrophobic interaction between the hydrophobic chain of the amphiphiles and hydrophobic residues of the peptide.
Lipopolysaccharide (LPS), the major constituent of the outer membrane of gram negative bacteria, shows strong binding affinity to NK-2, as determined by various experimental techniques, such as small angle X-ray diffraction, ζ potential, and isothermal titration calorimetry.10 It is believed that the main pathway to disrupt the integrity of the cellular membrane is the formation of transmembrane pores. Different AMPs seem to follow different pathways to create transmembrane pores.25 Therefore, in spite of a large number of attempts, the mechanism of transmembrane pore formation is still under dispute.6,26 For example, molecular electroporation was proposed as the mechanism of membrane pore formation, induced by NK-lysin.27
Biological membranes are complex, regulated by various membrane components. Therefore, it is often useful to study model membranes to understand more complex lipid–peptide interactions and hence to get some insight into the mechanism of cellular damage induced by AMP. Giant unilamellar vesicles (GUVs), made from lipid molecules, serve as an excellent model system to study many biological activities.28 For example, a kinetic process involving interaction of melittin and other AMP with PC vesicles have previously been demonstrated using the micropipette aspiration technique13 and leakage assay using fluorescence spectroscopy.14,16 It was found from previous studies of various AMP that the activity of pore formation initiates above a threshold lipid to the peptide ratio (∼70 for melittin).13,17 This threshold seems to be different for different peptides.
There have not been systematic studies on the interaction of NK-2 with phospholipid membranes. Therefore, there are several open questions which have not been addressed in the literature. Does NK-2 make pores on the membranes, as in the case of other AMPs? If NK-2 makes pores, what is the mechanism that NK-2 uses to form transmembrane pores? How does the size of pores depend on lipid composition and concentration of NK-2? Although there was a previous study on the interaction of NK-2 with LPS,11 the binding affinity of NK-2 with negatively charged phospholipid is still not well understood. It is also important to know how the binding affinity of NK-2 with phospholpids depends on the head group charge and size of the head group. It would also be interesting to observe any morphological change induced by NK-2 in the model membrane.
The major constituents of bacterial membranes are phosphatidylethanolamine (PE) and phosphatidyl-glycerol (PG) (∼4:1).20 Therefore, in our present study, we have chosen model systems, composed of dioleoyl phosphatidyl-glycerol (DOPG) and mixtures of DOPG with dioleoyl phosphatidylethanolamine (DOPE) and dioleoyl phosphatidylcholine (DOPC). These lipids also show fluid phase at room temperature (25 °C). As model membranes, we have used large unilamellar vesicles (LUVs) to study the interaction of NK-2 with different phospholipids using isothermal titration calorimetry (ITC), ζ potential, and dynamic light scattering (DLS). In particular, the electrostatic behavior as well as the size distribution of the membranes in the presence of NK-2 was systematically characterized using ζ potential and DLS, respectively. Thermodynamics of the interaction of this system have been thoroughly investigated using ITC study. We have determined, for the first time, the binding affinity of NK-2 with negatively charged phospholipid membranes.
2. Results
2.1. ζ Potential
The summary of results on ζ potential is illustrated in Figure 1. The ζ potential was measured in LUV dispersion, made from DOPC, DOPG, DOPE–DOPG (4:1) mixture, and mixtures of DOPC with DOPE and DOPG, before and after introducing peptides (i.e., before and after ITC measurements). As shown in Figure 1, ζ potential increases with increasing NK-2 to lipid molar ratio (NK-2/L) and charge compensation occurs at different NK-2/L for different lipid mixtures. Although phospholipids, such as DOPC and a mixture of DOPC–DOPE, are neutral, they exhibit a low negative value. A small negative ζ potential gets neutralized at NK-2/L, ∼1:250. In comparison, charge neutralization happens for DOPG at much higher NK-2/L (1:5). For DOPE–DOPG (4:1) mixtures, charge compensation occurs at intermediate NK-2/L (1:25). These differences are due to the fact that charge compensation occurs with respect to charge lipids. Interestingly, the ζ potential shows its saturation value, indicating overcharge compensation at different NK-2/L for various lipid mixtures (Figure 1). The ζ potential of DOPG shows a saturation at a much higher NK-2/L (3:10) than that of DOPC and DOPC–DOPE (1:250), whereas the ζ potential for DOPE–DOPG and DOPC–DOPG mixtures shows this at intermediate NK-2/L (1:20). The above result clearly indicates that NK-2 has a stronger affinity toward the negatively charged lipids.
Figure 1.
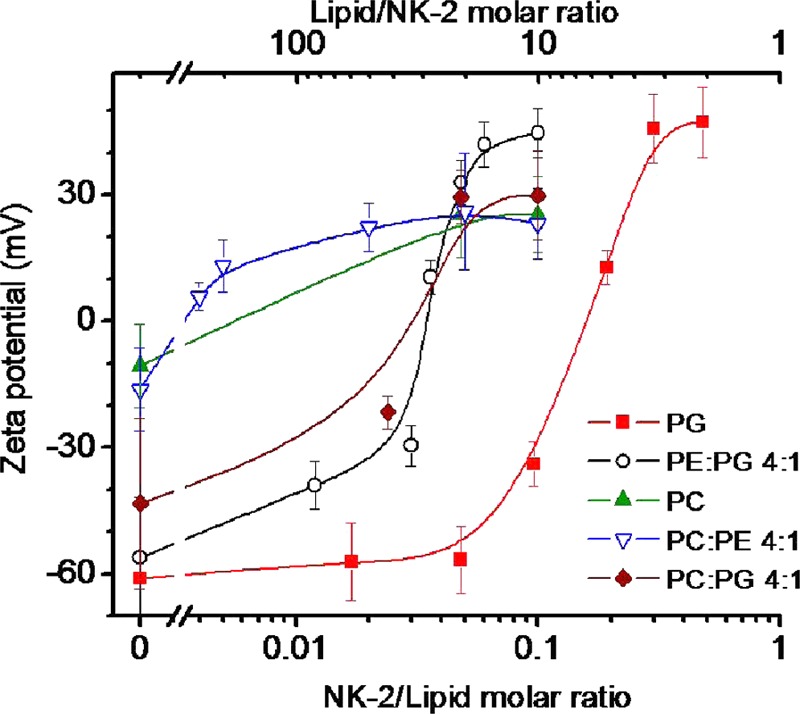
ζ Potential of phospholipid LUV at various NK-2 to lipid molar ratios. Solid lines are intended only as guides to the points. Error bars indicate the width of the distribution profile of ζ potential.
2.2. Size Distributions of LUV
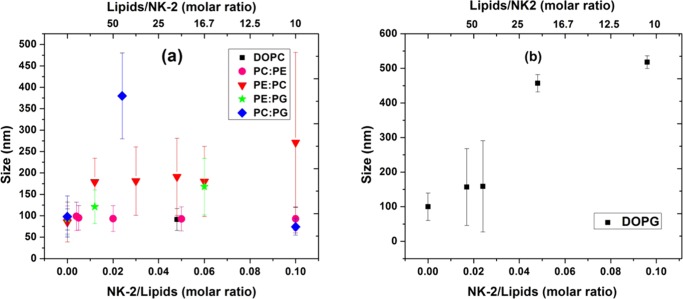
LUVs composed of pure DOPC and DOPG were found to be very stable, as no significant change in the size distribution was seen in DLS measurement even a couple of months later. The size distribution was measured for all lipid mixtures before (absence of NK-2) and after (presence of NK-2) ITC. The average diameter of LUV at different NK-2/lipid ratios is presented in Figure 2. The error bars in Figure 2 represent the width of the distribution, which is a measure of polydispersity of LUV. This error is relevant for understanding the effect of NK-2 on the membranes. However, errors, obtained from different measurements, are small and are not shown in the plot. Neutral LUVs, made from DOPC and a mixture of DOPC and DOPE, do not exhibit any significant change in their size distribution in the presence of NK-2 (Figure 2a). However, the average size of the negatively charged LUV increases with increasing Cnk2. Interestingly, LUVs made from pure DOPG show a dramatic increase in their average size in the presence of NK-2 (Figure 2b). The width of the size distribution (error bar in Figure 2), indicating polydispersity, also increases with the increase of Cnk2. In all samples containing DOPG, transparent LUV dispersion becomes turbid after ITC measurement. Therefore, as the NK-2/lipid ratio is increased, the sample exhibits a high value of size as well as high polydispersity and eventually shows large aggregates. After a couple of hours, the sample appears very turbid and hence the sample was not suitable for DLS measurement. This behavior clearly indicates that sample contains large aggregates induced by NK-2.
Figure 2.
Size distribution of LUV made from various lipid compositions in the presence of NK-2. (a) LUV are composed of DOPC and other phospholipid mixtures, as indicated by the figure legend. (b) LUV composed of DOPG. Error bar is the standard deviation and was obtained from the width of the distribution.
2.3. Binding Affinity of NK-2 with Model Membranes Measured from ITC
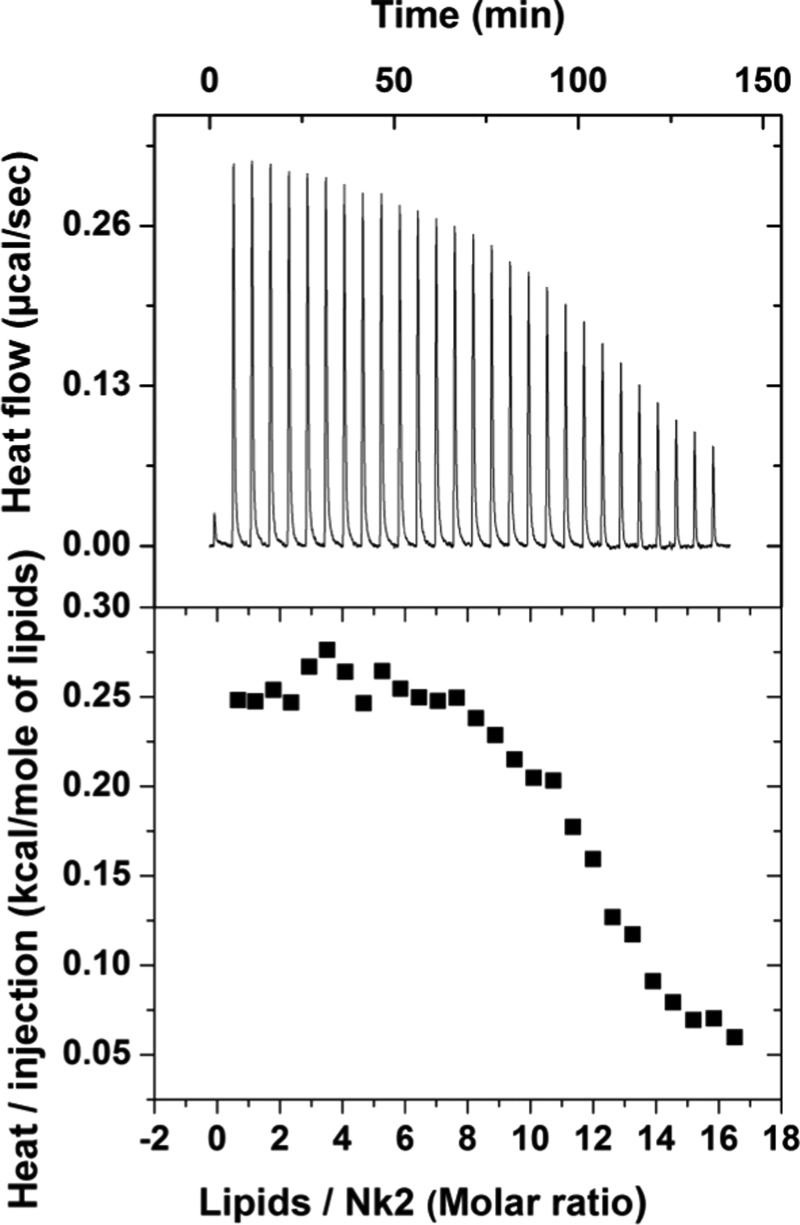
NK-2 of various concentrations, Cnk2 (100, 50, 40, 30, 25, and 10 μM) was titrated with 4 mM of LUV made from the DOPE–DOPG (4:1) mixture. For first few injections, heat flow remains constant, then starts decreasing as less and less NK-2 is available for binding. Typical raw data of ITC measurement at Cnk2 = 50 μM are shown in Figure 3. The lipid to NK-2 (L/NK-2) ratio at which saturation of the heat flow occurs is ∼20:1, taking into account all lipids (i.e., both monolayers of the LUV) interacting with the NK-2. The overall binding reaction was endothermic for all Cnk2. Interestingly, when the endothermic signal attains its saturation at ∼L/NK-2 = 20, further successive one to three injections show an exothermic signal and then successive injections contribute almost negligible heat (data not shown). This behavior is displayed in the raw ITC thermogram when lower Cnk2, typically <40 μM, was used. For these concentrations, saturation occurs before completing all injections of LUV. At the beginning of the titration, there are plenty of peptides to bind with lipids. Therefore, we have analyzed the data taking into account only the initial part of the endothermic heat signals or the data where all injections of LUV have been finished before the exothermic peaks appear, i.e., for Cnk2 > 40 μM. Although some of the isotherms can be fitted to one site binding model given by microcal origin, it gives us the apparent binding constant (Kapp), which is expected to vary with concentrations of unbound or free NK-2 concentration. However, the order of magnitude of the Kapp has been found to be consistent with the value obtained from the surface partition model. As the interaction of NK-2 with the negatively charged membranes is primarily driven by the surface charge of the membranes, it is desirable to fit the data taking into account the electrostatic contributions. Therefore, the more relevant parameter would be the intrinsic binding constant (Kint), where the surface concentration of peptide (CM) is more relevant than the bulk or free peptide concentration (Cf).
Figure 3.
Titration calorimetry of 50 μM NK-2 with 4 mM DOPE–DOPG (4:1) LUV (top); normalized heat of injection/mole of lipids, obtained from the integration of the individual peak (bottom). Heat of dilution, obtained from injecting 4 mM LUV into buffer, was subtracted from the actual measurement. Here we assume, lipids from both monolayers interact with the NK-2.
The model parameters, such as the extent of peptide binding (Xb), Cf, CM, Kint, etc, obtained numerically from experimental data, have been summarized in Table 1 (see Materials and Methods for details). In the case of DOPE–DOPG mixture, it is interesting to observe that CM versus Xb behaves linearly for lower lipid/NK-2, corresponding to 9–10 injections. However, the tendency to increase the value of Kint is evident from Table 1. Above 10 injections, the Kint increases with increasing the number of injections. Therefore, we have presented only the linear part of the data to estimate the Kint. The possible reason for increasing the value of Kint at higher lipid/NK-2 has been discussed later. The estimated values of molar binding enthalpy, ΔH, Kint, and binding entropy ΔS, obtained from the surface partition model with electrostatic contribution, have been summarized in Table 2.
Table 1. Parameters Obtained from Each Data Point in an ITC Experiment Using the Surface Partition Model Including Electrostatic Contributiona.
| lipid + peptide | lipid/NK-2 | Cf (mM) | CM × 10–6 (mM) | Xb | Kint (M–1) |
|---|---|---|---|---|---|
| DOPG (5 mM) + NK-2 (0.1 mM) | 0.34 | 0.08 | 3.29 | 0.420 | 1.28 × 108 |
| 0.62 | 0.07 | 2.86 | 0.414 | 1.45 × 108 | |
| 0.90 | 0.06 | 2.41 | 0.422 | 1.75 × 108 | |
| 1.19 | 0.05 | 1.97 | 0.422 | 2.14 × 108 | |
| 1.47 | 0.04 | 1.58 | 0.415 | 2.64 × 108 | |
| 1.76 | 0.03 | 1.20 | 0.407 | 3.41 × 108 | |
| 2.05 | 0.02 | 1.33 | 0.395 | 2.98 × 108 | |
| 2.34 | 0.01 | 1.07 | 0.381 | 3.56 × 108 | |
| 2.63 | 0.01 | 0.96 | 0.365 | 3.80 × 108 | |
| DOPE–DOPG (4:1—4 mM) + NK-2 (0.05 mM) | 1.79 | 0.047 | 16.2 | 0.121 | 7.52 × 106 |
| 2.36 | 0.045 | 15.4 | 0.112 | 7.30 × 106 | |
| 2.93 | 0.042 | 14.6 | 0.110 | 7.56 × 106 | |
| 3.51 | 0.040 | 13.8 | 0.108 | 7.85 × 106 | |
| 4.09 | 0.038 | 13.0 | 0.109 | 8.41 × 106 | |
| 4.67 | 0.035 | 12.1 | 0.110 | 9.11 × 106 | |
| 5.26 | 0.032 | 11.3 | 0.110 | 9.79 × 106 | |
| 5.85 | 0.030 | 10.5 | 0.109 | 10.4 × 106 |
Xb: binding fraction; Cf: free peptide concentration; CM: intrinsic peptide concentration, Kint: intrinsic binding constant. The lipid concentration used in the analysis is the total lipid concentration considering NK-2 interaction with both monolayers of the membrane.29
Table 2. Thermodynamical Parameters of Binding Kinetics of NK-2.a,b.
| lipids | ΔH (kcal/mol) | Kint (M–1) | ΔG (kcal/mol) | TΔS (kcal/mol) |
|---|---|---|---|---|
| DOPG | 0.8 ± 0.2 | 2.5 × 108 ± 3.5 × 107 | –13.8 ± 0.2 | 14.6 ± 0.4 |
| DOPE–DOPG (4:1) | 2.9 ± 0.8 | 7.3 × 106 ± 4.5 × 105 | –11.7 ± 0.6 | 14.6 ± 0.8 |
Binding enthalpy (ΔH), intrinsic binding constant Kint, entropy (ΔS), obtained numerically using surface partition model taking into account the electrostatic contribution.30
Here, the Kint is the mean value calculated from Table 1. Here, we have assumed NK-2 interacts with both leaflets of the membrane.29 The heat of dilution has been subtracted from all data. ζ Potential in the absence of NK-2 is also shown. The effective charge, zp, of the NK-2 when binding to the membrane has been taken as 5. Note that ΔH for DOPG was estimated from the first endothermic part (Figure 4) of the ITC thermogram.
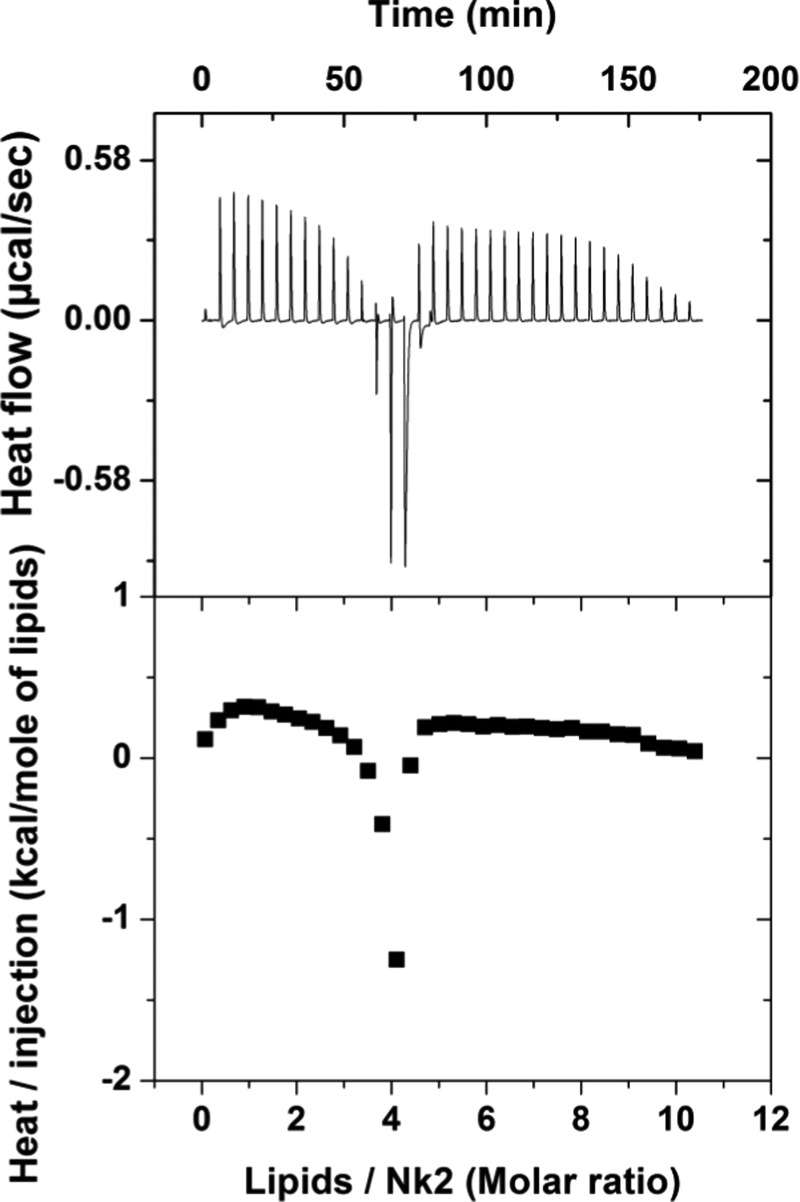
Titration isotherm of DOPG is shown in Figure 4. Surprisingly, it shows few exothermic signals at L/NK-2 (4:1) between two regions of endothermic response. In this case, exothermic peaks begin at much lower L/NK-2 (∼5). It is important to note that such an exothermic signal also occurs at a similar PG/NK-2 ratio for DOPE–DOPG (4:1) mixture. To understand the detailed behavior of two regions of the isotherm, 100 μM NK-2 was titrated with five different DOPG concentrations (10, 5, 2.5, 1.6, and 1 mM). The second region of the isotherm was accessed when two different Cnk2 (50, 35) were titrated with 10 mM DOPG LUV. At present, we are not able to fit the entire isotherm with the model available in the literature. However, we have determined the average thermodynamic parameters obtained from the first region using a partition model, taking into account the electrostatic contribution. The parameters obtained from the model have been presented in Table 1. In the model, we have reduced the effective charge of the NK-2 starting from the maximum charge +10 and found the linear relationship between Xb and CM at zp = 5. This can also be realized as L/NK-2 ∼5 to neutralize the membrane.
Figure 4.
Raw titration calorimetry data of DOPG, where NK-2 of 100 μM is titrated with 5 mM of DOPG LUV (top); the corresponding normalized heat per injection obtained from the integration of the individual peak (bottom). Here, we have assumed NK-2 interacts with all lipids.
The large binding constants in the case of DOPG and DOPE–DOPG mixture, as shown in Table 1, suggest that NK-2 strongly binds to negatively charged membranes. Therefore, it is interesting to check the affinity of NK-2 with neutral lipids, such as DOPC and DOPE. Unfortunately, LUVs from DOPE alone are not formed using the extrusion method used here. This is because PE bilayers are more rigid than PCs in the fluid phase due to hydrogen bonding between the head groups.30 Therefore, bending of PE bilayers costs more energy, which in turn prevents the formation of unilamellar vesicles. Therefore, a mixture of DOPE–DOPC (4:1) was used to investigate the influence of PE in the binding isotherm. A 100 μM NK-2 was titrated with 10 mM DOPE–DOPC (4:1). For comparison, 10 mM of DOPE/DOPC (1:4) mixture was injected in to three different Cnk2 (10, 100, and 200 μM). Similar experiments were done for DOPC. For DOPE–DOPC (4:1), the heat signal is stronger than that of DOPE–DOPC (1:4) but weaker than that of the DOPE–DOPG mixture. In all above mixtures, the binding reaction is endothermic, whereas the simple dilution experiment shows an exothermic response. The interaction of NK-2 with DOPC and DOPC–DOPE LUV is too weak to obtain a binding constant and other thermodynamic parameters. Considering all ITC results, we can easily conclude that the interaction of NK-2 with PE is stronger than with PC but weaker than with PG (PG ≫ PE > PC).
3. Discussion
A systematic investigation of the interaction of an important antimicrobial peptide NK-2 with model membranes shows strong binding affinity toward the negatively charged lipid, DOPG, as revealed from ITC and ζ potential. The adsorption of NK-2 on the membranes, as indicated by an increase in ζ potential (Figure 1), is primarily driven by electrostatic interaction between negatively charged membranes and positively charged NK-2. This is indeed an essential requirement for an AMP to exhibit antimicrobial activity. However, the interaction is very weak in the case of neutral DOPC and DOPC–DOPE membranes. The positive ζ potential (+10 mV) of DOPC LUV at very low NK-2/L (1:250) suggests that NK-2 adsorbs even in PC membranes, which has not been reported in any of the earlier studies. The ζ potential was measured previously for DPPC in the gel phase, suggesting no significant interaction with DPPC.22 However, a more biologically relevant study would be to measure the ζ potential in the fluid phase. X-ray scattering and Fourier transform infrared spectroscopy showed that NK-2 has no influence even on 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine vesicles that are in the fluid phase. They have not measured the ζ potential of PC vesicles in the fluid phase. Therefore, we cannot compare our results on DOPC with those obtained in ref (22). However, the behavior of the ζ potential of DOPG and DOPE–DOPG LUV were found to be consistent with those reported in the previous studies for DPPG and DPPE22 and for LPS.11 Binding of NK-2 to the negatively charged membranes results in charge neutralization. Therefore, the charge neutralization depends on the amount of charge lipids present on the outer membranes. This explains why very low NK-2/L (1:250) is required to neutralize the membrane charge for zwitterionic phospholipids. The charge neutralization at much higher NK-2/L (1:5) for DOPG suggests binding affinity to PG is much stronger than that to PC. If the binding of NK-2 to charged lipids is only due to electrostatic interaction, one would expect the charge overcompensation at the same ζ potential. The fact that we have obtained charge overcompensation at different ζ potential for different lipids (see Figure 1) implies entropic contribution in these systems. This is consistent with the ITC results in these mixtures. For DOPG, ITC shows saturation, indicating all of the NK-2 binds to the lipids at NK-2/L of ∼1:3, which is very similar to the NK-2/L (3:10) for charge overcompensation, as found from ζ potential. Similarly, ITC isotherm for DOPE–DOPG mixtures shows saturation at NK-2/L (1:20), which is again consistent with the results of ζ potential.
It is important to mention that change in the size distribution of the vesicles does not influence the ζ potential significantly. The ζ potential is estimated from the Smoluchowski approximation, where the Henry function f(κa) takes its maximum value as 1.5. In other words, ζ potential is determined from the electrostatic double layer formation, which does not depend on the size of the particle. Therefore, whatever change we observe in the ζ potential is not due to change in size but due to binding of peptide in the membrane.
The DLS technique can, in principle, show the evidence of membrane–membrane interaction mediated by NK-2 or the leakage of LUV induced by NK-2. Size distributions of LUV made from various compositions of phospholipids in the absence and presence of NK-2 clearly indicate stronger affinity of NK-2 toward negatively charged membranes. It is interesting to observe the turbid solution of LUV for those NK-2 concentrations in which the ITC shows saturation before completing all injections. This would mean that when there are no NK-2 available in the solution, LUV, introduced from successive injections can adhere due to electrostatic interaction between negatively charged injected LUV with positively charged LUV already present in the solution. Adhesion can eventually lead to the aggregation of LUV. This result clearly implies the antimicrobial activity of NK-2 toward negatively charged lipids and is consistent with the ζ potential result. Although size distributions do not alter significantly for pure DOPC, the mixture of DOPE and DOPC at 4:1 shows a slight increase in the average size (Figure 2a). Further, the presence of PE with PC enhances the heat signals in the ITC experiment. This indicates that PE plays a significant role in the interaction. Therefore, the PE–PG system is indeed an appropriate model system to look at the antimicrobial activity. Interestingly, this composition happens to be the major constituent of many bacterial membranes.
The binding of a positively charged AMP with negatively charged membrane usually leads to exothermic heat signal.31 The overall endothermic response observed in all isotherms is thus intriguing. The overall endothermic response, found in all lipid mixtures, can be explained in terms of entropy gain in liberating water molecules from the hydration shell of LUV due to adsorption of NK-2 at the interface. Entropic contribution can also arise due to conformational change of NK-2 (random coil to α helix) in the presence of lipids and also reorientation of NK-2 prior to the formation of pores. Such transitions were found for this peptide in a previous study by Olak et al.8 As the initial L/NK-2 ratio is small, we would expect pores in almost all LUVs. This is due to the fact that a threshold NK-2/L is required for the formation of pores and this condition is already achieved at the beginning of the isotherm.13,29 Our preliminary result on giant unilamellar vesicles also shows the leakage of internal fluid, supporting the pore formation on the membrane induced by NK-2 (data not shown). Although the appearance of the exothermic heat signal at PG/NK-2 ∼5:1 in both DOPE–DOPG and DOPG mixtures is very intriguing, the origin of these exothermic peaks is difficult to confirm at present. However, we believe that when there are no NK-2 available for binding, NK-2 can translocate through the pores and interact with the bare LUV present in the solution due to further injections. This process might lead to closing of pores, resulting in an exothermic heat signal. This hypothesis is based on the assumption that if the pore formation is endothermic, pore closure must be exothermic in nature. It is true that the resultant heat due to pore closure and binding of NK-2 together can cancel out. However, at this stage, the unbound peptide-to-lipid molar ratio is too small to produce considerable heat that can give rise to an endothermic response. Such an exothermic response in between two endothermic regions has not been observed in any of the earlier studies.
Surprisingly, a second set of endothermic regions were obtained in the case of DOPG (Figure 4), even though there are no NK-2s available for further binding with LUV. This can be explained qualitatively, as follows. It was known by a previous study that desorption kinetics of NK-2 are much slower than adsorption due to trapping of α helix at the membrane interface.8 Therefore, it is expected that no free NK-2 are available to give rise to a second region of isotherm. Further injections of LUV can lead to attraction toward positively charged LUV already present in the solution. When the membranes of negatively charged LUV come closer to the NK-2, water molecules in the hydration shell start to liberate giving rise to the entropic gain of two membranes of LUV. Such membrane–membrane interaction was also evidenced by the DLS measurement, as the average size of LUV was found to increase.
NK-2 has a strong binding affinity to the lipid bilayer interface, relative to its water solubility, as evidenced from the ζ potential. This leads to an excessive interfacial area due to NK-2 binding, which increases the membrane tension. Such an increase in the membrane tension results in the formation of transmembrane pores.29 It has been shown in the earlier study by Lee at al.29 that the asymmetry of interfacial tension due to one-sided binding could lead to translocation of peptide (melittin) via transient pores. The binding of peptide to both outer and inner monolayers forms a stable pore at a critical peptide-to-lipid ratio. Therefore, it is desirable to use total (current) lipid concentration in the ITC cell to estimate the binding constant. It was also reported earlier that some peptides are not able to translocate across the membrane and only the outer monolayer of the membrane (60% of total lipid) is available for binding.32 One of the striking features obtained in the present study, compared to those of other pore-forming peptides, such as melittin, is that the NK-2 interacts only with negatively charged membranes. On the contrary, melittin can interact significantly with the electrically neutral PC membrane.13
It is evident from Table 2 that entropic contribution (TΔS) is much larger than that of enthalpy (ΔH). This is not surprising, as hydrophobic interaction between the hydrophobic part of NK-2 and hydrophobic core of the membranes is entropic in origin. This is also necessary for the transmembrane pore formation, observed in this system. The intrinsic binding constant Kint (= 2.5 × 108 M–1) of NK-2 found in DOPG (see Table 2) LUV is 2 orders of magnitude higher than that obtained from earlier studies of different AMP.19,31 It is important to note that Kint changes significantly with the effective charge zp of the NK-2. We have optimized the value of zp at 5 in the model so that a linear relationship of CM versus Xb with a small intercept was maintained. This value can also be realized from the ratio L/NK-2 for which the charge compensation as well as the saturation of the heat signals occurs. Previous ITC measurements on the NK-2-LPS system have shown similar endothermic and exothermic response to the binding heat depending on the structure of LPS.11 However, these results were not analyzed. As evidenced from Table 1, the slight increase in the Kint with increasing lipid/NK-2 is the consequence of membrane–membrane interaction induced by NK-2. This result is also supported by DLS experiment, where we have observed an increase in the size distribution.
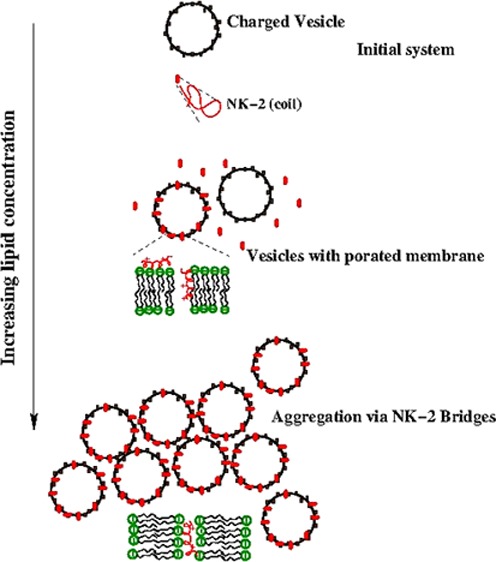
The mechanism of action of NK-2 on negatively charged membranes has been inferred from ITC result, as illustrated in Figure 5. Initially, positively charged NK-2 in the coiled configuration,8 when binds to an outer monolayer of the membranes, increases the membrane tension and induces transient pores to translocate NK-2 into the inner monolayer.29 The increase in membrane tension was also evidenced from the membrane thinning effect of melittin and other AMPs (13, 25, and 29). Such tension-induced (stretch-activated) pore formation has also been reported for an AMP Magainin 2.33 Although there have been no earlier reports on NK-2, we expect that NK-2 also induces membrane tension, as in the case of melittin or Magainin 2. As the concentration of lipid is increased (i.e., the number of LUV), the NK-2 may come out through the pores and negatively charged LUV move closer to the positively charged vesicles due to electrostatic attraction. This process eventually leads to aggregation of vesicles via NK-2 bridges. The process of aggregation has been clearly envisaged from the size distribution. The increase in the value of Kint, as mentioned in Results section, might be the consequence of the aggregation of vesicles at a higher lipid to NK-2 ratio.
Figure 5.
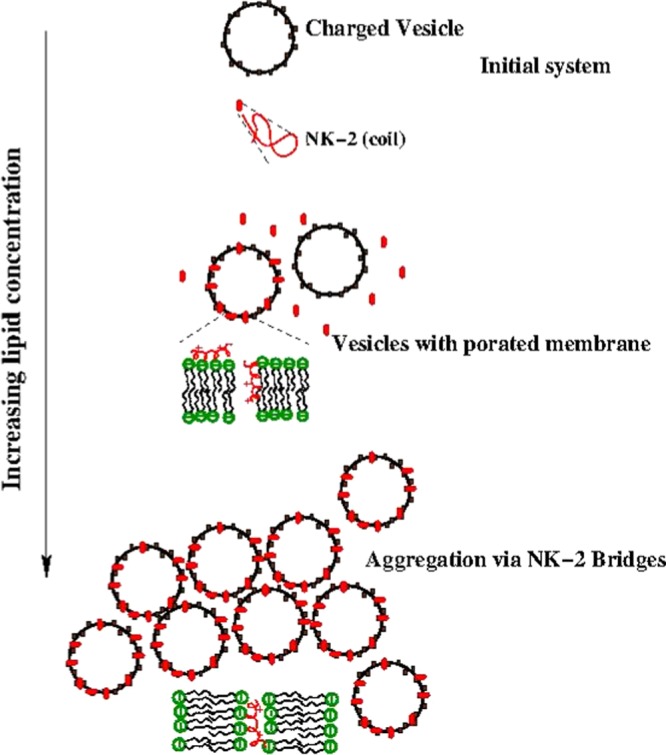
Interaction mechanism of NK-2 and vesicles.
4. Conclusions
We have systematically studied the interaction of NK-2 with phospholipid membranes to obtain insights into the antimicrobial activity. The binding affinity of NK-2 to the negatively charged membranes, PG, as well as the neutral phospholipids PC and PE was determined using ITC and ζ potential. We compare binding affinity of NK-2 to PG, PE, and PC as PG ≫ PE > PC. Weaker affinity toward neutral phospholipids suggests that interactions of NK-2 with lipids are mainly governed by negatively charged lipids, which are major constituents of the bacterial membranes. The very weak affinity of NK-2 toward the PC membrane (which is the major constituent of eukaryotic cell membranes) propels the development of peptide antibiotics. The evidence of pores on these membranes seen in the present study implies antimicrobial activity of NK-2. The significant increase in the size of negatively charged LUV, found in DLS measurement, confirms membrane–membrane interactions induced by NK-2 in these systems, which eventually leads to vesicle aggregates in the solution. Finally, we have proposed the mechanism of action of NK-2 based on our experimental results. More detailed studies are required to understand the mechanism of the kinetic process involved during pore formation. As already established, the NK-2 can be used as therapeutics to kill malaria parasite Plasmodium falciparum. It also shows activity against Escherichia coli and preferentially kills cancer cells. Further, low toxicity toward human cells is a great advantage for the development of antibiotics. Therefore, the present study will definitely reinforce the therapeutics applications. Nevertheless, our study provides important insights into the NK-2-lipids interaction.
5. Materials and Methods
5.1. Materials
Dioleoyl phosphatidylcholine (DOPC), dioleoyl phosphatidylethanolamine (DOPE), and dioleoyl phosphatidyl-glycerol (DOPG) were purchased from Avanti Polar Lipids and peptide NK-2 (KILRGVCKKIMRTFLRRISKDILTGKK-NH2) was purchased from WITA GmbH, Berlin, Germany. They were used without further purification.
5.2. Preparation of LUV
An appropriate amount of lipid solution in chloroform (concentration of stock solution is 10 mg/mL) was transferred to a 10 mL glass vial. The organic solvent was removed by gently passing nitrogen gas. The sample was then placed for a couple of hours in a desiccator connected to a vacuum pump to remove the traces of the solvent. Two and a half milliliters of 1 mM N-(2-hydroxyethyl)piperazine-N′-ethanesulfonic acid (HEPES) (pH 7.4 adjusted with 1 M KOH) was added to the dried lipid film so that final desired concentration was obtained. The lipid film with the buffer was kept overnight at 4 °C to ensure the better hydration of phospholipid heads. Vortexing of the hydrated lipid film for about 30 min produces multilamellar vesicles (MLVs). Sometimes long vortexing is required to make uniform lipid mixtures. LUVs were prepared by the extrusion method using LiposoFast-Pneumatic from AVESTIN (Canada). MLV suspensions are extruded successively through polycarbonate membranes having pore diameters of 400, 200, and 100 nm. This results in the formation of a well-defined size of LUV. This method produces vesicles of diameter ∼100 nm, as measured by dynamic light scattering.
5.3. Measurement of ζ Potential and Size Distributions Using DLS
ζ Potential and vesicle sizes were measured with a Zetasizer Nano ZS from Malvern Instruments. Same LUV, as used for ITC, was used for these measurements. The instrument uses 2 mW He–Ne laser of wavelength 633 nm to illuminate the sample. ζ Potential is obtained from the electrophoretic mobility by laser Doppler velocimetry using the Helmholtz–Smoluchowski equation.34
| 1 |
where η and ϵ are the coefficient of viscosity and the permittivity of the aqueous medium, respectively. The Henry function, f(κa) depends on the inverse Debye length (κ) and the radius (a) of the vesicle.
In DLS, back scattered light at
an angle of 173° is detected and sent to a digital signal processing
correlator. The rate of decay of intensity–intensity autocorrelation
function was measured, which was used to calculate the size of the
LUV using the Stokes–Einstein relation 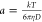 , D being the diffusion
constant and kT the thermal energy. The average ζ
potential and size were obtained from 3 to 4 successive measurements.
Each measurement includes 100–200 runs. The same cuvette is
used for both ζ potential and DLS measurements. All experiments
were performed at 25 °C.
, D being the diffusion
constant and kT the thermal energy. The average ζ
potential and size were obtained from 3 to 4 successive measurements.
Each measurement includes 100–200 runs. The same cuvette is
used for both ζ potential and DLS measurements. All experiments
were performed at 25 °C.
5.4. Isothermal Titration Calorimetry (ITC)
The binding affinity of NK-2 to the lipids was measured using a VP-ITC microcalorimeter produced by MicroCal Inc. (Northampton, MA). In all experiments, the injection syringe was filled with degassed LUV suspension. The sample cell (1.442 mL) contains various concentrations of NK-2 dissolved in 1 mM HEPES buffer (pH 7.4). The reference cell is filled with HEPES buffer only. All solutions were degassed prior to filling the syringe and ITC cells to eliminate air bubbles. A series of 28 injections, each of 8 μL, was introduced into the sample cell at 300 s intervals. All experiments were performed at 25 °C. Interaction of NK-2 with lipids produces a characteristic heat signal. The amount of heat of binding in every injection was obtained by integrating individual calorimetry traces. In a control experiment, LUV was injected into only buffer to measure the heat of dilution. The heat of dilution (∼−0.1 μcal/injection) was found to be small as compared to the actual measurement. Other heat of dilution (∼−0.07 μcal/injection), appearing from the dilution of NK-2, was even smaller, as compared to dilution of the former case. However, we have obtained heat per injection by subtracting heat of dilution, obtained from injecting LUV into buffer, from the actual measurement. ITC data have been analyzed without altering the lipid concentration. This would ensure that the peptides interact with both monolayers of the membrane. All dilution measurements show exothermic signal. The binding constant (K) and binding enthalpy (ΔH) and Gibbs free energy (ΔG = −RT ln K) and entropic contributions (TΔS = ΔH – ΔG) of the binding kinetics can be obtained from the model, as described by Domingues et al.31 A summary of the model is described below.
5.5. Surface Partition Model with Electrostatic Contributions
In a typical ITC experiment, when LUVs are injected into the peptide solution, the total concentration of the peptide is the sum of the concentration of bound peptides and the free peptides. The apparent binding constant Kapp is defined as Xb = KappCf, where Xb is the extent of peptide binding per mole of lipid and Cf is the free peptide concentration of the solution. When the charged peptide adsorbs, the membrane becomes changed. Hence, further adsorption of peptide onto the membrane is restricted by the electrostatic repulsion. Therefore, Kapp is no longer a constant but rather changes with Cf. Therefore, the most relevant binding parameter would be the intrinsic binding constant Kint (Xb = KintCM), which is assumed to be directly proportional to the surface concentration of the peptide in the membrane. The model essentially calculates Xb and CM for each injection of the ITC experiment. As the CM of the peptide is governed by the electrostatic contribution, it is determined by the Boltzmann distribution.
| 2 |
where zp is the effective peptide charge. The maximum charge of NK-2 is +10. F is the Faraday constant (= charge of 1 mol of electron = electronic charge × Avogadro’s number = 96 485 C/mol). ψ0 is the surface potential. R is the universal gas constant and T is the absolute temperature. As the ψ0 is related to surface charge density, σ, of the peptide, it can be estimated from the well-known Gouy–Chapman theory. As the ζ potential can be a good approximation to the surface potential, we have taken ψ0 same as the ζ potential. Now we need to know the ζ potential for each peptide-to-lipid molar ratio obtained after every injection. However, we have measured the ζ potential for few peptide-to-lipid ratios. To obtain the ζ potential for all peptide-to-lipid ratios required for the calculation of CM, we have fitted the ζ potential data to a Hill equation originally used to describe cooperative binding of ligand to macromolecules.35 Hence, we have obtained ζ potentials for all required concentrations from interpolation or extrapolation of the fitted curve. Now, for each data point, the concentration of the free peptide and ψ0 have been determined. Once Cf and ψ0 are known, CM can be calculated. We now discuss briefly how Xb and Cf have been estimated from an ITC experiment.
In an ITC experiment (lipids into peptide injection), the Xb and the enthalpy change ΔH per mole of peptides can be measured directly. The ΔH has been estimated from the sum over all heat per injection divided by the number of moles of peptide in the calorimeter cell.
| 3 |
where δhi is the heat per injection in the ITC experiment. Cp0 is the initial molar concentration of peptide in the ITC cell, and Vcell is the volume of the ITC cell. Now, the extent of peptide binding, Xb, per mole of lipid after completion of ith is given by
| 4 |
where Vinj is the volume of each injection with lipid of concentration CL. Now, the fraction of bound peptide after ith injection is given by
where the free peptide concentration Cf can be obtained from
| 5 |
Now, the Kapp can be obtained from the Xb and Cf. Therefore, CM and Kint can be estimated for each pair of Xb and Cf, obtained from experimental data, as discussed above.
Acknowledgments
This work was funded by the Department of Biotechnology (DBT), Govt. of India (BT/PR8475/BRB/10/1248/2013). P.M. and A.H. are grateful to UGC for providing research fellowship. We thank Drs. Rumiana Dimova and Volker Knecht, Max Planck Institute of Colloids and Interfaces, Potsdam, Germany for their keen interest in this study and for academic discussions.
The authors declare no competing financial interest.
References
- Zasloff M. Antimicrobial peptides of multicellular organisms. Nature 2002, 415, 389–395. 10.1038/415389a. [DOI] [PubMed] [Google Scholar]
- Strempel N.; Strehmel J.; Overhage J. Potential application of antimicrobial peptides in the treatment of bacterial biofilm infections. Curr. Pharm. Des. 2015, 21, 67–84. 10.2174/1381612820666140905124312. [DOI] [PubMed] [Google Scholar]
- Jacobs T.; Bruhn H.; Gaworski I.; Fleischer B.; Leippe M. NK-Lysin and its shortened analog NK-2 exhibit potential activities against Trypanosoma cruzi. Antimicrob. Agents Chemother. 2003, 47, 607–613. 10.1128/AAC.47.2.607-613.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciobanasu C.; Rzeszutek A.; Kubitscheck U.; Willumeit R. NKCS, a Mutant of the NK-2 Peptide, Causes Severe Distortions and Perforations in Bacterial, But Not Human Model Lipid Membranes. Molecules 2015, 20, 6941–6958. 10.3390/molecules20046941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.-j.; Gallo R. L. Antimicrobial peptides. Curr. Biol. 2016, 26, R14–R19. 10.1016/j.cub.2015.11.017. [DOI] [PubMed] [Google Scholar]
- Brogden K. A. Antimicrobial peptides: Pore formers or metabolic inhibitors in bacteria?. Nat. Rev. Microbiol. 2005, 3, 238–250. 10.1038/nrmicro1098. [DOI] [PubMed] [Google Scholar]
- Bechinger B. The structure dynamics and orientation of antimicrobial peptides in membranes by multidimensional solid-state NMR spectroscopy. Biochim. Biophys. Acta, Biomembr. 1999, 1462, 157–183. 10.1016/S0005-2736(99)00205-9. [DOI] [PubMed] [Google Scholar]
- Olak C.; Muenter A.; Andrä J.; Brezesinski G. Interfacial properties and structural analysis of the antimicrobial peptide NK-2. J. Pept. Sci. 2008, 14, 510–517. 10.1002/psc.954. [DOI] [PubMed] [Google Scholar]
- Banković J.; Andrä J.; Todorović N.; Podolski-Renić A.; Miloševića Z.; Miljković D.; Krause J.; Ruždijić S.; Tanić N.; Pešić M. The elimination of P-glycoprotein over-expressing cancer cells by antimicrobial cationic peptide NK-2: The unique way of multi-drug resistance modulation. Exp. Cell Res. 2013, 319, 1013–1027. 10.1016/j.yexcr.2012.12.017. [DOI] [PubMed] [Google Scholar]
- Andrä J.; Leippe M. Candidacidal activity of shortened synthetic analogs of amoebapores and NK-lysin. Med. Microbiol. Immunol. 1999, 188, 117–124. 10.1007/s004300050113. [DOI] [PubMed] [Google Scholar]
- Andrä J.; Koch M. J. H.; Bartels R.; Brandenburg K. Biophysical characterization of Endotoxin inactivation of NK-2, an antimicrobial peptide derived from mammalian NK-Lysin. Antimicrob. Agents Chemother. 2004, 48, 1593–1599. 10.1128/AAC.48.5.1593-1599.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M.; Li. M.-f.; Sun L. NKLP27: A Teleost NK-Lysin Peptide that Modulates Immune Response, Induces Degradation of Bacterial DNA, and Inhibits Bacterial and Viral Infection. PLoS One 2014, 9, e106543 10.1371/journal.pone.0106543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M.-T.; Hung W.-C.; Chen F.-Y.; Huang H. W. Mechanism and kinetics of pore formation in membranes by water-soluble amphipathic peptides. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 5087–5092. 10.1073/pnas.0710625105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambroggio E. E.; Separovic F.; Bowie J. H.; Fidelio G. D.; Bagatolli L. A. Direct visualization of membrane leakage induced by the antibiotic peptides: Maculatin, Citropin, and Aurein. Biophys. J. 2005, 89, 1874–1881. 10.1529/biophysj.105.066589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao H.; Mattila J.-P.; Holopainen J. M.; Kinnunen P. K. J. Comparison of the membrane association of two antimicrobial peptides, Magainin 2 and Indolicidin. Biophys. J. 2001, 81, 2979–2991. 10.1016/S0006-3495(01)75938-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamba Y.; Yamazaki M. Magainin 2-induced pore formation in the lipid membranes depends on its concentration in the membrane interface. J. Phys. Chem. B 2009, 113, 4846–4852. 10.1021/jp8109622. [DOI] [PubMed] [Google Scholar]
- Lee M.-T.; Chen F.-Y.; Huang H. W. Energetics of pore formation induced by membrane active peptides. Biochemistry 2004, 43, 3590–3599. 10.1021/bi036153r. [DOI] [PubMed] [Google Scholar]
- He K.; Ludtke S. J.; Worcester D. L.; Huang H. W. Neutron Scattering in the plane of membranes: structure of alamethicin pores. Biophys. J. 1996, 70, 2659–2666. 10.1016/S0006-3495(96)79835-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wieprecht T.; Apostolov O.; Beyermann M.; Seelig J. Membrane binding and pore formation of the antibacterial peptide PGLa: Thermodynamic and Mechanistic aspects. Biochemistry 2000, 39, 442–452. 10.1021/bi992146k. [DOI] [PubMed] [Google Scholar]
- Lohner K.; Prenne E. J. Differential scanning calorimetry and X-ray diffraction studies of the specificity of the interaction of antimicrobial peptide with membrane-mimetic system. Biochim. Biophys. Acta, Biomembr. 1999, 1462, 141–156. 10.1016/S0005-2736(99)00204-7. [DOI] [PubMed] [Google Scholar]
- Schröder-Borm H.; Bakalova R.; Andrä J. The NK-lysin derived peptide NK-2 preferentially kills cancer cells with increased surface levels of negatively charged phosphatidylserine. FEBS Lett. 2005, 579, 6128–6124. 10.1016/j.febslet.2005.09.084. [DOI] [PubMed] [Google Scholar]
- Willumeit R.; Kumpugdee M.; Funari S. S.; Lohner K.; Navas B. P.; Brandenburg K.; Linser S.; Andrä J. Structural rearrangement of model membranes by the peptide antibiotic NK-2. Biochim. Biophys. Acta, Biomembr. 2005, 1669, 125–134. 10.1016/j.bbamem.2005.01.011. [DOI] [PubMed] [Google Scholar]
- Vogel H.; Jähnig F. The structure of melittin in membranes. Biophys. J. 1986, 50, 573–582. 10.1016/S0006-3495(86)83497-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bechinger B.; Zasloff M.; Opella S. J. Structure and orientation of the antibiotic peptide magainin in membranes by solid-state nuclear magnetic resonance spectroscopy. Protein Sci. 1993, 2, 2077–2084. 10.1002/pro.5560021208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H. M.; Leung K. W.; Thakur N. N.; Tan A.; Jack R. W. Distinguishing between different pathways of bilayer disruption by the related antimicrobial peptides cecropin B, B1 and B3. Eur. J. Biochem. 2003, 270, 911–920. 10.1046/j.1432-1033.2003.03451.x. [DOI] [PubMed] [Google Scholar]
- Huang H. W.; Chen F.-Y.; Lee M.-T. Molecular Mechanism of peptide induced pores in Membranes. Phys. Rev. Lett. 2004, 92, 198304 10.1103/PhysRevLett.92.198304. [DOI] [PubMed] [Google Scholar]
- Miteva M.; Andersson M.; Karshikoff A.; Otting G. Molecular electroporation: a unifying concept for the description of membrane pore formation by antibacterial peptides, exemplified with NK-lysin. FEBS Lett. 1999, 462, 155–158. 10.1016/S0014-5793(99)01520-3. [DOI] [PubMed] [Google Scholar]
- Dimova R.; Aranda S.; Bezlyepkina N.; Nikolov V.; Riske K. A.; Lipowsky R. A practical guide to giant vesicles. Probing the membrane nanoregime via optical microscopy. J. Phys.: Condens. Matter 2006, 18, S1151–S1176. 10.1088/0953-8984/18/28/S04. [DOI] [PubMed] [Google Scholar]
- Lee M.-T.; Sun T.-L.; Hung W.-C.; Huang H. W. Process of inducing pores in membranes by melittin. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 14243–14248. 10.1073/pnas.1307010110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boggs J. M. Lipid intermolecular hydrogen bonding: influence on structural organization and membrane function. Biochim. Biophys. Acta, Rev. Biomembr. 1987, 906, 353–404. 10.1016/0304-4157(87)90017-7. [DOI] [PubMed] [Google Scholar]
- Domingues T. M.; Mattei B.; Seelig J.; Perez K. R.; Miranda A.; Riske K. A. Interaction of the Antimicrobial Peptide Gomesin with Model Membrane: A calorimetric Study. Langmuir 2013, 29, 8609–8618. 10.1021/la401596s. [DOI] [PubMed] [Google Scholar]
- Meier M.; Seelig J. Length dependence of the coil ⇆ β-sheet transition in a membrane environment. J. Am. Chem. Soc. 2008, 130, 1017–1024. 10.1021/ja077231r. [DOI] [PubMed] [Google Scholar]
- Karal M. A. S.; Alam J. M.; Takahashi T.; Levadny V.; Yamazaki M. Stretch-Activated Pore of the Antimicrobial Peptide, Magainin 2. Langmuir 2015, 31, 3391–3401. 10.1021/la503318z. [DOI] [PubMed] [Google Scholar]
- Hunter R. J.Zeta Potential in Colloid Science: Principles and Applications; Ottewill R. H., Rowell R. L., Eds.; Academic Press: New York, 1981; pp 59–124. [Google Scholar]
- Sannigrahi A.; Maity P.; Karmakar S.; Chattopadhyay K. Interaction of KMP-11 with Phospholipid Membranes and Its Implications in Leishmaniasis: Effects of Single Tryptophan, Mutation and Cholesterol. J. Phys. Chem. B 2017, 121, 1824–1834. 10.1021/acs.jpcb.6b11948. [DOI] [PubMed] [Google Scholar]