Using the Variable-Nearest Neighbor Method To Identify P-Glycoprotein Substrates and Inhibitors

Abstract

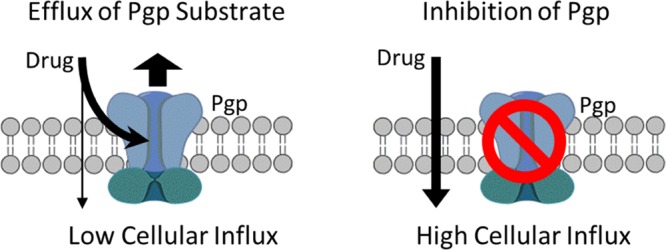
Permeability glycoprotein (Pgp) is an essential membrane-bound transporter that efficiently extracts compounds from a cell. As such, it is a critical determinant of the pharmacokinetic properties of drugs. Multidrug resistance in cancer is often associated with overexpression of Pgp, which increases the efflux of chemotherapeutic agents from the cell. This, in turn, may prevent an effective treatment by reducing the effective intracellular concentrations of such agents. Consequently, identifying compounds that can either be transported out of the cell by Pgp (substrates) or impair Pgp function (inhibitors) is of great interest. Herein, using publically available data, we developed quantitative structure–activity relationship (QSAR) models of Pgp substrates and inhibitors. These models employed a variable-nearest neighbor (v-NN) method that calculated the structural similarity between molecules and hence possessed an applicability domain, that is, they used all nearest neighbors that met a minimum similarity constraint. The performance characteristics of these v-NN-based models were comparable or at times superior to those of other model constructs. The best v-NN models for identifying either Pgp substrates or inhibitors showed overall accuracies of >80% and κ values of >0.60 when tested on external data sets with candidate Pgp substrates and inhibitors. The v-NN prediction model with a well-defined applicability domain gave accurate and reliable results. The v-NN method is computationally efficient and requires no retraining of the prediction model when new assay information becomes available—an important feature when keeping QSAR models up-to-date and maintaining their performance at high levels.

Introduction

Permeability glycoprotein (Pgp), a member of the ATP-binding cassette (ABC) transporter family, is an important cell-membrane protein that regulates the efflux of foreign substances out of the cell.¹⁻³ Pgp primarily exports hydrophobic compounds via an ATP-dependent process³ (Scheme 1). Compounds that interact with Pgp can be classified into three categories: substrates, inhibitors, and modulators.⁴ Pgp causes substrates to undergo efflux from the cell. By contrast, modulators and inhibitors both impair Pgp function; hence, these terms are often used synonymously. As shown in Scheme 1,the three most common ways to reduce Pgp function are (i) to block or competitively antagonize the substrate from attaching to the binding site (square), (ii) to inhibit the ATP binding site (triangle), and (iii) to interfere with the hydrolysis of ATP to ADP + P_i (star).

Scheme 1. Illustration of the Drug Efflux Mediated by ATP-Driven Pgp Transport.

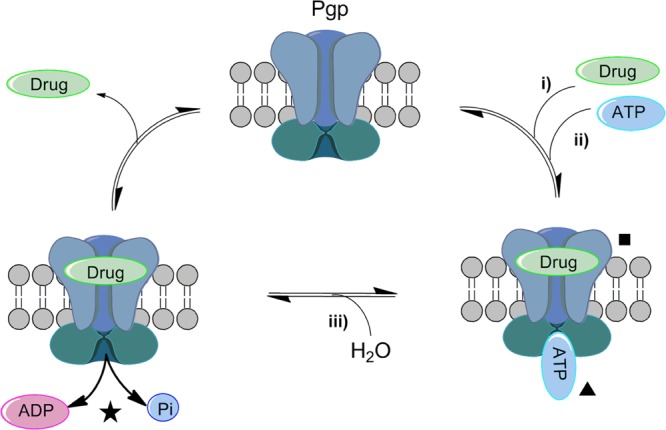
(i) Drug binds to the substrate binding site (■),⁵ (ii) ATP binds to the ATP-binding site (▲), and (iii) hydrolysis of ATP to ADP + P_i (★). Although only one binding site is shown for simplicity, multiple binding sites could contribute to substrate promiscuity.

In cultured cancer cell lines and tumor models, overexpression of Pgp generates drug-resistant phenotypes.² Pgp overexpression is a major factor that contributes to multidrug resistance (MDR), a phenomenon in which cells develop tolerance to drugs even at lethal doses by pumping them out, thereby reducing their cytotoxic effect.³ MDR is of great concern because it is one of the major reasons for the failure of cancer chemotherapy treatments, of which paclitaxel administration is perhaps one of the best-known examples. Considerable effort is also being devoted to identifying Pgp inhibitors that reduce drug resistance and improve drug effectiveness.^6,7 Several experimental assays, including the monolayer efflux, calcein-AM, and ATPase assays,^8,9 are available for assessing the compound transport across cellular membranes. These assays, however, are resource intensive. In this context, in silico models that identify inhibitors and substrates offer a valuable alternative for early prescreening efforts to guide the selection of compounds for experimental evaluation.

Several computational models have been proposed to predict the likelihood that a compound is a Pgp inhibitor¹⁰⁻¹⁵ or a substrate.¹⁵⁻¹⁷ Most of these models were developed using relatively small data sets, with concomitant limitations in their reliability. As such, the predictions of the models developed thus far are often difficult to validate. One aim of this study was to address this issue. We defined an applicability domain based on the premise that similar molecules have similar activities. In this way, we attempted to ensure that the models made a prediction only when a test molecule was similar to any of the molecules in the set of training compounds.

We also sought to test the utility of models that use an applicability domain in predicting Pgp substrates. As noted above, Pgp substrates are likely to be crucial for MDR because drugs that are Pgp substrates will accumulate less in cells than those that are not. This is why identifying Pgp substrates is often part of the early drug discovery screening process.¹⁸ Yet, despite the efforts that have been devoted to predicting Pgp inhibitors, the prediction of Pgp substrates themselves has received little attention. Predicting Pgp substrates is more challenging than predicting Pgp inhibitors because their structural variability is likely to be high, given the crucial role of Pgp in removing foreign substances from cells.

Here, we used our versatile variable-nearest neighbor (v-NN) method¹⁹ to develop the Pgp substrate and inhibitor identification models and compared how they performed in relation to previously published model constructs. We also combined the data sets from Chen et al.¹² and Broccatelli et al.¹⁰ to develop a v-NN Pgp inhibitor model and analyzed its performance. Our results show that these v-NN models perform well and suggest that reliable predictions can easily be made with the use of an applicability domain.

Results and Discussion

Prediction of Pgp Substrates

We applied our v-NN method to construct a Pgp substrate model, using experimentally determined substrates and nonsubstrates. The v-NN model predicts whether a test molecule is a substrate or a nonsubstrate on the premise that similar molecules have similar biological activities. If a test molecule is highly similar to a reference substrate molecule, it will be classified as a substrate. To increase the level of confidence in our predictions, we defined an applicability domain for the v-NN model by introducing a similarity threshold value (Tanimoto-distance threshold d₀) that had to be met to make a prediction. We selected the two v-NN parameters in eq 1 (smoothing factor h and Tanimoto-distance threshold d₀), according to the performance on the training set with respect to the κ value and overall coverage. We evaluated the performance of the model using the 10-fold cross validation, in which we randomly grouped the data set into ten equally sized groups and then used nine of the groups to construct the model and one to validate it. Subsequently, this process was repeated ten times so that all groups were left out once, and the final result was reported as the average.

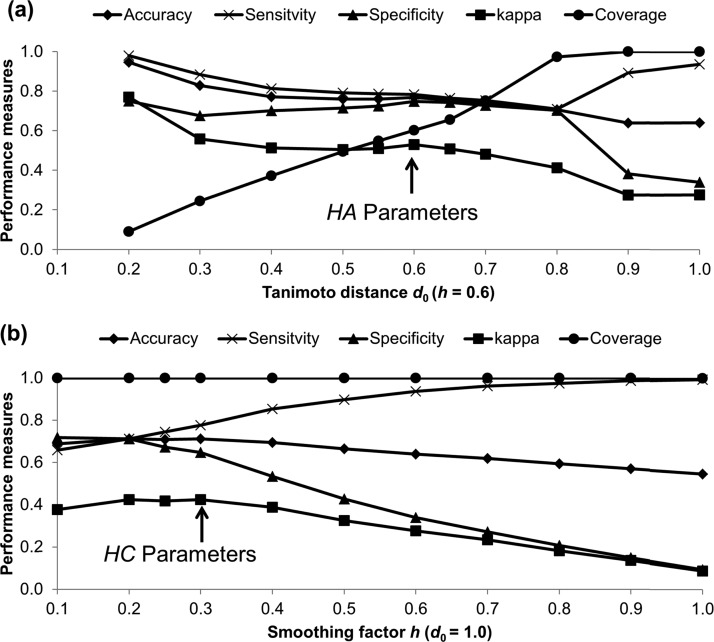
Figure 1a shows the performance measures of the model as a function of the Tanimoto-distance threshold d₀ at a constant smoothing factor h of 0.6. The best model performance, as measured by the κ value, was achieved at d₀ = 0.2, with an accuracy of 95%, sensitivity of 98%, specificity of 75%, and κ value of 0.77 (Figure 1a). However, this resulted in low coverage (9%), wherein the majority of compounds did not meet the Tanimoto-distance threshold.

Figure 1.

Performance measures of the v-NN Pgp substrate model as a function of the Tanimoto-distance threshold d₀ at a constant smoothing factor h of 0.6 (a) and as a function of the smoothing factor h at a constant Tanimoto-distance threshold d₀ of 1.0 (b), evaluated using the 10-fold cross validation.

A set of high-accuracy (HA) parameters (h = 0.6 and d₀ = 0.6; Figure 1a, arrow) was selected by adjusting the smoothing factor and the Tanimoto-distance threshold, which increased the coverage from 9 to 60%, while maintaining good performance measures (accuracy of 77%, sensitivity of 78%, specificity of 75%, and κ value of 0.53). In taking this approach, we sacrificed some coverage because we could not make predictions for 40% of the compounds. Although this inability may appear to be a limitation of our method, in our opinion, it is preferable not to make any prediction at all if these compounds are predicted merely by chance. Instead, these molecules should be tested experimentally. Once the results are known, the new data should then be included to the training set, so that the new model can make reliable predictions for similar compounds, effectively expanding the applicability domain of the model. Most published quantitative structure–activity relationship (QSAR) studies have not assessed the applicability domain of their models. Although this conveys the impression that these models are universally applicable, we and others have shown that the performance of a QSAR model rapidly deteriorates as new studies explore chemical spaces that differ from the space that was used to build the original model.^20,21 This is one of the great challenges in QSAR development. In tackling this problem, we consider the use of an applicability domain as a necessary step to establish reliable in silico methods.

The coverage of a QSAR model can be increased by the v-NN approach in a straightforward fashion. Our v-NN Pgp substrate model achieved nearly 100% coverage when we increased the Tanimoto-distance threshold to 0.8 (Figure 1a). This came at the cost of inferior prediction performance, as indicated by the smaller κ values as well as the slightly lower accuracy and specificity. To ensure a fair comparison of the performance of our v-NN Pgp substrate model with that of previously proposed models, we increased the Tanimoto-distance threshold to d₀ = 1.0 and varied the smoothing factor h to achieve a set of high-coverage (HC) parameters (h = 0.3 and d₀ = 1.0; Figure 1b, arrow) and enable our model to make predictions for all compounds.

To test the performance of the v-NN model in predicting Pgp substrates, we used the data set of Li et al.¹⁶ and their published Bayesian classifier (BC) model, which employs ECFP10 fingerprints and eight molecular properties (MPs). Table 1 summarizes the results of our v-NN model and the BC model. To compare the models directly, the table shows the model parameters with the 10-fold cross validation, the performance measures we calculated by using their data sets, and the BC model parameters reported by Li et al.

Table 1. Performance Measures in Predicting Pgp Substrates by Using the Data Set of Li et al.¹⁶.

method	parameters	accuracy	sensitivity	specificity	κ	coverage
Traininga
v-NN	HC (h = 0.3; d0 = 1.0)b	0.71	0.78	0.65	0.42	1.00
v-NN	HA (h = 0.6; d0 = 0.6)	0.77	0.78	0.75	0.53	0.60
BC	ECFP10 + 8MPc	0.72	0.65	0.79	0.44	1.00
Test
v-NN	HC (h = 0.3; d0 = 1.0)	0.76	0.80	0.71	0.51	1.00
v-NN	HA (h = 0.6; d0 = 0.6)	0.81	0.82	0.78	0.60	0.70
BC	ECFP10 + 8MP	0.73	0.66	0.81	0.47	1.00
Randomized Training Datad
v-NN	HC (h = 0.3; d0 = 1.0)	0.50	0.50	0.50	0.01	1.00
v-NN	HA (h = 0.6; d0 = 0.6)	0.52	0.50	0.54	0.04	0.65

^aPerformance in a 10-fold cross validation.

^bv-NN parameters (smoothing factor, h, and Tanimoto-distance threshold, d₀).

^cBayesian classifier that employs ECFP10 fingerprints and eight molecular properties (MPs).

^dTraining set compounds for Pgp were randomly assigned as substrates or nonsubstrates.

The best-performing v-NN model outperformed the BC + MP model with respect to accuracy, sensitivity, and κ value (Table 1). Of these three measures, high sensitivity is desirable because it assures high confidence in positive predictions. Even when we equated the v-NN model with the BC + MP model in terms of coverage (by using HC parameters), the sensitivity remained high in both the training and test sets, 0.78 and 0.80, respectively, compared with the corresponding sensitivities of 0.65 and 0.66 for the BC + MP model. However, the κ value is perhaps the most accurate measure for the performance of a prediction model because it takes into account the agreement occurring by chance. Although the v-NN model with the HC parameters performed on par with the BC + MP model on the training set with respect to the accuracy and the κ value, it performed better than the BC + MP model on the external test set. Furthermore, the v-NN model with the HA parameters showed superior accuracy and κ values on both the training and test sets.

To test the robustness of our model, we compared its performance when it was trained on the data set of Li et al. with that when it was trained on a randomized data set. As the bottom two rows of Table 1 show, the performance of the model deteriorated as expected. The accuracy, sensitivity, and specificity during randomized training were all approximately 0.5, a value much lower than the values during training with conventional data sets (0.65–0.78, top two rows of Table 1). In particular, the κ value was approximately zero, indicating that the model predictions were no better than those expected by chance. That our model is sensitive to relationships among compounds in the training data set suggests that it reliably predicts Pgp substrates.

Prediction of Pgp Inhibitors

Following the modeling procedure we pursued when constructing the Pgp substrate model, we collected Pgp inhibitor data from the studies of Broccatelli et al.¹⁰ and Chen et al.¹² and analyzed them separately for comparison, before combining them into one large data set. Broccatelli et al. developed a model by employing a combination of molecular interaction field-based technologies and by considering pharmacophore features as well as physicochemical properties related to membrane partitioning. They used VolSurf+ descriptors²² to model the physicochemical properties and fingerprints for ligands and proteins (FLAP)²³ to identify the most important pharmacophore features.

Table 2 shows the results of the v-NN model and the FLAP/VolSurf+ model of Broccatelli et al. As in the case of predicting Pgp substrates, we determined two sets of v-NN parameters to achieve HC and HA via a series of 10-fold cross validations. We selected the v-NN HA parameters (h = 0.2 and d₀ = 0.6) to establish a limited applicability domain and thereby optimize the performance. This resulted in an excellent performance on the training set, with an accuracy of 91%, sensitivity of 93%, specificity of 88%, κ value of 0.81, and coverage of 67%. The HC parameters (h = 0.2 and d₀ = 1.0) allowed us to make a prediction for all molecules (100% coverage). The v-NN models performed well compared with the FLAP/VolSurf+ model on all three data sets (training, internal test, and external test). The v-NN model with the HA parameters gave the best performance and the most reliable result on all data sets.

Table 2. Performance Measures in Predicting Pgp Inhibitors by Using the Data Set of Broccatelli et al¹⁰.

method	parameters	accuracy	sensitivity	specificity	κ	coverage
Traininga
v-NN	HC (h = 0.2; d0 = 1.0)b	0.85	0.86	0.84	0.70	1.00
v-NN	HA (h = 0.2; d0 = 0.6)	0.91	0.93	0.88	0.81	0.67
FLAP/VolSurf+		0.88	0.84	0.91	0.75	1.00
Internal Test
v-NN	HC (h = 0.2; d0 = 1.0)	0.84	0.84	0.83	0.67	1.00
v-NN	HA (h = 0.2; d0 = 0.6)	0.89	0.88	0.91	0.78	0.66
FLAP/VolSurf+		0.85	0.82	0.87	0.69	1.00
External Test
v-NN	HC (h = 0.2; d0 = 1.0)	0.76	0.81	0.67	0.48	1.00
v-NN	HA (h = 0.2; d0 = 0.6)	0.88	0.91	0.80	0.71	0.53
FLAP/VolSurf+		0.86	0.90	0.80	0.70	1.00
Randomized Training Datac
v-NN	HC (h = 0.2; d0 = 1.0)	0.55	0.41	0.67	0.08	1.00
v-NN	HA (h = 0.2; d0 = 0.6)	0.53	0.41	0.67	0.08	0.67

^aPerformance of 10-fold cross validation.

^bv-NN parameters (smoothing factor, h, and Tanimoto-distance threshold, d₀).

^cTraining set compounds for Pgp were randomly assigned as substrates or nonsubstrates.

We also compared the performance of our model when it was trained on the data set of Broccatelli et al. with that when it was trained on a randomized data set. The performance deteriorated as expected, and the low κ values indicated that the model predictions were no better than those expected by chance (bottom two rows of Table 2).

Table 3 compares the performance of v-NN models that used either HC parameters (h = 0.1 and d₀ = 1.0) or HA parameters (h = 0.4 and d₀ = 0.5) with that of the model developed by Chen et al.¹² using their data set. To directly compare our results with those of Chen et al., the training set was evaluated using the leave-one-out (LOO) cross validation instead of the 10-fold cross validation. Their model, which uses the BC model and eight molecular descriptors (BC + MP), performed as well as our v-NN models. The performance of the v-NN model with HA parameters was comparable to that of the BC + MP model, with an overall accuracy of 80%, sensitivity of 91%, and coverage of 72% for the test set. The v-NN models displayed excellent accuracy and sensitivity but showed low specificity. This may be attributed to our unbalanced data set, which included more Pgp inhibitors than noninhibitors. This asymmetry could have led to the low specificity of our models by increasing their likelihood of falsely classifying a proportionally greater number of noninhibitors as inhibitors.

Table 3. Performance Measures in Predicting Pgp Inhibitors by Using the Data set of Chen et al.¹².

method	parameters	accuracy	sensitivity	specificity	κ	coverage
Traininga
v-NN	HC (h = 0.1; d0 = 1.0)b	0.76	0.84	0.64	0.49	1.00
v-NN	HA (h = 0.4; d0 = 0.5)	0.83	0.91	0.63	0.57	0.68
BC + MP	FCFP4 + 8 MPc	0.81	0.80	0.82	0.61	1.00
Test
v-NN	HC (h = 0.1; d0 = 1.0)a	0.76	0.87	0.59	0.48	1.00
v-NN	HA (h = 0.4; d0 = 0.5)	0.80	0.91	0.50	0.45	0.72
BC + MP	FCFP4 + 8 MP	0.79	0.80	0.78	0.57	1.00
Randomized Training Datad
v-NN	HC (h = 0.1; d0 = 1.0)	0.53	0.59	0.43	0.02	1.00
v-NN	HA (h = 0.4; d0 = 0.5)	0.55	0.59	0.46	0.04	0.67

^aPerformance of LOO cross validation.

^bv-NN parameters (smoothing factor, h, and Tanimoto-distance threshold, d₀).

^cBayesian classifier that employs FCFP4 fingerprints and eight MPs.

^dTraining set compounds for Pgp were randomly assigned as substrates or nonsubstrates.

As in comparing the v-NN Pgp inhibitor model with a previous model by Broccatelli et al. (Table 2), we compared the performance of the former model when it was trained on the data set of Chen et al. with that when it was trained on a randomized data set. The performance again deteriorated as expected, and the low κ values indicated that the model predictions were no better than those expected by chance (bottom two rows of Table 3).

Prediction of Pgp Inhibitors in the Combined Data Set

The v-NN method relies on the diversity of the compounds used to construct the model. A large set of diverse molecules will result in a greater applicability domain of the model. We therefore combined the two inhibitor data sets into a single data set containing 1319 Pgp inhibitors and 957 noninhibitors. The data set was split into a training set of 1219 inhibitors and 857 noninhibitors and an evaluation set of 100 inhibitors and 100 noninhibitors. Table 4 shows the performance of the v-NN models in predicting Pgp inhibitors in this larger data set. The v-NN model with HA parameters (h = 0.3 and d₀ = 0.5) performed well on the training set as evaluated by the 10-fold cross validation, with an overall accuracy of 87% and a κ value of 0.68 in providing predictions for 75% of the compounds. The 75% coverage for the combined training set was greater than that achieved for the models constructed using only the data set of Broccatelli et al.¹⁰ or Chen et al.,¹² which showed coverage values of 67% and 68%, respectively (with the HA training values in Tables 2 and 3). On the evaluation set, the v-NN model generated predictions for 162 of the 200 compounds (81%) and correctly predicted 92% of the Pgp inhibitors. The v-NN model performed well even at 100% coverage, which was achieved by using the HC parameters (h = 0.1 and d₀ = 1.0); overall accuracies for the training and evaluation sets were 83 and 77%, respectively.

Table 4. Performance Measures in Predicting Pgp Inhibitors by Using All Inhibitor Data.

method	parameters	accuracy	sensitivity	specificity	κ	coverage
Traininga
v-NN	HC (h = 0.1; d0 = 1.0)b	0.83	0.87	0.77	0.65	1.00
v-NN	HA (h = 0.3; d0 = 0.5)	0.87	0.93	0.74	0.68	0.75
Evaluation
v-NN	HC (h = 0.1; d0 = 1.0)	0.77	0.88	0.66	0.54	1.00
v-NN	HA (h = 0.3; d0 = 0.5)	0.81	0.92	0.69	0.62	0.81

^aPerformance of 10-fold cross validation.

^bv-NN parameters (smoothing factor, h, and Tanimoto-distance threshold, d₀).

Klepsch et al.¹¹ also combined the data sets from Broccatelli et al.¹⁰ and Chen et al.¹² The models that performed best on their training set were the random forest (RF) and support vector machine (SVM) models, with overall accuracies of 86% and 75%, respectively. The corresponding accuracies of the RF and SVM models on their external test set were 75% and 73%, respectively. Klepsch et al. also presented a structure-based approach to predict Pgp inhibitors and noninhibitors by using the scoring function (ChemScore) in the docking program GOLD.²⁴ Even when they combined the scoring function with the logP value, they achieved only a total accuracy of 77%. This is lower than the accuracy of their ligand-based models. Although these results are comparable to our HC results, the v-NN model achieved higher accuracy with the HA parameters. We note, however, that their findings cannot be directly compared with our results because they used slightly different procedures for selecting their training and test sets.

Selectivity of the Pgp Substrate and Inhibitor Predictions

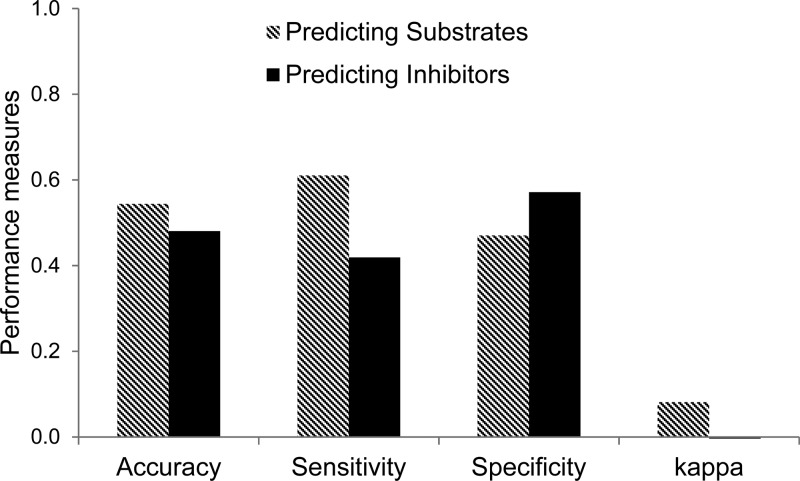
Previous studies have investigated the MPs of Pgp substrates and inhibitors. Poongavanam et al.¹⁵ analyzed the occurrence of different functional groups and found that (1) Pgp substrates are typically amphipathic (i.e., possessing both hydrophobic and hydrophilic parts) and lipophilic, with three commonly occurring features: an aromatic system, an ether moiety, and an amine group; and (2) Pgp inhibitors are lipophilic and nonpolar, often containing an alkyl aryl ether, an aromatic amine, and a tertiary aliphatic amine group. Although Pgp substrates and inhibitors differ in some respects, they also share the property of being hydrophobic. If our assumption that similar molecules have similar MPs is correct and if the MPs of Pgp substrates differ distinctly from those of Pgp inhibitors, then v-NN models that perform well in predicting Pgp substrates should be poor at predicting Pgp inhibitors. Conversely, those predicting Pgp inhibitors should be poor at predicting Pgp substrates. Therefore, we tested whether the models developed to predict Pgp substrates would show poor performance when tested with Pgp inhibitors and vice versa. In both cases, the accuracy levels were ∼50% and the κ values were close to zero (Figure 2). These results confirm that both the v-NN substrate and inhibitor models selectively identify the two different classes of Pgp compounds.

Figure 2.

Prediction of substrates by using the v-NN Pgp inhibitor model and the prediction of inhibitors by using the v-NN Pgp substrate model, as evaluated by the 10-fold cross validation.

Conclusions

Our v-NN-based models outperformed current models in predicting Pgp substrates and performed comparably to methods such as FLAP/VolSurf+ in predicting Pgp inhibitors. The advantages of using the v-NN method are as follows: (i) reliable predictions by using an applicability domain to ensure that only compounds within the chemical space of the compounds used to construct the model are selected for prediction and (ii) the absence of any need for retraining when new compounds are added to the model. We emphasize the importance of using a prediction model that is easily updated with new compound information and assay data, given our previous demonstration that feeding such models with even a small amount of assay data for truly novel compounds can greatly enhance their applicability domains.²⁰

Methods

Pgp Data Sets

We used the Pgp substrate data collected by Hou and co-workers from monolayer efflux, ATPase activity, and rhodamine-123/calcein-AM fluorescence assays.¹⁶ This data set consists of measurements for a training set of 313 substrates and 309 nonsubstrates and those for a test set of 109 substrates and 91 nonsubstrates.

We extracted the data sets for Pgp inhibitors from Chen et al.¹² and Broccatelli et al.¹⁰ The data set from Chen et al. consists of measurements for a training set of 609 inhibitors and 393 noninhibitors and those for a test set of 188 inhibitors and 112 noninhibitors. The data set from Broccatelli et al. consists of measurements for three sets of compounds: (i) a training set of 334 inhibitors and 438 noninhibitors, (ii) an internal test set of 37 inhibitors and 47 noninhibitors, and (iii) an external test set of 274 inhibitors and 144 noninhibitors.

Combining the Pgp inhibitor data sets from Chen et al. and Broccatelli et al. and removing duplicates resulted in a combined data set consisting of a training set of 1219 inhibitors and 837 noninhibitors and an evaluation set of 100 inhibitors and 100 noninhibitors. All data sets and corresponding simplified molecular input line entry specifications (SMILES) are available in the Supporting Information.

v-NN Method

The k-nearest neighbor (k-NN) method has been widely used to develop QSAR models.²⁵ This method rests on the premise that compounds with similar structures have similar activities. One difficulty with the k-NN method is that it always gives a prediction for a compound based on a constant number, k, of nearest neighbors regardless of the dissimilarity between the query and reference compounds. To correct for this shortcoming, we proposed a variable-nearest neighbor (v-NN) method¹⁹ that uses all nearest neighbors that meet a structural similarity criterion. When no nearest neighbor meets the criterion, the v-NN method makes no prediction. The predicted biological activity y is a weighted average across structurally similar neighbors

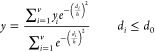1

where d_i denotes the Tanimoto distance between a query molecule for which a prediction is made and a molecule i of the training set, y_i is the experimentally measured activity value of molecule i, v denotes the total number of molecules in the training set that satisfy the condition d_i ≤ d₀, h is a smoothing factor that dampens the distance penalty, and d₀ is a Tanimoto-distance threshold beyond which two molecules are no longer considered to be sufficiently similar to be included in the average. The y_i values were set to 1 for predicting Pgp substrates or inhibitors and 0 for predicting nonsubstrates or noninhibitors. The v-NN method has two adjustable parameters that influence performance: the Tanimoto-distance threshold d₀ and the smoothing factor h. To identify structurally similar compounds, we used Accelrys extended-connectivity fingerprints with a diameter of four chemical bonds (ECFP4).²⁶ We wish to emphasize that h and d₀ are unique and that they need to be optimized for each set of fingerprints. In this study, we tested the performance of three frequently used fingerprints: ECFP, FCFP, and MDL Public Keys.²⁷ We have included the performance measures of v-NN models that used different fingerprints in Tables S8 and S9. All of the tested fingerprints allowed the v-NN model to perform well on the data sets, with comparable results. For this study, we chose the ECFP4 fingerprints that have previously been reported by Duan et al.²⁸ and Hert et al.²⁹ to show the best overall performance in retrieving the active compounds of many diverse data sets.

Model Performance Measures

We used the following metrics to measure the quality of the classification models

2

3

4

5

where TP, TN, FP, and FN denote true positive, true negative, false positive, and false negative, respectively. κ is a metric for assessing the quality of binary classifiers. Pr(e) is an estimate of the probability of a correct prediction by chance.³⁰ It is calculated as

6

Sensitivity is a measure of a model’s ability to correctly detect true positives, whereas specificity measures a model’s ability to detect true negatives. κ compares the probability of correct predictions to the probability of correct predictions by chance. Its value ranges from +1 (perfect agreement between model prediction and experiment) to −1 (complete disagreement), with 0 indicating no agreement beyond that expected by chance.

We also calculated the coverage, which is defined as the proportion of test molecules with at least one nearest neighbor that exceeded the similarity criterion. The coverage is a measure of how many test compounds are within the applicability domain of a prediction model.

Glossary

Abbreviations

ADP

adenosine diphosphate

ATP

adenosine triphosphate

BC

Bayesian classifier

ECFP

extended connectivity fingerprints

FCFP

functional connectivity fingerprints

FLAP

fingerprints for ligands and proteins

HA

high accuracy

HC

high coverage

MDR

multidrug resistance

MP

molecular properties

Pgp

permeability glycoprotein

QSAR

quantitative structure–activity relationship

v-NN

variable-nearest neighbor

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.6b00247.

• Computational details for optimizing v-NN parameters for HA and HC (Tables S1−S7 and Figures S1−S6); Results on the v-NN method using different fingerprints (Table S8 and S9) (PDF)

• Data sets and corresponding SMILES (XLSX)

The authors were supported by the US Army Medical Research and Materiel Command (Fort Detrick, MD) and the Defense Threat Reduction Agency grant CBCall14-CBS-05-2-0007.

The authors declare no competing financial interest.