Domain Meissner state and spontaneous vortex-antivortex generation in the ferromagnetic superconductor EuFe₂(As_0.79P_0.21)₂

Adding ferromagnetism to superconductor leads to spatially patterned phases of spontaneously generated vortex-antivortex pairs.

Abstract

The interplay between superconductivity and magnetism is one of the oldest enigmas in physics. Usually, the strong exchange field of ferromagnet suppresses singlet superconductivity via the paramagnetic effect. In EuFe₂(As_0.79P_0.21)₂, a material that becomes not only superconducting at 24.2 K but also ferromagnetic below 19 K, the coexistence of the two antagonistic phenomena becomes possible because of the unusually weak exchange field produced by the Eu subsystem. We demonstrate experimentally and theoretically that when the ferromagnetism adds to superconductivity, the Meissner state becomes spontaneously inhomogeneous, characterized by a nanometer-scale striped domain structure. At yet lower temperature and without any externally applied magnetic field, the system locally generates quantum vortex-antivortex pairs and undergoes a phase transition into a domain vortex-antivortex state characterized by much larger domains and peculiar Turing-like patterns. We develop a quantitative theory of this phenomenon and put forth a new way to realize superconducting superlattices and control the vortex motion in ferromagnetic superconductors by tuning magnetic domains—unprecedented opportunity to consider for advanced superconducting hybrids.

INTRODUCTION

The internal exchange energy in ferromagnets is usually significantly larger than the condensation energy of conventional superconductivity. Consequently, strong exchange fields destroy singlet Cooper pairs via the paramagnetic and orbital effects (1), making the coexistence of ferromagnetism and superconductivity a very rare phenomenon. Only a triplet superconductivity could coexist with a strong ferromagnetism—a situation expected in ferromagnetic (FM) superconductors UGe₂, URhGe, and UCoGe (2), in which the FM transition temperature T_FM is substantially higher than the superconducting (SC) critical temperature T_c. Therefore, the superconductivity appears in these compounds when a strong FM order already exists, resulting in the absence of the Meissner phase and in a domain structure of the vortex phase, as recently discovered by scanning superconducting quantum interference device (SQUID) microscopy in UCoGe (3). Consequently, the transition into the SC state at T_c ≪ T_FM does not significantly influence the already “frozen” FM domain structure. On the contrary, in EuFe₂(As_0.79P_0.21)₂, the superconductivity, associated with Fe-3d electrons and induced by the chemical pressure of P atoms, occurs above the temperature of the long-range FM ordering of Eu-4f spins, T_C > T_FM (see Fig. 1, A to C). Below T_FM, the two orders coexist (4–8). It is precisely the competition between them that results in unprecedented SC phases with internal spatial structure at nanoscale, as we show below. In this context, the FM transition in EuFe₂(As_0.79P_0.21)₂ below its SC critical temperature (see Fig. 1, A to C) is of great interest. The condition T_FM < T_c offers a unique opportunity to explore the influence of superconductivity on a weak emergent ferromagnetism at T ≲ T_FM and to follow the interplay between the two orders with temperature. To make ferromagnetism and superconductivity coexist at nanoscale, the paramagnetic effect should be switched off. In P-doped EuFe₂As₂ (the structure of the compound is presented in Fig. 1A), the superconductivity emerges in-between the Eu layers and is induced by the chemical pressure of P atoms on the sublattice (see the phase diagram in Fig. 1B). The superconductivity is associated with Fe-3d electrons and the FM response with the long-range ordering of Eu-4f spins [similar Eu-free compounds BaFe₂(As_1–xNi_x) and BaFe₂(As_1–xNi_x) are not FM (9, 10)]; the triplet character of superconductivity is quite improbable. Rather, a very weak exchange interaction between Eu atoms and conducting electrons could be a more plausible explanation (11–14). On this stage of development, the triplet superconductivity in EuFe₂(As_0.79P_0.21)₂ cannot be completely ruled out. However, as compared to all known triplet superconductors, the compound is characterized by very high critical temperature. Moreover, all experimental observations of the present work find the theoretical explanation without any need for a hypothesis on the triplet nature of Cooper pairs. In this case, the main mechanism of the interplay between the two orders is the orbital effect.

Fig. 1. Coexistence of superconductivity and ferromagnetism in EuFe₂(As_0.79P_0.21)₂.

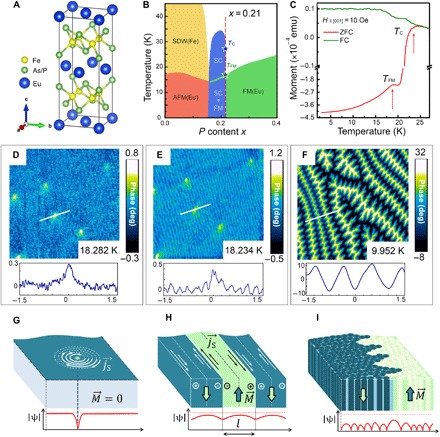
(A) Atomic structure of the material. (B) Phase diagram of EuFe₂(As_1-xP_x) as a function of P/As substitution. Vertical red dashed line marks the P content x = 0.21 of the studied samples. The stars denote the FM transition temperature T_FM and SC critical temperature T_C, T_FM < T_C. (C) Zero magnetic field cooled (ZFC; red line) and 10 Oe field cooled (FC; green line) magnetization curves. The onsets of superconductivity T_C and of ferromagnetism T_FM are marked by red arrows. emu, electromagnetic unit. (D to F) Local magnetic MFM maps acquired at the same sample area 8 μm × 8 μm at T = 18.28 K, T = 18.23 K, and T = 9.95 K in zero magnetic field. They demonstrate, respectively, a conventional Meissner state at T_FM < T < T_C, striped DMS discovered in a temperature range of 17.80 K < T < 18.25 K, and a domain vortex state revealed below T = 17.2 K. (G to I) Schematic views (not to scale) of the three discovered phases in (D) to (F). White arrows in (G) depict the vortex currents; white and black arrows in (H) depict the Meissner currents inside the Meissner domains; white and black dashed lines in (H) define vertical planes at the centers of FM domains, where Meissner currents are zero. Bold arrows mark the magnetization direction. Red solid lines define spatial evolution of the SC order parameter $|\mathrm{\psi }(\overrightarrow{\mathit{r}})|$ in the three states; red dashed lines depict |ψ₀(T)|—the maximum possible value of the order parameter at a given temperature (see explanations in the text).

Here, we explore the interplay at nanoscale between superconductivity and emerging magnetism in EuFe₂(As_0.79P_0.21)₂ by low-temperature magnetic force microscopy (MFM) (see the Supplementary Materials). Single crystals of EuFe₂(As_0.79P_0.21)₂ were grown using a self-flux method. The sample synthesis, chemical composition, structure, transport, and magnetic properties, preparation for experiments, as well as the details of the MFM experiments are presented in the Supplementary Materials. The global magnetic response of the system (Fig. 1C) witnesses the superconductivity and the ferromagnetism to establish at the expected temperatures T_FM ≈ 19 K < T_c ≈ 24 K.

RESULTS

Main experimental discoveries

Local MFM maps presented in Fig. 1 (D to F) summarize our discovery (full set of data is available in the Supplementary Materials). The maps were acquired at the same 8 μm × 8 μm region of the sample while cooling it in zero applied magnetic field. These maps are representative of the three temperature regions of the explored phase diagram: T_FM ≲ T < T_c, T ≲ T_FM < T_c, and T < T_FM < T_c. Above FM transition, the Meissner state in Fig. 1D is homogeneous, as expected for a conventional superconductor. Below T_FM, the Meissner state becomes spontaneously striped (Fig. 1E), characterized by the domain width l = 100 to 200 nm (inset in Fig. 1E). This domain Meissner state (DMS) lasts in a narrow temperature region ~1 K just below T_FM. At temperatures below 17 K, a new phase—a domain vortex-antivortex state (DVS)—is observed (Fig. 1F). It is characterized by large domain widths l ~ 350 nm (inset in Fig. 1F) and by up to 40 times stronger magnetic contrast. The first-order phase transition from DMS to DVS is rather complex. It is accompanied by a spontaneous vortex-antivortex (V-AV) generation at FM domain walls, filling of oppositely polarized FM domains with vortex and antivortex networks, and subsequent transformation of linear narrow DMS domains into enlarged interpenetrating DVS pattern. We not only studied this phase transition in detail, both experimentally and theoretically, but also explored the DVS phase down to 5 K, where the FM subsystem strongly dominates the total response.

Understanding the featureless map in Fig. 1D is straightforward, as the Meissner state of nonmagnetic superconductors is expected to be spatially homogeneous. As also expected, a few bright spots were observed in this map, which are magnetic signatures of individual Abrikosov vortices trapped in the sample at the SC transition, due to the residual external magnetic field (estimated to ~0.5 Oe). In our experiments, we used these vortices and other defects as location markers, which enabled us to probe the same region of the sample at all temperatures during several months’ period of the nonstop MFM study. Remarkably, when the temperature is lowered by only 50 mK, the map in Fig. 1E acquired at T = 18.23 K reveals a striped magnetic pattern—a fingerprint of a spatially inhomogeneous magnetic DMS. The striped pattern of the DMS reversibly disappears (appears) upon heating (cooling) the sample in a narrow temperature window around T_FM, yet it is not reproduced exactly at each temperature cycling. Thus, the DMS phase is linked to the onset of the FM order. The schematic drawings in Fig. 1 (G to I) depict the underlying nature of the observed phases. Above the FM transition, the Meissner state is conventional, characterized by a spatially homogeneous order parameter ψ (r) = const (Fig. 1G). The order parameter is only locally depleted in the trapped Abrikosov vortex cores on the scale ~2ξ, where ξ is the SC coherence length, ξ ≃ 5 to 10 nm in EuFe₂(As_0.79P_0.21)₂. The MFM is not sensitive to these tiny vortex cores; it probes the magnetic footprint of the vortex on a scale of the London penetration depth λ(~350 nm). The homogeneous Meissner state corresponds to the minimum of the free energy of the conventional SC system above T_FM. When the FM order sets in, the situation changes dramatically, as the FM subsystem generates magnetic domains (Fig. 1H). The SC subsystem reacts on the emerging magnetic induction by generating screening Meissner currents. This increases the kinetic energy of the SC subsystem and causes depairing, resulting in a local reduction of the SC order parameter. Theoretically, the situation was first addressed by Krey (15) who noted that the interaction between magnetic induction and superconductivity may strongly influence the FM properties and even cause an intrinsic domain generation. Precisely, the Meissner state of such an FM superconductor should be spatially inhomogeneous and should consist of intrinsic Meissner domains forming a DMS (see Fig. 1, E and H) (15). This DMS should have a narrow domain width l_DMS, which is shorter than not only the penetration depth but also the intrinsic domain width l_N of the same FM material in the absence of superconductivity. Later on, Fauré and Buzdin (16) and Dao et al. (17) predicted that the demagnetization effect should lead to the additional shrinkage of the DMS. This would correspond to the experimentally revealed short-period DMS in Fig. 1E. Because l < λ (T) in our sample, the Meissner screening in each domain is not perfect, and the MFM contrast in Fig. 1E can be seen as a superposition of the magnetic field due to FM domains weakened by a partial diamagnetic effect of Meissner currents. With lowering temperature, the MFM contrast of the DMS increases owing to the rising magnetization of FM domains. A remarkable effect of the DMS is the quasi-periodic modulation of the SC order parameter (Fig. 1H) due to the depairing effect of Meissner screening currents flowing along domain walls. This opens interesting perspectives that are discussed in the final section of the paper.

Domain Meissner state

The DMS exists in EuFe₂(As_0.79P_0.21)₂ in a narrow temperature range, 17.80 K ≲ T_DMS ≲ 18.25 K. Inside the DMS phase, the domain width is l_DMS = (120 to 140) nm (Fig. 2A). This is not only much shorter than the sample thickness d_F ~ 12 μm but also shorter than the zero-temperature penetration depth λ(0) ~ 350 nm of EuFe₂(As_0.79P_0.21)₂, in agreement with theoretical anticipations (15–17). The narrow DMS period and its smooth temperature evolution are the consequence of the competition between the emerging FM order and subsequent SC screening, both contributing to the total energy E_DMS of the DMS phase. In thin non-SC ferromagnets, the equilibrium domain width l_N originates from the energy balance between the magnetic induction energy, which tends to create alternating FM domains, and the energy cost of the domain walls ${\mathit{M}}^2\tilde{\mathit{w}}$ per unit surface, where M and $\tilde{\mathit{w}}$ are the magnetization and the effective width of the domain wall, respectively (18). As a result, the total energy E_FM of the FM state is a function of the domain width; it has a shallow minimum at l_N (Fig. 2B). The equilibrium FM domain width l_N is linked to d_F and $\tilde{\mathit{w}}$ as ${\mathit{l}}_{\mathrm{N}}\simeq \sqrt{{\mathit{d}}_{\mathrm{F}}\tilde{\mathit{w}}}$ (16) (exact relation is available in the Supplementary Materials) and usually lies in the range of 0.5 to 10 μm. In our case, however, the FM subsystem is magnetically coupled to the SC one, making the energy balance more subtle. While having too narrow domains (≪l_N) makes the FM energy very high, enlarging domains rapidly increases magnetic and kinetic energy contributions because of screening Meissner currents [see E_DMS(l) plot in Fig. 2B] (16, 19). The thermodynamically stable state corresponds to the minimum in E_DMS(l); it occurs at a significantly shorter domain width, l_DMS < l_N. Precise calculations using known T_DMS, λ, and d_F (see the Supplementary Materials) give the equilibrium l_DMS = 137 nm, that is, close to the experimentally found DMS domain width. Moreover, because E_DMS depends on λ and l_N, both E_DMS and l_DMS evolve with temperature. In superconductors, λ(T) ≃ λ(0)(1 − (T/T_c)⁴)^−1/2. In ferromagnets just below the Curie temperature, the domain walls are linear (20); when temperature lowers, the energy of the linear domain walls increases as ~(T_FM − T)^1/2 and results in l_N(T). These λ(T) and l_N(T) dependencies are reflected in l_DMS(T); they are nicely captured by the experiment.

Fig. 2. Energy of the domain phases in EuFe₂(As_0.79P_0.21)₂.

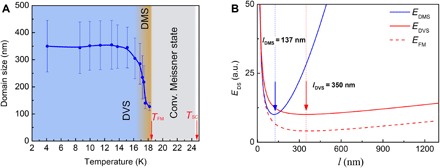
(A) Temperature evolution of the domain widths extracted from MFM maps (the error bars represent the variations of the domain period over the studied sample area). Domains appear just below T_FM, marking a transition from a conventional Meissner state to the DMS. Inside the DMS phase, the domain width slightly increases with lowering temperature. Around T = 17.5 K, the DMS/DVS phase transition takes place; the domain width rapidly increases. Below T = 15 K, deep in the DVS phase, the domain width is almost constant. (B) Total energy of the DMS E_DMS (blue curve), of the DVS E_DVS (red curve), and of the corresponding non-SC FM phase E_FM (dashed curve) as a function of the domain width l at DMS/DVS transition. The calculation is done for T = 18 K and λ(T) 420 nm (see the Supplementary Materials). In the DMS phase, the minimum energy corresponds to l = 137 nm and, in the DVS phase, to l = 350 nm, in agreement with the experiment. a.u., arbitrary units.

First-order transition into DVS

As the temperature is further lowered, the magnetic moments produced by the FM subsystem in each domain increase. When the local moment generated by a domain exceeds H_C1 significantly, the SC subsystem would transit to a vortex state (Fig. 1I). However, a conventional vortex phase is impossible because, in the absence of the external magnetic field, the global magnetization is zero. Rather, the first-order transition into a spontaneous V-AV state was predicted (19, 21), when the FM domains carry vortex lattices of opposite polarities. In the limit of a dense vortex lattice, the energy E_DVS of this new DVS differs from E_FM only by the vortex lattice energy: E_DVS ≃ E_FM + M H_c1 d_F (see Fig. 2B). Within this approximation, the equilibrium domain width in the DVS phase, l_DVS = l_N, that is, significantly larger than l_DMS. A simplified picture here is that, deep inside the DVS phase, the vortex magnetism compensates the Meissner diamagnetism. This compensation leaves the ferromagnetism to decide alone the width of the domains. That is why the equilibrium width l_DVS ≃ l_N, that is, as it would be in a case of a non-SC FM sample. Experimentally, we found that, at the DMS/DVS transition, the domain width rapidly increases (Fig. 2A). At low temperatures, that is, deep in the DVS, the domains are large, and their width l_DVS ≃ 350 nm does not vary significantly below 15 K.

We now follow the essential steps of the phase transition from DMS to DVS, which are presented in Fig. 3. In these maps, trapped Abrikosov vortices are surrounded by dashed circles. The onset of the transition takes place at T = 17.8 K, 1 K below T_FM, when new magnetic objects start to appear (follow the evolution from Fig. 3A to Fig. 3B, etc.). New objects are revealed as pairs of tiny dark and bright spots (surrounded by yellow circles). These pairs of spots are identified as locally generated V-AV pairs. They are never observed in the maps at T > T_FM. The magnetic contrast of the emerging V-AV pairs is significantly lower than that of single Abrikosov vortices, because, at nucleation, the V-AV distance is of the order of the effective width of the domain wall, $\tilde{\mathit{w}}\ll \mathrm{\lambda }$, and their oppositely directed magnetic fluxes partially cancel each other. Remarkably, the V-AV pairs nucleate systematically at locations where the SC order parameter is additionally weakened, such as normal cores of individual vortices or “Y”-shaped domain dislocations at which the “current crowding” effect at sharp turns (22) causes depairing and subsequent reduction of SC order parameter.

Fig. 3. Spontaneous V-AV generation and domain structure evolution at DMS/DVS transition.

(A to K) Local magnetic MFM maps acquired in a narrow temperature window ΔT ≈ 0.6 K from T = 17.86 K (A) to T = 17.25 K (K) in the same sample area 8 μm × 8 μm as in Fig. 1 (D to F). Pinned Abrikosov vortices are marked with dashed circles. Yellow arrows point to specific locations (Y-shaped dislocations of the domain structure, trapped Abrikosov vortices, newly nucleated V-AV pairs, etc.) that work as nucleation sites for V-AV pairs; the latter are surrounded by yellow circles in the following maps (see explanation in the main text). Already existing and growing V-AV clusters are marked by white ellipses. In (I) to (K), DMS and DVS coexist. (L) A map acquired at 16.53 K already resembles the low-temperature DVS of Fig. 1F. (M to O) Zoomed images on the upper region of the maps (A) to (C), showing single V-AV pair nucleation at a Y dislocation. (P) Once created, vortex and antivortex separate and serve as secondary nucleation centers for other V-AV pairs. The contrast in (M) to (P) was optimized for better visibility.

Local V-AV generation at the transition

The principal reason why the V-AV pairs generate, thus destroying DMS, resides in a continuous increase of the kinetic energy of Cooper pairs due to Meissner currents inside each FM domain as temperature is lowered and the magnetic moment inside each domain increases. At some temperature, the creation of vortices in a domain becomes energetically favorable. At the same moment, the appearance of antivortex becomes favorable in FM domains of the opposite polarity. Moreover, owing to peculiar distribution of Meissner currents in the DMS phase (Fig. 1H), the superconductivity at the domain walls is substantially weakened. Large screening currents circulate along the domain walls. Their amplitude (in the limit l ≪ λ) is j_wall = cMl/(6λ²) (16). Because, in our case, l ≃ 0.5λ, these currents can be strong, comparable to the critical current density j_c

$$\frac{{\mathit{j}}_{\text{wall}}}{{\mathit{j}}_{\mathrm{c}}(\mathit{T})}=\frac{2\mathrm{\pi }}{3}\frac{\mathit{M}}{{\mathit{H}}_{\mathrm{c}}}\frac{\mathit{l}}{\mathrm{\lambda }}$$

where H_c is the thermodynamic critical field. As a result, the SC order parameter at the domain wall ψ_wall is reduced compared to the maximum order parameter ψ₀(T) at the same temperature, (ψ₀(T) − ψ_wall)/ψ₀(T) ~ j_wall/j_c; the effect is depicted in Fig. 1H. Therefore, the peculiar geometry of the DMS phase offers a unique opportunity to nucleate V-AV cores locally at domain walls at a reduced energy cost. The presence of defects only facilitates the local V-AV nucleation. The simultaneous nucleation of V-AV pairs does not modify the total angular momentum of the system; this makes local V-AV generation topologically permitted. The experimentally demonstrated V-AV generation is at variance with the vortices in conventional superconductors, which carry a net angular momentum and nucleate at macroscopically distant sample edges. Therefore, the DMS/DVS transition is microscopically different from Meissner-to-vortex phase transitions in nonmagnetic superconductors. From the MFM maps in Fig. 3 (D to I), it is straightforward that the V-AV nucleation is followed by their separation and penetration into the oppositely oriented FM domains, where their presence reduces the total currents and the corresponding kinetic energy (the detailed scenario of V-AV nucleation is available in the Supplementary Materials) (23). Penetrating vortices and antivortices locally distort the quasi–one-dimensional order of the Meissner domains. As new V-AV pairs continue to nucleate at the locations where the SC order parameter is weakened, new domains filled with vortices appear. Once nucleated, the vortex domains proliferate (Fig. 3, I to L). Rapidly, several vortex domains nucleate at the locations where V-AV pairs are already present. Similar to Meissner domains, these new domains also have a quasi–one-dimensional topology, yet they are larger and have a complex internal structure. Because the propagation of the vortex domains is mainly parallel to the existing DMS domain walls, at some moment, a mixed phase is realized, consisting of alternating DMS and DVS clusters (Fig. 3, I to K). As the temperature lowers, new V-AV regions appear, and the DVS phase proliferates and finally occupies all available space. Note that, in Fig. 3, the contrast of each map is optimized for clarity, but the real contrast of the DVS increases at low temperatures and becomes approximately 30 times larger than the contrast of the DMS phase.

Spatial structure of the DVS

Deeply inside the DVS, we observed a puzzling fine structure of the vortex domains (Fig. 1F). This structure is not captured by the existing theories (15, 19) that consider only straight domain boundaries and, consequently, do not account for the internal structure of the DVS. There could be several mechanisms leading to such a complex DVS. The first to consider is the intrinsic domain structure of the ferromagnet, which is masked in the DMS but is recovered deep in the DVS. Many FM materials, especially when put in the form of thick samples, adopt such complex geometries (24). The second mechanism could involve an attractive interaction between vortices and antivortices of neighboring domains. This interaction tends to minimize V-AV distance and could also lead to the vortex and antivortex domain interpenetration and zigzagging domain walls in the DVS phase via vortex-domain coupling (25). Both these microscopic mechanisms are similar in that they locally promote a given order that is inhibited on a larger scale, similar to the Turing’s mechanisms of the pattern formation by the reaction of two substances with different diffusion rates (26) or patterns in biology stabilized by local activator and lateral inhibitor processes (27). The present solid-state counterpart is even richer as it involves two competing orders, each having its own “activation” and “inhibition” scales, although its evolution can be simply tuned by temperature. Third, in several weakly disordered superconductors, the avalanche dynamics of the vortex penetration led to a dendrite-like vortex clusters (28, 29), similar to “fractal” DVS domains that we observed here. Thus, the dynamic nature of the observed interpenetrating domains in DVS cannot be excluded. Moreover, because the minimum in E_DVS(l) is very shallow (see Fig. 2B), all above mentioned mechanisms could, in principle, destabilize the straight domain structure.

CONCLUSION

Finally, we experimentally revealed the existence of a new Meissner phase—the magnetic DMS and the subsequent first-order transition into the DVS in the FM superconductor EuFe₂(As_0.79P_0.21)₂. We also demonstrated the local generation of V-AV pairs directly inside this material. These phenomena should be common to weak FM superconductors with T_FM < T_c, as in Eu(Fe_0.91Rh_0.09)₂As₂, for instance (30). They enable one to anticipate several interesting effects. In the DMS, the quasi–one-dimensional modulation of the SC order parameter should lead to the angular anisotropy of critical currents. This modulation and resulting anisotropy could thus be simply controlled by temperature. By applying an external magnetic field, the Abrikosov vortex penetration and their guided motion inside the crystal along FM domains of a given polarity can also be controlled. Near DMS/DVS transition, external currents could be applied to generate, on demand, and manipulate individual V-AV pairs. All these effects could be exploited in advanced SC hybrids. At the present stage, however, the narrowness of the discovered DMS phase and the sharpness of the DMS/DVS transition would complicate the use of such hybrids. The search for novel FM superconductors (31) is therefore urgently required.

MATERIALS AND METHODS

Single crystals of EuFe₂(As_0.79P_0.21)₂ were grown using a self-flux method (8). The actual chemical composition of the studied samples was determined using energy-dispersive x-ray analysis on Carl Zeiss Supra 50VP scanning electron microscope. The FM superconductivity of EuFe₂(As_0.79P_0.21)₂ was verified by performing ZFC and FC M(T) magnetization cycles on a commercial SQUID magnetometer (MPMS-XL5, Quantum Design).

Atomic force microscopy (AFM) and MFM were performed using an attocube attoDRY 1000 closed-cycle cryogenic microscope with a base temperature of 4 K, supplied with a SC magnet up to 9 T. CoCr-coated silicon probes with a resonance frequency of 87 kHz, a spring constant of 2.8 N/m, and coercivity of 1400 Oe (MESP, Bruker) were used. The probes were magnetized at T = 30 K and H = 2000 Oe. All AFM/MFM images were taken in He buffer gas at pressure P = 0.5 mbar and at temperature that varied from 4 to 30 K, with the temperature stabilized within ±0.3 mK. Before MFM imaging, the EuFe₂(As_0.79P_0.21)₂ single crystals were cleaved in air and placed on the MFM sample holder with an out-of-plane c axis perpendicular to the scan directions. Hereinafter, MFM imaging of the domain structure at T < T_FM was performed in a dual-pass mode when, first, the topography was recorded along a single line in the tapping mode, after which the tip was raised above the surface and scanned along the same line in a lift mode. In this mode, the tip is lifted by 15 nm above the surface, thus avoiding the distortion of the magnetic structure maps due to the magnetic interaction with MFM tips. In general, the magnetic contrast was observed in both the tapping (amplitude and phase signals) and the lift (phase signal) modes.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/7/eaat1061/DC1

Section S1. Sample characterizations

Section S2. Interplay between superconductivity and ferromagnetism in EuFe₂(As_0.79P_0.21)₂: Supplementary MFM maps

Section S3. Energy balance between FM and SC states

Section S4. Simultaneous V-AV nucleation at FM domain boundaries

Fig. S1. Resistance temperature dependence.

Fig. S2. M(H) and χ(T) curves acquired on EuFe₂(As_0.79P_0.21)₂ crystal.

Fig. S3. Full set of images of spontaneous V-AV generation.

Fig. S4. Full set of maps demonstrating the domain structure evolution at DMS/DVS transition.

Fig. S5. The total energy of the domain structure Ẽ_DS in the Meissner and normal states.

Fig. S6. Schematics of the local V-AV nucleation.

Movie S1. Movie of the local V-AV nucleation and domain structure evolution at DMS/DVS.

References (32–38)