Extracting Compound Profiling Matrices from Screening Data

Abstract

Compound profiling matrices record assay results for compound libraries tested against panels of targets. In addition to their relevance for exploring structure–activity relationships, such matrices are of considerable interest for chemoinformatic and chemogenomic applications. For example, profiling matrices provide a valuable data resource for the development and evaluation of machine learning approaches for multitask activity prediction. However, experimental compound profiling matrices are rare in the public domain. Although they are generated in pharmaceutical settings, they are typically not disclosed. Herein, we present an algorithm for the generation of large profiling matrices, for example, containing more than 100 000 compounds exhaustively tested against 50 to 100 targets. The new methodology is a variant of biclustering algorithms originally introduced for large-scale analysis of genomics data. Our approach is applied here to assays from the PubChem BioAssay database and generates profiling matrices of increasing assay or compound coverage by iterative removal of entities that limit coverage. Weight settings control final matrix size by preferentially retaining assays or compounds. In addition, the methodology can also be applied to generate matrices enriched with active entries representing above-average assay hit rates.

1. Introduction

The practically elusive goal of chemogenomics is accounting for interactions between all biological targets and all potential small molecular ligands.¹ This idea naturally leads to the concept of compound profiling. In such experiments, compound libraries are tested against panels of targets, in different assays or the same assay format. Experimental profiling yields assay-compound matrices in which rows represent assays and columns represent small molecules. These entries (matrix cells) account for systematically assessed target–ligand interactions and represent a basic data structure for chemogenomics. If raw screening data are used, such matrices record binary active versus inactive annotations. If chemical optimization data are considered, quantitative activity measurements can be utilized, which typically limits the matrix size. In practice, profiling matrices often focus on individual target families such as kinases.² Profiling data is often incomplete, with only a fraction of all possible target–ligand interactions accounted for.³ For instance, the kinase SARfari version 6.0, curated by ChEMBL,⁴ contains 989 kinase domains, 54 189 active compounds, and 532 155 bioactivity data points, yielding a global coverage of only around 1% of all possible kinase–ligand interactions, given the number of targets and compounds.

Data-driven computational chemogenomics approaches, for instance, the investigation of compound promiscuity and selectivity or the prediction of activity profiles, rely on the availability of matrices capturing interactions between targets and collections of small molecules.² Given data sparseness,³ one of the tasks of computational chemogenomics is the prediction of missing interactions in target–ligand matrices.² Of course, matrices combining experimental results and predictions are of intrinsically limited accuracy. Ideally, complete experimental-only profiling matrices are desirable for practical applications and also the evaluation of machine learning approaches for activity profile prediction.

Herein, we introduce a methodology for generating large profiling matrices from experimental screening data, using PubChem as a data source.⁵ This approach was primarily developed to compensate for the lack of available profiling matrices covering diverse targets. Exemplary matrices reported herein have also provided the basis for a follow-up study exploring a variety of machine learning methods for matrix modeling and activity prediction.⁶

A heuristic approach is developed for iteratively generating submatrices of increasing density by stepwise removal of assays or compounds. Thus, these matrices contain a steadily decreasing proportion of “empty” cells until, ultimately, a matrix with complete coverage is obtained. The newly introduced algorithm is suitable for processing large data sets. It is applied to generate matrices comprising large numbers of assays and test compounds. For such arrays of assays, initial data coverage (i.e., matrix density) is very low, that is, only 10–20%, thus representing sparse matrices not suitable, for example, for multitask machine learning.

The algorithmic task of associating a set of assays with a set of compounds such that all compounds are tested in all, or nearly all, assays is accomplished by considering the biclustering concept.⁷ Biclustering is an NP-hard computational problem equivalent to finding the maximum edge biclique in a bipartite graph.^8,9 It has been of special interest for the analysis of large-volume genomics data for grouping genes with similar expression level patterns. In basic applications, biclustering algorithms attempt to identify submatrices with constant values. Biclustering methods of binary data (i.e., when only two values are distinguished) can also be applied to so-called “frequent item set mining”, which originates from market basket analysis and aims to identify sets of common items in collections of transactions.¹⁰ In the case of a compound profiling matrix, the clustering task corresponds to finding submatrices in which the entries indicate that a compound is tested in a given assay.

We introduce an algorithm for identifying such profiling submatrices. This approach is conceptually related to the biclustering algorithm of Cheng and Church,¹¹ a greedy algorithm for generating a bicluster of near constant values from a matrix by iteratively removing either rows or columns. Our method is based on iteratively removing assays or compounds of low coverage from an initially generated sparse matrix containing all possible assays and compounds. The algorithm generates matrices of increasing density until a matrix with complete coverage remains. Although the principal aim of the approach is retaining a matrix of maximal size, that is, with the largest possible number of entries, it is also applicable to put increasing emphasis on either retaining assays or compounds at the expense of overall matrix size. To this end, a weight parameter is used to preferentially retain assays or compounds. In addition, a variant of the algorithm is introduced to penalize the removal of active entries, hence aiming to generate a matrix representing above-average hit rates. Hence, the matrix generation algorithm detailed in the following is not only capable of generating complete profiling matrices but also capable of balancing compound and assay coverage for specific applications.

2. Results and Discussion

The starting point for the analysis is a collection of assays with overlapping sets of screening compounds. This is a typical output of high-throughput screening (HTS) campaigns using related compound libraries, for example, those that are shared and further expanded by publicly funded screening centers. Such a collection of assays yields a sparse matrix in which test results for multiple targets and varying numbers of compounds are reported. Sparse matrices provide the input for our methodology that is presented in detail in the Materials and Methods section below. A primary goal is the iterative removal of a minimum number of compounds or assays to convert a sparse matrix into a complete matrix. Alternatively, dense matrices with varying assay or compound composition or an enrichment of hits can be generated, as mentioned above.

2.1. Assembly of Sparse Matrices

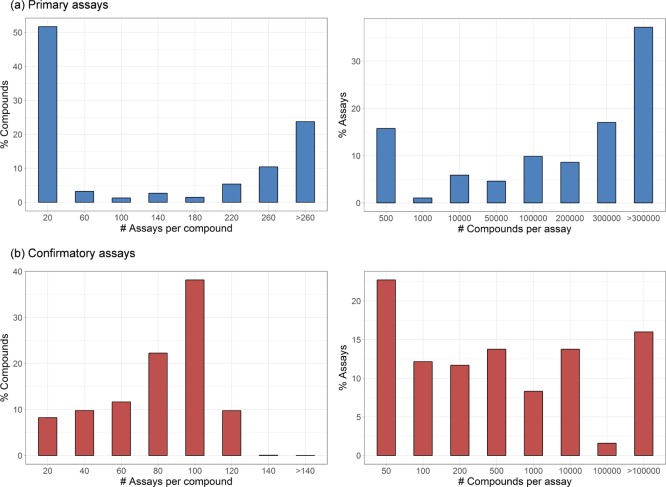
Initial collections of primary and confirmatory assays with overlapping screening compounds were separately assembled from PubChem applying the protocol described in the Materials and Methods section. Primary and confirmatory assays contained compounds tested against 476 and 625 different single protein targets, respectively. For 476 primary assays, the sparse matrix contained 767 895 compounds. For 625 confirmatory assays, the corresponding matrix contained 422 105 compounds. Initial coverage (density) of the matrices was 0.24 for primary and 0.11 for confirmatory data. Hence, 24% and 11% of all possible assay/compound combinations were tested in the sparse matrices. Of those entries, 0.67% (primary) and 1.15% (confirmatory) represented activity, yielding an activity density (i.e., the fraction of active entries in the whole matrix) of 0.24 × 0.67% = 0.16% for the primary assay matrix and 0.11 × 1.15% = 0.13% for the confirmatory assay matrix. Figure 1 shows the histograms reporting the number of assays per compound and the number of compounds per assay for these sparse matrices. More than 50% of the compounds from the primary assays was tested in 20 or fewer assays. However, approx. 40% of the compounds was screened in more than 200 assays. On the other hand, more than 50% of the assays contained more than 200 000 compounds. The distributions for confirmatory assays differed significantly. Here, the majority of compounds were tested in 100 or more assays. However, only approx. 15% of the assays contained more than 100 000 compounds.

Figure 1.

Assay and compound distribution. For selected and filtered PubChem assays, histograms report the number of assays each compound has been tested in (left) and the number of compounds tested in each assay (right). On the left, assay numbers are binned. The upper bound of each bin is given on the x-axis. The y-axis reports the percentage of compounds corresponding to each bin. On the right, assays are organized according to the number of tested compounds collected in bins. The upper bound of each bin is given on the x-axis. In (a), histograms are shown for primary and in (b) for confirmatory assays.

2.2. Generation of Dense and Complete Matrices

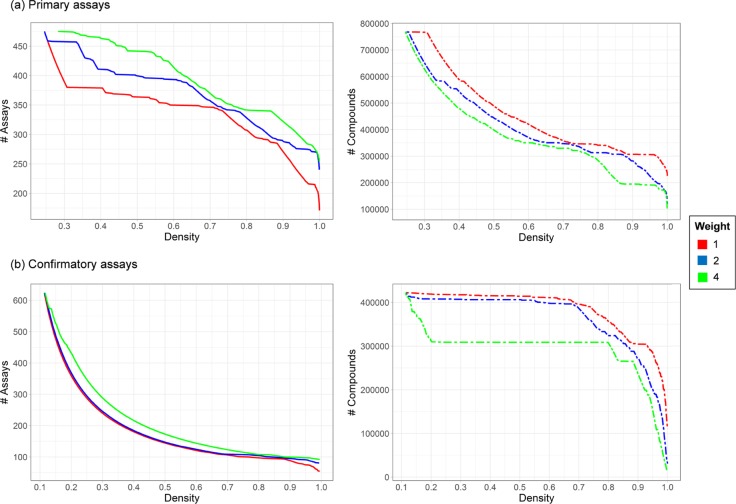
Next, the algorithm was applied to the sparse primary and confirmatory assay matrices. Three weights of 1, 2, and 4 were applied to increasingly prioritize the number of assays in matrices at the expense of compound numbers. The iterative nature of the algorithm yielded matrices of decreasing size but with increasing density by either eliminating assays or compounds. Figure 2 reports the number of assays and compounds as a function of matrix density and monitors the progression of matrices toward dense and ultimately complete matrices. Following the curves from the left to the right illustrates the progression. Depending on the initially assembled assay data, the order in which assays and compounds are removed from the matrix may vary when different weight settings are applied. The initial sparse primary assay matrix only contained relatively few assays with small compound numbers. As can be seen in Figure 2a, these assays were removed at early stages of algorithmic progression. Then, the compounds with low assay coverage were removed until a matrix density of approx. 75% was achieved. These progression characteristics varied slightly depending on the weights (1, 2, or 4), that is, increasing preference to retain assays over compounds. Notably, a larger number of primary assays were only removed during the latter stages of algorithmic progression when the density increased beyond 95%. In Table 1, sizes of the resulting matrix are reported for weights of 1 and 4 and different matrix densities. Compared to nearly complete matrices with 95–99% coverage, the complete matrix contained considerably fewer assays and compounds. Thus, if small amounts of missing data can be tolerated, preference might be assigned to nearly complete (dense) matrices over a complete matrix, given their larger size. In this context, it is important to consider the minimum assay coverage for all compounds and the minimum compound coverage for all assays, as also reported in Table 1. For the matrices generated using weight 1, the minimum percentage of assays covered by a single compound and the minimum percentage of compounds covered by a single assay were very similar; a desirable characteristic of the algorithm. For 90% density, the minimum coverage was approx. 58% in both instances, which further increased to 66% for the 95% dense matrix and to greater than 92% for the 99% dense matrix. A common concept in machine learning, known as “imputation”, is the replacement of missing data with substituted values such as the median.¹² For screening assays, the median would almost certainly correspond to an inactive data point. Because of the low coverage imputation on sparse screening matrices would make only little sense. By contrast, imputation would be applicable to dense matrices generated with our algorithm, which retain more assays and compounds than complete matrices.

Figure 2.

Assays and compounds as a function of matrix density. The curves show the effect of iterative removal of assays and compounds from the original matrix as a function of matrix density. Left, the number of assays and right, the number of compounds for matrices from (a) primary and (b) confirmatory assays.

Table 1. Size and Compound and Assay Coverage of Profiling Matrices^a.

	profiling matrix (primary assays)
	weight 1			weight 4
matrix density	matrix size	assay coverage	CPD coverage	matrix size	assay coverage	CPD coverage
0.75	330 × 346 368	0.17	0.17	352 × 317 322	0.39	0.029
0.90	270 × 307 224	0.58	0.58	322 × 194 924	0.74	0.30
0.95	229 × 305 944	0.66	0.66	294 × 191 440	0.84	0.49
0.99	210 × 267 419	0.92	0.93	272 × 172 204	0.92	0.74
1.00	171 × 225 550	1.00	1.00	254 × 93 317	1.00	1.00

	profiling matrix (confirmatory assays)
	weight 1			weight 4
matrix density	matrix size	assay coverage	CPD coverage	matrix size	assay coverage	CPD coverage
0.75	101 × 381 858	0.20	0.25	115 × 308 741	0.30	0.0076
0.90	88 × 304 509	0.63	0.63	100 × 236 778	0.76	0.36
0.95	75 × 284 486	0.80	0.81	98 × 152 594	0.91	0.71
0.99	56 × 189 513	0.96	0.97	93 × 35 435	0.98	0.93
1.00	53 × 110 636	1.00	1.00	91 × 12 341	1.00	1.00

^aFor five different matrix density levels and weights of 1 and 4, the size and assay/compound (CPD) coverage of profiling matrices extracted from primary (top) and confirmatory PubChem assays (bottom) are reported. Assay coverage refers to the minimum fraction of assays covered by a single compound and CPD coverage to the minimum fraction of compounds covered by a single assay.

Figure 2b shows the corresponding results for confirmatory assay matrices. The initial set of confirmatory assays contained many assays with only small numbers of compounds that were removed during the early stages. Consequently, the majority of compounds was only removed at later stages and higher matrix densities. Notably, the number of assays remained fairly constant (approx. 100) at higher densities. However, there was a sharp decrease in the number of compounds when the matrices became complete. For weight 1, compared to the 95% dense matrix, the complete matrix contained 70% of the assays but only less than 40% of the compounds, as reported in Table 1. By contrast, the minimum assay and compound coverage was greater than 80% for the 95% dense matrix. Thus, the 95% dense matrix contained much more experimental information than the complete matrix. These comparisons illustrate the ability of the algorithm to effectively balance assay and compound coverage with matrix density, an important feature.

2.3. Emphasizing Active Matrix Entries

2.3.1. Increasing Active Entry Density

Given the generally low hit rates in HTS assay, usually less than 1% for primary assays, one may want to enrich active entries in profiling matrices for some applications such as, for example, the comparison of virtual screening methods. Such enrichments represent a deliberate departure from experimental reality but are helpful on occasions, for example, to increase the number of positive training examples for machine learning. However, such enrichment also represents a methodological challenge for matrix design.

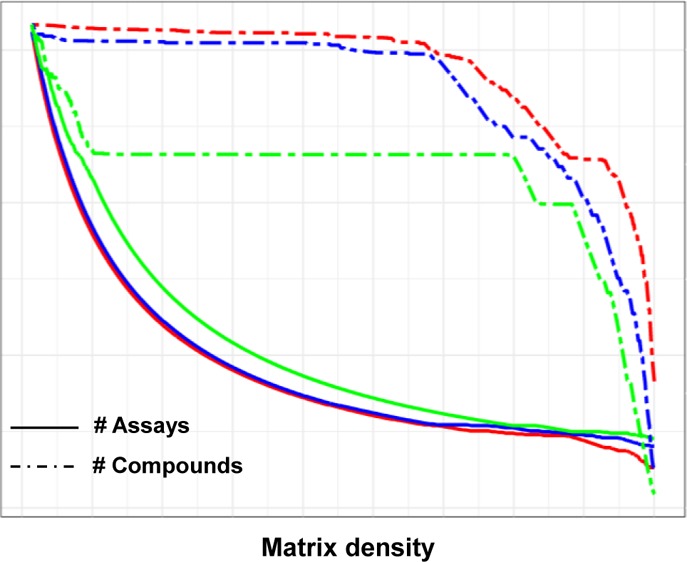
At the level of our algorithm, the enrichment of active entries can be achieved by preferentially retaining such entries at the expense of the global matrix size. To this end, a modification of the algorithm was developed. An “active weight” parameter was introduced to highly weight active matrix entries during iterative density improvement. The modified algorithm was applied to the confirmatory assay matrices using weights of 0 (i.e., no additional emphasis on active entries), 50, and 250. Figure 3 reports the resulting density of active entries for matrices of globally increasing density (and decreasing size). As can be seen, for positive active weight settings, the density of active entries slightly increased until a matrix density of approx. 0.85 was reached. Then, positive active weights led to an in part very strong increase in the density of actives (weight 250) until it reached a maximum at a matrix density of approx. 95%, before dropping off again sharply when the matrices reached completeness. Table 2 reports the results for different active weight settings for complete matrices and dense matrices where the density of actives reached its maximum. The effect of using an active weight of 50 was moderate, at best reaching a maximum active entry density of 1.30%, compared to 0.85% when no activity weight was applied. The number of assays was reduced from 79 to 62 and the number of compounds by less than 50% (from 294 912 to 166 255). In contrast, using a weight of 250 resulted in matrices with a maximum active entry density of 4.78% at a global matrix density of 98% and of 2.24% for a complete matrix. However, this significant increase in the density of active entries was achieved at the cost of reducing the number of assays to 28 and the number of compounds to 72 427 and 41 977 compounds, respectively. Thus, substantial reductions in matrix size must be accepted if an active entry density approaching 5% is desired for a given application.

Figure 3.

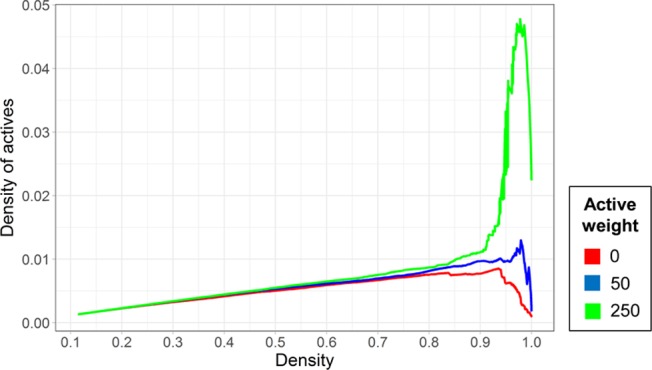
Density of active compounds as a function of matrix density. The curves report the density of active compounds as a function of matrix density for increasing “active weight” parameter settings. Densities are reported for matrices from confirmatory assays.

Table 2. Size, Compound and Assay Coverage, and Activity Density of Profiling Matrices^a.

activity weight	matrix density	matrix size	assay coverage	CPD coverage	activity density (%)
0	0.94	79 × 294 912	0.73	0.77	0.85
0	1.00	53 × 110 636	1.00	1.00	0.21
50	0.98	62 × 166 255	0.68	0.87	1.30
50	1.00	60 × 77 766	1.00	1.00	0.18
250	0.98	28 × 72 427	0.71	0.90	4.78
250	1.00	28 × 41 977	1.0	1.0	2.24

^aFor different activity weights and matrix density, the size and assay/compound (CPD) coverage and activity density of profiling matrices are reported. Assay coverage refers to the minimum fraction of assays covered by a single compound and CPD coverage refers to the minimum fraction of compounds covered by a single assay.

2.3.2. Assay-Based Hit Rates

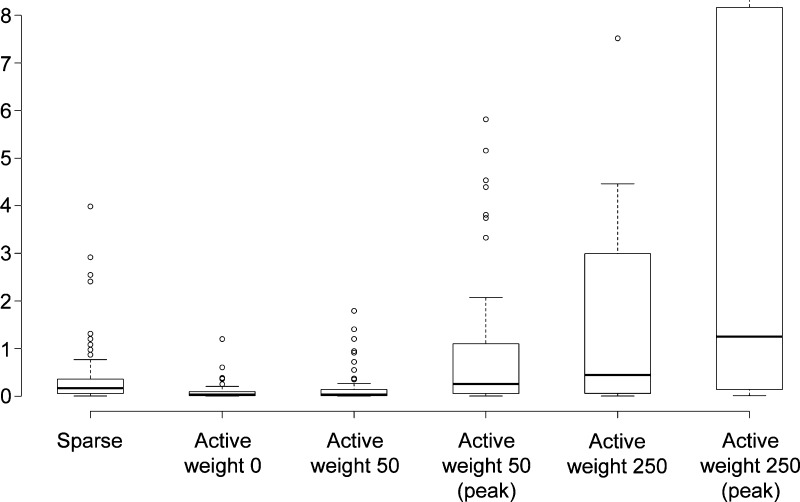
Figure 4 illustrates the effect of the algorithm on a per assay basis. The first two box plots report the distribution of hit rates for 53 assays of the complete matrix with no active weights. The first plot shows the distribution of hit rates for the original assays and the second plot shows the distribution for all compounds per assay retained in the completely filled matrix. The hit rates in the complete matrix were slightly reduced. This effect was partly compensated for by applying an activity weight of 50 to the complete matrix and reversed for the 98% dense matrix where the hit rates clearly increased. The effect was much stronger for the activity weight of 250. In this case, most assays displayed significantly increased hit rates in the complete matrix and even more so in the 98% dense matrix with maximal activity density. Hence, increases in hit rates were achieved across all assays retained in the modified matrices.

Figure 4.

Hit rates for individual matrix assays. The box plots report hit rate distributions for confirmatory assays in matrices generated with increasing “active weight” parameter settings for assays and compounds. The plot on the left (sparse) reports the hit rate distribution for the original matrix comprising 53 assays and the second plot to the right (active weight 0) the distribution for the complete matrix. The third and fourth plots report hit rates for active weight 50 for the complete matrix (third) and a matrix with density 0.98 (fourth) when the activity density reaches it maximum. The fifth and sixth plots show the corresponding distributions for activity weight 250 (fifth, complete; sixth, 98%). The box plots report the first quartile (lower boundary of the box), median value (thick line) and third quartile (upper boundary of the box); the whiskers extend to data points at distance of at most 1.5 interquartile ranges from the bottom or top line of the box; outliers beyond the whiskers are displayed as separate points.

2.4. Conclusions

The lack of large profiling matrices in the public domain is a limiting factor for many applications in computational medicinal chemistry and chemogenomics. Herein, we have presented an algorithm for the extraction of complete or nearly complete profiling matrices from screening data. We emphasize that the method does not involve data quality control and thus does not compensate for potentially limited quality of raw or even confirmatory screening data. If original data from which matrices are extracted are error-prone, limited data quality will carry over. Hence, one must generally be aware of potential data quality issues, which might affect the applicability of computed matrices (and compromise machine learning), especially if original data for matrix generation are taken from heterogeneous public sources.

Applying our approach, we have demonstrated how from an initial collection of more than 450 primary assays and 800 000 tested compounds a complete matrix with 170 assays and more than 225 000 compounds was extracted. A corresponding matrix from confirmatory assay data contained 53 assays and over 110 000 compounds because of the small size of many of confirmatory assays that were removed algorithmically. Depending on parameter settings, our algorithm is adaptable to put more emphasis on retaining assays or compounds in a matrix and balance its composition. Therefore, the generated profiling matrices represent a well-defined organization of experimental screening data accounting for original hit rates. Furthermore, applying additional active weights makes it possible to modify matrix composition and enrich active entries, if so desired. In addition to generating matrices that cover many diverse targets, which has been our major interest, the approach is equally applicable to assemble profiling matrices for individual target families of interest. Such matrices might contain smaller numbers of assays than contained in matrices generated in our proof-of-concept investigation but also large numbers of compounds. Through appropriate parameter settings, the assay-to-compound ratio of such matrices can also be modified to tune them for specific applications. Matrices reported herein will be made publicly available in an open access deposition. They provide a basis to, for example, investigate approaches for multitask machine learning or the prediction of complete matrices representing the experimental reality, which is of considerable interest to us.

3. Materials and Methods

3.1. Assays

Assay data representing chemical screens were extracted from the PubChem BioAssay database.⁵ The selected assays either represented primary screens (reporting the percentage of activity or inhibition for a single compound dose) or confirmatory assays for which activity is usually reported as AC₅₀ determined from dose–response data. Only assays with single protein targets were considered. For each qualifying assay, compounds were only selected if they were designated as “active” or “inactive”; compounds with other activity attributes such as “inconclusive” or “unspecified” disregarded. If multiple assays were available for the same target, only the assay with the largest number of tested compounds was retained. On the basis of these criteria, 476 primary and 632 confirmatory assays covering 825 187 and 450 464 unique compounds, respectively, were obtained that were directed against 476 and 632 unique targets, respectively. The compounds were screened for pan-assay interference compounds (PAINS),¹³ potentially causing assay artifacts, using three public PAINS substructure filters available in RDKit,¹⁴ ChEMBL,⁴ and ZINC.¹⁵ Filtering reduced the number of compounds to 767 895 and 422 105 for primary and confirmatory assays, respectively. Thus, for primary and confirmatory assays, initial assay/compound matrices of size 476 × 767 895 and 625 × 422 105 were formed, respectively.

3.2. Algorithm

A set of assays can be organized as a profiling (assay/compound) matrix in which rows represent assays and columns represent compounds. A matrix entry is set to 0 if the compound was not tested in the assay, set to 1 if the compound was active, and set to 2 if it was inactive. In the basic version of the algorithm detailed below, no distinction is made between active and inactive entries. Rather, the primary goal is constructing submatrices of decreasing size by removing either assays or compound entries such that the overall density, that is, the percentage of nonzero matrix entries (cells), increases monotonically until a complete (100% dense) matrix is obtained. In a complete matrix, each compound is tested in each assay. The basic algorithm follows a greedy approach.

• 1.Given an initial assay/compound matrix, we first consider a submatrix S = (s_ij) consisting of a set A of selected assays, represented by the rows of S, and a set C of selected compounds, represented by the columns of S. Let m = |A| and n = |C| be the number of rows and columns, respectively. The entry s_ij is 0 if the compound j is not tested in assay i, 1 if it tested active, and 2 if it tested inactive.
• 2.Initialize A and C to contain all assays and all compounds, respectively. Hence, C is the union of the tested compounds originating from all assays.
• 3.For each assay a in A, determine the density of the tested compounds for a, that is, the ratio of nonzero entries to the number of columns n: 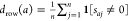. The indicator function 1[p] for a predicate p is defined to be 0 if p is false and 1 if p is true.
• 4.For each compound c in C, determine the density of the tested assays for c, that is, the ratio of nonzero entries to the number of rows m: .
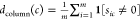• 5.Select the assay of A with minimum density a_min = argmin_a∈A(d_row(a)) and the compound of C with minimum density c_min = argmin_c∈C(d_column(c)). If multiple assays with minimum density or multiple compounds with minimum density are available, an arbitrary assay or compound with minimum density is selected.
• 6.If (c_min)^weight ≤ a_min remove c_min from C, that is, C ← C – {c_min}, else remove a_min from A, that is, A ← A – {a_min} and update matrix S accordingly.
• 7.Stop if S only contains nonzero elements, else continue with step 3.

The algorithm uses a parameter “weight” that controls the preferential removal of compounds (weight > 1) or assays (0 < weight < 1). In effect, the resulting dense matrix preferentially contains more assays at the cost of the number of compounds or vice versa. In addition, the overall size m × n of the resulting matrix is expected to be smaller compared to the case weight = 1 when, in each step, the row or column with the lowest density is removed.

The hit rates of the assays are usually low and one may also preferentially retain active compounds in a final matrix at the expense of the global matrix size. Therefore, a variant of the algorithm uses an “active weight” parameter to act against the removal of active compounds or assays with many active data points. It differs in steps 3 to 6 from the basic algorithm.

• 3′.
  For each assay a in A, determine

  
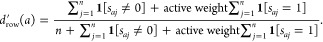
• 4′.
  For each compound c in C, determine

  
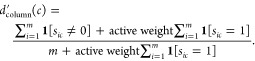
• 5′.Select the assay of A with the minimum density a_min^′ = argmin_a∈A(d_row(a)) and the compound of C with the minimum density c_min^′ = argmin_c∈C(d_column(c)). If multiple assays with minimum density or multiple compounds with minimum density are available, an arbitrary assay or compound with minimum density is selected.
• 6′.If (c_min^′)^weight ≤ a_min, remove c_min^′ from C, that is, C ← C – {c_min}, else remove a_min^′ from A, that is, A ← A – {a_min} and update matrix S accordingly.

In this variant, the condition active weight ≥ 0 applies. If active weight > 0, active measurements receive an increased weight when calculating densities d′.

Author Contributions

The study was carried out and the manuscript was written through contributions from all authors. All authors have approved the final version of the manuscript.

The authors declare no competing financial interest.