How Well Can DNA Rupture DNA? Shearing and Unzipping Forces inside DNA Nanostructures

Abstract

A purely DNA nanomachine must support internal stresses across short DNA segments with finite rigidity, producing effects that can be qualitatively very different from experimental observations of isolated DNA in fixed-force ensembles. In this article, computational simulations are used to study how well the rigidity of a driving DNA duplex can rupture a double-stranded DNA target into single-stranded segments and how well this stress can discriminate between unzipping or shearing geometries. This discrimination is found to be maximized at an optimal length but deteriorates as the driving duplex is either lengthened or shortened. This differs markedly from a fixed-force ensemble and has implications for the design parameters and limitations of dynamic DNA nanomachines.

1. Introduction

DNA is emerging as a programmable and versatile material for nanoengineering,^1,2 with techniques such as DNA origami allowing for a rich variety of geometries and structures,³ as well as dynamic transitions between structures that are kinetically controlled via toehold-mediated strand displacement. A variety of nanostructures have been built with DNA, including track-walking motors⁴⁻¹⁷ and nanorobots with Boolean logic control,¹⁸ with the potential to sense and manipulate intracellular environments.¹⁹

Alongside toehold-mediated strand displacement, DNA duplex rupture and re-formation is ideal for dynamically switching a DNA nanostructure between different states, with the process capable of storing or releasing up to 10 pN nm of chemical energy per base pair.²⁰ Investigating the mechanics of force-induced rupture is thus vital for developing DNA nanomachines, as well as for the wider understanding of DNA mechanics in general.

In particular, DNA requires two to three times more force to rupture when force is applied across opposite ends of the duplex, in a shearing geometry, as opposed to when forces are applied to the same end of the duplex to unzip it instead.²¹⁻²³ This difference has been used to distinguish between energetically and kinetically identical but geometrically different arrangements of DNA molecules.²⁴ The shearing–unzipping difference has also been used to implement selective dissociation between identical legs of DNA bipedal nanowalkers.^14,15

Such purely geometric discrimination in turn suggests that a DNA nanostructure could exhibit allosteric interactions, where binding to one part of the structure affects the energetics of a different part. This was recently demonstrated by a modular nanowalker which binds its rear foot in an unzipping geometry and its front foot in a shearing geometry^14,16 so that with both feet bound to the track, intramolecular tension preferentially unbinds the rear foot, achieving continuous forward movement without irreversible track damage.

Various theoretical and experimental approaches are used to study force-induced DNA rupture. Theoretically, the rupture of long duplexes can be treated as first-order thermodynamic transitions induced by sufficient force, 15–20 pN for unzipping^{21,22,25−27} and 60–70 pN for shearing.²³ However, the rupture of shorter DNA duplexes is of greater relevance to nanostructures. For such duplexes, rupture instead proceeds as an activated process whose rate is determined by the height of the transition barrier, as recently modeled.²⁸

Experimentally, in most measurements of rupture forces, the DNA molecule being studied is coupled to a larger system (e.g., the tip of an atomic force microscope), which applies a constant force. Rupture thus occurs over an isotensional or Gibbs ensemble.^29,30 By contrast, consider a DNA duplex with two “sticky ends” that, upon hybridizing, compress the duplex and reduce its average end-to-end distance, as shown in Figure 1. The reverse of this process corresponds to the stress in the main DNA duplex, rupturing the sticky ends apart either by unzipping or shearing. These seem at first glance to be nanomechanical analogues to constant force shearing and unzipping, but there is a vital difference: the tension in the main DNA duplex, and therefore the shearing or unzipping force, decreases as the duplex is allowed to relax into a less constrained state. Because of the finite elasticity of single-stranded and double-stranded DNA, the process therefore no longer occurs at constant force. Furthermore, because a duplex is generally longer than it is wide, a helix being sheared will generally experience different forces from a helix being unzipped, as well as the point of first contact being different. This is true rather generally for DNA shearing or unzipping that occurs within a DNA nanomachine. This study aims to clarify how this affects the energetics of shearing and unzipping, as well as the difference between them, which has implications for constructing DNA nanomachinery.

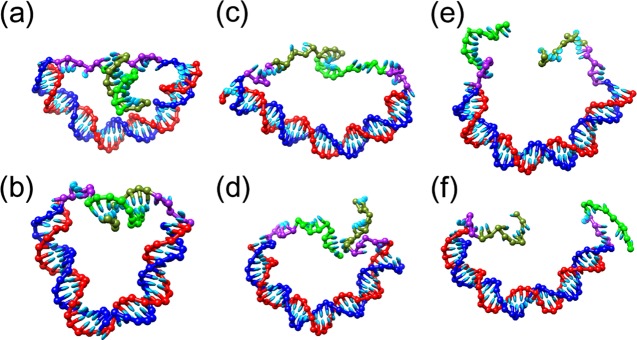
Figure 1.

As a short duplex DNA target attached to a longer main duplex (a, b) undergoes either unzipping (c) or shearing (d) to release single strands (e, f), the curvature and tension in the main duplex decreases. The different parts of each configuration are color-coded as follows: the main duplex is blue and red, whereas the overhangs are composed of green sticky ends that are complementary and come together to form the target duplex and purple linkers that provide mechanical flexibility. Configurations are shown for the main duplex length of 40 bp.

2. Results

2.1. DNA Systems

In this study, the nucleotide-level coarse-grained model oxDNA2³¹⁻³³ (parameterized to 1 M salt concentration) is used to simulate configurations shown in Figure 1, in which the stress across a double-stranded DNA main duplex of varying length is applied to either shear or unzip a duplex of 10 base pairs. The oxDNA2 model accurately represents the elastic properties of single and double-stranded DNA, together with the basic physics of base pairing. Despite treating each nucleotide as a rigid body, the oxDNA2 model has been useful in clarifying basic aspects of key processes, such as hybridization,³⁴ toehold-mediated strand displacement,³⁵ hairpin formation,³⁶ duplex strong bending and kinking,³⁷⁻³⁹ and force-induced melting and overstretching.⁴⁰ Instead of a specific sequence, sequence-averaged parameters are used for the nucleotide interaction potentials to exclude effects such as misbonding and the difference between A–T and C–G pair interaction strengths.

The molecular configurations consist of double-stranded DNA, between 20 and 60 base pairs long, with 15-nucleotide single strands added to either the 3′ and 5′ ends of one strand or the 3′ ends of both strands. In the former configuration, when the 10 terminal nucleotides on the single strands are hydrogen-bonded, they form a 10 base pair DNA duplex with unzipping stresses applied across one 3′–5′ end and two segments of 5-nucleotide single-stranded DNA left unbonded as linkers. In the latter configuration, the central duplex instead has shearing stresses applied at its 5′ ends. Both configurations evolve without external forces so that the unzipping or shearing forces come strictly from the stress of compressing the longer double-stranded DNA bridge.

Given the large free-energy changes expected, direct observation of rupture kinetics would be computationally demanding. As such, kinetics and energetics are instead inferred from free-energy landscapes of the shearing and unzipping processes. The virtual-move Monte Carlo (VMMC) algorithm of Whitelam and Geissler (the variant from the appendix of ref (41)) is used to simulate the model, and the free-energy profile is measured as a function of the reaction coordinate, either how many pair bonds remain along the target 10 bp duplex or the distance between the separated single strands, taken as the minimum of all distances between pairs of complementary nucleotides, in 0.85 nm bins (corresponding to 1 distance unit in the oxDNA2 model). Umbrella sampling⁴² and windowing based on the reaction coordinate is then used to further reduce the computational difficulty of accessing high-free-energy states and measuring their free energy accurately.

2.2. Energetic Features of Shearing and Unzipping

The free-energy landscapes for shearing and unzipping are shown in Figure 2. Both shearing and unzipping show qualitatively similar landscapes, with a monotonically increasing free-energy curve for bond-breaking leading to a reaction barrier at the state of highest free energy, which is always the state with exactly one pair bond remaining. As shown in Figure 3a, we define the transition barrier ΔG^‡ to be the free-energy difference between the 10-bond state and the one-bond reaction barrier state. After that last bond is broken, the free energy decreases again to a minimum at which both the main duplex and the sticky ends are in fully relaxed configurations, before rising again when the distance between sticky ends is large enough to require elastic stretching. We define the overall free-energy difference ΔG_tot to be the free-energy difference between the 10-bond state and the subsequent free-energy minimum over the ruptured configurations, which is negative if the 10-bond state has lower free energy than the ruptured free-energy minimum, indicating that rupture is energetically unfavorable and positive otherwise. The transition barrier and overall free-energy difference, respectively, control kinetic and energetic contributions to the relative rates of shearing and unzipping.

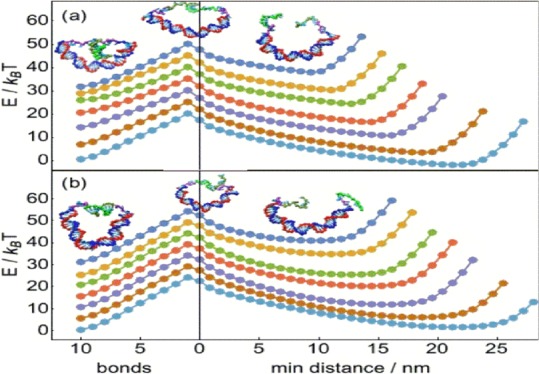
Figure 2.

As (a) unzipping or (b) shearing progresses, the free energy increases due to bond-breaking up until the reaction barrier, which is consistently the state with only one bond remaining. After this barrier is passed, the free energy steadily decreases to a relaxed minimum and only increases again when the distance between sticky ends is forced to be larger than the contour length of the main duplex. Free-energy curves are for main duplex lengths of (top to bottom) 20, 25, 30, 35, 40, 50, and 60 bp and are offset by 5 k_BT from each other at 0 bonds for clarity. Insets show characteristic configurations with either all 10 pair bonds intact, only one bond remaining, or completely unbound. Uncertainties are comparable to or smaller than the size of the symbols.

Figure 3.

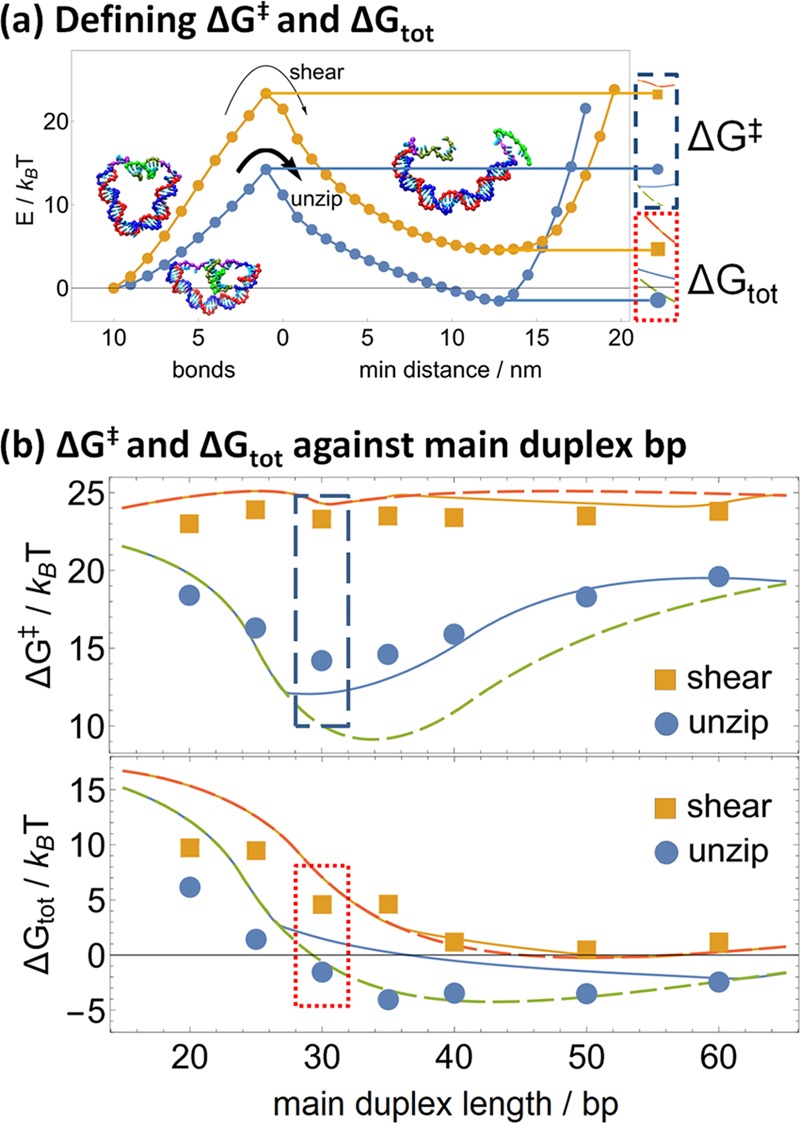
(a) For either shearing or unzipping (shown here for main duplex length 30 bp), the transition barrier ΔG^‡ and ΔG_tot can be defined by the free energy of the transition state (1 bond) and the minimum free energy of the unbound states, respectively, relative to the initial 10-bond state. Cut-outs on the right correspond to insets in graphs (b), depicting the derivation of these free energies graphically. (b) The transition barrier (top) remains largely constant for shearing and shows a minimum of around 30 bp for unzipping; the total free-energy change (bottom) mostly decreases with increasing main duplex length. These can be fitted to eqs 1 and 2 of Section 2.4, where allowing the main duplex to kink at a critical torque of 29 pN nm (solid lines) improves fitting of the transition barrier but degrades fitting of the total free-energy difference of unzipping, relative to a model in which the main duplex does not kink (dashed lines).

The variation in ΔG^‡ and ΔG_tot according to the length of the main duplex is shown in Figure 3b. At any main duplex length, both ΔG^‡ and ΔG_tot are higher for shearing than for unzipping. As the main duplex length increases, ΔG_tot decreases both for shearing and for unzipping until about 40 bp, after which it remains roughly constant, becoming negative for unzipping whereas remaining positive for shearing. Rupture is thus less energetically favorable with shorter main duplexes than longer main duplexes and less favorable for shearing than for unzipping; indeed, after 30 bp, unzipping becomes energetically favored, whereas shearing remains disfavored. On the other hand, ΔG^‡ is consistently 24–25 k_BT for shearing regardless of the main duplex length but varies nonmonotonically for unzipping, being minimized at 14 k_BT for a 30 bp main duplex, whereas rising as high as 19 k_BT for either shorter or longer main duplexes.

These trends can be qualitatively explained by considering the molecular geometries of shearing and unzipping. Because our systems require the same number of base pairs to be broken for shearing and unzipping, any difference in ΔG^‡ between them captures the difference in how the main duplex relaxes during the rupturing of the target duplex. Thus, the insensitivity of ΔG^‡ to main duplex length for shearing shows that the shearing of the target duplex does not allow the main duplex to relax. This is consistent with the molecular geometry of shearing, in which rupturing one base pair bond simply replaces one (double-stranded) base pair under tension with one (single-stranded) nucleotide’s worth of length. Indeed, the end-to-end distance across the main duplex changes minimally as shearing proceeds (Figure 4), with most of the relaxation occurring after the target duplex has been fully ruptured.

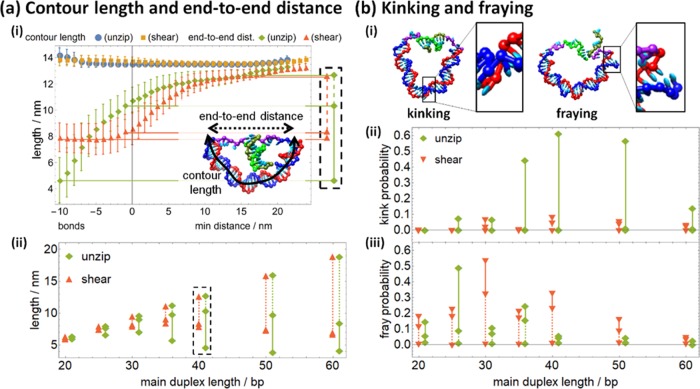
Figure 4.

(a) (i) As either shearing or unzipping proceeds (shown for main duplex length 40 bp), the end-to-end distance across the main duplex increases as it relaxes, whereas the contour length increases slightly at either high bond number or high min distance. (Here and in Figure 5, error bars are in-run fluctuations; the standard error of mean is the size of the symbols or smaller.) The inset shows how contour length (solid) and end-to-end distance (dashed) are calculated for a typical configuration. The end-to-end distance is extracted at 10 bonds, one bond, and the unbound energy minimum for subsequent analysis, with the cutout corresponding to the inset in graph (ii). Graph (ii) shows how the end-to-end length increases as shearing and unzipping proceed. (b) (i) The melting of base pairs in the main duplex results in either kinking or fraying. Graphs (ii) and (iii) show how kinking and fraying, respectively, decrease as shearing and unzipping proceed. In graphs (a) (ii), (b) (ii), and (b) (iii), solid lines show the relaxation from the 10-bond state to the one bond state and dashed lines show the subsequent relaxation to the fully relaxed unbound state; unzipping data points are shifted 1 bp right for clarity.

By contrast, unzipping the target duplex releases two nucleotides under tension per base pair broken, allowing the end-to-end distance across the main duplex to decrease by as much as 6 nm (Figure 4). The transition barrier ΔG^‡ is thus significantly lower for unzipping than for shearing, owing to the main duplex relaxation. The minimized ΔG^‡ for a 30 bp main duplex suggests that unzipping relaxation is maximized at this length. A shorter main duplex length has a shorter final end-to-end distance to relax to, reducing the relaxation and increasing ΔG^‡, whereas a longer main duplex remains substantially curved even after unzipping, again increasing ΔG^‡. The results for longer duplexes are consistent with experiments on molecular vises and point to either buckling or kinking of the main duplex.

The overall free-energy change ΔG_tot includes the cost of bringing the sticky ends into first contact, unlike the transition barrier ΔG^‡. Two effects compete as the main duplex length increases: the effective local concentration of the sticky ends decreases, increasing the cost of the first contact, but the increasing mechanical flexibility of the main duplex decreases the cost of the first contact. The observed decrease in ΔG_tot as the main duplex length increases suggests that the second effect predominates at shorter lengths, later being canceled out as the length of the main duplex increases past 40 bp.

2.3. Length Changes and Stacking Disruptions Accompanying Relaxation

The physical factors underlying the energetics of shearing and unzipping were further elucidated by characterizing simulation configurations according to two sets of characteristics, as shown in Figures 4a and 4b. For each configuration, the contour length and end-to-end distance of the main duplex were measured. In addition, a large enough stress can disrupt base pairing and stacking in the duplex, either fraying it at either end or kinking it at a base pair in its interior (as depicted in Figure 4b(i) and (ii), respectively). Thus, geometric criteria were also used to determine if kinking or fraying had disrupted stacking in the main duplex.

For each configuration, the midpoint of each base pair in the main duplex was located; the contour length was calculated as the sum of distances between each consecutive base pair midpoint along the duplex, whereas the end-to-end distance was calculated as the straight-line distance from the first base pair midpoint to the last. Trends in contour length and end-to-end distance as unzipping or shearing proceeds are shown in Figure 4a(i). Contour length increases slightly either in high-bond states or high min distance states, which can be attributed to kinking and fraying in the former cases and to elastic stretching in the latter.

More importantly, the end-to-end distance shows noticeable differences between shearing and unzipping. The initial distance (at 10 bonds) is much shorter for unzipping, reflecting the difference in orientation because the width of the target duplex (∼2 nm) is shorter than its length (∼3.3 nm). As seen in Figure 4a(ii), this persists for all main duplex lengths. However, unzipping steadily increases the end-to-end distance even during partial rupture of the target duplex, whereas the end-to-end distance remains roughly constant throughout shearing until the target duplex is fully ruptured. Thus, during shearing, most of the stress in the main duplex is relaxed only after the transition barrier, whereas some of that stress is released prebarrier during unzipping. This is consistent with the unzipping transition barrier being consistently lower than the shearing transition barrier, as noted earlier. Also, the total relaxation of the main duplex increases with increasing main duplex length, consistent with the reduction in total free-energy change (Figure 3b). The total relaxation is also always larger for unzipping than shearing, consistent with the total free-energy change being less for unzipping.

For each configuration, kinking and fraying were also detected via disruption of stacking. In oxDNA, the unit vectors a_i and a_i+1 encoding the orientation of neighboring nucleotides i and i + 1 are approximately parallel when the nucleotides are stacked in a relaxed duplex; that is, a_i · a_i+1 ≈ 1. Thus, stacking was defined to be disrupted between two nucleotides for which a_i · a_i+1 < 0.5, implying that the orientation of neighboring nucleotides differed by more than 60° (as described in ref (37) this criterion yields similar results to a direct calculation of stacking energies while being computationally less expensive; the criterion a_i · a_i+1 < 0, which is more stringent, yielded disruption rates about 25% smaller in all cases without any qualitative difference between different conditions). A stacking disruption was then defined as “fraying” when it occurred within the terminal three nucleotides on either end of the main duplex, and “kinking” elsewhere, as shown in Figure 4b(i).

Kinking is prevalent in the preunzipping state for main duplex lengths between 35 and 50 bp, decreasing for other lengths, as seen in Figure 4b(ii). However, as unzipping proceeds to the transition state, the kink probability becomes negligible. For shearing configurations, kinking is far rarer, although it is also relatively more common at intermediate main duplex lengths than for either shorter or longer main duplexes. Fraying is relatively common in both preunzipping and preshearing initial states when the main duplex is shorter than 40 bp, as seen in Figure 4b(iii). More fraying is seen for the unzipping configurations at 25 and 35 bp than for the shearing configurations and vice versa at 30 and 40 bp. This 10 bp periodicity indicates that fraying depends on the torsion in the main duplex. Also, unlike kinking, fraying only partially decreases during the initial relaxation to the transition state, with the remainder of the decrease occurring during relaxation to the final unbound state. We note that the near-zero fraying probabilities obtained for the relaxed structures are likely to be underestimates, as previously observed for the geometric criterion at intermediate curvatures,³⁷ and so the difference in fraying probability between bound or transition structures and relaxed structures in actual experiments may be even less than shown in Figure 4b(iii).

Kinking and fraying thus affect the energetics of shearing and unzipping, albeit in different ways. Kinking drastically reduces the effective rigidity of the main duplex, and primarily stabilizes the fully bound state relative to both the transition state and ruptured state; that is, it decreases the free-energy cost of forming the target duplex but not of bringing the sticky ends together beforehand. Thus, kinking of the main duplex increases both ΔG_tot and ΔG^‡ by similar, substantial amounts; it also appears primarily during unzipping but not during shearing. In contrast, fraying only reduces the effective length of the main duplex by a small amount, and affects both unzipping and shearing in a torsion-dependent manner. As such, subsequent modeling focuses on adding the effects of kinking to regular polymer mechanics.

2.4. Polymer Model for Shearing/Unzipping Energies

To describe the previous observations quantitatively, free-energy-extension functions are written down for single-stranded and double-stranded DNA and combined to estimate the mechanical contributions to ΔG^‡ and ΔG_tot. In bonded states, the extension x – x_offset of the single-stranded portion with n_nt nucleotides (with x_offset accounting for the inclusion of the target duplex where present) must match the end-to-end distance x of the main duplex with n_bp base pairs. Specifying energies of single-stranded DNA ΔG_ss(x – x_offset, n_nt) and double-stranded DNA ΔG_ds(x, n_bp) at a given extension x then allows us to find the equilibrium extension: it is the extension x_eq such that

1

which is equivalent to matching the tension in the single-stranded DNA with the compressive stress of the double-stranded DNA. A freely jointed chain is used for single-stranded DNA, and a wormlike chain is used for double-stranded DNA (see Figure 9 and Section 4.2 in Methods section for more details). The mechanical energy of that state can then be calculated as

2

Because the difference between shearing and unzipping is purely geometric, the differences in the transition barrier (ΔG^‡) and total free-energy change (ΔG_tot) should completely be accounted for in the mechanical energy. Base pairing then adds the same free-energy contribution to both ΔG^‡ and ΔG_tot under unzipping and shearing. This was empirically added in as an added constant 18 k_BT to ΔG^‡ and 22.5 k_BT to ΔG_tot (which thus includes the entropic cost of first contact), which gave the best fit to the free energies determined from simulations. More detail can be added to the model, such as by considering an ensemble of end-to-end distance fluctuations instead of a single energy-minimizing configuration or by varying the base-pairing contribution with the main duplex length via additional theory. Nonetheless, the current level of detail appears sufficient to capture key aspects of how the transition barrier and total free-energy difference vary with the main duplex length.

Figure 9.

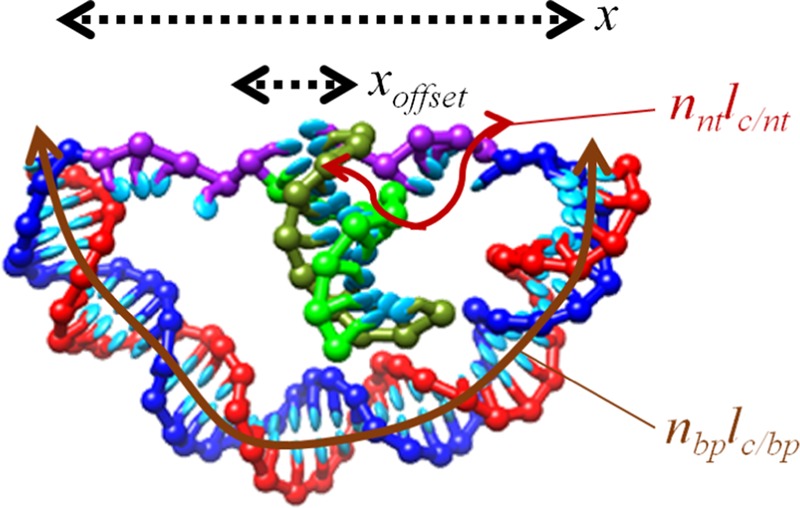
Physical variables x (end-to-end distance), x_offset (width or length of the target duplex), n_bpl_c/bp, and n_ntl_c/nt (the contour lengths of the main duplex and single-stranded linkers, respectively), depicted on a typical configuration.

As shown in Figure 3b, the resulting estimates are qualitatively accurate. ΔG^‡ and ΔG_tot are consistently larger for shearing than for unzipping, and the minimum in ΔG^‡ for unzipping at main duplex length of 30 bp is accurately reflected. However, there are some quantitative discrepancies, most noticeably the overestimate of the total free energy required for unzipping or shearing when the main duplex is 20 bp or shorter. In that regime, the contour length of the main duplex is 7 nm or shorter, comparable to the contour length of the target duplex and linkers so that instead single-stranded DNA under compression would exert a tensile stress on double-stranded DNA, both of which are outside the applicable ranges of the polymer models used.

More importantly, the simple models consistently overestimate the transition barrier difference between shearing and unzipping by 5–10 k_BT (dashed lines in Figure 3). This is attributable to kinking of the main duplex, which is observed in simulated configurations but not accounted for in the wormlike chain model of double-stranded DNA. Kinking would also have the largest effect at intermediate main duplex lengths, and indeed the discrepancy diminishes at a main duplex length of 60 bp, where the average curvature per base pair decreases, and hence kinking is less energetically relevant. As such, a term for critical torque kinking^43,44 was added, in which DNA kinks whenever a critical torque τ_c is exceeded, resulting in the kink free energy effectively linear in the angle: E(θ) = τ_c θ (the Vologodskii–Kamenetskii model,⁴⁵ which models the free energy of a kink as proportional to θ⁶, was also studied, but no significant improvement was observed).

With critical torque kinking, the transition barrier estimate was improved for main duplexes with lengths of 30–50 bp, consistent with the frequent observations of kinking at those lengths, as described in Section 2.3. However, quantitative agreement was still not perfect. This may simply indicate the inadequacy of the critical torque model, as its applicability has only been directly tested for nicked double-stranded DNA and not for a continuous helix.

However, as the critical torque model improves the estimates of transition barrier, it simultaneously degrades the estimates of the total energy difference, especially for unzipping. This may be due to the presence of fraying, as described in Section 2.3, which is not accounted for in this model. More importantly, the constant-offset approach does not account for the change in local concentration of the sticky strands with the main duplex length because a longer main duplex allows the sticky strands to achieve the first contact less often. Because this change in local concentration does not affect the unzipping or shearing from the fully bound state to the transition state, the constant-offset is less problematic in predicting the transition barrier. In addition, there may also be the influence of base stacking, which will be explored in the next section.

2.5. Single-Strand Stretching Points to Base-Stacking Contributions

Calculating the contour length and end-to-end distance for the 5 nt linkers (the total of distances between successive nucleotide base sites and the distance between first and last nucleotide base sites, respectively) reveals features that are incompatible with the simple freely jointed chain model used for single-stranded DNA, as shown in Figure 5. The end-to-end distance is consistently higher during unzipping than during shearing, again reflecting the higher tensions that are being relaxed in the process. However, the contour length is also significantly higher during unzipping, indicating that the tension is high enough to affect the assumption of an inextensible freely jointed chain. This is unlikely to involve elastic stretching of the backbone bonds, given a stretch modulus of 800 pN for single-stranded DNA,⁴⁶ and likely involves the disruption of base stacking in fully or partially bound states.

Figure 5.

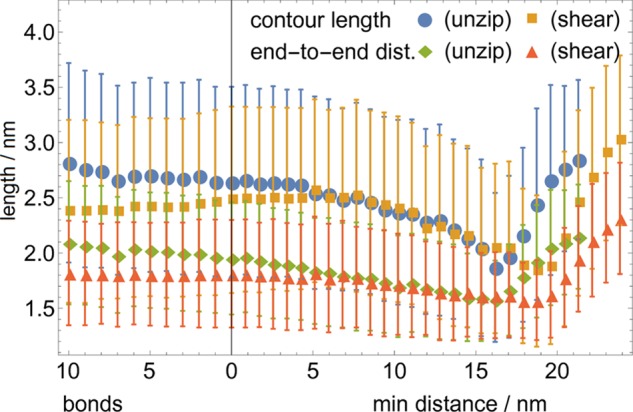
End-to-end length and contour length of the 5 nt single-stranded linker is consistently longer for unzipping than for shearing, showing the consistently higher tension throughout the structure during unzipping until the configuration is fully unbound and even for some small distance after. The consistent contour length decrease during unzipping indicates the recovery of base stacking, which may further decrease the energy cost of unzipping (the main duplex length is 40 bp; other lengths result in similar data).

Base stacking contributes a free energy on the order of 0.25 k_BT per stacked base and can be observed in experimental force-extension curves of single-stranded DNA.⁴⁷ For 10–30 nucleotides of single-stranded DNA, its energy contribution may therefore be 2.5–7.5 k_BT, which is comparable to the discrepancies seen in Figure 3. Base stacking is especially likely to be responsible for the large discrepancies in estimating the total energy due to the modeling methodology as follows: transition barrier is calculated as the difference between two modeled energies, during which the base-stacking omission cancels to some degree, whereas the total energy is calculated as the difference between one modeled energy and a constant energy and the base-stacking omission remains uncorrected. Furthermore, base stacking likely contributes to energetic changes when there is a larger change in tension across the single-stranded portions of the molecule and correspondingly the total energy discrepancy is much larger for unzipping than for shearing. Nonetheless, base stacking is difficult to account for quantitatively, especially in a manner that is sequence independent, and as such a quantitative model for its contribution is not attempted here.

2.6. Shearing and Unzipping as a Gating Mechanism for Artificial Molecular Walkers

The basic principle of tension enhancing unzipping preferentially to shearing is well understood, but it remains to be seen how much dissociation bias^48,49 can be extracted from this preference in the context of a real DNA nanowalker. Indeed, the tension exerted to rupture the target duplex can be estimated from the energy landscapes in Figure 2 by dividing the free-energy difference between the 0-bond state and the unbound free-energy minimum by the distance to that minimum. The resulting force estimates (shown in Figure 6a) lie between 3.5 and 6 pN, with the slightly higher forces for shearing than those for unzipping reflecting the fact that the first contact requires slightly more contraction of the main duplex. These forces might initially seem too low to sustain significant bias.

Figure 6.

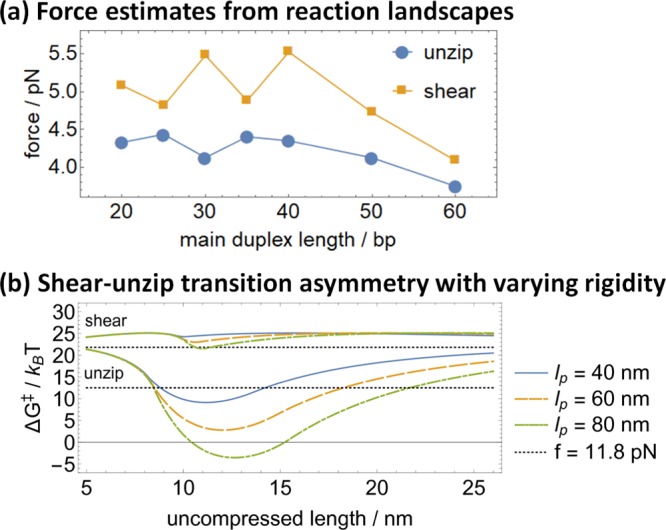
(a) Effective force driving shearing and unzipping in the studied structures ranges between 3.5 and 6 pN. (b) Replacing the main duplex with a polymer with higher persistence length dramatically increases the transition barrier difference between shearing and unzipping, as shown for hypothetical persistence lengths l_p = 60 and 80 nm. The activation energies from ref (28) at a constant force of 11.8 pN are also shown as a benchmark; the constant force shear–unzip gap is readily surpassed.

However, recent results²⁸ suggest that even at a comparatively low force of 11.8 pN, the activation barrier of unzipping 10 base pairs of DNA can be 9 k_BT lower than that for shearing 10 base pairs, which would imply that all else being equal unzipping would proceed 8000 times faster than shearing. Nonetheless, molecular vise experiments⁵⁰ suggest that it only takes 9 pN of force to bend a double helix of 40–50 base pairs of DNA or about 15 nm of double-stranded DNA. Furthermore, the force during unzipping or shearing will significantly decrease as the process proceeds if the released single-stranded DNA allows for additional relaxation.

This study demonstrates that the unzipping–shearing preference remains a viable mechanism for powering DNA-based nanomachines, even though the above-mentioned factors do reduce its magnitude. Even after accounting for kinking and progressive relaxation, the transition barrier difference between unzipping and shearing can indeed be as high as 10 k_BT under ideal conditions. Furthermore, as shown in Figures 3 and 6, the difference can be readily increased simply by preventing DNA kinking, perhaps with chemical intercalation or by using a more rigid structure such as DNA origami motifs.

The results also indicate that unzipping and shearing can be used to exert varying degrees of control over molecular dynamics, as shown in Figure 7. Suppose a DNA motor bound to a DNA track can be released either by unzipping or by shearing a set of base pairs. All else being equal, unzipping is both thermodynamically and kinetically favorable to shearing because it possesses both a lower transition barrier and a negative overall free-energy change; as such, the unzipping process will be overwhelmingly favored, allowing for clear discrimination between reaction pathways, as shown in refs (14, 15).

Figure 7.

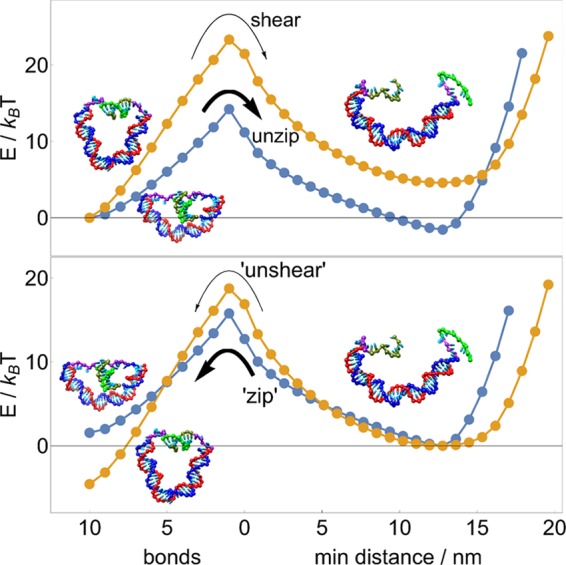
Between competitive DNA-rupturing pathways, unzipping is both kinetically and thermodynamically favored over shearing. The balance between reversed, DNA-binding processes “zipping” and “unshearing” is more subtle: zipping should proceed more quickly and be kinetically favored, but unshearing (or cyclization) is thermodynamically favored. Energy landscapes here are for a main duplex length of 30 bp.

However, should the same motor be designed to complete a forward step via a reverse of those processes, it faces two competing biases: zipping has a lower transition barrier and is thus kinetically favored, but unshearing is now thermodynamically favorable due to the negative overall free-energy change. The competition between kinetic and thermodynamic biases means that in principle, the reaction duration will be critical to favoring the correct reaction.

3. Conclusions

Bioanalogous molecular motors have been constructed from DNA using the difference between unzipping and shearing rates to ensure selective leg dissociation.^14,15 This study suggests that the DNA shearing versus unzipping asymmetry within the context of a real DNA motor can differ significantly from the asymmetry measured in a typical single-molecule setup. This study thus represents a first step toward a thorough derivation of the expected speed and efficiency of such devices from first principles rather than computationally expensive simulations. The intramolecular mechanics plays an important role in determining the performance of a molecular motor, as found in previous studies of biological molecular motors.⁵¹⁻⁵⁵

This study also supports that molecular vises are an effective probe of DNA bending and kinking.⁵⁶ The behavior of DNA under high curvature is an area of intense research. It serves as a stringent test of detailed mechanical models of DNA, as well as informing wider questions about how proteins bind, wind, and unwind DNA in various biological contexts. Various models propose that the force required to bend DNA undergoes a discontinuous change past a critical amount of curvature^45,57 or is even fundamentally not quadratic in the angle of curvature in so-called subelastic chain models.⁵⁸

Various methods have been proposed for probing DNA in the high-curvature regime, including cyclization experiments which measure how the chemical balance changes over time between a circular DNA molecule and alternative linearized forms. It can be seen in panels (b), (d), and (f) of Figure 1 that the process of shearing studied here has some analogies to (the reverse of) DNA cyclization and as seen in Figures 3b and 4b(ii), shearing is only minimally affected by high-curvature kinking. This contrasts with another computational study, suggesting that kinking is pertinent to cyclization experiments,³⁸ and points to the extra flexibility that even a few-nucleotides-long single-stranded linker can provide.

Also, kink free energy can change the transition barrier and total free-energy change of unzipping by a few k_BT, enough to make a measurable difference. As shown in ref (50) both Euler buckling and nonlinear kinking of the DNA duplex can be observed and controlled in similar configurations. As such, this study provides further evidence that “molecular vise” configurations can be used to reliably induce high curvature in a DNA duplex and study its effects rigorously.

4. Methods

4.1. Simulation

Umbrella sampling is used together with virtual-move Monte Carlo simulation (VMMC) to sample the behavior of the configurations. The VMMC is a numerical method to accelerate configurational sampling; the umbrella sampling is used to avoid long-time trapping at local free-energy minima. The two methods have been combined in oxDNA (see ref (59) for details). For each configuration, three simulation windows are defined: bound (1–10 pair bonds present), unbound (0 pair bonds remaining, and minimum distance between strands is at least 0.85 nm), or transitional (either 1–5 pair bonds present or 0 pair bonds and minimum distance between strands is at most 4.25 nm). A base pair bond is defined by a hydrogen bonding energy of less than 0.596 kcal mol^–1, around 15% of the typical hydrogen bonding energy in the model.

Each configuration is simulated within each window at temperature T = 27 °C for 10⁸–10⁹ VMMC steps, distributed over 4–12 independent simulations. Umbrella sampling⁴² is used to enhance sampling of higher-energy states and prevent simulations from leaving their respective windows, with the umbrella weights chosen iteratively such that sampling is uniformly distributed across different values of the reaction coordinate. The resulting free energies from different simulations in the same window agree with each other, showing that the number of steps used is sufficient for convergence. Furthermore, the simulation windows were chosen so that there is significant overlap in states between the transitional window and the bound or unbound windows. In these overlaps, the free energies from different windows also agree, further demonstrating simulation convergence. A typical set of results is shown in Figure 8. A similar free-energy matching is employed across different ranges of coordinates in a previous computational study of DNA bricks.⁶⁰

Figure 8.

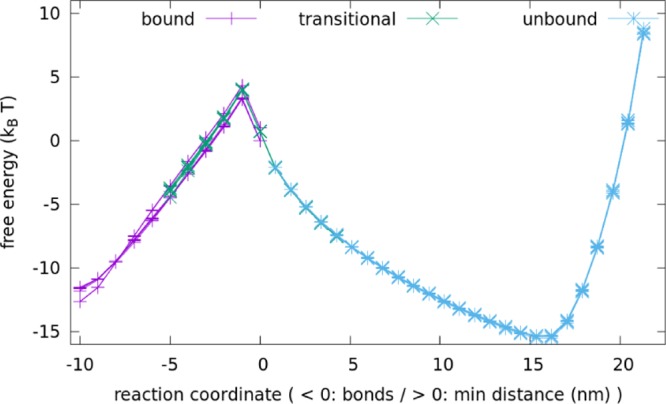
Free energies calculated from individual runs in the bound (purple), transitional (green), and unbound (blue) windows agree with other runs in the same windows and match the free energies from other windows where there is overlap. Data shown here are for unzipping for a 40 bp main duplex; other data are similar.

4.2. Polymer Modeling

Theoretical polymer energies are obtained by modeling the double-stranded DNA as a short wormlike chain with the contour length of 0.34 nm/bp and persistence length of l_p = 40 nm and modeling the single-stranded DNA as a freely jointed chain with the contour length of 0.6 nm/nt and Kuhn length of b = 1.25 nm. These parameters are consistent with established experimental ranges; attempts to more precisely fit the data by variation of parameters either failed or required highly unphysical parameter choices. In addition, as described in the main text, constant base-pairing contributions of 18 k_BT and 22.5 k_BT were added to the transition barrier ΔG^‡ and the total free-energy difference ΔG_tot, respectively. The configuration is then modeled in terms of the length x (end-to-end distance), x_offset (width or length of the target duplex), n_bpl_c/bp, and n_ntl_c/nt (the contour length of the main duplex and single-stranded linkers, respectively), as depicted in Figure 9 on a typical configuration.

The force F_FJC(x, l_c, b) at which a polymer of contour length l_c and the Kuhn segment length b has an average projection parallel to the force x is

3

where L(s) = coth s – 1/s is the Langevin function and the analytical approximation of its inverse⁶¹ is accurate to within 2%. The tensile energy G_FJC is then obtained by integration.

The bending energy G_WLC(x, l_c, l_p) at which a short wormlike chain of persistence length l_p and contour length l_c ≈ l_p has an end-to-end distance x is given by calculating the bending energy in the principal flexural mode, in which the chain assumes an “elastica” curve.^50,62

4

where K(μ) is the complete elliptic integral of the first kind. The parameter μ ≥ 0 monotonically specifies how bent the rod is, assuming a value of 0 when the rod is fully extended; it is the solution to x/l_c = 2E(μ)/K(μ) – 1, where E(μ) is the complete elliptic integral of the second kind. The following approximation is used

5

where M = 0.8261 is the value⁵⁰ of μ at x = 0.

Having specified the functional forms of the energy-extension functions, the equilibrium length x_eq for DNA molecules with n_bp base pairs in the main duplex and n_nt nucleotides along a single-stranded chain is found by equating the compression in the main duplex with the single-stranded tension

6

Here, x_offset accounts for the length or width of the target duplex, lying between the linkers, and its value in various situations is given below. l_c/bp = 0.34 nm is the contour length of a DNA duplex per base pair; l_c/nt = 0.6 nm is the contour length of a single-stranded DNA per nucleotide. Once x_eq is found, the energy can be substituted into the above energy functional forms.

In a fully bonded shearing configuration, the total length of the main duplex is equal to the length of two DNA single strands with 6 backbone bonds and an additional 10 base pairs of double-stranded DNA and x_offset is set to be 3.6 nm (the diagonal length across a double helix is 3.4 nm long and 1.8 nm wide). The transition configuration is considered to have two single strands, each with 10 backbone bonds. A value of x_offset = 0.63 nm is found to optimize the fitting to simulation values, which likely accounts for the width of the remaining base pair and its freedom of relative alignment. Nonetheless, varying x_offset from 0 to 1.8 nm for the transition configuration results in qualitatively similar plots.

In a fully or partially bound unzipping configuration, the width of the DNA duplex plays a similar role and x_offset is set to be 1.8 nm. As with shearing, the fully bound state has two DNA single strands with 6 backbone bonds; the transition state has 15 backbone bonds per single strand instead of 10, reflecting the difference between the first contact of the sticky ends for shearing and unzipping. Mathematically, the energy differences observed stem largely from the different values of x_offset and the different number of backbone bonds in the transition state due to the different binding geometries.

To incorporate DNA kinking, the critical torque model^43,44 was used. In this model, the energy of a DNA duplex with a kink angle θ is simply given by τ_cθ, where τ_c is the critical torque. For this article, a value of 29 pN nm was used, which falls within the range of 27–30 pN nm used in the literature. The double-stranded DNA energy G_WLC of any given state was modified to be the Boltzmann average of the kinked and unkinked energies; in practice, the transition width thus obtained is very narrow, and Boltzmann averaging essentially gives the minimum of both energies.

The authors declare no competing financial interest.