Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2017 Jul 27;2(7):4022–4029. doi: 10.1021/acsomega.7b00503

Superior Performance of the SQM/COSMO Scoring Functions in Native Pose Recognition of Diverse Protein–Ligand Complexes in Cognate Docking

Haresh Ajani †,‡, Adam Pecina †, Saltuk M Eyrilmez †,‡, Jindřich Fanfrlík †, Susanta Haldar †, Jan Řezáč †, Pavel Hobza †,§,*, Martin Lepšík †,*
PMCID: PMC6044937  PMID: 30023710

Abstract

graphic file with name ao-2017-00503q_0002.jpg

General and reliable description of structures and energetics in protein–ligand (PL) binding using the docking/scoring methodology has until now been elusive. We address this urgent deficiency of scoring functions (SFs) by the systematic development of corrected semiempirical quantum mechanical (SQM) methods, which correctly describe all types of noncovalent interactions and are fast enough to treat systems of thousands of atoms. Two most accurate SQM methods, PM6-D3H4X and SCC-DFTB3-D3H4X, are coupled with the conductor-like screening model (COSMO) implicit solvation model in so-called “SQM/COSMO” SFs and have shown unique recognition of native ligand poses in cognate docking in four challenging PL systems, including metalloprotein. Here, we apply the two SQM/COSMO SFs to 17 diverse PL complexes and compare their performance with four widely used classical SFs (Glide XP, AutoDock4, AutoDock Vina, and UCSF Dock). We observe superior performance of the SQM/COSMO SFs and identify challenging systems. This method, due to its generality, comparability across the chemical space, and lack of need for any system-specific parameters, gives promise of becoming, after comprehensive large-scale testing in the near future, a useful computational tool in structure-based drug design and serving as a reference method for the development of other SFs.

Introduction

In structure-based drug design, docking/scoring is a prime and well-established computational tool. Molecular docking generates ligand geometries bound to the protein (poses), whereas scoring using scoring functions (SFs) ranks them by the predicted affinity (score). Owing to the approximations embodied in docking/scoring methods for the sake of their acceleration, their accuracy has often been compromised.1 Nevertheless, recent methodological advances made docking/scoring methods an indispensable tool in discovering new protein ligands.2

The “docking power” or “sampling power”3,4 of a docking/scoring method is assessed by its ability to identify the native ligand pose (root-mean-square deviation (RMSD) from the crystal pose <2 Å) in protein–ligand (PL) complexes. Comprehensive testing across diverse PL complexes has shown that in up to 80% of PL complexes this task can be accomplished.4−8 However, classical SFs had troubles with the identification of the native binding mode as the best-scoring pose (especially in the case of metalloproteins, halogenated ligands, inorganic ligands, etc.).4 Thus, reliable identification of native PL poses within a diverse set of PL complexes using a single SF remains a challenging task.3,4,9

The four major approaches toward scoring are empirical,10−12 knowledge-based,8,13,14 statistical/machine learning,15,16 and physics-based.17,18 The first three approaches require a training set, and by use of parametrization and statistics, useful models can be obtained.19 However, because these approaches are dependent on the training set, their predictive power is limited. In contrast, physics-based methods rely on a generally valid description of PL interactions. Traditionally, such approaches were limited to molecular mechanics (MM) methods and simplified variants thereof. Thus, these approaches were inherently limited by the underlying approximations, most importantly the implicit treatment of electrons.

A general solution to the problem of accurately calculating noncovalent interactions in PL systems is the use of quantum mechanics (QM).20 With QM methods, phenomena of quantum origin, such as charge transfer, are described without further ad hoc parametrization. This is important for systems involving halogen bonding,21,22 metalloprotein binding,23 inorganic ligands,24−26 or covalent bond formation.27 But because of the high computational demands, QM calculations of sufficient quality (e.g., DFT-D3 level with a triple-ζ basis set) are limited to a few hundred atoms. This limitation can be overcome by use of fragmentation28,29 or a QM/MM approach.30−34 Another route is the use of semiempirical QM (SQM). The first QM-based SF was introduced by the Merz group.35 They combined the Austin model 1 (AM1) SQM method with empirical dispersion (D) and implicit solvation (Poisson–Boltzmann (PB) model). Its validation on a large dataset of PL complexes showed its superior performance, especially for metalloprotein–ligand complexes.36 Although this was an important pioneering step, the accuracy of the underlying methods, both for the vacuum part (AM1-D)37 and for solvation (PB),38 was not sufficient to yield quantitative results. More recently, Sulimov laboratory used the PM7 SQM method39 in conjunction with the conductor-like screening model (COSMO) implicit solvent model40 for identification of native ligand poses of 16 PL complexes in cognate docking.41,42 They showed superior performance of their SQM/COSMO SFs over force-field-based scoring. We should note here that PM7 results for noncovalent interactions can be slightly improved by using the latest version of empirical corrections to the PM6 SQM method (PM6-D3H4X, see below).43

In our laboratory, we have been systematically developing empirical corrections to SQM methods to accurately treat an array of noncovalent interactions.20 The latest version of empirical corrections for dispersion, hydrogen bonding, and halogen bonding yielded the PM6-D3H4X37,44 method, which, coupled with the COSMO implicit solvent model,40 forms the core of our SQM-based SF (eq 1).45,46

graphic file with name ao-2017-00503q_m001.jpg 1

The score (an estimate of the PL binding free energy) is expressed as an unweighted sum of thermodynamic terms. It consists of the gas-phase PL interaction energy (ΔEint), the change in solvation/desolvation free energy upon complex formation (ΔΔGsolv), the change in the conformation “free” energies of the protein and ligand [ΔG′wconf(P,L)], and the interaction entropy change upon binding (TΔSint).45,46 The PL complexes are optimized using the solution-phase SQM method before scoring. The ΔEint term is favorable for complex formation and usually is the largest in magnitude. It can reach a few hundreds of kcal/mol for charged or polar ligands. The ΔΔGsolv term opposes binding and can be nearly as large as the first term. These two dominant terms thus partially compensate for each other, and the final score is an order of magnitude smaller. Using this SF (eq 1), we have rationalized the binding of series of ligands to a dozen of protein targets,21,22,46−50 including covalent ligand binding.27 It should be noted that this SF can also be extended to evaluate explicit solvent effects.47,48,51

Recently, we have accelerated our SQM-based SF by considering only the first two dominant terms and replacing the time-demanding SQM optimization with a quick MM relaxation of hydrogens.23 We have shown in four difficult PL complexes that this SQM/COSMO SF at the PM6-D3H4X level outperforms eight widely used SFs in native ligand pose identification in cognate docking. The number of false-positive (FP) solutions (i.e., those poses that scored better than the native one) was up to 1 order of magnitude lower than that for the classical SFs.23 In three PL cases, it was even 0. In the challenging system of the tumor necrosis factor-α converting enzyme (TACE) metalloprotein featuring Zn2+ in the active site, which is bound by the thiolate group of the ligand, 39 FPs were found.23 A major improvement (FP = 0)52 was observed when the ΔEint term was calculated with a more robust SQM method, the self-consistent-charge density-functional tight-binding method augmented with empirical dispersion (previously shown to be useful for the description of biomolecules)53 and hydrogen-bonding corrections (SCC-DFTB3-D3H4, abbreviated DFTB3-D3H4).54 The high-quality description of the other three PL systems was retained.52 The price for the improvement was a higher but not unsurmountable computational cost. It should be noted that two recent studies used the uncorrected SCC–DFTB method in a QM/MM setup and reported success on the correct ligand binding geometries toward metalloproteins.31,32 Their approach toward the computationally expensive task was to use a rather small QM part consisting of Zn2+, its coordinating protein side chains, and the ligand on a large number of PL systems.31,32

In this study, we aim to validate our SQM/COSMO SFs23,52 for native pose identification in cognate docking on a data set consisting of 17 PL complexes from five diverse classes, selected using strict criteria for physics-based scoring. We apply two variants of the SQM/COSMO SF (ΔEint term at the PM6-D3H4X or DFTB3-D3H4X level)23,52 and compare them with four standard SFs (Glide XP,55 AutoDock4,56 AutoDock Vina,57 and UCSF Dock58). The performance criterion is the number of FPs23,52 with an extended definition presented here. We show here that the unique behavior of the SQM/COSMO SFs observed in our recent studies23,52 hold across 17 diverse PL complexes and gives promise of generality after comprehensive large-scale testing in the near future.

Results and Discussion

Data Set

In this work, we extend our previous pilot studies on four difficult PL systems23,52 to 17 pharmaceutically relevant and diverse PL complexes from five classes, including three enzyme classes (transferase, hydrolase, and lyase), one chaperone, and two nuclear receptor classes from the PBDbind “core set”59 (for details, see Methods section). We apply the strict criteria needed for physics-based scoring. Specifically, the crystal structures of the complexes have resolutions better than 2.5 Å, well-resolved electron densities for the ligands, and protein active sites. The ligands have variable chemistries, sizes (molecular weight of 305–666 Da), charges, and flexibilities (for details, see Methods section). Their binding constants toward their targets range from micro- to picomolar.

The crystal poses of the ligands were scored as reference. The ligand poses generated previously by docking4 with seven docking programs (for details, see Methods section) totaled 4566 poses. RMSD-based clustering (see Methods section) of the poses was carried out to avoid pose redundancy. After this, the number of poses decreased to 3328, corresponding to approximately 250 poses per target. A comprehensive evaluation of the recognition of near-native poses requires a balanced distribution of RMSDs of the docked ligand poses with respect to the crystal (native) geometry from very similar to very dissimilar (up to 10 Å). In most of the PL systems, 20–60% of poses had RMSD <2 Å (Figure S1A). Furthermore, poses were evenly distributed in RMSD ranges of 2–5 and 5–10 Å (roughly 20–40% for each category). Figure S1B shows minimal RMSD (RMSDmin) for the poses studied. Near-native poses within the experimental accuracy of X-ray crystallography of 0.5 Å60,61 were found in all but two cases (10GS: RMSDmin = 0.85 Å and 2VOT: RMSDmin = 0.70 Å). However, these cases only slightly exceeded the threshold.

Scoring

For each of the six SFs (two variants of SQM/COSMO SF and four standard SFs; for details, see Methods section), the scores of the docked ligand poses in their respective target proteins were calculated, transformed to relative scores with respect to the score of the crystal pose, and normalized (see Methods section).

The overall sampling power of all the SFs is shown as the enrichment plot (Figure S2), that is, the percent of PL cases (y axis) in which the best-scoring ligand of a given SF has defined RMSD (x axis) to the crystal pose. In the standard range of RMSD up to 2 Å, the SQM/COSMO SFs at the DFTB3-D3H4X level perform the best (88% of PL systems), followed by SQM/COSMO at the PM6-D3H4X level together with UCSF Dock (82% of PL systems). Slightly worse is the performance of Glide XP (76%), followed by AutoDock4 (71%), and AutoDock Vina (65%) (Figure S2). In recognition of near-native poses (RMSD < 0.5 Å), the two SQM/COSMO SFs together with AutoDock Vina perform the best (47%), followed by AutoDock4 and UCSF Dock (41%) and Glide XP, which recognize the poses only in 29% of cases.

The SQM/COSMO SFs also had the lowest number of PL complexes (two for DFTB3-D3H4X/COSMO, Table S1) for which the best-scoring pose exceeded the threshold for success of 2 Å. This was closely followed by SQM/COSMO at the PM6-D3H4X/COSMO level, UCSF Dock, and Glide XP (three cases). Five and six failures were found for Autodock4 and AutoDock Vina, respectively (Table S1). Averaging the RMSDs of the best-scoring poses across all 17 PL complexes (and counting all the failures >2 Å as 2.1 Å), DFTB3-D3H4X/COSMO was the winner (0.71 Å), closely followed by PM6-D3H4X/COSMO and UCSF Dock (0.77 and 0.79 Å, respectively; Table S1). Worse results (around 1 Å) were obtained for AutoDock Vina, AutoDock4, and Glide XP.

For detailed performance evaluations, we use the number of FP solutions criterion23,52 with an extended definition presented here. Previously, FPs were defined as those poses that scored better than the native pose (defined by a 0.5 Å RMSD cutoff from the crystal pose due to inaccuracies of crystal structures).23,52 Here, we allow room for larger uncertainties of native pose recognition by defining “hard FPs” (HFP) in which the cutoffs were increased to RMSD >2 Å and score better than −1 kcal/mol. The RMSD cutoff now also includes the effects of flexible parts of the ligands sticking out to the solvent, and the score cutoff corresponds roughly to 2–3 kcal/mol of unscaled energies, which are rough error bounds of the physics-based method. The HFPs for AutoDock Vina, AutoDock4, Glide XP, and UCSF Dock were high—211, 350, 425, and 635, respectively (Figure 1A). The SQM/COSMO SFs performed much better with the numbers of HFPs being up to 1 order of magnitude smaller—40 and 42 for the DFTB3-D3H4X and PM6-D3H4X levels, respectively (Figure 1A).

Figure 1.

Figure 1

Open in a new tab

Number of HFP solutions for the six SFs used here across all the 17 PL systems studied. (A) Number of HFPs and (B) HFPs for individual PL complexes sorted by ligand charge: neutral (left) and charged (right).

The number of HFPs for individual PL complexes (Figure 1B and Table S2) differed markedly with respect to the ligand charge: in the case of the neutral ligands (Figure 1B, left), they were by 1 order of magnitude smaller than that for the charged ones (Figure 1B, right). For SQM/COSMO at the PM6-D3H4X and DFTB3-D3H4X levels, the numbers of HFPs for neutral ligands were single-digit values (1 and 2, respectively). The classical SFs performed worse, with the number of HFPs ranging from 18 to 85 for neutral ligands (Figure 1B, left and Table S2). The complex with the largest number of HFPs was the RNA-dependent RNA polymerase/ligand complex (3GNW) with 71, 28, and 14 HFPs calculated with AutoDock4, UCSF Dock, and AutoDock Vina, respectively. A large number of HFPs (40) was also observed for the cyclin-dependent kinase 2 (CDK2)/ligand complex (2FVD) for Glide XP (Table S2).

The results show that the classical SFs had larger troubles in identifying the native binding poses for charged ligands (for the classical SFs, more than 90% of HFPs were found for charged ligands). The largest number of HFPs (140) was found with Glide XP for the α-l-fucosidase (2ZX6) PL complex, which had a positively charged ligand. For UCSF Dock, four systems, 2P4Y, 4GID, 2VOT, and 3NOX, yielded in total 403 HFPs, which is 70% of HFPs for the charged ligands in that method (577; Table S2). In contrast, the number of HFPs for the charged ligands for the SQM/COSMO was in total 38 and 41 for DFTB3-D3H4X and PM6-D3H4X, respectively. This is considerably lower than the classical SFs (193–577 HFPs) (Table S2). For SQM/COSMO at the DFTB3-D3H4X level, the largest number of HFPs was 20 and 8 for 2P4Y and 3NOX, respectively. Also, PM6-D3H4X/COSMO had some troubles with these systems (5 and 10 HFPs, respectively). In both 2P4Y and 3NOX complexes, the HFP poses have the ligand cores placed at very similar positions as the crystal pose, whereas moieties sticking out to the solvent (the benzisoxazol and morpholino groups, respectively) had fewer noncovalent interactions with the protein. This can be one reason why poses with higher RMSD could score well. Other reasons can be some of the approximations embedded in our protocol for speed, such as the neglected terms in the SQM/COSMO SF (change of conformational energy, entropy) or explicit water molecules, which may need to be included in some PL systems for reliable description of the energetics.47,51

Conclusions

The sampling (docking) power, that is, the ability to recognize a ligand native pose in cognate PL docking, of two variants of quantum-mechanics-based SQM/COSMO SFs is tested here on 17 PL systems from five diverse protein families carefully selected for physics-based SFs. For comparison, four standard SFs—Glide XP, AutoDock4, AutoDock Vina, and UCSF Dock, are used. The SQM/COSMO SFs at the PM6-D3H4X and DFTB3-D3H4X levels markedly outperform the standard SFs as judged by the number of HFP poses. The time requirements for the SQM/COSMO SF (Table S3) are higher than those for classical SFs, but given the supercomputer power, thousands of docking poses can be evaluated in a reasonable time. The results of the freely available SQM/COSMO SFs give promise of generality, and after comprehensive large-scale testing in the near future, this method could serve as a useful tool in structure-based drug design and reference for SF development.

Methods

Data Set

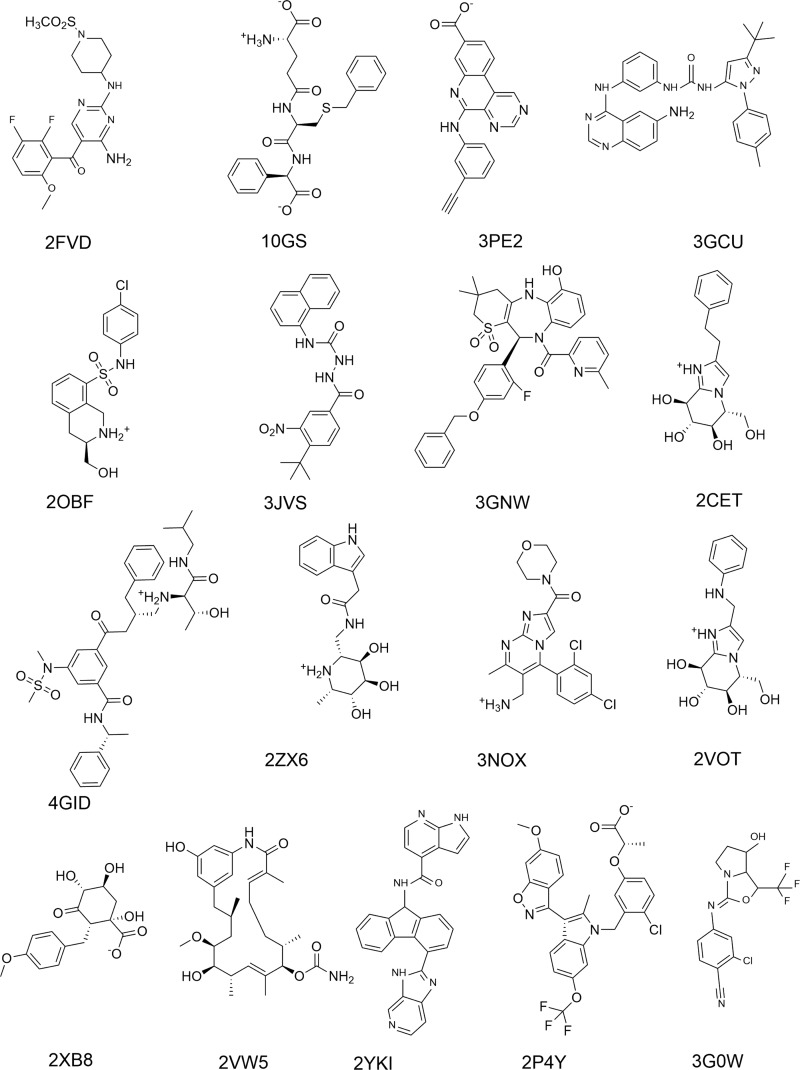
QM-based interaction energy calculations require sensible geometries and, therefore, we needed good-quality structures of PL complexes. The crystallographic structures should have fair resolution (<2.5 Å) with fully resolved electron density for the entire ligand and surrounding binding site residues. These criteria are fulfilled by the docking/scoring benchmark set PDBbind core set.3,59,62 In our study, 17 PL complexes (Figure 2 and Table 1) were used with targets from diverse protein families: three enzyme classes (transferase, hydrolase, and lyase), chaperone, and nuclear receptor (Table 1). The ligand structures are shown in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Two-dimensional structures of the ligands studied.

Table 1. Summary of the 17 PL Complexes Studied.

PDB code resolution (Å) protein name class ligand charge rotatable bonds in ligand
2FVD 1.8 CDK2 transferase (E.C.2) 0 6
10GS 2.2 glutathione S-transferase   –1 13
3PE2 1.9 casein kinase IIα   –1 4
3GCU 2.1 mitogen-activated protein kinase 14   0 6
2OBF 2.3 phenylethanolamine N-methyltransferase   +1 4
3JVS 1.9 checkpoint kinase 1   –1 5
3GNW 2.4 hepatitis C virus NS5B RNA-dependent RNA polymerase   0 5
2CET 1.9 β-glucosidase A hydrolase (E.C.3) +1 4
4GID 2.0 β-secretase I   +1 16
2ZX6 2.4 α-l-fucosidase   +1 4
3NOX 2.3 dipeptidyl peptidase 4   +1 3
2VOT 1.9 β-mannosidase   +1 4
2XB8 2.4 3-dehydroquinate dehydratase lyase (E.C.4) –1 4
2VW5 1.9 heat shock protein Hsp82 chaperone 0 3
2YKI 1.6 heat shock protein Hsp90-α   0 3
2P4Y 2.2 peroxisome proliferator-activated receptor γ nuclear receptor –1 9
3G0W 1.9 androgen receptor   0 2
Open in a new tab

Docking Poses

Ligand poses obtained by seven commonly used docking programs were collected from previously published work.4 These programs were AutoDock (version 4.2.6),56 AutoDock Vina (version 1.1.2),57 LeDock (version 1.0),63 UCSF Dock (version 6.7),58 Glide SP (version 67011),55 Glide XP (version 67011),55 and Surflex Dock (version 2.706.13302).64 For each target, the ligand poses were pooled, which amounted to approximately 350 poses per target. To reduce the redundancy, all poses per target were clustered using the “cluster_conformer” script in the Schrödinger suite65 with an RMSD cutoff of 0.5 Å. The number of poses was thus reduced to approximately 250 poses per PL system. Each ligand pose, as well as X-ray reference geometry, was scored “in-place” using four classical SFs (AutoDock,56 AutoDock Vina,57 UCSF Dock,58 and Glide XP55) and compared to that of two variants of SQM/COSMO SFs, see below.23,52

Protein and Ligand Preparation

Protein Structure Preparation

Following the standard virtual screening protocol,4 all the crystal waters were removed from the PL complexes. As noted previously,23 physics-based SFs require special care in preparing the PL structures. For all proteins, which were not deposited as monomers, chain A was used for protein preparation except 10GS and 2XB8 where the dimer interface makes important contributions to the binding. We used the LEaP program, which is part of the AMBER14 suite,66 to protonate the proteins. The protonation state of histidine residues was assigned manually on the basis of hydrogen-bonding patterns. Cysteine disulfide bonds were assigned manually on the basis of the sulfur–sulfur distance. In the case of the 3PE2 complex, the B conformation of M163 was used because it forms interactions with the ligand. Hydrogen atom positions in PL complexes were relaxed by the simulated annealing protocol using short molecular dynamics (MD) (for details see Supporting Information).

Ligand Preparation

The protonation states of the ligands were carefully checked by pKa calculations at pH 7 using Schrödinger “Propka”.65 The collected docking poses from seven different programs had different output file formats. Each ligand was made into one common MOL2 file format without any changes in X, Y, and Z coordinates. Partial charges were derived at the AM1-BCC level using RESP.67−69

RMSD Measurements

RMSD values of all the ligand poses were calculated with respect to the corresponding X-ray geometry of the ligand (without any further optimization) with the “heavy atom” option using the “rmsd.py” script by Schrödinger.

Scoring

SQM/COSMO SFs

All of the docked PL complexes with close contacts (cutoff of 1.5 Å) between the protein and the ligand were relaxed by short AMBER/GB optimization as in previous studies.52 Next, optimal hydrogen positions were localized in each complex using a short MDs run using AMBER/GB as in our previous studies.52 The SQM/COSMO score is a sum of ΔEint and ΔΔGsolv terms. For speed-up and without compromising the reliability,23 the former term was calculated on large parts of the protein (typically the ligand plus 10 Å protein surroundings) using two approaches: (i) the corrected PM6-D3H4X44 and (ii) DFTB3-D3H4X method, a third-order DFTB70,71 with the 3OB parameter set72,73 and the latest version of the D3H4X corrections for noncovalent interactions.74 The solvation free energy was calculated on the same truncated system as above using a COSMO implicit solvent model at the PM6 level.40

Glide XP Score

All scoring calculations were performed with Glide XP55 and run in the extra precision (XP) workflow framework. Docking grids were generated by Glide using the cocrystallized ligand at the center of the grid box. The compounds were scored with the option “score in place only”.

AutoDock4 and AutoDock Vina

For both AutoDock456 and AutoDock Vina,57 the centers of grid boxes were arranged according to the centers of the crystal ligand poses. The grid box sizes were adjusted to make scoring possible for all combinations of ligands and conformations. AM1-BCC RESP partial charges were used.

UCSF DOCK

The grid spacing was 0.3 Å. The cutoff for nonbonded interactions was not used. We used AMBER parameters. For ligands, we used AM1-BCC RESP partial atomic charges.

Score Scaling

The scores of all the poses of the 17 PL complexes obtained by the 6 SFs were transformed into relative numbers with respect to the score of the crystal pose and normalized as done previously.23,52

Acknowledgments

We thank Kristian Kříž for helpful ideas on the structures of PL complexes. This work was part of Research Project RVO: 61388963 of the Institute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic. This work was also supported by the Czech Science Foundation (H.A., S.H., S.M.E., J.F., A.P., P.H., and M.L. from grant No. P208/12/G016 and J.Ř. from grant No. P208/16-11321Y). This work was supported by the Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development, and Innovations project “IT4 Innovations National Supercomputing Center—LM2015070,” as well as from project LO1305 (P.H.).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b00503.

  • RMSD analyses of docking poses; enrichment plot; RMSD of the best-scoring poses; numbers of total and hard FPs; detailed computational protocols; timing of SQM/COSMO (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao7b00503_si_001.pdf (243.3KB, pdf)

References

  1. Schneider G. Virtual screening: an endless staircase?. Nat. Rev. Drug Discovery 2010, 9, 273–276. 10.1038/nrd3139. [DOI] [PubMed] [Google Scholar]
  2. Irwin J. J.; Shoichet B. K. Docking Screens for Novel Ligands Conferring New Biology. J. Med. Chem. 2016, 59, 4103–4120. 10.1021/acs.jmedchem.5b02008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cheng T.; Li X.; Li Y.; Liu Z.; Wang R. Comparative Assessment of Scoring Functions on a Diverse Test Set. J. Chem. Inf. Model. 2009, 49, 1079–1093. 10.1021/ci9000053. [DOI] [PubMed] [Google Scholar]
  4. Wang Z.; Sun H.; Yao X.; Li D.; Xu L.; Li Y.; Tian S.; Hou T. Comprehensive evaluation of ten docking programs on a diverse set of protein-ligand complexes: the prediction accuracy of sampling power and scoring power. Phys. Chem. Chem. Phys. 2016, 18, 12964–12975. 10.1039/C6CP01555G. [DOI] [PubMed] [Google Scholar]
  5. Yuriev E.; Agostino M.; Ramsland P. A. Challenges and advances in computational docking: 2009 in review. J. Mol. Recognit. 2011, 24, 149–164. 10.1002/jmr.1077. [DOI] [PubMed] [Google Scholar]
  6. Jain A. N.; Nicholls A. Recommendations for evaluation of computational methods. J. Comput.-Aided Mol. Des. 2008, 22, 133–139. 10.1007/s10822-008-9196-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Kontoyianni M.; McClellan L. M.; Sokol G. S. Evaluation of docking performance: comparative data on docking algorithms. J. Med. Chem. 2004, 47, 558–565. 10.1021/jm0302997. [DOI] [PubMed] [Google Scholar]
  8. Gohlke H.; Hendlich M.; Klebe G. Knowledge-based scoring function to predict protein-ligand interactions. J. Mol. Biol. 2000, 295, 337–356. 10.1006/jmbi.1999.3371. [DOI] [PubMed] [Google Scholar]
  9. Warren G. L.; Andrews C. W.; Capelli A.-M.; Clarke B.; LaLonde J.; Lambert M. H.; Lindvall M.; Nevins N.; Semus S. F.; Senger S.; Tedesco G.; Wall I. D.; Woolven J. M.; Peishoff C. E.; Head M. S. A critical assessment of docking programs and scoring functions. J. Med. Chem. 2006, 49, 5912–5931. 10.1021/jm050362n. [DOI] [PubMed] [Google Scholar]
  10. Böhm H.-J. The development of a simple empirical scoring function to estimate the binding constant for a protein ligand complex of known 3-dimensional structure. J. Comput.-Aided Mol. Des. 1994, 8, 243–256. 10.1007/BF00126743. [DOI] [PubMed] [Google Scholar]
  11. Wang R.; Lai L.; Wang S. Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J. Comput.-Aided Mol. Des. 2002, 16, 11–26. 10.1023/A:1016357811882. [DOI] [PubMed] [Google Scholar]
  12. Gohlke H.; Klebe G. Statistical potentials and scoring functions applied to protein-ligand binding. Curr. Opin. Struct. Biol. 2001, 11, 231–235. 10.1016/S0959-440X(00)00195-0. [DOI] [PubMed] [Google Scholar]
  13. Spitzmüller A.; Velec H. F. G.; Klebe G. MiniMuDS: A New Optimizer using Knowledge-Based Potentials Improves Scoring of Docking Solutions. J. Chem. Inf. Model. 2011, 51, 1423–1430. 10.1021/ci200098v. [DOI] [PubMed] [Google Scholar]
  14. Ishchenko A. V.; Shakhnovich E. I. SMall molecule growth 2001 (SMoG2001): An improved knowledge-based scoring function for protein-ligand interactions. J. Med. Chem. 2002, 45, 2770–2780. 10.1021/jm0105833. [DOI] [PubMed] [Google Scholar]
  15. Ain Q. U.; Aleksandrova A.; Roessler F. D.; Ballester P. J. Machine-learning scoring functions to improve structure-based binding affinity prediction and virtual screening. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2015, 5, 405–424. 10.1002/wcms.1225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Khamis M. A.; Gomaa W. Comparative assessment of machine-learning scoring functions on PDBbind 2013. Eng. Appl. Artif. Intell. 2015, 45, 136–151. 10.1016/j.engappai.2015.06.021. [DOI] [Google Scholar]
  17. Ewing T. J. A.; Makino S.; Skillman A. G.; Kuntz I. D. DOCK 4.0: Search strategies for automated molecular docking of flexible molecule databases. J. Comput.-Aided Mol. Des. 2001, 15, 411–428. 10.1023/A:1011115820450. [DOI] [PubMed] [Google Scholar]
  18. Morris G. M.; Goodsell D. S.; Halliday R. S.; Huey R.; Hart W. E.; Belew R. K.; Olson A. J. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998, 19, 1639–1662. . [DOI] [Google Scholar]
  19. Li L.; Wang B.; Meroueh S. O. Support vector regression scoring of receptor-ligand complexes for rank-ordering and virtual screening of chemical libraries. J. Chem. Inf. Model. 2011, 51, 2132–2138. 10.1021/ci200078f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Řezáč J.; Hobza P. Benchmark Calculations of Interaction Energies in Noncovalent Complexes and Their Applications. Chem. Rev. 2016, 116, 5038–5071. 10.1021/acs.chemrev.5b00526. [DOI] [PubMed] [Google Scholar]
  21. Fanfrlík J.; Kolář M.; Kamlar M.; Hurný D.; Ruiz F. X.; Cousido-Siah A.; Mitschler A.; Řezáč J.; Munusamy E.; Lepšík M.; Matějíček P.; Veselý J.; Podjarny A.; Hobza P. Modulation of Aldose Reductase Inhibition by Halogen Bond Tuning. ACS Chem. Biol. 2013, 8, 2484–2492. 10.1021/cb400526n. [DOI] [PubMed] [Google Scholar]
  22. Fanfrlík J.; Ruiz F. X.; Kadlčíková A.; Řezáč J.; Cousido-Siah A.; Mitschler A.; Haldar S.; Lepšík M.; Kolář M. H.; Majer P.; Podjarny A. D.; Hobza P. The Effect of Halogen-to-Hydrogen Bond Substitution on Human Aldose Reductase Inhibition. ACS Chem. Biol. 2015, 10, 1637–1642. 10.1021/acschembio.5b00151. [DOI] [PubMed] [Google Scholar]
  23. Pecina A.; Meier R.; Fanfrlík J.; Lepšík M.; Řezáč J.; Hobza P.; Baldauf C. The SQM/COSMO filter: reliable native pose identification based on the quantum-mechanical description of protein-ligand interactions and implicit COSMO solvation. Chem. Commun. 2016, 52, 3312–3315. 10.1039/C5CC09499B. [DOI] [PubMed] [Google Scholar]
  24. Ciancetta A.; Genheden S.; Ryde U. A QM/MM study of the binding of RAPTA ligands to cathepsin B. J. Comput.-Aided Mol. Des. 2011, 25, 729–742. 10.1007/s10822-011-9448-7. [DOI] [PubMed] [Google Scholar]
  25. Pecina A.; Lepšík M.; Řezáč J.; Brynda J.; Mader P.; Řezáčová P.; Hobza P.; Fanfrlík J. QM/MM calculations reveal the different nature of the interaction of two carborane-based sulfamide inhibitors of human carbonic anhydrase II. J. Phys. Chem. B 2013, 117, 16096–16104. 10.1021/jp410216m. [DOI] [PubMed] [Google Scholar]
  26. Mader P.; Pecina A.; Cigler P.; Lepšík M.; Šícha V.; Hobza P.; Grüner B.; Fanfrlík J.; Brynda J.; Řezáčová P. Carborane-Based Carbonic Anhydrase Inhibitors: Insight into CAII/CAIX Specificity from a High-Resolution Crystal Structure, Modeling, and Quantum Chemical Calculations. BioMed Res. Int. 2014, 389869 10.1155/2014/389869. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Fanfrlík J.; Brahmkshatriya P. S.; Řezáč J.; Jílková A.; Horn M.; Mareš M.; Hobza P.; Lepšík M. Quantum Mechanics-Based Scoring Rationalizes the Irreversible Inactivation of Parasitic Schistosoma mansoni Cysteine Peptidase by Vinyl Sulfone Inhibitors. J. Phys. Chem. B 2013, 117, 14973–14982. 10.1021/jp409604n. [DOI] [PubMed] [Google Scholar]
  28. Söderhjelm P.; Ryde U. How Accurate Can a Force Field Become? A Polarizable Multipole Model Combined with Fragment-wise Quantum-Mechanical Calculations. J. Phys. Chem. A 2009, 113, 617–627. 10.1021/jp8073514. [DOI] [PubMed] [Google Scholar]
  29. Berg L.; Mishra B. K.; Andersson C. D.; Ekström F.; Linusson A. The Nature of Activated Non-classical Hydrogen Bonds: A Case Study on Acetylcholinesterase-Ligand Complexes. Chem. – Eur. J. 2016, 22, 2672–2681. 10.1002/chem.201503973. [DOI] [PubMed] [Google Scholar]
  30. Wichapong K.; Rohe A.; Platzer C.; Slynko I.; Erdmann F.; Schmidt M.; Sippl W. Application of Docking and QM/MM-GBSA Rescoring to Screen for Novel Myt1 Kinase Inhibitors. J. Chem. Inf. Model. 2014, 54, 881–893. 10.1021/ci4007326. [DOI] [PubMed] [Google Scholar]
  31. Chaskar P.; Zoete V.; Röhrig U. F. Toward On-The-Fly Quantum Mechanical/Molecular Mechanical (QM/MM) Docking: Development and Benchmark of a Scoring Function. J. Chem. Inf. Model. 2014, 54, 3137–3152. 10.1021/ci5004152. [DOI] [PubMed] [Google Scholar]
  32. Chaskar P.; Zoete V.; Röhrig U. F. On-the-Fly QM/MM Docking with Attracting Cavities. J. Chem. Inf. Model. 2017, 57, 73–84. 10.1021/acs.jcim.6b00406. [DOI] [PubMed] [Google Scholar]
  33. Burger S. K.; Thompson D. C.; Ayers P. W. Quantum Mechanics/Molecular Mechanics Strategies for Docking Pose Refinement: Distinguishing between Binders and Decoys in Cytochrome c Peroxidase. J. Chem. Inf. Model. 2011, 51, 93–101. 10.1021/ci100329z. [DOI] [PubMed] [Google Scholar]
  34. Antony J.; Grimme S.; Liakos D. G.; Neese F. Protein-Ligand Interaction Energies with Dispersion Corrected Density Functional Theory and High-Level Wave Function Based Methods. J. Phys. Chem. A 2011, 115, 11210–11220. 10.1021/jp203963f. [DOI] [PubMed] [Google Scholar]
  35. Raha K.; Merz K. M. A quantum mechanics-based scoring function: Study of zinc ion-mediated ligand binding. J. Am. Chem. Soc. 2004, 126, 1020–1021. 10.1021/ja038496i. [DOI] [PubMed] [Google Scholar]
  36. Raha K.; Merz K. M. Large-scale validation of a quantum mechanics based scoring function: Predicting the binding affinity and the binding mode of a diverse set of protein-ligand complexes. J. Med. Chem. 2005, 48, 4558–4575. 10.1021/jm048973n. [DOI] [PubMed] [Google Scholar]
  37. Řezáč J.; Hobza P. Advanced Corrections of Hydrogen Bonding and Dispersion for Semiempirical Quantum Mechanical Methods. J. Chem. Theory Comput. 2012, 8, 141–151. 10.1021/ct200751e. [DOI] [PubMed] [Google Scholar]
  38. Kolář M.; Fanfrlík J.; Lepšík M.; Forti F.; Luque F. J.; Hobza P. Assessing the Accuracy and Performance of Implicit Solvent Models for Drug Molecules: Conformational Ensemble Approaches. J. Phys. Chem. B 2013, 117, 5950–5962. 10.1021/jp402117c. [DOI] [PubMed] [Google Scholar]
  39. Stewart J. J. P. Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. 10.1007/s00894-012-1667-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Klamt A.; Schüürmann G. COSMO - A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc., Perkin Trans. 2 1993, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
  41. Sulimov A. V.; Kutov D. C.; Katkova E. V.; Sulimov V. B. Combined Docking with Classical Force Field and Quantum Chemical Semiempirical Method PM7. Adv. Bioinf. 2017, 7167691 10.1155/2017/7167691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Oferkin I. V.; Katkova E. V.; Sulimov A. V.; Kutov D. C.; Sobolev S. I.; Voevodin V. V.; Sulimov V. B. Evaluation of Docking Target Functions by the Comprehensive Investigation of Protein-Ligand Energy Minima. Adv. Bioinf. 2015, 126858 10.1155/2015/126858. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Hostaš J.; Řezáč J.; Hobza P. On the performance of the semiempirical quantum mechanical PM6 and PM7 methods for noncovalent interactions. Chem. Phys. Lett. 2013, 568–569, 161–166. 10.1016/j.cplett.2013.02.069. [DOI] [Google Scholar]
  44. Řezáč J.; Hobza P. A halogen-bonding correction for the semiempirical PM6 method. Chem. Phys. Lett. 2011, 506, 286–289. 10.1016/j.cplett.2011.03.009. [DOI] [Google Scholar]
  45. Fanfrlík J.; Bronowska A. K.; Řezáč J.; Přenosil O.; Konvalinka J.; Hobza P. A Reliable Docking/Scoring Scheme Based on the Semiempirical Quantum Mechanical PM6-DH2 Method Accurately Covering Dispersion and H-Bonding: HIV-1 Protease with 22 Ligands. J. Phys. Chem. B 2010, 114, 12666–12678. 10.1021/jp1032965. [DOI] [PubMed] [Google Scholar]
  46. Lepšík M.; Řezáč J.; Kolář M.; Pecina A.; Hobza P.; Fanfrlík J. The Semiempirical Quantum Mechanical Scoring Function for In Silico Drug Design. ChemPlusChem 2013, 78, 921–931. 10.1002/cplu.201300199. [DOI] [PubMed] [Google Scholar]
  47. Vorlová B.; Nachtigallová D.; Jirásková-Vaníčková J.; Ajani H.; Jansa P.; Řezáč J.; Fanfrlík J.; Otyepka M.; Hobza P.; Konvalinka J.; Lepšík M. Malonate-based inhibitors of mammalian serine racemase: kinetic characterization and structure-based computational study. Eur. J. Med. Chem. 2015, 89, 189–197. 10.1016/j.ejmech.2014.10.043. [DOI] [PubMed] [Google Scholar]
  48. Cousido-Siah A.; Ruiz F. X.; Fanfrlík J.; Giménez-Dejoz J.; Mitschler A.; Kamlar M.; Veselý J.; Ajani H.; Parés X.; Farrés J.; Hobza P.; Podjarny A. D. IDD388 Polyhalogenated Derivatives as Probes for an Improved Structure-Based Selectivity of AKR1B10 Inhibitors. ACS Chem. Biol. 2016, 11, 2693–2705. 10.1021/acschembio.6b00382. [DOI] [PubMed] [Google Scholar]
  49. Dostál J.; Pecina A.; Hrušková-Heidingsfeldová O.; Marečková L.; Pichová I.; Řezáčová P.; Lepšík M.; Brynda J. Atomic resolution crystal structure of Sapp2p, a secreted aspartic protease from Candida parapsilosis. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2015, 71, 2494–2504. 10.1107/S1399004715019392. [DOI] [PubMed] [Google Scholar]
  50. Nekardová M.; Vymětalová L.; Khirsariya P.; Kováčová S.; Hylsová M.; Jorda R.; Kryštof V.; Fanfrlík J.; Hobza P.; Paruch K. Structural Basis of the Interaction of Cyclin-Dependent Kinase 2 with Roscovitine and Its Analogues Having Bioisosteric Central Heterocycles. ChemPhysChem 2017, 785. 10.1002/cphc.201601319. [DOI] [PubMed] [Google Scholar]
  51. Hylsová M.; Carbain B.; Fanfrlík J.; Musilová L.; Haldar S.; Köprülüoğlu C.; Ajani H.; Brahmkshatriya P. S.; Jorda R.; Kryštof V.; Hobza P.; Echalier A.; Paruch K.; Lepšík M. Explicit treatment of active-site waters enhances quantum mechanical/implicit solvent scoring: Inhibition of CDK2 by new pyrazolo[1,5-a]pyrimidines. Eur. J. Med. Chem. 2017, 126, 1118–1128. 10.1016/j.ejmech.2016.12.023. [DOI] [PubMed] [Google Scholar]
  52. Pecina A.; Haldar S.; Fanfrlík J.; Meier R.; Řezáč J.; Lepšík M.; Hobza P. SQM/COSMO Scoring Function at the DFTB3-D3H4 Level: Unique Identification of Native Protein-Ligand Poses. J. Chem. Inf. Model. 2017, 57, 127–132. 10.1021/acs.jcim.6b00513. [DOI] [PubMed] [Google Scholar]
  53. Elstner M.; Hobza P.; Frauenheim T.; Suhai S.; Kaxiras E. Hydrogen bonding and stacking interactions of nucleic acid base pairs: A density-functional-theory based treatment. J. Chem. Phys. 2001, 114, 5149–5155. 10.1063/1.1329889. [DOI] [Google Scholar]
  54. Miriyala V. M.; Řezáč J. Description of non-covalent interactions in SCC-DFTB methods. J. Comput. Chem. 2017, 38, 688–697. 10.1002/jcc.24725. [DOI] [PubMed] [Google Scholar]
  55. Friesner R. A.; Banks J. L.; Murphy R. B.; Halgren T. A.; Klicic J. J.; Mainz D. T.; Repasky M. P.; Knoll E. H.; Shelley M.; Perry J. K.; Shaw D. E.; Francis P.; Shenkin P. S. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem. 2004, 47, 1739–1749. 10.1021/jm0306430. [DOI] [PubMed] [Google Scholar]
  56. Morris G. M.; Huey R.; Lindstrom W.; Sanner M. F.; Belew R. K.; Goodsell D. S.; Olson A. J. AutoDock4 and AutoDockTools4: Automated Docking with Selective Receptor Flexibility. J. Comput. Chem. 2009, 30, 2785–2791. 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Trott O.; Olson A. J. Software News and Update AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2010, 31, 455–461. 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Allen W. J.; Balius T. E.; Mukherjee S.; Brozell S. R.; Moustakas D. T.; Lang P. T.; Case D. A.; Kuntz I. D.; Rizzo R. C. DOCK 6: Impact of New Features and Current Docking Performance. J. Comput. Chem. 2015, 36, 1132–1156. 10.1002/jcc.23905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Li Y.; Liu Z.; Li J.; Han L.; Liu J.; Zhao Z.; Wang R. Comparative Assessment of Scoring Functions on an Updated Benchmark: 1. Compilation of the Test Set. J. Chem. Inf. Model. 2014, 54, 1700–1716. 10.1021/ci500080q. [DOI] [PubMed] [Google Scholar]
  60. Kirchmair J.; Wolber G.; Laggner C.; Langer T. Comparative performance assessment of the conformational model generators omega and catalyst: A large-scale survey on the retrieval of protein-bound ligand conformations. J. Chem. Inf. Model. 2006, 46, 1848–1861. 10.1021/ci060084g. [DOI] [PubMed] [Google Scholar]
  61. Warren G. L.; Do T. D.; Kelley B. P.; Nicholls A.; Warren S. D. Essential considerations for using protein-ligand structures in drug discovery. Drug Discovery Today 2012, 17, 1270–1281. 10.1016/j.drudis.2012.06.011. [DOI] [PubMed] [Google Scholar]
  62. Zilian D.; Sotriffer C. A. SFCscore(RF): A Random Forest-Based Scoring Function for Improved Affinity Prediction of Protein-Ligand Complexes. J. Chem. Inf. Model. 2013, 53, 1923–1933. 10.1021/ci400120b. [DOI] [PubMed] [Google Scholar]
  63. Zhao H.; Caflisch A. Discovery of ZAP70 inhibitors by high-throughput docking into a conformation of its kinase domain generated by molecular dynamics. Bioorg. Med. Chem. Lett. 2013, 23, 5721–5726. 10.1016/j.bmcl.2013.08.009. [DOI] [PubMed] [Google Scholar]
  64. Jain A. N. Surflex: Fully automatic flexible molecular docking using a molecular similarity-based search engine. J. Med. Chem. 2003, 46, 499–511. 10.1021/jm020406h. [DOI] [PubMed] [Google Scholar]
  65. Small-Molecule Drug Discovery Suite 2016-1; Schrödinger, LLC: New York, NY, 2016.
  66. Case D. A.; Babin V.; Berryman J. T.; Betz R. M.; Cai Q.; Cerutti D. S.; Cheatham T. E.; Darden T. A.; Duke R. E.; Gohlke H.; Goetz A. W.; Gusarov S.; Homeyer N.; Janowski P.; Kaus J.; Kolossváry I.; Kovalenko A.; Lee T. S.; LeGrand S.; Luchko T.; Luo R.; Madej B.; Merz K. M.; Paesani F.; Roe D. R.; Roitberg A.; Sagui C.; Salomon-Ferrer R.; Seabra G.; Simmerling C. L.; Smith W.; Swails J.; Walker; Wang J.; Wolf R. M.; Wu X.; Kollman P. A.. AMBER 14; University of California: San Francisco, 2014. [Google Scholar]
  67. Wang J.; Wang W.; Kollman P. A.; Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graphics Modell. 2006, 25, 247–260. 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
  68. Jakalian A.; Bush B. L.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. . [DOI] [PubMed] [Google Scholar]
  69. Jakalian A.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
  70. Gaus M.; Cui Q.; Elstner M. DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. 10.1021/ct100684s. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Gaus M.; Goez A.; Elstner M. Parametrization and Benchmark of DFTB3 for Organic Molecules. J. Chem. Theory Comput. 2013, 9, 338–354. 10.1021/ct300849w. [DOI] [PubMed] [Google Scholar]
  72. Gaus M.; Lu X.; Elstner M.; Cui Q. Parameterization of DFTB3/3OB for Sulfur and Phosphorus for Chemical and Biological Applications. J. Chem. Theory Comput. 2014, 10, 1518–1537. 10.1021/ct401002w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Lu X.; Gaus M.; Elstner M.; Cui Q. Parametrization of DFTB3/3OB for magnesium and zinc for chemical and biological applications. J. Phys. Chem. B 2015, 119, 1062–1082. 10.1021/jp506557r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Kubillus M.; Kubař T.; Gaus M.; Řezáč J.; Elstner M. Parameterization of the DFTB3 method for Br, Ca, Cl, F, I, K, and Na in organic and biological systems. J. Chem. Theory Comput. 2015, 11, 332–342. 10.1021/ct5009137. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao7b00503_si_001.pdf (243.3KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES