Prediction of Compound Profiling Matrices Using Machine Learning

Abstract

Screening of compound libraries against panels of targets yields profiling matrices. Such matrices typically contain structurally diverse screening compounds, large numbers of inactives, and small numbers of hits per assay. As such, they represent interesting and challenging test cases for computational screening and activity predictions. In this work, modeling of large compound profiling matrices was attempted that were extracted from publicly available screening data. Different machine learning methods including deep learning were compared and different prediction strategies explored. Prediction accuracy varied for assays with different numbers of active compounds, and alternative machine learning approaches often produced comparable results. Deep learning did not further increase the prediction accuracy of standard methods such as random forests or support vector machines. Target-based random forest models were prioritized and yielded successful predictions of active compounds for many assays.

1. Introduction

Machine learning methods are widely used in computational compound screening, also termed virtual screening (VS), to select limited numbers of potentially active compounds from large libraries.¹ Algorithms such as support vector machine (SVM) or random forest (RF) are among the most popular approaches for activity prediction.² In addition, there is increasing interest in deep learning for VS and quantitative structure–activity relationship predictions.³⁻⁵

Public repositories for compounds and activity data are indispensable resources for developing, evaluating, and calibrating VS methods and protocols. For small molecules and data from medicinal chemistry and biological screening, ChEMBL⁶ (maintained by the European Bioinformatics Institute of the European Molecular Laboratory) and PubChem^7,8 (National Center of Biotechnology Information of the National Institutes of Health) have become primary resources, respectively. In addition, MoleculeNet has recently been introduced as a collection of curated compound activity data from diverse sources.⁹ For VS benchmark calculations, known active compounds and decoys are typically assembled.¹⁰⁻¹³ Active compounds are usually taken from medicinal chemistry sources. Evaluating VS approaches using high-throughput screening (HTS) data provides a more realistic scenario but is generally complicated by experimental variance and noise as well as natural unbalance of active and inactive compounds in HTS data sets.¹⁴⁻¹⁶ Hit rates in HTS typically range from about 0.1 to 2%,¹⁵ depending on the assays and targets, whereas most test compounds are inactive.¹⁶ Learning from data sets of such unbalanced composition generally provides substantial challenges for deriving predictive models. Hence, predictions using HTS data are only rarely reported.^17,18 Learning from unbalanced data has been addressed in a few studies.¹⁹⁻²¹

In addition to state-of-the-art machine learning methods such as SVM and RF, deep neural networks (DNNs) have also been applied for activity predictions.^{3−5,22−24} DNN applications sometimes report higher prediction accuracy compared with other methods. DNNs can either be trained on a per-target basis or by combining data from multiple activity classes, which are known as multitask DNNs.^23,24 Different results have been obtained by comparing the performance of single- and multitask DNNs.^23,24 A general limitation of DNN and, in particular, multitask learning is the rather limited ability to rationalize the failure of predictions.²⁴

A challenge in VS going beyond learning on the basis of HTS data is the prediction of compound profiling matrices, which are obtained by screening compound collections in a panel of assays.²⁵⁻²⁹ In these cases, the unbalance and screening data noise issues referred to above further escalate. Compounds might be active in one or more assays and inactive in others or they might be consistently inactive, yielding rather complex prediction scenarios. To our knowledge, machine learning predictions of large profiling matrices with more than just a handful of assays are yet to be reported. However, the inherent challenges of such predictions are not the only reason for their sparseness. Data unavailability is another. Although profiling matrices are frequently generated in the pharmaceutical industry, they are rarely disclosed. The few profiling data sets that are publicly available are essentially limited to kinase targets and partly incomplete. Thus, there is currently no sound basis for predictive modeling of profiling matrices.

In light of these limitations, we have developed a computational methodology to extract complete profiling matrices from available screening data.³⁰ Applying this approach, we have generated profiling matrices of different compositions including assays for a variety of targets. These matrices consist of “real life” screening data and are characterized by generally low hit rates and the presence of many consistently inactive compounds.

Prediction of compound profiling matrices is of high relevance for chemogenomics research, which ultimately aims at accounting for all possible small molecule–target interactions. For all practical purposes, reaching this goal will essentially be infeasible. Accordingly, there is a high level of interest in computational approaches that are capable of complementing profiling experiments with reliable ligand–target predictions. Moreover, profiling matrices also represent excellent model systems for HTS campaigns using a given compound deck. If experimental matrices are available, predicting the outcome of HTS runs against different targets can be attempted under realistic conditions. This provides much more informative estimates of computational screening performance than artificial benchmark settings that are typically used. In drug discovery, the prediction of HTS data has long been and continues to be a topical issue. For example, because the capacity of (compound) “cherry-picking” from screening plates has become more widely available in the industry, computational prescreening of compound decks can be used to prioritize subsets that are most likely to yield new hits. Cycles of computational screening followed by experimental testing are implemented in iterative screening schemes, which may significantly reduce the magnitude of experimental HTS efforts.

Herein, we have applied various machine learning approaches and strategies to predict newly derived compound profiling matrices. The results are presented in the following and provide an experimentally grounded view of expected accuracy of machine learning models in predicting the outcome of screening campaigns for diverse targets.

2. Results and Discussion

2.1. Profiling Matrices

Two HTS data matrices comprising the same 53 assays and targets (i.e., one assay per target) and 109 925 and 143 310 distinct compounds, respectively, were used for machine learning and VS. These matrices were assembled from confirmatory assays available in the PubChem BioAssay collection^7,8 by applying our new algorithm.³⁰ Assays, targets, and assay codes used in the following discussion are reported in Table 1. The density of the smaller matrix, termed matrix 1, was 100%, i.e., all possible matrix cells contained binary annotations of activity or inactivity. The number of compounds tested per assay initially ranged from 266 527 to 387 381 and 46 of the 53 assays in matrix 1 had a hit rate of less than 1%. Table 1 also shows that the number of active compounds per assay varied significantly, ranging from only a few to more than 1000. The 53 assays also included four assays without hits. For assays with only few active compounds, training of machine learning models was generally very difficult (if not impossible in some instances). However, if all test compounds were predicted to be inactive in such cases, satisfactory results would still be obtained (i.e., only very few actives would be missed), despite intrinsic limitations of model building.

Table 1. Assays and Targets^a.

assay ID	assay code	target name	organism	# active CPDs (matrix 2 training)	# active CPDs (matrix 2 test)	# active CPDs (matrix 1)
485313	A	Niemann-pick C1 protein precursor	Homo sapiens	3103	3142	395
485314	B	DNA polymerase β	Homo sapiens	1325	1326	125
485341	C	β-lactamase	Escherichia coli	458	478	420
485349	D	serine-protein kinase ATM isoform 1	Homo sapiens	191	175	118
485367	E	ATP-dependent phosphofructokinase	Trypanosoma brucei brucei	152	138	103
504466	F	ATPase family AAA domain-containing protein 5	Homo sapiens	1624	1586	424
588590	G	DNA polymerase iota	Homo sapiens	885	868	103
588591	H	DNA polymerase eta	Homo sapiens	1123	1129	39
624171	I	nuclear factor erythroid 2-related factor 2	Homo sapiens	367	391	118
624330	J	Rac GTPase-activating protein 1	Homo sapiens	491	536	156
1721	K	pyruvate kinase	Leishmania mexicana	433	425	39
1903	L	large T antigen	Simian virus 40	275	248	57
2101	M	glucocerebrosidase	Homo sapiens	73	58	41
2517	N	AP endonuclease 1	Homo sapiens	197	199	32
2528	O	Bloom syndrome protein	Homo sapiens	137	128	8
2662	P	histone-lysine N-methyltransferase MLL	Homo sapiens	10	15	3
2676	Q	relaxin/insulin-like family peptide receptor 1	Homo sapiens	215	195	223
463254	R	ubiquitin carboxyl-terminal hydrolase 2 isoform a	Homo sapiens	4	4	2
485297	S	Ras-related protein Rab-9A	Homo sapiens	3751	3810	410
488837	T	ryes absent homolog 2 isoform a	Homo sapiens	2	7	1
492947	U	β-2 adrenergic receptor	Homo sapiens	25	28	4
504327	V	histone acetyltransferase KAT2A	Homo sapiens	158	141	50
504329	W	nonstructural protein 1	influenza A virus	213	205	64
504339	X	lysine-specific demethylase 4A	Homo sapiens	4755	4757	1320
504842	Y	chaperonin-containing TCP-1 β subunit homolog	Homo sapiens	28	20	13
504845	Z	regulator of G-protein signaling 4	Homo sapiens	9	7	1
504847	AA	vitamin D3 receptor isoform VDRA	Homo sapiens	772	771	48
540317	AB	chromobox protein homolog 1	Homo sapiens	442	449	98
588579	AC	DNA polymerase kappa	Homo sapiens	354	362	6
588689	AD	genome polyprotein	dengue virus type 2	180	184	6
588795	AE	flap endonuclease 1	Homo sapiens	175	210	17
602179	AF	isocitrate dehydrogenase 1	Homo sapiens	75	81	28
602233	AG	phosphoglycerate kinase	Trypanosoma brucei brucei	28	40	1
602310	AH	DNA dC->dU-editing enzyme APOBEC-3G	Homo sapiens	60	66	11
602313	AI	DNA dC->dU-editing enzyme APOBEC-3F isoform a	Homo sapiens	202	183	28
602332	AJ	heat shock 70 kDa protein 5	Homo sapiens	15	15	6
624170	AK	glutaminase kidney isoform	Homo sapiens	162	186	65
624172	AL	glucagon-like peptide 1 receptor	Homo sapiens	7	7	2
624173	AM	hypothetical protein	Trypanosoma brucei brucei	136	141	32
624202	AN	breast cancer type 1 susceptibility protein	Homo sapiens	1469	1484	275
651644	AO	viral protein r	human immunodeficiency virus 1	208	209	74
651768	AP	Werner syndrome ATP-dependent helicase	Homo sapiens	278	325	5
652106	AQ	α-synuclein	Homo sapiens	111	102	57
720504	AR	serine/threonine-protein kinase PLK1	Homo sapiens	3357	3308	662
720542	AS	apical membrane antigen 1	Plasmodium falciparum	93	98	25
720707	AT	Rap guanine nucleotide exchange factor 3	Homo sapiens	50	62	3
720711	AU	Rap guanine nucleotide exchange factor 4	Homo sapiens	59	68	16
743255	AV	ubiquitin carboxyl-terminal hydrolase 2 isoform a	Homo sapiens	147	149	15
743266	AW	parathyroid hormone 1 receptor	Homo sapiens	66	70	79
493005	AX	Tumor susceptibility gene 101 protein	Homo sapiens	0	0	0
504891	AY	peptidyl-prolyl cis–trans isomerase NIMA-interacting 1	Homo sapiens	6	5	0
504937	AZ	sphingomyelin phosphodiesterase	Homo sapiens	5	9	0
588456	BA	thioredoxin reductase	Rattus norvegicus	1	8	0

^aReported are the PubChem assay IDs, codes used here, targets, and organisms, for all 53 assays. In addition, for each assay, numbers of active compounds in the matrix 2 training and test sets and in matrix 1 are reported.

A second matrix was generated by slightly reducing the density in favor of larger compound numbers.³⁰ From this matrix, all compounds contained in matrix 1 were removed, yielding matrix 2. The density of matrix 2 was 96%. Matrix 1 and matrix 2 contained 105 475 (96.0%) and 110 218 (76.9%) compounds, respectively, which were consistently inactive in all assays. In matrix 1, 3639 (3.3%) of the test compounds had single- and 811 (0.7%) had multitarget activity. For matrix 2, the corresponding numbers of active compounds were 19 069 (13.3%) and 14 023 (9.8%), respectively. Hence, the composition of these matrices was highly unbalanced and dominated by consistently inactive compounds. Overall, only 0.1 and 0.8% of the cells in matrix 1 and 2, respectively, contained activity annotations. Matrix composition is summarized in Table 2. In matrix 1, the number of active compounds per assay ranged from 0 to 1320, with a mean and median value of 110 and 32, respectively. In matrix 2, it ranged from 0 to 9512, with a mean and median value of 1077 and 348, respectively. Figure 1 shows exemplary active compounds from matrix 1. In Figure 2, intra- and interassay similarity of active compounds is reported. The heat map reveals low mean similarity of compounds active in different assays. Furthermore, interassay and intra-assay similarity were overall comparable. Taken together, these observations indicated that it would be challenging to detect compounds sharing the same activity on the basis of similarity calculations and distinguish between compounds with different activity.

Table 2. Matrix Composition^a.

	matrix 1	matrix 2
density	100%	96.4%
# compounds (CPDs)	109 925	143 310
# assays	53	53
percentage of active cells	0.1%	0.8%
# consistently inactive CPDs	105 475 (96%)	110 218 (76.9%)
# CPDs with single-target activity	3639 (3.3%)	19 069 (13.3%)
# CPDs with multitarget activity	811 (0.7%)	14 023 (9.8%)

^aFor matrix 1 and matrix 2, the density, number of compounds and assays, percentage of cells with activity annotations (active cells), number of consistently inactive compounds, and number of compounds with single- and multitarget activity are reported.

Figure 1.

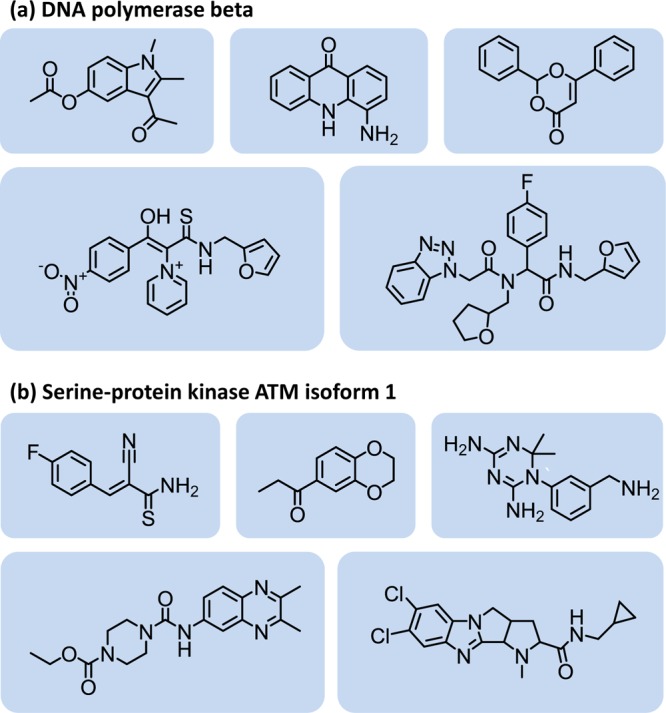
Exemplary active compounds. Shown are exemplary active compounds from two matrix 1 assays for (a) DNA polymerase β (assay code B) and (b) serine-protein kinase ATM isoform 1 (code D), respectively.

Figure 2.

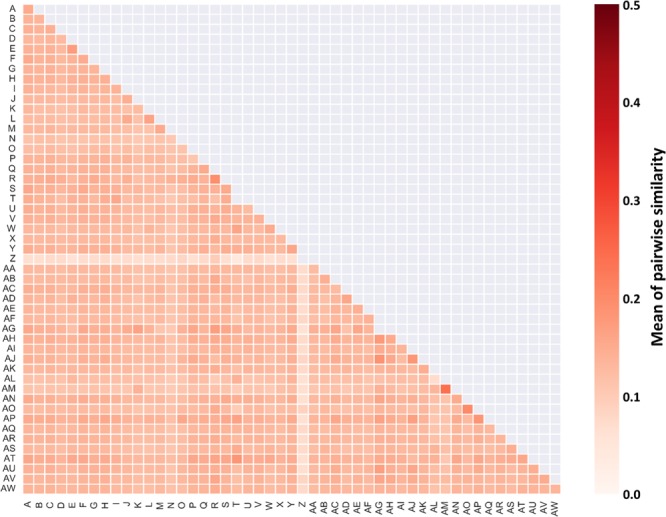
Pairwise Tanimoto similarity. The heat map reports mean pairwise Tanimoto similarity for active compounds from matrix 1. The extended connectivity fingerprint with bond diameter 4 (ECFP4; see Materials and Methods) was used as a molecular representation.

2.2. Prediction Strategy

The primary goal was predicting the entire matrix 1 by learning from matrix 2. Predictions were attempted at two levels including global predictions of active versus consistently inactive compounds as well as activity predictions for individual targets. For global models, training and test compounds with different activities were combined to yield the “active” class. Half of matrix 2 was randomly selected and used for training of global models using different methods. Global models were applied to predict active and inactive compounds for the other half of matrix 2 used as a test set as well as the entire matrix 1. Per-target models were derived in two ways: first, using half of matrix 2 and second, the entire matrix 2. The former per-target models were applied to predict the matrix 2 test set, and the complete matrix 1 and the latter models were applied to predict matrix 1. For per-target models, initial comparisons of different methods and optimization of calculation parameters were carried out for 10 assays from matrix 2 with large numbers of available training compounds (assay codes A–J in Table 1). These models were used to predict these 10 assays in the matrix 2 test set as well as in matrix 1. Further details are provided in the Materials and Methods section.

2.3. Global Models

Given that the vast majority of matrix compounds were consistently inactive in all assays, we reasoned that initial exclusion of these consistently inactive compounds followed by target-based predictions might be a promising strategy for activity prediction. Successful elimination of consistently inactive compounds would increase data balance and reduce the number of compounds to be predicted by per-target models. Therefore, global models were first built using SVM, RF, and DNN to distinguish between combined active and consistently inactive screening compounds. On the basis of test calculations (see Materials and Methods), models trained with all available data reached highest relative performance levels and the ECFP4 fingerprint was a preferred descriptor. Figure 3 shows the prediction results of the global models for the matrix 2 test set and for matrix 1. The performance of the different models was nearly identical in both cases. Although there was consistent early enrichment of active compounds, deprioritization of inactive compounds was accompanied by a substantial loss of active compounds, in particular, for matrix 1. In this case, eliminating 50% of the inactive compounds also led to a removal of 25% of the actives. For the minority class, the magnitude of this initial loss of active compounds limited the envisioned two-stage prediction approach.

Figure 3.

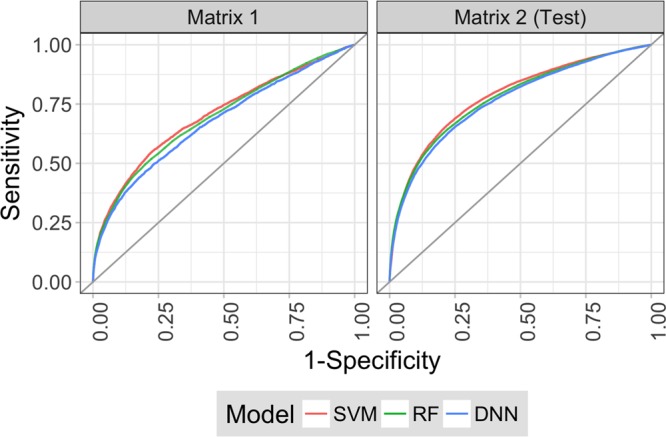
Receiver operating characteristic curves for global models. Receiver operating characteristic (ROC) curves are shown for SVM (red), RF (green), and DNN (blue) global models, which were trained with half of matrix 2 and used to predict the other half of matrix 2 (right) and matrix 1 (left).

2.4. Models for Assay-Based Predictions

Next, we used a subset of 10 assays with larger numbers of available active compounds (assay codes A–J in Table 1) for comparison of alternative machine learning methods and identification of best-performing models and preferred calculation conditions.

2.4.1. Method Comparison

Algorithms of different designs and complexities were systematically compared. Most of the implemented approaches resulted in single-task (per-target) models, but two multitask approaches were also included in the comparison. A multitask model yields probabilities of activity for compounds tested in different assays. Investigated methods included a similarity search-based approach termed the conditional correlated Bernoulli model (CCBM) to estimate rank positions of active compounds; popular machine learning approaches; such as naïve Bayes (NB) classification, SVM, and RF, single- and multitask DNN; and graph-convolutional NN (GraphConv). Test predictions were assessed by calculating area under the curve (AUC) values for receiver operating characteristic (ROC) curves and recall rates for the top 1% of ranked test sets.

Initially, we tested general training conditions. For each assay, available active training compounds were combined with increasing numbers of compounds inactive in the assay and a series of models were generated with different machine learning methods and evaluated. For all methods (except GraphConv), the folded version of the extended connectivity fingerprint with bond diameter 4 (ECFP4; see Materials and Methods) was used as a descriptor. Paralleling the findings for global models, preferred training sets generally consisted of all available active and inactive training compounds. Using these training sets, different methods were compared.

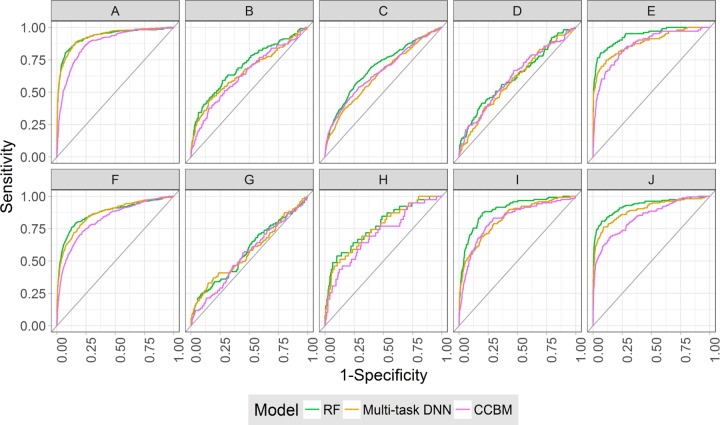
Tables 3 and 4 report benchmark results for the matrix 2 test set and for matrix 1, respectively. For the matrix 2 test set, best models consistently yielded AUC values >0.7 per assay and values >0.8 for eight assays. For matrix 1, prediction accuracy was overall lower but AUC values <0.7 were only obtained for three assays. Thus, different methods yielded models with at least reasonable prediction accuracy in most cases. Interestingly, although differences in prediction accuracy were often small, RF was the overall best-performing approach, achieving top predictions for eight assays in matrix 2 and five in matrix 1. As shown in Figure 4, it also compared favorably in multitasking DNN and performed better than the CCBM similarity search control. The performance level of RF was nearly matched by SVM, followed by GraphConv. Given overall comparable prediction accuracy achieved by different machine learning methods and high RF performance across different assays, RF was selected as a representative approach for further activity predictions.

Table 3. Area under the Curve Values for Prediction of 10 Assays of the Matrix 2 Test Set^a.

assay code	CCBM	NB	RF	SVM	single-task DNN	multitask DNN	GraphConv
A	0.85	0.84	0.91	0.92	0.91	0.91	0.90
B	0.77	0.79	0.85	0.85	0.82	0.82	0.83
C	0.64	0.71	0.73	0.72	0.69	0.67	0.72
D	0.63	0.72	0.69	0.65	0.67	0.62	0.64
E	0.81	0.82	0.86	0.84	0.84	0.85	0.85
F	0.82	0.82	0.88	0.88	0.87	0.87	0.86
G	0.73	0.79	0.84	0.84	0.81	0.79	0.82
H	0.80	0.85	0.90	0.90	0.88	0.87	0.89
I	0.80	0.85	0.89	0.89	0.88	0.85	0.89
J	0.84	0.87	0.92	0.92	0.91	0.86	0.92

^aReported are AUC values for prediction of 10 assays (codes A–J) using different machine learning methods. For each assay, best results are indicated in bold.

Table 4. Area under the Curve Values for Prediction of 10 Assays of Matrix 1^a.

assay code	CCBM	NB	RF	SVM	single-task DNN	multitask DNN	GraphConv
A	0.88	0.86	0.93	0.94	0.93	0.93	0.92
B	0.64	0.68	0.70	0.69	0.67	0.66	0.69
C	0.66	0.64	0.69	0.67	0.64	0.64	0.68
D	0.62	0.63	0.62	0.62	0.63	0.60	0.65
E	0.86	0.91	0.94	0.91	0.90	0.88	0.89
F	0.82	0.82	0.87	0.88	0.87	0.86	0.87
G	0.55	0.55	0.58	0.57	0.54	0.57	0.64
H	0.70	0.75	0.77	0.76	0.74	0.75	0.76
I	0.82	0.86	0.89	0.88	0.86	0.83	0.88
J	0.84	0.88	0.93	0.94	0.93	0.90	0.94

^aReported are AUC values for prediction of 10 assays (codes A–J) using different machine learning methods. For each assay, best results are indicated in bold.

Figure 4.

Per-target receiver operating characteristic curves. ROC curves are shown for target-based activity predictions with RF (green), multitask DNN (orange), and CCBM (pink) models. Curves represent 10 matrix 1 assays used for method comparisons. Codes A–J designate assays according to Table 1.

2.4.2. Alternative Molecular Representations

In the next step, RF models built using different molecular representations were compared. The results are reported in Table 5. In these calculations, ECFP4 emerged as the preferred descriptor, with nearly identical performance of its unfolded and folded (fixed length) version.

Table 5. Comparison of Different Molecular Representations^a.

assay code	MOE	MACCS	MOE + fold. ECFP4	nonfolded ECFP4	folded ECFP4
A	0.91	0.90	0.93	0.93	0.93
B	0.65	0.64	0.68	0.70	0.70
C	0.66	0.67	0.68	0.69	0.69
D	0.59	0.60	0.63	0.65	0.62
E	0.86	0.84	0.90	0.93	0.94
F	0.86	0.84	0.87	0.87	0.87
G	0.58	0.56	0.60	0.57	0.58
H	0.76	0.73	0.76	0.77	0.77
I	0.85	0.86	0.87	0.90	0.89
J	0.90	0.92	0.93	0.93	0.93

^aReported are AUC values for prediction of 10 assays (codes A–J) in matrix 1 using per-target RF models on the basis of different molecular representations, including 192 two-dimensional (2D) descriptors from the Molecular Operating Environment (MOE), 166 MACCS structural keys, the folded and unfolded version of ECFP4, and the combination of MOE descriptors and folded ECFP4 (MOE + fold. ECFP4). For each assay, best results are indicated in bold.

2.5. Per-Target Activity Predictions

On the basis of the comparisons above, final models for activity predictions on the 49 assays producing hits in matrix 1 were derived using RF, folded ECFP4, and all available active and inactive compounds per assay from the matrix 2 training set. As reported in Table 1, only few active training instances were available in a number of assays.

The results of activity predictions for all assays in the matrix 2 test set and in matrix 1 are reported in Figure 5. Predictions were overall superior for matrix 2 than matrix 1 (that did not share compounds with matrix 2). For matrix 2, AUC values of 0.8 or greater were achieved for 31 of 49 assays; an encouraging finding. For matrix 1, AUC values of at least 0.8 were obtained for 22 assays but there were also nine assays with low performance close to or even worse than random selection. In most cases, assays with low prediction accuracy only contained a limited number of actives (ranging from 1 to 79 compounds). As a control, matrix 1 predictions were also carried out with models trained on the entire matrix 2, shown in Figure 6. The availability of essentially twice as many active training compounds significantly improved prediction accuracy, with AUC values of 0.7 or greater obtained for 35 assays.

Figure 5.

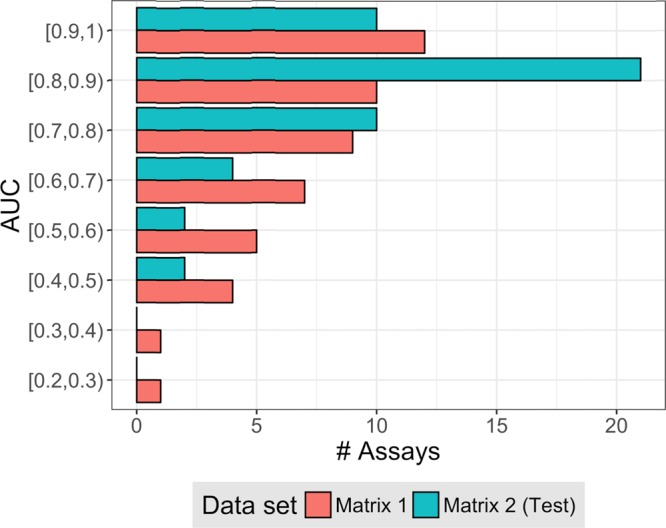
Area under the curve values for per-target models trained with half of matrix 2. AUC values are reported for predictions of compounds active in assays of the matrix 2 test set (blue) and matrix 1 (red).

Figure 6.

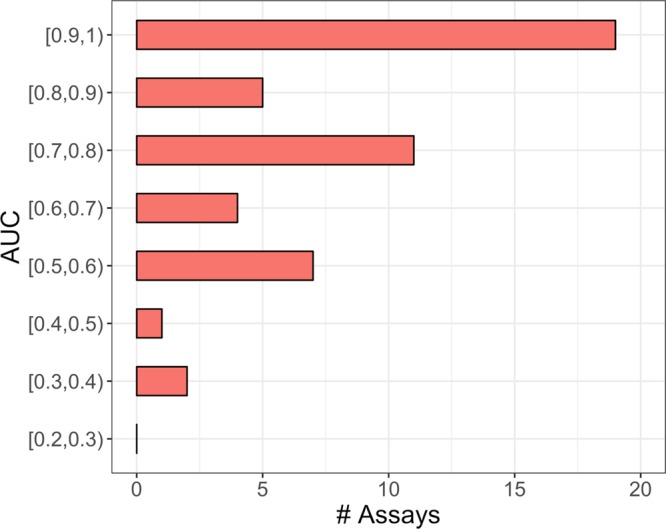
Area under the curve values for per-target models trained with matrix 2. AUC values are reported for predictions of compounds active in assays of matrix 1.

Table 6 reports the results for predictions on the 49 assays in matrix 1 after training RF models on the entire matrix 2. Recall rates among the top 1% of the ranking ranged from 0 to 100% and varied significantly, with mean and median values of 35 and 30%, respectively. Active compounds were successfully identified for 41 of 49 assays, and 26 models achieved recall rates of at least 30%. In instances where activity predictions completely failed, only few active compounds were available (ranging from two to eight). Interestingly, for many assays, there was a notable early enrichment of active compounds. In 22 cases, the first active compound was ranked among the top three database molecules and in 30 cases, it was ranked among the top 30. Thus, per-target models yielded promising predictions in many instances.

Table 6. Recall of Active Compounds in the Top 1% of Ranked Matrix 1^a.

assay code	# active CPDs in matrix 1	# active CPDs in top 1%	recall (%)	rank of first active CPD
X	1320	383	29	1
S	410	209	51	2
A	395	208	53	1
F	424	161	38	1
Q	223	120	54	1
J	156	113	72	2
AN	275	80	29	1
E	103	63	61	1
AR	662	59	9	1
C	420	56	13	4
AO	74	52	70	1
W	64	49	77	1
L	57	43	75	1
AB	98	36	37	5
I	118	35	30	10
AM	32	30	94	1
M	41	28	68	2
K	39	26	67	2
AK	65	25	38	3
AQ	57	17	30	7
D	118	16	14	1
B	125	15	12	2
AA	48	15	31	1
AF	28	15	54	1
G	103	7	7	42
H	39	7	18	39
AE	17	7	41	4
AS	25	7	28	1
AV	15	6	40	11
N	32	5	16	5
Y	13	5	38	1
AI	28	5	18	19
AD	6	3	50	72
V	50	2	4	192
AJ	6	2	33	88
T	1	1	100	38
Z	1	1	100	368
AG	1	1	100	146
AH	11	1	9	32
AU	16	1	6	249
AW	79	1	1	573
O	8	0	0	6758
P	3	0	0	12 637
R	2	0	0	31 266
U	4	0	0	1805
AC	6	0	0	2012
AL	2	0	0	26 430
AP	5	0	0	1156
AT	3	0	0	36 085

^aFor each assay, the number of active compounds in matrix 1, their recall in the top 1% of the ranking, and the highest-ranked active for RF models trained with matrix 2 are reported.

2.6. Conclusions

In this study, we have attempted to predict compound profiling matrices extracted from raw screening data. Large numbers of assays, small numbers of active compounds, their chemical diversity, and very large number of consistently inactive compounds challenged predictions in this case. Different machine learning methods were compared for their ability to identify active compounds across assays. Perhaps surprisingly, alternative methods often yielded comparable performance. Overall, RF emerged as a preferred approach, followed by SVM. Deep learning methods did not yield further improved prediction accuracy. In this context, we note that compound data sets used for activity predictions are still much smaller in size than many other data sets originating from life science research. In addition, compound data sets for activity prediction are also studied computationally using predefined molecular representations. Taken together, these features do not play into the strengths of deep learning in extracting patterns and feature representations from large data sets. This may explain the absence of significant performance increases through deep learning in predicting profiling matrices. Data sets originating from the life sciences that are more suitable for deep learning include, for example, images from high-content screening, data from large-scale gene expression analysis or next generation sequencing, and multipoint records from clinical trials. In these cases, performance increases through deep learning relative to other computational methods might be expected. Notably, image analysis in computer science has been one of the first applications where deep learning outperformed other machine learning approaches.

Initially, in our study, global models were designed aiming to eliminate large numbers of consistently inactive compounds. However, these models also deprioritized many active compounds, thus limiting their applicability as a first-path computational screen. By contrast, systematic activity predictions using per-target RF models yielded overall promising predictions on the basis of highly unbalanced training sets. A notable early enrichment of active compounds was frequently observed.

Compound matrices obtained from experimental screens provided a more realistic test system for machine learning than often applied benchmark settings. Under these conditions, prediction accuracy was lower than often reported for standard benchmarking exercises, as expected. Increasing complexity of machine learning methods did not scale with prediction accuracy, e.g., deep learning did not make a difference in this case. However, RF calculations yielded successful predictions for the majority of assays, indicating the ability of standard machine learning methods to identify novel active compounds under rather challenging experimental conditions. As an outlook, multitask learning should be further explored on the basis of profiling matrices for subsets of assays and we are also interested in focusing predictions specifically on small numbers of compounds with multitarget activity for which a different methodological framework might be required.

3. Materials and Methods

3.1. Matrices

A complete (100% density) assay-compound matrix (matrix 1) was generated from confirmatory assays in the PubChem BioAssay database⁷ using a newly introduced algorithm.³⁰ PubChem compounds yielding unique SMILES representations were retained in the matrix, which contained 109 925 compounds tested against a panel of 53 different confirmatory assays. Subsequently, matrix 2 with a final density of 96% was generated using the same algorithm. Initially, a matrix 2 precursor was assembled with 95% density that contained 281 943 compounds tested in the 53 assays. From the precursor, all matrix 1 compounds were removed. In addition, 28 708 inactive compounds tested in less than 50 assays were eliminated, yielding matrix 2 with 143 310 compounds. matrix 2 was then randomly divided into training and test sets each consisting of 71 655 compounds. Zero imputation³¹ was applied to missing values. Forty nine of the 53 assays produced hits, as reported in Table 1.

3.2. General Training Conditions

3.2.1. Global Models

Global models to distinguish between combined active and consistently inactive compounds were initially built using SVM, RF, and DNN on the basis of training sets of increasing size taken from the matrix 2 training set. A steady improvement in performance was observed with increasing training set size, consistent with earlier observations.³² Therefore, final global models were built using the entire matrix 2 training set.

3.2.2. Per-Target Models

Initially, per-target models were trained for 10 selected assays (codes A–J) for which larger numbers of active compounds were available (Table 1). Models were built using all active training compounds and different numbers of randomly selected compounds that were inactive in each assay. First, all available inactive compounds were used. Second, the number of randomly selected inactive compounds was set to 10 and 20 times the number of active compounds, following previously established rules for composition of training sets.³² Hence, three training sets with increasing ratio of inactive to active compounds were compared in model building.

3.3. Molecular Representations

Several descriptors were evaluated to represent compounds, including the extended connectivity fingerprints of bond diameter 4 (ECFP4)³³ and MACCS structural keys.³⁴ ECFP4 is a feature set fingerprint that enumerates layered atom environments and encodes them as integers using a hashing function. The feature set (“unfolded”) version of ECFP4 has variable size but can be “folded” to yield a constant number of bits. A 1024 bit folded version of ECFP4 was obtained through modulo mapping. MACCS is a binary keyed fingerprint, accounting for the presence or absence of 166 predefined substructures. The OEChem toolkit³⁵ and inhouse Python scripts were used to generate these fingerprints. In addition, 192 numerical 2D MOE descriptors were used.³⁶ Among others, these descriptors included physical properties, atom and bound counts, and various topological descriptors. Furthermore, graph-based representation known as graph-convolutional networks (GraphConv) was evaluated as an alternative to conventional chemical descriptors. GraphConv is a learnable representation inspired by the Morgan circular fingerprint representing compounds as undirected graphs and employs convolutional layers to create graph-based features.³⁷⁻³⁹ The DeepChem (version 1.3.2 dev)⁴⁰ implementation of GraphConv was used. Fingerprint similarity was quantified by calculating the Tanimoto coefficient (Tc).⁴¹

3.4. Machine Learning Models

Similarity searching, three state-of-the-art machine learning, and three types of DNNs were applied. For building predictive models, training compounds were represented as a feature vector 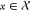and associated with a class label y ∈ {−1, 1}, encoding inactivity or activity for a given target. If the activity against all targets was predicted with a global model, y was expressed in a vector form.

3.4.1. Conditional Correlated Bernoulli Model (CCBM)

CCBM is an approach for modeling the distribution of Tc values of a screening database given a reference compound.⁴² For a specific target, each active compound from the matrix 2 training set was used once as the reference to search for active compounds in the test sets, i.e., matrix 2 test set and in matrix 1. Consistently inactive compounds from the matrix 2 training set were used as the database, and all active compounds present in matrix 2 test set and in matrix 1 were used as probes. A p-value representing the probability of finding a database compound with higher rank was calculated for every test compound. A nearest neighbor reference compound was determined and selected for each test compound having the highest Tc value, and the p-value corresponding to this reference compound was considered. If multiple nearest neighbors existed for a test compound, the mean p-values was taken. Finally, a ranking of test compounds was generated in the order of increasing p-values.

3.4.2. Support Vector Machine (SVM)

SVM is a supervised learning algorithm aiming to identify a hyperplane H that best separates two classes using the training data projected into the feature space 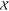.⁴³ This hyperplane is defined by a weight vector w and a bias b so that H = {x·w, x + b = 0} and maximizes the margin between the classes. To achieve better model generalization, slack variables can be added to permit errors of training instances falling within the margin or on the incorrect side of H. The trade-off between training errors and margin size can be controlled by the regularization hyperparameter C, which was optimized herein by 2-fold cross-validation using candidate values 0.1, 1, and 10. The preferred C values were 0.1 for 9 out of 10 models. In addition, the “kernel trick” enables projecting the training data into a higher dimensional space 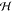without computing the explicit mapping of 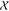into 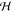. Class weights were considered to preferentially penalize errors in the minority class (active compounds).³² The Tanimoto kernel⁴⁴ was used to replace the standard scalar product.³² SVM models were generated using SVM-light.⁴⁵

3.4.3. Random Forest (RF)

RF consists of an ensemble of decision trees built from distinct subsets of the training data with replacement, known as bootstrapping.⁴⁶ A random subset of features is considered during node splitting for the construction of trees.⁴⁷ The number of trees was set at 500, and class weights were applied. The number of randomly selected features available at each split (max_features) and the minimum number of samples required to reach a leaf node (min_samples_leaf) were optimized via 2-fold cross-validation. Candidate values for max_features were the square root, the logarithm to base 2, or the total number of features; for min_samples_leaf, candidate values were 1, 5, and 10. RF calculations were carried out with scikit-learn.⁴⁸ The minimum number of samples for a leaf node was set to 5 for half of the assays and to 10 for the other half and the maximum number of features to 10 and 32, respectively. No preferred parameter combination was identified.

3.4.4. Naïve Bayes (NB)

NB uses Bayes’ theorem to predict the probability of a compound x to be active assuming feature independence^49,50

For binary descriptors, the Bernoulli NB implementation of scikit-learn was used.⁴⁸

3.4.5. Deep Feed Forward Neural Network (DNN)

DNN classifier approximates a function that maps an input value x to a class y, y = f(x; w), and learns the value of parameters w to achieve the best approximation.⁵¹ DNN consists of different layers with a number of neurons: an input layer, at least two hidden layers, and an output layer.⁵² Each hidden or output neuron assigns weights to the inputs, adds these weights, and passes the sum through a nonlinear function or activation function

where y is the output of neuron k, f is the activation function, x is the input variable (activation neuron in the previous layer), w is the weights connecting neuron k with x_j, and b_k is the bias. The summation includes all of the neurons adding connections to k.⁵³ Accordingly, each input is modified by a unique set of weights and biases. During the training phase, weights and biases are modified to obtain the correct output y, which is facilitated by following the gradient of the cost function (gradient decent) and efficiently calculated using backpropagation.⁵² Training is generally performed using subsets of data, and the weights and biases are updated accordingly. Single-task DNNs (with one DNN per assay) and a multitask DNN (i.e., a single DNN for predicting all active compounds) were investigated. For the multitask DNN, the matrix containing the activity profiles for training compounds was fed into the network as the set of desired outputs y and the output layer consisted of multiple nodes equaling the number of assays. Implementations were based on tensorflow⁵⁴ and keras.⁵⁵

Following previously formulated guidelines,^4,24,56 hyperparameters were either set to constant values or optimized by internal validation using 80 vs 20% data splits. For DNN, tested values for the learning rate (LR) were 0.01 and 0.001 and for the drop-out rate (DO), tested values were 25 and 50%. Investigated network architectures included [2000, 100], [2000, 1000], [500, 500, 500], [2000, 1000, 100], and [2000, 1000, 500, 100]. Therefore, both pyramidal and rectangular architectures were considered during hyperparameter optimization. Stochastic gradient descent was chosen as the optimizer, 128 as the batch size, and the “rectified linear unit” (ReLU) as the activation function. Output nodes were “softmax” for the single-task and “sigmoid” for the multitask DNNs. Different weights were also applied to the data according to the ratio of the number of active to inactive compounds to put more emphasis on actives. Finally, the maximum number of “epochs” was set to 100 for internal validation and 500 for the final model building.

For single-task DNN, two combinations of hyperparameters were preferentially selected including an optimum LR of 0.001, DO of 50%, and architecture [2000, 1000], as well as LR was of 0.01, DO of 25%, and architecture [2000, 100]. Multitask models require a single combination of optimized hyperparameters. Therefore, the median of AUC for all assays was used as a metric for multitask DNN hyperparameter optimization. The maximum value was obtained with a pyramidal architecture of two layers ([2000, 1000]), LR of 0.001, and DO of 25%.

3.4.6. Graph-Convolutional Neural Networks (GraphConv)

As mentioned above, GraphConv is based on features or descriptors with learnable parameters from a 2D molecular graph. Initially, a set of atom features, such as atom type or valence, and a neighbor list is obtained for every atom. Neighbor information is assigned to each atom by summing up the neighbors’ features. The learnable parameters include the weight matrices and biases used for posterior transformations. The same weight matrices and bias vectors are used in one layer depending on the degrees of atoms. After updating atom features, the pooling layer uses an activation function to generate a new set of feature values, which is the output vector in one layer. This procedure is repeated several times, and all of the outputs are summed up to obtain the final representation of the compound.⁵ Finally, this representation is the input of a fully connected DNN. Therefore, in this approach, feature extraction and model building are combined into one trainable module.³⁸ In our study, GraphConv models were carried out with DeepChem (version 1.3.2 dev),⁴⁰ which implemented a modified architecture of GraphConv. The pooling operator is max pool on an atom that returns the maximum activation across the atom and the atom’s neighbors without introducing additional parameters. Instead of summing several layers’ outputs, a graph gather layer is introduced. This layer sums all feature vectors for all atoms to obtain the final representation of a compound.

For GraphConv, internal validation (80–20%) was also applied and the number of epochs was set to 50 and the batch size to 256. The DO value was set to 25%. The numbers of output features in hidden graph-convolutional layers were [64], [64, 64], [64, 128, 64], [32, 32, 32, 32], and [64, 64, 64, 64]; for the dense layer dimension, which precedes the gather layer, they were 128 and 256; and for LR they were 0.01 and 0.001. Moreover, batch normalization, Adam optimizer, and ReLU were considered except for the gather (tanh), as the default settings in DeepChem. A single combination of hyperparameters was determined on the basis of the median value of AUCs for the 10 assays, as described for multitask DNN. The preferred architecture had three hidden convolutional layers with [64, 128, 64] neurons, 256 neurons in the dense layer, and an LR of 0.001.

Author Contributions

The study was carried out and the manuscript written with contributions of all authors. All authors have approved the final version of the manuscript.

The authors declare no competing financial interest.