Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2017 Oct 27;2(10):7343–7348. doi: 10.1021/acsomega.7b01089

Silver-Mediated Double Helix: Structural Parameters for a Robust DNA Building Block

Xi Chen †, Alexander Karpenko †, Olga Lopez-Acevedo †,‡,*
PMCID: PMC6045379  PMID: 30023548

Abstract

graphic file with name ao-2017-010899_0001.jpg

The DNA double helix is a versatile building block used in DNA nanotechnology. To potentiate the discovery of new DNA nanoscale assemblies, recently, silver cations have been introduced to pair DNA strands by base–Ag+–base bonding rather than by Watson–Crick pairing. In this work, we study the classical dynamics of a parallel silver-mediated homobase double helix and compare it to the dynamics of the antiparallel double helix. Our classical simulations show that only the parallel double helix is highly stable through the 100 ns simulation time. A new type of H-bond previously proposed by our collaboration and recently observed in crystal-determined helices drives the physicochemical stabilization. Compared to the natural B-DNA form, the metal-mediated helix has a contracted axial base pair rise and smaller numbers of base pairs per turn. These results open the path for the inclusion of this robust metal-mediated building block into new nanoscale DNA assemblies.

1. Introduction

The B-DNA double helix form is a pivotal biological structure for encoding information in living organisms and the basic building block in current DNA nanotechnology. B-DNA pairs strand antiparallel, one in the 5′ (phosphoryl) → 3′ (hydroxyl) orientation and the other in the 3′ → 5′ orientation. This helical form underpins recent designs for dynamic DNA machines1−3 and self-assembly schemes for elaborate DNA scaffolds4−7 that can control the separation between tethered molecules at sub-angstrom resolution.8 Yet depending on solution conditions, such as pH and ionic strength, distinctly different DNA structures may arise with noncanonical hydrogen (H)-bonding arrangements that are promoted by various base motifs. These include helical duplexes with parallel rather than antiparallel strands9,10 and folded forms, such as i-motifs and guanine (G) quadruplexes, which contain both parallel and antiparallel pairings.11−14

An important goal of biomolecular nanotechnology is the manipulation of the diverse forms of DNA. This has driven extensive research on alternatives to H-bonding. One attractive approach is base pairing by metal cations with high nucleobase affinities. This approach has potential for DNA-based nanomaterials with enhanced thermal, mechanical, and chemical properties and new functionalities.15−19 Silver cations have received particular attention due to their low toxicity, with numerous studies in artificial DNA containing unnatural bases.20−23 (In some cases, these modifications are available in commercially synthesized strands, albeit at high cost.) In natural DNA, Ag+-mediated pairings have potentially broader impacts that have begun to be explored in canonical duplexes with base mismatches24 and in strands without canonical pairings.25−28 However, understanding of structural changes produced by metal-mediated pairings is limited. This has largely precluded the incorporation of metal-mediated pairings into DNA nanotechnology, which relies on the use of well-established B-DNA parameters in sophisticated design schemes for multistrand assemblies.5,29

Previously, we studied the shortest possible Ag+-mediated cytosine (C) homobase duplex, a “tetramer” formed by Ag+ bridges between two 5′-C2-3′ DNA strands.30 We concluded that in aqueous solution Ag+ assembles these two-base strands in a parallel orientation, as supported by comparison of measured and computed circular dichroism spectra and in agreement with a previous proposal.27 Importantly, our calculations found that main stabilizing interactions include π–π nucleobase stacking and a novel interplanar H-bond between C bases in the adjacent C–Ag+–C pairs. We note that the silver cation increases the nucleobase–nucleobase distance and can indirectly affect the formation of (noncanonical) H-bonds. The existence of the interplanar H-bond was then found in a crystal structure of double helix forming silver-paired N1-hexylcytosines (which have no phosphate backbone) firstly and secondly between T–C and G–C bases in the crystal structure of an antiparallel silver-mediated DNA double helix. Both crystals support strongly the silver-mediated homobase forming a double helix in solution, but they leave open questions about their base and strand orientation and possible i-motif-like folding.

Here, we investigate whether the distinctive H-bonding, base orientations, and strand orientation in the silver-mediated tetramer are also characteristic of much longer Ag+-paired strands, as could be employed in designs for DNA nanostructures with regions of metal-mediated pairings. We employ strand lengths of up to 20 bases to test whether simple helices are preferred over an i-motif self-folded form. This work predicts structural parameters of Ag+-paired cytosine homobase DNA strands using a combination of quantum and classical calculations. Computationally, we show that a parallel double helix has high stability through the simulated dynamics, whereas an antiparallel double helix untwists to be almost nonhelical. The simulations’ atomistic level of description allows us to identify the main stabilization mechanisms. The Ag+–base bonds, base–base stacking interactions, and both planar and novel interplanar H-bonds all have central roles in the emergence of the double helix. The axis of the helix corresponds to a central spine of Ag+. This cationic spine reduces the average linear charge density by a factor of 2 relative to canonical duplex DNA, contributing to a contracted rise per base pair and increased rotation per base pair.

These results open a path for understanding how Ag+-mediated DNA duplexes in solution can share the outstanding properties of natural DNA in its double-helix form and open the door for targeted inclusion of this robust metal-mediated building block into new nanoscale DNA assemblies with enhanced properties.

2. Results

2.1. Test of the Classical Parameters

Because classical methods are required to simulate long duplexes, we must first determine the parameters under which quantum mechanics and molecular mechanics (QM/MM) dynamics in a solvent are reproduced by classical dynamics. We used previous results on a silver-mediated cytosine strand tetramer as a test case for such parameters (parameters specified in Tables S1 and S2, Supporting Information (SI)). The parameters are a combination of the improved AMBER99sb force field31 with the ParmBSC06 nucleic acid parameters,32 our own parameters for Ag+–base covalent bonds, a Lennard-Jones (LJ)-type of noncovalent model for the pairs involving Ag+ from the literature,33 and the use of linear constraint solver (LINCS) restrictions for the covalent bonds.34 Under these conditions, the classical dynamics simulations show good agreement with the QM/MM calculations, characterized by a similar Ag–Ag average distance and the correct formation of two interplanar H-bonds with significant residence time.

The parameters ParmBSC0632 have been already tested in parallel and antiparallel quadruplexes (see columns G-DNA ps and aps in Table 6 in ref (31)) using global geometrical quantities like the minor groove width and C1′–C1′ interstrand distance. Errors in minor groove and C1′–C1′ interstrand distance with respect to measurements are obtained with 3 and 1% for antiparallel and 3 and 0% for parallel quadruplex, respectively. Our test system, the tetramer, is a parallel assembly of C-strands mediated by silver cations. In the QM/MM simulation the average Ag–Ag distance was 3.5 ± 0.2 Å. A natural test distance to use is then the Ag–Ag distance because no metallic bond and almost no argentophilic interaction is expected at such distances. The Ag–Ag distance is used here as a test of the agreement of the overall solvated structure and its stabilization mechanisms.

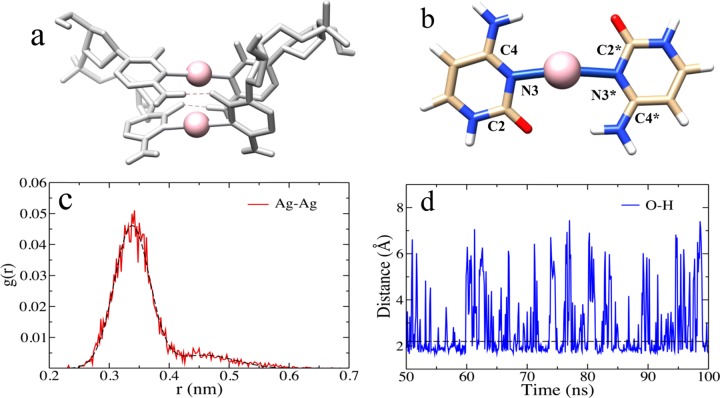
Figure 1a shows a typical snapshot of our test system, the classical Ag+-paired 5′-C2-3′ solvated atomic structure. In the classical simulation, we observe a Ag–Ag distance distribution with one major peak centered at 3.4 Å and one minor “shoulder” peak at longer Ag–Ag distances (Figure 1c). We can conclude that the short quantum trajectory with average Ag–Ag distance of 3.5 Å is reproduced by the first and most probable classical trajectory with Ag–Ag distance centered at 3.4 Å (corresponding to a 3% error). Importantly, the classical simulations exhibit the distinctive interplanar H-bonds found in prior QM simulations30 and crystal-determined metal-mediated helices35,36 contributing to the structure’s overall stability. Figure 1d shows the classical O–H distance dynamics on a 50 ns trajectory, indicating ∼2.2 Å as a reasonable bond cutoff with corresponding classical residence times of 56 and 49% for the two interplanar H-bonds. Using a time correlation function37 (C(t) = ⟨h(t)h(0)⟩/⟨h(t)⟩, where h(t) = 1 when the H-bond is present and 0 otherwise, with cutoff radius and angle of 3.5 Å and 30°, respectively) to estimate the classical H-bond lifetime gave 2.7 ± 0.4 ps, with the correlation function calculated from 10 different simulations each with 1 ns duration. Computational resources presently do not permit QM/MM simulations over long enough times to give a meaningful comparison of the quantum and classical H-bond lifetimes.

Figure 1.

Figure 1

Open in a new tab

Classical molecular dynamics (MD) of a Ag+-paired 5′-C2-3′ parallel duplex in explicit water. (a) Typical snapshot at 100 ns with the two stabilizing O–H bonds or interplanar H-bonds (dashed, red lines) and (b) atomic numbering; Ag atoms are in pink. (c, d) Dynamics characterization; (c) Ag–Ag distance distribution from five trajectories with 100 ns time each and (d) O–H distance as a function of time in the last 50 ns of one trajectory (2.2 Å cutoff bond distance used to calculate residence time is indicated by a dashed black line).

In the following, we apply sets of parameters tested in this section to longer chain structures. We explore and compare the two possible strand orientations.

2.2. Dynamics and Stability

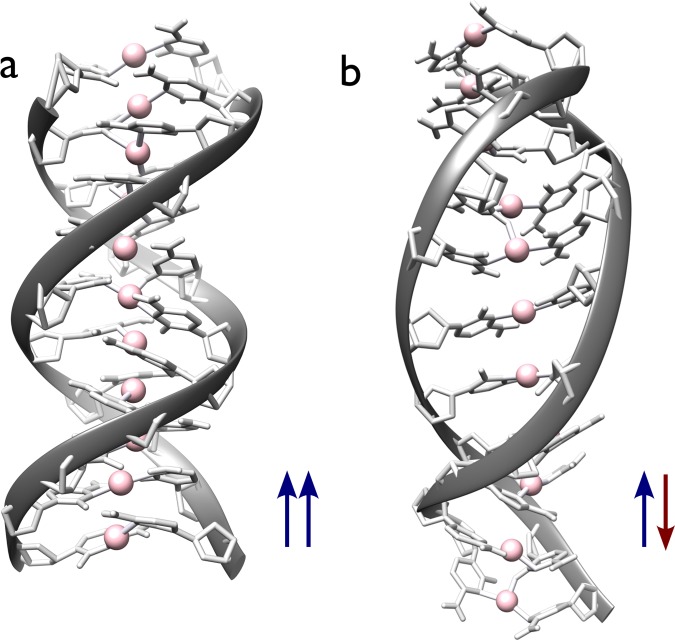
We applied our AMBER force-field parameters to C11–(Ag+)11–C11 (Figure 2) with both parallel and antiparallel strand orientations. Despite having similar parameters in the initial configurations, the duplexes evolved with completely different helicities during the dynamics.

Figure 2.

Figure 2

Open in a new tab

(a) Parallel and (b) antiparallel helices formed during the classical simulations of C11–(Ag+)11–C11. (a) A 100 ns snapshot of the parallel helix. The duplex is very stable and characterized with an average axial rise per base pair of 3.00 Å and angle twist of 41°. (b) Antiparallel helix is not stable and unfolds and reforms continuously during the trajectory, here showing a snapshot at 70 ns. A comparison of time evolution of average twist angle is shown in Figures S6 and S7, SI.

As previously discussed, base stacking, base hydrophobicity, and H-bonding drive natural DNA to emerge as a double helix. In the studied Ag+-mediated cytosine tetramer, π–π nucleobase interactions promote the stacking of bases. In addition, an interbase propeller twist of almost −90° allows the formation of interplanar H-bonds that in turn decrease the nucleobases’ exposed surface area. Because aromatic base stacking and hydrophobicity are key interactions in the formation of both Ag+-mediated cytosine tetramers and B-helices, we used B-form DNA as a template for the initial structures. These were prepared from a B-form double helix built by the 3DNA software program38 and then modified to the correct nucleobase content and to the parallel strand orientation in Figure 3a.

Figure 3.

Figure 3

Open in a new tab

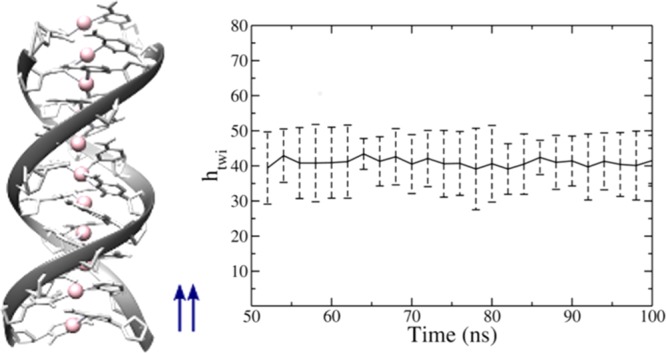
Parallel Ag+-mediated 20 base-long cytosine homobase double helix from a snapshot at 100 ns of the classical simulation. The average twist angle is 39°, higher than the twist angle between stacked C bases in C–G base pairs of B-DNA (34°), corresponding to a smaller number of bases per turn.

Both initial structures have the same Ag–Ag and Ag–N distances and no H-bond between cytosine bases. The simulation parameters are described in detail in “Computational Methods”, but can be summarized here as a 10 ns constant temperature and volume (NVT) equilibration and 100 ns constant temperature and pressure (NPT) production run, where the last 50 ns were used for analysis. The system’s charge was neutralized by Na+. Figure 2a,b shows typical snapshots at the end of the simulations. The initial structures and regularly spaced snapshots can be found in Figures S4 and S5.

In the C11–(Ag+)11–C11 parallel double helix (Figure 2a), using the last 50 ns of simulations, the time-averaged Ag–Ag distances range from 3.08 Å in the center of the helix to 3.35 Å toward the end of the helix, with an overall average of 3.17 ± 0.09 Å. All Ag–Ag distances are included in Table S3, SI. Both interplanar and planar hydrogen bonds are observed throughout the trajectory. The average number of H-bonds between the cytosine bases during the last 50 ns simulation is 6.6, using a cutoff N–O distance of 0.3 nm and O–H–N angle of 20°, including both planar and interplanar H-bonds. In contrast, the antiparallel duplex evolves (Figure 2b) to a remarkably different geometrical configuration with a much longer time-averaged Ag–Ag distance of 4.29 ± 0.16 Å, in agreement with the absence of H-bonds between the strands. Thus, even though the initial configuration is prepared close to antiparallel B-DNA, the dynamics drive the antiparallel Ag+-paired duplex away from such a structure. The Ag+-mediated parallel DNA helix stabilized by both Ag–N covalent bonds and H-bonds is for this reason likely to be more stable than the other parallel DNA structures only stabilized by H-bonds in reverse Watson–Crick or Hoogsteen pairs, or than the antiparallel silver-mediated duplex with no interstrand H-bond. Both the planar and interplanar H-bonds help stabilize the parallel double-helix structure and therefore play a key role in the parallel conformation’s preference.

A crystal structure of silver-paired N1-hexylcytosines (which has no phosphate backbone) has been published recently, which notably displays the presence of interplanar H-bonds stabilizing a parallel double-helix structure.35 The Ag–Ag distances in silver-paired N1-hexylcytosines crystal are slightly shorter than those obtained by simulations in average (3.1 Å in the crystal and 3.2 Å in simulated N = 11 helix). The backbone here may therefore constrain the complex close but away from the nucleobases-only minimum, allowing at the same time to create a more homogeneous double helix.

Our antiparallel double-helix simulations also agree with the more recent antiparallel silver-mediated double-helix crystal, where there is no interplanar H-bond between neighboring C–Ag–C base pairs.36 Such interplanar H-bonds appear in the crystal linking CG and CT nucleobases. In the antiparallel silver-mediated double-helix crystal, the Ag–Ag distances are similar to those obtained in the simulated and slightly longer than the N1-hexylcytosines crystal.

We also studied the parallel C20–(Ag+)20–C20 double helix to examine how the Ag+–DNA parallel double helix evolves as the length of the DNA strands grows. The initial structure was built by 3DNA. A 100 ns snapshot can be seen in Figure 3, whereas typical snapshots during the MD simulation are included in Figure S5. Simulation parameters are described in detail in “Computational Methods”. The time-averaged Ag–Ag distances do not show one unique minimum in the center of the helix but rather several local minima (Table S3, SI). In both CN Ag+-mediated duplexes, minimum values are close to each other. There is, accordingly, several local maxima Ag–Ag distances for the N = 20 duplex that are longer than those in the N = 11 duplex, where the longest Ag–Ag distances are located only at the end of the duplex. The overall time-averaged Ag–Ag distance of the N = 20 duplex is 3.5 ± 0.4 Å. This very large standard deviation is explained by the presence of the several local minima and maxima. The average numbers of H-bonds in Ag+-mediated CN duplexes with N = 2, 11, and 20 are 0.8, 6.6, and 12.3, respectively (about half the number of Ag+-mediated pairs). Because the three cases studied share similar geometrical parameters (Ag–Ag minima distances and relative number of H-bonds), we conclude that the same base stacking and planar and interplanar H-bonding interactions stabilize the studied duplexes despite their large differences in the length. These interactions seem likely to propagate to Ag+-mediated CN duplexes with N > 20, forming helical-type duplexes with similar geometric parameters.

2.3. Helical Characterization

As a final step, we characterize our metal-mediated double helices with the help of the software Curves+.39 We compute values for the N = 11 and 20 strands. We computed first the axial rise per base pair hris and the twist angle htwi, from which the number of base pairs per turn is derived as 360/htwi. For N = 11 and 20, respectively, we calculated the time average of the helical averages, and the result is hris = 3.00 ± 0.06 and 3.3 ± 1.1 Å; htwi = 41 ± 1 and 40 ± 1°. The time evolution is plotted in Figures S6 and S7, SI. The resulting numbers of base pairs per turn are thus 8.7 and 9.2, respectively. Although for both the N = 11 and 20 duplexes the axial rise is smaller than the axial rise of B-DNA (3.4 Å), the twist angle is higher than the twist angle in CC steps of B-DNA (33.7°), corresponding to a smaller number of bases per turn.40

The propeller twist angles for N = 11 and 20 are, respectively, −29 ± 4 and −20 ± 6°. For comparison, CC steps in B-DNA have a propeller twist angle of −8.11°.41 The increased value in the metal-mediated propeller twist is in accordance with the presence of interplanar H-bonding.

Looking at the groove parameters, we can distinguish a difference between the N = 11 and 20 helices. The N = 11 helix is very compact and has a homogeneous set of groove parameters, whereas the N = 20 helix has kinks in the backbone and therefore more variability in the groove parameters. The variation in the groove geometry is correlated to the variation we find in the Ag–Ag distance along the double helix. In contrast to B-DNA, which has distinct “major” and “minor” groove parameters formed by the antiparallel disposition of backbones, here the parallel disposition allows the short helix to have only one type of groove. In the case of a natural DNA double helix, it is well known that the exact parameters are environment- and base-dependent, causing interconversion between A-, B-, and Z-forms. For the Ag+-paired duplex, we can also expect some dependence on the nucleobase sequence and the solution counterions, which we plan to explore in future work.

3. Conclusions

In conclusion, we introduced and characterized parallel double-helix metal-mediated cytosine homobase strands. We used quantum simulations to derive parameters for classical simulations, which showed that strands with lengths of up to at least 20 bases form a double-helical duplex with a central Ag+ spine that is stable for an extensive simulation time (up to 100 ns). Although the duplex completes more than two full helical turns, simulations show no signs of conversion to an i-motif self-folded form. Finally, by comparison to simulations of the antiparallel duplex, which cannot preserve a helical configuration and presents no interstrand H-bonds, we conclude that the H-bonds play a central role in stabilizing the metal-mediated double helix. Because the B-form double helix is the basic building block not only in the genetic code of living organisms but also in DNA nanotechnology, metal-mediated double helices may be promising for binding proteins to alter protein function and for incorporation into self-assembled DNA nanostructures and dynamic DNA nanomachines. Our results lead to opportunities for devising new 3D metal-mediated DNA materials with enhanced resistance to thermal, chemical, and possibly enzymatic degradation due to the additional stability granted by Ag+-mediated base pairs.19

4. Computational Methods

In this work, we used the Gromacs 4.6 package42 and AMBER99sb force field31 with the ParmBSC032 nucleic acid parameters added, for the classical MD simulations. We derived the cation–nucleobase bonding parameters, including bond stretching, bond angle bending, and dihedral angle torsion, using potential energies from density functional theory.43 The energy of each step was calculated with GPAW code.44 The Tkatchenko–Scheffler scheme45 in combination with a gradient-corrected exchange correlation functional (PBE + TS09) was chosen to account van der Waals dispersion interactions. In the implementation, the values for the static polarizability and the van der Waals dispersion coefficient have been taken from Chu and Dalgarno.46 The bonded parameters for Ag+–cytosine obtained from energy curves fitting are listed in Table S1.

Adding Ag+ to cytosine strands rearranges the charge distribution of atoms. Therefore, the partial charges of the atoms need to be recalculated. In this work, the atomic partial charges were optimized with AmberTools12,47 following the two-step restrained electrostatic potential48 charge-fitting procedure recommended for AMBER. The electron density used to calculate the electrostatic potential was calculated by Gaussian 09 with B3LYP function and LANL2DZ basis set.49 Charges were also derived from a C–Ag+–C model system, where deoxyribose molecules are replaced by CH3. The partial charge of Ag+ is 0.38272. The charges of other atoms are given in Table S2. The 12-6 Lennard-Jones (LJ) model was used for van der Waals interactions. The van der Waals radii (Rmin/2) of 1.500 Å and energy parameter (ε) of 0.03899838 kcal/mol were taken for Ag+.33

Unless otherwise specified, all of the molecular dynamics were generated using the same procedure. The simulation was performed in GROMACS with explicit water. Initially, the structure was placed in a cubic box with at least 1.0 nm of water molecules in each direction. The structure was then minimized using a steepest-descent algorithm. After the minimization, 10 ns NVT followed by 10 ns NPT equilibration was performed. We then performed a 100 ns MD run and used the last 50 ns run for analysis. The MD simulations were run at a constant pressure of 1.0 bar and temperature of 300 K, with time constants of 1.0 and 0.1 ps for the pressure and temperature coupling, respectively. The LINCS algorithm was used to constrain bond lengths, allowing a time step of 2 fs in the simulations.

Acknowledgments

The authors are extremely grateful to Prof. Elizabeth Gwinn, Dr. Steven Swasey, and Dr. Stacy Copp for their ideas, comments, and contributions to an earlier version of this manuscript. This work was supported by the Academy of Finland Projects 279240, 284621, and 312556. The authors are also grateful to CSC, the Finnish IT Center for Science Espoo, and the Applied Physics Department of Aalto for computational resources.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b01089.

  • Force-field parameters (PDF)

    Atomic coordinates (xyz coordinates) (PDB)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ao7b01089_si_001.pdf (1.8MB, pdf)
ao7b01089_si_002.pdb (52.3KB, pdb)

References

  1. Bath J.; Turberfield A. J. DNA Nanomachines. Nat. Nanotechnol. 2007, 2, 275–284. 10.1038/nnano.2007.104. [DOI] [PubMed] [Google Scholar]
  2. Zhang D. Y.; Winfree E. Control of DNA Strand Displacement Kinetics Using Toehold Exchange. J. Am. Chem. Soc. 2009, 131, 17303–17314. 10.1021/ja906987s. [DOI] [PubMed] [Google Scholar]
  3. Wei B.; Ong L. L.; Chen J.; Jaffe A. S.; Yin P. Complex Reconfiguration of DNA Nanostructures. Angew. Chem., Int. Ed. 2014, 53, 7475–7479. 10.1002/anie.201402437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Sa-Ardyen P.; Vologodskii A. V.; Seeman N. C. The Flexibility of DNA Double Crossover Molecules. Biophys. J. 2003, 84, 3829–3837. 10.1016/S0006-3495(03)75110-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Rothemund P. W. K. Folding DNA to Create Nanoscale Shapes and Patterns. Nature 2006, 440, 297–302. 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
  6. Douglas S. M.; Dietz H.; Liedl T.; Högberg B.; Graf F.; Shih W. M. Self-Assembly of DNA into Nanoscale Three-Dimensional Shapes. Nature 2009, 459, 414–418. 10.1038/nature08016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Rangnekar A.; LaBean T. H. Building DNA Nanostructures for Molecular Computation, Templated Assembly, and Biological Applications. Acc. Chem. Res. 2014, 47, 1778–1788. 10.1021/ar500023b. [DOI] [PubMed] [Google Scholar]
  8. Funke J. J.; Dietz H. Placing Molecules with Bohr Radius Resolution Using DNA Origami. Nat. Nanotechnol. 2016, 11, 47–52. 10.1038/nnano.2015.240. [DOI] [PubMed] [Google Scholar]
  9. Germann M. W.; Kalisch B. W.; van de Sande J. H. Relative Stability of Parallel- and Anti-Parallel-Stranded Duplex DNA. Biochemistry 1988, 27, 8302–8306. 10.1021/bi00422a002. [DOI] [PubMed] [Google Scholar]
  10. Rippe K.; Jovin T. M. [11] Parallel-Stranded Duplex DNA. Methods Enzymol. 1992, 211, 199–220. 10.1016/0076-6879(92)11013-9. [DOI] [PubMed] [Google Scholar]
  11. Gehring K.; Leroy J.-L.; Guéron M. A Tetrameric DNA Structure with Protonated Cytosine-Cytosine Base Pairs. Nature 1993, 363, 561–565. 10.1038/363561a0. [DOI] [PubMed] [Google Scholar]
  12. Mergny J.; Lacroix L.; Han X.; Leroy J.; Helene C. Intramolecular Folding of Pyrimidine Oligodeoxynucleotides into an I-DNA Motif. J. Am. Chem. Soc. 1995, 117, 8887–8898. 10.1021/ja00140a001. [DOI] [Google Scholar]
  13. Hazel P.; Huppert J.; Balasubramanian S.; Neidle S. Loop-Length-Dependent Folding of G-Quadruplexes. J. Am. Chem. Soc. 2004, 126, 16405–16415. 10.1021/ja045154j. [DOI] [PubMed] [Google Scholar]
  14. Li J.; Correia J. J.; Wang L.; Trent J. O.; Chaires J. B. Not so Crystal Clear: The Structure of the Human Telomere G-Quadruplex in Solution Differs from That Present in a Crystal. Nucleic Acids Res. 2005, 33, 4649–4659. 10.1093/nar/gki782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yang H.; Metera K. L.; Sleiman H. F. DNA Modified with Metal Complexes: Applications in the Construction of Higher Order metal–DNA Nanostructures. Coord. Chem. Rev. 2010, 254, 2403–2415. 10.1016/j.ccr.2010.02.026. [DOI] [Google Scholar]
  16. Park K. S.; Park H. G. Technological Applications Arising from the Interactions of DNA Bases with Metal Ions. Curr. Opin. Biotechnol. 2014, 28, 17–24. 10.1016/j.copbio.2013.10.013. [DOI] [PubMed] [Google Scholar]
  17. Scharf P.; Müller J. Nucleic Acids With Metal-Mediated Base Pairs and Their Applications. ChemPlusChem 2013, 78, 20–34. 10.1002/cplu.201200256. [DOI] [Google Scholar]
  18. Clever G. H.; Shionoya M. Metal–base Pairing in DNA. Coord. Chem. Rev. 2010, 254, 2391–2402. 10.1016/j.ccr.2010.04.014. [DOI] [Google Scholar]
  19. Swasey S. M.; Gwinn E. G. Silver-Mediated Base Pairings: Towards Dynamic DNA Nanostructures with Enhanced Chemical and Thermal Stability. New J. Phys. 2016, 18, 045008 10.1088/1367-2630/18/4/045008. [DOI] [Google Scholar]
  20. Sinha I.; Fonseca Guerra C.; Müller J. A Highly Stabilizing Silver(I)-Mediated Base Pair in Parallel-Stranded DNA. Angew. Chem., Int. Ed. 2015, 54, 3603–3606. 10.1002/anie.201411931. [DOI] [PubMed] [Google Scholar]
  21. Johannsen S.; Megger N.; Böhme D.; Sigel R. K. O.; Müller J. Solution Structure of a DNA Double Helix with Consecutive Metal-Mediated Base Pairs. Nat. Chem. 2010, 2, 229–234. 10.1038/nchem.512. [DOI] [PubMed] [Google Scholar]
  22. Mandal S.; Hepp A.; Müller J. Unprecedented Dinuclear Silver(i)-Mediated Base Pair Involving the DNA Lesion 1,N6-Ethenoadenine. Dalton Trans. 2015, 44, 3540–3543. 10.1039/C4DT02663B. [DOI] [PubMed] [Google Scholar]
  23. Polonius F.-A.; Müller J. An Artificial Base Pair, Mediated by Hydrogen Bonding and Metal-Ion Binding. Angew. Chem., Int. Ed. 2007, 46, 5602–5604. 10.1002/anie.200700315. [DOI] [PubMed] [Google Scholar]
  24. Ono A.; Cao S.; Togashi H.; Tashiro M.; Fujimoto T.; Machinami T.; Oda S.; Miyake Y.; Okamoto I.; Tanaka Y. Specific Interactions between Silver(i) Ions and Cytosine–cytosine Pairs in DNA Duplexes. Chem. Commun. 2008, 4825. 10.1039/b808686a. [DOI] [PubMed] [Google Scholar]
  25. Swasey S. M.; Leal L. E.; Lopez-Acevedo O.; Pavlovich J.; Gwinn E. G. Silver(I) as DNA Glue: Ag+-Mediated Guanine Pairing Revealed by Removing Watson-Crick Constraints. Sci. Rep. 2015, 5, 10163 10.1038/srep10163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Berdakin M.; Taccone M. I.; Pino G. A.; Sánchez C. G. DNA-Protected Silver Emitters: Charge Dependent Switching of Fluorescence. Phys. Chem. Chem. Phys. 2017, 19, 5721–5726. 10.1039/C6CP08345E. [DOI] [PubMed] [Google Scholar]
  27. Megger D. A.; Müller J. Silver(I)-Mediated Cytosine Self-Pairing Is Preferred over Hoogsteen-Type Base Pairs with the Artificial Nucleobase 1,3-Dideaza-6-Nitropurine. Nucleosides, Nucleotides Nucleic Acids 2010, 29, 27–38. 10.1080/15257770903451579. [DOI] [PubMed] [Google Scholar]
  28. Ramazanov R. R.; Sych T. S.; Reveguk Z. V.; Maksimov D. A.; Vdovichev A. A.; Kononov A. I. Ag–DNA Emitter: Metal Nanorod or Supramolecular Complex?. J. Phys. Chem. Lett. 2016, 7, 3560–3566. 10.1021/acs.jpclett.6b01672. [DOI] [PubMed] [Google Scholar]
  29. Douglas S. M.; Marblestone A. H.; Teerapittayanon S.; Vazquez A.; Church G. M.; Shih W. M. Rapid Prototyping of 3D DNA-Origami Shapes with caDNAno. Nucleic Acids Res. 2009, 37, 5001–5006. 10.1093/nar/gkp436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Espinosa Leal L. A.; Karpenko A.; Swasey S.; Gwinn E. G.; Rojas-Cervellera V.; Rovira C.; Lopez-Acevedo O. The Role of Hydrogen Bonds in the Stabilization of Silver-Mediated Cytosine Tetramers. J. Phys. Chem. Lett. 2015, 6, 4061–4066. 10.1021/acs.jpclett.5b01864. [DOI] [PubMed] [Google Scholar]
  31. Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. 10.1021/ja00124a002. [DOI] [Google Scholar]
  32. Pérez A.; Marchán I.; Svozil D.; Sponer J.; Cheatham T. E.; Laughton C. A.; Orozco M. Refinement of the AMBER Force Field for Nucleic Acids: Improving the Description of A/γ Conformers. Biophys. J. 2007, 92, 3817–3829. 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Li P.; Song L. F.; Merz K. M. Systematic Parameterization of Monovalent Ions Employing the Nonbonded Model. J. Chem. Theory Comput. 2015, 11, 1645–1657. 10.1021/ct500918t. [DOI] [PubMed] [Google Scholar]
  34. Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
  35. Terrón A.; Moreno-Vachiano B.; Bauzá A.; García-Raso A.; Fiol J. J.; Barceló-Oliver M.; Molins E.; Frontera A. X-Ray Crystal Structure of a Metalled Double-Helix Generated by Infinite and Consecutive C*-Ag I-C* (C*:N1-Hexylcytosine) Base Pairs through Argentophilic and Hydrogen Bond Interactions. Chem. – Eur. J. 2017, 23, 2103–2108. 10.1002/chem.201604331. [DOI] [PubMed] [Google Scholar]
  36. Kondo J.; Tada Y.; Dairaku T.; Hattori Y.; Saneyoshi H.; Ono A.; Tanaka Y. A Metallo-DNA Nanowire with Uninterrupted One-Dimensional Silver Array. Nat. Chem. 2017, 9, 956–960. 10.1038/nchem.2808. [DOI] [PubMed] [Google Scholar]
  37. Luzar A.; Chandler D. Hydrogen-Bond Kinetics in Liquid Water. Nature 1996, 379, 55–57. 10.1038/379055a0. [DOI] [Google Scholar]
  38. Lu X.-J.; Olson W. K. 3DNA: A Software Package for the Analysis, Rebuilding and Visualization of Three-Dimensional Nucleic Acid Structures. Nucleic Acids Res. 2003, 31, 5108–5121. 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Lavery R.; Moakher M.; Maddocks J. H.; Petkeviciute D.; Zakrzewska K. Conformational Analysis of Nucleic Acids Revisited: Curves+. Nucleic Acids Res. 2009, 37, 5917–5929. 10.1093/nar/gkp608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Kabsch W.; Sander C.; Trifonov E. N. The Ten Helical Twist Angles of B-DNA. Nucleic Acids Res. 1982, 10, 1097–1104. 10.1093/nar/10.3.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Ussery D. W.DNA Structure: A-, B- and Z-DNA Helix Families. Encyclopedia of Life Sciences; John Wiley & Sons, Ltd: Chichester, U.K., 2002. [Google Scholar]
  42. Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  43. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  44. Enkovaara J.; Rostgaard C.; Mortensen J. J.; Chen J.; Dułak M.; Ferrighi L.; Gavnholt J.; Glinsvad C.; Haikola V.; Hansen H. A.; et al. Electronic Structure Calculations with GPAW: A Real-Space Implementation of the Projector Augmented-Wave Method. J. Phys. Condens. Matter 2010, 22, 253202 10.1088/0953-8984/22/25/253202. [DOI] [PubMed] [Google Scholar]
  45. Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
  46. Chu X.; Dalgarno A. Linear Response Time-Dependent Density Functional Theory for van Der Waals Coefficients. J. Chem. Phys. 2004, 121, 4083–4088. 10.1063/1.1779576. [DOI] [PubMed] [Google Scholar]
  47. Case D. A.; Cheatham T. E.; Darden T.; Gohlke H.; Luo R.; Merz K. M.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber Biomolecular Simulation Programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
  49. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09; Gaussian Inc.: Wallingford, CT, 2009. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao7b01089_si_001.pdf (1.8MB, pdf)
ao7b01089_si_002.pdb (52.3KB, pdb)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES