Standard Gibbs Energy of Metabolic Reactions: III The 3-Phosphoglycerate Kinase Reaction

Abstract

The glycolytic pathway is one of the most studied metabolic pathways to date. This work focuses on determining the standard Gibbs energy of reaction (Δ^Rg⁰) of the first adenosine triphosphate-yielding reaction step of glycolysis, namely, the 3-phosphoglycerate kinase (PGK) reaction. Trustworthy values of Δ^Rg⁰ are required for thermodynamic approaches to determine single reaction conversions or even fluxes of metabolic reactions. In literature, the observed Δ^Rg^0,obs values are usually determined directly from the experimental equilibrium composition data without accounting for the nonideality of the reaction mixture. That is the reason why the observed Δ^Rg^0,obs values do not present consistent standard data as they are a function of the concentration, pH, and pMg. In this work, a combination of experimentally determined equilibrium composition data and activity coefficients of the reacting agents was used to determine Δ^Rg⁰ values for the temperatures 303, 313, and 323 K at pH 7. The activity coefficients were predicted with the thermodynamic model electrolyte perturbed-chain statistical associating fluid theory (ePC-SAFT). The ePC-SAFT parameters were taken from literature or fitted to new experimental osmotic coefficients. At 313.15 K, a value for Δ^Rg⁰ of −16.2 ± 0.2 kJ/mol was obtained. This value is about 4 kJ/mol less negative than what is usually considered as an accepted standard value. The reason behind this discrepancy was found to be the activity coefficients of the reacting agents, which dramatically influence the equilibrium position of the PGK reaction. On the basis of the temperature-dependent Δ^Rg⁰ values, the standard enthalpy of reaction was determined and found to be Δ^Rh⁰ = −49 ± 9 kJ/mol.

Introduction

The glycolytic pathway represents the primary metabolic pathway for the oxidation of monosaccharides (e.g., glucose) to pyruvate in mostly all organisms, yielding adenosine triphosphate (ATP) in the process. The glycolytic pathway presents the best trade-off between the metabolic rate, ATP generation, and resource requirements for monosaccharide oxidation.^1,2 The interest of understanding the glycolytic pathway is also represented in the vast amount of literature available, covering the enzymes, substrates, cofactors, and regulation mechanics involved.³⁻⁸ Of further interest are accurate values for the standard Gibbs free energy of reaction Δ^Rg⁰ and the standard enthalpy of reaction Δ^Rh⁰. With the knowledge of Δ^Rg⁰, the driving force of the reaction can be calculated for any initial composition of the reaction mixture. Δ^Rh⁰ can be used to calculate Δ^Rg⁰ at different temperatures knowing only one reference value. Data for enzyme-catalyzed reactions covering Δ^Rg⁰ and Δ^Rh⁰ are reported in the literature under the assumption of an ideal mixture, that is, neglecting the activity coefficients of the reacting agents (γ_i = 1), which is regarded as a nonreasonable assumption for flux analysis from a thermodynamic standpoint.⁹⁻¹¹ At first glance, this seems reasonable for an aqueous buffered solution of a low concentration of reacting agents. However, previous publications showed that activity coefficients are important even at very low concentrations. Meurer et al.¹² determined an activity-based value for Δ^Rg⁰ of the hexokinase reaction and Hoffmann et al.¹³ determined Δ^Rg⁰ of the glucose-6-phosphate isomerization reaction. In both publications, a concentration-independent equilibrium constant K_a was obtained by explicitly taking into account the activity coefficients of the reacting agents.

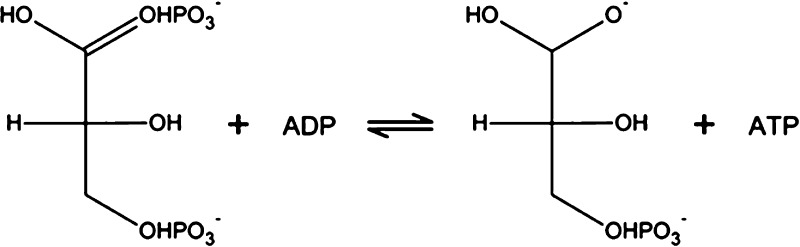
This work is focused on the first ATP-yielding reaction, namely, the 3-phosphoglycerate kinase (PGK) reaction. The reaction mechanism is shown in Scheme 1.

Scheme 1. Reaction Mechanism of the PGK Reaction.

The substrates are 1,3-BPG and ADP, which are converted to 3-PG and ATP by the enzyme PGK.

Regarding literature data on the Gibbs free energy of the PGK reaction, Bücher¹⁴ as well as Krietsch and Bücher¹⁵ provided a value of Δ^Rg^0,obs = −20 kJ/mol for a temperature of 298.15 K at pH 7; this value was calculated from the measured equilibrium composition. Cornell et al.¹⁶ reported vastly different experimental data for a temperature of 313.15 K at pH 7, leading to standard Gibbs free energy values between −17 and −22 kJ/mol. This wide range of Δ^Rg⁰ values provided by Cornell et al. can be explained by the different initial reaction conditions, for example, substrate and cofactor concentrations. Further, a value of Δ^Rg^0,obs = −18.8 kJ/mol for 313.15 K calculated by group contribution methods is reported in the literature.^9,17,18 An overview of the available data is given in Table 1.

Table 1. Overview over the Available Literature Data of the Observed (Apparent) Gibbs Free Energy of Reaction Δ^Rg^0,obs at the Respective Temperature and pH.

T [K]	pH [−]	ΔRg0,obs [kJ/mol]	source
298.15	7	–20	(14,15)
313.15	7	–19.3 ± 3.4	(16)
313.15	7	–18.8	(9,17,18)

From all the available data, it becomes obvious that different initial concentrations of substrates, temperatures, magnesium (cofactor), and buffer concentrations cause different Δ^Rg^0,obs values. Because a reliable standard value for Δ^Rg⁰ poses the first step into further investigations of the different cosolvent influences on the reaction in cellulo, an activity-based thermodynamic equilibrium constant K_a was determined in this work by combining reaction equilibrium measurements with activity coefficient values obtained with the thermodynamic equation of state electrolyte perturbed-chain statistical associating fluid theory (ePC-SAFT).

Theoretical Background

The driving force of every (bio)reaction is the Gibbs free energy of reaction Δ^Rg. It is defined as shown in eq 1

1

In eq 1, ν_i and μ_i denote the stoichiometric coefficient and the chemical potential of the reacting agent i at the respective temperature and pressure, respectively. The chemical potential of a liquid component can be described by eq 2 with the chemical potential of the pure component μ_0i, the universal gas constant R, the mole fraction x_i of component i, and the activity coefficient γ_i of component i.

2

Equations 3–5 relate the Gibbs free energy of reaction Δ^Rg to the standard Gibbs free energy of reaction Δ^Rg⁰ and the thermodynamic equilibrium constant K_a.

3

4

5

Equation 5 is the fundamental basis for the calculation of biochemical pathways and points to the importance of reliable values for Δ^Rg⁰. Instead of the classical chemical expression that takes into account each individual species, eq 5 can also be expressed biochemically by eq 6. The apostrophe in K_a^′ denotes the use of the species-averaged thermodynamic activities in contrast to the chemical definition of K_a, which is formulated in terms of true reacting species that are present in the reaction mixture at the specified reaction conditions. For the reaction considered, it shall be noted that the main reacting agents are 3-PG^2– and ATPMg₂^2– for the reaction conditions in this work. Nevertheless, K_a is then defined based on the sum of species activities; this definition assumes that all activity coefficients of all species of one component are equal. Equation 7 shows the expression for the biochemical K_a^′ for the PGK reaction

6

7

Equation 7 explicitly accounts for activity coefficients to provide an activity-based value for K_a^′ with the reference state one molal hypothetical ideal solution. Additionally to the mole fractions of the components, other concentration scales such as molality and molarity can be used.¹⁹ The connection between those is given in eq 8.

8

Activity coefficients related to molarity (γ_i,c) or to molality (γ_i,m) can be converted using textbook thermodynamics.

The standard enthalpy of reaction Δ^Rh^′0 can be calculated using the temperature-dependent K_a^′ values by the van’t Hoff eq 9.

9

Assuming a temperature-independent Δ^Rh^′0, integration of eq 9 leads to eq 10, from which a graphical determination of Δ^Rh^′0 is possible.²⁰

10

To calculate the activity coefficients required for eq 7, the ePC-SAFT equation of state was used in this work. ePC-SAFT was developed and proposed by Gross and Sadowski²¹ and extended by Cameretti et al.,²² leading to an expression for the residual Helmholtz energy a^res, as shown in eq 11

11

In eq 11, the hard-chain reference system is represented by a^hc. The perturbations to the hard-chain reference system accounted for ePC-SAFT are the molecular dispersive interactions, characterized by the van der Waals energy represented in a^disp and by the associative hydrogen-bonding forces a^assoc. In the case of an electrolyte system, which is considered in this work, the Coulomb interactions are expressed by a^ion which is based on a Debye–Hückel expression. The residual Helmholtz energy a^res is used to calculate the residual chemical potential μ_i^res and the fugacity coefficient φ_i of each component i in the solution. On the basis of the fugacity coefficients, the activity coefficients γ_i were expressed in this work as

12

where the superscript ∞ denotes the infinite dilution reference state. That is, eq 12 relates to infinite dilution at the same temperature T and pressure p as the actual solution of the composition x⃗. Thus, K_a^′ refers to the one molal hypothetically ideal reference state, which assumes that all activity coefficients are equal to one.

Results and Discussion

Osmotic Coefficients of the System Water + 3-PG Disodium Salt

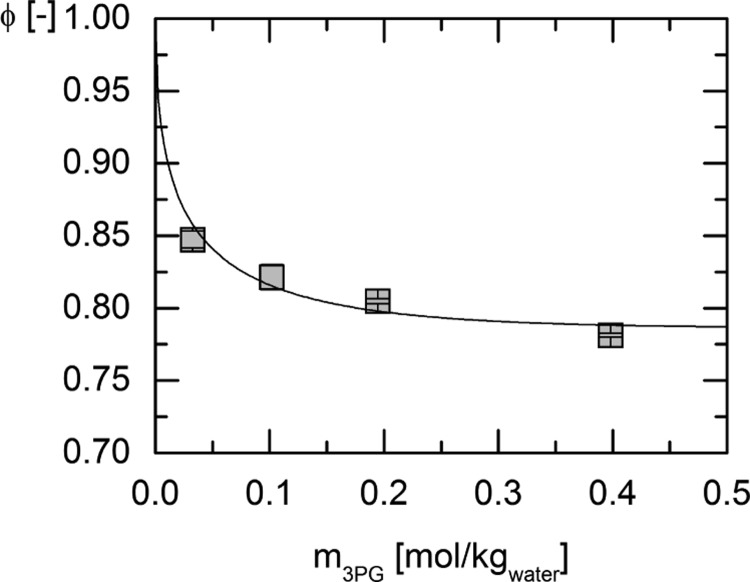
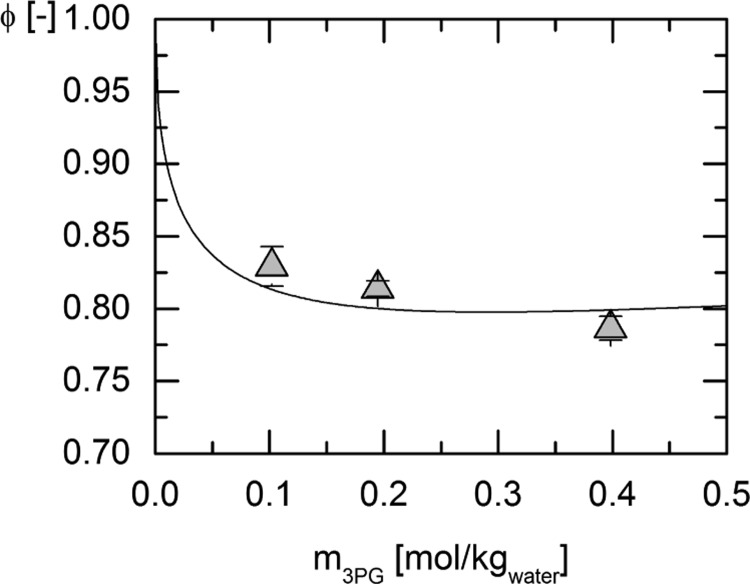
Experimental osmotic coefficient data of the system water + 3-phosphoglycerate (3-PG) disodium salt were used for fitting the ePC-SAFT parameters for 3-PG^2– and the binary interaction parameter between water and 3-PG^2–. The results of the measurements of the osmotic coefficients at 273.15 and 303.15 K and the respective modeling curves resulting from the parameter fit are shown in Figures 1 and 2, respectively. For the modeling of the osmotic coefficients with ePC-SAFT, the presence of Na⁺ has explicitly been accounted for. The experimental results are listed in Table 2.

Figure 1.

Osmotic coefficients of the system water + 3-PG disodium salt measured at 273.15 K for different initial molalities of 3-PG disodium salt (squares) and the modeling with ePC-SAFT (line) using the pure component and binary interaction parameters provided in Tables 6 and 7.

Figure 2.

Osmotic coefficients of the system water + 3-PG disodium salt measured at 303.15 K for different initial molalities of 3-PG disodium salt (triangles) and the modeling with ePC-SAFT (line) using the pure component and binary interaction parameters provided in Tables 6 and 7.

Table 2. Measured Osmotic Coefficients of the System Water + 3-PG Disodium Salt for the Temperatures 273.15 and 303.15 K.

273.15 K		303.15 K
m3-PG disodium salt [mol/kgwater]	ϕ [−]	m3-PG disodium salt [mol/kgwater]	ϕ [−]
0.033	0.847 ± 0.006	0.102	0.829 ± 0.014
0.102	0.821 ± 0.009	0.195	0.814 ± 0.005
0.195	0.805 ± 0.002	0.398	0.786 ± 0.008
0.398	0.781 ± 0.001

Equilibrium Constant of the PGK Reaction at 313.15 K

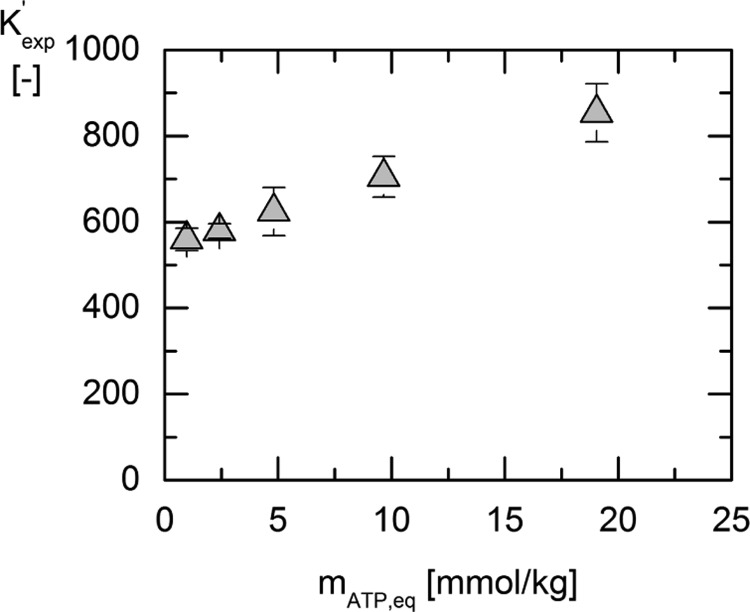
Reaction equilibrium measurements were performed for five different initial ATP concentrations between 1 and 20 mmol/kg_water. The results for the determined equilibrium composition ratio K_exp^′ are shown in Figure 3. The initial concentration of 3-PG for all experiments was prepared in equimolal ratio.

Figure 3.

Equilibrium composition ratio K_exp^′ vs the molality of ATP at equilibrium m_ATP,eq for different initial substrate concentrations at 313.15 K (triangles).

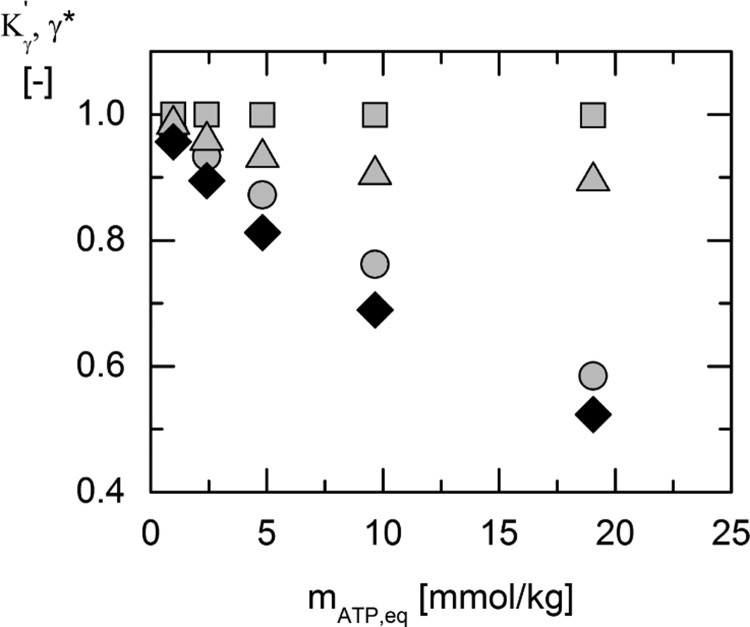
As can be seen in Figure 3, K_exp^′ strongly depends on the concentration, that is, K_exp is not constant as usually assumed in biochemistry. The equilibrium constant K_a^′ equals K_exp only for conditions for which all activity coefficients are one. This state exists theoretically if the concentrations of all reacting agents approach zero. On the basis of extrapolation of K_exp^′ to zero concentration, K_a will be about 520. For all other concentrations, activity coefficients have to be accounted for. In this work, activity coefficients were estimated using the ePC-SAFT equation of state with the parameters listed in Tables 6 and 7. The results of the predicted values of γ_i^* of each reacting agents are shown in Figure 4. It is noteworthy that in this work, nine components of the reaction mixture were taken into account [water, 3-PG^2–, ATP, adenosine diphosphate (ADP), Na⁺, Mg²⁺, Cl^–, NH₄⁺, and SO₄^2–]. 3-PG^2–, ATP, and ADP were considered as (averaged-species) reacting agents, whereas NH₄⁺ and SO₄^2– were part of the enzyme suspension and were regarded as impurities; these were also taken into account for the prediction of K_a. The enzyme was neglected for modeling because its exact concentration was estimated to be between 0.3 and 0.03 mmol/kg. The exact concentration of the enzyme in the suspension provided by Sigma-Aldrich was unknown/not provided.

Table 6. ePC-SAFT Pure Component Parameters Used in This Work^a.

	miseg [−]	σi [Å]	ui [K]	Niassoc	εAiBi [K]	κAiBi [−]	q [−]
water27	1.204	b	353.95	1:1	2425.7	0.0451	0
3-PG2–c	3.110	4.66	322.02	5:5	501.2	0.0001	–2
ATP12	50.16	2.14	165.92	7:7	862.4	0.0001	0
ADP12	18.83	2.33	169.54	6:6	1285.5	0.0001	0
Na+,28	1	2.82	230.00				+1
Mg2+,28	1	3.13	150.00				+2
NH4+,28	1	3.57	230.00				+1
SO42–,28	1	265	80.00				–2
Cl–,28	1	2.75	170.00				–1

^aParameters were taken from the literature or determined in this work.

^bσ_i = 2.7927 + 10.11·exp(−0.01775·T[K]) – 1.417·exp(−0.01146·T[K]).

^cThis work.

Table 7. ePC-SAFT Binary Interaction Parameters Used in This Work^a.

mixture	kij [−]
water–3-PG2–b	c
water–ATP12	–0.1719
water–ADP12	–0.1368
water–Na+,28	d
water–Mg2+,28	–0.2500
water–Cl–,28	–0.2500
water–NH4+,28	0.0640
water–SO42–,28	0.2500
Na+–Cl–,28	0.317
Na+–SO42–,28	–1.000
Mg2+–Cl–,28	0.817
Mg2+–SO42–,28	–1.000
NH4+–Cl–,28	–0.566
NH4+–SO42–,28	–1.000

^aParameters were taken from the literature or determined in this work, only valid with parameters from Table 6.

^bThis work.

^ck_ij(T) = −0.100167 + 0.0020333·(T − 298.15 K).

^dk_ij(T) = 0.00045485 – 0.007981·(T[K] – 298.15).

Figure 4.

ePC-SAFT predicted activity coefficients of ATP (circles), ADP (squares), 3-PG^2– (triangles), and the resulting value of K_γ^′ (black squares) vs the ATP molality m_ATP,eq at 313.15 K, resulting from the different initial substrate concentrations as listed in Table 5. Predictions in the multicomponent reaction mixtures were performed using the parameters from Tables 6 and 7.

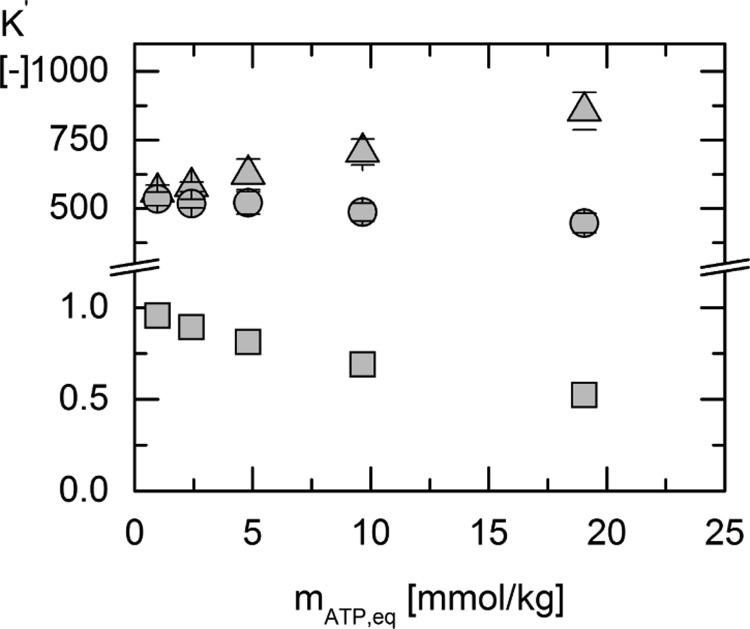
In Figure 4, the activity coefficient of 1,3-bisphosphoglycerate (1,3-BPG) is not shown. Because the concentration of ADP and 1,3-BPG at equilibrium was at least 25 times lower than the concentration of ATP and 3-PG, respectively, the activity coefficients of ADP and 1,3-BPG were assumed to be one. Figure 4 shows that γ* of 3-PG^2– and ATP is decreasing with increasing ATP concentrations, leading to a decrease in K_γ^′. Access to K_exp and K_γ^′ allows determining the activity-based equilibrium constant K_a. The results are shown in Figure 5 and Table 3.

Figure 5.

Calculated activity-based equilibrium constant K_a^′ (circles) from the equilibrium composition ratio K_exp (triangles) and the ePC-SAFT predicted activity coefficient ratio K_γ^′ (squares) using the parameters from Tables 6 and 7.

Table 3. Overview of the Measured ATP/ADP Ratio, the Measured Equilibrium Composition Ratios K_exp^′, Predicted Activity Coefficient Ratios K_γ, and the Resulting Equilibrium Constant K_a^′ for Different Initial Substrate Concentrations^a.

mATP,0 [mmol/kgwater]	m3-PG,0 [mmol/kgwater]	ATP/ADP ratio [−]	Kexp′ [−]	Kγ′ [−]	Ka′ [−]
1.02 ± 0.01	1.03 ± 0.01	23.52 ± 0.54	559.4 ± 25.9	0.9568	535.2 ± 24.8
2.51 ± 0.01	2.52 ± 0.01	24.02 ± 0.31	578.8 ± 17.3	0.8947	517.8 ± 15.5
5.00 ± 0.01	5.01 ± 0.02	25.24 ± 0.98	640.2 ± 51.0	0.8124	520.1 ± 41.4
10.03 ± 0.03	10.02 ± 0.03	26.55 ± 0.92	705.0 ± 47.3	0.6898	486.3 ± 32.7
19.62 ± 0.01	19.70 ± 0.03	29.27 ± 1.13	854.0 ± 67.6	0.5238	447.3 ± 35.4

^aMgCl₂ was added in a twofold molar excess to the ATP concentration for all samples. All measurements were performed at pH 7 and at a temperature of 313 K.

Comparing the values of K_exp^′ and K_a in Figure 5 and Table 3, the importance of taking activity coefficients of the reacting agents into account becomes clear. Although K_exp^′ and K_γ are strongly concentration-dependent, K_a^′ is a constant value within the error bars. The manifestation of a trustworthy activity-based equilibrium constant of the reaction in pure water is necessary because it allows for prediction concentrations and cosolvent influences, which are needed to understand the complexity of cellulo systems. On the basis of K_a, a value for Δ^Rg^0′ at 313.15 K was determined to be Δ^Rg^0′ = −16.18 ± 0.19 kJ/mol.

A comparison to the data of Cornell et al.¹⁶ at 311.15 K further highlights the importance of the thermodynamic activity. The experimental data presented in the work from Cornell et al.¹⁶ lead to a value of Δ^Rg^0′ = −19.34 ± 3.38 kJ/mol. This value is not a standard value but an apparent value, which explains the scatter in the data and the discrepancy to the value obtained in the present work. Unfortunately, the temperatures in this work and in the work of Cornell et al. are slightly different. Thus, quantitative comparisons require activity-based equilibrium constants at the same temperature. For this, the standard enthalpy of reaction Δ^Rh^0′ is required.

Standard Enthalpy of Reaction

The standard enthalpy of reaction was determined in this work by a linear regression of the van’t Hoff plot resulting from eq 10, assuming that Δ^Rh^0′ is temperature-independent. For this purpose, K_a^′ values were determined at three temperatures: 303, 313, and 323 K. For the temperatures of 303 and 323 K, a measurement of one equilibrium composition was performed for an initial substrate molality of 10 mmol/kg_water of ATP and 3-PG. The results of the measurements are listed in Table 4. The results are also illustrated in Figure 6.

Table 4. Overview of the Measured ATP/ADP Ratio, the Measured Equilibrium Composition Ratios K_exp^′, Predicted Activity Coefficient Ratios K_γ, and the Resulting Equilibrium Constant K_a^′ for Different Reaction Temperatures^a.

T [K]	mATP,0 [mmol/kgwater]	m3-PG,0 [mmol/kgwater]	ATP/ADP ratio [−]	Kexp′ [−]	Kγ′ [−]	Ka′ [−]
303	10.02 ± 0.01	10.06 ± 0.02	237.30 ± 3.04	1391.80 ± 226.22	0.6794	945.59 ± 153.70
313	10.03 ± 0.03	10.02 ± 0.03	26.55 ± 0.92	705.0 ± 47.3	0.6898	486.3 ± 32.7
323	10.08 ± 0.01	10.08 ± 0.03	20.07 ± 0.70	403.10 ± 27.20	0.6955	280.36 ± 18.92

^aMgCl₂ was added in a twofold molar excess to the ATP concentration for all samples. All measurements were performed at pH 7.

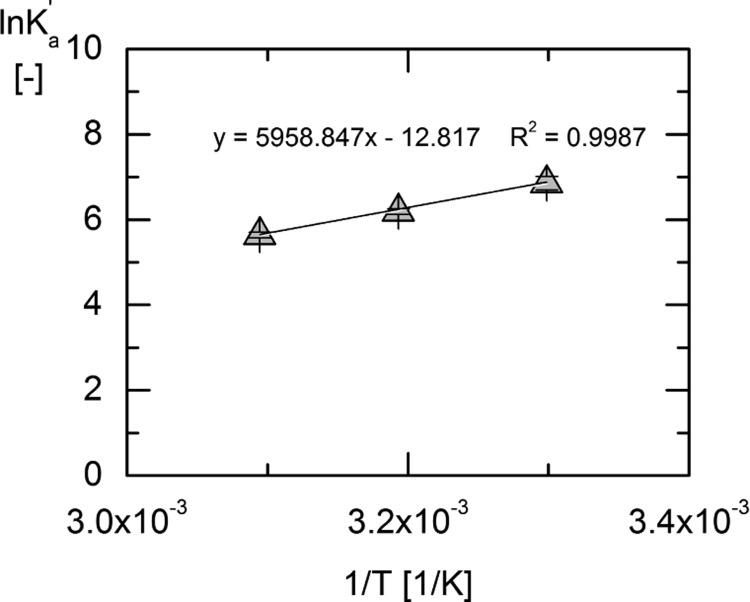
Figure 6.

Linear regression of van’t Hoff eq 10 of ln (K_a^′) over 1/T for the temperatures 303, 313, and 323 K to determine the standard enthalpy of reaction.

As can be seen from the linear regression in Figure 6, the assumption of a temperature-independent value of Δ^Rh^0′ is reasonable between 303 and 323 K for the PGK reaction. From the slope of the regression (equals −Δ^Rh^0′/R), the standard enthalpy of reaction was determined to be Δ^Rh^0′ = −49.19 ± 9.4 kJ/mol. The relatively high uncertainty arises from taking into account the uncertainties in the K_a^′ values using a Taylor series for error estimation.

Because no literature data for Δ^Rh^0′ of the PGK reaction are available, a validation of the determined value is not possible. Nevertheless, comparing this value to Δ^Rh^0′ data of other glycolytic reactions, namely, the hexokinase reaction⁹ (Δ^Rh^0′ = −67.7 kJ/mol), the phosphofructokinase reaction⁹ (Δ^Rh^0′ = −50.3 kJ/mol), or the aldolase reaction⁹ (Δ^Rh^0′ = −60.2 kJ/mol), indicates that the order of magnitude of standard reaction enthalpies of glycolytic reactions driven by ATP is all highly negative.

Conclusions

The reaction equilibrium of the 3-PGK reaction was investigated for three temperatures 303, 313, and 323 K at pH 7. Reaction equilibrium was measured by varying the equimolal initial substrate concentrations of ATP and 3-PG disodium salts. The equilibrium composition ratio K_exp^′ was determined using an enzyme assay that measures the ADP/ATP ratio based on the luciferase reaction. The results obtained for K_exp showed a very strong dependence on the initial substrate concentration. The reason for that was found to be the activity coefficients of the reacting agents, which strongly deviated from one even at low concentration. Activity coefficients were predicted with ePC-SAFT. The ePC-SAFT parameters were taken from the literature for all components except for 3-PG, which were fitted in this work to osmotic coefficient data. Overall nine species were explicitly taken into account for the prediction of the activity coefficients of the reacting agents. Combining these values with K_exp^′ allowed proposing an activity-based equilibrium constants K_a(T = 303.15 K) = 945 ± 153, K_a^′(T = 313.15 K) = 501 ± 35, and K_a(T = 323.15 K) = 280 ± 19. These values were used to calculate the respective standard Gibbs free energy of reaction and the enthalpy of reaction for the temperature range considered. The results were Δ^Rg^0′(T = 303.15 K) = −17.3 ± 0.4 kJ/mol, Δ^Rg^0′(T = 313.15 K) = −16.2 ± 0.2 kJ/mol, Δ^Rg^0′(T = 323.15 K) = −15.2 ± 0.2 kJ/mol, and Δ^Rh^0′ = −49.19 ± 9.4 kJ/mol. These results differ significantly from the literature values. The main reason is that literature data does not account for the activities of the reacting agents, while measuring a broad range of different initial substrate concentrations and ratios. The values determined in this work should be considered as thermodynamically exact and are recommended in all future works that are based on the Gibbs free energy determination of the glycolytic pathway.

Materials and Methods

Chemicals

PGK from baker’s yeast and d-3-PG disodium salt and magnesium chloride were purchased from Sigma-Aldrich. Adenosine-5′-triphosphate disodium salt was purchased from Roth, and sodium hydroxide was obtained from Merck. All samples were prepared using Millipore water from the Milli-Q system provided by Merck Millipore. A list of all chemicals used in this work is given in Table 5.

Table 5. Chemical Provenance Table^a.

compound	purity (%)	CAS	supplier
PGK from baker’s yeast		9001-83-6	S
d-3-PG disodium salt	>93	80731-10-8	S
magnesium chloride	>98	7786-30-3	S
adenosine-5′-triphosphate disodium salt	>98	987-65-5	R
sodium hydroxide	>99	1310-73-2	M

^aS = Sigma-Aldrich Chemie GmbH, R = Carl Roth GmbH + Co. KG, and M = Merck KGaA.

Measurement of Osmotic Coefficients

Osmotic coefficients of the system water and 3-PG disodium salt were measured to determine pure component and binary interaction parameters necessary for ePC-SAFT. Measurements were performed using a freezing point depression OSMOMAT 010 from Gonotec (Germany) at ambient pressure. The measurement is based on the freezing point depression of an aqueous solution as a function of known concentration of 3-PG disodium salt. After calibration with aqueous sodium chloride standards provided by Gonotec, the measured osmolality of the sample osm was related to the osmotic coefficient ϕ (eq 13)

13

In eq 13, ν and m characterize the amount of ions in which 3-PG disodium salt may dissociate and the initial molality of 3-PG disodium salt, respectively. 3-PG disodium salt was regarded as fully dissociated. Although this might not be true for the whole concentration range considered, this assumption was done due to the compatibility with the modeling strategy behind ePC-SAFT. Held and Sadowski²³ showed the ability to account for the nondissociated species, which was proven to be very difficult and even requires at least one more fit parameter and the ion-pairing constant. Thus, ν was set to three for 3-PG disodium salt independent of the concentration of 3-PG disodium salt.

Additional osmotic coefficients of the system water and 3-PG disodium salt were measured at 303 K and ambient pressure using vapor pressure osmometry, using a vapor pressure osmometer K-7000 from Knauer (Germany). The K-7000 measures the resistance between the two thermistors connected via a Wheatstone bridge. First, water was dropped on the tip of both thermistors, which were located in a water-saturated measurement cell. After the addition of the sample on the tip of one thermistor, vapor pressure differences between the droplets of both thermistors lead to a measurable current ΔI. With a calibration constant k_calib obtained from sodium chloride solutions of known osmolality, the osmotic coefficients were calculated with eq 14.

14

The data obtained were used to fit pure component ePC-SAFT parameters of 3-PG and the temperature-dependent binary interaction parameter k_ij while explicitly accounting for water, 3-PG and Na⁺. This is further explained in the next section.

Estimation of ePC-SAFT Parameters

The required pure component ePC-SAFT parameters for all components in the reaction mixture are the segment number m_i^seg, the segment diameter σ_i, the dispersion energy parameter u_i, and the association parameters ε^A_iB_i and κ^A_iB_i for components that are able to form hydrogen bonds (HBs). In this work, new pure component ePC-SAFT parameters for 3-PG^2– and the binary interaction parameter k_ij between 3-PG^2– and water were determined. The parameter fit was performed based on a Levenberg–Marquardt algorithm (damped least-squares method) which minimized the objective function OF shown in eq 15, in which ϕ_m and ϕ_m^exp denote the modeled and the experimental osmotic coefficients.

15

As proposed for the association ePC-SAFT parameters of ATP and ADP by Meurer et al.,¹² 3-PG was also regarded as a molecule forming strong HBs. This was accounted for by the association scheme N_i^assoc of 5 HB donor and 5 HB acceptor sites in agreement with the molecular structure. On the basis of the preliminary investigations within this work, the OF (eq 14) approached very low values by decreasing the association volume parameter κ^A_iB_i. Thus, κ^A_iB_i was set manually to 0.0001 and was excluded from the parameter estimation procedure. Further, 3-PG was modeled as charged species based on the dependence of experimental osmotic coefficients from 3-PG concentration, as shown in Figures 1 and 2. The steep decrease at small 3-PG concentrations indicates the electrolytic behavior.^24,25 The permittivity of ε_r = 78.45 was used for ePC-SAFT modeling as suggested in ref (22). 3-PG was allowed to cross-associate with water, ATP, and ADP, whereas all other ions were not considered as associating species.²⁶ Inorganic ions of equal charge were not allowed to interact via cross-dispersion, while dispersion between inorganic ions of the opposite charge sign was allowed. For organic ions, dispersion was treated for uncharged components (self-dispersion as well as cross-dispersion between organic ions and all other components was allowed).

The resulting 3-PG ePC-SAFT parameters are listed in Tables 6 and 7. The parameters are reasonable compared to other biological components. The association energy parameter and the segment number are comparably small values. All pure component and binary interaction parameters used in this work are listed in Tables 6 and 7.

Reaction Equilibria Measurements

Samples for the equilibrium measurements were prepared in 1.5 mL Eppendorf tubes. The initial reaction mixture contained equimolar concentrations of the substrates 3-PG disodium salt and ATP disodium salt. In addition, the necessary cofactor Mg²⁺ was added in the form of magnesium chloride in a twofold excess to the moles of ATP to guarantee a full saturation of the required ATP magnesia complex (ATPMg) required for the reaction. The pH of all samples was adjusted to 7 using sodium hydroxide. A constant reaction temperature and mixing was ensured using a ThermoMixer from Eppendorf at 1500 rpm and the according temperatures (303, 313, or 323 K). The reaction time was set to 3 h to ensure that equilibrium was reached. This was also verified by remeasuring the reaction equilibrium composition after readding the substrate after first reaction steps. On the basis of the findings, inactivation or denaturation of the enzyme was excluded (results not shown here). After reaction equilibrium was reached, the enzyme was separated from the reaction mixture using centrifugal filter tubes from VWR with a molecular weight cutoff of 3 kDa. Centrifugation took place in a Typ 5418R Eppendorf centrifuge for 20 min at 14 000 rpm. To ensure a constant temperature during the separation process, the centrifuge was preheated before the samples were inserted.

Determination of the equilibrium composition was performed based on measuring the ADP/ATP ratio. The procedure was adopted from Meurer et al.¹² and lead to reproducible results and thus is suited for glycolytic reactions. The determination of the ADP/ATP ratio is based on the luciferase reaction, during which the amount of photons emitted hν is equal to the moles of ATP converted. The luciferase reaction is shown in eq 16.

16

The principle of the measurement is based on measuring the decrease of the intensity of the emitted light through the conversion of ATP. Afterward, ADP is converted to ATP, and the initial step of the luciferase reaction is repeated to yield the ADP/ATP ratio as described by Meurer et al.¹² in detail. Measurement of the emitted light at 560 nm was performed in a FLUOstar Omega plate reader provided by BMG Labtech using the ADP/ATP ratio kit purchased from Sigma-Aldrich. Knowing the initial concentration of ATP, a mole balance was used to calculate the molality of ATP, ADP, 3-PG, and 1,3-BPG, as shown in eqs 17–20, where the subscript,0 denotes the initial molality of the compound.

17

18

19

20

For predictions with ePC-SAFT, molalities of the compounds were converted to mole fractions and the measured molalities were converted to the mole-fraction-based expression of K_exp^′, as shown in eq 21.

21

Glossary

Abbreviations

1,3-BPG

1,3-bisphosphoglycerate

3-PG

3-phosphoglycerate

ADP

adenosine diphosphate

ATP

adenosine triphosphate

ATPMg

adenosine triphosphate magnesia complex

eq

equilibrium

ePC-SAFT

electrolyte perturbed-chain statistical associating fluid theory

HB

hydrogen bonds

PGK

phosphoglycerate kinase

PPi

pyrophosphate

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors acknowledge funding from RESOLV Cluster of Excellence (EXC 1069). C.H. and A.W. gratefully acknowledge the financial support of DAAD (project number 57340264) funded by the Federal Ministry of Education and Research (BMBF).

The authors declare no competing financial interest.