A Bayesian framework for performance assessment and comparison of imaging biomarker quantification methods

Abstract

Quantitative biomarkers derived from medical images are being used increasingly to help diagnose disease, guide treatment, and predict clinical outcomes. Measurement of quantitative imaging biomarkers is subject to bias and variability from multiple sources, including the scanner technologies that produce images, the approaches for identifying regions of interest in images, and the algorithms that calculate biomarkers from regions. Moreover, these sources may differ within and between the quantification methods employed by institutions, thus making it difficult to develop and implement multi-institutional standards. We present a Bayesian framework for assessing bias and variability in imaging biomarkers derived from different quantification methods, comparing agreement to a reference standard, studying prognostic performance, and estimating sample size for future clinical studies. The statistical methods are illustrated with data obtained from a positron emission tomography challenge conducted by members of the NCI’s Quantitative Imaging Network program, in which tumor volumes were measured manually and with seven different semi-automated segmentation algorithms. Estimates and comparisons of bias and variability in the resulting measurements are provided along with an R software package for the technical performance analysis and an online web application for sample size and power analysis.

1 Introduction

Due to recent advances in medical imaging technology, the biological features of cancerous tumors can be characterized with large numbers of quantitative features, including measures of tumor image intensity, variability, texture, shape, and size. Radiomics is an emerging discipline that utilizes such features as quantitative imaging biomarkers (QIBs) to predict clinical outcomes. Unfortunately, radiomic extraction and analysis of QIBs is subject to measurement variability and bias. In particular, extracted biomarkers are affected by the imaging technologies themselves as well as the tumor segmentation methods used to define regions over which to calculate them. Moreover, institutions often differ with respect to quantification methods used, thus making it challenging to develop and implement multi-institutional standards for the use of biomarkers to guide therapy or to diagnoses disease, guide treatment, and predict clinical outcomes.

The statistical methods presented in this paper are motivated by an application comparing biomarkers derived from different tumor segmentation methods. Tumor segmentation is the process of drawing a boundary around the anatomical structures on a medical image that are believed to be cancerous. Current medical practice is for segmentation to be performed manually by trained oncologists. However, semi and fully automated methods have been proposed to reduce segmentation time and potentially increase quality.¹ Several such methods were employed in a recent positron emission tomography (PET) segmentation challenge conducted by center members of the NCI Quantitative Imaging Network (QIN).² The segmentations and biomarkers obtained from that challenge serve as the data application in this paper.

As noted by others, formal evaluations and comparisons of methods used to derive imaging biomarkers have received relatively little attention in the past.³ Nevertheless, there is a general understanding that assessment of method quality should take into account bias, defined as the expected difference between biomarker measurements and the true value, and variability, defined as the differences between biomarker measurements repeated on the same experimental unit. Moreover, appropriately designed studies are crucial for comparable quality assessments.⁴ A complicating factor in the study of imaging biomarkers measured on humans is that the true biomarker values are often unknown. When the truth is unknown, comparisons are often made to a reference standard. Such is the case in the motivating application.

In the following sections, statistical methods are developed and applied for the comparison of multiple quantitative methods. A measurement error modeling approach is taken, similar to the linear mixed effects reproducibility model considered in Raunig et al.⁵ However, separate inter and intra-operator variance components are added to the reproducibility model’s between and within-subject components, and all quantitative methods are modeled and compared simultaneously. From our proposed model, performance metrics commonly used in the technical validation of imaging biomarkers are derived and presented, including bias, operator variance, repeatability coefficient, intraclass correlation coefficient (ICC), coefficient of variation, and between-method correlation. The model is then extended to facilitate clinical validation where interest lies in estimating associations with health events.⁶ In particular, a model-based simulation approach is presented to assess the impact of quantification method measurement errors on odds ratio estimation in the context of a binary health event, such as presence or absence of a new disease, treatment response, or disease recurrence. An illustrative example is given for the simulation approach to show how the effects of measurement errors on bias, variability, study power, and sample size can be quantified. An understanding of these effects is important in practice to ensure proper design of studies, including clinical trials, to test imaging biomarkers in patient populations. Underlying the methods development in this paper is a Bayesian approach which allows direct probability statements to be made about performance metrics and avoids approximate inferential methods. In contract, previous statistical methods for imaging biomarker assessment have traditionally relied on large sample asymptotic theory, finite series approximations, and the bootstrap⁷ to estimate confidence intervals and test statistics.

2 QIN PET segmentation challenge

A medical imaging segmentation challenge was conducted among academic center members of the NCI’s QIN program.⁸ The QIN is designed to promote research and development of quantitative imaging methods for the measurement of tumor response to therapies in clinical trial settings, with an overall goal of facilitating clinical decision-making. Participating members of the challenge were presented with 47 lesions identified in pre-treatment PET scans of head and neck cancer patients acquired at the University of Iowa. Each member then used a method of their choosing to segment the lesions. Methods included manual segmentation as well as commercially available software and in-house-developed semi-automated segmentation algorithms. An overview of the methods and credentials of the operator(s) of each is given in Table 1. Additional detail about the challenge, image acquisition, and segmentation methods are contained in the main findings paper.²

Table 1.

Summary of quantitative image analysis methods and operators in the QIN PET segmentation challenge.

Method	Description	Operator
1	Manual segmentation	Radiation oncologists
2	Active contour segmentationa	PhD research scientist
3	Graph-based optimizationa	Radiation oncologist
4	Mirada Medical RTxb	Imaging physicist
5	VCAR and PMODb	Medical physics postdoc
6	MIMb	Imaging physicist
7	PMODb	Image analyst
8	3D level-set segmentationa	Medical image analysis graduate student

^aIn-house algorithm.

^bCommercial software.

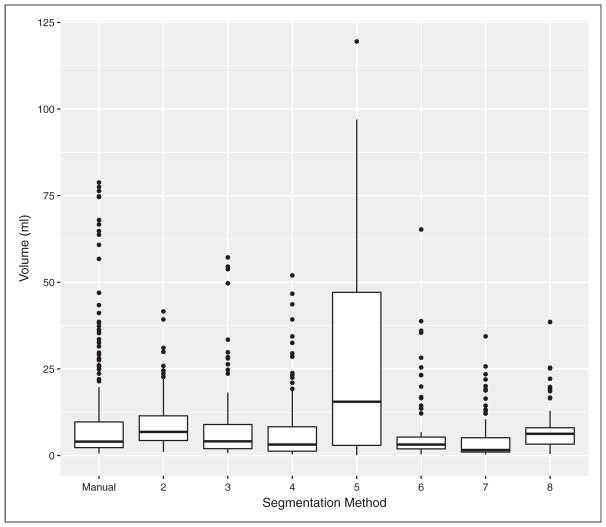
Challenge participants segmented all 47 lesions twice, with a waiting period of at least one week between repeated segmentation. Manual segmentation (Method 1) was performed by three experienced radiation oncologists; whereas, the other methods were performed by a single operator. Lesion volumes (ml) were derived from the segmentations and are the quantitative biomarker measurements upon which the methods and application of this paper focus. Their distributions are summarized with boxplots in Figure 1. The skewed nature of the plots reflect the inherently positive nature of tumor volumes and the relatively small number of large head and neck lesions. Also noteworthy are the volume measurements from Method 5 which stand out from the rest as being decidedly larger. Method 5 was ultimately excluded from parts of the main challenge findings due to its lack of consistency with other methods and concerns about the appropriateness of its segmentation approach. The method, however, will be included in the present analysis, which includes statistical methods that explicitly account for and characterize the impact of its volumetric differences.

Figure 1.

Distributions of segmented tumor volumes from different quantitative image analysis methods.

3 Statistical methods

The methodological approach taken aims to characterize the bias and variability that can result when estimating the risk of clinical outcomes associated with an imaging biomarker derived from different quantification methods. In order to do so, an underlying Bayesian model is specified for the joint distribution of method-specific biomarker measurements and sources of measurement error. Based on the model, a measurement-error-free reference biomarker is obtained and used to simulate clinical outcomes for user-specified risk associations and sample sizes. Then, based on the modeled joint distribution, risks estimated from method-specific biomarkers measured with error are compared. Also provided in this section are software procedures for fitting the Bayesian model; algorithms for the risk simulations; and an online web application for interactive comparison of method-specific risk estimates, statistical powers, and coverage probabilities.

3.1 Quantitative imaging biomarker model

To begin the methodological development, a linear mixed effects statistical model is specified for the biomarker measurements of interest. In particular, measurements are modeled as a function of systematic and random sources of variability. The model is designed for settings in which biomarker measurement b_mijk is obtained from method m = 1, … ,M applied to a common set of i = 1, … , I independent medical images by operator j = 1, … , J_m and repeatedly for k = 1, … ,K_m number of times. Accordingly, measurements on the images are obtained from all methods, but the operators and number of repeats may vary by method. The functional form of the model is

$$\begin{gathered} b_{\mathit{mijk}}={\iota }_{mi}+{\omega }_{mj}+{(\iota \omega )}_{\mathit{mij}}+{\epsilon }_{\mathit{mijk}} \\ {({\iota }_{1i},\dots ,{\iota }_{Mi})}^{\top }~N_M(\mathit{\mu },{\mathrm{\sum }}_{\iota }) \\ {\omega }_{mj}~N(0,{\sigma }_{{\omega }_m}^2) \\ {(\iota \omega )}_{\mathit{mij}}~N(0,{\sigma }_{{(\iota \omega )}_m}^2) \\ {\epsilon }_{\mathit{mijk}}~N(0,{\sigma }_{{\epsilon }_m}^2), \end{gathered}$$ (1)

where μ = (μ₁, … ,μ_M)^⊤ represent systematic method effects, ι_mi a random image effect, ω_mj and (ιω)_mij random operator and image-by-operator interaction effects, and ε_mijk a repeat error. Normal distributions are specified for the random effects and repeat error. With respect to the image effect, the distribution is multivariate normal with an unstructured M × M covariance matrix Σ_ι. Independent univariate normals are otherwise specified with method-specific operator variances ${\sigma }_{{\omega }_m}^2$ and ${\sigma }_{{(\iota \omega )}_m}^2$ and repeat error variance ${\sigma }_{{\epsilon }_m}^2$.

As noted above, sources of variability are incorporated with the systematic method, random, and repeat error model terms. Random effects ι_mi represent image means within methods, ω_mj) (ιω)_mij observer deviations about the image means, and ε_mijk repeat deviations about the observer means. Moreover, the ι_mi effects imply that the I measured images are a random sample from a larger population of images. For instance, quantitative biomarker measurements might be obtained from randomly selected cancer patients imaged at the time of diagnosis. The Σ_ι matrix accounts for both between-image variances ( ${\sigma }_{{\iota }_m}^2:={({\mathrm{\sum }}_{\iota })}_{m,m}$) and between-method covariances (σ_ιm,m′ := (Σ_ι)_m,m′), the latter of which being a consequence of the repeated application of different methods to the same set of images. Accordingly, covariances and correlations between biomarker measurements from different methods are represented by the model parameters

$$\begin{gathered} cov(b_{\mathit{mijk}},b_{m^{\prime }{i}^{\prime }{j}^{\prime }{k}^{\prime }})={\sigma }_{{\iota }_{m{m}^{\prime }}} \\ \text{cor}(b_{\mathit{mijk}},b_{m^{\prime }{i}^{\prime }{j}^{\prime }{k}^{\prime }})={\sigma }_{{\iota }_{m{m}^{\prime }}}\sqrt{{\sigma }_{{\iota }_m}^2{\sigma }_{{\iota }_{m^{\prime }}}^2}. \end{gathered}$$

The variance terms ${\sigma }_{{\omega }_m}^2+{\sigma }_{{(\iota \omega )}_m}^2$ and ${\sigma }_{{\epsilon }_m}^2$ can be viewed as inter and intra-operator variability, respectively. In general terms, the images are the study units, or subjects, with a population mean for method m of μ_m, between-subject variance ${\sigma }_{{\iota }_m}^2$, and within-subject variance ${\sigma }_{{\omega }_m}^2+{\sigma }_{{(\iota \omega )}_m}^2+{\sigma }_{{\epsilon }_m}^2$.

3.2 Prior and posterior distributions

A Bayesian analysis approach is taken by specifying prior distributions, denoted p(·), on the biomarker model parameters so as to base inference on the joint posterior distribution

$$\begin{gathered} p(\mathit{\theta }\mid \mathit{b})\propto \prod _{m,i,j,k}p\left(b_{\mathit{mijk}}\mid {\mu }_m,{\iota }_{mi},{\omega }_{mj},{(\iota \omega )}_{\mathit{mij}},{\sigma }_{{\epsilon }_m}^2\right)p\left({\mathit{\iota }}_i\mid {\sum }_{\iota }\right)p\left({\omega }_{mj}\mid {\sigma }_{{\omega }_m}^2\right) \\ \times p\left({(\iota \omega )}_{\mathit{mij}}\mid {\sigma }_{{(\iota \omega )}_m}^2\right)p({\mu }_m)p\left({\sum }_{\iota }\right)p({\sigma }_{{\omega }_m}^2)p\left({\sigma }_{{(\iota \omega )}_m}^2\right)p\left({\sigma }_{{\epsilon }_m}^2\right), \end{gathered}$$ (2)

where $\mathit{\theta }=(\mathit{\mu },\mathit{\iota },\mathit{\omega },(\mathit{\iota }\mathit{\omega }),{\mathrm{\sum }}_{\iota },{\mathit{\sigma }}_{\omega }^2,{\mathit{\sigma }}_{(\iota \omega )}^2,{\mathit{\sigma }}_{\epsilon }^2)$ is the collection of all model parameters. Markov chain Monte Carlo (MCMC) computational methods will be used to simulate draws from the posterior. MCMC provides autocorrelated draws of the model parameters that start with a set of initial values and must have converged to draws from the posterior distribution in order for their use in inference to be valid.⁹ Convergence will be assessed by generating three parallel MCMC chains started at different initial values and assessed visually with time series (trace) plots and analytically with the diagnostic of Gelman and Rubin.¹⁰ Prior distributions for the analysis include normals for μ_m, inverse-Wishart for Σ_ι, and uniforms for σ_ωm, σ_(ιω)m, and σ_εm. Uniforms were employed for the standard deviation parameters to represent weakly informative priors, as suggested by Gelman.¹¹ Semi-conjugate inverse-gammas for the variance forms of these parameters are additionally available in our software implementation of the model to accommodate more informative priors. The overall choices of priors have the desirable properties of supporting a wide range of weak to strong prior information. Moreover, the mean normal and variance inverse-gamma priors are conjugate to the normal distributions on the random effects and repeat errors that condition on them. Conjugacy, in particular, tends to produce more efficient MCMC simulations by lowering autocorrelation and improving convergence.

Bayesian rather than frequentist methods were selected for the statistical modeling due to several advantages offered for the intended application. First and foremost, inference is based on the joint posterior distribution and thus accounts for uncertainty and relationships among all biomarker model parameters. Thus, conclusions about the parameters are made in terms of probability statements, conditional on the observed biomarker measurements. Second, inference can be made about future biomarker measurements b̃ based on the posterior predictive distribution p(b̃|b). This feature is utilized in subsequent sections to obtain method-specific disease risk estimates, powers, and coverage probabilities. Third, inference about transformations or combinations of model parameters is conceptually straightforward, given draws from the posterior distribution, and does not rely on large sample asymptotic theory or approximation methods. Other advantages include formal quantification and incorporation of prior information in the analysis and its ability to combine information from multiple sources. Conversely, criticisms of Bayesian approaches include subjectivity introduced through prior distributions and the extra computational burden of obtaining draws from the posterior.¹² Computing for the proposed biomarker model is rather minimal since it can be implemented and fit with off-the-shelf software programs. With respect to priors, vague specifications will be employed to minimize subjectivity. The sensitivity of results to the priors can be examined over a range of specifications and also assessed with posterior predictive model checks.

3.3 Posterior predictive model checks

Model fit is assessed with posterior predictive p-values¹³ of the form

$$Pr(T_m({\mathit{b}}^{\text{rep}},\mathit{\theta })\ge T_m(\mathit{b},\mathit{\theta })\mid \mathit{b})$$

where b are observed biomarker measurements, b^rep are measurements replicated from the posterior predictive distribution p(b̃|b) and with the same structure as the observed, and T_m is the goodness-of-fit quantity for method m

$$\begin{gathered} T_m(\mathit{b},\mathit{\theta })=\sum _{i,j,k}\frac{{(b_{\mathit{mijk}}-\mathrm{E}(b_{\mathit{mijk}}))}^2}{var(b_{\mathit{mijk}})} \\ =\sum _{i,j,k}\frac{{(b_{\mathit{mijk}}-({\mu }_m+{\iota }_{mi}+{\omega }_{mj}+{(\iota \omega )}_{\mathit{mij}}))}^2}{{\sigma }_{{\epsilon }_m}^2} \end{gathered}$$

Separate posterior predictive checks are performed for each of the methods to assess their model fits individually. In general, posterior predictive p-values compare the test statistic distribution on the observed measurements to the distribution on observations replicated from the model with the same set of fixed and random effects. p-Values that deviate from 0.5 indicate discrepancies in the test quantities T_m between observed and replicated data. Such discrepancies could be due to model misspecification or to differences in information contained in the prior specifications and data.

3.4 Posterior predictive distributions

Bayesian inference provides the posterior predictive distribution of future observations on model parameters, data, or any function thereof that would be predicted based on the posterior distribution. The end goal of the proposed methodology is to characterize bias and uncertainty in risk estimates derived from different quantitative imaging methods. Two statistical algorithms are presented in this section to accomplish that goal: one which simulates posterior predictive odds ratios and another which uses the simulated values to estimate power and coverage probability. In essence, characteristics of odds ratio estimates are studied using a simulation approach in which the posterior predictive distribution serves as the data-generating mechanism and reflects the additional uncertainty in predicting future observations from available study data.

Algorithm 1, as shown, describes a process for simulating posterior predictive odds ratios estimated from the different quantification methods applied to a future study sample of specified size N. Clinical outcomes for the odds ratio estimation are simulated from a logistic model that relates outcome probability π to “reference” biomarker b according to

$$\text{logit}(\pi )={\beta }_0+{\beta }_1\frac{b}{\mathrm{\Delta }}$$

where values of β₀ and β₁ are fixed based on user-specified (1) odds ratio OR = exp{β₁} for a Δ unit increase in b and (2) outcome prevalence π̄ at biomarker value b̄. The “reference” biomarker is taken to be the posterior predictive image effects from one of the methods. Without loss of generality, the ι̃₁₁, … , ι̃_1N from method 1 are taken. By using the image effects, measurement error due to within-image variability is removed from the simulation of clinical outcomes. Simulation results will vary depending on the choice of reference method since they are affected by differences in the population mean effects μ_m and between-image variances ${\sigma }_{{\iota }_m}^2$. Ideally, a ground truth method would be used as the reference. However, the ground truth is often unknowable in patient-imaging studies, in which case a reference standard, such as manual segmentation, might be a desirable alternative. Once Bernoulli outcomes ỹ_i are simulated from the reference biomarker as indicated on line 15 of the algorithm, a logistic regression model is fit to the posterior predictive biomarker values b̃_mi from each method, and estimated odds ratio OR_m and geometric standard error SE_m are obtained. The process is repeated to simulate S posterior predictive draws of the odds ratios.

Method-specific odds ratio estimates are expected to reflect similarities and differences in the posterior predictive biomarker measurements according to their shared and individual variance components. With respect to shared components, the image random effects for all measurements are drawn from a multivariate normal distribution with covariance matrix Σ_ι. This matrix controls the method-specific variances between image means and the correlations in means between methods, the largest sources of variability in biomarker measurements. Thus, methods with similar between-subject variances and with high correlations will tend to be similar with respect to their biomarker measurements and resulting odds ratios. The mean effects μ_m represent systematic differences between method measurements. Mean shifts like these will not affect odds ratio estimates. On the other hand, differences in the inter and intra-observer variability can have an effect since measurement error tends to attenuate risk estimates.^14,15

Algorithm 1.

Posterior predictive odds ratios.

Input:
Odds ratio OR for a Δ unit increase in the reference biomarker.
Outcome prevalence π̄ at reference biomarker value b̄.
Sample size N at which odds ratios are to be estimated.
Output: S simulated odds ratios ORm and geometric standard errors SEm for quantification methods m = 1, … ,M.
1:	β1 ← log(OR)	▻ Reference logistic slope
2:	${\beta }_0\leftarrow \text{logit}(\overline{\pi })-{\beta }_1\frac{\overline{b}}{\mathrm{\Delta }}$	▻ and intercept.
3:	for s=1 to S do
4:	$\text{Draw}({\mathit{\mu }}^{(s)},{\mathrm{\sum }}_{\iota }^{(s)},{\mathit{\sigma }}_{\omega }^{2(s)},{\mathit{\sigma }}_{(\iota \omega )}^{2(s)},{\mathit{\sigma }}_{\epsilon }^{2(s)})~p(\mathit{\theta }\mid \mathit{b})$
5:	for i=1 to N do
6:	$\text{Draw}{({\stackrel{\sim }{\iota }}_{1i},\dots ,{\stackrel{\sim }{\iota }}_{Mi})}^{\top }~N_M({\mathit{\mu }}^{(s)},{\mathrm{\sum }}_{\iota }^{(s)})$
7:	for m=1 to M do
8:	$\text{Draw}{\stackrel{\sim }{\omega }}_{mi}~N(0,{\sigma }_{{\omega }_m}^{2(s)})$
9:	$\text{Draw}{(\stackrel{\sim }{\iota \omega })}_{mi}~N(0,{\sigma }_{{(\iota \omega )}_m}^{2(s)})$
10:	$\text{Draw}{\stackrel{\sim }{\epsilon }}_{mi}~N(0,{\sigma }_{\epsilon m}^{2(s)})$
11:	${\stackrel{\sim }{b}}_{mi}\leftarrow {\stackrel{\sim }{\iota }}_{mi}+{\stackrel{\sim }{\omega }}_{mi}+{(\stackrel{\sim }{\iota \omega })}_{mi}+{\stackrel{\sim }{\epsilon }}_{mi}$
12:	end for
13:	b̃i ← ι̃1i	▻ Reference biomarker value,
14:	${\stackrel{\sim }{\pi }}_i\leftarrow \text{invlogit}({\beta }_0+{\beta }_1\frac{{\stackrel{\sim }{b}}_i}{\mathrm{\Delta }})$	▻ outcome probability,
15:	Draw ỹi ~ Bernoulli(π̃i)	▻ and simulated outcome.
16:	end for
17:	for m=1 to M do
18:	$({\widehat{\beta }}_{1m},\widehat{\text{se}}({\widehat{\beta }}_{1m}))\leftarrow \text{estimates}\text{from}\text{logistic}\text{regression}$ $$\begin{gathered} {\stackrel{\sim }{y}}_i~\text{Bernoulli}({\pi }_{mi});i=1,\dots ,N \\ \text{logit}({\pi }_{mi})={\beta }_{0m}+{\beta }_{1m}\frac{{\stackrel{\sim }{b}}_{mi}}{\mathrm{\Delta }} \end{gathered}$$
19:	$O{R}_m^{(s)}\leftarrow exp\{{\widehat{\beta }}_{1m}\}$
20:	$S{E}_m^{(s)}\leftarrow exp\{\widehat{\text{se}}({\beta }_{1m})\}$
21:	end for
22:	end for

In Algorithm 2, method-specific power and (1 − α)100% confidence interval coverage probability are computed from the S posterior predictive odds ratios simulated by Algorithm 1. Power is defined as the probability of rejecting the null hypothesis H₀ : OR = 1 or, equivalently, H₀ : β₁ = 0 of no association between the biomarker and clinical outcome. User inputs to the algorithm include the direction of the alternative hypothesis (one or two-sided), the α level at which to assess statistical significance and construct confidence intervals, and the reference odds ratio under which method-specific odds ratios were estimated. Statistical testing and confidence intervals are based on the Wald test statistic

$$\frac{\widehat{{\beta }_1}}{\widehat{\text{se}}({\widehat{\beta }}_i)}\stackrel{H_0}{\sim }N(0,1).$$

A test is performed and confidence interval constructed for each of the S posterior predictive draws. As presented, testing is done by checking whether the Wald confidence interval includes the null odds ratio value of 1. If not, then the test is rejected. Power is thus estimated as the proportion of times the null is rejected. Coverage probability is the proportion of times the confidence intervals contain the reference odds ratio.

Algorithm 2.

Posterior predictive power and coverage.

Input:
S simulated odds ratios ORm and geometric standard errors SEm for quantification methods m = 1, … ,M.
Level α at which to assess significance of statistical testing and to compute 100(1 − α)% confidence intervals.
Specification of a one or two-sided alternative HA to the null hypothesis H0 : OR = 1.
Reference odds ratio OR.
Output: Statistical powerm to accept the alternative hypothesis, and confidence interval coveragem of the reference odds ratio.
1:	if HA : OR ≠ 1 then
2:	α ← α2
3:	end if
4:	for m = 1 to M do
5:	powerm ← 0
6:	coveragem ← 0
7:	for s = 1 to S do
8:	lower ← 0	▻ Initialize interval lower
9:	upper ← ∞	▻ and upper bounds.
10:	if HA : OR ≠ 1 or HA : OR > 1 then
11:	$\mathit{lower}\leftarrow O{R}_m^{(s)}/{(S{E}_m^{(s)})}^{z_{1-\alpha }}$
12:	end if
13:	if HA : OR ≠ 1 or HA : OR < 1 then
14:	$\mathit{upper}\leftarrow O{R}_m^{(s)}\times {(S{E}_m^{(s)})}^{z_{1-\alpha }}$
15:	end if
16:	A ← {x : lower < x < upper}
17:	powerm ← powerm + 1Ā (1)/S
18:	coveragem ← coveragem + 1A(OR)/S
19:	end for
20:	end for

3.5 Posterior simulation

In the proposed approach, MCMC methods will be used to draw samples from the joint posterior distribution. Posterior predictive samples will then be simulated from the posterior draws. Since the process of simulating draws can be computationally intensive, several strategies are employed to improve computing runtimes. First, MCMC draws will be obtained once, prior to their use in Algorithm 1, since the joint posterior does not depend on any user inputs to the algorithms. Second, Algorithm 1 is executed only if its user inputs for the reference odds ratio (OR, Δ, π̄, or b̄) or sample size (N) change. Algorithm 2 depends only on output from the first algorithm and the user inputs for statistical inference (α level and alternative hypothesis direction). Thus, it is only executed if those change. By partitioning and conditionally executing these tasks, the greater computational expenses of joint posterior simulation with MCMC and posterior predictive simulation with Algorithm 1 are minimized. Likewise, power and coverage probabilities can be estimated quickly for different testing scenarios with the computationally inexpensive Algorithm 2.

Another practical computational consideration is the number of posterior samples S to simulate. Posterior inference will be based on summary statistics computed from the samples. In particular, posterior predictive power and coverage probability will be estimated with sample proportions. As estimates, each proportion p is subject to sampling variability which could be quantified with the standard error

$$\widehat{\text{se}}(p)=\sqrt{\frac{p(1-p)}{S}}$$

if the simulated samples were independent. However, the MCMC samples obtained are not independent. Rather, the standard error is increased due to lag-s autocorrelation (ρ_s) generally exhibited by MCMC sequences and is better approximated by replacing S with an estimate of the effective sample size¹⁶

$$\mathit{ESS}=\frac{S}{1+2{\sum }_{s=1}^{\infty }{\rho }_s}.$$

Terms “naive error” and “simulation error” will be used to distinguish between the standard error formulations for independence and autocorrelation, respectively. Values of S are typically sought to keep simulation error below some desired upper bound, say err_upper. Finding such values is challenging since the ESS, sample proportions p, and thus the resulting errors are not known prior to the simulation, when the choice of S must be made. The approach taken here is to set the maximum naive error, which occurs at p=0.5, equal to the desired upper bound and solve to obtain S = (0.5 × err_upper)². Although this solution for S guarantees an upper bound on the naive error, the actual simulation error will be larger due to MCMC autocorrelation. Therefore, thinning of MCMC sequences will be employed in which the S values are taken at set intervals of the sampler to reduce autocorrelation and help ensure that the simulation error is close to the bounded naive error.

3.6 Software

Statistical programming and analysis were conducted with the R environment¹⁷ in conjunction with the following software. JAGS¹⁸ and the rjags R interface¹⁹ were used to implement and execute the Bayesian models. Convergence diagnostics and assessment of MCMC output from the Bayesian analyses was performed with the coda package.²⁰ An R package for fitting the Bayesian model is available at https://github.com/brian-j-smith/qibm and was used to perform the data application analysis (see Supplementary material). Finally, a web application for power and sample size calculations was created with the R Studio shiny package.²¹

4 Application

4.1 Modeled tumor volumes

The Bayesian biomarker model was applied to log-transformed tumor volume measurements from the 8 QIN PET challenge methods each used to segment a common set of 47 head and neck cancer lesions. The log-transformation was needed to satisfy the model assumption of normally distributed, homoscedastic, and additive errors. Manual segmentation was considered the reference standard in the challenge and thus designated as Method 1 in the model. All images were segmented manually by each of three trained operators, whereas segmentation with each of the other methods was performed by separate individual operators. Accordingly, operator random effects were included for Method 1 but not for the others. Operators segmented the images twice to produce replicate measurements. Vague prior distributions on the model parameters were specified as

$$\begin{gathered} {\mu }_m~N(0,1e6) \\ {\mathrm{\sum }}_{\iota }~\text{Inverse}-\text{Wishart}({\mathit{I}}_M,M) \\ {\sigma }_{{\omega }_1},{\sigma }_{{(\iota \omega )}_1},{\sigma }_{{\epsilon }_m}~\text{Uniform}(0,2) \end{gathered}$$ (3)

for m = 1, … , 8. Draws from the posterior distribution were simulated with MCMC methods. An initial burn-in sequence of 5000 iterations was discarded to allow for convergence, and 10,000 subsequent iterations with a thinning interval of 20 iterations were retained for inference. Model parameters are summarized with posterior means and 95% highest posterior density credible intervals (CrI) computed with the method of Chen and Shao.²²

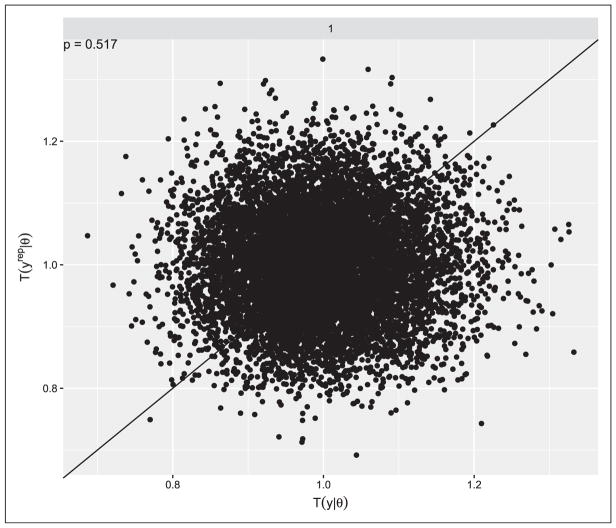
Model fit was assessed with posterior predictive p-values based on the goodness-of-fit quantity described in the Methods Section. Fit was assessed separately for each of the methods and resulted in p-values of 0.517, 0.515, 0.514, 0.517, 0.523, 0.519, 0.521, and 0.521 for Methods 1–8, respectively. The values being close to 0.5 suggest good model fit and prior information that is consistent with that in the data. Figure 2 shows a plot of the observed versus replicated data distributions of the goodness-of-fit statistic for Method 1. The apparent random scattering about the 45-degree line is consistent with the p-value in suggesting good model fit. Similar patterns occur for the other methods (not shown).

Figure 2.

Distribution of posterior predictive goodness-of-fit quantities evaluated at replicated data from the fitted Bayesian model and observed study data. Values of the posterior predictive p-value Pr(T(y^rep|θ) ≥ T(y|θ)| y) close to 0.5 indicate agreement between the model and data.

4.2 Posterior summaries of model parameters

Posterior summaries of the model parameters are given in Table 2. Care should be exercised when interpreting the parameters since Methods 2–8 each involved a single operator. As such, the mean effect μ_m for each of these methods is confounded with the corresponding operator. In other words, the mean effects of the operator and method are inseparable. Likewise, the image variances for these methods include variability due to interaction between the operator and method which cannot be separated. Conversely, Method 1 mean μ₁ averages over the three operators, and inter-operator variability is separated out as ${\sigma }_{{\omega }_1}^2+{\sigma }_{{(\iota \omega )}_1}^2$. Therefore, the mean and image variance are most comparable across Methods 2–8. The intra-operator variability σ_εm is comparable across all methods as the variability in repeated segmentations about the corresponding operator mean. The approach taken for interpretation will be to view the results within the study context in which they were obtained. In particular, Method 2–8 results reflect performance when each is applied by a single operator. Method 1 is the reference standard whose image mean effect is free of inter and intra-operator variability and reflects the ideal in this study.

Table 2.

Posterior means (95% CrI) of the method-specific mean and variance parameters from the joint Bayesian analysis of segmented tumor volumes (ml).

Method	Mean volume exp{μm}	Between-image variability exp{σιm}	Repeat error exp{σm}
1a	5.09 (2.65, 7.48)	2.96 (2.33, 3.65)	1.29 (1.25, 1.33)
2	7.01 (5.58, 8.51)	1.91 (1.60, 2.24)	1.62 (1.48, 1.78)
3	4.67 (3.32, 6.18)	2.98 (2.35, 3.71)	1.28 (1.22, 1.34)
4	3.55 (2.39, 4.87)	3.30 (2.52, 4.27)	1.74 (1.58, 1.91)
5	10.99 (5.46, 17.27)	6.51 (4.18, 9.38)	1.14 (1.11, 1.18)
6	3.60 (2.67, 4.65)	2.41 (1.93, 2.94)	1.82 (1.64, 2.01)
7	2.30 (1.64, 3.11)	3.06 (2.40, 3.86)	1.42 (1.33, 1.53)
8	5.55 (4.13, 6.94)	2.36 (1.96, 2.85)	1.33 (1.25, 1.41)

^aInter-operator variability: $exp\left\{\sqrt{{\sigma }_{{\omega }_1+{\sigma }_{{(\iota \omega )}_1}^2}^2}\right\}=1.35(1.02,2.26)$.

Since modeling was performed on log-transformed volumes, posterior estimates are reported for exponentiated (geometric) means and standard deviations on the original scale. Relative to the manual reference, Method 5 appears to be the most dissimilar. Its measured volumes are systematically larger (10.99 vs. 5.09), indicating that the segmentations produced are more liberal in their inclusion of tumor and surrounding structures. Likewise, image variability is higher (6.51 vs. 2.96), although repeat variability is advantageously lower (1.14 vs. 1.29). Method 3 is the most similar in performance to the reference, followed closely by Method 8. Associations between the methods are summarized with correlations in Table 3. Consistent with the other posterior summaries, Method 3 exhibits a high degree of correlation with the reference (0.945), as do Methods 4 (0.939) and 7 (0.900); and Method 5 exhibits the least amount of correlation (0.346). Method 8, which had similar mean and variances, exhibits only moderate correlation (0.605). Inter-operator standard deviation $exp\left\{\sqrt{{\sigma }_{{\omega }_1}^2+{\sigma }_{{(\iota \omega )}_1}^2}\right\}$ was additional available for Method 1 and had posterior mean of 1.35 (95% CrI 1.02–2.26). As discussed in the next section, analogous similarities and differences show up in the odds ratio estimates predicted from the posterior distribution obtained and summarized here.

Table 3.

Posterior means (95% CrI) of the between-method correlations from the joint Bayesian analysis of segmented tumor volumes (ml).

	1	2	3	4	5	6	7	8
1	1
2	$0.761\left(\begin{array}{l}0.607\hfill \\ 0.902\hfill \end{array}\right)$	1
3	$0.945\left(\begin{array}{l}0.911\hfill \\ 0.975\hfill \end{array}\right)$	$0.764\left(\begin{array}{l}0.606\hfill \\ 0.901\hfill \end{array}\right)$	1
4	$0.939\left(\begin{array}{l}0.895\hfill \\ 0.975\hfill \end{array}\right)$	$0.742\left(\begin{array}{l}0.562\hfill \\ 0.893\hfill \end{array}\right)$	$0.920\left(\begin{array}{l}0.862\hfill \\ 0.967\hfill \end{array}\right)$	1
5	$0.346\left(\begin{array}{l}0.086\hfill \\ 0.607\hfill \end{array}\right)$	$0.450\left(\begin{array}{l}0.166\hfill \\ 0.701\hfill \end{array}\right)$	$0.406\left(\begin{array}{l}0.147\hfill \\ 0.642\hfill \end{array}\right)$	$0.301\left(\begin{array}{l}0.013\hfill \\ 0.569\hfill \end{array}\right)$	1
6	$0.880\left(\begin{array}{l}0.794\hfill \\ 0.952\hfill \end{array}\right)$	$0.743\left(\begin{array}{l}0.565\hfill \\ 0.897\hfill \end{array}\right)$	$0.871\left(\begin{array}{l}0.777\hfill \\ 0.948\hfill \end{array}\right)$	$0.896\left(\begin{array}{l}0.818\hfill \\ 0.962\hfill \end{array}\right)$	$0.265\left(\begin{array}{c}-0.043\\ 0.561\end{array}\right)$	1
7	$0.900\left(\begin{array}{l}0.836\hfill \\ 0.955\hfill \end{array}\right)$	$0.780\left(\begin{array}{l}0.629\hfill \\ 0.905\hfill \end{array}\right)$	$0.902\left(\begin{array}{l}0.840\hfill \\ 0.960\hfill \end{array}\right)$	$0.905\left(\begin{array}{l}0.836\hfill \\ 0.963\hfill \end{array}\right)$	$0.287\left(\begin{array}{l}0.008\hfill \\ 0.555\hfill \end{array}\right)$	$0.898\left(\begin{array}{l}0.823\hfill \\ 0.959\hfill \end{array}\right)$	1
8	$0.605\left(\begin{array}{l}0.418\hfill \\ 0.791\hfill \end{array}\right)$	$0.550\left(\begin{array}{l}0.301\hfill \\ 0.773\hfill \end{array}\right)$	$0.590\left(\begin{array}{l}0.385\hfill \\ 0.777\hfill \end{array}\right)$	$0.526\left(\begin{array}{l}0.292\hfill \\ 0.747\hfill \end{array}\right)$	$0.545\left(\begin{array}{l}0.321\hfill \\ 0.757\hfill \end{array}\right)$	$0.478\left(\begin{array}{l}0.204\hfill \\ 0.712\hfill \end{array}\right)$	$0.469\left(\begin{array}{l}0.224\hfill \\ 0.706\hfill \end{array}\right)$	1

4.3 Performance of quantification methods

In addition to posterior inference on the model parameters, the Bayesian approach allows for posterior inference on any transformation or combination of model parameters. Furthermore, posterior statistics, such as means and credible intervals, can be computed directly from the MCMC samples and do not require large sample asymptotic theory, finite series approximations, numerical optimization routines, or resampling from approximating distributions. Posterior summaries of several metrics for evaluating and comparing imaging method performances are given in Table 4.

Table 4.

Posterior means (95% CrI) of method-specific agreement and precision metrics computed from the joint Bayesian analysis of segmented tumor volumes (ml).

	Agreement			Precision
Method	Bias	C-Index	ICC	wCV	RDC	RC
1	0.00	1.00	0.88 (0.61, 0.97)	0.45 (0.25, 1.03)	1.05 (0.67, 2.36)	0.70 (0.62, 0.78)
2	1.92 (−0.04, 4.33)	0.69 (0.61, 0.77)	0.64 (0.47, 0.78)	0.51 (0.41, 0.63)	1.34 (1.09, 1.60)	1.34 (1.09, 1.60)
3	−0.43 (−1.99, 2.08)	0.83 (0.74, 0.89)	0.95 (0.92, 0.98)	0.25 (0.20, 0.30)	0.68 (0.55, 0.82)	0.68 (0.55, 0.82)
4	−1.54 (−3.22, 0.86)	0.79 (0.71, 0.85)	0.82 (0.73, 0.90)	0.60 (0.48, 0.72)	1.53 (1.26, 1.79)	1.53 (1.26, 1.79)
5	5.90 (0.25, 12.44)	0.58 (0.52, 0.63)	0.99 (0.99, 1.00)	0.14 (0.11, 0.16)	0.37 (0.29, 0.45)	0.37 (0.29, 0.45)
6	−1.49 (−3.64, 0.67)	0.73 (0.65, 0.80)	0.68 (0.54, 0.80)	0.66 (0.53, 0.79)	1.66 (1.39, 1.94)	1.66 (1.39, 1.94)
7	−2.79 (−4.93, −0.65)	0.79 (0.71, 0.85)	0.91 (0.85, 0.95)	0.36 (0.29, 0.44)	0.98 (0.79, 1.17)	0.98 (0.79, 1.17)
8	0.46 (−1.73, 2.87)	0.67 (0.61, 0.73)	0.90 (0.84, 0.95)	0.29 (0.23, 0.36)	0.78 (0.62, 0.96)	0.78 (0.62, 0.96)

C-Index: concordance index; ICC: intraclass correlation coefficient; wCV: within-subject coefficient of variation; RDC: reproducibility coefficient; RC: repeatability coefficient.

Three agreement metrics are provided: population Bias, C-Index, and ICC. Bias is computed as the differences

$${\text{Bias}}_m=exp\{{\mu }_m\}-exp\{{\mu }_1\}$$

between population means (on the original scale) relative to the reference standard. C-Index is a non-parametric (rank) measure of concordance^23,24 comparing the I model-derived biomarker measurements ${{\stackrel{\sim }{b}}^{\prime }}_{mi}={\iota }_{mi}+{\stackrel{\sim }{\omega }}_{mi}+{(\stackrel{\sim }{\iota \omega })}_{mi}+{\stackrel{\sim }{\epsilon }}_{mi}$ from Method m to those from the reference standard, where ε̃ mi , ${(\stackrel{\sim }{\iota \omega })}_{mi}$, and ω̃ mi are as defined in Algorithm 1. Concordance values of 1 and 0.5 represent perfect and chance rank agreement, respectively. Given next is the ICC defined as the variance between images relative to the total.

$${\text{ICC}}_m=\frac{{\sigma }_{{\iota }_m}^2}{{\sigma }_{{\iota }_m}^2+{\sigma }_{\omega }^2+{\sigma }_{\iota \omega }^2+{\sigma }_{\epsilon }^2}$$

It is a measure of the consistency in repeated measurements relative to the total population variability.^25,26 The agreement metrics differ in that ICC measures consistency within methods, whereas Bias and C-Index measure consistency between. With respect to the latter two, Bias measures mean shifts between methods that are not captured by the shift and scale invariant C-Index. Differences in the metrics are particularly evident for Method 5, which has nearly perfect ICC (0.99), but very low concordance (0.58) and high bias (5.90). Conversely, Method 3 has consistently high agreement internally and with the reference (Bias=−0.43, C-Index=0.83, ICC=0.95). Method 7 has relatively high concordance (0.79) but also high bias (−2.79).

The reported precision metrics are within-subject coefficient of variation (wCV), reproducibility coefficient (RDC), and repeatability coefficient (RC). In our setting, wCV is the inter and intra-operator standard deviation divided by the population mean. Since measurements were log-transformed for the analysis, wCV can be computed on the original scale²⁷ as

$$\text{wCV}=\sqrt{exp\{\sqrt{{\sigma }_{\omega }^2+{\sigma }_{\iota \omega }^2+{\sigma }_{\epsilon }^2}\}-1}.$$

The reproducibility and repeatability coefficients measure variability between two measurements taken on the same image. The former applies to measurements taken under two different conditions while the latter applies when the condition is the same.^4,28, Both represent the interval within which the two measurements are expected to occur 95% of the time. Here, operators represent different conditions so that

$$\begin{gathered} \text{RDC}=1.96\sqrt{2({\sigma }_{\omega }^2+{\sigma }_{\iota \omega }^2+{\sigma }_{\epsilon }^2)} \\ \text{RC}=1.96\sqrt{2{\sigma }_{\epsilon }^2}. \end{gathered}$$

Since the non-reference methods were evaluated in the present study as being performed by a single operator, their inter-operator variances are zero, resulting in RDC and RC being the same. Lower wCV, RDC, and RC values are desirable in a method as they indicate less operator measurement variability. In looking at the precision measures, Method 5 exhibits the lowest variability (wCV=0.14, RDC=RC=0.37) and hence the highest precision. This is in contrast to its poor measures of agreement with the reference. Overall, its measurements are precise but not in accord with the reference. Method 3 has the second highest precision (wCV=0.25, RDC=RC=0.68) to accompany its high agreement with the reference.

4.4 Posterior predictive odds ratios, power, and coverage

Posterior predictive odds ratios, powers, and coverage probabilities were simulated according to Algorithms 1 and 2. Posterior predictive samples were generated for the S=10,000 joint posterior draws described in the previous section. The number of samples ensures a maximum naive error of 0.005 for posterior power and coverage probability estimates. Observed simulation errors were also less than the maximum. Manual segmentation was utilized as the reference method designated in the study. A reference odds ratio of OR=1.5 and an outcome prevalence of 0.5 at the reference biomarker mean were specified. Method-specific odds ratios were then estimated for sample sizes of N=250 and 500, and power and coverage probabilities computed for two-sided α = 0.05 level statistical testing and confidence intervals. Posterior predictive results are presented in Table 5.

Table 5.

Posterior predictive odds ratio means (95% CrI), root mean squared errors, powers, and 95% confidence interval coverage probabilities for clinical outcomes simulated from reference manual segmentations and a specified odds ratio of 1.5.

Method	N	Odds ratio	RMSE	Power	Coverage
1	250	1.45 (1.07, 1.85)	0.212	0.809	0.897
2	250	1.41 (0.93, 1.95)	0.284	0.457	0.908
3	250	1.45 (1.10, 1.88)	0.207	0.802	0.930
4	250	1.34 (1.05, 1.65)	0.224	0.731	0.783
5	250	1.09 (0.92, 1.28)	0.421	0.209	0.028
6	250	1.36 (1.00, 1.74)	0.240	0.599	0.857
7	250	1.39 (1.04, 1.75)	0.214	0.739	0.874
8	250	1.34 (0.90, 1.79)	0.283	0.421	0.839
1	500	1.44 (1.12, 1.73)	0.162	0.967	0.873
2	500	1.40 (1.05, 1.80)	0.217	0.736	0.870
3	500	1.45 (1.17, 1.73)	0.151	0.972	0.909
4	500	1.33 (1.12, 1.55)	0.201	0.946	0.633
5	500	1.09 (0.95, 1.22)	0.419	0.358	0.002
6	500	1.35 (1.10, 1.65)	0.204	0.862	0.760
7	500	1.39 (1.13, 1.64)	0.173	0.948	0.816
8	500	1.33 (1.02, 1.66)	0.241	0.681	0.742

RMSE: root mean squared error.

The posterior predictive odds ratio estimates reflect method-specific measurement error due to inter and intra-operator variability as well as correlations between the manual reference and other methods. Deviations (bias) in their posterior means from the 1.5 reference odds ratio value and the credible interval widths (variability) are measures of the degrees to which an underlying biomarker-disease relationship can be estimated with the different quantification methods. Lower bias and variability are indicative of better estimation. The manual odds ratio is closest to the reference odds ratio as expected. However, the posterior means (1.45 and 1.44) are attenuated as is known to happen for a logistic regression covariate measured with error. Odds ratio estimates for Method 3 are just as close, which can be attributed to its relatively low measurement errors and high correlation with the manual method. Methods 2, 4, and 6–8 odds ratios are further shifted to the 1.3–1.4 range, and the Method 5 odds ratios (1.09) are clearly the most affected by its measurement error and low correlation with the manual method. As noted previously, the methods differ with respect to their systematic mean effects. These differences are unlikely to have impacted the results, since odds ratios are invariant to mean shifts in the covariate.

Also presented are root mean squared error (RMSE), power, and coverage estimates. RMSE is computed as the square root of the bias squared plus variance

$${\text{RMSE}}_m=\sqrt{{(\mathrm{E}({OR}_m)-OR)}^2+var({OR}_m)}.$$

It provides a composite performance measure of bias and variability in estimated odds ratios. As such, Methods 1, 3, and 7 are judged to have the best performance based on their low RMSE values. Power is the probability of rejecting the null hypothesis of no biomarker association (H₀: OR=1). If designing a study, the differences in power identify which methods would require a smaller or larger sample size to achieve a desired study power. Methods 1, 3, 4, and 7 are clearly leading the pack with advantageously high powers. Coverage is the probability that 95% confidence intervals contain the reference odds ratio. Ideally, 0.95 coverage would be achieved to match the confidence level. However, biases and unaccounted-for measurement error can lead to confidence intervals with incorrect coverages. Such is the case here, with all methods falling short of the 0.95 nominal level, although Method 3 is relatively close. Moreover, the shortfalls get worse as the sample size gets larger.

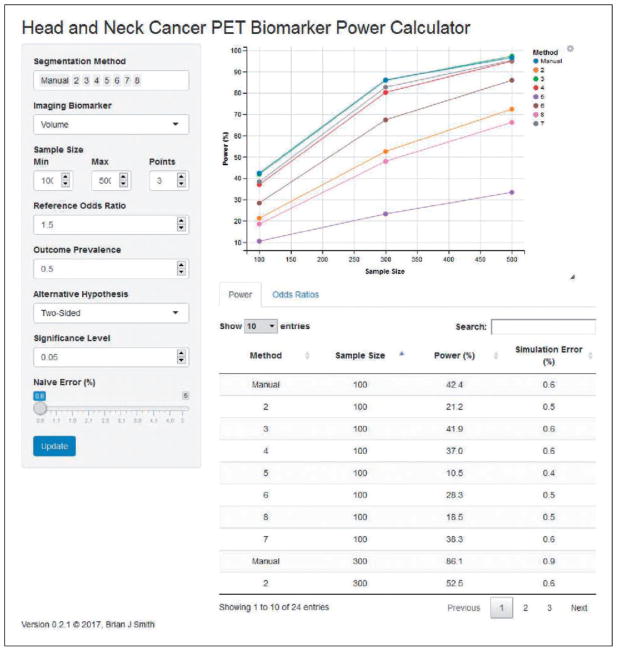
An online web application was developed to provide interactive estimation of odds ratios, powers, and coverage probabilities; and is available directly at https://ph-shiny.iowa.uiowa.edu/bjsmith/QIB/PET/HNC/Power/ or through the University of Iowa QIN website at http://qin.iibi.uiowa.edu. As shown in Figure 3, the application interface consists of three main components.

Figure 3.

Power and sample size web application for quantitative imaging biomarkers.

1. User inputs: Controls for specifying the segmentation methods and biomarker for which to simulate odds ratios as well as simulation parameter values for the sample size, reference odds ratio, outcome prevalence, alternative hypothesis, and significance level.

2. Power curves: Plots of simulated power estimates as a function of the specified sample sizes.

3. Tabular summaries: Under the plots are “Power” and “Odds Ratios” tabs containing simulation estimates. The first tab provides a sortable and subsettable table of the power estimates displayed graphically in the power curves as well as the associated simulation errors. Likewise, the second tab provides a table of odds ratio estimates, posterior CrI, RMSE, and coverage probabilities.

To improve responsiveness, a slider input is included for users to set the maximum naive error for power estimates. Larger values reduce the number of posterior predictive samples S used for estimation and decrease the time needed to update the application. Ten-thousand previously generated posterior samples are supplied to the application at startup to eliminate the need for them to be generated at runtime. Otherwise, the application executes Algorithms 1 and 2 as described previously and does so only when their respective inputs change. For instance, if the reference odds ratio is changed, both algorithms are executed; whereas, if the alternative hypothesis or significance level change, only the second algorithm is run. Since the latter runtime is much shorter, the application reduces update times when it can. Overall, the application is designed to be plug-and-play so that other segmentation methods or biomarkers can be added or the data updated without needing to make changes to the implementation.

5 Conclusion

With this paper, a unified Bayesian approach has been presented for the assessment, comparison, and clinical study design of quantitative imaging biomarkers. At the core is a mixed-effects model that characterizes sources of systematic and random variability within and between different quantification methods. As demonstrated in the application, the covariance matrix specified on the image random effects allows for direct estimation of correlations between methods. Likewise, measures of bias and concordance relative to a reference standard are directly estimable from the model parameters, as are measures of intraclass correlation and precisions (within-subject coefficient of variation, reproducibility coefficient, and repeatability coefficient). The importance of reporting more than one performance metric was discussed in relation to complementary information provided by bias, concordance, and precision measures. With respect to inference, the joint posterior distribution provided by the Bayesian approach allows for probability statements to be made about measures of interest, including credible intervals that can be interpreted as containing the true value with a specified probability. Computationally, credible intervals and any other posterior statistic are straightforward to calculate given MCMC samples, and do not require asymptotic, numerical, or resampling approximations. Potential downsides to the Bayesian approach include prior specification which may be criticized as being subjective and computational challenges of obtaining MCMC samples. The former is minimized with the use of vague priors, and the latter due to standard Bayesian software that can fit the proposed model and the accessible R model-fitting function provided.

For study design, algorithms and an online web application are provided to determine power for and to assess the effects of estimating odds ratios with different quantification methods. The results from these provide another means of comparing method performances. Whereas the mixed model assesses performance on the measurement scale, the study design metrics assess performance in predicting clinical outcomes — the ultimate goal of a biomarker. For instance, bias, precision, mean-squared error, power, and probability coverage can be compared to study the accuracies and precisions in risk estimates. The power algorithms can aid in the design of clinical trials to directly study the prognostic performance of biomarkers.

Although the application in this paper focused on tumor volume as the biomarker, the analytic methods and software can be applied to other biomarkers. Indeed, several others can be derived from the QIN PET challenge and analyzed with the approach presented. Of particular interest will be the robustness of different biomarkers in estimating risk. One might expect that the commonly used SUV_max, which is a maximum voxel value, would be more similar across different segmentation methods than biomarkers that take into account all values within the segmented region. Nevertheless, rigorous statistical comparisons of such biomarkers will be crucial given the growing number of quantification methods and increasing interest in using biomarkers in clinical research and practice.