Molecular model of J-aggregated pseudoisocyanine fibers

Abstract

Aggregated cyanines form ordered supramolecular structures with the potential to transport energy efficiently over long distances, a hallmark of photosynthetic light-harvesting complexes. In concentrated aqueous solution, pseudoisocyanine (PIC) spontaneously forms fibers with a chiral J-band red-shifted 1600 cm⁻¹ from the monomeric 0–0 transition. A cryogenic transmission electron microscopy analysis of these fibers show an average fiber width of 2.89 nm, although the molecular-level structure of the aggregate is currently unknown. To determine a molecular model for these PIC fibers, the calculated spectra and dynamics using a Frenkel exciton model are compared to experiment. A chiral aggregate model in which the PIC monomers are neither parallel nor orthogonal to the long axis of the fiber is shown to replicate the experimental spectra most closely. This model can be physically realized by the sequential binding of PIC dimers and monomers to the ends of the fiber. These insights into the molecular aggregation model for aqueous PIC can also be applied to other similar cyanine-based supramolecular complexes with the potential for long-range energy transport, a key building block for the rational design of novel excitonic systems.

I. INTRODUCTION

Photosynthetic light-harvesting complexes feature molecular aggregates that can efficiently harvest light and transport energy to reaction centers for energy conversion,¹ a result of high absorption cross-sections amenable for light-absorption and fast energy transport through the aggregates. Mimicking the hierarchical structure of photosynthetic light-harvesting antennae may lead to efficient artificial devices operating under the same design principles.^2–4 1,1′-Diethyl-2,2′-cyanine or pseudoisocyanine (PIC) was one of the earliest molecular aggregates investigated and was discovered independently by Jelley^5,6 and Scheibe.^7,8 While the physicochemical properties of PIC aggregates have been investigated, the molecular structure remains to be understood.

In two early studies, Czikkely et al. used a brick-like structural model for the PIC J-aggregates⁹ and Daltrozzo et al. postulated four alternatives for the J-aggregate structure based on quasi-one-dimensional threads of parallel-displaced PIC monomers.¹⁰ Later, cryogenic transmission electron microscopy (cryo-TEM) measurements of PIC chloride in aqueous solution showed a homogeneous network of rod-like particles with a diameter of ∼2.3 nm, with a proposed structural model of six one-dimensional stacks of PIC threads forming a star-like or tubular arrangement.^11,12 More recently, molecular dynamics simulations have been used to elucidate structural dynamics of amphiphilic PIC aggregates^13,14 and the initial phase of PIC aggregation using both a pile of coins (H-aggregate) and parallel-displaced (J-aggregate) initial geometry.¹⁵ In addition to its self-aggregation properties in aqueous solution, PIC also shows promise as a scaffolded chromophoric material on DNA nanostructures.^16,17

In this study, we first perform an interaction energy scan of PIC dimerization, in order to quantify a potential physical model for the initial mode, or seed, of J-aggregation. Next, both thread-like and superstructural models of PIC molecular aggregates are investigated, and photophysical and excitonic characteristics are calculated and compared to prior and new experimental results obtained here. With these results, we present new superstructural models for PIC molecular aggregation that more closely resemble the absorption and circular dichroism (CD) data shown in experimental results.

II. EXPERIMENTAL METHODS

A. General

Pseudoisocyanine (PIC) iodide (catalog number: 323764), Dowex 1x2 chloride-form resin (200–400 mesh, catalog number: 217395), anhydrous ethanol (catalog number: 459836), and chromatography-grade diethyl ether (catalog number: 309966) were purchased from Millipore Sigma (St. Louis, MO) and were used as received. Sample preparations were all carried out in air and protected from light. High-resolution mass spectra (HRMS) were recorded on a Bruker Daltonics APEXIV 4.7 Tesla Fourier Transform Ion Cyclotron Resonance Mass Spectrometer (FT-ICR-MS) by electron spray ionization time-of-flight (ESI-TOF). Elemental analysis was performed by Robertson Microlit Laboratories (Ledgewood, New Jersey) using optimal combustion conditions to determine carbon, hydrogen, and nitrogen content in the sample and ion chromatography for chloride determination.

B. Steady-state spectroscopy

Optical spectra (linear absorbance, fluorescence, and circular dichroism) were measured using a demountable cuvette with 0.01 mm path length (catalog number: 20/O-Q-0.01, Starna Cells, Inc., Atascadero, CA). PIC chloride samples used for measurement were prepared by diluting a 15 mM stock solution of PIC in deionized water to a final concentration of 12.5 mM PIC chloride in deionized water. All samples were prepared only prior to measurement. The absorbance spectra of samples were measured using an Evolution 260 Bio UV-Visible spectrophotometer (Thermo Fisher, Waltham, MA) at room temperature. The fluorescence spectra of samples were measured using a Horiba Fluoromax-4C fluorimeter (Horiba Jobin Yvon, Edison, NJ) at room temperature. Fluorescence from samples was collected using front-collection geometry. Circular dichroism spectra were measured using a JASCO Model J-1500 circular dichroism spectrometer (JASCO, Inc. Easton, MD).

C. Synthesis of 1,1′-diethyl-2,2′-cyanine chloride (PIC chloride)

PIC chloride was obtained by converting commercially available PIC iodide to chloride form using anion-exchange chromatography, as described previously.¹⁸ Briefly, 80 mg of PIC iodide was dissolved in 200 cm³ of deionized water at 60 °C under sonication for 1 h. The sample was cooled to room temperature and loaded onto a Dowex 1X2 (200–400, chloride form) anion-exchange column (75 mm × 300 mm). The solution was allowed to flow by gravity without pressure at a rate of approximately 20 drops per minute. The resulting solution was filtered through a filter paper and water was removed under reduced pressure. The residue was dissolved in minimum amount of ethanol (20 cm³) and warmed to 50 °C until all residue was dissolved. The dark red solution was then rapidly poured to a chilled diethyl ether (kept at −20 °C for 1 h) and kept at −20 °C overnight. The mixture was then filtered, washed with chilled 1:1 ethanol:diethyl ether (kept at −20 °C for 1 h), and dried overnight in a 80 °C oven to obtain a red crystalline solid (55 mg, 86% yield).

HRMS (m/z): calculated for C₂₃H₂₃N₂Cl [(M + Cl)⁺] 362.1550, found 362.2137.

Elemental analysis for C₂₃H₂₃N₂Cl·H₂O: Expected: 72.52% C, 6.62% H, 7.35% N, and 9.31% Cl. Measured: 67.61% C, 6.43% H, 6.78% N, and 10.38% Cl.

D. Cryogenic transmission electron microscopy (Cryo-TEM) of PIC J-aggregates

A volume of 3 μL of 12.5 mM PIC J-aggregate in deionized water was dropped on a lacey copper grid coated with a continuous carbon film and blotted to remove excess sample without damaging the carbon layer using Gatan Cryo Plunge III. The sample grid was mounted on a Gatan 626 single tilt cryo-holder. The specimen and holder tip were cooled down by liquid nitrogen to maintain cryogenic temperatures during sample transfer into the microscope and subsequent imaging. Samples were imaged using a JEOL 2100 field-emission electron gun (FEG) microscope, minimizing electron dose to reduce sample damage under the electron beam. The microscope was operated at 200 kV and with a magnification in the range of 10 000–60 000 for assessing fiber sizes and distribution. All images were recorded on a Gatan 2k × 2k UltraScan CCD camera.

E. PIC fiber annotation

We annotated 175 fibers in 27 total cryo-TEM images and extracted fiber measurements from image subregions defined by user annotations. Only linear sections of fibers were annotated and analyzed. Cryo-TEM images were rotated using nearest-neighbor interpolation such that the fibers were oriented vertically. Image rotation did not impact the observed fiber width, as illustrated in Fig. S17(a) of the supplementary material. An 80 pixel wide crop was then taken from the cryo-TEM image centered on the fiber, where fiber annotations varied from 59 to 238 pixels in height [Fig. S17(b) of the supplementary material]. These images of the fibers were vertically concatenated into a single image 21 895 pixels in height and 80 pixels in width. To create the average image in Fig. 1(e), the concatenated fiber image was averaged with a window of 200 pixels. To create the average fiber line scan, the concatenated fiber image was averaged along the vertical dimension. To extract the fiber width from this image, the extent of the fiber is taken to be where the fiber line scan crosses the noise floor.^19,20 The noise floor of the image was estimated by a linear fit to points on the line scan greater than 5 nm away from the center of the fiber, and 50 points in total were used for this fit. This linear baseline estimation was then subtracted from the average fiber, and the center 40 points are shown in Fig. 1(f). The width of the fiber was found by where the line scan crosses zero after baseline subtraction, estimated by linear interpolation of the 3 closest points to where the line scan crosses zero. The standard deviation of the errors in this interpolation was added to the standard deviation of the baseline estimation to find the overall uncertainty of the fiber width measurement.

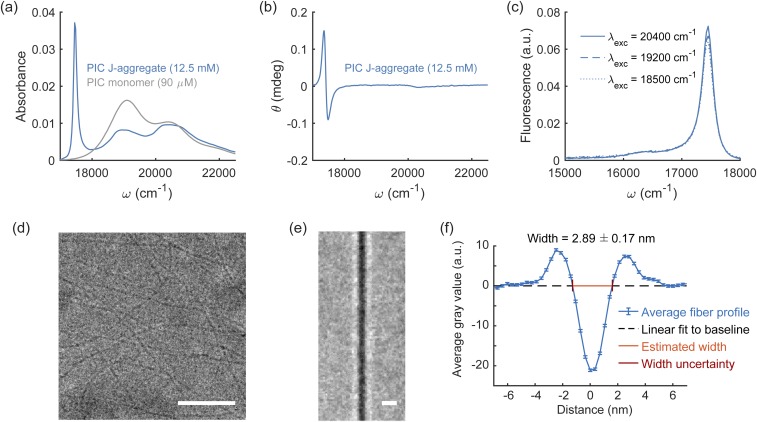
FIG. 1.

Spectroscopic and cryo-TEM images of PIC J-aggregates. PIC self-assembles into J-aggregates at high molar concentrations in deionized water (12.5 mM). (a) Formation of PIC J-aggregates leads to a bathochromic shift to 17 500 cm⁻¹ and narrowing in the absorbance spectrum (area normalized) compared to the monomer absorption maximum at 19 100 cm⁻¹. (b) In addition, PIC J-aggregates also exhibit an induced positive Cotton effect in the circular dichroism spectra wherein the optical rotation signal initially peaks then reaches a trough with increasing photon energy. (c) The fluorescence spectra of PIC J-aggregates have a narrow intensity peak at 17 500 cm⁻¹, which coincides with the J-aggregate absorbance maximum peak, and a vibronic sideband peak at 16 300 cm⁻¹. (d) Representative cryo-TEM image of PIC J-aggregates. (e) Average line scan of J-aggregate fibers. (f) Average fiber profile and estimated J-aggregate fiber width. The gray value is a measure of intensity of the transmitted electron beam. Scale bar: (d) 25 nm, (e) 5 nm.

III. COMPUTATIONAL METHODS

A. PIC coordinate system and transformations

To form PIC dimer structures, a Cartesian coordinate system is introduced with its origin at the point midway between atoms C4 and C8 of the right-hand quinoline structure. Using the Python package ProDy,²¹ a right-handed orthonormal basis $\left(\mathbf{x},\mathbf{y},\mathbf{z}\right)$ is then defined by the three principal axes of the point cloud generated by the atomic positions of the heavy atoms (C2, N3, C4, C5, C6, C7, C8, C9, and C10) in the right-hand quinoline structure, where x is coincident with the first principal axis and points in the direction of the vector from atom C2 to C6, y is coincident with the second principal axis and points in the direction of the vector from atom C4 to C8, and z = x × y. We define the coordinate systems for right- and left-handed PIC identically [Fig. 2(a)].

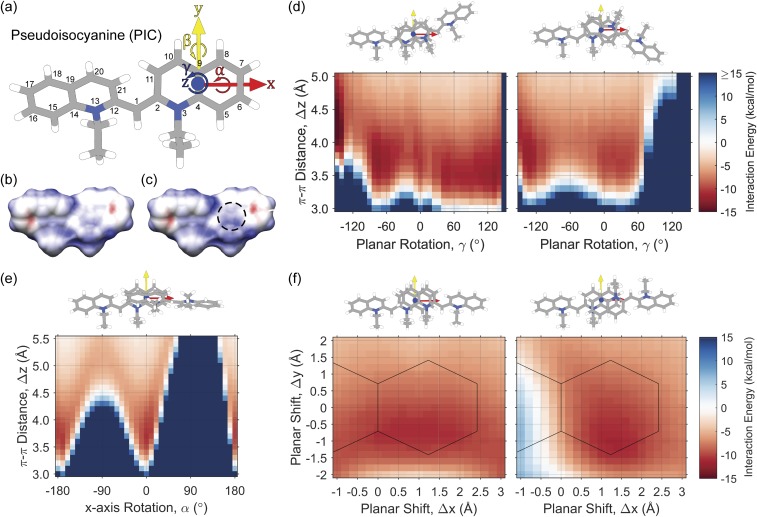
FIG. 2.

Interaction energies for PIC dimerization. (a) PIC coordinate system for J-aggregate dimerization. (b) Electrostatic potential of a monomer of PIC in aqueous solution. (c) Electrostatic potential of dimerized PIC in aqueous solution. The dashed region shows a decrease in electronegativity near the N atom upon dimerization. Red—negative potential, blue—positive potential. (d) Interaction energy surface of PIC dimers based on π–π stacking distance, Δz, and planar rotation, γ, with coordinate transformations $\left\{0.0,0.0,z,\mathrm{0,180},\gamma \right\}$ (left) and $\left\{0.0,0.0,z,\mathrm{180,180},\gamma \right\}$ (right). (e) Interaction energy surface of PIC dimers based on π–π stacking distance, Δz, and x-axis rotation, α, with coordinate transformation $\left\{0.0,0.0,z,\alpha ,\mathrm{180,0}\right\}$. (f) Interaction energy surface of PIC dimers based on planar x shift, Δx, and planar y shift, Δy, at a π–π stacking distance of Δz = 3.7 Å, with coordinate transformations $\left\{x,y,3.7,\mathrm{0,180,0}\right\}$ (left) and $\left\{x,y,3.7,\mathrm{180,180,0}\right\}$ (right). Solid lines outline the heavy atoms of the right-hand quinoline ring of the first PIC molecule. Interaction energies are calculated using dispersion-corrected DFT [DFT-D3/B3LYP/6-31+G(d)] with implicit water solvation using COSMO.

With this (x, y, z) coordinate system, we define a rotation about the x-axis as α, a rotation about the y-axis as β, and a rotation about the z-axis as γ. Throughout the manuscript, we refer to a PIC coordinate transformation using the following six degrees of freedom: {x, y, z, α, β, γ}, where distances are reported in Ångstroms and angles are reported in degrees. The Python package ProDy²¹ is then used to create PIC dimers using the appropriate transformation matrix.

B. Interaction energy calculations

Interaction energy calculations between two PIC molecules require the comparison of ground-state energies of the PIC monomer and the combined PIC dimers. The density functional theory (DFT)²² energies for each PIC monomer and dimer are calculated using dispersion-corrected DFT,²³ with the B3LYP functional,²⁴ and the 6-31+G(d) basis set^25,26 with implicit water solvation using the conductor-like screening model (COSMO)^27,28 as implemented in the NWChem 6.6 software package.²⁹ We test the basis set dependence of interaction energies in Fig. S1 of the supplementary material, showing no significant difference when using basis sets larger than or equal to 6-31+G(d). First, we perform ground-state DFT optimization of the PIC monomer, where the optimized right-handed molecule is shown in Fig. 2(a). Next, after a coordinate transformation to create a combined PIC dimer using the ground-state structure, we perform a single-point DFT energy calculation. The interaction energy of each PIC dimer is then calculated as E_int = E_dimer − 2E_monomer.

C. Electronic coupling calculations

After calculating PIC dimer interaction energies, the excited state properties of the PIC monomer fragments are calculated in order to compute the electronic couplings between each PIC dimer pair. PIC transition densities of the S₀ → S₁ excited state transition for each monomer are calculated with time-dependent density functional theory (TD-DFT),^22,30 using dispersion-corrected DFT,²³ the B3LYP functional,²⁴ the 6-31+G(d) basis set,^25,26 and implicit COSMO^27,28 water solvation, all implemented in the NWChem 6.6 software package.²⁹

TD-DFT calculations of a PIC monomer show a 0–0 transition energy of 2.75 eV (22 180 cm⁻¹) with a transition dipole strength of 6.7 D. The experimental absorption spectra of the PIC monomer (90 µM in water) show a 0–0 transition energy of 19 100 cm⁻¹, indicating a red-shifted value calculated using TD-DFT. In subsequent calculations, it is important to use an accurate experimental value for the transition dipole moment strength. The experimental oscillator strength, f, is calculated as³¹

$$f=4.319\times 10^{-9}\int \epsilon \left(\nu \right)d\nu ,$$ (1)

where ν is the frequency in cm⁻¹ and ε(ν) is the molar absorption coefficient in L mol⁻¹ cm⁻¹, and can be related to the transition dipole moment, μ, using³¹

$$f=\frac{4\pi m_e\nu }{3e^2\hslash }{\mu }^2.$$ (2)

When integrating over the experimental absorption spectra of the PIC monomer, an oscillator strength of 0.55 and transition dipole moment strength of 6.2 D is calculated. In addition, Haverkort et al. recently calculated an oscillator strength of 0.68 (6.8 D) for the similar amphi-PIC molecule.¹⁵ As the transition dipole moment strengths are in good agreement between TD-DFT and the experiment, no subsequent scaling is necessary.

The transition density cube (TDC) method³² is employed to accurately estimate the electronic couplings, which discretizes the transition densities onto a volumetric grid. The electronic coupling, V_DA, using the TDC method is represented as

$$V_{DA}\approx V_{TDC}=\sum _{i,j}\frac{M_D\left(i\right)M_A\left(j\right)}{4\pi {\epsilon }_0{r}_{ij}},$$ (3)

where M_D,A represents the discretized transition densities calculated from the ground and first excited state wavefunctions of the donor (D) and acceptor (A) dye molecules,

$$M_{D,A}\left(x,y,z\right)=V_{\delta }{\int }_z^{z+{\delta }_z}{\int }_y^{y+{\delta }_y}{\int }_x^{x+{\delta }_x}|{\psi }_0⟩⟨{\psi }_1|dxdydz,$$ (4)

with grid size, δ, and volume element, V_δ.

Using Eq. (3), we are assuming that the electronic coupling, V_DA, consists solely of long-range Coulombic interactions and that any short-range exchange interactions are negligible.³³

D. PIC linear and superstructural aggregation models

Linear aggregation models for PIC are formed by sequential coordinate transformations using the aforementioned PIC coordinate system on right-handed, left-handed, and racemic mixtures of PIC monomers. To perform the sequential coordinate transformations, we utilize the Python package ProDy.²¹ Racemic linear aggregation models additionally require the ground-state PIC structure to be switched as the aggregate alternates between right- and left-handed PIC molecules. This is achieved by overlapping the right- and left-handed PIC coordinate systems prior to the coordinate transformation.

For linear PIC aggregation models as shown in Figs. 3(a)–3(e), the first twenty monomeric sites are retained for subsequent excited state and electronic coupling analysis. Using TD-DFT^22,30 as described above, the transition densities of the S₀ → S₁ excited state transition for each monomer are calculated, and the electronic couplings between each PIC monomer pair in the linear aggregate are calculated using the TDC method³² to form a site-basis electronic Frenkel Hamiltonian, Ĥ_elec, for each aggregate model for N monomeric units, which is described as

$${Ĥ}_{elec}=\sum _i^N{\nu }_i|{\psi }_i⟩⟨{\psi }_i|+\sum _i^N\sum _{j\ne i}^N{V}_{ij}|{\psi }_j⟩⟨{\psi }_i|,$$ (5)

where ν_i is the site energy of the S₀ → S₁ electronic transition of the ith PIC molecule, |ψ_i⟩ describes the excited state molecular wavefunction for the monomeric site, and V_ij is the Coulombic electronic coupling between the ith and jth monomeric sites.³⁴

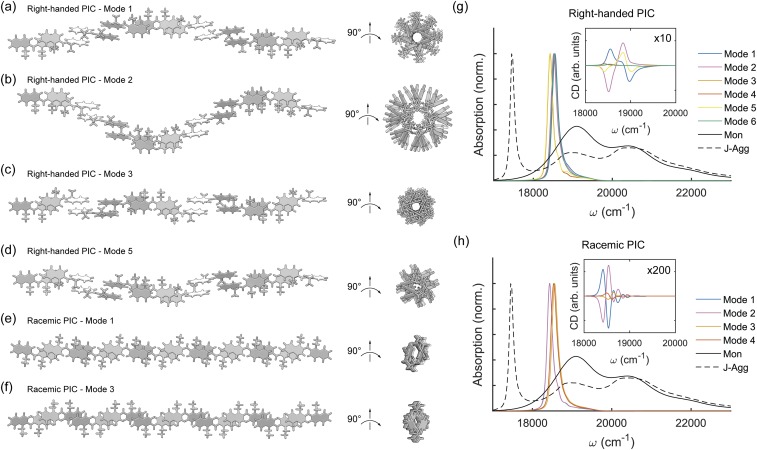
FIG. 3.

Linear PIC aggregation models. (a) PIC right-handed linear aggregation using Δx = 1.2 Å, Δz = 3.7 Å, and β = 180°. (b) PIC right-handed linear aggregation using Δx = 1.2 Å, Δz = −3.7 Å, and β = 180°. (c) PIC right-handed linear aggregation using Δx = 1.2 Å, Δz = 3.7 Å, α = 180°, and β = 180°. (d) PIC right-handed linear aggregation using Δx = 1.2 Å and β = 180° and alternating between Δz = 3.7 Å and −3.7 Å. (e) PIC racemic linear aggregation using Δx = 1.2 Å, α = 180°, and β = 180° and alternating between Δz = 3.7 Å and −3.7 Å. (f) PIC racemic linear aggregation using Δx = 1.2 Å, α = 180°, and β = 180°, where PIC is alternated between Δz = 3.7 Å and −3.7 Å, as well as right- and left-handed stereoisomers. Calculated PIC absorption and circular dichroic spectra for (g) right-handed and (h) racemic linear aggregates compared to the PIC monomer (Mon) and J-aggregate (J-Agg) spectra. Other modes of linear aggregation including left-handed PIC not shown here are detailed in Figs. S2–S4 of the supplementary material. Site-basis Hamiltonians for each model are also shown in Figs. S2–S4 of the supplementary material. Calculated absorption and circular dichroism spectra for left-handed linear aggregates is shown in Fig. S7 of the supplementary material.

The superstructural aggregation models for PIC require similar sequential coordinate transformations to the linear aggregation models, but these transformations are multi-step processes, outlined further in Figs. 4(a)–4(d). Similarly, the first forty (“chiral fiber” and “crystal”), thirty-nine (“stacked disk”), or thirty-six (“cylinder”) monomeric sites are retained for subsequent electronic coupling analysis. The aggregate sizes are chosen so that the model system is several times larger than the hypothesized excitonic coherence length, while balancing the computational cost of running the excitonic analysis.

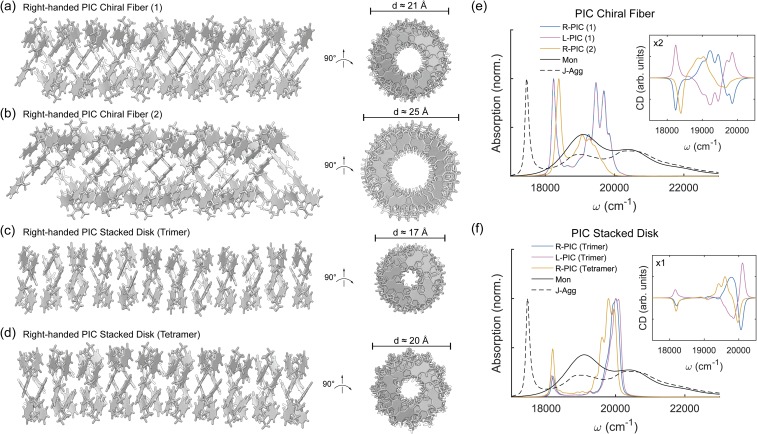
FIG. 4.

Chiral PIC superstructure models. (a) PIC right-handed linear aggregation using x = 1.2 Å, z = 3.7 Å, β = 180°, and γ = 78°, creating a rod-like superstructure with diameter d ≈ 21 Å. (b) PIC right-handed linear aggregation using two chiral threads of x = 1.2 Å, z = 3.8 Å, β = 180°, and γ = 60°, creating a rod-like superstructure with diameter d ≈ 25 Å. (c) PIC right-handed stacked disk superstructure where trimeric disks are built using x = 1.4 Å, y = 1.4 Å, z = 3.7 Å, β = 180°, and γ = 120°, with diameter d ≈ 17 Å. (d) PIC right-handed stacked disk superstructure where tetrameric disks are built using z = 3.7 Å, α = 10°, β = 180°, and γ = 90°, with diameter d ≈ 20 Å [(e) and (f)] Calculated PIC absorption and circular dichroic spectra for the right- and left-handed chiral and stacked aggregates compared to PIC monomer (Mon) and J-aggregated (J-Agg) spectra. Electronic couplings are calculated using the transition density cube (TDC) method from excited states calculated using TD-DFT [DFT-D3/B3LYP/6-31+G(d)] with implicit water solvation using COSMO. Site-basis Hamiltonians for each model are shown in Fig. S5 of the supplementary material.

E. Computed absorption and circular dichroism spectra

The absorption and circular dichroism spectra can be computed by first diagonalizing the site-basis Frenkel Hamiltonian to solve the stationary Schrödinger equation in the excitonic basis, Ĥ|ϕ_k⟩ = ε|ϕ_k⟩, where the excitonic wavefunctions, |ϕ_i⟩, are expanded over the set of monomeric wavefunctions, |ϕ_k⟩ = ∑_iU_ik|ψ_i⟩. From this procedure, the excitonic wavefunction energies, ε_i and amplitudes, U_ik, are obtained^34,35 and can be used to calculate the spectral properties of the PIC aggregates.

The absorption and circular dichroism stick spectra are calculated using the excitonic site energies and amplitudes from the diagonalized Frenkel Hamiltonian and the transition dipole moments, μ, of the monomeric excited states. The absorption stick-spectra intensities are calculated using

$${\mu }_i^2=\sum _{j,k=1}^N\left({\overrightarrow{\mu }}_j\cdot {\overrightarrow{\mu }}_k\right)U_{ji}{U}_{ki},$$ (6)

and the circular dichroism stick-spectra intensities are calculated using

$${\mathcal{R}}_i=1.7\times 10^{-5}\cdot \sum _{j,k=1}^N{\epsilon }_i\left[{\overrightarrow{R}}_{jk}\cdot \left({\overrightarrow{\mu }}_k\times {\overrightarrow{\mu }}_j\right)\right]U_{ji}{U}_{ki},$$ (7)

with units of μ in Debye, ε in cm⁻¹, μ² in Debye², R in nm, and $\mathcal{R}$ in Debye-Bohr magnetons.^34,35 To compare the amplitudes of absorption and CD spectra, the CD amplitudes are calculated in units of Debye², by changing the pre-factor in Eq. (7) to (π/2)·10⁻⁷, and an additional pre-factor of (1/3) is also included in Eqs. (6) and (7) due to the random spatial orientation of the absorbers.³⁴ For spectral calculations of PIC aggregates, we use an S₁ site energy of ν = 19 100 cm⁻¹, with a FWHM of 400 cm⁻¹, due to line narrowing in the aggregate based on less static disorder than in the monomer. This homogeneous linewidth is estimated using $W_{agg}=W_{mon}/N_{agg}^{1/2}$, where W_agg is the FWHM of the aggregate, W_mon is the FWHM of the monomer (1200 cm⁻¹), and N_agg is the effective delocalization length of the exciton in the aggregate.³⁵ In Fig. S6 of the supplementary material, homogeneous and inhomogeneous linewidths are varied, and we use W_agg = 400 cm⁻¹ and γ = 25 cm⁻¹ based on this qualitative analysis. Homogeneous linewidths of PIC iodide and PIC bromide have previously been estimated with values ranging from ∼10–50 cm⁻¹ in varying conditions.^36–39 Static disorder is included in the spectral calculations by randomizing the diagonal site energies based on a normal distribution. Each of the individual absorption and circular dichroism spectra includes homogeneous broadening, which is included using a Cauchy distribution as follows:

$$A\left(\omega \right)=\sum _i^N{\mu }_i^2\left(\frac{{\gamma }^2}{\left(\omega -{\epsilon }_i\right)+{\gamma }^2}\right),$$ (8)

$$CD\left(\omega \right)=\sum _i^N{\mathcal{R}}_i\left(\frac{{\gamma }^2}{\left(\omega -{\epsilon }_i\right)+{\gamma }^2}\right),$$ (9)

and then, the calculated individual spectra are averaged from 10 000 trial aggregate systems with randomized site energies.

F. Exciton transport calculations and properties

To study the exciton transport properties of the PIC aggregates, we employ the Frenkel exciton Hamiltonian as Ĥ_tot = Ĥ_elec + Ĥ_ph + Ĥ_reorg + Ĥ_el−ph, where Ĥ_elec is the electronic Hamiltonian in the absence of environmental phonon modes, Ĥ_ph is the phonon Hamiltonian of the thermal bath, Ĥ_reorg is the reorganization of the electronic states with respect to the thermal bath, and Ĥ_el–ph is the coupling between the electronic and phonon degrees of freedom.⁴⁰ In the weak electron-phonon coupling regime, the standard full Redfield approximation is reached where the time-evolution of the quantum master equation in the exciton basis is written as^40–42

$$\frac{\partial }{\partial t}{\rho }_{ab}\left(t\right)=-i{\omega }_{ab}{\rho }_{ab}\left(t\right)+\sum _{c,d}{R}_{ab,cd}{\rho }_{cd}\left(t\right),$$ (10)

where ρ_ab is the reduced density matrix in the exciton basis and R_ab,cd is the relaxation matrix, also called the Redfield tensor, which is described as

$$\begin{array}{ccc}\hfill R_{ab,cd}& =\hfill & {\delta }_{ac}\sum _e{\mathrm{\Gamma }}_{be,ed}\left({\omega }_{dc}\right)+{\delta }_{bd}\sum _e{\mathrm{\Gamma }}_{ae,ec}\left({\omega }_{ce}\right)\hfill \\ \hfill & \hfill & +{\mathrm{\Gamma }}_{ca,bd}\left({\omega }_{db}\right)-{\mathrm{\Gamma }}_{db,ac}\left({\omega }_{ca}\right),\hfill \end{array}$$ (11)

where the damping matrix elements, Γ_ab,cd, are written as

$${\mathrm{\Gamma }}_{ab,cd}\left({\omega }_{dc}\right)=\frac{1}{{\hslash }^2}\sum _{i,j}⟨{\varphi }_a|V_i|{\varphi }_b⟩⟨{\varphi }_c|V_j|{\varphi }_d⟩C_{ij}\left({\omega }_{dc}\right),$$ (12)

and C_ij(ω_dc) is the response of the phonon correlation function at frequency ω_dc = (ε_d − ε_c)/ℏ. The phonon correlation function is written as

$$C_{ij}\left(t\right)=\frac{\hslash }{\pi }{\int }_{-\infty }^{\infty }\mathcal{J}\left(\omega \right)[n_{BE}\left(\omega \right)+1]e^{-i\omega t},$$ (13)

with the Bose-Einstein distribution, n_BE = 1/(e^βℏω − 1), and a Drude-Lorentz spectral density described as

$$\mathcal{J}\left(\omega \right)=2\lambda \frac{\omega \gamma }{{\omega }^2+{\gamma }^2},$$ (14)

where reorganization energy λ = 29 cm⁻¹ and bath correlation energy γ = 150 cm⁻¹.¹⁶

For exciton dynamics using Redfield theory, we again use an S₁ site energy of ν = 19 100 cm⁻¹, with a FWHM of 400 cm⁻¹, the same parameters as in the spectral calculations. Diagonal disorder is included in the exciton dynamics by randomizing the site energies based on a normal distribution. The excitonic properties are averaged from 50 trial aggregate systems with randomized site energies, where the quantum master equation is propagated for 5 ps with the exciton initialized locally on the first site.

The extent of delocalization of the excitons, or exciton coherence length, L_p, can be calculated using the inverse participation ratio of the time-dependent density matrix as

$$L_p\left(t\right)=\frac{{\left({\sum }_{mn}|{\rho }_{mn}\left(t\right)|\right)}^2}{N{\sum }_{mn}|{\rho }_{mn}\left(t\right){|}^2},$$ (15)

where ρ_mn(t) is the time-dependent reduced density matrix in the site basis.⁴³

IV. RESULTS AND DISCUSSION

A. Experimental characterization of PIC J-aggregate

PIC chloride spontaneously forms J-aggregates in pure water at high monomer concentrations. At 12.5 mM PIC chloride in water, a narrow band that is bathochromically shifted by 1600 cm⁻¹ relative to the PIC monomer peak absorbance at 19 100 cm⁻¹ emerges, indicating the formation of PIC J-aggregates^8,11,44 [Fig. 1(a)]. The circular dichroism (CD) [Fig. 1(b)] spectrum of the PIC J-aggregates in aqueous solution show a bisignate CD trace with a positive Cotton effect; i.e., the CD signal initially peaks and then progresses to a trough with increasing photon energy. The positive couplet in the CD spectra occurs at the same photon energy bandwidth (17 500–18 000 cm⁻¹) as in the J-aggregate absorbance spectra, which suggests that the CD signal may originate from exciton coupling in J-aggregates. The fluorescence spectra of PIC J-aggregates excited at different energies [Fig. 1(c)] consistently show a peak at 17 500 cm⁻¹ and a weak vibronic sideband at 16 300 cm⁻¹. Using the relative fluorescence intensities of the 0–0 J-aggregate band at 17 500 cm⁻¹ (I₀₋₀) and the 0–1 J-aggregate band at 16 300 cm⁻¹ (I₀₋₁), the exciton coherence length N_coh can be estimated by⁴⁵

$$\frac{I_{0\text{–}0}}{I_{0\text{–}1}}=\frac{N_{coh}}{{\lambda }^2},$$ (16)

where λ² is the Huang-Rhys factor of the coupled vibrational mode (0.605 for PIC¹⁵). We have observed previously¹⁷ that Eq. (16) provides a comparable estimate of N_coh for PIC J-aggregates when compared to radiative enhancement measurements as an estimate for N_coh. The estimated exciton coherence length for PIC J-aggregates formed from 12.5 mM PIC solutions is 8.9 ± 2.9 (mean ± s.d. of three independent replicates). The exciton coherence length of DNA-templated PIC J-aggregates,^16,17 by contrast, has been measured to be 1.5–2.0, which is attributed to smaller J-aggregates formed on the templating DNA sequence^16,17 compared to the long continuous PIC J-aggregate fibers observed here.

Cryo-TEM images of J-aggregates formed from 12.5 mM PIC in water show dense fiber-like structures [Fig. 1(d)]. We manually annotated straight sections of fibers and used these annotations to estimate the width of fibers. We rotated, cropped, and averaged these images in order to produce the average fiber shown in Fig. 1(e). By averaging the collection of fibers in the y-direction and subtracting a linear fit to the background, we produce the average fiber profile shown in Fig. 1(f). Individual fiber profiles are in good agreement with average fiber profiles but have increased noise [Fig. S18(a) of the supplementary material]. Estimated widths of individual fiber profiles are distributed normally around an average of 2.99 ± 0.19 nm [Fig. S18(b) of the supplementary material], and the estimated width of the average fiber was found to be 2.89 ± 0.17 nm [Fig. 1(f)].

B. Energy surface of PIC dimerization

There is evidence that PIC dimerizes in solution above a critical concentration prior to forming a J-aggregate, noticeable as an increase and blue-shift of the monomer 0–1 vibronic progression.⁴⁶ Assuming that this dimerization is necessary for subsequent formation of the J-aggregate, it is important to quantify the relative interaction energy surface of PIC dimerization to gauge how the PIC monomers may interact in solution. In Fig. 2, the interaction energy potential surface for PIC dimerization is sampled based on the PIC coordinate system centered on the heavy atoms of the quinoline rings [Fig. 2(a)].

Monomeric PIC carries a positive charge, which is delocalized evenly over the two quinoline rings [Fig. 2(b)], with an electron-deficient region near the nitrogen atoms and an electron-rich region on the face of the outer rings. For this reason, the face-centered parallel π-stacking configuration is not likely to be the most favorable to PIC dimerization. Instead, an offset parallel configuration will allow the electron-deficient nitrogens to face the electron-rich outer rings, leading to a more favorable aromatic donor-acceptor interaction.⁴⁷ In the case of a strongly interacting PIC dimer, the positive charge on each monomer is redistributed, strengthening both the electron-deficient nitrogens and the electron-rich outer rings [Fig. 2(c)].

In order to determine the most favorable interaction energies of PIC dimerization, we rotate parallel face-centered PIC dimers around their z-axis [Fig. 2(d)], rotate perpendicular PIC dimers around their x-axis [Fig. 2(e)], and shift parallel face-centered PIC dimers along the x-y plane [Fig. 2(f)]. When rotating the γ angle with cis-ethyl groups between PIC dimers, the following minima are noted: −16.7 kcal/mol {0.0, 0.0, 4.2, 0, 180, −150}, −12.9 kcal/mol {0.0, 0.0, 3.5, 0, 180, −75}, −10.9 kcal/mol {0.0, 0.0, 3.7, 0, 180, −5}, −11.8 kcal/mol {0.0, 0.0, 3.5, 0, 180, 45}, and −12.9 kcal/mol {0.0, 0.0, 3.5, 0, 180, 135}. While the parallel face-centered π-stacking interaction is favorable, it is energetically preferred to rotate both clockwise and counter-clockwise around the z-axis. Clockwise rotation brings the nitrogens in line, requiring a greater π-stacking distance for favorable interactions, and counter-clockwise rotation moves the nitrogens away from each other, allowing for closer dimerization due to the aromatic donor-acceptor interaction. At γ = −150°, both quinoline rings are interacting, forming an H-aggregated dimer with noticeably lower interaction energy than the J-aggregated dimers.

Next, we rotate the γ angle with trans-ethyl groups between PIC dimers [Fig. 2(d), right] and note the following two minima: −10.4 kcal/mol {0.0, 0.0, 3.7, 180, 180, 35} and −12.2 kcal/mol {0.0, 0.0, 3.8, 180, 180, −130}. Here, the parallel face-centered orientation is part of the broad energetically favorable area when rotating counter-clockwise around the z-axis, as the nitrogens are already in a favorable position over the outer rings. Slightly more energetically favorable is the dimer conformation when rotating clockwise to −130° and beyond, as this begins to form an H-aggregated complex with both quinolines interacting.

As edge-to-face interactions are important in other aromatic dimer complexes (e.g., benzene^47,48), we rotate the α angle between PIC dimers to compare interaction energies to the face-centered orientations [Fig. 2(e)]. We note the following two minima, which correspond to the face-centered orientations: −10.3 kcal/mol {0.0, 0.0, 3.6, −170, 180, 0} and −10.6 kcal/mol {0.0, 0.0, 3.7, 0, 180, 0}. Thus, the edge-to-face interactions are not energetically favorable in PIC dimers when compared to the face-centered orientations.

Finally, we compare the shifted face-centered orientations of PIC dimers [Fig. 2(f)] to the rotated face-centered orientations, and we note the following two minima: −11.0 kcal/mol {1.6, −0.8, 3.7, 0, 180, 0} and −11.3 kcal/mol {1.2, −1.0, 3.7, 180, 180, 0}. The resulting minima are offset from the face-centered orientation due to a combination of van der Waals repulsion between the ethyl groups and quinoline rings and dispersive attraction as the electron-deficient nitrogens move apart and closer to the electron-rich outer rings.

C. PIC linear J-aggregation models

In the work of Daltrozzo et al.,¹⁰ several linear structural models are proposed for the PIC J-aggregate. We extend this analysis here to build all possible linear motifs for PIC J-aggregates, as shown in Fig. 3. (Due to the assumed linearity, the possible degrees of freedom for dimerization of PIC are above/below, cis/trans, and right/left-handedness. Randomized sequential models are not considered.) For each linear motif, we fix Δx = 1.2 Å, Δy = 0.0 Å, β = 180°, and γ = 0°. We use an offset Δx value due to the offset local minima shown in Fig. 2(f). By alternating between Δz = 3.7 Å (above) and −3.7 Å (below), and α = 0° (N-atoms same side) and 180° (N-atoms opposite sides), chiral linear chains using either R- or L-PIC can be built. In Fig. 3, right-handed mode 3 is equivalent to model A2 in the work of Daltrozzo et al.; likewise, right-handed mode 5 is equivalent to model B2.¹⁰ All six right- and left-handed linear models are detailed in Figs. S2 and S3 of the supplementary material.

In addition, 1:1 racemic mixtures of PIC can form achiral linear structures, as shown in Figs. 3(e) and 3(f). Racemic mode 1 is equivalent to model A1 in the work of Daltrozzo et al. All four racemic linear models are detailed in Fig. S4 of the supplementary material. We extend each linear model to twenty monomeric PIC units to study their respective excitonic characteristics. Electronic couplings are calculated between each set of monomeric units using the transition density cube (TDC) method to form a site-basis Hamiltonian, and absorption and circular dichroism spectra are calculated from the exciton-basis Hamiltonian as detailed in Sec. III.

While it is unlikely that the aqueous structure of PIC fibers is due to an ideal linear chain, these models are useful as building blocks for more complicated superstructural models. The linear J-aggregation models all contain open π-bonded regions along the long-axis, suggesting that a homogeneous PIC fiber cannot be built using one ideal linear chain, as lateral PIC aggregation will be favorable. All linear chain models contain strong J-aggregation absorption signatures (red-shifted 0–0 energies) and no H-aggregation absorption signatures (blue-shifted 0–0 energies), as expected. Strong chirality is observed in linear modes 1 and 2, for both right- and left-handed PIC molecules, with a positive Cotton effect observed in left-handed linear mode 1. Symmetrical features are seen in right-handed PIC mode 1 and left-handed PIC mode 2, and vice versa. The chiral signature most closely resembling that of the experimental CD spectra belongs to the left-handed PIC mode 1 (opposite chirality to right-handed PIC mode 2), suggesting that a similar motif may be present in the PIC fiber.

The chiral linear models can be directly compared to the achiral racemic models. While the J-aggregation absorption signature is still strong, the magnitude of the computed CD spectra shows little-to-no chirality, with oscillator strengths an order of magnitude smaller than the chiral models. Unfortunately, the magnitude of CD chirality cannot be directly compared to the experimental spectra, as the concentration of PIC aggregates in solution is unknown. Thus, racemic linear chains are unlikely to be present as a structural motif in the PIC fiber.

D. PIC superstructural J-aggregated models

As the number of variables to consider when forming a superstructural model is quite daunting, several assumptions are implemented in order to reduce the structural space. First, we assume a homogeneous design motif along the long axis of the PIC fiber so that ideal superstructural models can be compared. The width of the fiber from cryo-TEM points toward relative homogeneity, so while it is possible that several distinct fiber types are present in the sample, we assume for simplicity in the subsequent models that the sample is homogeneous. Second, the atomic coordinates of the PIC monomer are maintained in their ground-state orientation from DFT. The rigidity of this ground-state model during aggregation is uncertain but would require extensive molecular dynamics simulations to uncover any deviations, so the ground-state structure of PIC is assumed to be a reasonable average. Third, these superstructural models are built in gas-phase conditions with no salt ions present. While the anions (Cl⁻) in solution are likely to be important factors in stabilizing the PIC fiber, it is assumed that they do not contribute to the excitonic behavior of the PIC aggregates.

Three distinct types of superstructural fiber models are compared to a 2D crystal lattice in Figs. 4 and 5. The first type of model considered is denoted as a “chiral fiber,” due to the x-axis of PIC residing parallel to neither the long- or short-axis of the fiber [Fig. 4(a)]. This “chiral fiber” model is formed by starting from PIC linear mode 1 [Fig. 3(a)] and rotating the γ-angle to 78°. At this angle, a full lateral rotation occurs slightly after every fourth PIC monomer. Upon extension into a fiber, this superstructural model combines the characteristics of linear modes 1 and 2 with rotated γ angles. A second “chiral fiber” model is considered, where the γ-angle is rotated to 60° so that a full lateral rotation occurs after every fifth PIC monomer. The second model requires two separate threads to be rotated simultaneously. Physically, the “chiral fiber” model could form in solution either by monomers individually aggregating or by prior PIC dimerization, followed by dimers aggregating. The first “chiral fiber” model is approximately 21 Å in diameter, which is less than the experimental value of 29 Å. While this diameter estimate is outside of experimental error measurements from cryo-TEM, the structural placement of Cl⁻ anions around the PIC fiber could potentially add 3–4 Å to the width. The second “chiral fiber” model is larger, at approximately 25 Å in diameter, and would closely match the experimental width when including anions.

FIG. 5.

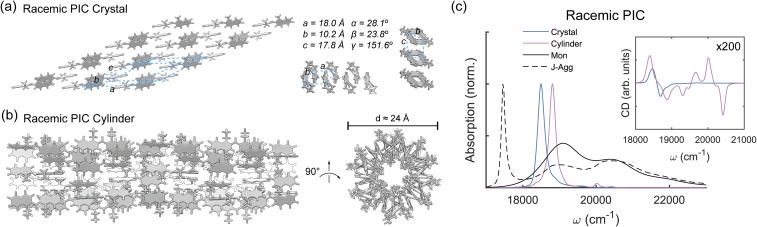
Racemic PIC superstructure models. (a) PIC racemic crystal structure with 8 × 5 monomeric units. (b) Star-like PIC racemic cylinder with four stacked units. (c) Calculated PIC absorption and circular dichroic spectra for the racemic PIC superstructures compared to PIC monomer (Mon) and J-aggregated (J-Agg) spectra. Electronic couplings are calculated using the transition density cube (TDC) method from excited states calculated using TD-DFT [DFT-D3/B3LYP/6-31+G(d)] with implicit water solvation using COSMO. Site-basis Hamiltonians for each model are shown in Fig. S5 of the supplementary material.

Using 40 PIC monomers, the excitonic characteristics of the “chiral fiber” models are calculated as before. For the first model (γ = 78°), the calculated absorption spectra shows both a sharp J-aggregate peak at 18 250 cm⁻¹ and a set of H-aggregate peaks centered around 19 500 cm⁻¹ [Fig. 4(e)]. The second model (γ = 60°) has a J-aggregate peak at 18 400 cm⁻¹ and a set of smaller H-aggregate peaks from 19 050 to 19 500 cm⁻¹. These J- and H-aggregate signatures are not as red- and blue-shifted (respectively) as the experimental results, but this could be due to several reasons. First, by including more PIC monomers in the excitonic calculation, the J- and H-aggregation would strengthen in coherence length, potentially shifting both peaks further from the monomeric 0–0 transition energy. Second, the site-site electronic couplings neglect the short-range exchange interactions, which are important for closely packed dimers. Third, small changes in superstructural patterning can affect the excitonic characteristics. The experimental fiber structure may be close to this idealized model but may have optimized excitonic properties. Calculated circular dichroism shows strong chirality of both the J- and H-aggregate regions of the structure. The left-handed J-aggregate peak matches the experimental CD result, but the H-aggregate chirality is stronger than that seen in experiment. This, again, may be due to deviations in the experimental structure from this idealized model. The second “chiral fiber” model, which has weaker H-aggregate chirality than the first “chiral fiber” model, is closer to the experimental CD spectra.

The second type of model considered is denoted as a “stacked disk,” due to the x-axis of PIC residing nearly parallel to the short-axis of the fiber [Fig. 4(b)]. This “stacked disk” model is built by first forming disks (rotating the γ-angle of PIC linear mode 1 to 120° for a trimer and 90° for a tetramer). Next, the disks are stacked to maximize π–π bonding between separate disks. Physically, a two-step mechanism in solution would involve prior formation of disks, followed by disk aggregation to form the fiber. The “stacked disk” model with a trimer disk is approximately 17 Å in diameter, and the “stacked disk” model with a tetramer disk is approximately 20 Å in diameter. As mentioned previously, structural placement of anions around the fiber could add 3–4 Å to this diameter measurement.

Using 39 PIC monomers for the trimer model and 40 PIC monomers for the tetramer model, the excitonic characteristics of the “stacked disk” model are calculated as before. The calculated absorption spectra for both the trimer and tetramer models show a sharp J-aggregate peak near 18 200 cm⁻¹ and a sharp H-aggregate peak near 20 000 cm⁻¹ (trimer) and several H-aggregate peaks centered near 19 775 cm⁻¹ (tetramer). In the “stacked disk” model, the J-aggregate intensity is lower than the H-aggregate intensity, which does not match the experimental results. Additionally, the calculated CD results show stronger H-aggregate chirality than J-aggregate chirality, also not indicated in the experimental CD spectra. So, while the physical model of disk aggregation seems reasonable, the calculated spectral properties do not point to the “stacked disk” model being the correct structural form of the PIC fiber.

The third type of model considered is denoted as a “cylinder,” due to the x-axis of PIC residing nearly parallel to the long-axis of the fiber [Fig. 5(b)]. Due to the racemic composition of the “cylinder,” the excitonic characteristics are compared to a 2D racemic “crystal” lattice, as seen in Fig. 5(a). The 2D “crystal” is formed by combining linear racemic modes 1 and 3 (Fig. 3). The “cylinder,” inspired by the “star-like” model proposed by von Berlepsch et al.,¹¹ requires a complicated formation process. First, monomeric “cylinders” (12 PIC monomers) are formed by rotating the α-angle by 30°. Monomeric “cylinders” alternating between right- and left-handed PIC regions are then brought into contact in a gear-like manner. This “cylinder” model does not relate to any of the linear models presented in Fig. 3 and does not seem likely to form physically because of the complicated formation process.

Nevertheless, the excitonic characteristics of the “cylinder” can be analyzed to compare to the “chiral fiber” and “stacked disk” models. Using 36 PIC monomers for the “cylinder” (12 PIC monomers in each “gear”-like section) and 40 PIC monomers for the “crystal” (an 8 × 5 lattice), the absorption and CD spectra are calculated as before. The calculated absorption spectra for the “crystal” and “cylinder” show strong J-aggregate peaks near 18 500 cm⁻¹ and 18 800 cm⁻¹, respectively. No blue-shifted absorption peaks are noted in the calculated absorption spectra. In addition, the calculated CD spectra of both the “crystal” and “cylinder” show very weak chirality of the J-aggregate band, with a magnitude ∼100 times lower than the “chiral fiber” or “stacked disk” models. Since the experimental results show both J- and H-aggregated spectral characteristics with structural chirality, it is not likely that the PIC fiber is formed in this manner.

E. Accuracy of excitonic predictions

In all of the calculated absorption spectra presented (Figs. 3–5), the J-aggregate peaks are not as red-shifted from the monomer 0–0 band as predicted from the experiment (∼17 500 cm⁻¹). If it is assumed that the quantum mechanical wavefunctions for the S₁ excited state of PIC are qualitatively accurate (quantitative accuracy of the transition dipole moment is achieved by scaling to the experimental value), then there are several potential sources of error in the calculated excitonic energy levels. First, in the site basis, the electronic couplings between monomers are assumed to contain no short-range electron exchange interactions. This assumption is adequate for monomers which share no atomic orbital overlap but is problematic between PIC monomers which are in direct atomic orbital contact. Because of this, the electronic couplings between closely packed PIC monomers are too low, requiring an additional electron exchange interaction term.³³ Additionally, any charge-transfer exciton states are ignored in the Frenkel Hamiltonian model, which may not be an adequate assumption based on recent evidence in tetracene crystals, which show strong Davydov splitting due to the charge-transfer excitons.⁴⁹ Second, in the exciton basis, the number of monomers included in the Hamiltonian should be larger than the system’s maximum exciton coherence length, to allow excitonic transport in the system. Third, the electronic-vibrational coupling to the high-frequency mode present in PIC (∼1400 cm⁻¹) is ignored in this model.

The first source of error, the neglect of electron exchange interaction between closely packed monomers, is difficult to compute due to the complexity of interacting monomeric wavefunctions. (The Coulombic interaction assumes non-interacting monomeric wavefunctions.) Nevertheless, to test the effect of an increase in electron exchange interaction to the closely packed monomeric site energies, an empirical interaction term can be added to the existing site Hamiltonian. Assuming the form of the electron exchange interaction is similar to Dexter electron transfer (DET), a distance-dependent empirical formula is used, $V_{exch}\approx \alpha \exp \left(-\beta R\right)$, where β = 2/L, R is the distance between donor and acceptor, L is the average orbital radius of the donor and acceptor, and α is an empirical scaling factor.^42,50 In Fig. S6 of the supplementary material, the effect of an empirical electron exchange interaction term on the excitonic energies of the PIC “chiral fiber” is shown. It is clear that an electron exchange interaction term between the closely packed monomers is necessary to accurately reproduce the experimental excitonic energies. For the “chiral fiber” model, the electron exchange interaction terms, V_exch, necessary to red-shift the J-aggregate band to near 17 500 cm⁻¹ are between 250 and 400 cm⁻¹ for the closely packed monomeric sites, around the same order of magnitude as the Coulombic couplings from TDC calculations. This empirical analysis does assume that the short- and long-range interactions in the Frenkel Hamiltonian are additive and that no additional charge transfer excitons are present.

The second source of error, the finite size of the calculated fiber, is difficult to test due to computational limitations, since the size of the Hamiltonian increases with N², where N is the number of PIC monomers. The excitonic coherence length using the inverse participation ratio can be calculated for each aggregate model using the equilibrated excitons from a series of Redfield dynamics calculations. The computational details and results of these Redfield calculations are presented in Figs. S9–S16 of the supplementary material. The superstructural excitonic coherence lengths using the inverse participation ratio are around 15–20 sites, larger than the experimentally derived value of 8.9 ± 2.9 derived from super-radiance enhancement and much larger than the calculated coherence lengths for the linear models. It must be noted that there are many different methods of quantifying the coherence length, and a direct comparison between theory and the experiment may not be useful in this case.⁵¹ Nevertheless, in all present cases, the number of sites, N, is more than twice the exciton coherence length of the aggregate. Therefore, it is unlikely that the finite size of the fiber is a significant source of error in the excitonic calculations.

Finally, the inclusion of the electronic-vibrational coupling to the high-frequency mode of PIC (∼1400 cm⁻¹) would resolve the spectral bands around 19 100 cm⁻¹ and 20 400 cm⁻¹ in the aggregated spectra, as calculated in previous theoretical work on the PIC dimer structure.⁴⁶ Inclusion of these electronic-vibrational couplings, though, will require more accurate knowledge of the electronic couplings and aggregate structure of PIC and will be considered in the future.

V. CONCLUSIONS

A theoretical model for pseudoisocyanine (PIC) dimerization and superstructural aggregation reveals how PIC may form spontaneous homogeneous chiral fibers in aqueous solution with intense J-aggregate spectral signatures. The experimental absorption spectra of the J-aggregated fibers reveal a strong J-band residing at 17 500 cm⁻¹, red-shifted 1600 cm⁻¹ from the monomeric 0–0 transition at 19 100 cm⁻¹, as well as a broad H-band near 20 400 cm⁻¹, overlapping with the monomeric 0–1 vibronic progression. In addition, strong chirality of the J-band is evident from experimental circular dichroism measurements. The average PIC J-aggregated fiber is estimated at 2.89 ± 0.17 nm, determined from an averaged line scan of cryo-TEM images (Fig. 1).

A physical model for spontaneous aggregation of PIC must go through an intermediate step, which is analyzed by calculating the interaction energy potential between geometrically distinct dimers of PIC. From this analysis, it is noted that a linear J-aggregated 1D chain of PIC monomers is energetically unfavorable compared to a rotated chiral chain of monomers, while still maintaining face-centered π-stacking. Since PIC is a cationic molecule, this effect is mainly due to an aromatic donor-acceptor interaction as the electron-deficient nitrogen atoms are rotated away from each other. Interestingly, degrees of rotation far from a linear chain are preferred, with broad regions of stability when rotating both clockwise and counter-clockwise around a face-centered axis (Fig. 2).

This non-linear preference of PIC dimerization is key to the formation of spontaneous chiral aggregates, in which PIC dimers or PIC monomers are sequentially bound to the ends of the fiber. By analyzing the computed spectra and excitonic properties of several PIC superstructural models, it is likely that PIC forms homogeneous fibers in a sequential chiral arrangement where the long-axis of the PIC monomer is neither parallel nor orthogonal to the long-axis of the fiber. In this arrangement, a strong red-shifted J-aggregate band is seen in the calculated absorption spectra, and this J-aggregate band in the left-handed PIC formation shows similar chirality from the calculated circular dichroism spectra. In addition, a set of weaker blue-shifted H-aggregate bands are indicative of this PIC aggregate arrangement. This set of spectral features, which is also observed in the experimental spectra, is not seen in the other superstructural models tested (Figs. 4 and 5) or in the linear aggregate models (Fig. 3). This chiral arrangement would have an estimated fiber width of 25–29 Å when including the anionic layer as well as the PIC monomers, similar to the experimental value of 29 Å estimated from cryo-TEM analysis.

While the qualitative excitonic features present in the sequential chiral fiber model are in reasonable agreement with experimental characterization, the quantitative accuracy of the excitonic energy levels requires improvement. Specifically, the absence of the short-range electronic coupling between PIC monomers, especially of those sharing π-orbital electrons, contributes to this inaccuracy. By including an empirical short-range electronic coupling between the closest PIC dimers, the excitonic spectra much more closely resemble the experiment. In the future, it may be important to calculate the short-range coupling between closely stacked molecules more accurately, instead of relying on empiricism. Additionally, the stability of these aggregation models can be modeled using molecular dynamics, along with an improved estimate of the spectral density of the PIC monomers aggregated in aqueous solution. These molecular models for PIC aggregation in aqueous solution may have implications for structural aggregation of other dyes^{19,20,52–57} and for using these dyes as a structural biological mimics of long-range energy transport in photosynthetic complexes.

SUPPLEMENTARY MATERIAL

See supplementary material for additional data regarding the choice of DFT functionals, the linear PIC aggregation models, the electronic couplings for each PIC aggregate model, a qualitative analysis of static and dynamic disorder on the PIC J-aggregate band, an empirical analysis of electronic exchange interaction on the electronic couplings, Redfield site populations and coherence lengths for each PIC aggregate, and the cryo-TEM analysis of PIC fiber widths.