Abstract
Key points
The brain is vulnerable to damage from too little or too much blood flow. A physiological mechanism termed cerebral autoregulation (CA) exists to maintain stable blood flow even if cerebral perfusion pressure (CPP) is changing.
A robust method for assessing CA is not yet available. There are still some problems with the traditional measure, the pressure reactivity index (PRx).
We introduce a new method, the wavelet transform method (wPRx), to assess CA using data from two sets of controlled hypotension experiments in piglets: one set had artificially manipulated arterial blood pressure (ABP) oscillations; the other group were spontaneous ABP waves.
A significant linear relationship was found between wPRx and PRx in both groups, with wPRx providing a more stable result for the spontaneous waves.
Although both methods showed similar accuracy in distinguishing intact and impaired CA, it seems that wPRx tends to perform better than PRx, although not significantly so.
Abstract
We present a novel method to monitor cerebral autoregulation (CA) using the wavelet transform (WT). The new method is validated against the pressure reactivity index (PRx) in two piglet experiments with controlled hypotension. The first experiment (n = 12) had controlled haemorrhage with artificial stationary arterial blood pressure (ABP) and intracranial pressure (ICP) oscillations induced by sinusoidal slow changes in positive end‐expiratory pressure (‘PEEP group’). The second experiment (n = 17) had venous balloon inflation during spontaneous, non‐stationary ABP and ICP oscillations (‘non‐PEEP group’). The wavelet transform phase shift (WTP) between ABP and ICP was calculated in the frequency range 0.0067–0.05 Hz. Wavelet semblance, the cosine of WTP, was used to make the values comparable to PRx, and the new index was termed wavelet pressure reactivity index (wPRx). The traditional PRx, the running correlation coefficient between ABP and ICP, was calculated. The result showed a significant linear relationship between wPRx and PRx in the PEEP group (R = 0.88) and non‐PEEP group (R = 0.56). In the non‐PEEP group, wPRx showed better performance than PRx in distinguishing cerebral perfusion pressure (CPP) above and below the lower limit of autoregulation (LLA). When CPP was decreased below LLA, wPRx increased from 0.43 ± 0.28 to 0.69 ± 0.12 (P = 0.003) while PRx increased from 0.07 ± 0.21 to 0.27 ± 0.37 (P = 0.04). Moreover, wPRx provided a more stable result than PRx (SD of PRx was 0.40 ± 0.07, and SD of wPRx was 0.28 ± 0.11, P = 0.001). Assessment of CA using wavelet‐derived phase shift between ABP and ICP is feasible.
Keywords: cerebral autoregulation, experimental hypotension, low limit of autoregulation, pressure reactivity index, wavelet transform
Key points
The brain is vulnerable to damage from too little or too much blood flow. A physiological mechanism termed cerebral autoregulation (CA) exists to maintain stable blood flow even if cerebral perfusion pressure (CPP) is changing.
A robust method for assessing CA is not yet available. There are still some problems with the traditional measure, the pressure reactivity index (PRx).
We introduce a new method, the wavelet transform method (wPRx), to assess CA using data from two sets of controlled hypotension experiments in piglets: one set had artificially manipulated arterial blood pressure (ABP) oscillations; the other group were spontaneous ABP waves.
A significant linear relationship was found between wPRx and PRx in both groups, with wPRx providing a more stable result for the spontaneous waves.
Although both methods showed similar accuracy in distinguishing intact and impaired CA, it seems that wPRx tends to perform better than PRx, although not significantly so.
Introduction
Cerebral autoregulation (CA) refers to the ability of cerebrovascular resistance to follow low frequency (<0.05 Hz) changes in cerebral perfusion pressure (CPP) to keep cerebral blood flow (CBF) constant (Kvandal et al. 2013). It is a universal physiological mechanism, depicted by the Lassen curve, with intact autoregulation delimited by lower limit of autoregulation (LLA) and upper limit of autoregulation (ULA)(Lassen, 1959; Lassen & Agnoli, 1972). Dysfunction of CA has been reported in pathologies such as stroke, traumatic brain injury, various brain lesions and infections, and such dysfunction may influence the patient outcomes (Paulson et al. 1990; Tarumi et al. 2014; Kenosi et al. 2015; Addison, 2015a ; Liu et al. 2016). It is therefore important to have an effective tool for assessment and monitoring of CA.
The interrelationship between arterial blood pressure (ABP), intracranial pressure (ICP) and cerebral arterial blood flow velocity (FV) provides information about functioning of CA (Aaslid et al. 1986; Shigemori et al. 1989; Giller, 1990; Chan et al. 1992; Schmidt et al. 1999; de Jong et al. 2017). Invention of the pressure reactivity index (PRx), calculated as a moving correlation coefficient between ABP and ICP, has allowed for continuous monitoring of CA over extended periods of time (Czosnyka et al. 1997). Negative PRx values reflect a reduction in ICP in response to an increase in ABP indicating intact CA, whereas positive PRx values, conversely, indicate impaired CA (Muizelaar et al. 1989; Lang & Chesnut, 1995). Because ICP and ABP are two commonly measured modalities in traumatic brain injury patients in intensive care units and no external ABP manipulations are necessary, PRx has become widely accepted as a marker for cerebral autoregulatory status (Lang et al. 2015). However, PRx, being a simple correlation coefficient, is noisy due to its indiscriminate nature and inherent, incoherent, physiological variability of ABP and ICP (Diedler et al. 2011; Brady et al. 2012). Transfer function analysis and other frequency methods have also been developed to assess CA (Tzeng et al. 2012; Tzeng & Ainslie, 2014; Tian et al. 2016; Labrecque et al. 2017; Chi et al. 2018; van der Scheer et al. 2018). However, these methods are based on the assumptions of linearity and stationarity (i.e. time invariance of statistical properties) of transmission between input (ABP) and output (cerebral blood flow, velocity or volume) of the autoregulation system.
With the clarification of the non‐stationarity and non‐linearity of CA (Panerai et al. 1999; Panerai, 2014), there is motivation to perform more sophisticated analyses to quantify the coupling mechanism of ABP and CBF (Placek et al. 2017). The wavelet transform method is a powerful mathematical tool for analysing intermittent, noisy and non‐stationary signals, such as measured in studies of the autonomic nervous system (Pichot et al. 1999; Addison, 2002; Davrath et al. 2003; Keissar et al. 2009), making it also a natural candidate for assessing cerebral pressure reactivity (Bishop et al. 2012; Garg et al. 2014; Tian et al. 2016; Chalak & Zhang, 2017; Chalak et al. 2017; Wszedybyl‐Winklewska et al. 2017). One advantage of wavelet analysis is the ability to reveal signal features with the right balance of the temporal and frequency resolution, appropriate to the frequencies studied. The two parameters typically extracted from wavelet analysis are the wavelet phase shift (WTP), which produces maps of the localised delay (phase difference) between the two signal components over a range of frequencies and time points (Addison, 2015b ); and the wavelet transform coherence (WTC), which characterises time‐ and frequency‐dependent (cross‐) correlations between those two signals (Grinsted et al. 2004). A value of WTC = 1 indicates entirely linear transmission of power between two time series at a certain time and frequency point, while a value of WTC = 0 signifies no such association (Rowley et al. 2007; Kvandal et al. 2013). Enforcing a certain minimal threshold of WTC can be used to find correlated areas in the time–frequency map and improve reliability (decreasing variance) of phase estimation (Grinsted et al. 2004).
In this study, we set out to apply wavelet transform analysis to assessment of CA using ABP and ICP signals and to validate the algorithm through two groups of experimental piglet data: one group with induced, sinusoidal, regular ABP waves (Brady et al. 2012) and the other with spontaneous ABP waves (Brady et al. 2008). The two specific objectives of the study were: (1) to validate the new method for CA assessment in conditions of high‐power, regular, periodic waves of ABP (high signal to noise scenario); and (2) to establish advantages and disadvantages of the wavelet method vs. the traditional, well‐established parameter, PRx.
Methods
Ethical approval
Two separate piglet models were analysed in this study. In the first study, with induced, sinusoidal ABP waves, 12 subjects were approved by the Institutional Animal Care and Use Committee of Baylor College of Medicine (Brady et al. 2012). In the other study, with spontaneous ABP waves, 17 subjects were approved by Johns Hopkins Animal Care and Use Committee (Brady et al. 2008). Both animal experiments were performed in accordance with the laws of the USA (under animal protocol numbers 1010 and 1046) and the ethical standards mandated by the Journal of Physiology (Grundy, 2015). Both studies conformed fully to the standards of animal experimentation described in the Guide for the Care and Use of Laboratory Animals, Eighth Edition (National Research Council), including sourcing of the animals, their preoperative care and housing, access to water and food, anaesthesia and euthanasia protocols (National Research Council, 2011).
Experimental piglets
Piglets (domestic swine, weight:1.0–5.0 kg, Keeling Center for Comparative Medicine and Research at the University of Texas, M.D. Anderson Cancer Center, Bastrop, TX, USA) arrived at 1–2 days of age and were housed in stainless steel cages in temperature‐ and light‐controlled rooms (room temperature 21–23°C, humidity 30–70%, normal light cycle: on at 07:00 h off at 7:00 h). Cages were changed and cleaned daily by staff. The cages had supplemental warmth provided by a water circulating heated blanket. Pigs were feed pig replacement formula ad libitum. The pigs were weighed daily to verify growth and weight gain. Bottle feeding was added if the piglets lost weight. They were taught to drink from an automatic water (Birthright formula) feeder on the day they arrived and were housed in pairs to reduce stress. Piglets were acclimated for at least 24 h prior to surgery. The model necessitates the use of very young piglets, no more than 4–5 days of age because the neonatal piglet brain develops at least 20 times faster than the human brain (Gressens et al. 2008). Piglets were nothing by mouth (NPO) for 8 h before surgery to reduce the risk of reflux or vomiting on induction. The piglets were killed while under complete sedation with an iv injection of pharmaceutical‐grade euthanasia solution before any brain harvesting or tissue removal.
ABP wave manipulated group
Current PRx estimation is noisy due to the presence of incoherent, physiological variability of mean ABP and ICP (Diedler et al. 2011; Brady et al. 2012). This is probably due, at least partially, to the influence of intracranial sources of variation in cerebral blood volume, not directly related to ABP, under conditions of low‐power slow waves in the latter. To minimise influences of those incoherent covariates that are not related with CA, we first analysed a data set from a piglet model with induced high‐amplitude slow waveforms in ABP (Brady et al. 2012). Such controlled ABP waves provoke coherent changes in blood volume and thus ICP, improving stability of PRx calculation and making the time series of PRx considerably less noisy.
This data set included recordings from 12 piglets, in which regular, sinusoidal (1 min period), strong ABP oscillations were induced using modulated positive end‐expiratory pressure (PEEP) during volume‐controlled ventilation (Brady et al. 2012). The subjects were anaesthetised with isoflurane, intubated by tracheotomy, and maintained under 0.8% isoflurane, 50% nitrous oxide and 50% oxygen. Fentanyl was infused at 50 μg kg−1 h−1 in 0.45 normal saline with 5% dextrose and 50 Meq l–1 sodium bicarbonate added at 4 ml kg−1 h−1. Femoral arterial and venous cannulation was performed bilaterally. ABP and central venous pressure (CVP) were transduced with a clinical monitor (GE Healthcare, Little Chalfont, UK). Craniotomy was performed for placement of an external ventricular drain, transduced as a fluid‐filled column. Additional craniotomies were performed over each parietal cortex for placement of bilateral laser Doppler probes (Moor Instruments, Axminster, UK). The laser Doppler probe tips were juxtaposed to the underlying cortex. The drain and probes were secured in place with dental cement. Subjects were given 20 ml kg−1 normal saline and recovered from surgery for 30 min while maintained under general anaesthesia at normothermia (38–39°C) with arterial blood gas measurements of pH 7.37–7.43, 38–42 mmHg and 150–200 mmHg. A customised ventilator was used (Impact Instrumentation, West Caldwell, NJ, USA). A primary wave component was applied for ventilation, which was a fixed tidal volume of 50 cm3 at a rate between 15 and 25 per minute. Volume control ventilation prevented changes in minute ventilation with varying PEEP. A secondary slow wave component was introduced into the PEEP control. PEEP was oscillated between 5 and 10 cmH2O in a sine‐wave pattern with a period of 60 s. Once stable recording was obtained, the piglets were haemorrhaged by syringe‐pump withdrawal at a rate of 12% calculated blood volume h–1, which allowed ABP to be gradually reduced over 3–4 h before death. For later analysis, this group was labelled the PEEP Group. The data have been published as part of a validation study of the pressure‐reactivity index (Brady et al. 2012).
Spontaneous ABP wave group
After the validation study using the ‘PEEP’ data set described above, a comparison between the wavelet method and traditional PRx was conducted in a more clinically relevant setting of spontaneous ABP waves at two ICP levels: naïve (ICP = 10 mmHg, n = 10) and elevated ICP (ICP = 20 mmHg, n = 7). For the wavelet‐based PRx and traditional PRx, the stability and the ability to distinguish CPP above LLA (indicating good CA) and below LLA (indicating poor CA) was compared.
After tracheostomy and mechanical ventilation (goal pH, 7.35–7.45; , 200–300 mmHg, , 35–45 mmHg), the 17 infant piglets were anaesthetised with isoflurane, intubated by tracheotomy, and maintained under 0.8% isoflurane, 50% nitrous oxide and 50% oxygen combined with iv dosing of vecuronium (5 mg bolus and 2 mg h–1 infusion) and fentanyl (25 μg bolus and 25 μg h–1 infusion). Warming pads were applied to maintain brain and rectal temperature at 38.5–39.5°C. For the seven piglets with elevated ICP, artificial cerebrospinal fluid (KCl 3.0 mmol l–1, MgCl2 0.6 mmol l–1, CaCl2 1.3 mmol l–1, NaCl 131.8 mmol l–1, NaHCO3 24.6 mmol l–1, urea 6.7 mmol l–1, glucose 3.6 mmol l–1) was infused in an external ventricular drain catheter at varying rates to achieve and maintain a steady‐state ICP of ≈20 mmHg throughout the experiment(Brady et al. 2008, 2009).
Once the piglets were anaesthetised, a central venous line and a 5 Fr oesophageal balloon catheter (Cooper Surgical, Trundall, CT, USA) were placed in the femoral veins. Gradual inflation of the balloon catheter by infusion of saline from a syringe pump at the level of the inferior vena cava was used to induce hypotension in the piglets. CPP was slowly decreased to approximately 10 mmHg over 3 h before death.
The femoral artery was cannulated for placement of a pressure monitoring line. ABP was continuously monitored after setting the transducer to zero at the level of the external auditory meatus, which was also at the level of the left atrium. For piglets in the naïve ICP group, a single external ventricular drain catheter was placed 4 mm lateral and 4 mm rostral to the bregma at midline through a 2–3 mm craniotomy. Piglets in the elevated ICP group required an additional contralateral 2–3 mm craniotomy for placement of a second external ventricular drain for infusion of cerebrospinal fluid. Continuous ICP was monitored by transduction of the external ventricular drain in all animals with pressure lines set to zero at the external auditory meatus. Craniotomy was also performed 4 mm lateral and 4 mm rostral to the first craniotomy in all piglets for placement of a laser Doppler probe (Moor Instruments), positioned against the surface of the frontoparietal cortex. Craniotomies were sealed with dental cement. Later, this group was labelled the non‐PEEP Group. The data of spontaneous waves have been used to test the lower limit of cerebral autoregulation (Brady et al. 2008, 2009).
Data collection
In both experiments, ABP, ICP and CBF were monitored continuously. ABP was transduced invasively with a clinical monitor (Marquette Solar 8000, GE Healthcare). ICP was monitored through an external ventricular drain after craniotomy. Bilateral laser Doppler probes (Moor Instruments) were placed to monitor CBF after additional craniotomies over each parietal cortex. The signals were all sampled at 200 Hz, digitised using an A/D converter (DT9801, Data Translation, Marlboro, MA, USA), and were recorded using a laptop computer with ICM+ software (Cambridge Enterprise Ltd, Cambridge, UK, http://icmplus.neurosurg.cam.ac.uk). The same software was later used for retrospective analysis of all stored signals.
Data analysis
Wavelet semblance (wPRx)
WTP between ABP and ICP in the low‐frequency range of 0.0067–0.05 Hz was calculated through a complex, continuous wavelet transform (Torrence & Compo, 1998; Highton et al. 2015; Tian et al. 2016; Liu et al. 2017a). In brief, the WTP at each scale‐frequency point was calculated from 500 s data segments (moving window, with update every 10 s), and subsequently WTC was used to reject corresponding unreliable phase values. In this paper, the WTC threshold of 0.48 was used, determined through 10,000 Monte Carlo simulations (detailed description can be found in Liu et al. 2017a). Individual phase shift values with coherence higher than 0.48 were kept, while data points with coherence lower than the threshold were deleted. Wavelet semblance (Cooper & Cowan, 2008), the cosine of wavelet phase shift, was calculated, and labelled wavelet pressure reactivity index (wPRx). Finally, the values were averaged along the frequency domain, resulting in one wPRx value at each time point. A 500 s window length was chosen to make it comparable to the standard PRx calculation period of 300 s but accounting for edge effects of the wavelet transform (Addison, 2002, 2016). The application of wavelet semblance limits wPRx range from −1 (180 deg phase shift, inversely correlated) to 0 (uncorrelated) to +1 (0 deg phase shift, fully and positively correlated), giving a metric with direct correspondence to PRx (Cooper & Cowan, 2008). In addition, the cosine operation offers a practical solution to the problem of phase wrapping, as in effect the value obtained is equal to the normalised real part of the wavelet transfer function, and therefore not subject to the wrapping effects.
Determining the lower limit of autoregulation
In both experiments, CPP was gradually decreased either through syringe‐pump withdraw (PEEP group) or through a balloon catheter (non‐PEEP wave) until values of CPP well below the lower limit of autoregulation (LLA) were reached. Each subject's LLA was determined through a scatter plot of 1‐min average laser Doppler flow versus CPP (Brady et al. 2008; Lee et al. 2009). The CPP value at the left intersection of two lines defined by a piecewise linear regression model was defined as LLA (Fig. 1). The ability of wPRx and PRx in distinguishing CPP above LLA and below LLA was compared.
Figure 1.
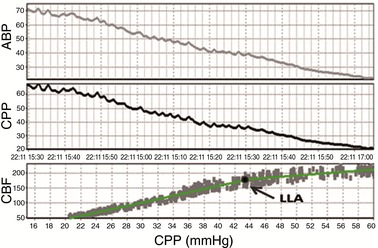
Demonstration of lower limit of autoregulation (LLA) using laser Doppler cerebral blood flow (CBF) and cerebral perfusion pressure (CPP) as a breakpoint between two linear sections estimated using the least mean square distance (data from one piglet)
Pressure reactivity index (PRx)
The PRx was calculated according to previously published methods (Czosnyka et al. 1997). First, ABP and ICP were filtered to remove pulse and respiratory frequency waveforms with 10 s averaging. A moving Pearson correlation coefficient of 30 consecutive samples (300 s) provides the standard PRx (Czosnyka et al. 1997). All the abbreviations were summarised in Table 1.
Table 1.
Abbreviations used in the article
| Abbreviation | Full name | Abbreviation | Full name |
|---|---|---|---|
| ABP | Arterial blood pressure | AUC‐ROC | Area under receiver–operator characteristic curve |
| CA | Cerebral autoregulation | CBF | Cerebral blood flow |
| CPP | Cerebral perfusion pressure | FV | Cerebral blood flow velocity |
| ICP | Intracranial pressure | LLA | Lower limit of autoregulation |
| PEEP | Positive end‐expiratory pressure | PRx | Pressure reactivity index using 300 s window |
| ROC | Receiver‐operator characteristic | ULA | Upper limit of autoregulation |
| wPRx | Wavelet semblance | WTC | Wavelet transform coherence |
| WTP | Wavelet transform phase shift |
Statistics
SPSS software (version 21, IBM, Armonk, NY, USA) was used for statistical analysis. Linear regression was used to describe the relationship between PRx and wPRx. Pearson's correlation coefficient (r) was used to examine the linearity of the relationship. A paired t test was used to compare the ability of PRx and wPRx to distinguish intact CA (CPP above LLA) and impaired CA (CPP below LLA). A receiver‐operator characteristic (ROC) test was also done, providing an area under the ROC curve (AUC‐ROC) for each parameter. Statistical differences between AUC‐ROC curves were verified using the DeLong's test for two correlated ROC curves (R package pROC; Robin et al. 2011). Bland–Altman plots were used to investigate the agreement between the two variables. A Kruskal–Wallis test was used to compare the standard deviation of PRx and wPRx. Results were considered significant at P < 0.05.
Results
Wavelet transform calculation
A representative example of wavelet phase shift and wavelet coherence between ABP and ICP from a single experimental dataset (PEEP group) is shown in Fig. 2. While ABP was gradually decreased (Fig. 2 A), wavelet phase shift showed a synchronised decrease at the frequency of 1 min–1 (PEEP wave frequency), demonstrated by the colour change from red to blue in Fig. 2 C. This phase shift change from roughly 3 radians (red) to less than 1 radian (blue) is interpreted as the transition from intact CA to impaired CA due to CPP below LLA. The phase semblance result is shown in Fig. 2 D. In this protocol, the wavelet coherence in the same frequency remained stable and high across the whole period, shown by the red colour (Fig. 2 E). Figure 2 F shows the average coherence across the whole frequency range at each time point, and it was clear that for this sample, the frequency‐averaged WTC was generally above the threshold level of 0.48.
Figure 2. Changing wavelet phase (WTP), wavelet semblance and coherence (WTC) between ABP and ICP of one piglet in the PEEP group.
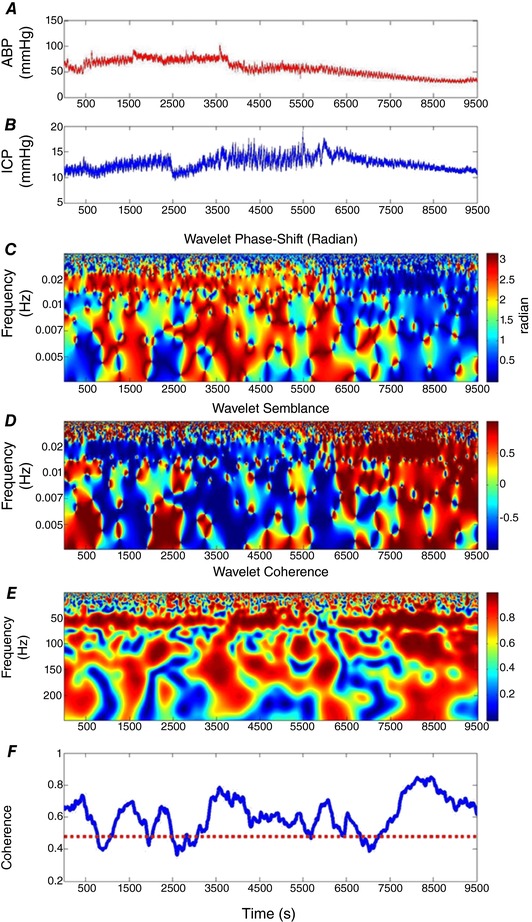
A, arterial blood pressure, ABP. B, intracranial pressure, ICP. C, the WTP map between ABP and ICP. Red colour indicates higher values and blue colour indicates lower values. D, the wavelet semblance map. E, the WTC map. F, the average value of WTC across the whole frequency average at each time point. The dashed line is the significance level of WTC. The Morlet wavelet characteristic angular frequency w0 = 2π. Wavelet semblance: cosine of wavelet phase shift.
The relationship between wPRx and PRx
The relationship between wPRx and PRx was analysed using 30 min average values (n = 118 in the PEEP group, n = 262 in the non‐PEEP group, Fig. 3). wPRx was positively related to PRx and PRx in the PEEP group (R = 0.88, Fig. 3 A) and non‐PEEP group (R = 0.56, Fig. 3 C). The Bland–Altman chart showed a tendency of a negative PRx–wPRx difference (Fig. 3 B,D). The mean difference between PRx and wPRx was −0.23 [95% confidence interval (CI): −0.64 to 0.18] in the PEEP group and −0.4 (95% CI: −0.91 to 0.11) in the non‐PEEP group.
Figure 3. Relationship between PRx and wPRX.
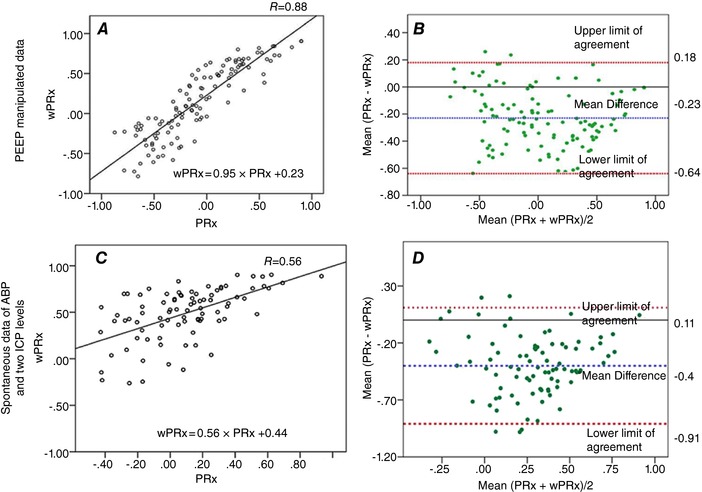
Relationship between PRx and wPRX in the PEEP group (A) and in the non‐PEEP group (C). The Bland–Altman plot between PRx and wPRx in the PEEP group (B) and in the non‐Peep group (D). PRx: pressure reactivity index; wPRx: wavelet semblance; PEEP: positive end‐expiratory pressure. The Bland–Altman plot was used to analyse the agreement of the two indices. CI: confidence interval. [Color figure can be viewed at http://wileyonlinelibrary.com]
Stability of PRx and wPRx
Stability of the two parameters was compared through mean standard deviation when CPP was above LLA. Because of the induced regular ABP oscillations, there was no difference between PRx and wPRx in the PEEP group (SD of PRx = 0.47 ± 0.06, SD of wPRx = 0.48 ± 0.07, n = 12, P > 0.05). However, the better performance of wPRx was demonstrated in the spontaneous non‐PEEP group, with smaller SD of wPRx (SD of PRx = 0.40 ± 0.07, and SD of wPRx = 0.28 ± 0.11, P = 0.001).
Comparing wPRx and PRx against LLA in the PEEP group
The average LLA of the PEEP group was 33.75 mmHg (95% CI: 27.6–39.9 mmHg), and average LLA of the non‐PEEP group was 36.4 mmHg (95% CI: 29.5–43.2 mmHg). Figure 4 shows an example of averaged PRx and wPRx in (CPP‐LLA) bins. Both PRx and wPRx were increased significantly while CPP was decreased below LLA, indicating worse autoregulation.
Figure 4. Comparison of PRx and wPRx against a standard LLA in the PEEP group (data from one piglet).
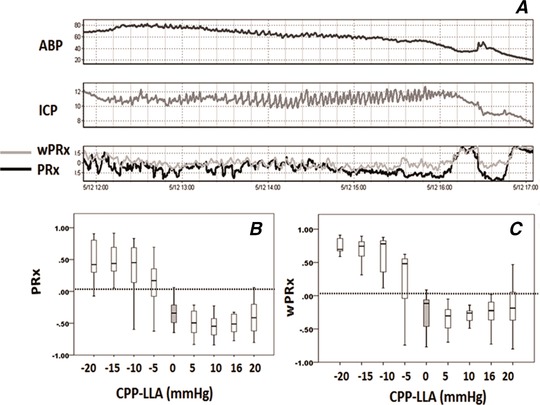
A, an example of ABP, ICP, PRx and wPRx along a continuous ABP decrease. Cerebral autoregulation indices are binned in 5 mmHg increments of CPP for comparison against the LLA. B, PRx; C, wPRx. A positive CPP‐LLA value indicates intact CA, while negative CPP‐LLA indactes impaired CA. PRx: pressure reactivity index; wPRx, wavelet pressure reactivity index, cosine of wavelet phase shift between arterial blood pressure and intracranial pressure, using wavelet coherence as threshold. Analysed frequency was 0.0067–0.05 Hz. LLA: lower limit of autoregulation.
In the PEEP group, mean PRx increased significantly from −0.22 ± 0.33 to 0.41 ± 0.20 (P < 0.001, Fig. 5 A) and wPRx increased from −0.02 ± 0.35 to 0.58 ± 0.21 (P < 0.001, Fig. 5 B) while CPP decreased below LLA. In the non‐PEEP group, wPRx showed a more significant increase (from 0.43 ± 0.28 to 0.69 ± 0.12, P = 0.003, Fig. 5 D) than PRx (from 0.07 ± 0.21 to 0.27 ± 0.37, P = 0.04, Fig. 5 C).
Figure 5. Performance of PRx and wPRx in distinguishing CPP above LLA and below LLA.
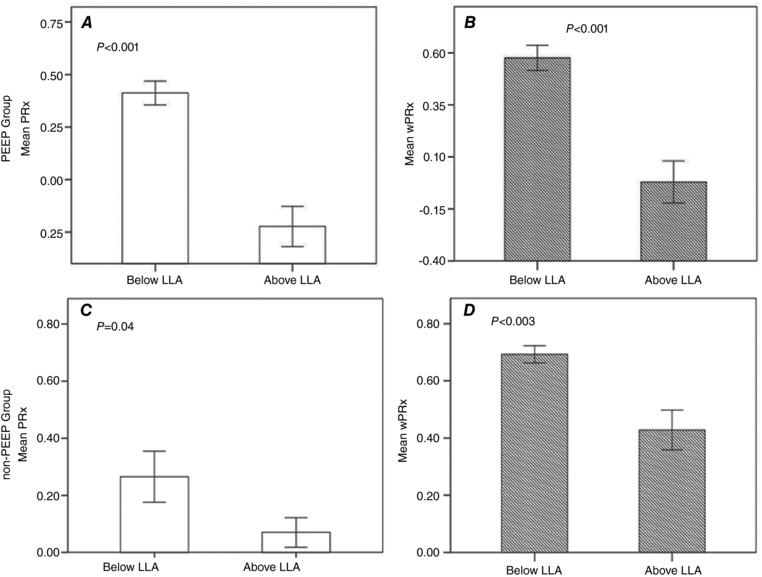
A, in the PEEP group, mean PRx increased significantly while CPP decreased below LLA (P < 0.001); B, in the PEEP group, wPRx increased significantly while CPP decreased below LLA (P < 0.001). C and D, in the non‐PEEP group, wPRx (D) showed a more significant increase (p < 0.003) than PRx (C, P = 0.04) while CPP decreased below LLA. P < 0.05 implies a significant difference. Open bars, mean PRx; striped bars, mean wPRx result. Error bar: standard error. PRx: pressure reactivity index; wPRx: wavelet semblance; ICP, intracranial pressure; CPP, cerebral perfusion pressure; LLA, lower limit of autoregulation; CA: cerebral autoregulation.
The AUC‐ROC curve showed that both wPRx and PRx can differentiate CPP above or below LLA (Fig. 6). In PEEP wave, AUC‐ROC of PRx and wPRx were 0.94 (95% CI: 0.76–1) and 0.96 (95% CI: 0.79–1) respectively. In non‐PEEP wave, AUC‐ROC of PRx and wPRx were 0.73 (95% CI:0.55–0.87) and 0.83 (95% CI: 0.66–0.93), respectively, although possibly because of the small sample size, the DeLong's test showed no significant difference between the two AUC‐ROC curves of PRx and wPRx in the two groups.
Figure 6. Delong's test to compare the two AUC‐ROC curves of PRx and wPRx in distinguishing CPP above LLA and below LLA in the PEEP group and non‐PEEP group.
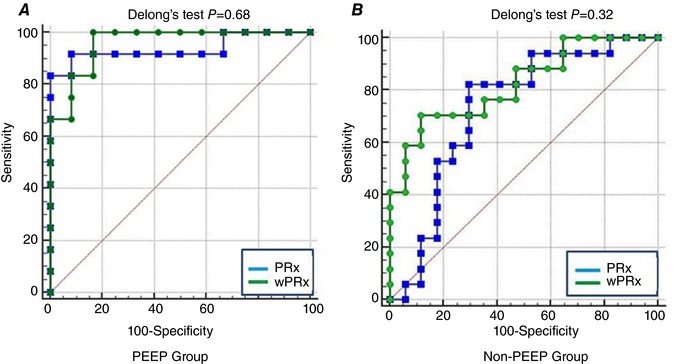
A, PEEP group; B, non‐PEEP group. The area under the curve is where a value of 1 indicates maximum sensitivity and specificity. CA: cerebral autoregulation; PEEP: positive end‐expiratory pressure. AUC‐ROC: area under the receiver‐operator characteristic (ROC) curve. LLA: lower limit of autoregulation. [Color figure can be viewed at http://wileyonlinelibrary.com]
Discussion
Because cerebral slow‐wave activity is generally non‐periodic and non‐stationary, it poses a challenge for traditional, Fourier based signal‐processing techniques. The wavelet technique, well suited to this type of signal, has previously been described in several studies for assessment of cerebral autoregulation (Latka et al. 2005; Peng et al. 2010; Highton et al. 2015; Tian et al. 2016; Chalak & Zhang, 2017; Chalak et al. 2017; Liu et al. 2017a). In this paper, we have applied a wavelet semblance algorithm first in two piglet experiments and used wavelet coherence as a measure of a reliable ABP–ICP phase relationship. The main finding was that wPRx produced a more stable result than PRx and could distinguish CPP above and below LLA more significantly when spontaneous ABP and ICP waves were analysed.
Validation of wPRx
To validate the wavelet method against the well‐established PRx index, this study used a piglet model with regular ABP oscillations by adding sinusoidal variations in PEEP during volume‐controlled ventilation (Brady et al. 2009, 2012). This significantly improved stability (lowered variance) of PRx and therefore wPRx was not expected to perform any better than PRx, as the strong, deterministic component of approximately fixed frequency and amplitude induced in ABP removed any advantages of a non‐stationary approach. However, the resulting strong linear relationship between the two parameters validated wPRx. As wPRx directly reflects the phase shift between ABP and ICP, this result indicates that high positive PRx values reflect near 0 phase shift (cosine close to 1) between ABP and ICP (i.e. completely impaired autoregulation), while negative values of PRx correspond to highly positive phase shifts (90 deg to 180 deg, negative cosine, highly active autoregulation).
The potential advantages of wPRx lie in dealing with spontaneous waves in ABP of varying intensity and frequency. Transmission of these variable waves into the output signal (ICP) waveforms may be partially masked by other independent (intracranial) sources of fluctuations in ICP, thus making PRx less reliable (noisy), because of its indiscriminate nature. These circumstances will also lead to reduced coherence between ABP and ICP. Thus, using coherence as a filter should produce a more stable result, and that was indeed demonstrated by increased stability of wPRx in the non‐PEEP group.
Wavelet analysis
The wavelet transform expands time series into a time–frequency space with desired temporal–frequency resolution, to fit various needs for non‐stationary signal analysis (Grinsted et al. 2004). In his review, Smith discussed the use of wavelet‐based techniques to aid the interpretation of complex time‐variant signals by producing qualitative and quantitative evidence of cerebrovascular autoregulation that is otherwise ‘not possible using other methods’ (Smith, 2011; Addison, 2015a ). The Morlet wavelet, a complex function, is a natural choice when phase feature extraction is needed. Coherence (in this case WTC) threshold is often used to ensure a reliable estimate of phase relationship between input and output. This combination of wavelet‐derived instantaneous phase accompanied by coherence‐derived quality control makes constitutes, in general, a more robust method for non‐stationary signal analysis.
However, defining an appropriate threshold for coherence is generally not trivial as it will vary depending on the values of various parameters of the estimation process (Faes et al. 2004). Therefore, we chose to establish that threshold using Monte Carlo simulations in which surrogates of ABP and ICP with destroyed phase relationship were generated and analysed. As ultimately the method needs to be applicable to real‐time analysis, and given that Monte Carlo simulations carry a significant performance penalty, we chose to calculate a single threshold for the whole dataset, rather than estimating it for each individual recording. Reassuringly this threshold matched our previous result in a large cohort of traumatic brain injury patients (Liu et al. 2017a).
However, it must be acknowledged that there may be considerable variability in the coherence threshold in different acute brain injury patients (Highton et al. 2015), because of the differences in autocorrelation in individual datasets. Ideally, therefore, an individual coherence threshold should be considered in the future.
Wavelet transform coherence
WTC characterises cross‐correlations between two signals. A value of WTC close to 1 indicates a high common power (more precisely highly correlated variability in power) between two time series at a certain time and frequency area, and it guarantees linear relationships between two signals at that point in time and frequency (and thus a reliable estimation of phase at that point). On the other hand, a low value of WTC indicates a vanishing correlation, possibly caused by external noise or a non‐linear relationship (Zhang et al. 1998). In the case of transmission between ABP and CBF, it can also be argued that coherence per se could be an indicator of CA, with high coherence indicating impaired CA (slow variations in ICP are linearly and passively related to slow variations in ABP), and low coherence indicating properly functioning CA because of the strong (and possibly non‐linear) fluctuation attenuating effect of CA (Giller, 1990; Zhang et al. 1998). Rejecting low coherence as ‘noise’ may therefore dismiss areas that still contain valid information about CA and in effect this may lead to disproportionately low sampling from regions of intact autoregulation. As a result, fewer semblance values will contribute to the final summary (mean) value, potentially increasing its variance. However, our results showed overall improvement of stability of wPRx over PRx, suggesting a good balance between removing seemingly uncorrelated data points and decreasing valid data points for averaging. Additionally, the apparently better ability of wPRx, with the coherence mask, to distinguish CPP above and below LLA is reassuring.
Potential clinical use
PRx has been used for estimation of the optimal, or safe, range of CPP for patients with traumatic brain injury (Donnelly et al. 2017; Liu et al. 2017b) . Deviation from optimal CPP defined by PRx monitoring is associated with death and permanent neurological disability (Aries et al. 2012). Maintenance of CPP at the optimal range defined by PRx monitoring is associated with the highest rate of survival with intact neurological function. However, it is known that the PRx can be imprecise, due to transient fluctuations in the ABP and ICP signals unrelated to autoregulation. This imprecision necessitates prolonged time windows to delineate optimal CPP reliably. Four hours is the agreed minimal period for estimation of optimal CPP (Aries et al. 2012), and so far there is no evidence that shorter windows are feasible. Also, the yield of optimal CPP is not high (around 50%) using PRx (Aries et al. 2012; Depreitere et al. 2014). Improvements in the precision of PRx monitoring have the potential to improve the optimal CPP yield and this has been shown in a recent publication (Liu et al. 2017a). The use of a wavelet transform with coherence filtering, as demonstrated in this study, is a viable method to improve the signal to noise ratio, and has the potential to improve optimal CPP yield for future clinical usage.
Conclusion
In this study, a new wavelet‐transform‐based method, suitable for non‐stationary signals, was introduced to assess CA. The new method, termed wavelet transform pressure reactivity index (wPRx), was validated through two groups of experimental piglet data. The results showed a strong, linear relationship and high agreement between wPRx and the time‐correlation‐based index, PRx. Both PRx and wPRx can distinguish CPP above and below LLA, while wPRx demonstrated more stable results than PRx.
Additional information
Conflicts of interest
ICM+ Software is licensed by Cambridge Enterprise, Cambridge, UK (http://icmplus.neurosurg.cam.ac.uk). M.Cz. and P.S. have a financial interest in a fraction of the licensing fee.
Author contributions
K.B. designed the animal experiment, acquired, analysed and interpreted the data and revised the manuscript. P.S. and M.Cz. designed the work, interpreted the data and revised the manuscript. X.Y.L. analysed and interpreted the data and wrote the manuscript. J.D. and D.C. interpreted the data and revised the manuscript. M.Ca. analysed the data and revised the manuscript. P.J.H. interpreted the data and revised the manuscript. X.H. interpreted the data and revised the manuscript. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.
Funding
The authors received no specific funding for this work.
Acknowledgements
PJH is supported by a NIHR Research Professorship and the NIHR Cambridge Biomedical Research Centre.
Biography
Xiuyun Liu received her B.S. and M.S. in Biomedical Engineering from Tianjin University (China) in 2009 and 2012, respectively. She received her PhD degree in Clinical Neurosciences from University of Cambridge (UK) in 2017. She joined the Department of Physiological Nursing at University of California, San Francisco, as a postdoctoral researcher in 2017. Her research focuses on cerebral autoregulation assessment, physiological signal processing, intracranial waveform analysis and biomedical models and she has a particular interest in cerebral blood flow dynamics.

Edited by: Harold Schultz & Laura Bennet
Linked articles This article is highlighted by a Perspective by Highton. To read this article, visit https://doi.org/10.1113/JP276290.
References
- Aaslid R, Lundar T, Lindegaard KF & Nornes H (1986). Estimation of Cerebral Perfusion Pressure from Arterial Blood Pressure and Transcranial Doppler Recordings. Intracranial Press VI 226–229.
- Addison PS (2002). The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, 1st Edition, CRC Press, Boca Raton. [Google Scholar]
- Addison PS (2015a). A review of wavelet transform time‐frequency methods for NIRS‐based analysis of cerebral autoregulation. IEEE Rev Biomed Eng 8, 78–85. [DOI] [PubMed] [Google Scholar]
- Addison PS (2015b). Identifying stable phase coupling associated with cerebral autoregulation using the synchrosqueezed cross‐wavelet transform and low oscillation morlet wavelets. Conf Proc IEEE Eng Med Biol Soc 8, 5960–5963. [DOI] [PubMed] [Google Scholar]
- Addison PS (2016). The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, Second Edition, CRC Press, Taylor & Francis Group, Boca Raton. [Google Scholar]
- Aries MJH, Czosnyka M, Budohoski KP, Steiner LA, Lavinio A, Kolias AG, Hutchinson PJ, Brady KM, Menon DK, Pickard JD & Smielewski P (2012). Continuous determination of optimal cerebral perfusion pressure in traumatic brain injury. Crit Care Med 40, 2456–2463. [DOI] [PubMed] [Google Scholar]
- Bishop SM, Yarham SI, Navapurkar VU, Menon DK & Ercole A (2012). Multifractal analysis of hemodynamic behavior: intraoperative instability and its pharmacological manipulation. Anesthesiology 117, 810–821. [DOI] [PubMed] [Google Scholar]
- Brady KM, Easley RB, Kibler K, Kaczka DW, Andropoulos D, Fraser CD, Smielewski P, Czosnyka M, Adams GJ, Rhee CJ & Rusin CG (2012). Positive end‐expiratory pressure oscillation facilitates brain vascular reactivity monitoring. J Appl Physiol 113, 1362–1368. [DOI] [PubMed] [Google Scholar]
- Brady KM, Lee JK, Kibler KK, Easley RB, Koehler RC, Czosnyka M, Smielewski P & Shaffner DH (2009). The lower limit of cerebral blood flow autoregulation is increased with elevated intracranial pressure. Anesth Analg 108, 1278–1283. [DOI] [PubMed] [Google Scholar]
- Brady KM, Lee JK, Kibler KK, Easley RB, Koehler RC & Shaffner DH (2008). Continuous measurement of autoregulation by spontaneous fluctuations in cerebral perfusion pressure: comparison of 3 methods. Stroke 39, 2531–2537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalak L, Tian F, Adams‐Huet B, Vasil D, Laptook A, Tarumi T & Zhang R (2017). Novel wavelet real time analysis of neurovascular coupling in neonatal encephalopathy. Sci Rep 7, 45958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalak LF & Zhang R (2017). New wavelet neurovascular bundle for bedside evaluation of cerebral autoregulation and neurovascular coupling in newborns with hypoxic‐ischemic encephalopathy. Dev Neurosci 39, 89–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan KH, Miller JD, Dearden NM, Andrews PJ & Midgley S (1992). The effect of changes in cerebral perfusion pressure upon middle cerebral artery blood flow velocity and jugular bulb venous oxygen saturation after severe brain injury. J Neurosurg 77, 55–61. [DOI] [PubMed] [Google Scholar]
- Chi N, Wang C, Chan L & Hu H (2018). Comparing different recording lengths of dynamic cerebral autoregulation: 5 versus 10 minutes. Biomed Res Int DOI: 10.1155/2018/7803426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper GRJ & Cowan DR (2008). Comparing time series using wavelet‐based semblance analysis. Comput Geosci 34, 95–102. [Google Scholar]
- Czosnyka M, Smielewski P, Kirkpatrick P, Laing RJ, Menon D & Pickard JD (1997). Continuous assessment of the cerebral vasomotor reactivity in head injury. Neurosurgery 41, 11–19. [DOI] [PubMed] [Google Scholar]
- Davrath LR, Goren Y, Pinhas I, Toledo E & Akselrod S (2003). Early autonomic malfunction in normotensive individuals with a genetic predisposition to essential hypertension. Am J Physiol Heart Circ Physiol 285, H1697–704. [DOI] [PubMed] [Google Scholar]
- Depreitere B, Güiza F, Van den Berghe G, Schuhmann MU, Maier G, Piper I & Meyfroidt G (2014). Pressure autoregulation monitoring and cerebral perfusion pressure target recommendation in patients with severe traumatic brain injury based on minute‐by‐minute monitoring data. J Neurosurg 120, 1451–1457. [DOI] [PubMed] [Google Scholar]
- Diedler J, Zweifel C, Budohoski K, Kasprowicz M, Sorrentino E, Haubrich C, Brady K, Czosnyka M, Pickard J & Smielewski P (2011). The limitations of near‐infrared spectroscopy to assess cerebrovascular reactivity: the role of slow frequency oscillations. Anesth Analg 113, 849–857. [DOI] [PubMed] [Google Scholar]
- Donnelly J, Czosnyka M, Adams H, Robba C, Steiner LA, Cardim D, Cabella B, Liu X, Ercole A, Hutchinson PJ, Menon DK, Aries MJH & Smielewski P (2017). Individualizing thresholds of cerebral perfusion pressure using estimated limits of autoregulation. Crit Care Med 45, 1464–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faes L, Pinna GD, Porta A, Maestri R & Nollo G (2004). Surrogate data analysis for assessing the significance of the coherence function. IEEE Trans Biomed Eng 51, 1156–1166. [DOI] [PubMed] [Google Scholar]
- Garg A, Xu D, Laurin A & Blaber AP (2014). Physiological interdependence of the cardiovascular and postural control systems under orthostatic stress. Am J Physiol Heart Circ Physiol 307, H259–264. [DOI] [PubMed] [Google Scholar]
- Giller CA (1990). The frequency‐dependent behavior of cerebral autoregulation. Neurosurgery 27, 362–368. [DOI] [PubMed] [Google Scholar]
- Gressens P, Dingley J, Plaisant F, Porter H, Schwendimann L, Verney C, Tooley J & Thoresen M (2008). Analysis of neuronal, glial, endothelial, axonal and apoptotic markers following moderate therapeutic hypothermia and anesthesia in the developing piglet brain. Brain Pathol 18, 10–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinsted A, Moore JC & Jevrejeva S (2004). Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process Geophys 11, 561–566. [Google Scholar]
- Grundy D (2015). Principles and standards for reporting animal experiments in The Journal of Physiology and Experimental Physiology . Exp Physiol 100, 755–758. [DOI] [PubMed] [Google Scholar]
- Highton D, Ghosh A, Tachtsidis I, Panovska‐Griffiths J, Elwell CE & Smith M (2015). Monitoring cerebral autoregulation after brain injury: multimodal assessment of cerebral slow‐wave oscillations using near‐infrared spectroscopy. Anesth Analg 121, 198–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Jong DLK, Tarumi T, Liu J, Zhang R & Claassen JAHR (2017). Lack of linear correlation between dynamic and steady‐state cerebral autoregulation. J Physiol 595, 5623–5636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keissar K, Davrath LR & Akselrod S (2009). Coherence analysis between respiration and heart rate variability using continuous wavelet transform. Philos Trans A Math Phys Eng Sci 367, 1393–1406. [DOI] [PubMed] [Google Scholar]
- Kenosi M, Naulaers G, Ryan CA & Dempsey EM (2015). Current research suggests that the future looks brighter for cerebral oxygenation monitoring in preterm infants. Acta Paediatr 104, 225–231. [DOI] [PubMed] [Google Scholar]
- Kvandal P, Sheppard L, Landsverk SA, Stefanovska A & Kirkeboen KA (2013). Impaired cerebrovascular reactivity after acute traumatic brain injury can be detected by wavelet phase coherence analysis of the intracranial and arterial blood pressure signals. J Clin Monit Comput 27, 375–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labrecque L, Rahimaly K, Imhoff S, Paquette M, Le Blanc O, Malenfant S, Lucas SJE, Bailey DM, Smirl JD & Brassard P (2017). Diminished dynamic cerebral autoregulatory capacity with forced oscillations in mean arterial pressure with elevated cardiorespiratory fitness. Physiol Rep 5, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang EW & Chesnut RM (1995). Intracranial pressure and cerebral perfusion pressure in severe head injury. New Horiz 3, 400–409. [PubMed] [Google Scholar]
- Lang EW, Kasprowicz M, Smielewski P, Santos E, Pickard J & Czosnyka M (2015). Short pressure reactivity index versus long pressure reactivity index in the management of traumatic brain injury. J Neurosurg 122, 588–594. [DOI] [PubMed] [Google Scholar]
- Lassen N (1959). Cerebral blood flow and oxygen consumption in man. Physiol Rev 39, 183–238. [DOI] [PubMed] [Google Scholar]
- Lassen NA & Agnoli A (1972). The upper limit of autoregulation of cerebral blood flow – on the pathogenesis of hypertensive encepholopathy. Scand J Clin Lab Invest 30, 113–116. [DOI] [PubMed] [Google Scholar]
- Latka M, Turalska M, Glaubic‐Latka M, Kolodziej W, Latka D & West BJ (2005). Phase dynamics in cerebral autoregulation. Am J Physiol Heart Circ Physiol 289, H2272–2279. [DOI] [PubMed] [Google Scholar]
- Lee JK, Kibler KK, Benni PB, Easley RB, Czosnyka M, Smielewski P, Koehler RC, Shaffner DH & Brady KM (2009). Cerebrovascular reactivity measured by near‐infrared spectroscopy. Stroke 40, 1820–1826. [DOI] [PubMed] [Google Scholar]
- Liu J, Tseng BY, Khan MA, Tarumi T, Hill C, Mirshams N, Hodics TM, Hynan LS & Zhang R (2016). Individual variability of cerebral autoregulation, posterior cerebral circulation and white matter hyperintensity. J Physiol 594, 3141–3155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Donnelly J, Czosnyka M, Aries MJH, Brady K, Cardim D, Robba C, Cabeleira M, Kim D‐J, Haubrich C, Hutchinson PJ & Smielewski P (2017a). Cerebrovascular pressure reactivity monitoring using wavelet analysis in traumatic brain injury patients: a retrospective study. PLoS Med 14, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Maurits N, Aries M, Czosnyka M, Ercole A, Donnelly J, Cardim D, Kim D, Dias C, Cabeleira M & Smieleweski P (2017b). Monitoring of optimal cerebral perfusion pressure in traumatic brain injured patients using a multi‐window weighting algorithm. J Neurotrauma 34, 3081–3088. [DOI] [PubMed] [Google Scholar]
- Muizelaar J, Ward J, Marmarou A, Newlon P & Wachi A (1989). Cerebral blood flow and metabolism in severely head‐injured children Part 2: Autoregulation. J Neurosurg 71, 72–76. [DOI] [PubMed] [Google Scholar]
- National Research Council (2011). Guide for the Care and Use of Laboratory Animals, 8th Ed, National Academies Press, Washington (DC). [Google Scholar]
- Panerai RB (2014). Nonstationarity of dynamic cerebral autoregulation. Med Eng Phys 36, 576–584. [DOI] [PubMed] [Google Scholar]
- Panerai RB, Dawson SL & Potter JF (1999). Linear and nonlinear analysis of human dynamic cerebral autoregulation. Am J Physiol 277, H1089–1099. [DOI] [PubMed] [Google Scholar]
- Paulson OB, Strandgaard S & Edvinsson L (1990). Cerebral autoregulation. Cerebrovasc Brain Metab Rev 2, 161–192. [PubMed] [Google Scholar]
- Peng T, Rowley AB, Ainslie PN, Poulin MJ & Payne SJ (2010). Wavelet phase synchronization analysis of cerebral blood flow autoregulation. IEEE Trans Biomed Eng 57, 960–968. [DOI] [PubMed] [Google Scholar]
- Pichot V, Gaspoz JM, Molliex S, Antoniadis A, Busso T, Roche F, Costes F, Quintin L, Lacour JR, Barthélémy JC, Busso T, Roche F, Costes F, Quintin L, Lacour JR & Barthélémy JC (1999). Wavelet transform to quantify heart rate variability and to assess its instantaneous changes. J Appl Physiol (1985) 86, 1081–1091. [DOI] [PubMed] [Google Scholar]
- Placek MM, Wachel P, Iskander DR, Smielewski P, Uryga A, Mielczarek A, Szczepański TA & Kasprowicz M (2017). Applying time‐frequency analysis to assess cerebral autoregulation during hypercapnia. PLoS One 12, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez J & MüllerEmail M (2011). pROC: an open‐source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics 12, 77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowley AB, Payne SJ, Tachtsidis I, Ebden MJ, Whiteley JP, Gavaghan DJ, Tarassenko L, Smith M, Elwell CE & Delpy DT (2007). Synchronization between arterial blood pressure and cerebral oxyhaemoglobin concentration investigated by wavelet cross‐correlation. Physiol Meas 28, 161–173. [DOI] [PubMed] [Google Scholar]
- van der Scheer J, Kamijo Y, Leicht C, Millar P, Shibasaki M, Goosey‐Tolfrey V & Tajima F (2018). A comparison of static and dynamic cerebral autoregulation during mild whole‐body cold stress in individuals with and without cervical spinal cord injury: a pilot study. Spinal Cord 10.1038/s41393-017-0021-7. [DOI] [PubMed] [Google Scholar]
- Schmidt B, Czosnyka M, Schwarze JJ, Sander D, Gerstner W, Lumenta CB, Pickard JD & Klingelhöfer J (1999). Cerebral vasodilatation causing acute intracranial hypertension: a method for noninvasive assessment. J Cereb Blood Flow Metab 19, 990–996. [DOI] [PubMed] [Google Scholar]
- Shigemori M, Nakashima H, Moriyama T, Tokutomi T, Nishio N, Harada K & Kuramoto S (1989). Noninvasive study of critical thresholds of intracranial pressure and cerebral perfusion pressure for cerebral circulation and brain function. Neurol Res 11, 165–168. [DOI] [PubMed] [Google Scholar]
- Smith M (2011). Shedding light on the adult brain: a review of the clinical applications of near‐infrared spectroscopy. Philos Trans A Math Phys Eng Sci 369, 4452–4469. [DOI] [PubMed] [Google Scholar]
- Tarumi T, Dunsky DI, Khan MA, Liu J, Hill C, Armstrong K, Martin‐Cook K, Cullum CM & Zhang R (2014). Dynamic cerebral autoregulation and tissue oxygenation in amnestic mild cognitive impairment. J Alzheimers Dis 41, 765–778. [DOI] [PubMed] [Google Scholar]
- Tian F, Tarumi T, Liu H, Zhang R & Chalak L (2016). Wavelet coherence analysis of dynamic cerebral autoregulation in neonatal hypoxic‐ischemic encephalopathy. NeuroImage Clin 11, 124–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrence C & Compo GP (1998). A practical guide to wavelet analysis. Bull Am Meteorol Soc 79, 61–78. [Google Scholar]
- Tzeng YC & Ainslie PN (2014). Blood pressure regulation IX: Cerebral autoregulation under blood pressure challenges. Eur J Appl Physiol 114, 545–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng YC, Ainslie PN, Cooke WH, Peebles KC, Willie CK, MacRae BA, Smirl JD, Horsman HM & Rickards CA (2012). Assessment of cerebral autoregulation: the quandary of quantification. Am J Physiol Heart Circ Physiol 303, H658–671. [DOI] [PubMed] [Google Scholar]
- Wszedybyl‐Winklewska M, Wolf J, Swierblewska E, Kunicka K, Gruszecka A, Gruszecki M, Kucharska W, Winklewski PJ, Zabulewicz J, Guminski W, Pietrewicz M, Frydrychowski AF, Bieniaszewski L & Narkiewicz K (2017). Acute hypoxia diminishes the relationship between blood pressure and subarachnoid space width oscillations at the human cardiac frequency. PLoS One 12, 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Zuckerman JH, Giller CA & Levine BD (1998). Transfer function analysis of dynamic cerebral autoregulation in humans. Am J Physiol 274, 233–241. [DOI] [PubMed] [Google Scholar]


