Abstract
Key points
Cytotoxic T lymphocytes (CTLs) and natural killer (NK) cells are required to eliminate cancer cells.
We analysed the Ca2+ dependence of CTL and NK cell cytotoxicity and found that in particular CTLs have a very low optimum of [Ca2+]i (between 122 and 334 nm) and [Ca2+]o (between 23 and 625 μm) for efficient cancer cell elimination, well below blood plasma Ca2+ levels.
As predicted from these results, partial down‐regulation of the Ca2+ channel Orai1 in CTLs paradoxically increases perforin‐dependent cancer cell killing.
Lytic granule release at the immune synapse between CTLs and cancer cells has a Ca2+ optimum compatible with this low Ca2+ optimum for efficient cancer cell killing, whereas the Ca2+ optimum for CTL migration is slightly higher and proliferation increases monotonously with increasing [Ca2+]o.
We propose that a partial inhibition of Ca2+ signals by specific Orai1 blockers at submaximal concentrations could contribute to tumour elimination.
Abstract
Cytotoxic T lymphocytes (CTLs) and natural killer (NK) cells are required to protect the human body against cancer. Ca2+ is a key metabolic factor for lymphocyte function and cancer homeostasis. We analysed the Ca2+ dependence of CTL and NK cell cytotoxicity against cancer cells and found that CTLs have a bell‐shaped Ca2+ dependence with an optimum for cancer cell elimination at rather low [Ca2+]o (23–625 μm) and [Ca2+]i (122–334 nm). This finding predicts that a partial inhibition of Orai1 should increase (rather than decrease) cytotoxicity of CTLs at [Ca2+]o higher than 625 μm. We tested this hypothesis in CTLs and indeed found that partial down‐regulation of Orai1 by siRNA increases the efficiency of cancer cell killing. We found two mechanisms that may account for the Ca2+ optimum of cancer cell killing: (1) migration velocity and persistence have a moderate optimum between 500 and 1000 μm [Ca2+]o in CTLs, and (2) lytic granule release at the immune synapse between CTLs and cancer cells is increased at 146 μm compared to 3 or 800 μm, compatible with the Ca2+ optimum for cancer cell killing. It has been demonstrated in many cancer cell types that Orai1‐dependent Ca2+ signals enhance proliferation. We propose that a decrease of [Ca2+]o or partial inhibition of Orai1 activity by selective blockers in the tumour microenvironment could efficiently reduce cancer growth by simultaneously increasing CTL and NK cell cytotoxicity and decreasing cancer cell proliferation.
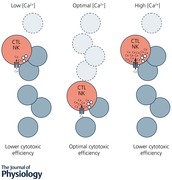
Keywords: cytotoxic immune cells, cancer cells, killing efficiency
Introduction
Cytotoxic T lymphocytes (CTLs) and natural killer (NK) cells kill their targets, virally infected or cancer cells, by several different mechanisms, the most prominent being the release of cytotoxic or lytic granules (LGs) containing perforin and granzymes at the immune synapse (IS) between cytotoxic cells and target cells. Already 40 years ago it was shown that cytotoxicity of CTLs is strongly dependent on Ca2+ influx from the extracellular medium (Golstein & Smith, 1976; Plaut et al. 1976; Gately & Martz, 1977). Ten years later it became clear that for granule exocytosis at the IS like exocytosis at neuronal synapses, a Ca2+‐dependent step is required for CTL‐induced cytotoxicity (Lancki et al. 1987; Takayama & Sitkovsky, 1987; Lyubchenko et al. 2001). This further strengthened the analogy between these two types of synapses (Becherer et al. 2012) but raised the question of which channels would conduct the Ca2+ currents required for vesicle fusion in the non‐excitable cells of the haematopoietic system. With the identification of Ca2+ release‐activated Ca2+ (CRAC) channels as the main source for Ca2+ entry in mast cells and Jurkat T cells (Hoth & Penner, 1992, 1993; Zweifach & Lewis, 1993), a valid hypothesis was that CTLs and NK cells also use CRAC channels as a Ca2+ source to mediate LG release. Following the identification of CRAC channel‐dependent Ca2+ influx in CTLs during target cell engagement (Zweifach, 2000) and the identification of Orai1 as an essential component of endogenous CRAC channels (Feske et al. 2006; Vig et al. 2006; Zhang et al. 2006), it was finally reported that Ca2+ entry through Orai1 channels is required for LG exocytosis and target cell killing by primary human NK cells (Maul‐Pavicic et al. 2011).
Considering these findings, it is obvious that Ca2+ influx through Orai1 channels is necessary to kill cancer cells (as reviewed in Schwarz et al. 2013). The overall impact of Orai1 function on cancer progression is not determined only by its involvement in CTL and NK function, since Orai channels are also major players in proliferation, migration and metastasis of cancer cells (reviewed in Hoth, 2016; Iamshanova et al. 2017). In many cancer types changes of expression levels and/or mutations of Orai channels and their activators, stromal interaction molecule (STIM) proteins, have been reported (Chen et al. 2011; Bergmeier et al. 2013; Vashisht et al. 2015). While it is widely believed that Orai channel activity modulates cancer cell growth (Yang et al. 2009; Feng et al. 2010; Chen et al. 2011; Prevarskaya et al. 2011; Bergmeier et al. 2013; Vashisht et al. 2015; Xu et al. 2015; Hoth, 2016; Iamshanova et al. 2017), mutations in Orai channels and other Ca2+ channels are probably not causally linked to cancer development (Hoth, 2016). However, considering the prominent role of Orai channels for cytotoxicity of CTLs and NK cells on one hand and for cancer growth on the other hand, Ca2+ influx through Orai channels has at least a dual role in the tumour microenvironment. This makes Ca2+ influx an interesting target to influence overall cancer growth. It is thus of relevance to understand if and how Ca2+ determines the efficiency of human immune cell cytotoxicity against cancer cells. We have analysed the role of Ca2+ for cancer cell elimination by primary human CTLs and NK cells, and we have investigated the potential underlying mechanisms.
Methods
Ethical approval
This research has been approved by the local ethic committee (84/15; Prof. Dr Rettig‐Stürmer). Leukocyte reduction system (LRS) chambers, a byproduct of platelet collection from healthy donors, were kindly provided by the local blood bank in the Institute of Clinical Hemostaseology and Transfusion Medicine at Saarland University Medical Center. Prior to the sample being taken, blood donors provided written consent to use their blood for research purposes. The study conformed to the standards set by the Declaration of Helsinki, except for registration in a database.
Cells
Human peripheral blood mononuclear cells (PBMCs) of healthy donors were isolated from LRS chambers (Institute of Clinical Haematology and Transfusion Medicine, Homburg) by density gradient centrifugation using Lymphocyte Separation Medium 1077 (PromoCell, Heidelberg, Germany). Primary human NK cells and CD8+ T cells were negatively isolated from PBMCs using Dynabeads Untouched Human NK Cells or T Cells Kits (11349D and 11348D, Thermo Fisher Scientific, Darmstadt, Germany). Negative isolation avoids pre‐stimulation of the isolated subtypes because antibody‐coated beads against all other cell types are used for isolation and thus isolated subtypes do not come into contact with antibodies against any of their own plasma membrane proteins. Staphylococcal enterotoxin A (SEA)‐stimulated CD8+ T cells were prepared as described before (Qu et al. 2011). Briefly, positive isolation of CD8+ T cells was carried out following PBMC stimulation with 1 μg ml−1 SEA for 5 days and subsequent isolation by using Dynabeads CD8 Positive Isolation Kit (11333D, Thermo Fisher Scientific), which contains anti‐CD8‐coated beads. In the last step of the isolation process, anti‐CD8‐coated beads were removed from the cells by the DETACHaBEAD reagent (Thermo Fisher Scientific). PBMCs and isolated subtypes were maintained in AIM V medium (Thermo Fisher Scientific) supplemented with 10% fetal bovine serum (FBS). Jurkat T cells, Raji cells, P815 cells and K562 cells were maintained in RPMI 1640 medium (Thermo Fisher Scientific) supplemented with 10% FBS and 1% penicillin–streptomycin (Thermo Fisher Scientific). NK‐92 cells were from DSMZ (Braunschweig, Germany) and cultivated in MEMα (Thermo Fisher Scientific) supplemented with 12.5% FBS (Thermo Fisher Scientific), 12.5% horse serum (Thermo Fisher Scientific), 2 mm l‐glutamine (Sigma‐Aldrich, Munich, Germany) and 10 ng ml−1 IL‐2 (Thermo Fisher Scientific).
Reagents
Calcein‐AM (C3100) and Fura‐2/AM (F1211) were purchased from Thermo Fisher Scientific. Anti‐CD3 (B‐B11) antibody was from Diaclone (Besancon, France), lymphocyte function‐associated antigen 1 (anti‐LFA1) antibody (SM3100AS) was from Acris Antibodies (Herford, Germany). Anti‐human CD28 (555725) was from BD Biosciences (Heidelberg, Germany). Fibronectin (F4759), phorbol 12‐myristate 13‐acetate (PMA, P1585), ionomycin (I0634), SEA (S9399) and EGTA (E4378) were from Sigma‐Aldrich. All other chemicals and reagents not specifically mentioned were from Sigma‐Aldrich.
Real‐time killing assay
The real‐time killing assay was carried out as previously described (Kummerow et al. 2014). Briefly, cancer cells (Raji for CTL killing, K562 for NK/NK‐92 killing) were loaded with 500 nm calcein‐AM in AIM V medium containing 10 mm Hepes. Raji target cells were pulsed with 1 μg ml−1 SEA in AIM V medium for 30 min in the incubator before loading them with calcein‐AM, and were then settled at 2.5 × 104 cells per well into the 96‐well black plate with clear‐bottom (353219, Corning, Amsterdam, Netherlands). Primary NK cells, NK‐92 or SEA‐expanded CD8+ T cells were added subsequently onto cancer cells at the indicated effector to target ratio. Target lysis was measured either in an M200 Infinite plate reader (Tecan, Crailsheim, Germany) or a Genios Pro (Tecan) using bottom reading function at 37°C.
To study the impact of concanamycin A (CMA; Santa Cruz Biotechnology, Dallas, TX, USA) on cytotoxicity, NK cells or SEA‐stimulated CTL were pre‐incubated for 4 h in AIM V with 10% FBS and 10 mm Hepes containing 100 nm CMA (200 μm stock solution in dimethyl sulfoxide) at 37°C, 5% CO2 at a density of 2 × 106 cells ml−1. To exclude CMA effects on cancer cells, NK cells or CTLs were centrifuged and re‐suspended in AIM V with 10% FBS with10 mm Hepes without CMA before measurement.
For analysis of real‐time killing in modified Ringer solution with different extracellular Ca2+ concentrations ([Ca2+]o), variable concentrations of CaCl2 were added to the solution containing 155 mm NaCl, 4.5 mm KCl, 10 mm glucose and 5 mm Hepes. The sum of [CaCl2] and [MgCl2] was kept constant at 3 mm. pH was adjusted to 7.4 with 1 m NaOH. Modified Ringer solution for experiments in Fig. 1 H (analysing the influence of extracellular Mg2+ concentrations) contained 145 mm NaCl, 4 mm KCl, 10 mm glucose, 10 mm Hepes and MgCl2 and CaCl2 as indicated. Mg2+ was added from a 1 m stock of MgCl2.
Figure 1. Ca2+ dependence of perforin‐dependent CTL cytotoxicity.
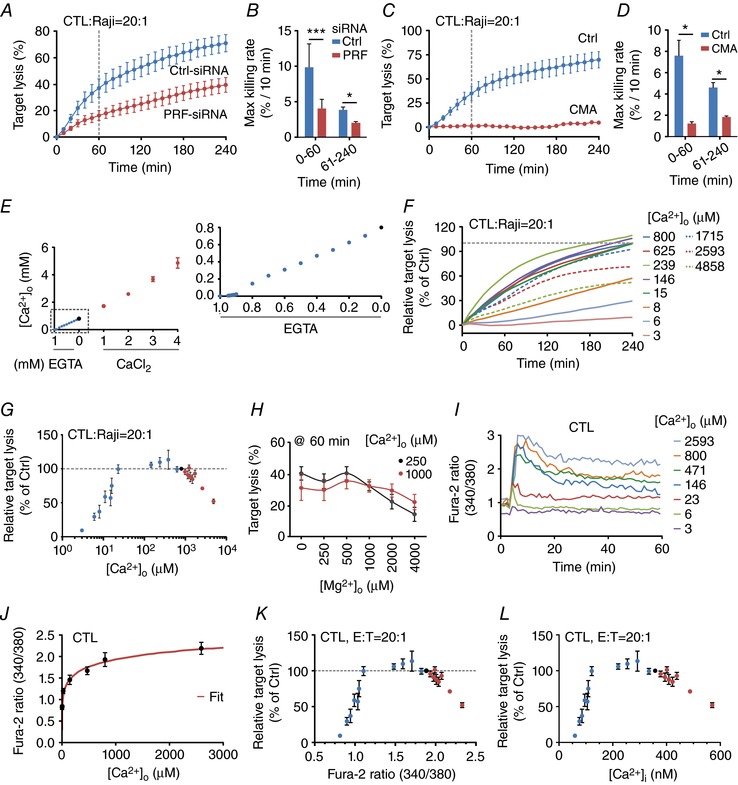
A and B, real‐time killing assay using SEA‐stimulated CTLs as effector and SEA‐pulsed Raji cells as target cells with an E:T ratio of 20:1 (A) and the statistical analysis of the maximal killing rate (B) in perforin down‐regulated CTLs (PRF‐siRNA, n = 4 independent experiments) in comparison to the mean of control siRNA transfected CTLs (Ctrl‐siRNA, n = 4 independent experiments). C and D, real‐time killing assay in CMA‐treated CTLs with SEA‐pulsed Raji cells as target cells with an E:T ratio of 20:1 (C, CMA n = 2 or Ctrl n = 4 independent experiments) and the statistical analysis of the maximal killing rate (D). E, measurement of [Ca2+]o in AIM V medium (black circle) with the addition of EGTA (blue circles) or CaCl2 (red circles) using a Ca2+‐selective electrode or a blood gas analyser. Each data point was measured independently 2–6 times. If no error bars are shown, they are smaller than the points themselves. F, real‐time killing assay with SEA‐pulsed Raji cells as target cells with an E:T ratio of 20:1 in different [Ca2+]o (values as indicated) manipulated by the addition of EGTA (continuous lines) or CaCl2 (dashed lines). Data are normalized to target lysis in 800 μm [Ca2+]o after 4 h. Data are from 2–17 different donors and 4–24 experiments for each [Ca2+]o. G, statistical analysis of the relative target lysis after 4 h plotted against the [Ca2+]o. Data are from 2–17 different donors and 4–24 experiments. Data points in blue represent AIM V medium with added EGTA, in red AIM V medium with added CaCl2 and the data point in black represents AIM V medium. H, statistical analysis of real‐time killing assay with SEA‐pulsed Raji cells as target cells with an E:T ratio of 20:1 at 60 min plotted against different Mg2+ (0–4000 μm) concentrations. The Ca2+ concentration was fixed to 250 and 1000 μm. Data are shown as mean ± SEM from 5–15 donors with 5–18 experiments. I, average Ca2+ ratio values of CTL forming an IS with Raji target cells in AIM V medium with the indicated [Ca2+]o. Fura‐2 ratio kinetics were temporally aligned before averaging. J, steady state values for Fura‐2 ratios of CTLs in contact with target cells (shown in I) plotted against the corresponding [Ca2+]o values. Data were fitted by a Hill equation using Igor Pro 6.22A (red line). K, relative target lysis of CTLs (normalized to target lysis in AIM V medium) is plotted against plateau Fura‐2 ratios during target contact. Fura‐2 ratios were calculated based on [Ca2+]o using the Hill function from Fig. 1J. Data points in blue represent AIM V medium with added EGTA, in red AIM V medium with added CaCl2 and the data point in black represents AIM V medium. L, relative target lysis of CTLs (normalized to target lysis in AIM V medium) plotted against plateau [Ca2+]i of CTLs during contact with target cells. [Ca2+]i values were derived by in situ calibration of Fura‐2 as described in Methods. Data points in blue represent AIM V medium with added EGTA, in red AIM V medium with added CaCl2 and the data point in black represents AIM V medium.
Quantification of free Ca2+ concentration in AIM V medium supplemented with different amounts of Ca2+ or EGTA
To modify [Ca2+]o, different Ca2+‐containing solutions were prepared by adding 0.1–1 mm of the Ca2+ chelator EGTA (100 mm stock solution, pH 8.0, sterile filtered) or 1–4 mm CaCl2 (1 m stock solution), respectively to AIM V with 10 mm Hepes. Both stock solutions were pre‐diluted to 10–20 mm with AIM V with 10 mm Hepes. Solutions were equilibrated overnight at 37°C and 5% CO2 prior to measurements the next day. Solutions were stirred during measurements. Free [Ca2+] was measured using a Ca2+‐selective electrode (perfectION Combination Calcium Electrode, Mettler Toledo, Gießen, Germany) or the blood gas analyser Rapidpoint 405 (Siemens, Erlangen, Germany) following the manufacturer's instruction. With the blood gas analyser three independent experiments were carried out and each free [Ca2+] was determined at least in triplicate. For calibration of the Ca2+‐selective electrode, standard solutions were prepared by a serial dilution of the provided Ca2+ standard solution ([Ca2+] = 1 g l−1) in distilled water. Ca2+ ionic strength adjuster (ISA) was added to calibration solutions to ensure a similar ionic strength. Two different calibration modes were used as described in the manufacturer's protocol: the direct or the low‐level calibration technique. For direct calibration four different solutions (2.5 × 10−2, 2.5 × 10−3, 2.5 × 10−4, 2.5 × 10−5 mol l−1) and for low‐level calibration five different solutions (100 × 10−6, 40 × 10−6, 10 × 10−6, 1 × 10−6, 1 × 10−7 mol l−1) were prepared. Measurements were performed at room temperature as described in the manufacturer's protocol. To determine the free [Ca2+]o of AIM V with 0.2, 0.4, 0.5, 0.6 and 0.8 mm CaCl2 added, measured free [Ca2+]o of AIM V manipulated with 0 or 1–4 mm CaCl2 was fitted by a sigmoid function (f(x) = −3738.1 + {25229/[1 + exp(7.1 − x)/4.7]}) in Igor Pro 6.22A (Wavemetrics, Lake Oswego, OR, USA). Similarly, to determine the free [Ca2+]o of AIM V with 0.1, 0.3, 0.4, or 0.6 mm EGTA added, measured free [Ca2+]o of AIM V with 0, 0.2, 0.5, 0.7, 0.8, 0.9, 0.91, 0.92, 0.93, 0.94, 0.95 or 1 mm EGTA was fitted by a sigmoid function (f(x) = 6127.7 + {−8379/[1 + exp(−1.27 − x)/2.27]}) in Igor Pro 6.22A. This function was then used to calculate the remaining values.
Single cell Ca2+ imaging by epifluorescence microscopy
Single cell Ca2+ imaging was performed as previously described (Quintana et al. 2007). To analyse Ca2+ dynamics in cells, cells were loaded with 2 μm Fura‐2/AM in FBS‐free AIM V and were subsequently settled onto poly‐d‐ornithine‐coated coverslips. Cells were monitored with an Olympus IX71 microscope equipped with an Olympus UPLSAPO ×20 (NA 0.75) objective and a camera controlled by TillVision software. Cells were excited at 340 and 380 nm with a polychrome V monochromator (T.I.L.L. Photonics, FEI Munich GmbH, Munich, Germany) using an ET Fura‐2 filter set (Chroma Technology Corp., Rockingham, VT, USA). The emitted light at wavelength >400 nm (T400 LP dichroic beamsplitter, ET510/80 nm emission filter) was acquired by a CCD camera (SensiCam, T.I.L.L. Imago, T.I.L.L. Photonics). Images were acquired every 5 s. Cells were perfused with a solution containing 0 mm Ca2+/1 mm EGTA and thapsigargin (TG) after 100 s to deplete intracellular Ca2+ stores. Solutions with Ca2+ were applied to the cells by perfusion after 700 s. The captured images were analysed by T.I.L.L. Vision software.
Single cell Ca2+ imaging with a 96‐well plate bioimager
A BD Pathway Bioimager 855 system (BD Biosciences) was used. NK‐92 cells and SEA‐stimulated CTLs were loaded with 2 μM Fura‐2/AM (Thermo Fisher Scientific) for 30 min at room temperature, washed and seeded into black, clear‐bottom 96‐well plates in medium containing desired concentrations of EGTA. Target cells were added and fluorescence images at excitation 334/10 nm and 380/10 nm and emission 540/50 nm were acquired. Ratiometric images and single cell ratio values were calculated with ImageJ 1.46r for every NK‐92 cell or CTL making contact with a target cell. Data were temporally aligned according to the Ca2+ rise after target contact and average ratio values were calculated. [Ca2+]i was determined according to the method described by Grynkiewicz et al. (1985): [Ca2+]i = K d × ((R − R min)/(R max − R)) × (S f2/S b2). The K d was determined by a patch‐clamp calibration, and R min, R max, S f2 and S b2 were determined from an in situ calibration in Jurkat T cells, which are used as a standard cell system to calibrate our set‐ups. We have previously confirmed that Jurkat T cells and primary human T cells have very similar calibration values (Schwarz et al. 2007).
Total internal reflection fluorescence microscopy imaging
Vesicle fusion was observed with a Leica DMI6000 B total internal reflection fluorescence (TIRF) MC microscope (Leica, Wetzlar, Germany). The emission line of a 561 nm solid state laser was used for excitation in TIRF mode and a Hamamatsu EMCCD 9100‐02 camera (Hamamatsu, Japan) was used to acquire fluorescence images. Human anti‐CD3/anti‐CD28 bead‐stimulated CTL overexpressing granzyme B–mCherry or perforin–mCherry were activated by an antibody cocktail of anti‐CD3 (30 μg ml−1), anti‐CD28 (90 μg ml−1) and anti‐LFA1 (30 μg ml−1) coated onto the coverslip. Cells were settled onto the antibody‐coated coverslips in modified Ringer solution with 0 mm [Ca2+]o for 5 min. After one wash with fresh 0 mm [Ca2+]o to flush away unsettled CTLs, images were acquired at indicated channels every 42 ms. Granzyme B–mCherry or perforin–mCherry overexpressing CTLs were monitored at 561 nm for LG fusion. After 20 s of acquisition, desired concentrations of [Ca2+]o in AIM V medium were applied to the cells. LG fusion was analysed by ImageJ using the time series analyser 2.0 plugin. Vesicles were marked in regions of interest (ROIs) and the mean fluorescence intensity within ROIs was analysed over time.
CellTiter‐Blue‐based proliferation assay
The Ca2+ dependence of CD8+ T cell proliferation was measured as described previously (Schwarz et al. 2007). Experiments were carried out as triplicates in 96‐well plates (no. 353219, black/transparent bottom, Corning). For each data point 2.5 × 104 CTLs were seeded in a total volume of 200 μl in each well and cultured for 72 h at standard culture conditions in AIM V medium with 10% FBS. After 72 h, the numbers of living cells were determined by CellTiter‐Blue (Promega (Madison, WI, USA)) following the manufacturer's instruction. Results are presented as percentage of relative fluorescence units (RFU). CTLs were stimulated with anti‐CD3/anti‐CD28‐coated beads (no. 111.32D, Dynabeads Human T‐Activator CD3/CD28, Thermo Fisher Scientific) at a ratio of 1:1 (bead/cell). To analyse cell proliferation under limiting Ca2+ conditions, 0.8–4 mm EGTA (from the 100 mm stock solution in H2O, pH 8.0, sterile filtered) was added in a total volume of 100 μl into the plates to partially chelate Ca2+ (see above for details). To investigate cell proliferation under elevated Ca2+ conditions, 2–8 mm CaCl2 (from the 1 m stock solution in H2O, sterile filtered) was added into the medium. To equilibrate pH, plates were pre‐incubated for at least 2 h at 37°C, 5% CO2 and 95% humidity before CTLs were mixed with antibody‐coated beads and applied in a total volume of 100 μl. Proliferation was measured with the plate reader Genios Pro (Tecan) using the bottom reading function at 37°C.
Electroporation
SEA stimulated CTLs were transfected as described earlier (Bhat et al. 2016). Briefly, for the siRNA transfection, 100 μl cell suspension was nucleofected with 8–10 μl (20 μm stock solution) or 4 μl (40 μm stock solution) of the following siRNA stock solutions: FlexiTube GeneSolution GS5551 for perforin 1 (Qiagen, Hs_PRF1_1, _3, _4 and _5, pool, 2.5 μl each), Orai1_1 and Orai1_2 (Qiagen, Hilden, Germany, no. SI03196207 and no. SI04215316, modified, 5 μl each) and various control siRNAs, AllStars negative control siRNA (Qiagen, no. 1027280, 20 μm), negative control siRNA (Qiagen, no. 1027310, 20 μm, unmodified and modified), control siRNA (Microsynth, Balgach, Switzerland, 40 μm, modified). Modifications were introduced according to Mantei et al. (2008) by Microsynth. Twelve to sixteen hours following siRNA transfection, cells were washed and plated at 1.5 × 106 cells ml−1 in fresh AIM V plus 10% FBS media with 20 μg ml−1 IL‐2 added and incubated until further use (36–44 h for perforin or 1 and 3 days for Orai1‐transfected CTLs). For the protein over‐expression, 100 μl cell suspension of anti‐CD3/anti‐CD28 bead‐stimulated CTLs was nucleofected with 0.5 μg granzyme B–mCherry construct or 0.75 μg perforin–mCherry construct using the 4D Nucleofector system from Lonza (Cologne, Germany). The medium was replaced 6 h post transfection and cells were used 15–24 h after the transfection.
Modified primer sequences are identical as previously published (Holzmann et al. 2013):
Orai1_1_mod, sense: 5′ OMeC OMeG GCCUGAUCUUUAUCG d(UCU) OMeU OMeT OMeT 3′
Antisense: 3′ OmeG OmeC CGGACUAGAAAUAGCAGA d(A) 5′
Orai1_2_mod, sense: 5′ OMeC OMeA ACAUCGAGGCGGUGA d(GCA) OMeA OMeT OMeT 3′
Antisense: 3′ OMeG OMeT UGUAGCUCCGCCACUCGU d(U) 5′
Negative control siRNA_mod, sense: 5′ OMeA OMeA UUCUCCGAACGUGUC d(ACG) OmeU OmeT OMeT 3′
Antisense: 3′ OmeT OMeT AAGAGGCUUGCACAGUGC d(A) 5′
Control siRNA_mod, sense: 5′ OMeA OMeA AGGUAGUGUAAUCGC d(CUU) OMeG OMeT OMeT 3′
Antisense: 3′ OMeT OMeT UCCAUCACAUUAGCGGAA dC 5′
RNA isolation and qRT‐PCR
Experiments were carried out as described before (Wenning et al. 2011). In brief, total RNA was isolated from 1.5 × 106 SEA‐stimulated CTLs using TRIzol reagent (Thermo Fisher Scientific) supplemented with 1 μl glycogen (5 μg μl−1, Thermo Fisher Scientific). Total RNA (0.8 μg) was reverse transcribed and 1 μl of cDNA was used for quantitative real‐time polymerase chain reaction (qRT‐PCR). Real‐time PCR was carried out in a CFX96 Real‐Time System C1000 Thermal Cycler (Bio‐Rad Laboratories, Munich, Germany) (software: Bio‐Rad CFX Manager, Version 3.0) as described before (Wenning et al. 2011). Primer sequences for reference genes RNAPolII (accession NM_000937) and TBP (accession NM_003194) and for Orai1 are taken from (Wenning et al. 2011), and for perforin from (Bhat et al. 2016).
Migration
The observable area of an Ibidi (Martinsried, Germany) cell culture μ‐dish (81156) was coated with 100 μl bovine fibronectin (Sigma‐Aldrich, F4759) solution with a concentration of 0.1 mg ml−1 (stock solution at 1 mg ml−1 in distilled H2O, dilution to 0.1 mg ml−1 in PBS) and allowed to dry for 45 min at room temperature under a sterile bench. Remaining fibronectin was then removed with a cell culture aspirator. SEA‐stimulated CTLs (1 × 104) were seeded in AIM V medium with 10% FBS and incubated at 37°C for 1 h. Medium was then replaced by buffer solutions containing 155 mm NaCl, 4.5 mm KCl, 10 mm glucose, 5 mm Hepes and variable concentrations of CaCl2. In the case of the Ca2+‐free buffer, 1 mm EGTA was added. Imaging was performed at 37°C on a Zeiss Cell Observer HS with an AxioCam MRm camera (Carl Zeiss Microscopy, Jena, Germany) and a Fluar ×5/0.25 objective in brightfield mode at 6 frames min−1. The cells were slightly defocused to facilitate subsequent tracking. Cell tracking was performed in ImageJ 1.46r using a combination of automatic tracking with MTrack2 (https://valelab4.ucsf.edu/~nstuurman/IJplugins/MTrack2.html by N. Stuurman (2003), MTrack2, retrieved 6 September 2017) and manual correction with Speckle Tracker (Smith et al. 2011). Quantification of the obtained trajectories was done in Igor Pro 6.31.
The displacement is the distance between the centroid of a cell at time and a time , , where r(t) is the position vector of a centroid at time t. The instantaneous velocity v(t) is given by , where is the time between two successive frames. From these quantities, the mean‐squared displacement is given by = 〈〉 and the velocity autocorrelation is given by = 〈〉. In both cases, brackets indicate averages with respect to the cells in a batch. Within experimental error, the velocity autocorrelation is independent of the time t and thus the VAC will be averaged also over a sliding window for the reference time t. The velocity distributions shown have been obtained after averaging the tracks using a sliding window.
Statistical analysis
Data are presented as the mean ± SEM (n = number of experiments) if not stated otherwise. Data were tested for significance using one‐way ANOVA or Student's t test (if Gaussian distribution was confirmed): * P < 0.05, ** P < 0.01, *** P < 0.001; ns, no significant difference. Statistics were calculated using Microsoft Excel 2010, Igor Pro6 or Prism 7 (GraphPad Software, La Jolla, CA, USA) software.
Killing assays in Figs 1 and 2 were analysed as described before (Kummerow et al. 2014). Killing assays for CTLs, primary NK or NK‐92 cells were assumed as appropriate when the proportionality factor r was 0.8 < r < 1.2 (r = F live(0)/F exp(0), where F live is fluorescence of target cells only, and F exp is fluorescence of the wells with target and effector cells). Out of all killing experiments performed in this publication, only four single experiments with CTLs and none from primary NK or NK‐92 cells did not meet this criterion and were thus not included in the analysis.
Figure 2. Ca2+ dependence of perforin‐dependent NK cell cytotoxicity.
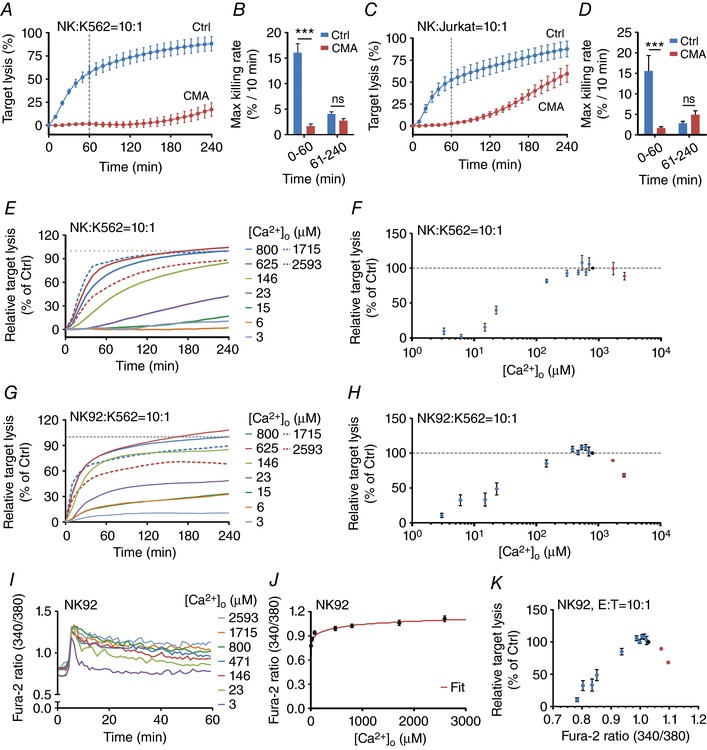
A and B, real‐time killing assay with K562 cells as target cells with an E:T ratio of 10:1 (A) and the statistical analysis of the maximal killing rate (B) of CMA‐treated NK cells (100 nm CMA, 4 h pre‐incubation, n = 3 independent experiments) in comparison to the mean of untreated NK cells (n = 3 independent experiments). C and D, real‐time killing assay of CMA‐treated NK cells with Jurkat T cells as target cells with an E:T ratio of 10:1 (n = 3 independent experiments) and the statistical analysis of the maximal killing rate (D). E–H, Ca2+ dependence of NK cell‐mediated cytotoxicity. Killing kinetics was determined using the real‐time killing assay for primary NK cells (E and F) or NK‐92 cells (G and H). K562 cells were used as target cells with an E:T ratio of 10:1. Target lysis of the condition with AIM V (800 μm [Ca2+]o) at 240 min was set as 100%. The relative target lysis at 240 min from various [Ca2+]o from E and G are plotted against the corresponding [Ca2+]o in F and H, respectively. Results are shown as mean (E and G) or mean ± SEM (F and H) from 3–10 independent experiments. I, average Fura‐2 ratios of NK‐92 cells in contact with K562 target cells at different [Ca2+]o. Fura‐2 ratio kinetics were temporally aligned before averaging. J, plateau values for Fura‐2 ratios of NK‐92 cells in contact with target cells (in Fig. 2I) were determined and plotted against the corresponding [Ca2+]o values. Data were fitted by a Hill equation using Igor Pro 6.22A (red line). K, relative target lysis of NK‐92 cells (normalized to target lysis in AIM V medium) is plotted against plateau Fura‐2 ratios during target contact. Fura‐2 ratios were calculated based on [Ca2+]o using the Hill function from Fig. 2J.
Results
Ca2+ dependence of perforin‐dependent CTL cytotoxicity
To quantify perforin‐dependent cytotoxicity of primary human CTLs and NK cells, we used a real‐time cytotoxicity assay (Kummerow et al. 2014). For CTLs, staphylococcal enterotoxin A (SEA)‐pulsed Raji cells were used as target (cancer) cells. Figure 1 A shows the kinetics of cancer cell killing by primary human CTLs (blue curve). Quantification of maximum killing rates in two time periods (0–60 and 61–240 min) reveals that the killing efficiency is higher during the first hour compared to the next 3 h (Ctrl‐siRNA in Fig. 1 A and B). The two major cytotoxic mechanisms of CTLs are based on perforin/granzyme or the Fas/FasL system (Henkart, 1994). To assess the contribution of the perforin/granzyme system on CTL cytotoxicity, perforin mRNA levels were down‐regulated by a pool of siRNAs against perforin to about 50% of control levels as confirmed by qRT‐PCR relative to control siRNA‐transfected CTLs normalized to the reference genes, TBP and RNAPol. Down‐regulation of perforin was paralleled by a clear reduction of the cytotoxic efficiency of CTLs against cancer cells (Fig. 1 A, PRF‐siRNA, red curve). Maximum killing rates and in particular the maximal rate during the first 60 min are reduced to about 40% of control (Fig. 1 B). Considering the significant killing rate reduction during the first 60 min following perforin down‐regulation, we conclude that a majority of cancer cells are killed during the first 60 min in a perforin‐dependent way. The imperfect down‐regulation by the perforin siRNA to only 50% suggests that the role of perforin in CTL killing is even more pronounced than determined with this type of assay.
To further test the importance of perforin, we used concanamycin A (CMA), which has been reported to inhibit perforin function by disrupting the pH value within LGs (Kataoka et al. 1996) without interfering with the Fas/FasL system at the low concentration used here (100 nm). Figure 1 C shows that CMA almost completely abolished cancer cell killing by CTLs compared to control conditions. Quantification of the rates reveals that CMA reduced the maximal killing rate during the first 60 min to about 11% of control (Fig. 1 D). Thus we conclude that, in our experimental setting, CTLs kill the majority of cancer cells during the first 60 min in a perforin‐dependent manner.
IS formation between CTLs and Raji cells activates Ca2+ entry through Orai channels and Ca2+ entry has been shown to be important for CTL cytotoxicity mediated by perforin and granzyme release from LGs (Lyubchenko et al. 2001; Maul‐Pavicic et al. 2011). To test the dependence of perforin‐mediated CTL cytotoxicity on Ca2+ entry through Orai channels, one feasible method is to change the electrochemical driving force for Ca2+ by changing the extracellular Ca2+ concentration ([Ca2+]o). We chose AIM V medium to quantify the cytotoxicity of CTLs against their targets because it is optimized for immune cell functionality. To change [Ca2+]o in AIM V, either EGTA or CaCl2 was added. Free [Ca2+]o was determined with the help of a Ca2+‐selective electrode or a blood gas analyser. Figure 1 E depicts free [Ca2+]o in AIM V as a function of added EGTA or CaCl2. AIM V with different [Ca2+]o was then used to analyse cancer cell killing by CTLs (Fig. 1 F). Quantification of cancer cell killing reveals that target lysis is very low at very low [Ca2+]o (3–6 μm) and increases up to a value of 384 μm (Fig. 1 G). Surprisingly the killing efficiency dropped at higher [Ca2+]o, which is most evident at the highest [Ca2+]o of 2593 or 4858 μm (Fig. 1 F and G). Averaging all experiments shows that CTLs work most efficiently against cancer cells at relatively low [Ca2+]o in the range between 23 and 625 μm (Fig. 1 G), which is below average blood plasma free [Ca2+]o of about 1200 μm.
The unexpected Ca2+ dependence of CTL‐dependent cytotoxicity against cancer cells was tested in another set of experiments using modified Ringer solution instead of AIM V medium. Real‐time killing assays of CTLs with SEA‐pulsed Raji cells as target cells (E:T ratio of 20:1) were carried out in modified Ringer solution with varying [Ca2+]o. Target cell lysis was analysed at 240 min in 2–11 experiments from 2–10 independent donors. Consistent with the data obtained in AIM V medium, a Ca2+ optimum for CTL cytotoxicity at [Ca2+]o of ∼500 μm was observed in modified Ringer solution, thereby confirming the data obtained in AIM V medium.
In the modified Ringer solution [Ca2+] and [Mg2+] were kept constant at 3 mm total. Since it was previously shown that decreased intracellular free Mg2+ impairs cytolytic responses against Epstein–Barr virus by CTLs and NK cells, the latter by downregulating the expression of the natural killer activating receptor (NKG2D) (Chaigne‐Delalande et al. 2013), we analysed whether changes in extracellular Mg2+ concentrations influence CTL cytotoxicity. Mg2+ dependence of CTL‐dependent cytotoxicity against cancer cells was analysed in modified Ringer solution with defined extracellular Ca2+ and Mg2+ concentrations (Fig. 1 H). At physiological [Ca2+]o (1000 μm), Mg2+ dependence was weak during the first 60 min (Fig. 1 H) and likewise at 240 min. Only at lower [Ca2+]o (250 μm) did addition of higher Mg2+ concentrations (>1 mm) decrease CTL efficiency. In conclusion, [Mg2+] slightly influences cytotoxicity and interferes with the Ca2+ dependence if analysed in modified Ringer solution if combined [Ca2+] and [Mg2+] are kept constant, as done in many studies of Ca2+ signalling.
[Ca2+]o determines the amplitude of Ca2+ influx into CTLs, which determines the intracellular Ca2+ concentration ([Ca2+]i) during IS formation. To analyse [Ca2+]i as a function of [Ca2+]o, Ca2+ imaging experiments with CTLs activated by SEA‐pulsed Raji cells with different [Ca2+]o were performed (Fig. 1 I). The correlation between [Ca2+]o and steady state [Ca2+]i is presented in Fig. 1 J, showing a strictly monotonously rising function as expected, which could be fitted by an exponential function. This function was used to calculate cancer cell lysis as a function of Fura‐2 ratios (340/380) (Fig. 1 K) or [Ca2+]i (Fig. 1 L). As expected from the dependence of cytotoxic efficiency on [Ca2+]o, also the dependence on [Ca2+]i shows an optimum, which is between 122 and 334 nm. In summary, we conclude that CTLs kill their targets most efficiently at a Ca2+ optimum defined by relatively low Ca2+ entry through CRAC/Orai1 channels and thus at relatively low [Ca2+]i.
Ca2+ dependence of perforin‐dependent NK cell cytotoxicity
NK cells use similar mechanisms to kill their respective target cells, but their mode of activation is different. In contrast to antigen‐specific activation of CTLs, NK cells are activated as a result of the balance between the stimulation of activating and inhibiting NK receptors (Lanier, 2005; Guillerey et al. 2016). A standard target for primary human NK cells is K562 cells or Jurkat T cells (Langhans et al. 2005), which are both killed very efficiently as measured by the real‐time killing assay (Fig. 2 A and C, blue curves). NK cells kill very fast within the first 60 min and quantification of killing rates revealed that the killing efficiency is much higher during the first 60 min compared to the next 3 h (compare blue bars in Fig. 2 B and D). The difference between the two targets is that Jurkat T cells can be killed by both LGs (containing perforin and granzyme) and Fas/FasL‐dependent pathways, whereas K562 can only be killed by LGs but not by Fas/FasL because they lack the Fas receptor (Owen‐Schaub et al. 1995). Primary human NK cells cannot easily be transfected and thus we relied on only CMA to test the contribution of perforin‐dependent cancer cell killing rather than perforin down‐regulation as used for CTLs. Figure 2 A and B show that CMA almost completely blocked K562 cell killing by NK cells compared to control conditions. In particular the maximal rate during the first 60 min was reduced from 16%/10 min to 1.5%/10 min. For Jurkat T cells, the results during the first 60 min were identical (reduced from 15% to 1.3%/10 min), but at later time points significant killing occurred (Fig. 2 C and D), indicating that Fas/FasL was still working properly between NK and Jurkat T cells. From both sets of experiments we conclude that more than 90% of the initial killing by NK cells during the first 60 min is perforin dependent, very similar to CTLs. For K562 cells, close to 100% should theoretically be killed in a perforin‐dependent manner because they lack the Fas receptor (Owen‐Schaub et al. 1995). In conclusion, the killing assay used in this study reports mostly perforin dependent cancer cell death following target cell encounter with either CTLs or NK cells.
To test the Ca2+ dependence of perforin‐mediated NK cytotoxicity against cancer cells, we used primary human NK cells and also NK‐92 cells, a well‐established human NK cell line (Klingemann et al. 2016). As targets we used K562 cells because they cannot be killed by Fas/FasL. As for CTLs, [Ca2+]o was varied in AIM V by adding either EGTA or CaCl2 (Fig. 1 E–H). Similarly to CTLs, NK or NK‐92 cell cytotoxicity against cancer cells is very low at very low [Ca2+]o (3–15 μm; Fig. 2 E–H). Optimal NK or NK‐92 cytotoxicity is observed at [Ca2+]o between 384 and 800 μm (Fig. 2 F and H). In primary NK cells, cytotoxicity does not drop much at higher [Ca2+]o (Fig. 2 F), whereas this effect is slightly more pronounced in NK‐92 cells (Fig. 2 H).
As for CTLs, [Ca2+]i measured as the Fura‐2 ratio (340/380) was determined as a function of [Ca2+]o by Ca2+ imaging experiments of NK‐92 cells in contact with K562 cells (Fig. 2 I). The correlation between the Fura‐2 ratio and [Ca2+]o is presented in Fig. 2 J, showing a strictly monotonously rising function as expected, which could be fitted by a Hill function. This function was used to calculate the cancer cell lysis as a function of the Fura‐2 ratio in NK‐92 cells (Fig. 2 K). As expected from the dependence of cytotoxic efficiency on [Ca2+]o, the dependence on the Fura‐2 ratio also showed an optimum. This optimum is at a Fura‐2 ratio of about 1.0 with a decline for lower and higher ratios.
Orai1 down‐regulation increases perforin‐mediated killing
The free [Ca2+]o in blood plasma is around 1200 μm (total Ca2+ around 2400 μm). In the tumour microenvironment, free [Ca2+]o is not known. Considering the relatively low Ca2+ optimum of CTL cytotoxicity, our data predict that under certain conditions a reduction of Orai1 expression (or Orai1 inhibition) should not decrease but rather increase the perforin‐dependent killing efficiency of cancer cells by CTLs.
We down‐regulated Orai1 in primary human CTLs using an siRNA approach. Effective down‐regulation is shown in the mRNA level (Fig. 3 A). As expected, Orai1 down‐regulation decreased [Ca2+]i signals in CTLs by about 50% following store depletion by thapsigargin (Fig. 3 B–D) or following stimulation with SEA antigen‐presenting cells (Fig. 3 E). In parallel experiments we tested the killing efficiency of CTLs (Fig. 3 F) from the same blood donors as shown in Fig. 3 E. The killing efficiency was analysed with AIM V medium containing 800 μm free [Ca2+]o, which is above the range optimal for CTL cytotoxicity (23–625 μm). Figure 3 F shows that, as predicted from the Ca2+ dependence described in Fig. 1 K and L, a decrease in Orai1 expression and Orai1‐dependent Ca2+ signals correlated with an increase in killing efficiency under these conditions (Fig. 3 F and G). The overall cancer cell lysis and in particular the maximal killing rate of cancer cells were significantly enhanced in Orai1 down‐regulated CTLs (Fig. 3 G). We conclude that cancer cell lysis by CTLs can be increased by a decrease of Orai1 activity.
Figure 3. Orai1 down‐regulation increases perforin‐dependent killing.
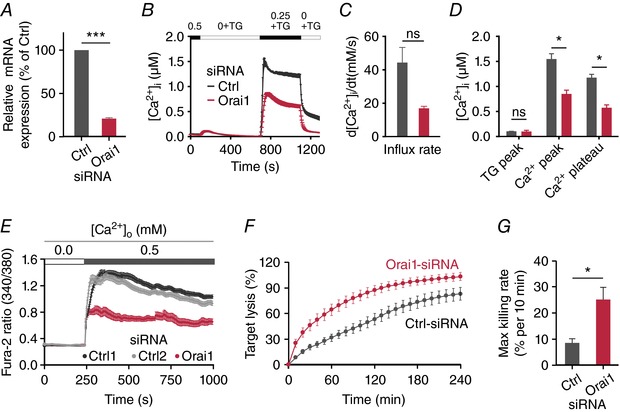
A, relative expression of Orai1 mRNA analysed in control siRNA‐ (Ctrl) and Orai1 siRNA‐ (Orai1) transfected CTLs by qRT‐PCR after 70 h. Expression was normalized to the reference genes TBP and RNAPolII. Data are shown as mean ± SEM from 3 independent experiments. B, store‐operated Ca2+ entry in SEA‐stimulated CTLs transfected with non‐silencing RNA or siRNA against Orai1 for 3 days. Cells were initially kept in buffer solution containing 0.5 mm of CaCl2. After store depletion in Ca2+‐free solution containing thapsigargin (TG, 1 μm), a solution containing 0.25 mm [Ca2+]o was added back to record the influx rate and the resulting plateau value. Subsequently, [Ca2+]o was removed again. C and D, quantification of single cell parameters from B as indicated. E, Ca2+ influx of CTLs upon target recognition 70 h after the transfection with control siRNAs (Ctrl1 (dark grey) or Ctrl2 (light grey)) and Orai1 siRNA (red); 2 × 105 CTLs were loaded with 2 μm Fura‐2/AM and settled on the coverslip in modified Ringer solution containing 0 mm Ca2+. Images were acquired every 5 s at both 340 nm and 380 nm excitation (n = 21 cells Orai1 siRNA, n = 44 cells Ctrl1; n = 74 cells Ctrl2). F, real‐time killing assay with SEA‐pulsed Raji cells as target cells with an E:T ratio of 20:1. CTLs were transfected with Orai1 siRNA (red) or control siRNA (dark grey). Data are from 4 donors (n = 8 independent experiments for two different Ctrl siRNA; n = 4 for Orai1 siRNA). G, statistical analysis of the maximal killing rate from data is shown in F.
Mechanisms to tune Ca2+‐dependent CTL cytotoxicity
There are several steps during the CTL‐mediated killing process of cancer cells which could confer the Ca2+ dependence with a [Ca2+]o optimum between 23–625 μm (Fig. 1 G). In principle, Ca2+‐dependent CTL proliferation, migration, LG accumulation at the IS and/or LG release at the IS could determine the Ca2+ optimum. We tested these possibilities.
Proliferation
Considering that we only analysed target cell killing over 4 h, it appears unlikely that proliferation was responsible for the Ca2+ optimum of CTL cytotoxicity. Nevertheless we analysed the [Ca2+]o dependence of CTL proliferation. In contrast to the Ca2+ dependence of cytotoxicity with a [Ca2+]o optimum between 23 and 625 μm in AIM V medium, CTL proliferation showed no detectable [Ca2+]o optimum. Non‐stimulated CTLs (Fig. 4, naïve, grey circles) did not proliferate much, whereas CTL stimulation with anti‐CD3/anti‐CD28‐coated beads resulted in a monotonously increasing proliferation with increasing [Ca2+]o but without a maximum (Fig. 4, red and blue circles). EGTA was not toxic, as CTLs in AIM V medium supplemented with equal amounts (1.0 mm or 1.5 mm) EGTA and Ca2+ proliferated similarly to those without additional EGTA and Ca2+ (Fig. 4, green circles).
Figure 4. Ca2+ dependence of CTL proliferation.
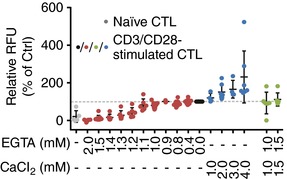
A, proliferation of anti‐CD3/anti‐CD28 bead‐stimulated CTLs compared to non‐stimulated CTLs (naïve, grey circles) was determined after 72 h. [Ca2+]o was manipulated by the addition of EGTA (red circles) or CaCl2 (blue circles) or both at the same concentration as control (green circles). AIM V medium alone (no manipulation) is set to 100% (black circles). Data are shown as mean ± SD of 4 independent experiments from 2–9 different donors.
Migration
One could argue that there are too many CTLs per well and thus migration does not play a role in this assay. However, the majority of SEA‐stimulated CTLs usually kill inefficiently, and thus migration of the ‘competent’ killers may be of importance. To study CTL migration at different [Ca2+]o, we used time‐lapse microscopy. On a short time scale (seconds or minutes), CTLs show directional persistence, whereas migration on a long time scale (minutes or hours) is random. Representation of random migration tracks starting at the same origin are shown in the absence of extracellular Ca2+ (0 mm [Ca2+]o) or in the presence of 1 mm [Ca2+]o (Fig. 5 A). It is immediately obvious that CTLs can still migrate without any [Ca2+]o present (1 mm EGTA was added), at least during the investigated time of 1 h, which was quite surprising to us. We speculate that acute removal of [Ca2+]o does not completely inhibit migration due to residual Ca2+ contained in the intracellular stores of CTLs. The distance travelled under this condition is, however, shorter. This is also evident by the analysis of the mean square displacement (MSD) in 0 mm and 1 mm [Ca2+]o (Fig. 5 B).
Figure 5. Ca2+ dependence of CTL migration.
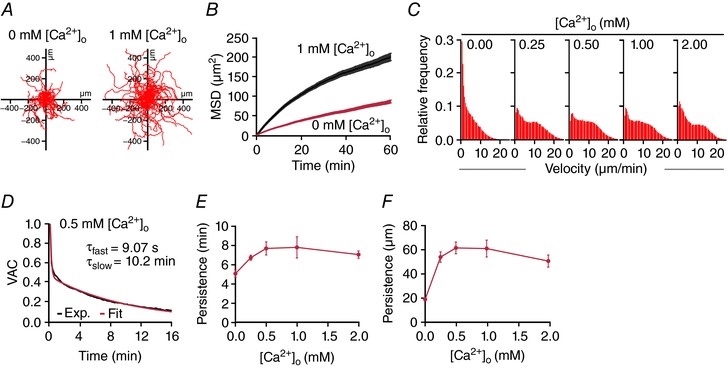
CTL migration was visualized at 37°C every 10 s for 1 h using a Zeiss Cell Observer HS. CTLs were not fluorescently labelled. CTLs were tracked with ImageJ (Plugin Specle TrackerJ) with manual correction. A, representative tracks of SEA‐stimulated CTLs migrating for 60 min. B, mean squared displacement of about 500 cells per condition from 5 independent experiments of 2‐3 donors as for the ones shown in A. C, velocity distribution of CTLs at different [Ca2+]o. D, the velocity autocorrelation function of CTL tracks was fitted with a double exponential function to yield two time constants reflecting the directional persistence of cell movement. E and F, average persistence time (slow exponential component from 5D) and average persistence distance (as calculated from the MSD) of CTLs as a function of [Ca2+]o.
To analyse the Ca2+ dependence of migration in more detail, we carried out experiments as the ones shown in Fig. 5 A at different [Ca2+]o. The distribution of cell velocities was Ca2+ dependent as evident from the histograms shown in Fig. 5 C. Lower velocities are more frequent at 0 mm [Ca2+]o but also at higher [Ca2+]o (1 or 2 mm Ca2+). Finally, to quantify directional migration we determined the velocity autocorrelation as depicted for example at 500 μm [Ca2+]o in Fig. 5 D. The velocity autocorrelation function is a measure for how long a cell's direction of motion persists. It typically falls off exponentially where τ is the persistence time. The analysis reveals that persistence time (Fig. 5 E) and persistence displacement (Fig. 5 F) vary with different [Ca2+]o.
In summary, CTLs move fastest and with the highest directional persistence at 500–1000 μm [Ca2+]o and slower and with less persistence at lower or higher Ca2+. This maximum is, however, not very prominent and is also shifted slightly to the right compared to the Ca2+ optimum of 23–625 μm [Ca2+]o for perforin‐dependent cancer cell killing.
LG accumulation at the IS
Granzyme B–mCherry was transiently transfected into CTLs to label LGs. TIRF microscopy was used to count LGs at the IS formed between the antibody‐coated surface of the glass and the cell as previously reported (Qu et al. 2011). Figure 6 A shows an example of LGs located at the IS for three different [Ca2+]o (3, 146 and 800 μm) which are below, in between or above the optimal [Ca2+]o range of 23–625 μm for CTL cytotoxicity. The data are quantified in Fig. 6 B. At 146 μm [Ca2+]o (grey curve) about 13 LGs are present at the IS. This number is increased at higher and lower [Ca2+]o. Two possibilities may explain this result: at 146 μm [Ca2+]o (1) more LGs were released, or (2) fewer LGs were recruited to the IS. The latter would not explain the phenotype that CTLs kill very well at 146 μm.
Figure 6. Ca2+ dependence of lytic granule release.
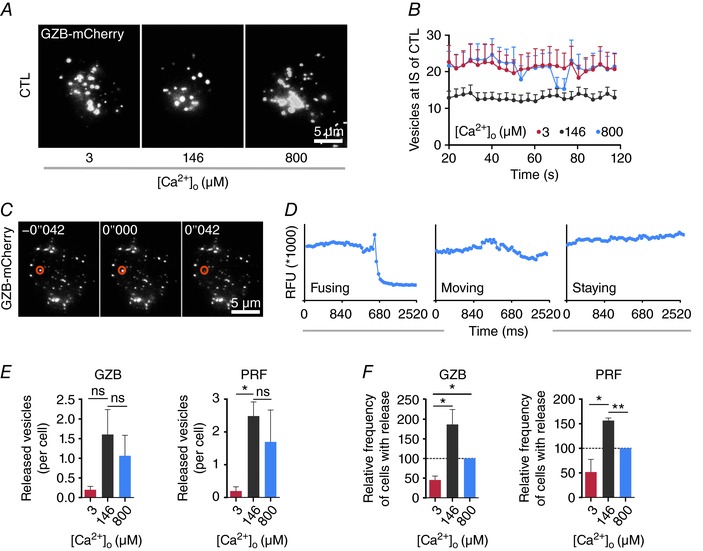
A, snapshots of LG accumulation stained with granzyme B–mCherry at the IS. Anti‐CD3/anti‐CD28 bead‐stimulated CTLs were transfected with granzyme B–mCherry and settled onto anti‐CD3/anti‐CD28/anti‐LFA‐1 antibody‐coated coverslips in modified Ringer solution containing 0 mm Ca2+ and then switched to AIM V with indicated [Ca2+]o. Images were taken at TIRF mode with a penetration depth of 110 nm. Scale bar is 5 μm. B, quantification of the accumulated granzyme B‐positive LGs at the IS. Data are shown as mean + SEM from 3 independent experiments. C, sequential images of a fusing LG at IS. CTLs were transfected with granzyme B–mCherry and were settled onto anti‐CD3/anti‐CD28/anti‐LFA‐1 antibody‐coated coverslips in modified Ringer solution containing 0 mm Ca2+ and then switched to AIM V with indicated [Ca2+]o. The orange cycle indicates a LG fusing at 42 ms. Scale bar is 5 μm. D, defining LG release by analysing the fluorescence intensity. The region of interest (ROI) covers the individual LG and the fluorescence intensity of the ROI is depicted over time. E, quantitative analysis of granzyme B or perforin positive LG fusion at different [Ca2+]o. CTLs were transfected with granzyme B–mCherry or perforin–mCherrry. The number of released LGs containing either granzyme B or perforin was analysed at different [Ca2+]o (3, 146 or 800 μm) during an interval of 2 min after Ca2+ application (n = 49 cells for 3 μm, n = 48 cells for 146 μm and n = 43 cells for 800 μm [Ca2+]o). Data are from 4 independent experiments from 4 donors. F, quantification of the relative frequency of cells with LG release (at least one fused LG). Cells are taken from E (n= 20 cells for 3 μm, n = 22 cells for 146 μm and n = 15 cells for 800 μm [Ca2+]o). Frequency at 800 μm [Ca2+]o was set as 100%. Data are from 4 independent experiments of 4 donors.
LG release at the IS
Considering the reduction of LGs at the IS at 146 μm, it is reasonable to assume that more LGs are released at the IS under these conditions. We tested this hypothesis by TIRF microscopy under the same conditions as described above. Figure 6 C shows three images of LGs in a CTL stained by granzyme B–mCherry. The fluorescence signal of each individual LG was recorded over time with fastest possible acquisition (one image every 42 ms). Fluorescence changes of each LG were analysed as shown in Fig. 6 C and D. Release of LGs is evident by a sharp drop of fluorescence usually preceded by a very brief increase of fluorescence due to neutral pH‐induced higher fluorescence of mCherry during fusion (Liu et al. 2011). For the LG marked with a red circle in Fig. 6 C, a sharp drop of fluorescence signal kinetics within 42 ms was observed indicating that it was released (Fig. 6 D), whereas other LGs showed more constant fluorescence signals, indicating either moving or stationary LGs (Fig. 6 D). Release of LGs stained with either granzyme B–mCherry or perforin–mCherry was quantified at 3, 146 or 800 μm [Ca2+]o. The number of released LGs was counted during an interval of 2 min after Ca2+ application. Quantification revealed that the average number of released LGs, containing either granzyme B or perforin, was highest at 146 μm [Ca2+]o compared to lower or higher [Ca2+]o (Fig. 6 E). Similarly, the relative frequency of cells showing at least one release event was highest at 146 μm [Ca2+]o (Fig. 6 F). We conclude that LG release has a Ca2+ optimum in the same range as the Ca2+ optimum of cancer cell killing efficiency, between 23 and 625 μm. In summary, the Ca2+ dependence of LG release can in principle explain the finding that CTLs kill their targets most efficiently at a relatively low Ca2+ optimum.
Discussion
A pro‐oncogenic tumour microenvironment is one key factor for uncontrolled tumour growth. The immune system is in principle well positioned to control and eliminate tumour cells. However, if the immune system is not fast enough, the tumour has the potential to develop measures to mask itself, or even worse, may hijack the immune system for its own purposes (Hanahan & Weinberg, 2011). It is clear that the efficiency of tumour elimination in its early stages is a key factor for a successful immune response. Many metabolic factors, hormones or messengers influence the tumour‐immune microenvironment, Ca2+ being one of them.
Ca2+ is a central factor for cell proliferation and it is thus no surprise that many studies have provided good evidence that Ca2+ channels are upregulated in cancerous tissues. The rationale behind this is that more Ca2+ channels will – slightly – increase the cellular Ca2+ concentration and thereby increase or modulate cancer cell proliferation, invasion, migration and metastasis. This is also true for the CRAC channel components STIM and Orai (Yang et al. 2009; Feng et al. 2010; Chen et al. 2011; Prevarskaya et al. 2011; Bergmeier et al. 2013; Vashisht et al. 2015; Xu et al. 2015; Hoth, 2016; Iamshanova et al. 2017). It should, however, be noted, that CRAC channel genes cannot be considered cancer drivers but rather passengers considering cancer genome analyses as discussed in Hoth (2016). Nevertheless inhibiting Ca2+ influx into tumour cells should slow down their proliferation rate.
This benefit should, however, come at the cost of reduced cytotoxic functionality of human CTLs and NK cells as evident by the necessity of Orai1 activity for cytolytic immune cell functions as clearly shown by Maul‐Pavicic et al. (2011) and Klemann et al. (2017). Thus, it is widely believed that the benefit of inhibiting CRAC/Orai activity to reduce tumour growth will be counteracted by a reduced eradication of cancer cells through CTLs and NK cells. Considering these results it seems questionable if inhibition of CRAC/Orai‐dependent Ca2+ entry into CTLs and NK cells could be a therapeutic option in a multimodal cancer therapy as proposed by many groups from the Ca2+ signalling field (Yang et al. 2009; Feng et al. 2010; Chen et al. 2011; Prevarskaya et al. 2011; Bergmeier et al. 2013; Vashisht et al. 2015; Xu et al. 2015).
The results of the present study point in another direction. The finding that CTLs and NK cells have an unexpectedly low Ca2+ optimum for efficient cancer cell elimination well below blood plasma Ca2+ levels offers an interesting future therapy option against cancer. A partial reduction of Orai1 channel activity and the concomitant decrease in [Ca2+]i increases rather than decreases the cytotoxic efficiency of CTLs due to the Ca2+ optimum of target cell killing described here. Only at very low [Ca2+]o and [Ca2+]i is CTL and NK cell cytotoxicity abolished. The drastic reduction of CTL cytotoxicity at values below 23 μm [Ca2+]o is explained by the fact that at less than 100 μm [Ca2+]o, binding of perforin to the plasma membrane of target cells is inhibited (Voskoboinik et al. 2005). In addition, this reduction could also be explained by our finding that below 23 μm [Ca2+]o LG release is impaired.
While the importance of Orai1/CRAC channel activity for cytolytic immune cell functions has been convincingly demonstrated (Lyubchenko et al. 2001; Maul‐Pavicic et al. 2011; Schwarz et al. 2013; Klemann et al. 2017), there are several reports that cytotoxicity is only slightly reduced in tumour‐specific murine CTLs following a drastic reduction of Ca2+ signals by the application of 1 μm BTP2 (Weidinger et al. 2013), one of the most potent CRAC channel blockers (Zitt et al. 2004). In murine NK cells, it was recently reported that degranulation was persisting in the complete absence of Ca2+ (Freund‐Brown et al. 2017). This finding was based on in vivo data in STIM1/2 double knock‐out NK cells and on in vitro data in the absence of [Ca2+]o. Our data may reconcile these different findings. The very low Ca2+ optimum for CTL and NK cell cytotoxicity (between 122 and 334 nm for [Ca2+]i and between 23 and 625 μm for [Ca2+]o in case of CTLs) indicates that Ca2+ influx can probably be reduced dramatically but still allow very good perforin‐dependent cytotoxicity. Considering this, we would like to point out the problem of controlling [Ca2+]o in external cell culture media. We needed, in the range of 1 mm EGTA, to reduce [Ca2+]o to very low micromolar levels in AIM V medium with no FBS added. FBS in our experiments added a large amount of Ca2+ and we therefore chose to leave it out. In the experimental set‐up used by (Freund‐Brown et al. 2017), FBS was added together with 250 μm EGTA to Ca2+‐free medium (S‐MEM). Depending on the Ca2+ concentration in FBS, 250 μm may not be sufficient to reduce [Ca2+]o to very low micromolar levels. Considering our findings, we expect that under these circumstances, NK cells would maintain significant degranulation and killing capacity as observed in the study. We therefore question the conclusion that store‐operated Ca2+ entry is not required for NK cell degranulation and perforin‐dependent cytotoxicity. A Ca2+ optimum at very low Ca2+ entry, on the other hand, is in good agreement with the other published data sets (Lyubchenko et al. 2001; Maul‐Pavicic et al. 2011; Weidinger et al. 2013; Klemann et al. 2017).
The reason for the unexpected low cytotoxic Ca2+ optimum of CTLs and NK cells is probably related to the Ca2+ optimum for LG release at the IS, which is in the same range as the cytotoxic efficiency against target cells. However, there is an apparent inconsistency. Whereas at 800 μm [Ca2+]o, LG release is significantly reduced in CTLs, the overall global killing is only slightly affected. This inconsistency could in principle be explained as follows. (1) The relationship between LGs and killing efficiency could be non‐linear, as are many biological correlations. (2) The CTL population is heterogeneous, which means that some cells kill very efficiently and others do not (Vanherberghen et al. 2013). (3) The efficiency of target cell killing depends on several Ca2+‐dependent mechanisms, which is the case in CTLs as also shown in the present paper. CTL migration (velocity and persistence) have a maximum at 500–1000 μm [Ca2+]o. As both processes, LG release and migration, likely contribute to the efficiency of target cell killing, it is reasonable that the Ca2+ optimum for target cell killing is higher than the optimum of LG release.
The [Ca2+]o optimal for cancer cell killing (between 23 and 625 μm) is far below the normal concentrations in blood plasma (1.2 mm). While it is intriguing to speculate on the effect of hyper‐ or hypocalcaemia on immune cell killing, it is unlikely that blood plasma [Ca2+] could vary so much as to be relevant for killer cell function: free [Ca2+] is tightly regulated and levels below 1.1 mm are already considered as severe hypocalcaemia with heavy generalized symptoms such as neuro‐muscular dysfunction (tetany, seizures). We do, however, believe that [Ca2+]o in the extracellular space of different tissues could vary to such a degree, considering, for example, that tumours are densely populated by malignant cells, stroma and infiltrating lymphocytes while vascularization and thus perfusion is often very limited.
One disadvantage of our measurement is that we have only analysed global [Ca2+]i signals. In CD4+ T cells, local Ca2+ signals at the IS are very inhomogeneous (Quintana et al. 2011) and it has been recently shown that targeted Ca2+ entry in CTLs increases cytotoxic functions against tumour cells (Kim et al. 2017). Thus, to fully understand the Ca2+ dependence of LG release in CTLs and NK cells, local domains at the IS have to be analysed and potential Ca2+ sensors need to be identified. A potential candidate is synaptotagmin VII, which is expressed in murine CTLs and probably regulates Ca2+‐dependent LG exocytosis (Fowler et al. 2007). Interestingly, local Ca2+ domains are also very important to selectively activate different isoforms of the transcription factor nuclear factor of activated T cells (NFAT; Kar & Parekh, 2015; Kar et al. 2016), which are key transcription factors in T cells. One of these, NFATc1, has recently been shown to control cytotoxicity of murine CTLs (Klein‐Hessling et al. 2017). Thus, there is another highly relevant Ca2+‐dependent process in CTLs that might contribute to the Ca2+ optimum of CTLs and NK cell cytotoxicity.
The cytotoxic Ca2+ optimum is an interesting mechanism to tune the immune response against cancer and potentially also during inflammation. CTLs and NK cells may operate best at rather modest Ca2+ entry through CRAC/Orai channels with an apparent Ca2+ optimum for CTLs at unexpectedly low [Ca2+]o between 23 and 625 μm and [Ca2+]i between 122 and 334 nm. Efficient cancer cell killing by human CTLs and NK cells at their respective Ca2+ optimum opens the possibility of inhibiting Orai1 channels in tumour tissue resulting in a dual effect: reduced cancer growth but increased cytotoxicity.
Additional information
Author's present address
Bernd Bufe: Molecular Immunology, University of Applied Sciences Kaiserslautern, Zweibrücken, 66482, Germany.
Competing interests
The authors declare no competing or conflicting interests.
Author contributions
X.Z., K.S.F., H.L., Y.Z., R.S., A.K., S.M., C.H., A.A., C.S.B., C.M., R.Z., S.C., G.S., C.H., A.L., B.Q., C.K. and E.C.S. performed experiments and analysed results. X.Z., B.Q., C.K., E.C.S. and M.H. designed the study. B.B. and F.Z. contributed to high‐throughput Ca2+ imaging. M.N. and K.K. helped with migration analysis. X.Z., B.A.N., A.L., B.Q., C.K., E.C.S. and M.H. designed experiments. X.Z., B.Q., C.K., E.C.S. and M.H. coordinated all data analysis and designed final figure layout. M.H. wrote the paper in constant discussion with E.C.S. and with help from X.Z., B.A.N., A.L., B.Q. and C.K. All authors carefully checked the paper and provided critical feedback. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.
Funding
This project was funded by grants from the Deutsche Forschungsgemeinschaft (DFG) SFB 894 (projects A1 to M.H., A2 to B.A.N. and A17 to F.Z.) and IRTG 1830 (to B.A.N. and M.H.). A.L. acknowledges DFG grant LI 1750/4‐2 and B.Q. and K.K. acknowledge SFB 1027 (project A1 and A2).
Acknowledgements
We very much appreciate the help of Prof. Hermann Eichler and the Institute of Clinical Hemostaseology and Transfusion Medicine at Saarland University Medical Center for obtaining human blood cells. We thank Shruthi S. Bhat for initial experiments to determine CTL cytotoxicity in Ringer solution. We thank Prof. Matthias W. Laschke and Janine Becker (Department of Experimental Surgery) for the access to the blood gas analyser and kind support for using the machine at the Institute for Clinical and Experimental Surgery, Saarland University, Homburg. We thank Prof. Jens Rettig (CIPMM, Saarland University, Homburg) for the modified pMAX vector and Dr Rongxi Yang (German Cancer Research Center, Heidelberg) for the granzyme B‐mCherry construct. We thank all lab members for insightful discussions.
Biography
Xiao Zhou completed his B.Sc. degree in Bioengineering (2005) and his M.Sc. degree in Pharmacology (2012) at the China Pharmaceutical University in Nanjing, China. During his master's degree program, Xiao worked with Prof. Hong Liao and focused on the role of the Nogo receptor in neuronal regeneration after CNS injury. In 2012, Xiao joined the group of Prof. Markus Hoth at the Saarland University (Germany) as a PhD candidate. Xiao investigated the impact of bystander cells and external Ca2+ on immune system functions, particularly on the efficiency of immune cell‐mediated cytotoxicity. In 2017, Xiao completed his study and obtained his PhD in Biophysics from the Saarland University.

Edited by: Ole Petersen & Maike Glitsch
References
- Becherer U, Medart MR, Schirra C, Krause E, Stevens D & Rettig J (2012). Regulated exocytosis in chromaffin cells and cytotoxic T lymphocytes: how similar are they? Cell Calcium 52, 303–312. [DOI] [PubMed] [Google Scholar]
- Bergmeier W, Weidinger C, Zee I & Feske S (2013). Emerging roles of store‐operated Ca2+ entry through STIM and ORAI proteins in immunity, hemostasis and cancer. Channels (Austin) 7, 379–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhat SS, Friedmann KS, Knorck A, Hoxha C, Leidinger P, Backes C, Meese E, Keller A, Rettig J, Hoth M, Qu B & Schwarz EC (2016). Syntaxin 8 is required for efficient lytic granule trafficking in cytotoxic T lymphocytes. Biochim Biophys Acta 1863, 1653–1664. [DOI] [PubMed] [Google Scholar]
- Chaigne‐Delalande B, Li FY, O'Connor GM, Lukacs MJ, Jiang P, Zheng L, Shatzer A, Biancalana M, Pittaluga S, Matthews HF, Jancel TJ, Bleesing JJ, Marsh RA, Kuijpers TW, Nichols KE, Lucas CL, Nagpal S, Mehmet H, Su HC, Cohen JI, Uzel G & Lenardo MJ (2013). Mg2+ regulates cytotoxic functions of NK and CD8 T cells in chronic EBV infection through NKG2D. Science 341, 186–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen YF, Chiu WT, Chen YT, Lin PY, Huang HJ, Chou CY, Chang HC, Tang MJ & Shen MR (2011). Calcium store sensor stromal‐interaction molecule 1‐dependent signaling plays an important role in cervical cancer growth, migration, and angiogenesis. Proc Natl Acad Sci USA 108, 15225–15230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng M, Grice DM, Faddy HM, Nguyen N, Leitch S, Wang Y, Muend S, Kenny PA, Sukumar S, Roberts‐Thomson SJ, Monteith GR & Rao R (2010). Store‐independent activation of Orai1 by SPCA2 in mammary tumors. Cell 143, 84–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feske S, Gwack Y, Prakriya M, Srikanth S, Puppel SH, Tanasa B, Hogan PG, Lewis RS, Daly M & Rao A (2006). A mutation in Orai1 causes immune deficiency by abrogating CRAC channel function. Nature 441, 179–185. [DOI] [PubMed] [Google Scholar]
- Fowler KT, Andrews NW & Huleatt JW (2007). Expression and function of synaptotagmin VII in CTLs. J Immunol 178, 1498–1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freund‐Brown J, Choa R, Singh BK, Robertson TF, Ferry GM, Viver E, Bassiri H, Burkhardt JK & Kambayashi T (2017). Cutting edge: Murine NK cells degranulate and retain cytotoxic function without store‐operated calcium entry. J Immunol 199, 1973–1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gately MK & Martz E (1977). Comparative studies on the mechanisms of nonspecific, Con A‐dependent cytolysis and specific T cell‐mediated cytolysis. J Immunol 119, 1711–1722. [PubMed] [Google Scholar]
- Golstein P & Smith ET (1976). The lethal hit stage of mouse T and non‐T cell‐mediated cytolysis: differences in cation requirements and characterization of an analytical "cation pulse" method. Eur J Immunol 6, 31–37. [DOI] [PubMed] [Google Scholar]
- Grynkiewicz G, Poenie M & Tsien RY (1985). A new generation of Ca2+ indicators with greatly improved fluorescence properties. J Biol Chem 260, 3440–3450. [PubMed] [Google Scholar]
- Guillerey C, Huntington ND & Smyth MJ (2016). Targeting natural killer cells in cancer immunotherapy. Nat Immunol 17, 1025–1036. [DOI] [PubMed] [Google Scholar]
- Hanahan D & Weinberg RA (2011). Hallmarks of cancer: the next generation. Cell 144, 646–674. [DOI] [PubMed] [Google Scholar]
- Henkart PA (1994). Lymphocyte‐mediated cytotoxicity: two pathways and multiple effector molecules. Immunity 1, 343–346. [DOI] [PubMed] [Google Scholar]
- Holzmann C, Kilch T, Kappel S, Armbruster A, Jung V, Stockle M, Bogeski I, Schwarz EC & Peinelt C (2013). ICRAC controls the rapid androgen response in human primary prostate epithelial cells and is altered in prostate cancer. Oncotarget 4, 2096–2107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoth M ( 2016). CRAC channels, calcium, and cancer in light of the driver and passenger concept. Biochim Biophys Acta 1863, 1408–1417. [DOI] [PubMed] [Google Scholar]
- Hoth M & Penner R (1992). Depletion of intracellular calcium stores activates a calcium current in mast cells. Nature 355, 353–356. [DOI] [PubMed] [Google Scholar]
- Hoth M & Penner R (1993). Calcium release‐activated calcium current in rat mast cells. J Physiol 465, 359–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iamshanova O, Fiorio Pla A & Prevarskaya N (2017). Molecular mechanisms of tumour invasion: regulation by calcium signals. J Physiol 595, 3063–3075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kar P, Mirams GR, Christian HC & Parekh AB (2016). Control of NFAT isoform activation and NFAT‐dependent gene expression through two coincident and spatially segregated intracellular Ca2+ signals. Mol Cell 64, 746–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kar P & Parekh AB (2015). Distinct spatial Ca2+ signatures selectively activate different NFAT transcription factor isoforms. Mol Cell 58, 232–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kataoka T, Shinohara N, Takayama H, Takaku K, Kondo S, Yonehara S & Nagai K (1996). Concanamycin A, a powerful tool for characterization and estimation of contribution of perforin‐ and Fas‐based lytic pathways in cell‐mediated cytotoxicity. J Immunol 156, 3678–3686. [PubMed] [Google Scholar]
- Kim KD, Bae S, Capece T, Nedelkovska H, de Rubio RG, Smrcka AV, Jun CD, Jung W, Park B, Kim TI & Kim M (2017). Targeted calcium influx boosts cytotoxic T lymphocyte function in the tumour microenvironment. Nat Commun 8, 15365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein‐Hessling S, Muhammad K, Klein M, Pusch T, Rudolf R, Floter J, Qureischi M, Beilhack A, Vaeth M, Kummerow C, Backes C, Schoppmeyer R, Hahn U, Hoth M, Bopp T, Berberich‐Siebelt F, Patra A, Avots A, Muller N, Schulze A & Serfling E (2017). NFATc1 controls the cytotoxicity of CD8+ T cells. Nat Commun 8, 511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klemann C, Ammann S, Heizmann M, Fuchs S, Bode SF, Heeg M, Fuchs H, Lehmberg K, Zur Stadt U, Roll C, Vraetz T, Speckmann C, Lorenz MR, Schwarz K, Rohr J, Feske S & Ehl S (2017). Hemophagocytic lymphohistiocytosis as presenting manifestation of profound combined immunodeficiency due to an ORAI1 mutation. J Allergy Clin Immunol 140, 1721–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingemann H, Boissel L & Toneguzzo F (2016). Natural killer cells for immunotherapy – advantages of the NK‐92 cell line over blood NK cells. Front Immunol 7, 91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kummerow C, Schwarz EC, Bufe B, Zufall F, Hoth M & Qu B (2014). A simple, economic, time‐resolved killing assay. Eur J Immunol 44, 1870–1872. [DOI] [PubMed] [Google Scholar]
- Lancki DW, Weiss A & Fitch FW (1987). Requirements for triggering of lysis by cytolytic T lymphocyte clones. J Immunol 138, 3646–3653. [PubMed] [Google Scholar]
- Langhans B, Ahrendt M, Nattermann J, Sauerbruch T & Spengler U (2005). Comparative study of NK cell‐mediated cytotoxicity using radioactive and flow cytometric cytotoxicity assays. J Immunol Methods 306, 161–168. [DOI] [PubMed] [Google Scholar]
- Lanier LL ( 2005). NK cell recognition. Annu Rev Immunol 23, 225–274. [DOI] [PubMed] [Google Scholar]
- Liu D, Martina JA, Wu XS, Hammer JA 3rd & Long EO (2011). Two modes of lytic granule fusion during degranulation by natural killer cells. Immunol Cell Biol 89, 728–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyubchenko TA, Wurth GA & Zweifach A (2001). Role of calcium influx in cytotoxic T lymphocyte lytic granule exocytosis during target cell killing. Immunity 15, 847–859. [DOI] [PubMed] [Google Scholar]
- Mantei A, Rutz S, Janke M, Kirchhoff D, Jung U, Patzel V, Vogel U, Rudel T, Andreou I, Weber M & Scheffold A (2008). siRNA stabilization prolongs gene knockdown in primary T lymphocytes. Eur J Immunol 38, 2616–2625. [DOI] [PubMed] [Google Scholar]
- Maul‐Pavicic A, Chiang SC, Rensing‐Ehl A, Jessen B, Fauriat C, Wood SM, Sjoqvist S, Hufnagel M, Schulze I, Bass T, Schamel WW, Fuchs S, Pircher H, McCarl CA, Mikoshiba K, Schwarz K, Feske S, Bryceson YT & Ehl S (2011). ORAI1‐mediated calcium influx is required for human cytotoxic lymphocyte degranulation and target cell lysis. Proc Natl Acad Sci USA 108, 3324–3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owen‐Schaub LB, Zhang W, Cusack JC, Angelo LS, Santee SM, Fujiwara T, Roth JA, Deisseroth AB, Zhang WW, Kruzel E & Radinsky R (1995). Wild‐type human p53 and a temperature‐sensitive mutant induce Fas/APO‐1 expression. Mol Cell Biol 15, 3032–3040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plaut M, Bubbers JE & Henney CS (1976). Studies of the mechanism of lymphocyte‐mediated cytolysis. VII. Two stages in the T cell‐mediated lytic cycle with distinct cation requirements. J Immunol 116, 150–155. [PubMed] [Google Scholar]
- Prevarskaya N, Skryma R & Shuba Y (2011). Calcium in tumour metastasis: new roles for known actors. Nat Rev Cancer 11, 609–618. [DOI] [PubMed] [Google Scholar]
- Qu B, Pattu V, Junker C, Schwarz EC, Bhat SS, Kummerow C, Marshall M, Matti U, Neumann F, Pfreundschuh M, Becherer U, Rieger H, Rettig J & Hoth M (2011). Docking of lytic granules at the immunological synapse in human CTL requires Vti1b‐dependent pairing with CD3 endosomes. J Immunol 186, 6894–6904. [DOI] [PubMed] [Google Scholar]
- Quintana A, Pasche M, Junker C, Al‐Ansary D, Rieger H, Kummerow C, Nunez L, Villalobos C, Meraner P, Becherer U, Rettig J, Niemeyer BA & Hoth M (2011). Calcium microdomains at the immunological synapse: how ORAI channels, mitochondria and calcium pumps generate local calcium signals for efficient T‐cell activation. EMBO J 30, 3895–3912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quintana A, Schwindling C, Wenning AS, Becherer U, Rettig J, Schwarz EC & Hoth M (2007). T cell activation requires mitochondrial translocation to the immunological synapse. Proc Natl Acad Sci USA 104, 14418–14423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz EC, Kummerow C, Wenning AS, Wagner K, Sappok A, Waggershauser K, Griesemer D, Strauss B, Wolfs MJ, Quintana A & Hoth M (2007). Calcium dependence of T cell proliferation following focal stimulation. Eur J Immunol 37, 2723–2733. [DOI] [PubMed] [Google Scholar]
- Schwarz EC, Qu B & Hoth M (2013). Calcium, cancer and killing: the role of calcium in killing cancer cells by cytotoxic T lymphocytes and natural killer cells. Biochim Biophys Acta 1833, 1603–1611. [DOI] [PubMed] [Google Scholar]
- Smith MB, Karatekin E, Gohlke A, Mizuno H, Watanabe N & Vavylonis D (2011). Interactive, computer‐assisted tracking of speckle trajectories in fluorescence microscopy: application to actin polymerization and membrane fusion. Biophys J 101, 1794–1804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takayama H & Sitkovsky MV (1987). Antigen receptor‐regulated exocytosis in cytotoxic T lymphocytes. J Exp Med 166, 725–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanherberghen B, Olofsson PE, Forslund E, Sternberg‐Simon M, Khorshidi MA, Pacouret S, Guldevall K, Enqvist M, Malmberg KJ, Mehr R & Onfelt B (2013). Classification of human natural killer cells based on migration behavior and cytotoxic response. Blood 121, 1326–1334. [DOI] [PubMed] [Google Scholar]
- Vashisht A, Trebak M & Motiani RK (2015). STIM and Orai proteins as novel targets for cancer therapy. Am J Physiol Cell Physiol 309, C457–C469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vig M, Peinelt C, Beck A, Koomoa DL, Rabah D, Koblan‐Huberson M, Kraft S, Turner H, Fleig A, Penner R & Kinet JP (2006). CRACM1 is a plasma membrane protein essential for store‐operated Ca2+ entry. Science 312, 1220–1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voskoboinik I, Thia MC, Fletcher J, Ciccone A, Browne K, Smyth MJ & Trapani JA (2005). Calcium‐dependent plasma membrane binding and cell lysis by perforin are mediated through its C2 domain: A critical role for aspartate residues 429, 435, 483, and 485 but not 491. J Biol Chem 280, 8426–8434. [DOI] [PubMed] [Google Scholar]
- Weidinger C, Shaw PJ & Feske S (2013). STIM1 and STIM2‐mediated Ca2+ influx regulates antitumour immunity by CD8+ T cells. EMBO Mol Med 5, 1311–1321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wenning AS, Neblung K, Strauss B, Wolfs MJ, Sappok A, Hoth M & Schwarz EC (2011). TRP expression pattern and the functional importance of TRPC3 in primary human T‐cells. Biochim Biophys Acta 1813, 412–423. [DOI] [PubMed] [Google Scholar]
- Xu Y, Zhang S, Niu H, Ye Y, Hu F, Chen S, Li X, Luo X, Jiang S, Liu Y, Chen Y, Li J, Xiang R & Li N (2015). STIM1 accelerates cell senescence in a remodeled microenvironment but enhances the epithelial‐to‐mesenchymal transition in prostate cancer. Sci Rep 5, 11754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang S, Zhang JJ & Huang XY (2009). Orai1 and STIM1 are critical for breast tumor cell migration and metastasis. Cancer Cell 15, 124–134. [DOI] [PubMed] [Google Scholar]
- Zhang SL, Yeromin AV, Zhang XH, Yu Y, Safrina O, Penna A, Roos J, Stauderman KA & Cahalan MD (2006). Genome‐wide RNAi screen of Ca2+ influx identifies genes that regulate Ca2+ release‐activated Ca2+ channel activity. Proc Natl Acad Sci USA 103, 9357–9362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zitt C, Strauss B, Schwarz EC, Spaeth N, Rast G, Hatzelmann A & Hoth M (2004). Potent inhibition of Ca2+ release‐activated Ca2+ channels and T‐lymphocyte activation by the pyrazole derivative BTP2. J Biol Chem 279, 12427–12437. [DOI] [PubMed] [Google Scholar]
- Zweifach A ( 2000). Target‐cell contact activates a highly selective capacitative calcium entry pathway in cytotoxic T lymphocytes. J Cell Biol 148, 603–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zweifach A & Lewis RS (1993). Mitogen‐regulated Ca2+ current of T lymphocytes is activated by depletion of intracellular Ca2+ stores. Proc Natl Acad Sci USA 90, 6295–6299. [DOI] [PMC free article] [PubMed] [Google Scholar]


