Daytime Ionosphere Retrieval Algorithm for the Ionospheric Connection Explorer (ICON)

Abstract

The NASA Ionospheric Connection Explorer Extreme Ultraviolet spectrograph, ICON EUV, will measure altitude profiles of the daytime extreme-ultraviolet (EUV) OII emission near 83.4 and 61.7 nm that are used to determine density profiles and state parameters of the ionosphere. This paper describes the algorithm concept and approach to inverting these measured OII emission profiles to derive the associated O⁺ density profile from 150–450 km as a proxy for the electron content in the F-region of the ionosphere. The algorithm incorporates a bias evaluation and feedback step, developed at the U.S. Naval Research Laboratory using data from the Special Sensor Ultraviolet Limb Imager (SSULI) and the Remote Atmospheric and Ionospheric Detection System (RAIDS) missions, that is able to effectively mitigate the effects of systematic instrument calibration errors and inaccuracies in the original photon source within the forward model. Results are presented from end-to-end simulations that convolved simulated airglow profiles with the expected instrument measurement response to produce profiles that were inverted with the algorithm to return data products for comparison to truth. Simulations of measurements over a representative ICON orbit show the algorithm is able to reproduce hmF2 values to better than 5 km accuracy, and NmF2 to better than 12% accuracy over a 12-second integration, and demonstrate that the ICON EUV instrument and daytime ionosphere algorithm can meet the ICON science objectives which require 20 km vertical resolution in hmF2 and 18% precision in NmF2.

Introduction

The Ionospheric Connection Explorer (ICON) is a NASA mission that will answer key questions about the response of the ionosphere to energy and momentum drivers in the troposphere and stratosphere below. The overarching mission goals are described by Immel et al. (2016 submitted), which specifically calls out (in their Table 1) the need to measure the peak ion density of the F-layer (or its corollary in electron density, commonly referred to as NmF2) and the altitude of that layer peak (hmF2). The method chosen to meet this requirement for the ICON mission during the daytime segments of its orbit uses the measurement of naturally-occurring airglow emissions of singly-ionized atomic oxygen (O⁺) at 83.4 nm, along with a complementary emission at 61.7 nm, that are used to infer the concentration altitude profile of this species. The ion concentration of the F-layer is approximately 95% O⁺, and because of charge neutrality the measurement serves as a proxy for electron density in this layer, and thus hmF2, and NmF2. The measurements will be made by the ICON EUV spectrograph (ICON EUV) described by Sirk et al. (2016 submitted).

The concept for using limb-viewing altitude profiles of the OII 83.4 nm emission feature to infer the concentration profile of the sunlit O⁺ was first developed by McCoy et al. (1985). The main source of this emission is photoionization of an inner shell electron of atomic oxygen by either solar EUV (λ < 43.6 nm) or a photoelectron, followed by the (2p^{4 4}P → 2p^{3 4}S) transition from the triplet exited-state to its singlet ground state along with the emission of a photon. The 83.4 nm emission triplet consists specifically of emission lines at (vacuum) wavelengths 83.2759, 83.3330, and 83.4466 nm (Martin et al., 1993). These excitation processes peak in the lower thermosphere, below 200 km, but the photons that are generated undergo multiple resonant scattering by O⁺ in the ionosphere that peaks in density at higher altitudes. A small contribution above ~400 km has been observed from the direct scattering of solar 83.4 nm photons, although simulations were conducted that demonstrated that this source is insignificant for the ICON measurements and retrievals (see also Stephan, 2016), in agreement with other studies (Feldman et al., 1981; Meier, 1990). The altitude profile of the 83.4 nm emission that is measured by ICON when viewed toward the limb from its 575 km orbit thus depends on both the brightness of the original excitation sources in the lower thermosphere and the O⁺ ion density in the F-region of the ionosphere.

To resolve the ambiguity between changes in the initial photoemission source in the lower thermosphere and the ionospheric scattering effects of the 83.4 nm emission, ICON will additionally measure the OII 61.7 nm feature that derives from the same ionization processes in the lower thermosphere, but is optically thin to the ionosphere. This feature also is a triplet emission (3s ²P → 2p^{3 2}D) comprised of lines at (vacuum) wavelengths 61.6303, 61.6378, and 61.7063 nm (Martin et al., 1993). As suggested by McCoy et al. (1985) and Picone (2008), and more fully developed by Stephan et al. (2012) and Stephan (2016) using data from the Remote Atmospheric and Ionospheric Detection System (RAIDS), the 61.7 nm emission solely reflects changes in the brightness of the photoionization source in the lower thermosphere. Pairing measurements of these two emissions allows the analysis to isolate changes in two environmental conditions and therefore more accurately infer the ionospheric profile that only affects the 83.4 nm emission.

Measurement Requirements

In order to meet the ICON science objectives, the algorithm must be able to take the ICON EUV measurements taken between sunrise and sunset and invert the profiles to obtain the ionospheric characteristics. Because the measurement concept requires sunlit conditions, this means that not only does the ICON EUV need to be in sunlight, but the entire path along all lines of sight within the entire field of regard must also meet that condition. In practice, the accuracy of the algorithm may also be reduced near the largest allowable solar zenith angles as the path of the solar ionizing radiation through the three-dimensional thermosphere becomes increasingly large. Additionally, early-morning ionospheres are significantly less-developed and thus may not contain sufficient opacity to create a measurable scattering effect. These conditions will be monitored and marked through the examination of the on-orbit data.

While the ICON science objectives require a minimum temporal resolution of one minute that is equivalent to 500 km horizontal sampling, in practice the sampling cadence will be every 12 seconds, meaning that spectra can be co-added to improve the signal-to-noise of each profile, or a set of profiles can be merged after processing to the Level 2 stage by this algorithm. The algorithm will be able to determine the vertical profile between 100 km and 450 km, and thus specifically obtain hmF2 that falls within this range, with 20 km vertical resolution. The density at the F2 peak, NmF2, will be determined with 18% precision. Although accuracy in the NmF2 product is not a driving science requirement, this will be evaluated by the algorithm and the science team throughout the mission.

Ionospheric Density Retrieval Algorithm

The core of the ICON inversion algorithm to derive the daytime ionospheric parameters was originally developed and described by Picone et al. (1997a, 1997b). The concept adapts the approach used by Meier and Picone (1994) to measure O, N₂, and O₂ in the thermosphere using far-ultraviolet airglow, and most recently implemented to successfully invert measurements from the Global Ultraviolet Imager (GUVI) instrument on the NASA Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) Explorer mission (Meier, et al., 2015). The daytime ionospheric algorithm described here for the ICON mission has most recently been applied to analyze measurements from the Special Sensor Ultraviolet Limb Imager (SSULI) instruments on the Defense Meteorological Satellite Program (DMSP) F18 and F19 satellites (see Stephan, 2016). A flow chart depicting the main algorithm sequence is shown in Figure 1, and is described in more detail in the following paragraphs.

Figure 1.

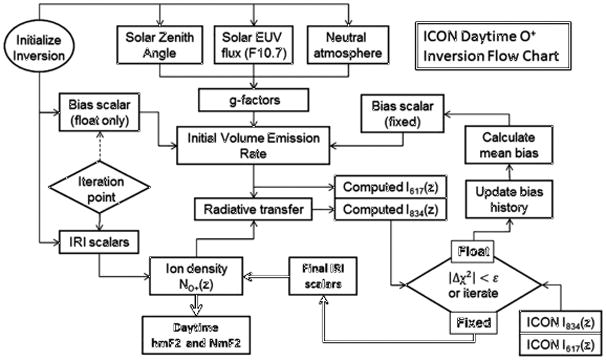
This flow chart shows the main sequence of steps to obtain daytime ionospheric parameters using measurements from the ICON EUV instrument, starting from the initialization point in the upper left. The algorithm uses a two-phase process to improve estimation of the initial volume emission rate from photoionization of atomic oxygen in the lower thermosphere. The first pass through the algorithm iterates on all parameters and measurements but archives only the resulting bias term. Then the recent history of results is used to determine a mean bias term to fix and re-run the inversion, modifying only the ionospheric parameters to fit the 83.4 nm emission profile.

A forward model is used to calculate the expected emission intensities as a function of look angle for direct comparison to the ICON EUV measurements. The model includes a calculation of the initial volume excitation of photons in the lower thermosphere, a representation of the ion density, and a calculation of the resonant scattering by O⁺ ions as well as the absorption by O⁺ ions and neutrals. Although the ionosphere can be most simply represented within the forward model by a Chapman parameterization, the ICON algorithm preferentially implements the 2007 International Reference Ionosphere (IRI) (Bilitza, 2001; Bilitza and Reinisch, 2008) to define the O⁺ profile in order to enable a higher-accuracy and more complete representation of the ionospheric density profile by providing additional framework to an inherently underdetermined problem, particularly for ionospheres where hmF2 is low. It is important to note that the algorithm does not require the IRI model to produce an accurate ionosphere for a given time or set of conditions, but only that it is able to quickly generate different ionospheric profiles that can be tested to obtain the best fit to the EUV emissions. Because of the successful heritage of the algorithm with SSULI and the testing completed in preparation for ICON (some of which is presented here), newer versions of IRI have not been evaluated for use.

The forward model is iteratively adjusted using a set of parameters, m, until the output produces the best match to the ICON EUV measurements. These model parameters are selected to be the necessary and sufficient set of model inputs and/or outputs that enable the model to describe the most comprehensive set of possible airglow measurements, and thus ionospheric profiles. For the ICON mission, based on experience developing this algorithm concept for the SSULI program (see Stephan, 2016), the model employs only three model parameters: two to adjust the profiles of the IRI model that describe the O⁺ density using the 12-month running mean of sunspot number (Rz12) and the ionosonde-based 12-month running mean of the ionospheric global (IG12) index, and one to compensate for systematic biases within the forward model and measurements. This latter parameter is discussed in more detail in the next section. Additional parameters could be included in the call to IRI to improve the ability to modify the ionospheric profile, but this pair can be user-specified as predictive inputs for all solar conditions. Testing with SSULI data has found these two to be sufficient to present a solution for most ionospheric conditions, with Rz12 driving changes in hmF2 and IG12 affecting primarily NmF2.

The initial volume excitation of the 83.4 and 61.7 nm emissions by solar photoionization of atomic oxygen in the lower thermosphere, the number of excitations per second per atom, is calculated using the g-factor g(r) at position r in the atmosphere that is given by:

$$g(\mathit{r})={\int }_{{\nu }_0}^{\infty }\sigma (\nu )F(\mathit{r},\nu )d\nu ,$$ (1)

where F is the attenuated solar flux of wavelength ν at atmospheric position r, and σ is the excitation cross section to the excited state for each emission feature (2p^{4 4}P for 83.4 nm, and 3s ²P for 61.7 nm). The algorithm uses a parameterized representation of the g-factors derived from the Atmospheric Ultraviolet Radiance Integrated Code (AURIC) (Strickland et al., 1999) that enables a rapid computation of the g-factors as a function of the solar zenith angle, solar F10.7 index, and the total vertical column density of neutral species above location r. A calculation of the solar 83.4 nm source contribution based on the solar flux model of Hinteregger, et al. (1981) is included in the ICON algorithm for completeness. As described in extensive mathematical detail in the appendix to Picone et al. (1997b), the forward model calculates this excitation at a discrete set of altitudes, z_i, that are then used to complete the radiative transfer and absorption calculations, and the integration along the line of sight. The key algorithm steps from Picone et al. (1997a, 1997b) are summarized here. With the approximation that horizontal transport is effectively zero due to spherical symmetry, r translates directly to z. Then the volume excitation rate j_k(z) of line k in each emission feature, at altitude z, is given by:

$$j_k(z)=j_{0k}(z)+{\sigma }_{0k}{N}_{O^{+}}(z){\int }_{z_0}^{\infty }{j}_k(z^{\prime })H(\mid {\tau }_k^{\prime }-{\tau }_k\mid ,\mid t_k^{\prime }-t_k\mid )d{z}^{\prime },$$ (2)

which includes the production source from the initial photoionization of atomic oxygen in the lower thermosphere, j_0k, that is calculated from the appropriate photoionization g-factor from (1) and the number density of atomic oxygen, N_O, using

$$j_{0k}(z)=\mathrm{g}(z)N_O(z).$$ (3)

The contribution from scattering by the population of O⁺ (N_O⁺) at all other altitudes into the altitude z is given by the Holstein probability function, H, which describes the probability that a photon will resonantly scatter from altitude z′ to the altitude z (Holstein, 1947), and the scattering cross section σ_0k. This volume emission rate field is then used to integrate along the line of sight and calculate the measured emission intensity, 4πI, in Rayleighs which, if I is the radiance in megaphotons cm⁻² s⁻¹ ster⁻¹, is then given by:

$$4\pi I(\mathit{r},\widehat{\mathit{e}})={10}^{-6}\int \sum _k{j}_k[{\mathit{r}}^{\prime }(s)]T_k({\mathit{r}}^{\prime },\mathit{r})ds$$ (3)

where T_k is the transmission probability that a photon emitted from region r′ along the line of sight ê, will reach the sensor located at r.

The algorithm uses the Levenberg-Marquardt scheme to minimize χ² between the data and the model, with convergence determined by evaluating a threshold in change in the χ² between successive results. The resulting best fit is determined to be most probable values for the model parameters, and a covariance matrix for the model parameter vector is calculated. The variances in the ionospheric density profile and the hmF2 and NmF2 values are calculated at each altitude using standard error propagation equations with the covariance matrix, the retrieved model parameters, and the partial derivatives of the density with respect to the model parameters. The level 2 data product for the EUV measurement will include the retrieved O⁺ density profile and the correlated hmF2 and NmF2 values along with uncertainties in each. Additionally, data quality flags and metrics from the level 1 data will be passed through to the level 2 data, as well as new flags to identify the quality of the fit from the algorithm, along with other data quality and metrics from the fitting process (e.g. convergence issues, model parameters driven to functional limits) that users should consider when conducting an analysis with the ICON EUV data products.

Error Propagation

The ICON EUV level 1 data products include a separate determination of the random and systematic uncertainties. Random uncertainties are a product of the photon-counting nature of the measurement and are handled directly by the inversion algorithm. While systematic uncertainties can be included as part of the inversion process, they are best handled by the inclusion of a bias term as demonstrated by Picone (2008). Even using a state-of-the-art, best-practices approach for calibration of the EUV sensor, the systematic uncertainty in instrument response, and thus absolute intensity of the ICON EUV L1 data products is expected to be on the order of 13% (Sirk, et al., 2016 submitted). Early on-orbit characterization will play an important role in identifying these factors and defining the best approach to handle these within the inversion algorithm. Additionally, the ICON algorithm will incorporate a multiplicative bias as described by Picone (2008) and Stephan (2016) that will evaluate and compensate, in part, for this uncertainty. It is noted that this approach does not compensate for an additive bias created by an inappropriate background subtraction, or an altitude-dependent bias caused, for example, by non-uniform background contributions across the passband due to out-of-band light that unknowingly changes the shape of the emission profiles.

Additionally, a multiplicative bias term is a necessary component of the forward model to mitigate potential systematic errors in not only the absolute intensity of the EUV measurements but also in the physics of the forward model itself. Systematic uncertainties in the forward model are most likely to stem from the specification of the production of photons in the lower thermosphere, also referred to as the “initial source” (Picone, 2008). However, the manifestation of these sources in the data are expected to be significantly different, with instrument calibration errors steady or slowly changing over time, and physics-based errors governed more by solar and global thermospheric conditions that change and alter the generation of airglow profiles with scales on the order of a day (Stephan, 2016).

The science requirement for ICON is to measure with precision in NmF2 to 18%, and accuracy in hmF2 to 20 km. However, the goal of the algorithm is to meet that target while providing the highest possible accuracy to all products. The inclusion of a bias term adds flexibility in the fitting process to allow for systematic errors in the measurements and the forward model, but comes at a cost as the additional parameter reduces the precision of the result (Picone, 2008), effectively resulting in a larger uncertainty in the returned products. Therefore, the ICON algorithm adopts a two-phase inversion developed for the SSULI missions that first inverts the data with a multiplicative bias term allowed to change as part of the fitting process. Subsequently, a time-history of the bias terms is evaluated (see Stephan, 2016) and a second inversion is conducted with a fixed bias term that is determined from the historical set of measurements. With the SSULI program, the median of the multiplicative bias from the 24-hour span prior to the current measurement has been found to return the best results. Because the ICON orbit is different from the Sun-synchronous platforms of SSULI where this approach has been previously applied, and ICON contains additional information in the 61.7 nm feature that is not available in the SSULI passband, the best approach for the evaluation of the final fixed bias for ICON will, by necessity, be determined early in the mission and updated as necessary throughout the course of the mission. However, in testing the algorithm performance for ICON, a two-color inversion was conducted that fit the measured emission profiles from both colors with a single bias, determined by the median from a single orbit and applied to the emission profiles of both colors equally. This is only appropriate for the simulation because the airglow generation and inversion was completed with identical, known physical cross sections and constants, with the only systematic errors being introduced by the calibration uncertainties in the simulator of the ICON EUV. In practice, the products will have to be carefully verified for additional biases and systematic errors in the retrieval.

Validation

Validation of the ICON EUV daytime ionosphere algorithm was completed through a series of end-to-end simulations. A representative set of ICON orbit and EUV viewing geometry data was generated and used in combination with the existing forward model to create a noise-free set of airglow volume emission rates and limb-viewing intensity profiles for both the 61.7 and 83.4 nm emission features. The range of ionospheres in this orbit included hmF2 values ranging from 245 to 340 km, and NmF2 values ranging from 1.0 × 10⁵ to 1.6 × 10⁶ cm⁻³. These were then run through an instrument simulator that used the pre-flight instrument characterization (Sirk et al., submitted to Space Science Reviews, 2016) to generated a full set of EUV viewing images and to create ICON EUV level 1 data profile sets with realistic representation of the algorithm inputs. In all, 138 ICON EUV profiles were simulated over the orbit. The algorithm was then used to process these data in a flight-like test, starting with an analysis of all the data that allowed the bias term to float in the fitting process, and followed by a second pass that used a fixed, single bias value based on a statistical evaluation of the full orbit of bias results. The bias factor determined for this simulated orbit is 0.91, equivalent to a 9% systematic offset that is within the 13% systematic uncertainty in the ICON EUV L1 data products (Sirk et al., submitted). It is noteworthy that all retrievals started from the same ionospheric profile (represented by the dashed lines in the upper panels of Figure 2 for the starting emission and ion density profile) to ensure that the algorithm truly identified the correct ionosphere from the measurements without any preconditioned expectation. It has been demonstrated through numerous validation tests for ICON and the inversion of tens of thousands of SSULI limb scans that the final ionospheric profile is independent of the starting point, although certainly this independence cannot be rigorously proven for all measurement and inversion scenarios.

Figure 2.

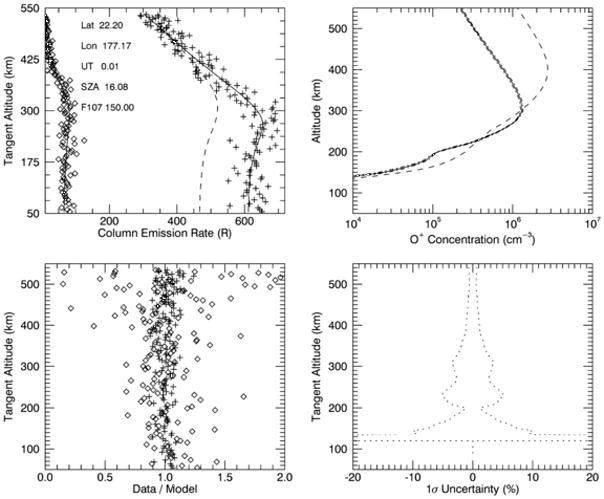
Top left, a sample from the simulated ICON EUV 83.4 nm (+ symbols) and 61.7 nm (⋄ symbols) measurements, the 83.4 nm profile based on an initial guess of the ionospheric profile (dashed line) and the final fit (solid lines). The ratio of the data to the final fit shown in the bottom left panel. Top right, the initial guess of the ionospheric profile (dashed line), and the final result (solid line), with 1σ uncertainties propagated through the inversion (dash-dot lines) also shown in the bottom right panel.

Figure 3 shows the fraction of all the profiles within the simulated ICON orbit for which the algorithm was able to determine hmF2 and NmF2 to within various ranges of accuracy to the known ionospheric conditions used to generate the sample emission profiles. This figure includes both the first pass through the data when the bias term is allowed to vary as part of the model fitting process (dashed lines), and the final pass when the bias is fixed based on the values returned (solid line). These curves are used as a representative sample of measurements to identify the accuracy of the algorithm based on the expected performance of the ICON EUV based on a simplified approximation for a 1-σ precision value to mean that the accuracy of two-thirds of the samples are within that range. These results show that the ICON EUV can measure hmF2 with 3 km accuracy and NmF2 to 12% accuracy. It is also shown that the impact of the bias is most significant for the determination of NmF2, with little impact on the accuracy of the aggregate of hmF2 products that are more strongly dependent on the shape of the limb profile. Picone et al. [1997a] showed that this bias parameter is expected to be most accurate when hmF2 is above 350 km, a condition not tested in these simulations.

Figure 3.

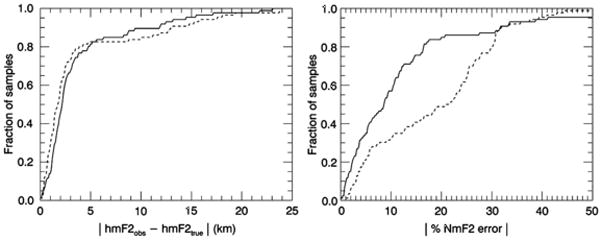
The left panel shows the fraction of the 86 limb profile samples from one simulated ICON orbit with a retrieved hmf2 value within the range of the known input true value. The dashed line represents the first run with a floating bias, and the solid line represents the second pass with a fixed bias set to the median value of all the biases. The right panel shows the same representation for NmF2 that is more strongly dependent on the absolute intensity of the 83.4 nm emission, and thus the bias in the measurement.

These simulations were conducted with 12-second integrations, the inherent cadence of the EUV sensor, but a factor of 5 less than the 60-second sampling required to achieve the 500 km spatial resolution that is needed for these measurements to support the analysis that will address the ICON science questions (Immel et al., 2016). However, even at this most strict test condition, the performance of the algorithm meets the ICON performance requirements to measure hmF2 and NmF2 in both accuracy and precision. Additional validation of the algorithm will be possible on-orbit by comparison of algorithm products to available ground-based ionosonde measurements. This will include a detailed analysis of the biases that are returned by the algorithm in order to refine and tune the algorithm to return the highest-accuracy results.

Summary

The NASA Ionospheric Connection Explorer (ICON) mission will use an advanced version of an algorithm, developed at the U.S. Naval Research Laboratory using data from the SSULI and RAIDS programs, to infer the daytime ionosphere from measurements of the OII 83.4 and 61.7 nm emissions made by the Extreme Ultraviolet (EUV) spectrograph. The algorithm uses the multiple scattering effects of the 83.4 nm emission feature of O⁺ to infer the altitude profile of this species covering 150–450 km in altitude, and thereby obtain a measure of the ionospheric F-region peak density, NmF2, and height, hmF2. With the additional measurement of the 61.7 nm emission and the high responsivity of the sensor, the ICON EUV will directly address ambiguities that are inherent in measurements of the 83.4 nm emission feature alone. The algorithm also incorporates a bias evaluation and feedback step that is able to effectively mitigate the effects of systematic instrument calibration errors and inaccuracies in the original photon source within the forward model to improve the accuracy in NmF2. The hmF2 accuracy is largely unaffected by uncorrected measurement bias. Pre-flight simulations of ICON EUV measurements over a representative orbit have been conducted that show the accuracy of the algorithm is able to reproduce hmF2 values to better than 5 km accuracy, and NmF2 to better than 12% accuracy over a 12-second integration, both well within the science requirements for the NASA ICON mission.