Rapid Method To Determine Intracellular Drug Concentrations in Cellular Uptake Assays: Application to Metformin in Organic Cation Transporter 1–Transfected Human Embryonic Kidney 293 Cells

Abstract

Because of the importance of intracellular unbound drug concentrations in the prediction of in vivo concentrations that are determinants of drug efficacy and toxicity, a number of assays have been developed to assess in vitro unbound concentrations of drugs. Here we present a rapid method to determine the intracellular unbound drug concentrations in cultured cells, and we apply the method along with a mechanistic model to predict concentrations of metformin in subcellular compartments of stably transfected human embryonic kidney 293 (HEK293) cells. Intracellular space (ICS) was calculated by subtracting the [³H]-inulin distribution volume (extracellular space, ECS) from the [¹⁴C]-urea distribution volume (total water space, TWS). Values obtained for intracellular space (mean ± S.E.M.; μl/10⁶ cells) of monolayers of HEK cells (HEK-empty vector [EV]) and cells overexpressing human organic cation transporter 1 (HEK-OCT1), 1.21± 0.07 and 1.25±0.06, respectively, were used to determine the intracellular metformin concentrations. After incubation of the cells with 5 µM metformin, the intracellular concentrations were 26.4 ± 7.8 μM and 268 ± 11.0 μM, respectively, in HEK-EV and HEK-OCT1. In addition, intracellular metformin concentrations were lower in high K⁺ buffer (140 mM KCl) compared with normal K⁺ buffer (5.4 mM KCl) in HEK-OCT1 cells (54.8 ± 3.8 μM and 198.1 ± 11.2 μM, respectively; P < 0.05). Our mechanistic model suggests that, depending on the credible range of assumed physiologic values, the positively charged metformin accumulates to particularly high levels in endoplasmic reticulum and/or mitochondria. This method together with the computational model can be used to determine intracellular unbound concentrations and to predict subcellular accumulation of drugs in other complex systems such as primary cells.

Introduction

Intracellular unbound drug concentrations are critical determinants of drug interactions with targets and enzymes because most drug metabolizing enzymes and drug targets are located inside cells (Overington et al., 2006; Dollery, 2013). In general, because intracellular unbound concentrations of drugs cannot be measured in vivo, extracellular drug concentrations are used as a proxy and are most often measured in plasma, with or without correction for plasma protein binding. Increasingly it is being recognized that because of active transport proteins that mediate drugs across cellular membranes, intracellular drug concentrations may be different from their levels in the extracellular environment.

Because of the difficulty in measuring intracellular concentrations, a number of methods have been developed to estimate unbound intracellular concentrations of drugs (Chu et al., 2013). However, many of these methods are complicated and costly. Measurement of intracellular concentrations in vivo is especially difficult. Recently, new technology based on mass spectrometry imaging techniques (matrix-associated laser desorption/ionization, secondary ion mass spectrometry (SIMS) and nanoSIMS has been used to determine intracellular drug levels in vivo (Dollery, 2013); however, use of this technology is limited because of the need for special equipment and the high costs associated with these imaging methods. Thus, in silico methods to predict intracellular drug concentrations in vivo represent a better alternative; however, in silico methods require information from in vitro assays to accurately estimate in vivo concentrations.

For many drugs to reach their intracellular target, passage through the lipoprotein bilayer of the cell membrane is facilitated by membrane transporters (Giacomini et al., 2010). For a compound that is a substrate of a particular transporter, the number of transporter proteins on the cell surface and the K_m of the compound for the transporter are major determinants of its rate of influx. Once in the cell, some molecules become highly concentrated in organelles, such as lysosomes (Dollery, 2013) or mitochondria (Durazo et al., 2011). Thus, knowledge of the drug concentration within cells is becoming increasingly important in drug development to determine the effect of new compounds at the site of action, binding to targets, and hence drug activity. For example, the IC₅₀ values for cytotoxicity of adefovir and cidofovir, anti-human immunodeficiency (HIV) drugs, substrates of organic anion transporters (OATs), is significantly influenced by the intracellular concentrations of these drugs (Zhang et al., 2013, 2015).

Metformin, one of the world’s most widely prescribed antidiabetic drugs, requires membrane transporters such as organic cation transporter 1 (OCT1) to gain access to intracellular targets (Wang et al., 2002; Tzvetkov et al., 2009; Li et al., 2013; Chen et al., 2014). We developed a method to measure the intracellular concentrations of metformin in vitro in cells expressing OCT1 to assess whether the drug accumulates in subcellular compartments. We applied this method to measure the binding and accumulation of metformin, aminoguanidine, and guanidine in cultured human embryonic kidney 293 cells (HEK293). Our simple step-by-step procedure coupled with the mechanistic model provides a novel method for predicting the subcellular compartment accumulation of drugs. This method can be applied to in vitro/in vivo modeling to predict intracellular drug levels and pharmacologic responses.

Materials and Methods

Cell Culture.

The cells were generated and cultured as previously described elsewhere (Shu et al., 2007). HEK293 Flp-In-293 cells were transfected with pcDNA5/FRT vector (Invitrogen, Invitrogen, Carlsbad, CA) containing the OCT1 cDNA insert (HEK-OCT1) or vector only (HEK-EV [empty vector]) using Lipofectamine 2000 (Invitrogen) following the manufacturer’s protocols. The cells were maintained in Dulbecco’s modified Eagle’s medium of high glucose supplemented with 10% FBS, 100 U/ml penicillin and 100 μg/ml streptomycin, and 75 μg/ml hygromycin B, at 37°C in a humidified 5% CO₂ atmosphere.

Chemicals and Uptake Buffers.

Uptake was performed in Hank’s balanced salt solution (HBSS), 5.4 mM KCl, and 140 mM KCl buffers. The HBSS buffer was purchased from Life Technologies (Carlsbad, CA). Potassium buffers were made as described elsewhere (Klapperstück et al., 2009). Briefly, the buffer composition was 5.4 mM KCl buffer containing 1 mM CaCl₂, 1 mM MgCl₂, 10 mM HEPES, 140 mM NaCl, 5.4 mM KCl, and 10 mM glucose. The 140 mM KCl buffer was identical to the 5.4 mM KCl buffer with the exception of the sodium and potassium being iso-osmotically adjusted (the sum was 145.4 mM). We purchased ¹⁴C-metformin (ARC1738) and ¹⁴C-urea (ARC0150A) American Radiolabeled Chemicals (St. Louis, MO). The ¹⁴C-aminoguanidine (MC215) and ¹⁴C-guanidine (MC145) were purchased from Moravek Biochemicals and Radiochemicals (Brea, CA). ³H-Inulin (NET086L001MC) was purchased from PerkinElmer Life and Analytical Sciences (Waltham, MA).

Distribution Spaces of Individual Markers in Monolayers.

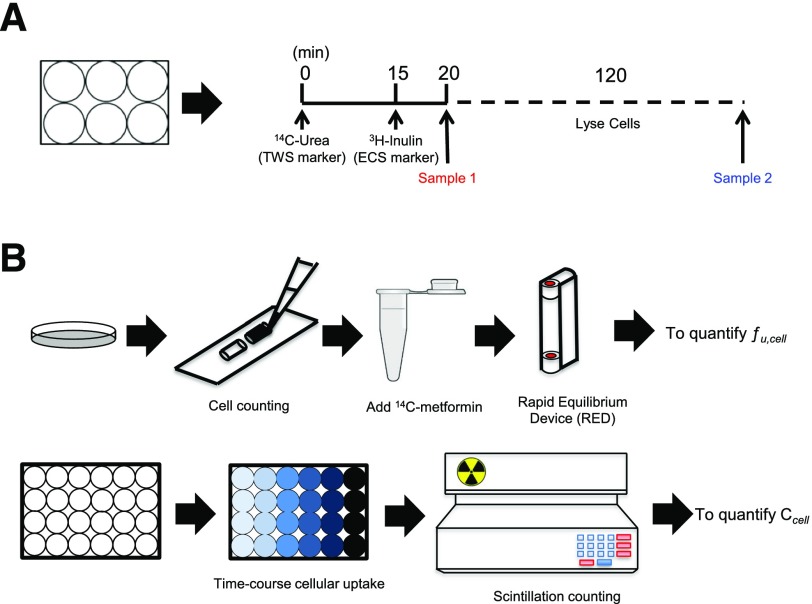
HEK-EV and HEK-OCT1 cells were grown in six-well plates. The monolayers were rinsed with HBSS and then equilibrated at 37°C for 10 minutes. After removal of the buffer, 950 μl of radioactively labeled total water space (TWS) marker (¹⁴C-urea, final concentration 1.0 μCi/ml) was added to the cells at time zero, 50 μl of the marker for extracellular space (ECS) (³H-inulin, final concentration 1.0 μCi/ml) was added after 15 minutes, and the incubations were terminated after 20 minutes (Vasquez et al., 1982).

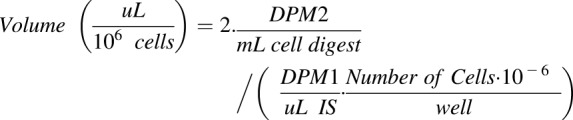
At the indicated times, the incubation of the cells with the marker was terminated by placing the plate on ice. Triplicate aliquots (25 μl) of incubated solution (IS) were removed to determine total radioactivity (DPM 1); then the cells were rinsed twice rapidly with 1.0 ml of ice-cold HBSS per rinse. After aspiration of the final rinse, cells were digested for 2 hours at room temperature with 2.0 ml lysis buffer (0.1 N NaOH, 0.1% SDS). A 1.0-ml aliquot of cell digest from each well was used to measure radioactivity (DPM 2). The distribution volume of the radioactive marker (μl/10⁶ cells) was calculated as follows:

(1)

In this equation, Volume represents the marker distribution volume. DPM1 and DPM2 represent radioactivity of incubated solution (IS), and cell digest after lysis, respectively. The protein concentration from each well was measured by the BCA Protein Assay Kit (Thermo Fisher Scientific, Waltham, MA) and converted into cell number using a standard curve as described herein.

Standard Curve of Cell Number.

To simplify cell number calculations, we constructed a standard curve of cell number versus protein amount. Various numbers of cells (10,000∼200,000) were seeded in a 48-well plate. Cells from half of a plate were lysed and measured for protein concentration with the BCA Protein Assay Kit (Thermo Scientific); the other half plate of cells were trypsinized and the number of cells were counted by the TC20 cell counter (Bio-Rad Laboratories, Hercules, CA). Three replicates for each condition were used to plot the standard curve.

Measurement of Drug Binding.

Compound binding to HEK cells was measured through equilibrium dialysis as previously described elsewhere (Mateus et al., 2013). The cells were harvested from a six-well plate using 0.05% trypsin, then centrifuged at 500g for 5 minutes. Cells were washed once with HBSS, counted using a TC20 cell counter (Bio-Rad Laboratories), and centrifuged again at 500g for 5 minutes. The pellet of HEK293 cells was suspended in buffer, and the buffer was adjusted to a concentration of 10 × 10⁶ cells/ml. We incubated ¹⁴C-metformin with the homogenate at a concentration of 5 μM for 30 minutes at 37°C.

Samples were dialyzed using a rapid equilibrium dialysis (RED) device (Thermo Fisher Scientific) by transferring 200 μl of compound-spiked cell suspension to one chamber of the dialysis unit (cell chamber) and 350 μl of HBSS to the other chamber (buffer chamber). The dialysis unit was incubated at 37°C and 900 rpm on an orbital shaker for 4 hours. At the end of the incubation, triplicated aliquots (25 μl) of each sample from the buffer and cell chambers were taken to determine radioactivity.

The unbound fraction of metformin in the cells was calculated as C_buffer/C_cell, where C_buffer is the metformin concentration in the buffer chamber and C_cell is the metformin concentration in the cell chamber. The unbound fractions of guanidine and aminoguanidine were measured and calculated using same procedure.

Osmolarity Study.

To determine whether the uptake of metformin was due to intracellular accumulation or binding to membranes, a method that relies on assessing uptake under conditions of varying osmolarity was applied (Gisclon et al., 1987). In short, uptake of metformin was determined at 1 hour in the presence of varying concentrations of the impermeable solute, sucrose (0.2 mM to 0.8 mM). Uptake of 5 μM metformin was determined in HEK-EV and HEK-OCT1 cells at varying osmolarities. Theoretically, at infinite sucrose osmolarity, intracellular space volume is negligible because the cells shrink, and metformin associated with the cells represents membrane bound. Thus, the intercept of a linear plot of metformin uptake versus inverse sucrose osmolarity, divided by metformin uptake in the absence of sucrose, represents the fraction of metformin bound to the cellular membranes.

Statistical Analysis.

In general, triplicate data points were generated in each experiment and experiments were repeated three times unless otherwise stated. Data are presented as mean ± S.E.M. Statistical inference was calculated using Student’s t test.

Mathematical Modeling.

A model similar to that published previously elsewhere was used to characterize the uptake of metformin into HEK-EV cells (Trapp and Horobin, 2005; Trapp et al., 2008; Ghosh et al., 2014). Briefly, the flux of metformin across a cell membrane, J_{A → B} is assumed to follow the electrochemical potential of a monoprotic base (eq. 2):

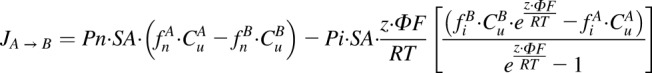(2)

where P_n and P_i represent intrinsic permeability of the neutral and ionized species of metformin; SA, z, F, ∆φ, R, and T represent the membrane surface area, molecular charge, Faraday’s constant, electric potential, gas constant, and absolute temperature; and f_n, f_i, and C_u are the neutral fraction, ionized fraction, and unbound concentration on either side of the membrane, respectively. The fractional ionization was calculated using the Henderson-Hasselbalch equation according to the pH and an assumed metformin pKa of 12.4 (DrugBank: (http://www.drugbank.ca).

As previously described, this conceptualization of flux was incorporated into a physiologic cell model containing representations of media, cytosol, nucleus, lysosomes, endoplasmic reticulum (ER), and mitochondria. Concentrations for each compartment were characterized by accounting for the volumes and fluxes between compartments as shown for the cytosol (eq. 3).

(3)

The HEK cell volume was assumed to be 1.23 pl, with 40, 10, 0.7, 9.3, and 40% being represented by cytosol, mitochondria, lysosome, ER, and nucleus, respectively. Under 5.4 mM extracellular KCl conditions, values for ∆φ were assumed to be −20, −180, 18.6, and −9.2 mV (Trapp and Horobin, 2005; Trapp et al., 2008; Ghosh et al., 2014) for the outer membrane, mitochondria, lysosome, and nucleus, respectively.

Due to uncertainty in the appropriate ∆φ values for the ER, data were modeled under an assumed value of −80 mV and 0 mV to cover a range consistent with reported values (Somlyo et al., 1981; Tang et al., 1989; Burdakov et al., 2005; Qin et al., 2011). The value assumed for the outer membrane is within the range of internal electrophysiologic measures on these cells (−19 to −27 mV, data not shown) and independent literature (Søgaard et al., 2001). Under 140 mM KCl conditions, ∆φ was assumed to be 0 mV for the cell membrane (Søgaard et al., 2001; Yamada et al., 2001). Values for pH were assumed to be 7.4, 7.2, 8.0, 4.7, 7.2, and 7.2 for the media, cytosol, mitochondria, lysosome, ER, and nucleus, respectively (Trapp and Horobin, 2005; Trapp et al., 2008; Ghosh et al., 2014). Under these assumptions, the P_n and P_i values of metformin were estimated from the time course of cellular uptake in HEK-EV cells under low and high extracellular KCl conditions by the maximum likelihood method.

Consistent with a mechanism of equilibrative, saturable transport according to electrochemical potential, the kinetics of metformin uptake in OCT1 transfected cells were characterized by incorporating a bidirectional saturable effect on the ionized permeability of metformin (eq. 4):

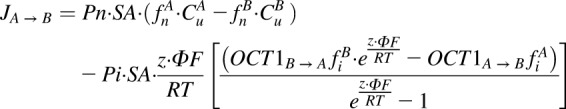(4)

where

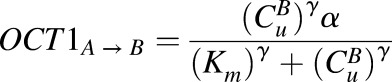and

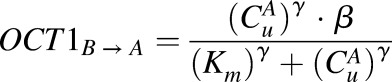The effect of OCT1 on flux was only applied to the outer cell membrane. All other physiologic parameters of the HEK-OCT1 cells were assumed to be equivalent to that previously stated for HEK-EV cells, except the time course for the model was 20 minutes for the HEK-EV and 60 minutes for the HEK-OCT1.

Exposure to the 140 mM KCl solution resulted in poor viability of the HEK-EV cells compared with the HEK-OCT1 cells. In addition, the P_n and P_i values for metformin were assumed to be the same as estimated in HEK-EV cells, and the value of γ was fixed to 1.12. Under these assumptions, the values of α, β, and K_m were estimated from the time course of cellular uptake in HEK-OCT1 cells under low and high extracellular KCl conditions by the maximum likelihood method.

Results

Intracellular Space Measurement.

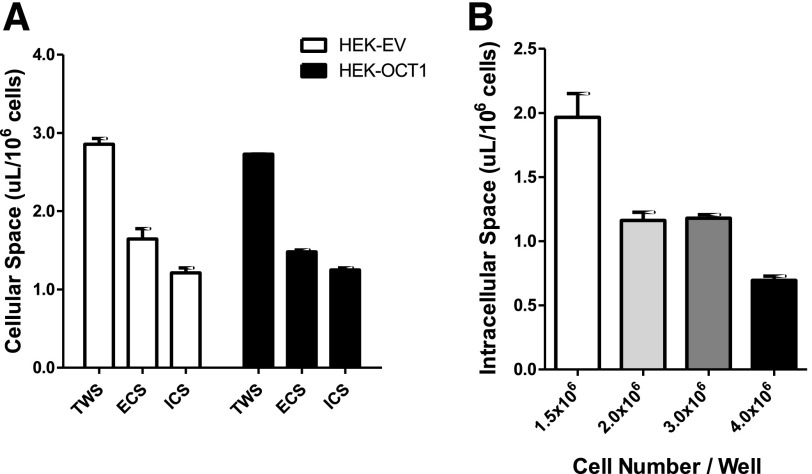
Total water space (TWS: the sum of ECS and intracellular space [ICS]) was estimated by the equilibrium distribution volume of ¹⁴C-urea, which reached a steady state in 20 minutes and was independent of the urea concentration (Fig. 1A, modified from Vasquez et al., 1982). The TWS of HEK-EV and HEK-OCT1 was 2.860.12 µl/10⁶ cells and 2.730.01 µl/10⁶ cells, respectively (Fig. 2A). The ECS distribution volume of HEK-EV was 1.64 0.23 µl/10⁶ cells and was 1.48 0.04 µL/10⁶ cells for HEK-OCT1. Thus, the total intracellular space of HEK-EV and HEK-OCT1 was calculated to be 1.210.07 µl/10⁶ cells and 1.25 0.06 µl/10⁶ cells, respectively.

Fig. 1.

Step-by-step procedure for determining the intracellular unbound drug concentration in adherence cells in culture. (A) To determine intracellular space in monolayers, the marker for total water space (TWS, [¹⁴C]-urea) was added at time zero, and the marker for extracellular space (ECS, [³H]-inulin) was added after 15 minutes. The incubation was terminated at 20 minutes. Sample 1 and 2 were taken before and after cells were lysed. The distribution volume of the radioactivity labeled marker was calculated with eq. 1 (see Materials and Methods). ICS was obtained by subtracting ECS volume from TWS volume. (B) Upper panel: Cells were harvested and counted, then spiked with ¹⁴C-metformin or other tested radiolabeled compounds. Samples were dialyzed using a rapid equilibrium dialysis (RED) device. The unbound drug fraction of cells (fu_cell) was calculated by C_buffer/C_cell. Lower panel: Time-course of cellular uptake was assessed. Compound solutions were prepared in HBSS buffer and then added to cells. After uptake, wash, and cell lysis, the radioactivity was determined, and the amount of compound in the cell lysate, A_cell, was determined. The intracellular unbound drug concentration Cu_cell was calculated by fu_cell × (A_cell/V_cell). V_cell is intracellular space obtained from A.

Fig. 2.

Cellular space measurement of human HEK cells. (A) TWS, ECS, and ICS of HEK-EV and HEK-OCT1 cells. Intracellular space was calculated from the distribution volume of [¹⁴C]-urea (20 minutes) and [³H]-inulin (5 minutes) in monolayers of cells. (B) ICS of HEK-OCT1 cells at different cell densities. Data are presented as mean ± S.E.M.

In addition, we measured cell diameter using a cell sorter (Supplemental Table 1). The cell volume of HEK-EV and HEK-OCT1 was calculated to be 2.28 ± 0.68 µl/10⁶ cells and 2.33 ± 0.71 µl/10⁶ cells, respectively. We also tested the effect of different cell densities, ranging from 1.5 × 10⁶ to 4.0 × 10⁶/well and we found that the ICS was smaller when the cells were present at higher densities, such as ICS was 0.70 μl/10⁶ cells when cell density was 4 × 10⁶/well (Fig. 2B). The smaller ICS associated with high-cell density is a result of many cells squeezed into a limited surface area resulting in a smaller intracellular volume per cell. Thus, cell density is an important determinant of intracellular volume.

Measurement of Unbound Drug Fraction.

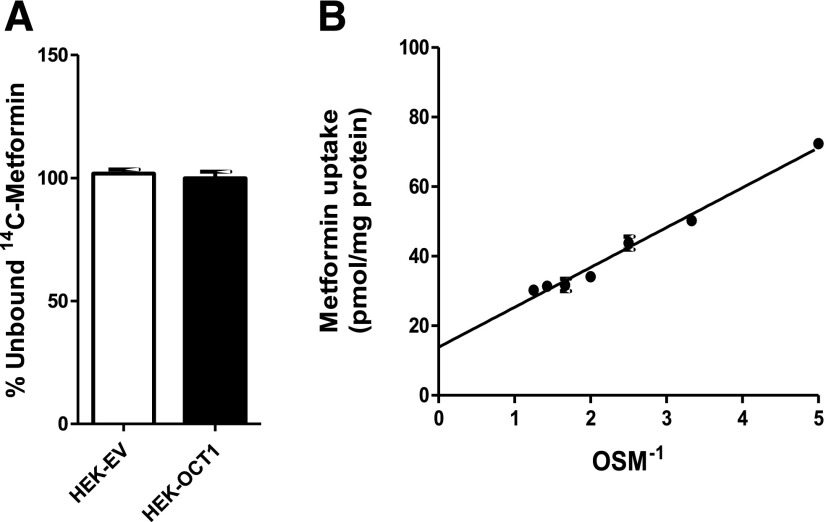
Measurements of drug binding to HEK293 cells using the RED device showed that very little metformin was bound (Figs. 1B and 3A). A very low cell-bound fraction of metformin (<2%) was observed in other cell lines including HepG2-OCT1, HepaRG-OCT1, and HEK-mOCT1 (data not shown). Furthermore, the unbound fraction of metformin measured in human plasma was also very low (∼2%), consistent with previous results in the literature (Eyal et al., 2010).

Fig. 3.

Unbound fraction of metformin of human HEK cells. (A) Unbound fractions of metformin in HEK-EV and HEK-OCT1 cells determined by dialysis using a rapid equilibrium device (see Materials and Methods). No significant difference was found between HEK-EV and HEK-OCT1. (B) Equilibrium (1 hour) uptake of metformin as a function of inverse osmolarity of sucrose (OSM-1) in HBSS buffer. Each point represents the mean ± S.E. of data obtained from uptake values in three wells. The line was generated by linear regression. Membrane binding was determined to be 2.5% ± 0.1%, as calculated by (Intercept × 100)/(Uptake in the absence of sucrose).

The osmolarity studies were also used to assess the cellular binding of metformin (Fig. 3B). Theoretically, at infinite sucrose osmolarity, intracellular volume is negligible, and the metformin associated with the cells represents membrane-bound compound (Gisclon et al., 1987). Thus, the intercept of a linear plot of metformin uptake versus inverse sucrose osmolarity, divided by metformin uptake in the absence of sucrose, represents the fraction of metformin bound to the membranes. Similar to the measures using the RED device, a small fraction of metformin (2.50% ± 0.11% of the uptake) represented bound metformin. Both methods showed metformin exhibits low cell binding, and its binding is negligible in comparison with its intracellular concentrations.

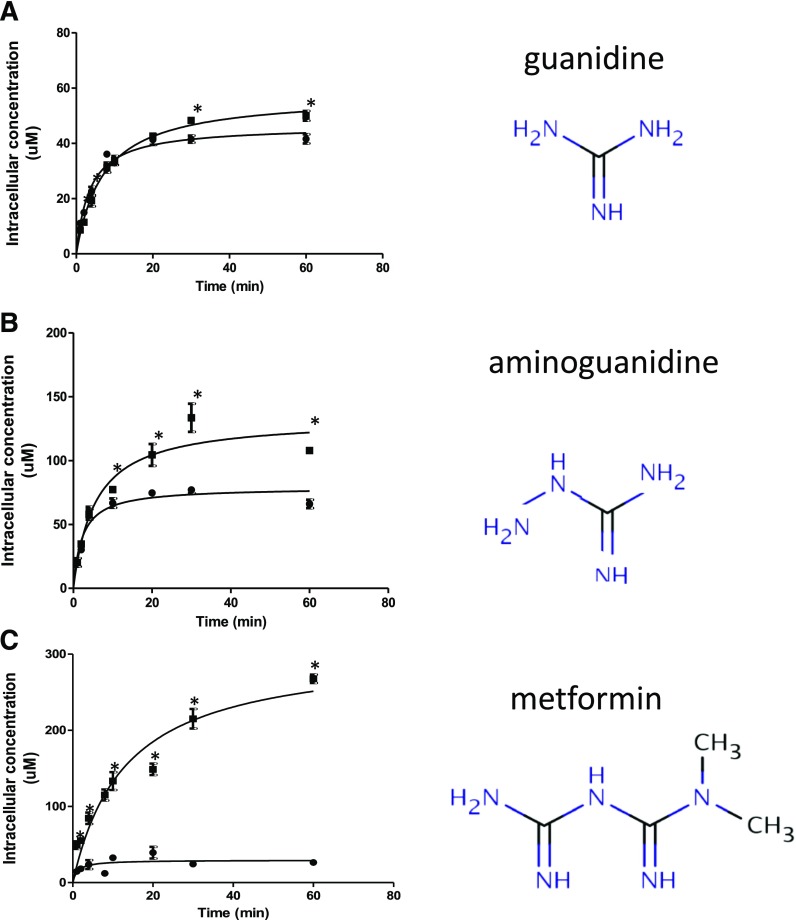
Intracellular Concentrations of Guanidine Compounds.

We compared unbound intracellular concentrations of a series of guanidine compounds including guanidine, aminoguanidine, and metformin (dimethylbiguanidine). Intracellular guanidine concentrations were very similar in HEK-EV and HEK-OCT1 cells, consistent with the compound not being a substrate of OCT1 (Fig. 4A). In contrast, intracellular aminoguanidine concentration in HEK-OCT1 was 2-fold higher than in HEK-EV cells (Fig. 4B), and the intracellular metformin concentration in HEK-OCT1 was 10-fold higher than in HEK-EV cells (Fig. 4C). Interestingly, the metformin accumulation was greater than the accumulation of guanidine and aminoguanidine, consistent with the drug being a substrate for OCT1.

Fig. 4.

Intracellular concentrations of guanidine compounds in human cells in HBSS buffer. Time course of intracellular concentration of (A) guanidine, (B) aminoguanidine, and (C) metformin in HEK-EV (●) and HEK-OCT1 (▪) cells. We incubated 5 µM extracellular drug concentration with the cells. Cell binding of the compounds was determined by dialysis using a rapid equilibrium device (RED). Intracellular space of HEK-EV (1.21 µl/10⁶ cells) and HEK-OCT1 (1.25 µl/10⁶ cells) were used to calculate the unbound intracellular concentrations of three guanidine compounds. Data are presented as mean ± S.E.M. *P < 0.05.

We then compared the unbound drug accumulation ratio (K_puu), defined as the intracellular concentration divided by the medium concentration, for unbound guanidine, aminoguanidine, and metformin using 5 μM compound concentrations in HBSS uptake buffer. Guanidine exhibited the lowest K_puu (10), and metformin had the highest ratio (53.6).

Intracellular Concentration of Metformin in Buffers Containing KCl.

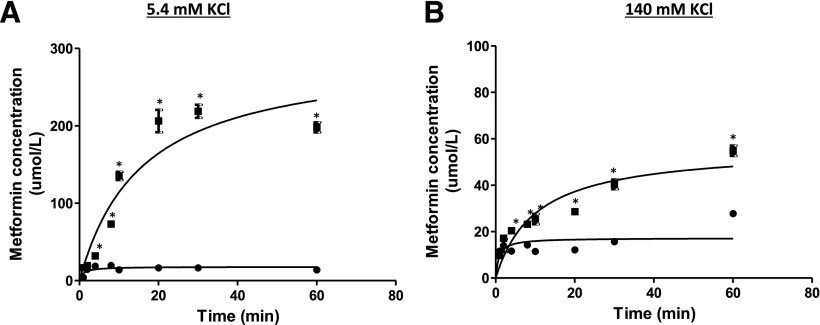
The effect of membrane potential on intracellular accumulation of metformin was studied using low K⁺ (5.4 mM KCl) and high K⁺ buffers (140 mM KCl). Similar intracellular concentrations of metformin were observed between the standard HBSS uptake buffer (K⁺ concentration = 5.4 mM) (Fig. 4C) and the low K⁺ buffer (Fig. 5A), reflecting the similar K⁺ concentrations and the similar membrane potential difference between in the cells incubated in the prepared low K⁺ buffer and the standard HBSS buffer. In contrast, intracellular metformin concentrations were much lower in HEK-OCT1 in high K⁺ buffer (Fig. 5B), consistent with an electrical potential sensitive accumulation of the drug into the cells.

Fig. 5.

Intracellular metformin concentration in human HEK cells in different buffers. Time course of intracellular metformin concentrations in HEK-EV (●) and HEK-OCT1 (▪) in (A) low K⁺, 5.4 mM KCl buffer, and (B) high K⁺, 140 mM KCl buffer. The ICS of HEK-EV (1.21 µl/10⁶ cells) and HEK-OCT1 (1.25 µl/10⁶ cells) was used to calculate the metformin unbound intracellular concentrations in two different buffers. Data are presented as mean ± S.E.M. *P < 0.05.

Mathematical Modeling.

The proposed mechanistic model captured the uptake of metformin in HEK-EV cells well (Fig. 6A). The results are consistent with the contribution of ionized permeation to the overall flux and accumulation of metformin in HEK-EV cells. Despite the fact that P_n is estimated to be nearly 40,000-fold greater than P_i (Table 1), the ionized form of metformin is expected to be in even greater excess of the neutral form at pH 7.4 (i.e., 100,000-fold based on the Henderson-Hasselbalch equation). As such, the difference in uptake between low and high extracellular KCl concentrations is attributed to permeation according to differential electrochemical potential under these conditions. In addition, the steady-state accumulation of metformin in excess of that predicted by the Nernst equation with a −20 mV potential difference is attributed to differential accumulation in organelles in accordance with the associated pH and membrane potential at these subcellular sites.

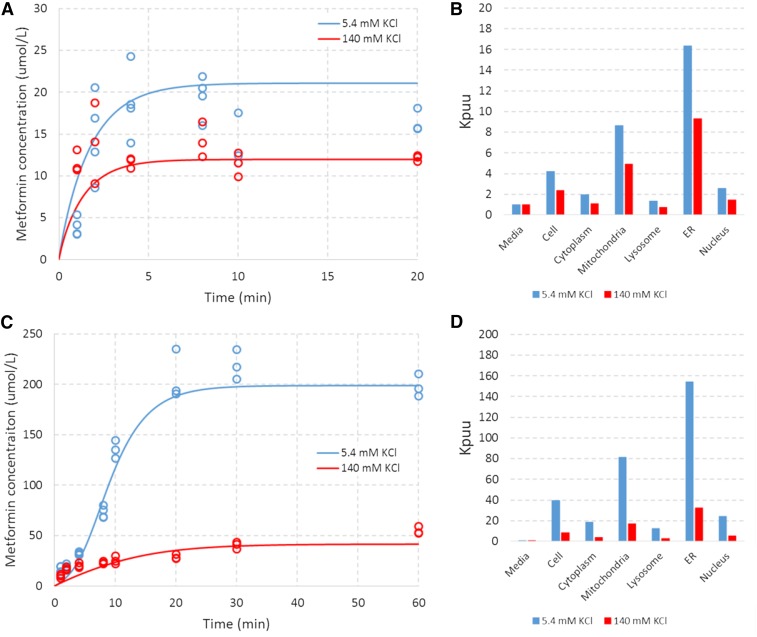
Fig. 6.

Model-based characterization of metformin uptake in HEK-EV and HEK-OCT1 cells under an assumed ER ∆Φ of −80mV. Blue and red symbols represent data of (A) HEK-EV and (C) HEK-OCT1 under extracellular KCl concentrations of 5.4 mM and 140 mM, respectively. Associated lines represent the model-based characterization associated with the derived parameters from Table 1. Blue and red bars represent subcellular accumulation (relative to media concentration) associated with the model-based characterization of uptake in (B) HEK-EV and (D) HEK-OCT1 under extracellular KCl concentrations of 5.4 mM and 140 mM, respectively.

TABLE 1.

Parameter estimates derived from application of the mechanistic model to metformin uptake in HEK-EV and HEK-OCT1 cells

Parameter	ER ∆φ = −80 mV		ER ∆φ = 0 mV
	Estimates	Standard Error (%)	Estimates	Standard Error (%)
Pn (cm/sec)	0.247	42	0.249	86
Pn/Pi	39,932	17	24,242	24
α	12.15	23	8.24	14
β	9.18	26	5.56	18
Km (µM)	68.04	29	83.61	18

Under the assumed ER ∆φ value of −80 mV, the model suggests that metformin accumulates to particularly high levels (relative to the medium) in both the mitochondria and ER (Fig. 6B). The proposed mechanistic model also captures the uptake of metformin in HEK-OCT1 cells well with the addition of four parameters (one fixed, three estimated) serving as modifiers to the ionized permeability (Fig. 6C). The effect of OCT1 is parameterized as a nonlinear function with a single K_m, but a differential directional capacity. This parameterization was chosen as it represents the simplest biologically plausible codification that provided an adequate characterization of the data (Table 1, Fig. 6C).

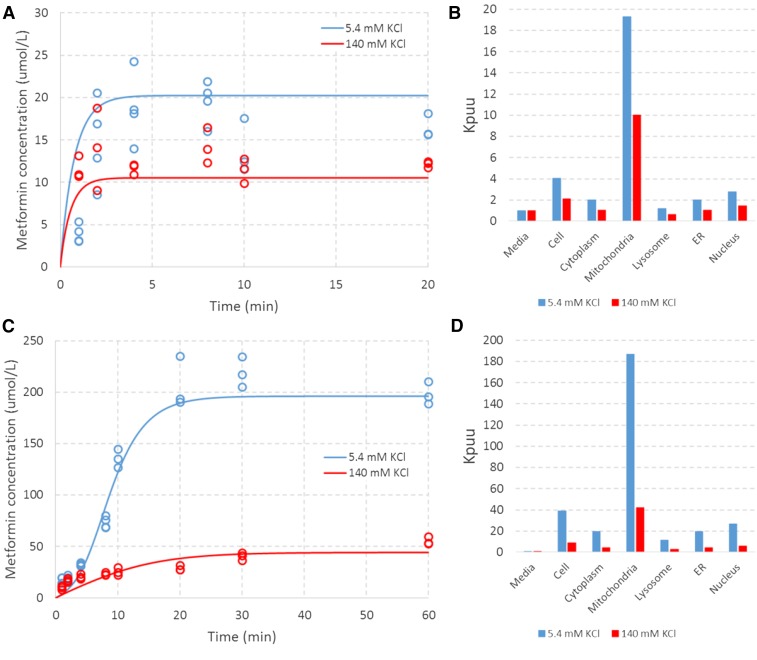
As expected, the model suggests an even greater accumulation in subcellular locations in the presence of OCT1 due to the multiplicative nature of accumulation across the cytosol and organelles (Fig. 6D). The data were equally well characterized under the assumed ER ∆φ value of 0 mV (Fig. 7, A and C). Under this assumption, the parameters governing the distribution of ionized species (e.g., P_i, α, β, and K_m) changed by approximately 20% to 40% (Table 1). Under this condition, the ER and cytosol concentrations (relative to the medium) are comparable, and subcellular accumulation is most significant in mitochondria (Fig. 7, B and D). These results indicate that, although the implications for the site of accumulation differ, the data characterization and derived parameters are relatively insensitive to the assumed ER ∆φ value. This is most likely the result of the relatively small volume of the ER (i.e., 10% of cell) and the presence of another strongly electronegative organelle capable of accounting for the observed net uptake with minor changes to estimated parameters (i.e., mitochondria ∆φ = −180 mV).

Fig. 7.

Model-based characterization of metformin uptake in HEK-EV and HEK-OCT1 cells under an assumed ER ∆Φ of 0 mV. Blue and red symbols represent data in (A) HEK-EV and (C) HEK-OCT1 under extracellular KCl concentrations of 5.4 mM and 140 mM, respectively. Associated lines represent the model-based characterization associated with the derived parameters from Table 1. Blue and red bars represent subcellular accumulation (relative to the medium concentration) associated with the model-based characterization of uptake of (B) HEK-EV and (D) HEK-OCT1 under extracellular KCl concentrations of 5.4 mM and 140 mM, respectively.

Metformin Uptake in ER (Microsomes) and Mitochondria.

The mechanistic model proposes that metformin accumulates to high levels in the ER and mitochondria (Figs. 6 and 7). To assess the validity of the model, we determined the metformin uptake in mouse liver microsomes and mitochondria (Supplemental Fig. 1). We tried the uptake experiment in a “cytosol-like” buffer (see the Supplemental Methods). The data showed that metformin accumulated in microsomes and mitochondria. Furthermore, with the pore-forming reagent alamethicin, metformin accumulation in both organelles was dramatically reduced.

Discussion

The estimated ICS for HEK-EV and HEK-OCT1 cells was 1.21 and 1.25 μl/10⁶ cells, respectively, at 37°C, suggesting that OCT1 expression does not affect intracellular volume. These measured volumes are similar to the values estimated previously using 4/3 πr³ = cell volume, and r = 6.95 μm or 6.5 μm for HEK293 cells (Mateus et al., 2013; Zhang et al., 2015). It should be noted, however, that all measurements of intracellular volume that are derived from distribution volumes of marker compounds yield average values and do not permit identification of subpopulations of cells of different sizes within the culture. For ECS estimates, in addition to inulin, sucrose may be used as a marker (Vasquez et al., 1982). We obtained similar results for ECS estimates using either ¹⁴C-inulin or ¹⁴C-sucrose (data not shown).

In addition, we measured cell diameter using a cell sorter. Highly uniform polystyrene microspheres were used as size markers. The cell diameters were used to estimate the cell volume of HEK-EV and HEK-OCT1 cells (Supplemental Table 1). Although this method is widely used to estimate cell size, the surrogate parameters (e.g., Forward Scatter-Width [FSC-W] or Forward Scatter-Area [FSC-A]) can greatly affect measurement results (Tzur et al., 2011). Optical microscopy can also be used to assess cell diameter, but the method is biased as many cell types are not spherical. Our current procedure (Fig. 1), which combines elements of several methods published previously, provides a step-by-step measurement of drug concentration in vitro. The procedure required no special instruments such as cell sorters or mass spectrometers, so scientists can easily measure the intracellular cell volume, unbound fraction, and intracellular drug concentrations in a 1-day experiment.

Combining the cellular binding and uptake experiments allowed us to determine the unbound drug accumulation ratio (K_puu) in the HEK293 cells. Metformin accumulates to higher concentrations inside the cell through OCT1 and the favorable electrical potential difference across the plasma membrane; however, its concentrations were even higher than expected (50-fold inside the cells), potentially as a result of subcellular trapping of the ionized species.

Metformin as well as the other guanidine compounds may accumulate in the cells as a result of subcellular trapping in mitochondria because the accumulation of positively charged compounds is facilitated by the high negative potential inside mitochondria. Surprisingly, our model predicted that metformin would accumulate to high concentrations in the ER and mitochondria (Figs. 6 and 7).

We then tried metformin uptake in ER preparations (liver microsomes) and mitochondria (Supplemental Fig. 1). Because isolated organelles are different from organelles in intact cells, we tested metformin uptake in microsomes as well as mitochondria in the cytosol-like buffer (Supplemental Fig. 1). Interestingly, the metformin uptake in microsomes was ∼25% higher than in mitochondria. Because organelle behavior in intact cells is not identical to these isolated membrane fractions, the results of our studies will need to be validated further in vivo or in intact cells.

The equilibrium potential was defined by considering ionic movements through a selectively permeable membrane. Each permeable ionic species tends to move by the process of diffusion from the compartment containing a high concentration to that of the lower one. There are two requirements for establishing an electrical membrane potential: 1) ion concentration across the membrane, and 2) selective ion channels in the membrane (http://www.physiologyweb.com/). When the chemical and electrical gradients are equal in magnitude, the ion is in electrochemical equilibrium, and the membrane potential that is established at equilibrium is termed the equilibrium potential (V_eq). Thus, the equilibrium potential is calculated based on the nature of ions (i.e., valence of ion) as well as the ion concentration gradient that exists across the membrane.

V_eq = (RT/zF) * ln([X]_o/[X]_i) is known as Nernst equation, where R is the gas constant, T is the absolute temperature, F is the Faraday constant, and z is the valence of ion. This equation allows us to calculate the potential that will be established across the membrane based on the valence and concentration gradient of ions. If the ion in the equation is K⁺ and the ratio of [K⁺]_o/[K⁺]_i is 0.1, the Nernst equilibrium potential for K⁺ will be −61.5 mV (when T = °C + 273.15 K, R = 8.314 J.K⁻¹.mol⁻¹, F = 96,485 C.mol⁻¹, and z = 1). So, at an extracellular K⁺ concentration of 5.4 mM, a large electrochemical difference (inside negative) across the plasma membrane is created, which in turn triggers more metformin to accumulate in the cells. Conversely, at an extracellular K⁺ concentration of 140 mM, the membrane potential difference is minimized, which restricts metformin uptake into cells.

Interestingly, at physiologic pH of 7.4, the valences of guanidine, aminoguanidine, and metformin are all +1, but the K_puu of metformin is larger than the other two compounds. Because the pK_as of metformin, aminoguanidine, and guanidine are similar (12.4, 12.0, and 12.5 [DrugBank: (http://www.drugbank.ca]), respectively), it seems unlikely that differences in the subcellular compartment pH would result in differences in subcellular accumulation of these three guanidine compounds.

It has long been known that basic molecules become highly concentrated in organelles, such as lysosomes (Dollery, 2013) or mitochondria (Durazo et al., 2011). Furthermore, mitochondrial respiratory chain complex I is the primary target of metformin (Viollet et al., 2012). These data collectively suggest that metformin is concentrated in a subcellular compartment(s) in comparison with the other two compounds. The differences between the compounds could be due to differences in P_n/P_i for the compounds (which the model is using to drive the subcellular accumulation of metformin). Our model suggests that metformin will accumulate to high levels in ER and/or the mitochondria (depending upon the assumed value of ∆φ for the ER). Ideally, methods in intact cells rather than isolated subcellular fractions will reflect the in vivo situation more accurately. However, such procedures are fraught with technical difficulties. Our results using isolated mitochondria and microsomes (Wells, 2005) show that metformin accumulates in both organelles.

Our results indicate that OCT1 transport is saturable (K_m = 68–84 µM) and that the capacity to accentuate ionized permeability is about 30% to 50% greater in the direction of uptake over efflux (Table 1). Though the estimated K_m of metformin for OCT1 is considerably lower than the K_m values in the literature (1.47 mM; Kimura et al., 2005), this is likely attributable to the application of a mechanistic model (e.g., Fick-Nernst-Planck versus Eadie-Hofstee) to a different set of experimental conditions (time course of metformin to steady-state versus concentration dependent initial uptake). These two methods rely on different assumptions. For example, the traditional method assumes that there are negligible intracellular concentrations of metformin under initial conditions, but our mechanistic model does not make this assumption. Further application of this model framework to standard initial rates of uptake experiments (in concert with equilibrium studies) is warranted to better understand these apparent differences. There are other factors such as pH and temperature, with or without inhibitor (e.g., ions), that may have affected our K_m determinations. However, it is not possible to discern which factor caused the large difference.

Although the significance and mechanistic implications of this apparent relative directional capacity remain to be determined, the results are generally consistent with OCT1-mediated metformin uptake being a function of cell physiology (e.g., pH, electrochemical potential, subcellular volumes, transport capacity), the physiochemical properties of metformin (e.g., pKa, P_n, and P_i), and the interaction between metformin and OCT1 (e.g., K_m).

In vitro assays are frequently used to assess the transmembrane flux of drugs to predict clinical pharmacokinetic parameters (in vitro/in vivo correlations). However, to obtain reliable in vitro/in vivo correlations, it is critical to accurately determine the intracellular concentrations in vitro (Houston and Galetin, 2003). The procedure we have presented should be applicable to the measurement of ICS as well as the intracellular compound concentration of drugs and other solutes under steady-state conditions in a variety of adherent cultured cells. Our procedure, coupled with a mechanistic model, provides a novel method for predicting subcellular compartment accumulation of drugs.

Abbreviations

ECS

extracellular space

ER

endoplasmic reticulum

EV

empty vector

HBSS

Hank’s balanced salt solution

HEK

human embryonic kidney 293 cells

ICS

intracellular space

OCT1

organic cation transporter 1

RED

rapid equilibrium dialysis

TWS

total water space

Authorship Contributions

Participated in research design: Chien, Zur, Maurer, Scott, Giacomini.

Conducted experiments: Chien, Zur, Maurer, Tolsma, Jasper.

Performed data analysis: Chien, Zur, Maurer, Yee, Tolsma, Jasper, Giacomini.

Wrote or contributed to the writing of the manuscript: Chien, Zur, Maurer, Yee, Giacomini.