Functional transformation of Fourier-transform mid-infrared spectrum for improving spectral specificity by simple algorithm based on wavelet-like functions

Graphical abstract

Abstract

Herein a simple algorithm for the mathematical transformation of FTIR spectrum was developed, evaluated, and applied for description of different systems. Water, ethanol, n-butanol, n-hexanol, formic acid, acetic acid, citric acid, and water-acetic acid mixtures at different concentrations were used as model systems. We found that functional transformation of FTIR spectrum can be performed by functionally-enhanced derivative spectroscopy approach using the Function P, which is defined as P = (1 + a_j)(s)^−0.5 where a_j and s are the absorbance and the scale factor, respectively. It is also demonstrated that Function P can be used for qualitative and quantitative analysis of pure substances and mixtures. It is concluded that Function P can be understood as a wavelet transformation, which is evaluated at small times and displacements, with scaling factor given by the change of absorbance inverse.

Introduction

Infrared (IR) spectroscopy is an analytical technique, which is currently used in the study of a wide range of samples of different nature from pure substance to mixtures. However, the spectral analysis of substances, mixtures, and materials generates frequently a poorly resolved spectrum, owing to the existence of highly overlapped and hidden peaks. Spectral signal overlapping (SSO) is produced by the finite resolution of the measuring device and causes spectral line distortion. SSO can be solved by increasing the instrumental resolution when it is not associated with intrinsic physical factors of investigated material. The SSO resulting of intrinsic factors is usually observed in spectra of materials with random structures, such as glass or aqueous systems. In addition, it is strongly characterized by fewer bands and peak broadening [1]. Therefore, interpretation not only hindered by the presence of hiding signals in mixture and by a poor molecular resolution, but also, some applications are seen to be limited as a result of external or internal factors (e.g., environmental humidity, water as sub-product or water as inherent constituent).

Different steps are commonly used to study the SSO by hidden and overlapped peaks; these are: (i) to collect all available information on the system under investigation, (ii) to increase the resolution by separation of overlapped peaks into their components and (iii) to make a curve fitting of the experimental spectrum by a function, which is the sum of the individual peaks [2], [3]. Generally, it is widely accepted that the reliability analysis depends to a large extent on the degree of progress of these steps.

Among methods to evaluate the existence of overlapped and hidden peaks and determine their positions are: (i) spectral deconvolution [1], [4], [5], [6] and (ii) spectral differentiation (or derivative spectroscopy) [7], [8].

From the above, the ideal mathematical method for narrowing of an FTIR spectrum should eliminate, or at least to reduce the SSO, and this way to allow a direct estimation of the number of overlapping bands and their position, in order to achieve the separation of signals associated with different components or contributions in complex samples, and therefore, to improve the molecular specificity of spectral analysis. But also, spectral information should be keeping, or at least recovered, as far as possible, to permit the adaptability of methodology for different analytical systems. In addition, algorithms with a reduced data structure and calculation requirements ease the adaptability of computer systems applied to new technologies based on web, remote sensing or mobile operating system. In consequence, the mathematical narrowing of FTIR spectra has a significant relevance for new applications of FTIR spectroscopy as metabolomics, cellular differentiation and complex sample analysis (e.g., soil, biological fluids, biomolecules, foods and other) [9], [10], [11], [12].

Herein a simple algorithm for the mathematical transformation of FTIR spectrum was developed, evaluated, and applied for description of different systems (pure water and water-acetic acid mixtures as model systems). These systems were selected because water and molecules with carboxylic groups are important constituents of many engineered, natural, and biological systems.

Functionally-enhanced derivative spectroscopy (FEDS): Algorithm

The “functional transformation” approach to modify data produces a code, which often faster to program, more expressive, and easier to debug and maintain than a more traditional programming [13]. By functional transformation, a set of functions define how to transform a set of structured data from its original form into another form. It is expected that transforming functions are “pure functions” and therefore these are self-contained (i.e., data can be freely ordered and rearranged without entanglement or interdependencies) and stateless (i.e., that executing of the same function or specific set of functions on the same input will always result the same output data) [13], [14], [15]. Here, a strategy based on “non-pure” functions are used because a FTIR spectrum is a data set with a fixed order in function of vibrational energy. However, transformation was based on mathematical functions and logical association defined from original data [13].

In this case, finite approximation method was used to compute the derivatives of the spectra. Usually, derivative algorithm utilizes a set of signal resolution to compute differences (Δv = |v_j − v_i| where Δv is the separation between adjacent data). Eq. (1) showed the finite approximation of the first derivative for FTIR spectrum, which is plotted usually in function of v:

$$y^{\prime }=\frac{\mathit{ds}}{\mathit{dv}}\approx \frac{\mathrm{\Delta }s}{\mathrm{\Delta }v}=\frac{s(v_j)-s(v_i)}{v_j-v_i}$$ (1)

where s and Δs denote the signal for a specific values of v and the difference between adjacent signals, respectively. For another spectrum usually used in analytical sciences, the ultraviolet-visible spectrum, the plotting of data is typically described as a function of λ.

Function P is the algorithm proposed in this work (the name P is given by the word “primera” in Spanish). Basically, Function P can be understood as a functional transformation that contracts the signals of FTIR spectrum in function of critical points without changing the relative position of them. It is expected that this transformation could be useful from analytical point of view. The sequence of steps associated for the obtaining of Function P is:

Normalization of absorbance data (a) respect to the maximum absorbance (a_max)

$$a_N=\frac{a}{a_{\text{max}}}$$ (2)

Transformation of data from a_N to a_N⁻¹, and later, to carry out the determination of derivative spectrum from values of a_N⁻¹ using the finite approximation method

$$\frac{{\mathit{da}}_N{(v)}^{-1}}{\mathit{dv}}\approx \frac{\mathrm{\Delta }{a}_N{(v)}^{-1}}{\mathrm{\Delta }v}=\frac{a_N{(v_j)}^{-1}-a_N{(v_i)}^{-1}}{v_j-v_i}$$ (3)

Assuming that v_j − v_i is always a constant (this assumption is valid for almost all instrumental equipment), Eq. (3) can be written as

$$\frac{{\mathit{da}}_N{(v)}^{-1}}{\mathit{dv}}\mathrm{\Delta }v\approx a_N{(v_j)}^{-1}-a_N{(v_i)}^{-1}=p$$ (4)

where p denotes an auxiliary function in order to simplify the notation. Since Eq. (4) defines positive and negative values, and these are decreased as a result of mathematical transformation, |p| is calculated and the signals are amplified by the calculation of square root; but also, it is suggested to comeback to “more natural scale” a_N⁻¹ → a_N and to search an adequate congruence with absorbance data by 1 + a_N. By the above, Function P is defined to be

$$P=\frac{(1+a_N)}{\sqrt{|p|}}$$ (5)

Finally, Eq. (5) can be normalized using the maximum value of P (p_max), thus

$$P_N=\frac{(1+a_N)}{p_{\text{max}}\sqrt{|p|}}$$ (6)

Note that, equations have no limitations related to technique. Consequently, equations can be used to analyze spectra from other techniques such as Raman spectroscopy or ultraviolet–visible spectroscopy.

Material and methods

Reagents and equipment

Alcohols (Aldrich, St Louis, MO, USA) and carboxylic acids (Aldrich, St Louis, MO, USA) with different molecular weight were used as target samples. Alcohols were ethanol and n-butanol and n-hexanol, whereas carboxylic acids were formic acid, acetic acid and citric acid. Deionized water was used in all cases. These compounds were selected by practical importance of main functional groups associated with them: carboxylic acid (—COOH), carbonyl (—C O) and hydroxyl (—OH). All reagents were analytical grade. Samples were analyzed by FTIR spectroscopy by attenuated total reflectance (ATR-FTIR) using an IRAffinity-1S spectrophotometer from Shimadzu Co (Kyoto, Japan).

Collection of spectra

Spectra of pure compounds were collected by direct analysis of sample. For that, sample was placed in the ATR device. This procedure was performed along different days to include the variation associated to analyst in order to evaluate the reproducibility of FEDS. Spectra were collected in the mid-IR, using a SeZn crystal. After, data were filed no changes in “.txt” format in order to run the algorithm without the use of specialized software (Excel spreadsheet of Microsoft was used).

Spectra of acetic acid/water mixture were collected in order to evaluate the capacity of FEDS to improve the molecular differentiation and its potential quantitative application (mixture were performed in triplicate with 10, 20, 40, 60 and 80% of water).

Smoothing the noise by average-based spectral filter

Since derivative spectrum is strongly sensitive to noise in the original signal, smoothing the noise was decreased by the use of average-based spectral filter (ABSF) [16]. ABSF is given by

$$a_N=\frac{1}{3}{\displaystyle \sum _w^{w+2}}\left(\frac{a_w}{a_{\text{max}}}\right)=\frac{1}{3}{\displaystyle \sum _w^{w+2}}{a}_{N,w}$$ (7)

where w denotes the position of absorbance values.

As function is modified by the use of Eq. (7), the same transformation of data should be performed on function domain in order to correct small displacements respect to original spectrum (i.e., maximum points in original spectrum should be the same in the Function P).

Data analysis

Spectral comparison

Data were transformed by the use of Function P and compared with original spectrum. In order to evaluate the capacity to differentiate two substances, from pure spectra and mixture spectra, the comparison of spectra was performed using the Pearson correlation coefficient (r) as similarity index [17]. For that, signal values at each v in two spectra were two-dimensionally plotted to describe the similarity by numerical values. Thus, if r is closer to 1, then a greater similarity is observed. This comparison was performed with normalized spectra using as variable the normalized signal intensity in function of v later to the use of ABSF.

Analysis of spectral signal overlapping (SSO)

In order to show the potential application of FEDS in the analysis of spectral signal overlapping, Gaussian approach was used [18]. This is given by

$$f(a_j)=\frac{A}{\sigma \sqrt{2\pi }}\exp \left(\frac{-{(a_j-a_{\text{max}})}^2}{{\sigma }^2}\right)$$ (8)

where σ and a_max are parameters analogous to standard deviation and average value for Gauss distribution, and A is the scaling factor.

In order to show the FEDS capacity for the deconvolution of overlapped spectral signals, acetic acid spectrum was selected and analyzed in the region between 1100 cm⁻¹ and 1400 cm⁻¹ (for acetic acid, this region is seen to be particularly overlapped and different vibrations associated with C—O bonds appear in this region). Data corresponding to target region, in triplicate, were averaged and algorithm ABSF was used to eliminate the noise. FEDS-FTIR and derivative-FEDS spectra were determined in order to identify the parameters associated to Eq. (10).

Illustration of quantitative applications

In order to exemplified the potential use of FEDS for quantitative applications, the determination of composition of a binary mixture water:acetic acid was analyzed by the making of analytical calibration fit. Correlation was analyzed using absorbance signals in the original spectrum and modified spectrum and compared by parametric statistics. In addition, capacity of FEDS to ease the study the hydrogen bond interaction was evaluated; thus, water-acrylic acid mixture was used as model system.

To study dimerization of acetic acid, the following dimerization reaction is assumed 2CH₃COOH CH₃COOH⋯HOOCCH₃; where “⋯” denotes the hydrogen bond formation [19]. Thus, dimerization constant (K_D) can be easily calculated by

$$K_D=\frac{[\text{dimer}]}{{[\text{monomer}]}^2}=\frac{x}{{(C_0-2x)}^2}$$ (9)

where x is the amount dimerized acetic acid and C₀ is the acetic acid initial concentration, and [dimer] and [monomer] are the concentrations are dimer and monomer at equilibrium, respectively. From infrared data, x can be easily calculated by

$$x=\frac{a_2{C}_0}{a_1+2a_2}$$ (10)

where a₁ and a₂ are the absorbance values associated to monomer and dimer, respectively [19].

Results and discussion

Model comparison with Gaussian functions

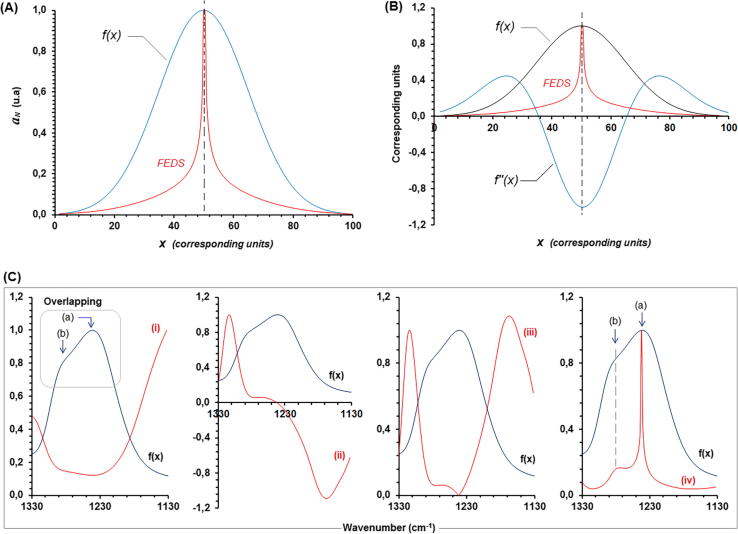
Fig. 1 had shown different comparison of effect to apply the functional transform on typical Gaussian function. In the first case, Fig. 1A, the effect of FEDS on Gaussian curve is shown, it can be seen that the graph shape is contracted near of mean point. In consequence, for FTIR spectrum the maximum absorption is not affected. Fig. 1B had shown the comparison with transformation based on the second derivative. It can be seen that minimum value in the derivative spectrum is corresponded with maximum value in the FEDS transformation. Whereas second derivative method permits the identifying of inflexion points of original function, the complexity of spectrum is increased by derivative method being an important difference compared with FEDD transformation. So, for a simple Gaussian function, with only one maximum point, a function with two maximum and one negative minimum value is obtained by second derivative method. However, by FEDS transformation, the complexity of resulting spectrum is increased only when overlapped signals are evidenced.

Fig. 1.

(A) Illustration of effect of FEDS transformation on Gaussian function. (B) Comparison of second derivative transformation and FEDS transformation for a Gaussian function and (C) Illustration step-to-step of effect of FEDS transformation on overlapped signals.

On the other hand, Fig. 1C had shown the effect of FEDS transformation illustrating the main steps. In the first plot (from left to right) can be seen an example of overlapping. Note that the point identified to be b is not associated with a change of concavity of function as wavenumber is increased to achieve the point identified to be b; therefore, second derivative transformation cannot be used to evaluate the overlapping between these adjacent points. In addition, it can be seen that the first operational change is related with change the maximum absorbance point by a minimum absorbance point. In the second plot (ii), since minimum absorbance point is associated with concavity change, this point is related with the value of zero. However, it is important to note that transformation is highly sensitive and in consequence the value associated with b is differentiated. The third plot shows that differentiation of point is increase for finally to be amplified in (iv).

From Fig. 1C we can also see the sequence of plots named to be (i), (ii), (iii) and (iv) (from left to right). Thus, sequential transformation can be visualized step-by-step:

• •From f(x) to (i): It is calculated the inverse function of f(x) which was previously normalized using a_max as normalization criterium.
• •From (i) to (ii): Derivative spectrum of normalized inverse function is obtained by the use of Eq. (4). Clearly, a_max corresponds to zero.
• •From (ii) to (iii): The transformation based on the use of equation 4 is modified by the use of by Eq. (5). In this case, a_max is transformed in the minimum value, but also, lower values of absorbance in the original spectrum are increased.
• •From (iii) to (iv): The use of mathematical operator 1/x^0.5 where x is defined to be any function, lower data are increased and larger data are decreased permitting to obtain the end transformation of original spectrum. Finally, by functional transformation, data are compared and adjusted to be congruent with the a_max.

Spectral comparison

FEDS-FTIR spectrum for water

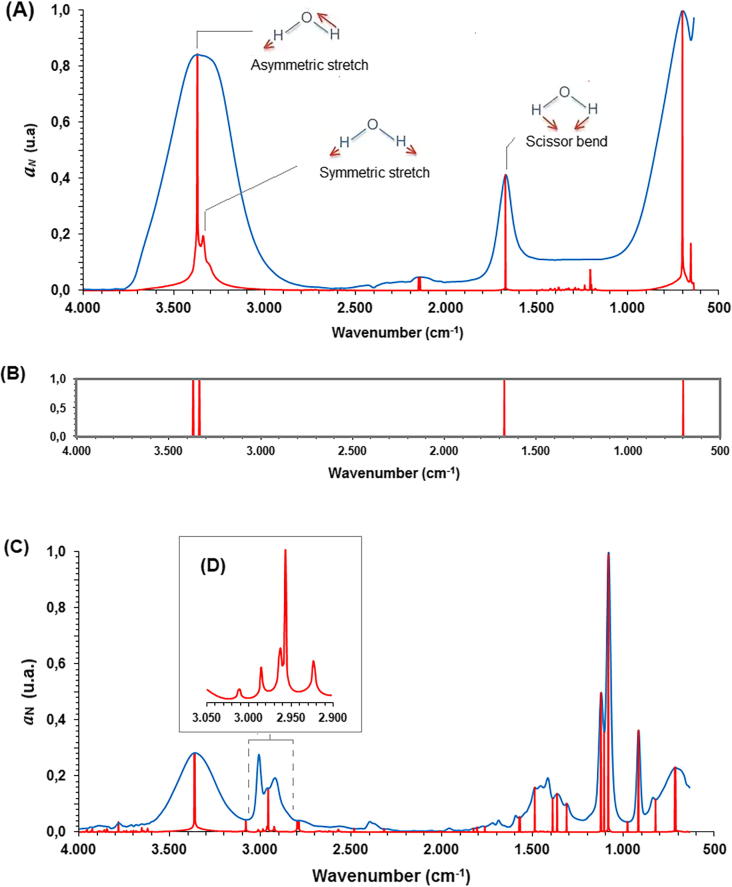
Comparison of original and modified FTIR spectra (i.e., FTIR and FEDS-FTIR) for water was shown in Fig. 2A. Water was selected as testing substance because it is very important for many processes and, in consequence, its quality, purity, presence or absence is continuously monitored at different systems. It can be seen that modified spectrum shows the same signals associated to water molecule FTIR spectrum (i.e., ∼700, ∼1670 and ∼3357 cm⁻¹). But also, new signals can be identified, thus, signals at 1200 and 3340 cm⁻¹ cannot be evidenced from original spectrum. However, signal at 1200 cm⁻¹ in the FEDS-FTIR spectrum is the result of a small change in the absorbance values between 1100 and 1400 cm⁻¹ and is not directly associated to molecular vibration phenomena (the above was verified by modification of data in this region, by this procedure was seen that small values associated to relative minimum and maximum points are transformed in signals with a relatively high intensity; however, to offset this effect, factor 1 + a_N was introduced in Eq. (5)).

Fig. 2.

FTIR and FEDS-FTIR spectra for water (A) and line plot from FEDS-FTIR spectra (B), FTIR and FEDS-FRIT spectra for ethanol (C) and FEDS-FTIR in the region 2900–3050 cm⁻¹ (D).

For water, at FTIR spectrum, vibration of O—H bonds around 2800–3600 cm⁻¹ is the most important absorption region because usually this band overlaps other absorption signals of important functional groups in mixtures or hydrated systems. As it was previously indicated, in this region, two main vibrations can be visualized from FEDS-FTIR spectrum (Fig. 2A). This is congruent with vibrational studies of water molecules [20], [21]. Thus, two vibrations are expected in the regions between 2800 and 3600 cm⁻¹, the first one is associated with symmetric stretch whereas the second one is associated to asymmetric stretch [20], [21]. On the other hand, signal at ∼1670 cm⁻¹ is associated with scissors bend and ∼700 with characteristic vibrations (fingerprint-zone vibrations). In addition, it’s clear that one of the main characteristics of the water spectrum is its simplicity. The presence of only four relevant signals in the FEDS-FTIR spectrum means that the presence of any strange organic substance can be easily evaluated. On the contrary, in the FTIR spectrum, the vibration band of O—H can overlap many signals in a wide range of wavenumbers, being most important the overlap when concentration of exogenous substance is very low.

Reproducibility of signals for water molecules was verified by spectra collected at the same experimental conditions, in different days, by different analyst, different de-ionized water samples and at different values of pH. From the information obtained, Pearson correlation coefficients are calculated and summarized in Table 1. Though Pearson correlation coefficient can be used as a quantitative descriptor of spectral similarity, an erratic behavior is evidenced from respective plots. On the other hand, from Pearson coefficient for FEDS-FTIR spectra, a poor correlation was seen for replicates at the same conditions. The above can be explained considering that FEDS-FTIR spectrum is associated to changes of absorbance inverse instead of absorbance values. Similar results were observed when derivative FTIR spectra were correlated by Pearson coefficient (Table 1). In consequence, in order to ease the spectral comparison of FEDS-FTIR spectra, a line plot or absorption pattern is suggested and this can be made considering only the main signals, which can be selected by comparison with FTIR spectrum (Fig. 2B). In consequence, at standard conditions, absorption bands defined in a range of v can be associated with absorption lines defined by a single value, and therefore, evaluation of similarity can be easily carried out.

Table 1.

Pearson correlation coefficients for FTIR, FEDS-FTIR and derivative FTIR spectra of water at different values of pH: replicates of coefficient (r₁, r₂ and r₃), mean (r_prom), standard deviation (σ) and coefficient of variation (CV).

pH	Parameter	FTIR	FEDS-FTIR	Derivative FTIR
3.0	r1	0.9759	0.0702	0.3843
	r2	0.9168	0.1978	0.0539
	r3	0.8224	0.0979	0.0115
	rprom ± σ	0.91 ± 0.07	0.12 ± 0.07	0.15 ± 0.20
	CV	8.6	55.0	136.2
6.0	r1	0.7426	0.4524	0.2314
	r2	0.7268	0.3755	0.5746
	r3	0.9927	0.3695	0.1502
	rprom ± σ	0.82 ± 0.15	0.40 ± 0.05	0.35 ± 0.23
	CV	18.2	11.6	78.7
10.0	r1	0.9787	0.2728	0.8805
	r2	0.9631	0.2516	0.2965
	r3	0.9933	0.3494	0.2031
	rprom ± σ	0.98 ± 0.02	0.29 ± 0.05	0.46 ± 0.37
	CV	1.5	17.7	79.8

FEDS-FTIR spectra of alcohols and organic acids

As an illustration, FTIR and FEDS-FTIR for ethanol are shown in Fig. 2C; in addition, it can be seen that a better resolution can be obtained when a short wavelength region is analyzed (Fig. 2D). It can be seen that as spectral complexity of substance increases, the complexity of FEDS-FTIR spectrum is greater. However, it is important to note that the real application of functional transformation is achieved only if some specific signal associated to molecular structure can be identified and differentiate from a mixture containing the target molecule.

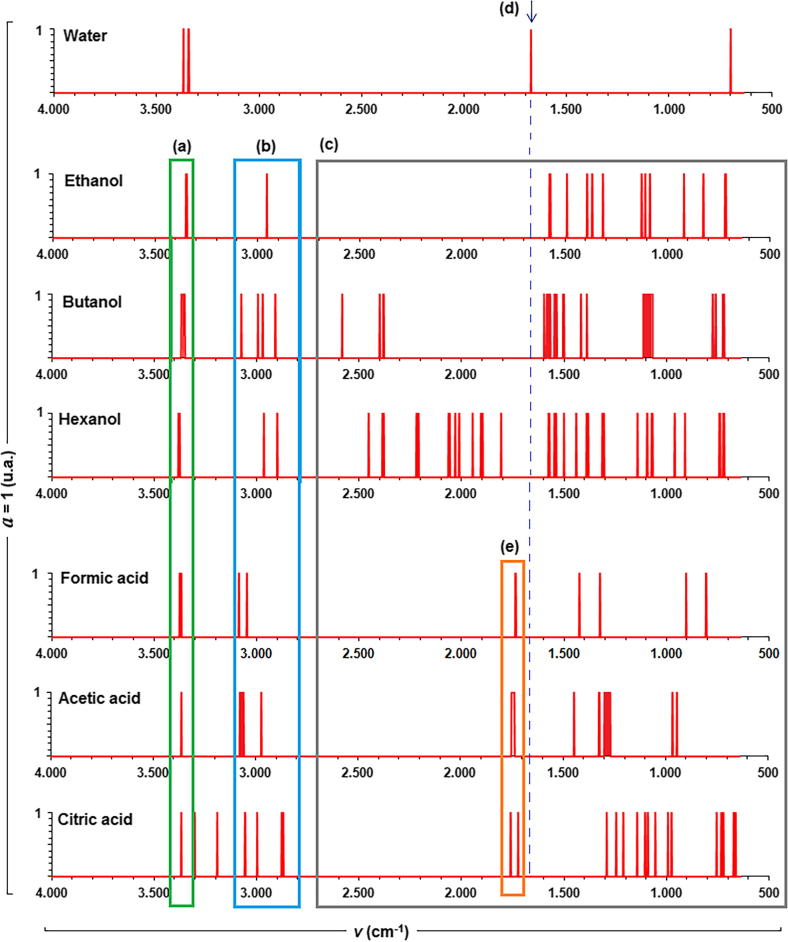
Plot lines for water, alcohols, and carboxylic acid are shown in Fig. 3; it can be seen that: signals associated to O-H vibrations can be hardly differentiated from FTIR spectrum. From FEDS-FTIR, molecular differentiation can be achieved by small displacement of maximum absorption associated to —OH respect to water signals (Fig. 3a). However, signals associated to —CH₂ and —CH₃ groups are seen to show a higher difficulty (Fig. 3b). Zone related with fingerprint region shows different signals that can be used to achieve a proper differentiation (Fig. 3c), however, for identification of specific signals and their respective comparison suggest that a small region of visualization was used. It should be noted that water can be differenced from other test molecules by the signal at ∼1670 cm⁻¹ from FEDS-ATR spectrum (Fig. 3d and e).

Fig. 3.

Line plots for water, ethanol, butanol, hexanol, formic acid, acetic acid and citric acid. Comparison of vibration bands associated to hydroxyl groups (a), methyl and methylene groups (b), other vibrations associated to fingerprints (c), scissor vibration for water (d) and vibration of carbonyl groups (e).

Analysis of spectral signal overlapping (SSO)

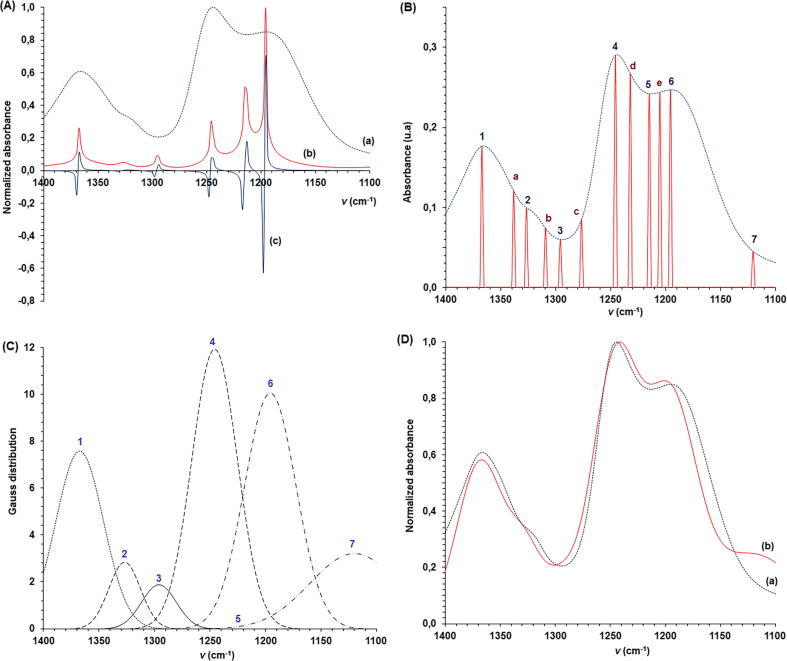
A comparison between FTIR, FEDS-FTIR and derivative-FEDS was shown in Fig. 4A. It can be seen that application of FEDS at a smaller spectral region eases the assignation of signals and identifications of possible overlaps. On the other hand, derivative-FEDS is useful for the computing and selecting of data. The effect of using the selection algorithm can be seen in Fig. 4B. Thus, critic points, from a point of view of function theory, were identified by numbers (from 1 to 7) whereas inflection points were denoted by letters.

Fig. 4.

Sequence to transformation for the analysis of spectral signal overlapping into the FTIR spectrum: (A) FTIR spectrum (a), FEDS-FTIR spectrum (b) and derivative FEDS-FTIR spectrum (c); (B) comparison of FTIR spectrum and derivative FEDS-FTIR modified by the third conditional transformation, 1, 2, 3, 4, 5, 6, and 7 denote the critic points whereas a, b, c, d, and e denote the inflexion points considered to define sigma; (C) splitting of the spectral signals by Gaussian modeling and (D) comparison of total Gaussian function calculated by the additive contributions of partial Gaussian functions (b) and FTIR spectrum (a).

On the other hand, the different contribution obtained using Gauss distribution model are shown in Fig. 4C. However, in order to determine if there is an adequate congruence between Gaussian contributions and FTIR spectrum Pearson correlation coefficient was used to compare the FTIR spectrum and total Gaussian FTIR spectrum (this was calculated by the sum of all Gaussian contributions identified). Correlation coefficient obtained was 0.9365 (FTIR and Gaussian spectra are compared in Fig. 5D). In general, it can be concluded that FEDS was useful for determination of maximum number of Gaussian contributions required to unfold the different signals studied in FTIR spectrum.

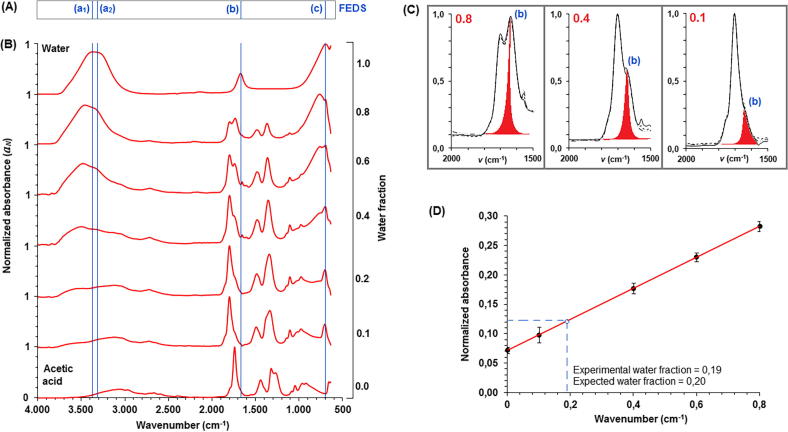
Fig. 5.

(A) Line FEDS-FTIR plot for water: a₁, a₂, b, and c denote the vibration signals for water molecule; (B) normalized FTIR spectra for water, acetic acid and water-acetic acid at different proportions; (C) identification of water scissor vibration, it was identified as “b” in Fig. 5A, by FEDS for different water-acetic acid mixtures (0.8, 0.4, and 0.1 v/v of water); and (D) calibration fit used to determine the water concentration in a water-acetic acid mixture.

Illustration of quantitative applications

Determination of water content

Line plot based on FEDS-FTIR for water was shown in Fig. 5A and contrasted with FTIR spectra of water-acetic acid mixtures at different compositions (Fig. 5B). A displacement of signals associated to water can be identified in the mixtures, but also, a displacement of vibration at ∼1750 cm⁻¹ associated to carbonyl group on acetic acid is clearly identified. On the other hand, Fig. 5C illustrated the change in the vibrations between 1500 and 2000 cm⁻¹. These signals are associated to vibrations of water molecule and carbonyl group of acetic acid, but the correct assignment of groups can be difficult because of the obvious overlap. So far, FEDS is useful for the discrimination on signal associated scissor vibration of water molecule and carbonyl group vibration on acetic acid. It can be evidenced that signal denoted as “b” in Fig. 5A appears to the right of vibration of carbonyl group and, in consequence, it can be easily identified, even if they are overlapping. Thus, FEDS can be useful for signal assignation because a small change in the FTIR spectrum can be easily enhanced in FEDS-FTIR. Since it was possible the association of specific values of wavenumbers in the spectra with one component of the mixture, calibration fit was performed and was shown in Fig. 5D. It is evident that an incorrect assignation of signals should produce a non-linear behavior. According to Beer-Lambert law, concentration of water in the mixture should be associated to linear increase in absorbance.

Hydrogen bond interaction and dimerization of acetic acid in water

Dimerization of acetic acid has been widely evaluated [19], [22]. Usually the dimerization phenomenon is easily described in dissolution of acetic acid in aprotic polar solvents; and it can be understood as the formation of molecular association by hydrogen bonds between acid proton on carboxylic acid group and electronegative oxygen on carbonyl group (Fig. 6A). In water acetic acid dimerization also is produced, but the overlapping and displacement of signals makes it difficult to analyze in aqueous solution. The advance of FEDS respect to derivative spectroscopy is that derivative is less sensible to small changes, and in some cases, signals cannot be easily differentiated from noise; but also, as a result of overlapping, signals could not be associated to relative maximum and in consequence these not could be identified. An illustration of the above was shown in Fig. 6B; it can be seen in the illustration (i) that a₁ > a₂ > a₃ (left) and their respective values of v are v₁ > v₂ > v₃, in consequence, a₁ and a₂ are relative maximum whereas a₃ is a relative minimum, in this case, a₁ and a₂ can be associated to vibrational signals and identified easily by derivative spectroscopy. However, the illustration (ii) had shown that a₁ > a₃ > a₂ (right) being v₁ > v₂ > v₃ their respective values of v, and therefore, only a relative maximum can be identified.

Fig. 6.

(A) Chemical equation for dimerization of acetic acid; (B) Graphical representation of limitations of derivative FTIR spectroscopy to unfold overlapped signals (a₁, a₂ and a₃ are critic points: (i) a₁ and a₂ can be identified by derivative FTIR spectroscopy whereas into (ii) a₂ cannot be identified as a critic points because a₁ > a₃ > a₂; (C) illustration of effect of capacity of FEDS technique to separate the overlapped signals and ease the identification of no-evident signals into FTIR spectra of water, acetic acid and their mixtures.

Monomer is associated to signal of carbonyl group at ∼1680 cm⁻¹ whereas dimer is associated to the signal at low frequencies, ∼1770 cm⁻¹, in the vicinity of monomer signal [22]. FTIR and FEDS-FTIR spectra, in the region between ∼1650 and ∼1800 cm⁻¹, are shown in Fig. 6C. From FTIR spectra we can that the overlapping is more significant as acid concentration increases and the spectral study of hydrogen bonds associated to dimerization was not possible. However, from FEDS-FTIR spectra, signals can be easily identified. Results of FEDS analysis and determination of dimerization constant are summarized in the Table 2; the decrease of values of K_D as acid concentration is increased can be explained by the other association forms different to cyclic dimer. Average value for K_D was 0.042 ± 0.029 whereas reported value is 0.033 [22].

Table 2.

Determination of dimerization constant (K_D), monomer concentration ([mnomer]) and dimer concentration ([dimer]) from FEDS-FTIR (C₀, a₁ and a₂ are initial concentration of acetic acid and normalized absorbances at 1680 and 1770 cm⁻¹, respectively).

C0	a1	a2	[monomer]	[dimer]	KD
(mol/L)	(u.a.)	(u.a.)	(mol/L)	(mol/L)	(mol/L)
2.50	0.866	0.193	2.419	0.539	0.092
7.00	0.989	0.197	5.002	0.996	0.040
10.49	0.999	0.221	7.273	1.609	0.030
13.99	1.000	0.236	9.503	2.243	0.025
15.74	1.000	0.223	10.883	2.427	0.020

u.a.: absorbance units.

Wavelet interpretation

Mathematical transformations are applied to signals in order to obtain further information to those initially available (e.g., FTIR spectrum is transformed to FEDS by a mathematical function which is applied to data set). However, it can be interesting the understanding of why Function P becomes a proper transformation from mathematical concepts. Thus, the connection point between Function P and wavelet concept is analyzed because both functions show the same mathematical structure in their generalized expressions. First, change of signals can be defined to be a time-domain function and frequency-domain function. A typical example of frequency-domain function is FTIR spectrum; and the change though the time of FTIR spectrum corresponds to time-frequency domain function. Thus, whereas Fourier transform is used to analyze the change in the signal through frequency domain, wavelet is used to analyze the change by time-frequency domain.

Wavelet is a concept described in pure mathematical which has been applied to digital signal treatment. Wavelets are generated from a single basic wavelet (“mother wavelet”: Y(t) where t is the time) and is defined by the following general expression

$$Y(t)=\frac{1}{\sqrt{|s|}}\mathrm{\Psi }\left(\frac{t-\theta }{s}\right)$$ (11)

where s and θ are scale factor and translation factor, respectively. Basis function (Ψ) is a difference between the wavelet transform and other transforms (e.g., Fourier transform). In addition, wavelet must be square-integrable function, Fourier transform of Ψ must be zero at the zero frequency and average value of the wavelet in the time domain must be zero; therefore, it must be oscillatory.

If Ψ = 1 + a_j then Eq. (12) can be written to be P(t) = Y(t); however, Ψ must be a function of w = (t − θ)/s. Note that, it is possible to define a wavelet set from mother wavelet to satisfy the above condition,

$$Y(t)=\frac{1}{\sqrt{|s|}}{\displaystyle \sum _{t=0}^t}\left(\frac{a_j^m}{1+t^{t-1}}\right)\text{where}m=\left(\frac{t+w}{1+w}\right)t$$ (12)

Eq. (12) is a valid function for θ ≪ 1 (i.e., small displacements of the function at the time), and in this situation, w ≈ t/s. A small time can be defined to be t = 1; however, as time increases the function rapidly decreases as a result of factor 1/(1 + t^t−1). For instance, for times of 1, 2, 3, and 4 the obtained factor were 1/2, 1/3, 1/10 and 1/65, respectively; whereas for time lower than 1 (for example, 0.5, 0.05, and 0.005) the obtained factors were 0.414, 0.055, and 0.005, respectively. In this order of ideas, Function P can be defined as a wavelet evaluated at small times and displacements, with scaling factor given by the change of absorbance inverse (i.e., s = (a_j−1 − a_j)/a_ja_j−1).

Scaling factor for Function P can be understood when the fact that data should oscillate throughout its domain is considered. Since FTIR does not meet the above requirement, derivative spectrum can be used to produce the data oscillation. In addition, for s < 1, wavelet is decreased whereas, for s > 1, wavelet is increased; in consequence, as normalized absorbance is always lower than 1, the transformation of the absorbances by its inverse produces an expansion of wavelet.

Conclusions

Transformation of FTIR spectrum can be performed by FEDS approach based on the named Function P. FEDS can be used for qualitative and quantitative analysis of pure substances and mixtures. In addition, FEDS and derivative-FEDS showed to be useful to visualize and compare the analysis of FTIR spectrum of complex systems, to analyze the spectral signal overlapping and to ease the quantitative analysis from specific signals. In addition, line plot is suggested for the comparison of FEDS-FTIR spectra instead of Pearson coefficient. Finally, it is concluded that Function P can be understood to be a wavelet transformation which is evaluated at small times and displacements, with scaling factor given by the change of absorbance inverse (i.e., s = (a_j−1– a_j)/a_ja_j−1).

Conflict of interest

The authors have declared no conflict of interest.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.