Proper inference from Simon’s two-stage designs

SUMMARY

Simon’s two-stage designs are very popular for phase II clinical trials. A literature review revealed that the inference procedures used with Simon’s designs almost always ignore the actual sampling plan used. Reported P values, point estimates and confidence intervals for the response rate are not usually adjusted for the design’s adaptiveness. In addition, we found that the actual sample size for the second stage is often different from that planned. We present here a method for inferences using both the planned and the actual sample sizes. The conventional and the preferred inference procedures usually yield similar P values and confidence intervals for the response rate. The conventional inference, however, may contradict the result of the corresponding hypothesis testing.

1. INTRODUCTION

Two-stage designs are commonly used in phase II clinical trials and especially in cancer clinical trials. Simon [1] has proposed two criteria, minimax and optimal, for selecting sample sizes and critical values for these two-stage designs. The maximum sample size and the expected sample size under H₀ are minimized in the minimax and optimal designs, respectively. Simon’s two-stage designs have been gaining influence; his 1989 paper [1] has been cited more than 700 times. Since it was cited twice in 1991, the number of citations per year has increased steadily, to 50 times in 2001 and over 100 times in each of 2005 and 2006.

There have been a number of extensions proposed for Simon’s designs. These include consideration of toxicity [2, 3, 4, 5], inclusion of more than one treatment [6, 7, 8, 9], addition of the third stage [10], consideration of partial and complete responses [11, 12], and consideration of multiple strata [13]. Banerjee and Tsiatis [14] proposed to extend a Simon’s design by allowing different stage 2 sample sizes for different values of X₁. Their more flexible designs have advantages over the original Simon’s designs with respect to the expected sample sizes under the null and alternative hypotheses. Others have considered optimality in 2 stage designs and proposed to improve on Simon’s designs [15, 16, 17].

Due to the adaptive nature of the design, the inference procedures for Simon’s designs are not straightforward. A maximum likelihood estimator of the response rate, number of positive responses / total number of patients, is biased [18, 19]. Confidence interval and P value should not be computed as if the data were obtained in a single stage. There are relatively few papers that discuss the inference procedures used with two-stage designs in phase II clinical trials. Whitehead [18] has studied the bias of the maximum likelihood estimator and has proposed a bias-reduced estimator that was further studied by Chang et al [19]. Jung and Kim [20] have provided a comprehensive study of estimators from a multi-stage design. For general group sequential designs, the inference procedures have been considered by Fairbanks and Madsen [21], Tsiatis, Rosner and Mehta [22], Lin, Wei and DeMets [23], Yi and Yu [24], Fan and DeMets [25], among others.

It could be argued that these two-stage designs are primarily for decision making and that estimation is a secondary objective of a phase II clinical trial. It is preferable, however, to compute a P value, a confidence interval and an estimate of the response rate at the termination of the trial. The latter two are especially useful when the design of a new phase III clinical trial is based on the findings of a phase II trial. As a matter of fact, our literature review revealed that the majority of studies using Simon’s two-stage designs report an estimate of the response rate with a confidence interval.

Our literature review also revealed that the actual sample size of stage 2 is often different from the planned stage 2 sample size. It is not straightforward to conduct a hypothesis testing when the stage 2 sample size is changed in a Simon’s design. We will further extend the inference procedures to handle the cases in which the actual sample size is different from the one planned.

In Section 2, a brief introduction of Simon’s designs will be given. We will apply the inference procedures developed for multi-stage group sequential designs to Simon’s designs in Section 3. Then in Section 4, we will present general inference procedures for Simon’s designs when stage 2 sample size is different from the one planned.

We have developed and made widely available a software program that makes inference from a Simon’s design based on the method discussed in this paper.

2. SIMON’S DESIGNS

In a study with a Simon’s design, the null hypothesis is concerned with a response rate, π. Without loss of generality we assume that a higher value of π is more favorable and write H₀ : π ≤ π₀. The power of the study is set at some π₁ that is greater than π₀.

A Simon’s design is usually indexed by four numbers that represent stage 1 sample size (n₁), stage 1 critical value (r₁), final sample size (n_t), and final critical value (r_t). In stage 1, a sample of size n₁ is taken. Let X₁ be the number of successes in stage 1. If X₁ ≤ r₁, the trial is stopped for futility; otherwise, an additional sample is taken until total of n_t observations are obtained. Let X₂ be the number of successes in stage 2, and let X_t = X₁ + X₂. If X_t ≤ r_t, futility is concluded; otherwise efficacy is concluded by rejecting H₀.

We depart from convention and use R₁ ≡ r₁ + 1 and R_t ≡ r_t + 1 to denote the critical values of a Simon’s design. This new notation is a simpler one in certain extensions that we will consider in later sections. It will also be necessary to consider the stage 2 critical value, and we will use the notation, R₂(x₁), which is a function of X₁ and can be written simply as R₂(x₁) ≡ R_t − x₁ for R₁ ≤ X₁ < R_t, and 0 for R_t ≤ X₁ in a usual Simon’s design.

To present the power function of a Simon’s design, we first introduce the conditional power of stage 2 given the stage 1 result, X₁ = x₁. It is P_π[X₂ ≥ R₂(x₁)] for X₁ ≥ R₁, where X₂ ~ Binomial(n₂, π). Throughout the paper, the notation P_π[E] represents the probability of the event E at a specific π. We use the notation A(x₁, π) to denote the conditional power, which can be written as:

$$A(x_1,\pi )=\sum _{x_2=R_2(x_1)}^{n_2}\left(\begin{array}{c}\hfill n_2\hfill \\ \hfill x_2\hfill \end{array}\right){\pi }^{x_2}{(1-\pi )}^{(n_2-x_2)}.$$ (1)

If the trial is terminated in stage 1 because the results indicated futility (X₁ < R₁), we let A(x₁, π) = 0. We note that the conditional power at π = π₀ is the conditional type I error rate.

The power function of a Simon’s design is

$$\beta (\pi )=P_{\pi }[\text{Reject }{H}_0]=\sum _{x_1=R_1}^{n_1}{P}_{\pi }[X_1=x_1]A(x_1,\pi ).$$ (2)

A design, (n₁, R₁, n_t, R_t), is usually chosen so that β(π₀) ≤ α and β(π₁) ≥ 1 − β.

3. INFERENCE PROCEDURES

Inference procedures for multi-stage designs have been discussed by many [21, 22, 23, 24, 25, 26], and we will review them in this section and extend them in the subsequent section.

3.1. P value

Suppose that the number of successes is X₁ = x₁ ≥ R₁ and X₂ = x₂ for stage 1 and 2, respectively. It is a common practice to compute a P value at the end of the stage 2, incorrectly assuming that the data are collected in a single stage. Let us call this a conventional P value and denote it by p_c. We can write

$$p_c=\sum _{x_1=0}^{n_1}{P}_{{\pi }_0}[X_1=x_1]P_{{\pi }_0}[X_2\ge x_t-x_1].$$ (3)

The summand of the right hand side of the above equation include impossible sample paths in which X₁ < R₁ and X₂ = X_t − X₁. A preferred P value may be

$$p_p=\sum _{x_1=R_1}^{n_1}{P}_{{\pi }_0}[X_1=x_1]P_{{\pi }_0}[X_2\ge x_t-x_1],$$ (4)

which does not include these impossible sample paths. Clearly, p_c ≥ p_p.

The P value is the probability of obtaining the result that is at least as extreme as the observed one under the null hypothesis. In (3) and (4), we are implicitly assuming that the larger value of X_t, regardless of X₁ and X₂, is more extreme. When X₁ < R₁ and futility is concluded in stage 1, the P value is P_π0 [X₁ ≥ x₁]. Because we use the total number of successes to order the possible outcomes in (4), it is applicable only if n₂ is a constant for all X₁. In certain extensions of Simon’s design in which stage 2 sample size is not a constant in X₁ (e.g., Banerjee and Tsiatis [14]), the P value in (4) is not applicable. We will also show in Section 4 that, when the realized stage 2 sample size is different from the one planned in a simple design with a constant n₂, (4) may not be applicable.

3.2. Confidence Interval

A 95% two-sided confidence interval is reported in many of the papers that we have studied. It is not wrong to report a 95% two-sided confidence interval. If, however, it is desirable that a confidence interval and hypothesis testing be consistent, because Simon’s design is used in one-sided hypothesis testing, then a 95% one-sided confidence interval of the form, (π_L, 1] for α = .05 is required. The method described below can be used to form a more common two-sided confidence interval of the form, (π_L, π_U). We will use a 90% two-sided confidence interval to allow consistency with the one-sided hypothesis testing at α = .05. In other words, we can interpret this confidence interval in a usual way: the two statements, “π₀ is not contained in a confidence interval” and “H₀ is rejected” are equivalent.

We can compute a P value for testing $H_0:\pi \le {\pi }_0^{\prime }$ using (4) for any ${\pi }_0^{\prime }$. A 90% two-sided confidence interval that we use is a collection of ${\pi }_0^{\prime }$ such that the corresponding P value is within [.05, .95]. This is a simple application of the method based on “stage-wise ordering” of group sequential methodology, and is a methodology that produces an interval [26, 27].

3.3. Point Estimate of the Response Rate

The maximum likelihood estimator of the response rate, π̂ = x_t/n_t if x₁ ≥ R₁ or π̂ = x₁/n₁ if x₁ < R₁, underestimates the true response rate in Simon’s designs that we are considering. When x₁/n₁ is larger than π, the trial tends to proceed to stage 2, and the upward bias tends to be corrected. On contrary, when x₁/n₁ is smaller than π, the trial tends to be terminated without a chance for the downward bias to be corrected.

A bias reduced estimator due to Whitehead [18], denoted here by π̂_w, is the solution to E_π̂w[π̂] = π̂ [19]. The characteristics of this and other estimators have been studied previously [20, 28]. Generally, it is more favorable than the maximum likelihood estimator in terms of the mean square errors.

3.4. Example

We will consider as an example a design (n₁ = 10, R₁ = 2, n_t = 29, R_t = 6) that is the minimax design for π₀ = .1, π₁ = .3 with α = .05, β = .2. Suppose that we observe X₁ = 2 and X_t = 6. This sample path leads to rejection of H₀ in stage 2. We can compute for this example, p_c = .064 and p_p = .047 using (3) and (4). A 90% confidence interval is (.094, .368) with (3) and (.102, .401) with (4). The conventional P value (3) yields a P value that is greater than α and a confidence interval that contains π₀ although H₀ is rejected. And π̂ = .207, π̂_w = .243.

4. EXTENDING OR SHORTENING THE STUDY

Our literature review reveals that the actual sample size is often different from the planned sample size in many studies that use a Simon’s design. Depending on the predicted and actual accrual rates and drop-out rates, the actual sample size may be larger or smaller.

Extending or shortening a study is simple in a single-stage design since it is easy to recalculate a new critical value or the correct P value and make the correct decision regarding H₀. With a Simon’s two-stage design, however, extending or shortening a study is not as straightforward. A common practice to conduct a hypothesis testing is to compute the conventional P value that is based on incorrect distributional assumption, and use it to make a decision. Equivalently, the critical value is re-computed as if the new sample size were originally planned in a single stage design. Unlike the simple two-stage designs with no sample size change, where the preferred P value in (4) is always smaller than or equal to the conventional one in (3), it is now possible to make an incorrect decision and inflate the type I error rate. We will discuss in this section how to calculate the new critical value and how to make a new inference based on the actual sample size.

A subtle but critical issue is that the decision to use a different sample size must be made blinded to any part of the data including the stage 1 result. A legitimate situation in which a sample size is different from that planned can occur when the sample size is planned with anticipation of a certain number of uninformative drop-outs, but a different number of patients actually finish the study. On the other hand, it is not permissible to decide at the end of stage 1 (or during the stage 2) to extend the study because there are fewer positive responses than expected, or to shorten the study because there are more positive responses than expected. There may be designs that allow such adaptive changes and still protect type I error rates. In order to make a proper inference, an additional assumption is also required about the sample size that would have been used if a different number of successes were observed in stage 1 [29, 30]. We will only consider noninformative sample size change in this paper.

As a notational convention, we use a prime to indicate that the sample size has changed. For example, $n_2^{\prime }$ is the new sample size for stage 2 and $x_2^{\prime }$ is the number of successes among $n_2^{\prime }$ in stage 2.

4.1. Hypothesis Testing

We have introduced the term, conditional power, in Section 3.1 and have denoted it by A(x₁, π), which is the probability of rejecting H₀ in stage 2 given the result of stage 1. Rejecting H₀ if X₂ ≥ R₂(x₁) and rejecting H₀ if cp(x₁, x₂, n₂, π₀) ≡ P_π0 [X₂ ≥ x₂ | X₁ = x₁] ≤ A(x₁, π₀) are equivalent. We call cp(x₁, x₂, n₂, π₀) the conditional P value, which is the P value of stage 2 given the result of stage 1. The conditional P value is compared to the conditional type I error rate in decision making at termination of stage 2.

The conditional P value can be computed regardless of the sample size of the actual stage 2, and the decision to reject H₀ can be made by comparing the conditional P value and conditional type I error rate evaluated at the observed x₁. The same conclusion may be based on the new critical value, $R_2^{\prime }(x_1)$, which is defined as the largest R, such that

$$P_{{\pi }_0}[X_2^{\prime }\ge R|X_1=x_1]\le P_{{\pi }_0}[X_2\ge R_2(x_1)|X_1=x_1],$$ (5)

where $X_2^{\prime }~\mathit{\text{Binomial}}(n_2^{\prime },{\pi }_0)$. With the new critical value, $R_2^{\prime }(x_1)$, we define $A\prime (x_1,\pi )=P_{\pi }[X_2^{\prime }\ge R_2^{\prime }(x_1)|X_1=x_1]$. Because we set the new critical value so that the new conditional type I error rate is always equal to or smaller than the original conditional type I error rate, the overall unconditional type I error rate is controlled.

An alternative method of hypothesis testing may be to re-compute the critical value as if the new sample size, $n_2^{\prime }$, were planned originally. This involves a simple numerical search of the critical value that produces the type I error rate less than α given n₁, R₁ and $n_t^{\prime }$. This method only attempts to control the unconditional type I error rate even though the stage 1 has already been terminated. If we apply the same reasoning and only attempt to control the unconditional type I error rate, we could have as much conditional type I error rate at the observed X₁ = x₁ as α/P_π0 [X₁ = x₁], and 0 elsewhere. Then the result of computation of (2) at π = π₀ with A(x₁, π₀) replaced by A′(x₁, π₀) would be at most α. The type I error rate, however, is not actually controlled because we would have used different critical values if X₁ were different. In other words, this method fails to protect the conditional type I error rate, which is relevant and needs to be protected after stage 1. Thus we prefer the first method of re-computing the critical value (5) because it guarantees that the conditional type I error is protected given the stage 1 result.

When the new critical value, $R_2^{\prime }(x_1)$, is obtained from (5), the total number of positive responses, $x_1+R_2^{\prime }(x_1)$, necessary to reject H₀ may be different for different values of X₁ as the following example demonstrates.

We will consider a new design, (n₁ = 19, R₁ = 7, n_t = 39, R_t = 17), as an example. This is the minimax design for π₀ = .3, π₁ = .5 with α = .05 and β = .2. Suppose that we observe X₁ = 7 in stage 1. Then H₀ would be rejected if the stage 2 P value is smaller than the conditional type I error rate, A(7, .3) = P_π0 [X₂ ≥ 10] = .0480. Further suppose that the stage 2 sample size is increased from the planned 20 to 23. If we observe 11 successes in these 23 stage 2 observations, the conditional P value is $P_{{\pi }_0}[X_2^{\prime }\ge 11]=.0546$, and the null hypothesis should not be rejected. The critical value at X₁ = 7 with n₂ = 23 is $R_2^{\prime }(7)=12$ from (5).

In a different scenario, suppose that we observe X₁ = 10 in stage 1; the conditional type I error rate is A(10, .3) = .3920. With the new sample size, $n_2^{\prime }=23$, the critical value is $R_2^{\prime }(10)=8$ from (5). Thus in the first scenario, H₀ is rejected with 19 or more positive responses, but in the second scenario, the number of necessary positive responses is 18.

In the second scenario above, the conditional type I error rate is .3920 at X₁ = 10, and H₀ would be rejected with a stage 2 P value that is less than or equal to .3920. When compared to the usual unconditional type I error rate, α, the conditional type I error rate sometimes seems very high. It may be unintuitive that H₀ is rejected with a such a high (conditional) type I error rate. The unconditional type I error rate can be viewed in (2) as a weighted average of the conditional type I error rate. Thus, when P_π0 [X₁ = x₁] is very small for a particular x₁, the conditional type I error rate at this x₁ may be very high, and the unconditional type I error rate is still protected.

4.2. Inference When Sample Size is Changed

As shown in 4.1, even when the stage 2 sample size is changed, hypothesis testing can be conducted with the conditional P value and conditional type I error rate. These conditional quantities may not be intuitive because they can not be compared directly to the usual unconditional type I error rate, α. Together with the original motivation for computing unconditional P value, confidence interval and an estimate of π, this compels us to make unconditional inference when the stage 2 sample size is changed.

The formula for P value in (4) needs to be extended because this formula is only valid when the stage 2 sample size is not changed. The unconditional P value may be written as follows:

$$p_p=\sum _{x_1=R_1}^{n_1}{P}_{{\pi }_0}[X_1=x_1]\mathit{\text{ cp}}(x_1,x_2,n_2,{\pi }_0),$$ (6)

where cp(x₁, x₂, n₂, π₀) is the conditional P value for testing H₀ : π ≤ π₀. It is only observed at one (x₁, x₂), but it needs to be extended to the entire range of X₁ ∈ [R₁, n₁] to evaluate (6). When stage 2 sample size is constant and not changed (Section 3.1), this extension is based on X_t. When, however, stage 2 sample size is changed, we cannot extend the conditional P value based on X_t. It is demonstrated in Section 4.1 that the same value of X_t may or may not lead to rejection of H₀ depending on the sample paths. Moreover, as per the work of Banerjee and Tsiatis [14], if the planned stage 2 sample size is not constant for different values of X₁ extending the conditional P value based on X_t would not make sense.

We propose the following approach for extending cp(x₁, x₂, n₂, π) to the potential values of X₁. We find a conditional power function, A(x₁, π*), for some π* that goes through the observed conditional P value. It requires solving numerically for π* such that A(x₁, π*) = cp(x₁, x₂, n₂, π₀). This A(x₁, π*) function can be extended to the potential values of x₁ using (1) with the original n₂ and the original R₂. We propose that the sample paths that lead to the same π* have the same magnitude of evidence against H₀. In other words, it is possible to order different sample paths with different x₁ and the realized sample size for stage 2 by comparing π*. The smaller π*, the more extreme the evidence against H₀. This ordering is coherent with the hypothesis testing procedure described in 4.1; the P value based on this ordering is smaller than the type I error rate if and only if the null hypothesis is rejected. To compute the P value, we replace cp(x₁, x₂, n₂, π₀) in (6) by A(x₁, π*) so that

$$p_p=\sum _{x_1=R_1}^{n_1}{P}_{{\pi }_0}[X_1=x_1]A(x_1,{\pi }^{\ast }).$$ (7)

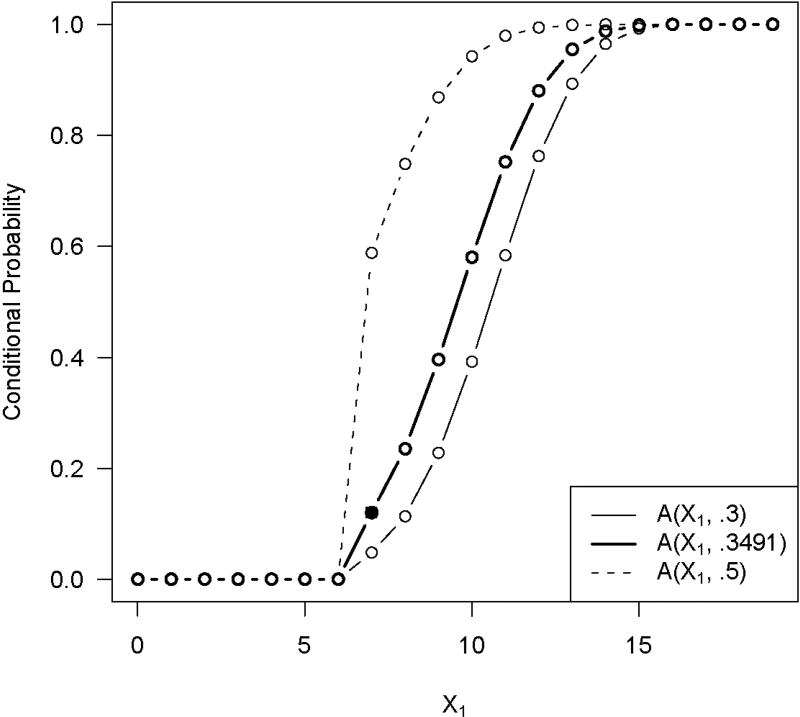
Suppose that we observe in the same example that X₁ = 7 and $X_2^{\prime }=10(n_2^{\prime }=23)$. Then the conditional P value is .1201, and H₀ is not rejected because the conditional type I error rate at X₁ = 7 is .0480. We compute to find that π* = .3491. We can then extend the conditional power to the different potential values of X₁. This is represented by the bold line, A(x₁, .3491), in Figure 1 which also shows the conditional type I error rate, A(x₁, .3), and the conditional power at the original alternative, A(x₁, .5). Finally, we find the P value using (7) to be p_p = .0828.

Figure 1.

Extension of the observed conditional P value to other x1 values based on π*. The solid line is the conditional type I error rate, and the dotted line is the conditional power under the alternative. The conditional P value is indicated by a solid circle. The bold line is the conditional power function that goes through this point.

A confidence interval and a reasonable point estimate of π can be obtained by “inverting the hypothesis testing.” A 90% confidence interval is a collection of ${\pi }_0^{\prime }$ such that $H_0:\pi ={\pi }_0^{\prime }$ would be rejected by the sample path. We can use (7) with ${\pi }_0={\pi }_0^{\prime }$ to compute a P value for testing $H_0:\pi ={\pi }_0^{\prime }$. We note that different π* are used for different values of ${\pi }_0^{\prime }$. And the value of ${\pi }_0^{\prime }$ that makes the P value = .5 can be used as a heuristically reasonable estimate of π. The properties of this estimator in contrast with a simple estimator, $(x_1+x_2^{\prime })/(n_1+n_2^{\prime })$, would need further exploration.

For the current example, X₁ = 7 (n₁ = 19) and $X_2^{\prime }=10(n_2^{\prime }=23)$, a 90% confidence interval for π is (.282, .546). And the value of ${\pi }_0^{\prime }$ which gives the P value = .5 in this example is .405.

5. DISCUSSION

The simplicity of Simon’s designs may account for their popularity. Our literature review revealed that, frequently, the inference procedures used with Simon’s designs are often not corrected for these designs’ adaptive nature.

Also, when the sample size is changed, the inference procedures become more complicated. In this paper, we have shown how to make a preferred inference taking into account the planned and actual sample sizes when a Simon’s design is used. When the actual sample size is the same as the planned sample size, the inference procedure is rather simple. When, however, the actual sample size is different from that planned, we need to take into consideration both the realized and the planned sample sizes when computing the P value and confidence interval of the response rate.

The concept of “conditional power” is well studied in the context of adaptive phase III clinical trials, and it is directly applicable in phase II methodologies that we have considered in this paper. When the sample size is changed, the critical value needs to be updated so that the conditional type I error rate is not inflated. As shown in this paper, more obvious methods of updating the design may not control type I error rate.

Finally, we have developed and made widely available a web-based program to compute a P value and a point estimate and a confidence interval for the response rate from data obtained from a Simon’s design.