Abstract
The activity of the single synapse is the base of information processing and transmission in the brain as well as of important phenomena as the Long Term Potentiation which is the main mechanism for learning and memory. Although usually considered as independent events, the single quantum release gives variable postsynaptic responses which not only depend on the properties of the synapses but can be strongly influenced by the activity of other synapses. In the present paper we show the results of a series of computational experiments where pools of active synapses, in a compatible time window, influence the response of a single synapse of the considered pool. Moreover, our results show that the activity of the pool, by influencing the membrane potential, can be a significant factor in the NMDA unblocking from increasing the contribution of this receptor type to the Excitatory Post Synaptic Current. We consequently suggest that phenomena like the LTP, which depend on NMDA activation, can occur also in subthreshold conditions due to the integration of the dendritic synaptic activity.
Keywords: Synaptic transmission, Synaptic modeling, AMPA, NMDA, LTP
Introduction
Excitatory glutamatergic synapses (Glut) are the main structures involved either in the transfer of information among neurons and in the neuronal computational ability of the brain (London and Häusser 2005). They represent more than the of the total brain synapses and are active both for short and long range neuronal connections (Megías et al. 2001; Bourne and Harris 2011). A single typical pyramidal neuron located in the cortex, CA1 or CA3 subfields of hippocampus, receives from to synaptic inputs and of them are of Glut type (Megías et al. 2001). These numbers give a clear idea of why a huge amount of both experimental and modeling oriented papers can be found in literature due to the big effort that neuroscientists spent to unveil and clarify the basic mechanisms of neuronal functionality. However, the parameters involved in synaptic transmission are many and so, despite such a big effort, still a huge amount of work is needed. Synaptic response variability, even for the single synaptic event (see for example Forti et al. 1997; Schikorski and Stevens 1997), is due both to stochastic and activity dependent factors as for example the vesicle position (eccentricity) (Ventriglia and Di Maio 2000a, 2002, 2003a, b) or the number, type and position of receptors (Allam et al. 2015, and for a review Di Maio et al. 2017) and this in turn, is the main factor why the neural code (spike sequences) of a single neuron, which is dependent on the synaptic inputs, still remains a problem to solve. Synaptic contribute to the spike generation is due to the Excitatory Post Synaptic Current (EPSC) which, generated at the synaptic spine in the dendritic tree produces a depolarizing wave (Excitatory Post Synaptic Potential, EPSP) which travels across dendrites. The time course and amplitude of this depolarization decreases in time and space according to the cable equation (Rall 1962; Rall and Rinzel 1973).
The depolarizing waves of all the active synapses integrate at the hillock, which is the region of the soma of the neuron where the spike sequences are generated. If depolarization at the hillock crosses a threshold value, the neuron emits spikes (For an example of integration at the hillock, see Ventriglia and Di Maio 2006). This is the generalized path followed by the “information” to pass among chains of neurons in the form of spike sequences which are considered to be the coded information. The large number of synapses which can be active inside a given time window, the different possible combination of their activation sequences, their relative distance from the hillock, the intrinsic stochastic variability of each synapse and the dendritic biophysical properties along the path (Rall 1962; Rall and Rinzel 1973; Di Maio 2007, 2008; Spruston 2010) are the main factors influencing the large variability of the spike sequences (neural code) even for the same presynaptic stimuli. Among all these factors influencing the neural code formation, the key role is played by the synaptic transmission but, because each single synapse gives at the hillock a very low contribution and because of its variability, the larger part of modeling scientists prefer to consider the far synaptic inputs as simply integrated into a Gaussian like noise (Musilla and Lansky 1991; Lansky and Sato 1999; Carfora and Pirozzi 2017; Pirozzi 2017, see for example) and only few consider the integration effect of the single synaptic event at the hillock (Ventriglia and Di Maio 2005, 2006, see for example).
Apparently, synaptic transfer of information is rather simple in a Glut synapse. A presynaptic spike induces influx at the presynaptic terminal which activates a molecular mechanism of fusion of a vesicle containing glutamate (Glu) molecules producing their diffusion into the synaptic cleft. Diffusion of Glu into the cleft activates two types of post-synaptic receptors: the -amino-3-hydroxy-5-methyl-4-isoxazole propionic acid sensitive receptors (AMPARs) and the N-methyl-D-aspartic acid sensitive receptors (NMDARs) positioned on the post-synaptic membrane of a dendritic spine. AMPARs and NMDARs are ionotropic receptors that, once activated, produce the flow of a ionic depolarizing current (AMPA-EPSC and NMDA-EPSC). Differences between the AMPA and NMDA EPSCs are that, although both are non specific for a particular ion type, enter NMDA but not AMPA channels. Moreover, they have different activation mechanisms since the AMPA component of the EPSC is much faster than the NMDA once (see model below). Several intrinsic factors contribute to the single synaptic event variability and in the recent years we have contributed to their study by using a model of synaptic transmission based on a very fine description of the synaptic geometry and on a very fine time step in the order of s (40 fs) (Ventriglia and Di Maio 2000a, b, 2002, 2003a, b; Ventriglia 2011; Ventriglia and Di Maio 2013a, b; Di Maio et al. 2015, 2016a, b, c). All these study, however, as well as in the larger part of papers found in literature on the same topic, considered the single synaptic as an independent event due to the open of a vesicle. However, by considering that a typical pyramidal neuron contains a number of synapses in the order of – it is reasonable to assume that in a given time window a certain number of synapses are active and that a sort of mutual influence can be among the synapses producing extrinsic factors of variability. In this perspective, we have to consider that the larger part of Glut synapses are located into dendritic districts which cannot be considered as isopotential regions (see for example, Reznik et al. 2016). The main source of non isopotentiality are the different activity of synapses on different areas of dendrites.
In the present paper, we want consider a non intrinsic source of the single synaptic response variability by considering the possible influence of pools of synapses, located at distance from our synapse () such that their depolarizing wave (EPSP) can influence the membrane voltage at the level of , in a time window compatible with the time at which produces a response (). We have conservatively chosen a pool of 100 synapses and randomized their response such to simulate different distances from and the intrinsic variability of the EPSP of each of them. The different activity of the pool has been simulated varying by a Poisson process the firing frequency of the synapses belonging to the pool. In other words, as for the case of the single neuron spiking activity where we integrated the activity of thousands of synapses at the hillock (Ventriglia and Di Maio 2006), in the present work we have integrated the synaptic activity of a restricted pool under the spine where is located. Because we want only see the influence of a pool of synapse on the single synaptic response, all the results must be considered as obtained in subthreshold conditions. This means that, whatever the synaptic frequency is, it will never generate spikes in the neuron. This correspond to those electrophysiological experiments intended to study the synaptic transmission where (tetrodoxin) TTX is used to abolish spikes in order to have a clean and clear readable synaptic response.
Model
As in the case of our previous papers, we used a simulation system divided into two parts. A first module, by considering a fine description of the synaptic geometry, simulates the diffusion and binding of Glu to AMPARs and NMDARs producing a matrix of the binding of the second molecule of Glu to the receptors. The second one simulates, off line, the post synaptic response by using this matrix .
Geometry of the synaptic space and diffusion
Geometry
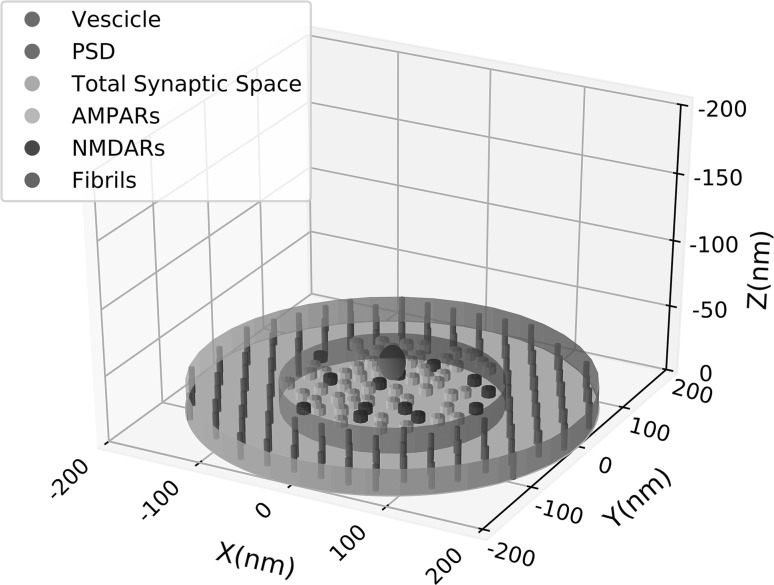
Our model considers the presynaptic and postsynaptic membranes as the roof and the floor of the synaptic space approximated to a flat cylinder with height () of nm. The radius depends on the number of receptors and can vary between and nm (Clements et al. 1992a; Clements 1996) but, for the present simulations, where we used a fixed number of receptors, a fixed radius was used (see below and Table 1). A schematic representation of the simulated geometry of the synaptic space is shown in Fig. 1.
Table 1.
Main geometrical and diffusion parameters
| Parameter | Value | |
|---|---|---|
| Synaptic radius | 220 nm | |
| PSD radius | 110 nm | |
| Height of the cleft | 20 nm | |
| Height of the fusion pore | 12 nm | |
| Receptor radius | 7 nm | |
| Fibril radius | 7 nm | |
| Fibril interspacing | 22 nm | |
| Vesicle radius | 12.5 nm | |
| Total number of receptors | 68 | |
| Number of AMPARs | 55 | |
| Number of NMDARs | 13 | |
| Number of Glu in a vesicle | 780 | |
| Diffusion coeff. of Glu | D | |
| Mass of Glu | m | |
| Temperature | T | |
| Radial velocity | ||
| Time step | ||
| Presynaptic binding probability |
Fig. 1.
Schematic 3D representation of the simulated synaptic space. Each component of the synaptic space is shown in the legend and detailed explanation of the properties of the components are in the text. Height of the synaptic cleft is 20 nm, PSD diameter is 110 nm and total synaptic space has a diameter of 220 nm. AMPARs (yellow) and NMDARs (blue) protrude from the base of 7 nm. (Color figure online)
The cylinder containing all the synaptic space, encloses a smaller one which is delimited at the floor level by a central region (modelled of circular shape), where AMPARs and NMDARs are allocated, called Post Synaptic Density (PSD) and by an equivalent area at the roof, called Active Zone (AZ), behind which docked vesicles, filled of Glu molecules, are positioned. The event of release consists essentially in the formation of a fusion pore between one of the docked vesicle and the cell membrane. This pore, the height of which we assumed of 12 nm (twice the tickness of a cell membrane), opens with a radial velocity permitting the Glu molecules to diffuse in the synaptic cleft according to their Brownian motion (Glavinovic 1999; Ventriglia and Di Maio 2000a, b).
For our computation, although of circular shape, we have considered the PSD as a matrix () where we have randomly allocated [but excluding the angles, (see Fig. 2 in Ventriglia and Di Maio 2000b)] 55 AMPARs and 13 NMDARs computed by considering the AMPA/NMDA proportion (Takumi et al. 1999) and the size of the single receptor with respect to the size of the synapse (Nakagawa 2010; Mayer 2011; Ventriglia and Di Maio 2013a). For this number of receptors the radius of the PSD was 110 nm and the total synaptic space radius was 220 nm. This size can be considered a medium size synapse of hippocampus (for glutamatergic synapse size see Clements et al. 1992a, b). Each receptor needs to be bound by at least 2 molecules of Glu to have some significant probability to open. Receptors were modelled as cylinders protruding from the PSD surface of 7 nm. Each of them had on the top 2 binding sites modelled as circles randomly positioned. The interspace between the outer and inner cylinder contains microfibrills which connect pre and postsynaptic cell membrane (Zuber et al. 2005). They have a diameter of 7 nm and are interspaced each other of 22 nm (Zuber et al. 2005; Ventriglia 2011; Ventriglia and Di Maio 2013a, b). These fibrils are important because they can produce a variability of the response of with respect to simulations performed with no fibrils (Ventriglia 2011)
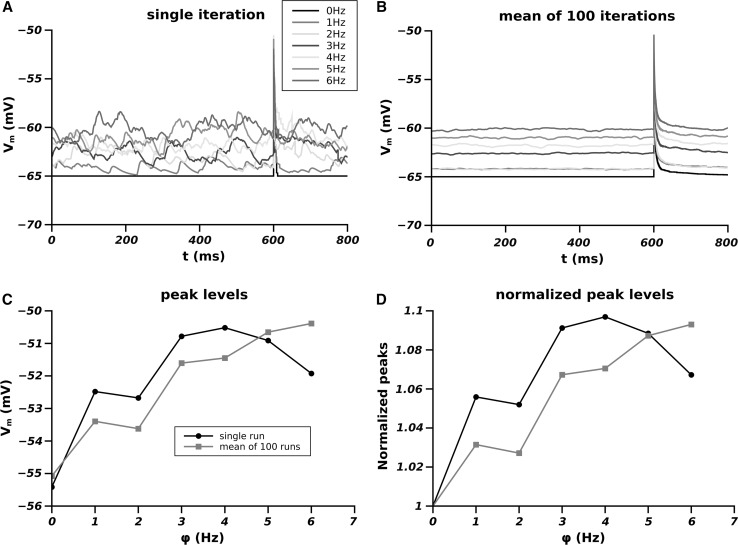
Fig. 2.
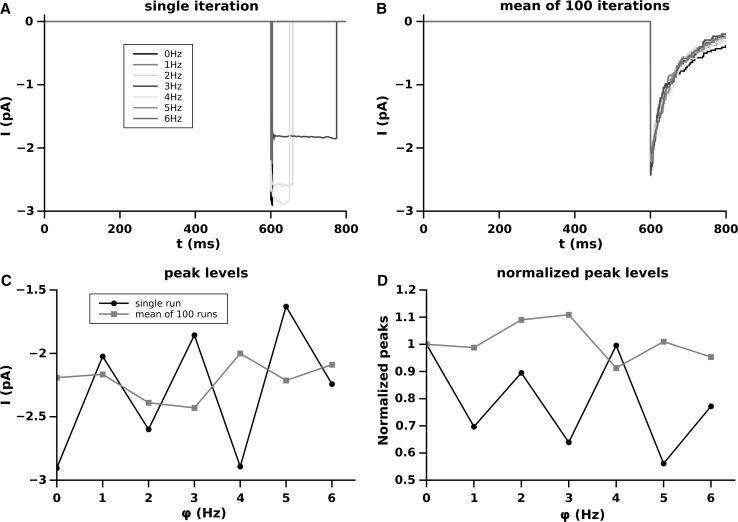
Effect of the different firing frequency of the synaptic pools on the membrane potential. A Single run for each frequency; B average of over 100 runs; C peak levels of the EPSPs as function of the firing frequency of the pool (black single run, red averaged over 100 runs); D dependence of the peak level as a function of the firing frequency of the pool normalized to the peak level at (black single run and red average on 100 runs). (Color figure online)
On the top of the synaptic space (behind the presynaptic surface), a single centered () vesicle, simulated as a sphere, with an internal diameter of 24 nm and containing 780 molecules of Glu (Ventriglia and Di Maio 2000a, b), starts to fuses with the presynaptic membrane forming a fusion pore at time . The pore then opens with its radial velocity (see Table 1) and when its diameter becomes equal to that of a molecule of Glu, molecules can flow into the synaptic cleft.
Diffusion and binding
The molecules of Glu move freely in the synaptic space following Brownian motion limited only by the geometry of the synaptic sub-components shown in Fig. 1. If a molecule hits one of the synaptic structure it is reflected continuing its motion. In only three cases a different behaviour can occur: (a) if the molecule crosses the lateral surface of the outer cylinder; (b) if it hits the presynaptic surface (the roof of the outer cylinder); (c) if it hits the upper surface of a receptor. About the point (a), we have considered for this model an absorbing boundary. All around the synaptic space, in fact, are located glial cells which have a large density of Glu receptors and this make unlikely that a molecule who has crossed the boundary can return back to the synaptic space. For the point (b) we considered that the few presynaptic metabotropic receptors can catch the Glu molecules although with a very low probability () (semi-absorbing boundary). The last condition (c) is the most important and concerns the case in which a molecule hits the upper surface of an AMPA or NMDA receptor. In this case there is some probability to bind to the receptor and this is the main point for the postsynaptic response and will be discussed later in the appropriate section.
At time , molecules of Glu are all enclosed in the spherical vesicle moving with a velocity chosen according to a Maxwell distribution. The diffusion in the cleft started once the fusion pore diameter reached a value greater than the diameter of a molecule of Glu. Brownian diffusion was simulated according to the following Langevin equations:
| 1 |
| 2 |
where is a vector of the position of the ith molecule in the space at time t, is its velocity, m is the molecular mass of a molecule of Glu (see Table 1), is a friction parameter depending on the absolute temperature with being the Boltzman constant, D the diffusion coefficient, T the temperature in Kelvin. A white Gaussian noise was used as stochastic force with intensity . For the numerical simulations, the following discretized form of Eqs. (1) and (2) were used
| 3 |
| 4 |
where is a random vector with Gaussian components having mean 0 and standard deviation 1.
To have a good dumping term in the above equations and a fine description of the molecular movements, a very small time step () of s (40 fs) and no space discretization were used.
The main parameters used in the diffusion simulations are shown in Table 1.
Molecules were considered massless (identified only by their 3D coordinates) during all the diffusion process except when they approach a binding site of a receptor. In this case an ovoid shape was considered. This approach was necessary to compute the binding probability of Glu molecules to the receptors. We consider, in fact, meaningless the use of the classical mass equation when time step in the femtoseconds time scale is used. Moreover, computed by mass equations consider an equilibrium of the Glu concentration which is to exclude during a single synaptic event (Ventriglia 2011; Ventriglia and Di Maio 2000a, 2002, 2003a, b, 2013a, b; Di Maio et al. 2016a, b, c). For these reasons, our () was computed according to some geometrical considerations. We know, in fact, that Glu can bind to receptors only from its -carboxyl group (one side of the simulated ovoid). Assuming a circular shape of the binding site, we can compute () as the ratio between the volume of the cone angle, which enclose all the useful orientation for binding of the -carboxyl group of Glu, and the volume of a sphere which includes all its possible spatial orientations [see Fig. 3 in Ventriglia and Di Maio (2013a)].
The total diffusion simulation time was of s () and produced two matrices of . One matrix () was not used for the computation of the response because it contained the binding time of a first molecule of Glu to a receptor. This state of the receptor has an open probability negligible and so it was excluded because we are interested only to the receptor states which produce a response in terms of conductance and so we used only the second time of binding matrix ). The matrix was used with the matrix , which coded the position i, j of the receptor types, as follows
| 5 |
Here, is the binding time of the second molecule of Glu to the receptor which is allocated at the position i, j in the matrix .
The matrices and produced as result of the diffusion simulation were used offline to simulate the postsynaptic response.
Postsynaptic response
EPSC computation
To simulate the postsynaptic response it is necessary to consider the different dynamics of the two receptor types. While for the AMPA receptors, in fact, the binding of two molecules of Glu is a necessary and sufficient condition, the same does not hold for the NMDA receptors. NMDARs, in fact, at the resting level of the membrane potential are blocked by and, before they can open, need to be unblocked. Their blocking depends on the concentration and on the membrane voltage (). Jahr and Stevens (1990) and Vargas-Caballero and Robinson (2004) have shown that NMDA-dependent conductance follows a sigmoid relationship depending on the membrane potential and that the slope of the function essentially depends on the concentration. To manage the NMDA contribution to the postsynaptic response in our simulation system, we have converted this relationship in a probability function (Di Maio et al. 2016a, b, c) such that
| 6 |
where is the unblocking probability which depends on the variation of membrane potential () expressed in mV and x is the concentration in mM. Being the most likely concentration in the synaptic cleft of of mM for our simulation the equation has been reduced to
| 7 |
Since at the resting level of the membrane potential the blocking results to be complete and at a level of mV all is fully unblocked (Jahr and Stevens 1990; Vargas-Caballero and Robinson 2004), the probability was adjusted to be at mV and at mV (Di Maio et al. 2016a, b, c). The following simplified Markov chains for AMPA and NMDA receptors have been then adopted.
| 8 |
where , , represent respectively the non active configurations of the receptors and the state is the only active one. The denotes the blocked condition of NMDA receptors. The steps of the above Markov chains are computed in the simulation of diffusion (see above) with the exception of the passage for the AMPARs and for the NMDARs which, being the crucial state transitions for the postsynaptic response, are considered here. The detailed mechanism used in our simulations for the opening and closing of receptors can be found in our previous papers (Di Maio et al. 2015, 2016a, b, c).
The states and , being the close and open states are those contributing to the total conductance of our synapse S which is then computed as
| 9 |
where is the conductance of the receptor positioned at .
Single receptor conductance varies not only between AMPARs and NMDARs but also in the same type. These receptors, in fact, are tetrameric proteins which can be composed of different subunits (Dingledine et al. 1999; Traynelis et al. 2010). To account for this variability, we have randomized the values of the single receptor conductance by a Gaussian distribution and then
| 10 |
For the values of and of AMPARs and NMDARs conductances, see Table 2. The EPSC of , () is then computed as
| 11 |
where is the reversal potential which for the glutamatergic synapse is at mV.
Table 2.
Main parameters for simulation of membrane potential
| Parameter | Value | |
|---|---|---|
| Resting potential | mV | |
| Synaptic reversal potential | 0 mV | |
| Full unblocking | mV | |
| Spine resistance | 500 MΩ | |
| AMPAR conductance | pS | |
| NMDAR conductance | pS |
Computation of
The value of is crucial for the synaptic dynamics in the dendritic tree. On one side, the current (EPSC), for a given value of the synaptic conductance, depends on the driving force [ such that it decreases by increasing ] as clearly visible in Eq. 11. On the other side, the activation of NMDARs being dependent on (see Eqs. 6 and 7) increases the total conductance increasing the total current (EPSC). In the present paper, we have considered the influence of a pool of 100 synapses on the membrane potential at the level of the spine where our synapse is allocated in order to see how they affect the EPSC produced by a single synaptic release of . The influence of each single synapse belonging to pool depends on the distance from and on the amplitude at the origin which, according to the cable theory (Rall 1962; Rall and Rinzel 1973), decreases exponentially with distance depending on the space constant . However, in our simplified model, we have not defined a precise distance of each synapse from because it was randomized across the runs and it was defined by the parameters of the model we used to simulate the single synaptic activity in the pool (see below). The variation of the membrane voltage under the spine where is allocated due to the single synapse belonging to the pool has been computed as the difference of two exponentials according to the following equation
| 12 |
where is the peak value of the synapse, is its rising time constant, its decay time constant and is the time at which it starts to fires. We randomized the parameters by uniform distributions such that: (in mV); (in ms); and (in ms). Please note that by the above Uniform distributions we ensured that always . This randomization produced different shapes of the single EPSP emitted by the synapses of the pool. The combination of different values of simulated both of the stochastic variability of the single synaptic response and the distance of each synapse from . For example, a high value and small values of and well agree with the contribution given by a synapse located in the proximity of . The same previous value of and combined with a smaller value of produces a shape of the EPSP simulating a synapse located at the same distance but with a different response due to its intrinsic stochastic processes (for stochastic variability in the same synapse Ventriglia and Di Maio 2002, 2003a, b; Ventriglia 2011; Ventriglia and Di Maio 2013a, b; Di Maio et al. 2017). Alternatively, higher values of and simulate inputs arriving from more distant synapses. In summary, we are confident that by this method we have simulated the random distances and amplitudes of synaptic inputs arriving to .
The total synaptic pool contribution to at the spine level of will be then
| 13 |
where is the total contribution of the synaptic pool. The total variation of will be then
| 14 |
being the resting potential, the spine resistance (Di Maio et al. 2016b, c) and the EPSC produced by . Since we consider the current computed at the origin (under or inside the spine), being the free area of the spine membrane extremely small, we neglected in the above equation the capacitative component of the current because much less than 1 pA.
The frequency at which the synaptic pool fires is, of course, a crucial point in determining the contribution of the pool to . This frequency depends on the firing frequency of the presynaptic neurons. A spontaneous firing frequency of Hz is common in pyramidal neurons (see references in Ventriglia and Di Maio 2006) but it cannot be excluded higher firing frequencies due to subthreshold stimulation of some dendritic area. For this reason we have used firing frequency of the synaptic pool () ranging from 0 (no contribution of the pool) to 6 Hz. We determined the time (see Eq. 12) at which each synapse of the pool starts to fire by a Poisson distribution P the parameter of which was
| 15 |
Our total simulation time was of 1 s with a time step of s (0.01 ms). Simulation started with the membrane potential fixed at the resting level of mV. By visual inspection of the first runs we determined that after 150 ms the system arrived to a regime level. For this reason, we cut off from results the first 200 ms of simulation and set ms. The onset of the synapse was fixed at ms which, being ms appears to be 600 ms in the figures. For each frequency between 0 and 6 Hz, a single run (to show the real behaviour of the membrane potential) and 100 runs simulations were performed and compared. A summary of the main parameters used for the simulation of the electrical output is presented in Table 2.
Results
In Fig. 2 are shown the results of the membrane potential computed according to our model.
The panel A of Fig. 1 shows the single run computation of . The real membrane oscillations are visible for each frequency of the pool activity. The flat line (black) corresponds to the simulation with no pool contribution ( Hz) where the value remains equal to until the synapse fires. Although confusing, should be evident that the different frequencies in the single runs simulations produces oscillation to a level which depends on . The panel B shows this level as the result of the average point by point of over 100 runs. In this case the flattening of shows clearly the different levels of the mean oscillation as dependent on . This mean level of has to be considered as the most likely value (expected value) of at which the onset of the EPSC of occurs for a given frequency of the pool. The effect of this is visible in panels C and D. In fact, independently from its amplitude, the EPSP of , occurring at levels of depending on , reaches at the peak a level which depends itself on . In these panels, the single run peak level (black line) shows a trend similar to the averaged one. This means that in our single runs the larger part of the EPSP of occurred in proximity of its expected value for any given frequency. Panel D shows the same as panel C but the peak levels are normalized to that reached by the EPSP of when there is no synaptic pool influence. In summary Fig. 2 shows an approximately linear dependence of the peak levels of the EPSP of as dependence of the frequency of activity of the pool and this effect is independent on the amplitude of the peak.
The peak level as well as the level of the pool activity before onset of the EPSP of is of fundamental importance because the contribution of the NMDA receptors to the synaptic response depends on the level of .
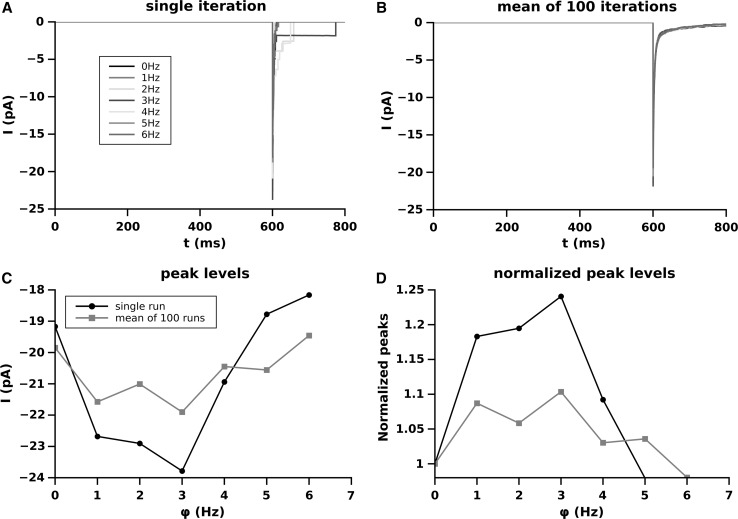
The Fig. 3 shows the effect of the synaptic pool contribution to the current (EPSC) produced by the synapse . Since we consider only the ionic current produced by the the synapse , and the contribution to the membrane potential of the synaptic pool is considered only as variations of , the current level in this case is always 0 and the peak levels coincide to the peak amplitudes.
Fig. 3.
Effect of the different firing frequency of the synaptic pool on EPSC amplitude produced by the synapse S. A single run for each frequency; B average over 100 runs; C amplitude of the EPSC as function of the firing frequency of the pool; D dependence of the EPSC peak amplitude, as a function of the firing frequency of the pool, normalized to the peak amplitude at
The panel A of Fig. 3 shows the EPSC produced for a single run. The square shaped tail of the EPSCs are due to the activation of the NMDARs. Single channels currents approximate a square (rectangular) waves and so, if a single receptor is still open, the shape assumes the rectangular shape of the current produced by that receptor. Tails of EPSC involving NMDA receptors are always contributed only by NMDARs because of the faster decay of the AMPA current with respect to the NMDA one (see for example Di Maio et al. 2016c). The peak amplitude of the EPSCs produced by mediated over 100 runs are visible in panel B and their dependence on is plotted in panel C and, normalized, in panel D. The EPSC peak amplitude of , on the contrary of the EPSP level, does not follow a quasi liner increase as a function of . The non linearity of the current is due to two main factors which some time contrast each other. The increasing of , in fact, increasing rises proportionally the number of activated NMDARs increasing the total conductance and consequently the EPSC peak. However, the increase of also decreases the driving force reducing the EPSC amplitude. The level of balancing (or unbalancing) of these two opposite forces for any given frequency is the base of the observed non linearity. Panel D shows that, on average, the synaptic pool frequency at most increases of the EPSC peak amplitude with respect to the situation where no synapses are active in the synaptic pool (). In Figs. 4 and 5 the AMPA and NMDA-dependent components concurring to the total EPSCs of Fig. 2 are presented for each frequency of the pool.
Fig. 4.
Effect of the different firing frequency of the synaptic pool on AMPA-EPSC amplitude produced by the synapse S. A single run for each frequency; B average over 100 runs; C amplitude of the AMPA-EPSC as function of the firing frequency of the pool; D dependence of the AMPA-EPSC peak amplitude, as a function of the firing frequency of the pool, normalized to the peak amplitude at
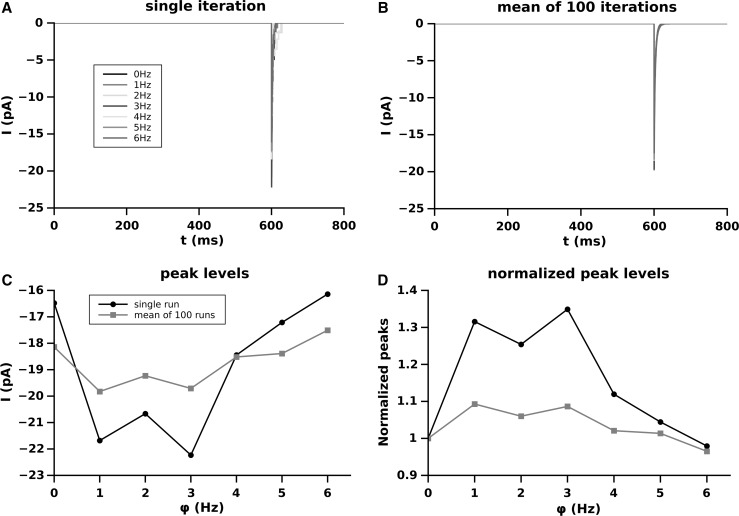
Fig. 5.
Effect of the different firing frequency of the synaptic pool on NMDA-EPSC amplitude produced by the synapse S. a single run for each frequency; b average over 100 runs; c amplitude of the NMDA-EPSC as function of the firing frequency of the pool; d dependence of the NMDA-EPSC peak amplitude, as a function of the firing frequency of the pool, normalized to the peak amplitude at
AMPA-EPSC is the maximal component of the EPSC produced by the synapse and so it is not surprising that the trend and amplitude of the AMPA-EPSC peaks is similar (but not equal) to the total EPSC shown in Fig. 2.
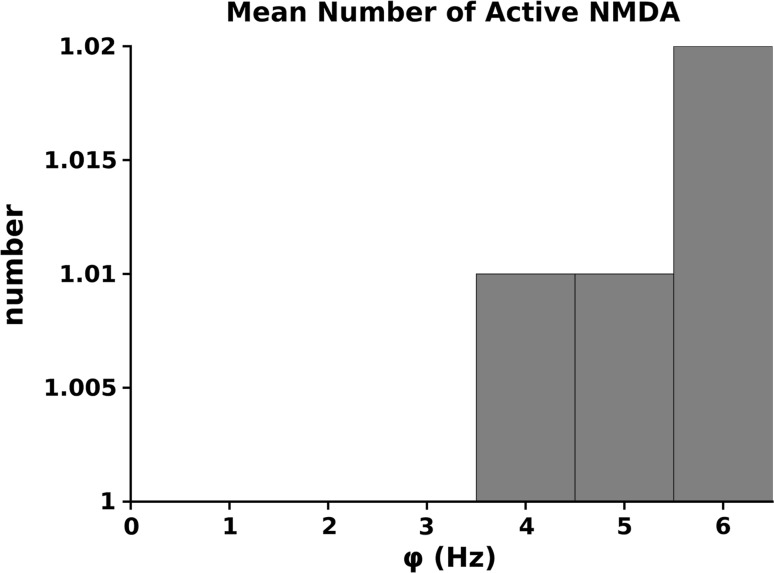
A little more complex situation is given by the NMDA-EPSC component because this effect is depending on the fact that they are or not unblocked and this is dependent on the level of . The number of activated NMDARs as a function of the firing frequency of the synaptic pool is given in Fig. 6. In our simulations we, conservatively, used a relatively small number of synapses and low frequencies for the synaptic pool activity. This is the reason why, at most, we have only 2 NMDARs activated. Although this number can be considered small, it represents a non negligible value on a total of 13 NMDARs used in the simulation ().
Fig. 6.
Average number of NMDA receptors of the synapse activated at the different frequencies of the synaptic pool
Discussion
The basic structures involved in information transfer in the brain are the synapses. They not only transfer information from one neuron to another but contribute to the code generation of each single neuron. Neurons integrate synaptic inputs to reach a threshold level of the membrane potential at the hillock and to produce sequences of spike which encode the information. So far, if code is formed as a consequence of computation over the information arrived by synapses, it is obvious that their role is fundamental in neural computation, too.
Although simple in principle, the mechanism of information transfer and integration is rather complex. It involves several molecules and several control mechanisms both at the pre and postsynaptic side. Even at the level of the single synapse it is possible to observe a large variability for a single event such that the EPSC of a synapse can range 5–100 pA (Forti et al. 1997; Schikorski and Stevens 1997; Liu et al. 1999). This variability cannot be longer attributed only to intrinsic stochastic or/and activity-dependent processes (for a review, see Di Maio et al. 2017), but the key role of the other active synapses has to be considered, too.
In the present paper we have proposed a simple model which proves that the activity of other synapse can influence the response of a single one. We used a pool limited to 100 synapses and showed that, when they fires in a compatible time window, they can significantly influence the output of the single synapse. This point is very important for several reasons. One important point is that each synapse can give a contribution to modulate the activity of any other synapse and so the code generated by the postsynaptic neuron strongly depends on the pool of synapses which are active in a given time window. This means also that the information coded by the neuron is primarily modulated at the dendritic level and this support the idea that information is primarily processed by a sort of “dendritic computation” at the dendritic level (for a review on this topic, see for example London and Häusser 2005). Models dealing with single neuron code generation and interpretation should carefully consider this important point in order to solve primarily the problem of variability of the code following a given stimulus.
Another important point revealed by our simulation results is that NMDA receptors can be activated also in subthreshold conditions. As shown by Vargas-Caballero and Robinson (2004), Jahr and Stevens (1990), Allam et al. (2015) the activation of NMDA due to their unblocking depends on the membrane depolarization. This means that any activity which can produce membrane depolarization can activate the NMDA-conductance which, consequently, does not need necessarily the firing of a spike in the postsynaptic cell. This point is of great importance because it is well known the role of these receptors in the formation of LTP which is the base of important cognitive phenomena like memory and learning (see for example, Malinow and Malenka 2002; Nicoll and Schmitz 2005; Rao and Finkbeiner 2007; Raymond 2007; Volianskis et al. 2015). Although in our simulations the activation of NMDA is relatively small, we must stress that the number of synapses as well as their frequency was conservatively chosen small and it cannot be excluded that, for an average number of , a number much grater than 100 synapses can influence the synapse and even at a frequency greater than the maximal we used (6 Hz). In our simulations we have been even very conservative by choosing the maximal peak value (1 mV) of each synapse in the pool ( in Eq. 12). We assumed this limit considering the values of the EPSP usually registered at soma. However, our EPSP of computed at spine level is mV (see Fig. 2) and this means that, a similar synapse, placed in the close proximity of would give a contribution to the membrane potential under much greater than 1 mV.
Conclusion
Our simulations have shown that the activity of any synapse can virtually affect and modulate the response of any other synapse once assumed that the mutual distance and the time of activation of the two synapses are compatible. A direct consequence of this assumption is that probably the neuronal code formation strongly depends not only on the mutual interaction of synapses (integration at the hillock) but also on their ability to modulate each other by a sort of “dendritic computation”.
Another important point is related to the ability that this sort of synaptic cooperativeness can have in modulating LTP of single synapse. Our simulations give a strong indication that even the LTP in a single synapse is not only a process depending on the activity of the synapse but is modulated by the cooperative effect of other active synapses. This aspect could be not apparent in experiments for the studies of the single synapse, but should be considered when results of these studies are generalized to in vivo conditions.
References
- Allam S, Bouteiller JMC, Hu EY, Ambert N, Greget R, Bischoff S, Baudry M, Berger TW. Synaptic efficacy as a function of ionotropic receptor distribution: a computational study. PLoS ONE. 2015 doi: 10.1371/journal.pone.0140333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourne JN, Harris KM. Coordination of size and number of excitatory and inhibitory synapses results in a balanced structural plasticity along mature hippocampal CA1 dendrites during LTP. Hippocampus. 2011;21:354–373. doi: 10.1002/hipo.20768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carfora MF, Pirozzi E. Linked Gauss-diffusion processes for modeling a finite-size neuronal network. Biosystems. 2017 doi: 10.1016/j.biosystems.2017.07.009. [DOI] [PubMed] [Google Scholar]
- Clements JD. Transmitter timecourse in the synaptic cleft: its role in central synaptic function. Trends Neurosci. 1996;19:163–171. doi: 10.1016/S0166-2236(96)10024-2. [DOI] [PubMed] [Google Scholar]
- Clements JD, Lester RA, Tong G, Jahr CE, Westbrook GL (1992a) The time course of glutamate in the synaptic cleft. Science 258(5087):1498–1501. 10.1126/science.1359647. http://www.ncbi.nlm.nih.gov/pubmed/1359647%5Cn, http://www.sciencemag.org/cgi/doi/10.1126/science.1359647 [DOI] [PubMed]
- Clements JD, Lester RA, Tong J, Jahr CE, Westbrook GL. The time course of glutamate in the synaptic cleft. Science. 1992;258:11,498–11,501. doi: 10.1126/science.1359647. [DOI] [PubMed] [Google Scholar]
- Di Maio V. Excitatory synaptic interaction on dendritic tree. In: Mele F, Ramella G, Santillo S, Ventriglia F, editors. Brain, vision and arificial intelligence. Lecture notes in computer science. Berlin: Springer; 2007. pp. 388–397. [Google Scholar]
- Di Maio V. Regulation of information passing by synaptic transmission: a short review. Brain Res. 2008;1225:26–38. doi: 10.1016/j.brainres.2008.06.016. [DOI] [PubMed] [Google Scholar]
- Di Maio V, Ventriglia F, Santillo S. A model of dopamine modulated glutamatergic synaspe. Biosystems. 2015;136:59–65. doi: 10.1016/j.biosystems.2015.05.001. [DOI] [PubMed] [Google Scholar]
- Di Maio V, Ventriglia F, Santillo S. A model of cooperative effect of AMPA and NMDA receptors in glutamatergic synapses. Cogn Neurodyn. 2016;10:315–325. doi: 10.1007/s11571-016-9383-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Maio V, Ventriglia F, Santillo S. A model of dopamine modulation of glutamatergic synapse on medium size spiny neurons. Biosystems. 2016;142–143:25–31. doi: 10.1016/j.biosystems.2016.03.001. [DOI] [PubMed] [Google Scholar]
- Di Maio V, Ventriglia F, Santillo S (2016c) AMPA/NMDA cooperativity and integration during a single synaptic event. J Comput Neurosci 41(2):127–142. http://dblp.uni-trier.de/db/journals/jcns/jcns41.html#MaioVS16, http://dx.doi.org/10.1007/s10827-016-0609-5 [DOI] [PubMed]
- Di Maio V, Ventriglia F, Santillo S. Stochastic, structural and functional factors influencing AMPA and NMDA synaptic response variability: a review. Neuronal Signal. 2017;1:1–11. doi: 10.1042/NS20160051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dingledine R, Borges K, Bowie D, Traynelis S. The gutamate receptor ion channels. Pharmacol Rev. 1999;51:7–61. [PubMed] [Google Scholar]
- Forti L, Bossi M, Bergamaschi A, Villa A, Malgaroli A. Loose path recording of single quanta at individual hippocampal synapses. Nature. 1997;388:874–878. doi: 10.1038/42251. [DOI] [PubMed] [Google Scholar]
- Glavinovic MI. Monte Carlo simulation of vesicular release, spatiotemporal distribution of glutamate in synaptic cleft and generation of postsynaptic currents. Pflügers Arch Eur J Physiol. 1999;437:462–470. doi: 10.1007/s004240050802. [DOI] [PubMed] [Google Scholar]
- Jahr C, Stevens C. Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci. 1990;10:3178–3182. doi: 10.1523/JNEUROSCI.10-09-03178.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lansky P, Sato S. The stochastic diffusion models of nerve membrane depolarization and interspike interval generation. J Peripher Nerv Syst. 1999;4:27–42. [PubMed] [Google Scholar]
- Liu G, Choi S, Tsien RW. Variability of neurotransmitter concentration and nonsaturation of postsynaptic AMPA receptors at synapses in hippocampal cultures and slices. Neuron. 1999;22:395–409. doi: 10.1016/S0896-6273(00)81099-5. [DOI] [PubMed] [Google Scholar]
- London M, Häusser M. Dendritic computation. Annu Rev Neurosci. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- Malinow R, Malenka RC. AMPA receptor trafficking and synaptic plasticity. Annu Rev Neurosci. 2002;25:103–26. doi: 10.1146/annurev.neuro.25.112701.142758. [DOI] [PubMed] [Google Scholar]
- Mayer ML. Structure and mechanism of glutamate receptor ion channel assembly, activation and modulation. Curr Opin Neurobiol. 2011;21:283–290. doi: 10.1016/j.conb.2011.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Megías M, Emri Z, Freund TF, Gulyàs AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience. 2001;102:527–540. doi: 10.1016/S0306-4522(00)00496-6. [DOI] [PubMed] [Google Scholar]
- Musilla M, Lansky P. Generalized stein model for anatomically complex neurons. Biosystems. 1991;25:179–191. doi: 10.1016/0303-2647(91)90004-5. [DOI] [PubMed] [Google Scholar]
- Nakagawa T. The biochemistry, ultrastructure, and subunit assembly mechanism of AMPA receptors. Mol Neurobiol. 2010;15:161–184. doi: 10.1007/s12035-010-8149-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicoll R, Schmitz D. Synaptic plasticity at hippocampal mossy fibre synapses. Nat Rev Neurosci. 2005;6:863–876. doi: 10.1038/nrn1786. [DOI] [PubMed] [Google Scholar]
- Pirozzi E (2017) Colored noise and a stochastic fractional model for correlated inputs and adaptation in neuronal firing. Biol Cybern. 10.1007/s00422-017-0731-0. http://dx.doi.org/10.1016/j.biosystems.2017.07.009 [DOI] [PubMed]
- Rall W. Electrophysiology of a dendritic neuron model. Biophys J . 1962;2:145–167. doi: 10.1016/S0006-3495(62)86953-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rall W, Rinzel J. Branch input resistance and steady attenuation for input to one branch of a dendritic neuron model. Biophys J . 1973;13:648–688. doi: 10.1016/S0006-3495(73)86014-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao VR, Finkbeiner S. NMDA and AMPA receptors: old channels, new tricks. Trends Neurosci. 2007;30(6):284–91. doi: 10.1016/j.tins.2007.03.012. [DOI] [PubMed] [Google Scholar]
- Raymond CR. LTP forms 1, 2 and 3: different mechanisms for the “long” in long-term potentiation. Trends Neurosci. 2007;30(4):167–75. doi: 10.1016/j.tins.2007.01.007. [DOI] [PubMed] [Google Scholar]
- Reznik RI, Barreto E, Sander E, So P (2016) Effects of polarization induced by non-weak electric fields on the excitability of elongated neurons with active dendrites. J Comput Neurosci 40(1):27–50. http://dblp.uni-trier.de/db/journals/jcns/jcns40.html#ReznikBSS16 [DOI] [PubMed]
- Schikorski T, Stevens CF. Quantitative ultrastructural analysis of hippocampal excitatory synapses. J Neurosci. 1997;17:5858–5867. doi: 10.1523/JNEUROSCI.17-15-05858.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N. Dendritic signal integration. Encycl Neurosci. 2010;1:445–452. [Google Scholar]
- Takumi Y, Matsubara A, Rinvik E, Ottersen OP. The arrangement of glutamate receptors in excitatory synapses. Ann N Y Acad Sci. 1999;868:474–482. doi: 10.1111/j.1749-6632.1999.tb11316.x. [DOI] [PubMed] [Google Scholar]
- Traynelis S, Wollmuth L, CJ M, Menniti F, Vance K, Ogden K, Hansen K, Yuan H, Myers S, Dingledine R. Glutamate receptor ion channels: structure, regulation, and function. Pharmacol Rev. 2010;62:405–496. doi: 10.1124/pr.109.002451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vargas-Caballero MI, Robinson H. Fast and slow voltage-dependent dynamics of magnesium block in the NMDA receptor: the asymmetric trapping block model. J Neurosci. 2004;24:6171–6180. doi: 10.1523/JNEUROSCI.1380-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ventriglia F. Effect of filaments within the synaptic cleft on the response of excitatory synapses simulated by computer experiments. Biosystems. 2011;104:14–22. doi: 10.1016/j.biosystems.2010.12.008. [DOI] [PubMed] [Google Scholar]
- Ventriglia F, Di Maio V. A Brownian model of glutamate diffusion in excitatory synapses of hippocampus. Biosystems. 2000;58:67–74. doi: 10.1016/S0303-2647(00)00108-8. [DOI] [PubMed] [Google Scholar]
- Ventriglia F, Di Maio V. A Brownian simulation model of glutamate synaptic diffusion in the femtosecond time scale. Biol Cybern. 2000;83:93–109. doi: 10.1007/s004220000150. [DOI] [PubMed] [Google Scholar]
- Ventriglia F, Di Maio V. Stochastic fluctuation of the synaptic function. Biosystems. 2002;67:287–294. doi: 10.1016/S0303-2647(02)00086-2. [DOI] [PubMed] [Google Scholar]
- Ventriglia F, Di Maio V. Stochastic fluctuation of the quantal EPSC amplitude in computer simulated excitatory synapses of hippocampus. Biosystems. 2003;71:195–204. doi: 10.1016/S0303-2647(03)00117-5. [DOI] [PubMed] [Google Scholar]
- Ventriglia F, Di Maio V. Synaptic fusion pore structure and AMPA receptors activation according to Brownian simulation of glutamate diffusion. Biol Cybern. 2003;88:201–209. doi: 10.1007/s00422-002-0375-5. [DOI] [PubMed] [Google Scholar]
- Ventriglia F, Di Maio V (2005) Neural code and irregular spike trains, vol 3704. In: Gregorio MD, Di Maio V, Frucci M, Musio C (eds) BVAI, lecture notes in computer science, pp 89–98. Springer. http://dblp.uni-trier.de/db/conf/bvai/bvai2005.html#VentrigliaM05, http://dx.doi.org/10.1007/11565123_9
- Ventriglia F, Di Maio V (2006) Multisynaptic activity in a pyramidal neuron model and neural code. Biosystems 86:18–26. 10.1016/j.biosystems.2006.02.014. http://www.sciencedirect.com/science/article/pii/S0303264706000633 [DOI] [PubMed]
- Ventriglia F, Di Maio V. Effects of AMPARs trafficking and glutamate-receptor binding probability on stochastic variability of EPSC. Biosystems. 2013;112:298–304. doi: 10.1016/j.biosystems.2013.01.010. [DOI] [PubMed] [Google Scholar]
- Ventriglia F, Di Maio V. Glutamate-AMPA interaction in a model of synaptic transmission. Brain Res. 2013;1536:168–176. doi: 10.1016/j.brainres.2013.04.051. [DOI] [PubMed] [Google Scholar]
- Volianskis A, France G, Jensen MS, Bortolotto ZA, Jane DE, Collingridge GL (2015) Long-term potentiation and the role of N-methyl-d-aspartate receptors. Brain Res 1621:5–16. 10.1016/j.brainres.2015.01.016. http://www.sciencedirect.com/science/article/pii/S000689931500027X. (Brain and memory: old arguments and new perspectives) [DOI] [PMC free article] [PubMed]
- Zuber B, Nikonenko I, Klauser P, Muller D, Dobochet J. The mammallian central nervous synaptic cleft contains a high density of periodically organized complexes. Proc Natl Acad Sci USA. 2005;102:19,192–19,197. doi: 10.1073/pnas.0509527102. [DOI] [PMC free article] [PubMed] [Google Scholar]