Kinetics teach that electronic coupling lowers the free-energy change that accompanies electron transfer

Significance

Nature’s use of electronic coupling (H_DA) and free-energy (ΔG^o) gradients to vectorially control electron transport provides inspiration for artificial photosynthesis. Theoretical predictions indicate that H_DA and ΔG^o are not independent parameters, and are instead linked. Reported here is a broadly applicable kinetic approach that was utilized to demonstrate such behavior for four acceptor–bridge–donor compounds. When the electronic coupling was large and electron transfer was adiabatic, the free energy of the reaction |ΔG^o| was less than that for nonadiabatic transfer. This finding should be taken into account in the design of hybrid materials for solar energy conversion and has broad implications to the many classes of electron-transfer reactions in biology and chemistry.

Abstract

Electron-transfer theories predict that an increase in the quantum-mechanical mixing (H_DA) of electron donor and acceptor wavefunctions at the instant of electron transfer drives equilibrium constants toward unity. Kinetic and equilibrium studies of four acceptor–bridge–donor (A-B-D) compounds reported herein provide experimental validation of this prediction. The compounds have two redox-active groups that differ only by the orientation of the aromatic bridge: a phenyl–thiophene bridge (p) that supports strong electronic coupling of H_DA > 1,000 cm⁻¹; and a xylyl–thiophene bridge (x) that prevents planarization and decreases H_DA < 100 cm⁻¹ without a significant change in distance. Pulsed-light excitation allowed kinetic determination of the equilibrium constant, K_eq. In agreement with theory, K_eq(p) were closer to unity compared to K_eq(x). A van’t Hoff analysis provided clear evidence of an adiabatic electron-transfer pathway for p-series and a nonadiabatic pathway for x-series. Collectively, the data show that the absolute magnitude of the thermodynamic driving force for electron transfers are decreased when adiabatic pathways are operative, a finding that should be taken into account in the design of hybrid materials for solar energy conversion.

Electron flow in natural photosynthesis is controlled, to a large extent, by the spatial arrangement of redox-active species in the electron transport chain whose formal reduction potentials provide a free-energy gradient (1–5). In artificial photosynthesis, this same strategy has been employed to vectorially translate electrons away from interfaces or toward catalytic sites (6–9). In each case, ideal electron flow occurs rapidly and quantitatively in one desired forward direction, without a significant loss in the Gibbs free energy, ΔG^o. In reality, electron transfer exists as an equilibrium with forward and reverse reactions regulated by the free energy that separates the redox-active species, |ΔG^o|. When |ΔG^o| approaches zero, the reverse reactions become more significant, resulting in electron flow in undesired directions. Strong electronic coupling between redox centers facilitates rapid electron transfer, but theoretical considerations indicate that this will result in a free-energy loss (10, 11). Many scientists in the growing fields of artificial photosynthesis for electrical power generation or solar fuel production do not consider the influence of electronic coupling on ΔG^o. This may be due to the fact that the theory that relates electronic coupling and ΔG^o has received little experimental attention (12, 13).

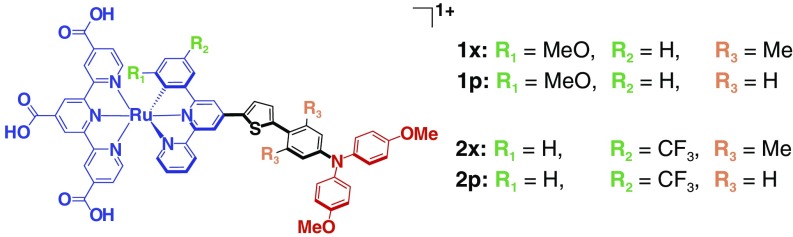
Herein, we describe a kinetic approach for quantifying the influence of electronic coupling on ΔG^o that was applied to acceptor–bridge–donor (A-B-D) compounds of the type shown in Fig. 1. The four cyclometalated ruthenium compounds shown contain an aromatic thiophene bridge to a triphenylamine (TPA) donor group. Electron withdrawing (-CF₃) or donating (-OMe, methoxy) substituents on the cyclometalating phenyl ring were used to tune the Ru^III/II potentials while the identity of the TPA^+/0 was fixed. These compounds are ideal for fundamental study as they provide TPA → Ru^III electron-transfer reactions that are thermodynamically unfavored (1x, 1p), ΔG^o > 0, or favored (2x, 2p), ΔG^o < 0. The influence of electronic coupling on the free-energy change was elucidated by the introduction of groups that disrupt conjugation in the aromatic bridge. For compounds (1p, 2p), a phenyl bridge unit allows planarity with the thiophene and thus promotes strong electronic coupling. On the contrary, the two methyl groups on the xylyl bridge of compounds (1x, 2x) inhibit planarity with the thiophene and decrease electron coupling. The 14-Å geometric distance between the amine N and the Ru center, garnered from density-functional theory (DFT) optimized structures, is the same for all four compounds such that the through-space electronic coupling is constant. The intense color changes associated with the Ru^III/II and TPA^+/0 redox chemistry enables small concentrations to be detected spectroscopically. To our knowledge, the combined optical, redox, and structural properties of these compounds are the most optimal available in the literature for determination of how electronic coupling influences the free-energy change of an electron-transfer reaction (14).

Fig. 1.

The A-B-D compounds. Four cylcometalated ruthenium compounds with carboxylic acid groups (for binding to TiO₂) and an aromatic bridge to a TPA. Methyl substituents in the R₃ positions––xylyl bridge (x)––lowers electronic coupling relative to the phenyl-bridge (p). The R₁ and R₂ substituents allow the E°(Ru^III/II) potentials be controlled for the 1 and 2 series while the E°(TPA^+/0) was held at parity.

Theoretical Prediction That Electronic Coupling, H_DA, Lowers ΔG^o

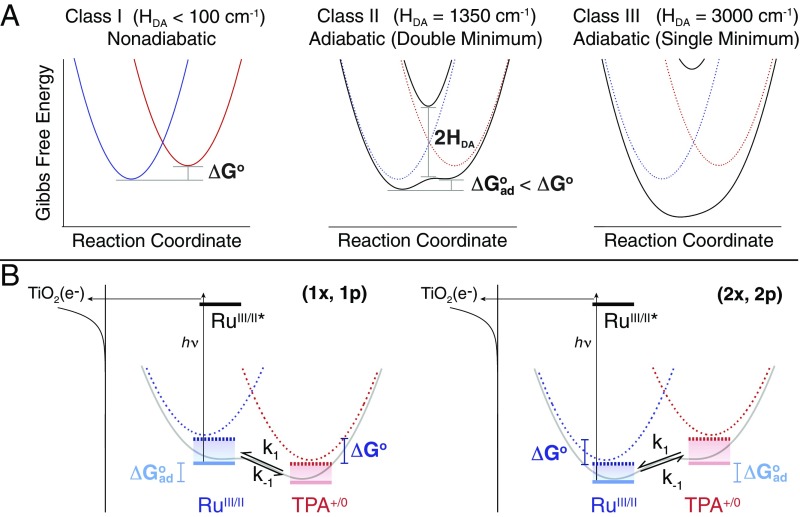
Consider a simplified A-B-D compound in which the quantum-mechanical interaction between an electron acceptor (A) and an electron donor (D) wavefunction is controlled by the bridge (B) that links them. The degree of mixing is quantified by the electronic coupling matrix element H_DA. Marcus theory holds that the many-fold potential surfaces for electron transfer can be represented as parabolic Gibbs free-energy surfaces (GESs) with fixed force constants, for the A-B-D “reactants” and the A⁻-B-D⁺ “products,” that are a function of a single reaction coordinate, Eq. 1 and Fig. 2 (10, 11, 15). Robin and Day have categorized the degree of electronic coupling between A and D in three distinct classes, Fig. 2A (16). When the bridge is insulating and no coupling occurs during the electron transfer, A and D retain their original identities and electron transfer occurs by a jump from the reactant to the product GES (Class I or nonadiabatic). At the opposite extreme where the bridge facilitates strong electronic coupling, the A and D GESs collapse to a single minimum GES (adiabatic Class III). Most common electron-transfer reactions in biology and chemistry, however, occurs with intermediate electronic coupling in the double-minimum GES (adiabatic Class II). Note that as H_DA increases in the progression from nonadiabatic to adiabatic Class II electron transfer, |ΔG^o| decreases to an adiabatic value, ΔG^o_ad, i.e., |ΔG^o| > |ΔG^o_ad|. This would indicate that the equilibrium and thus the directionality of electron transfer can be controlled by the nature of the bridge and its ability to promote electronic coupling. It is therefore of interest to test this prediction experimentally under a variety of conditions that include both weak and strong (12, 13) coupling.

Fig. 2.

The Gibbs free-energy surfaces and the kinetic approach. (A) GESs that represent a redox equilibrium between A-B-D (blue) and A⁻-B-D⁺ (red) as the electronic coupling matrix element (H_DA) is increased from 0 (nonadiabatic) to over 3,000 cm⁻¹ (adiabatic). Emphasis is placed herein on the reduction in the Gibbs free-energy change, |ΔG^o| > |ΔG^o_ad| that accompanies the transition from nonadiabatic to adiabatic electron transfer in the double-minimum regime. (B) The approach consists of a Ru^II-B-TPA compound anchored to the surface of mesoporous thin films of TiO₂ (the secondary acceptor). Light absorption induces excited-state electron injection from the Ru^II unit into the TiO₂ to form TiO₂(e⁻)|-Ru^III-B-TPA. Within the timeframe of charge recombination, the dynamic equilibrium Ru^III-B-TPA $\mathrm{\leftrightharpoons }$ Ru^II-B-TPA⁺ was quantified through a kinetic model that afforded the forward, k₁, and reverse, k₋₁, electron-transfer rate constants.

Kinetic Approach

The approach reported here exploits the dynamic aspect of equilibrium reactions through a broadly applicable kinetic model. Although equilibrium, as a “balance of opposing forces,” oftentimes invokes the false perception that the competing forces stop altogether when concentrations become time invariant (17), in fact, a dynamic equilibrium is emphasized in introductory science classrooms where the opposing forces are rate constants (Eq. 1), whose values can be quite large and depend only on the absolute temperature (18).

$$\text{A}-\text{B}-\text{D}\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{\text{A}}^{\mathrm{-}}-\text{B}-{\text{D}}^{+}.$$ [1]

Rate constants provide a direct measure of the equilibrium constant, K_eq, that may also be computed from the difference in the acceptor (A) and the donor (D) formal reduction potentials, ΔE^o = E^o(A^0/−) − E^o(D^+/0) through Faraday’s constant (F), Eq. 2

$${\text{K}}_{\text{eq}}=e^{\text{F}\mathrm{\Delta }{\text{E}}^{\text{o}}/\text{RT}}=e^{\left(-\mathrm{\Delta }{\text{G}}^{\text{o}}\right)/\text{RT}}=\frac{k_1}{k_{-1}}.$$ [2]

While relations like those given in Eq. 2 can be found in most introductory science books, direct estimates of K_eq values through independent electrochemical measurements of ΔE^o are only strictly correct for nonadiabatic electron transfer. Strong electronic interactions of the donor and acceptor redox orbitals at the instant of electron transfer will result in adiabatic electron transfer that is expected to decrease |ΔG^o| as was described above (10, 11, 15). Indeed, under such conditions ΔE^o is no longer an accurate indicator of the equilibrium or the true free-energy change. An alternative approach is to use kinetic data, yet previous attempts to quantify dynamic equilibria with pulsed-laser or line-broadening techniques have met limited success and have not provided temperature-dependent K_eq values (12, 13, 19–21). Kubiak and coworkers (12, 13) have previously investigated the influence of H_DA on ΔG° through the use of vibrational spectroscopy on “mixed-valence isomers,” which has shown that |ΔG°| in strongly coupled systems was less than values expected for nonadiabatic electron transfer.

The kinetic strategy, schematically shown in Fig. 2B, utilizes a pulsed laser to initiate electron transfer to a secondary acceptor whose recombination kinetics are sufficiently slow such that the approach to A-B-D $\mathrm{\leftrightharpoons }$ A⁻-B-D⁺ equilibrium can be time resolved spectroscopically. In this study, A-B-D compounds of the general form Ru^II-B-TPA were anchored to the surface of TiO₂ anatase nanocrystallites that serves as the secondary acceptor. Upon light absorption by the Ru^II constituent, a charge-transfer excited state injects an electron into TiO₂ to form TiO₂(e⁻)|-Ru^III-B-TPA, where Ru^III-B-TPA represents the A-B-D state of interest. Following electron injection, the TPA donor may transfer an electron to the oxidized Ru^III acceptor to give Ru^II-B-TPA⁺, which establishes the A⁻-B-D⁺ state (14). For all four compounds studied in this work, the Ru^III-B-TPA is the initial and reference A-B-D state after excited-state electron injection, such that electron transfer from the TPA donor to the Ru^III acceptor is thermodynamically unfavored for (1x, 1p), and favored for (2x, 2p) (Table 1). The millisecond lifetime of the injected TiO₂(e⁻) electron and the intense color changes associated with the Ru^III/II and TPA^+/0 redox chemistry, enabled the Ru^III-B-TPA $\mathrm{\leftrightharpoons }$ Ru^II-B-TPA⁺ dynamic equilibria to be measured spectroscopically and quantified through the proposed kinetic model. It is recognized that this light-initiated reaction technically yields a “quasi-equilibrium” since true equilibrium is achieved only when the injected electrons recombine with the oxidized compound. Nevertheless, related photochemical strategies have been widely utilized in fluid solution to characterize excited-state “equilibrium” reactions, most notably for the determination of excited-state pK_a* values of photoacids and photobases in aqueous solutions (22, 23). Consequently, this kinetic approach is expected to be of general utility for characterization of free-energy changes that accompany electron transfer in chemistry and biology.

Table 1.

Thermodynamic and electronic coupling parameters at room temperature

	Electrochemistry*,†			Kinetics*,‡	HDA, cm−1§
comp	Eo, TPA+/0	Eo, RuIII/II	−ΔGo/F	−ΔGo/F
1x	940	860	−80 (0.044)	−80 (0.044)	<100 (0.01)
1p	940	860	−80 (0.044)	−62 (0.089)	1,350 (0.17)
2x	940	1,010	+70 (16)	+68 (15)	<100 (0.01)
2p	940	1,030	+90 (35)	+54 (8.4)	1,350 (0.17)

^*Values given in millivolts vs. NHE.

^†Calculated with Eq. 2, using the electrochemical data, where F is the Faraday constant. Values in parentheses are the equilibrium constants, K_eq.

^‡Calculated with Eq. 2, using the kinetic data. Uncertainties in the values are ±10%. Values in parentheses are the equilibrium constants, K_eq.

^§Values in parentheses are given in electron volts.

Results and Discussion

The A-B-D Compounds.

All four compounds were available from our previous studies and their measured redox properties are summarized in Table 1 (14). Of note is the fact that the E^o(TPA^+/0) = 0.94 V vs. the normal hydrogen electrode (NHE) for all four compounds and E^o(Ru^III/II) was 1.03 V for 2p, 1.01 V for 2x, and 0.86 V for 1x and 1p. For 2p in particular, where the TPA redox center was oxidized first, the more positive E^o(Ru^III/II) value likely emanates from the inductive influence of the oxidized TPA group transmitted through the strongly coupled phenyl bridge. Nevertheless, ΔE^o = E^o(Ru^III/II) − E^o(TPA^+/0) was insensitive to the bridge identity for 1p and 1x and changed by 20 mV for 2p and 2x (Table 1).

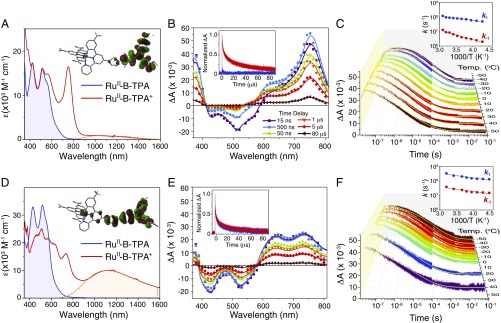
Representative UV-vis absorption spectra of 2x and 2p anchored to an oxide surface (Fig. 3 A–D) show extinction coefficients for the phenyl-bridged 2p compound that were about 30–50% larger than those measured for its xylyl-bridged analog 2x; consistent with greater electronic coupling afforded by the phenyl bridge (14, 24). DFT calculations (Fig. 3 A–D, Insets) reveal that the highest occupied molecular orbital (HOMO) for 2p is more delocalized over the thiophene bridge and has both Ru and TPA character, while the HOMO for 2x was localized predominantly on the TPA group. The appearance of an intervalence transition “IT” absorption band centered around 1,100 nm in the one-electron oxidized mixed-valent Ru^II-B-TPA⁺ state enabled quantitative analysis of the electronic coupling. Application of the two-state generalized Mulliken–Hush expression (25, 26) provided H_DA = 1,350 cm⁻¹ for 2p, and H_DA < 100 cm⁻¹ for 2x. Electronic coupling values for (1x, 1p) were estimated to be equivalent to those measured for (2x, 2p), respectively, which indicated that the identity of the bridge unit, either xylyl or phenyl, determines the degree of electronic coupling (27). The details of this analysis are given in SI Appendix.

Fig. 3.

Electronic properties and transient absorption data. (Left) The visible absorption spectra of 2x (A) and 2p (D) anchored to In₂O₃:Sn thin films. Highlighted in the shaded orange area are the intervalence transition bands. (Insets) Molecular structure with the overlaid HOMOs generated from DFT calculations. (Center) Absorption difference spectra measured at the indicated delay times after laser excitation for 2x (B) and 2p (E). (Insets) Normalized single-wavelength kinetic data monitored at 700 nm (that report predominantly on TPA⁺ concentrations) and at 510 nm (due to Ru^III). (Right) Single-wavelength data that report on the time-dependent TPA⁺ concentration as a function of temperature for 2x (C) and 2p (F). Overlaid in yellow are fits to the kinetic model used, as described in SI Appendix. (Insets) Arrhenius plots of the forward, k₁, and reverse, k₋₁, rate constants. All experiments were performed in 0.1 M LiClO₄/CH₃CN solution.

Application of the Kinetic Approach.

The transient spectra measured after pulsed green-light excitation of 2x and 2p are given in Fig. 3 B–E, respectively. The room-temperature spectra reveal the appearance of an absorption band at ∼750 nm that is characteristic of the oxidized donor TPA⁺ that could not be time resolved for 2p. Hence the transient spectra alone provide direct evidence that the redox equilibrium is established more quickly for the adiabatic electron-transfer reaction. In fact, the transient spectra recorded at any delay time after light excitation of 2p were superposable when normalized, demonstrating that equilibrium was achieved on a sub-10-ns time scale at room temperature, whereas at lower temperatures, the appearance of TPA⁺ could be partially time resolved (see below). The insets show kinetic data that correspond to recombination of the injected electron with TPA⁺ and the Ru^III center, the latter of which was much faster for the xylyl bridge (14).

Temperature-dependent kinetic data, over an 80° range, that report on the transient TPA⁺ concentration for compounds 2x and 2p (Fig. 3 C–F) are shown with overlaid kinetic fits. Under all conditions, the transient data fully recovered to initial values within 10 ms with no evidence of net photochemistry. The kinetic model utilized has previously been reported for excited-state acid base equilibria (22, 23) and was constrained here with kinetic data from a model compound, that did not contain the pendant TPA group, which accounted for the nonexponential nature of the interfacial back-electron-transfer reaction (SI Appendix). The insets show the classical Arrhenius analysis of the k₁ and k₋₁ values extracted from the kinetic data. The observed temperature dependence, evident for all four compounds, is indicative of a significant activation barrier that provides clear evidence that the electronic coupling was insufficient to collapse the GES to a single minimum, i.e., Class III behavior, Fig. 2A.

For 1p and 2p (see SI Appendix, Fig. S1B for 1p data), the forward and reverse rate constants displayed the same temperature dependence. In sharp contrast, the introduction of the methyl substituents in 2x decreased the forward rate constant by over an order of magnitude, while k₋₁ also decreased significantly and became more temperature dependent. The expectation from transition-state theory that the rate constant for the thermodynamically uphill reaction would increase with increasing H_DA was realized. The generality of this finding held true for the endothermic equilibrium of 1x, where kinetic analysis demonstrated that the uphill reaction, Ru^III-B-TPA → Ru^II-B-TPA⁺, was more temperature dependent (SI Appendix, Fig. S1A, Inset). This is understood by an increased H_DA that lowers the barrier for the uphill reaction to a greater extent than for the exothermic reaction. For both xylyl-bridged compounds (1x, 2x), the slow unfavored reaction rate constant approached the same value of that for the favored reaction as the temperature was raised. Classical Arrhenius analysis provided the barriers, E_a, and preexponential factors, ln(A), for electron transfer (Table 2). The similar ln(A) values indicated that differences between adiabatic and nonadiabatic kinetics do not originate from changes in dynamic crossing events, but are instead controlled by a smaller activation barrier E_a for the uphill process, Ru^III-B-TPA → Ru^II-B-TPA⁺ for 1p, and Ru^II-B-TPA⁺ → Ru^III-B-TPA for 2p.

Table 2.

Arrhenius parameters extracted from temperature-dependent rate constants

	ln(A)		Ea
Comp.	k1	k−1	k1	k−1	ΔHo	ΔSo
1x	22.0	21.8	14.4	6.44	7.9	1.5
1p	21.2	19.1	4.8	5.40	0.0	−18
2x	20.5	20.8	5.4	12.5	−7.0	−2.6
2p	21.7	19.6	5.8	6.1	0.0	17

E_a and ∆H° values are in kJ mol⁻¹. ∆S° values are in J mol⁻¹⋅K⁻¹. SE: ln(A) ± 0.2, E_a ± 0.5, ∆H° ± 0.4, ∆S° ± 1.5. Arrhenius equation, $\text{k}=\text{A}*\exp \left(-{\text{E}}_{\text{a}}/\text{RT}\right)$. The rate constants for electron transfer are: k₁ (TPA → Ru^III) and k₋₁ (Ru^II → TPA⁺).

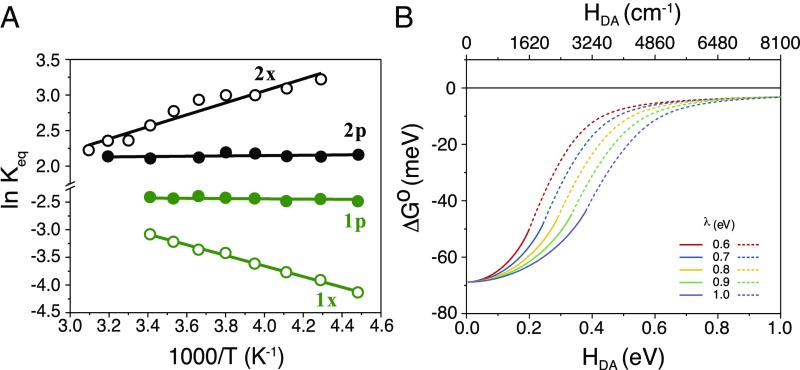
Classical van’t Hoff representations (18) of the temperature-dependent equilibrium data given in Fig. 4A and Eq. 3,

$$\text{ln}\hspace{0.17em}{\text{K}}_{\text{eq}}=-\frac{\mathrm{\Delta }{\text{G}}^{\text{o}}}{\text{RT}}=-\frac{\mathrm{\Delta }{\text{H}}^{\text{o}}}{\text{RT}}+\frac{\mathrm{\Delta }{\text{S}}^{\text{o}}}{\text{R}},$$ [3]

provide a vividly clear demonstration that K_eq was closer to unity for the phenyl-bridged (1p, 2p) compounds, and hence |ΔG^o| was smaller for the more strongly coupled equilibrium. This finding is completely in line with theoretical predictions and the pioneering work of Kubiak and coworkers (12, 13). Before discussing the broader impacts it is worthwhile to consider more carefully the specific data in Fig. 4A.

Fig. 4.

van’t Hoff analysis and the influence of electronic coupling on Gibbs free energy. (A) A van’t Hoff plot, ln K_eq vs. 1,000/T, of the electron-transfer equilibrium constants with overlaid best-fit lines that demonstrates an adiabatic mechanism for (1p, 2p) and nonadiabatic for (1x, 2x). (B) Effect of electronic coupling on the Gibbs free energy for electron transfer calculated from numerical analysis of the GESs (Eq. 4) with the indicated reorganization energies, λ. The solid lines represent the progression of the nonadiabatic ΔG^o to the adiabatic value, ΔG^o_ad, limited to the double-minimum regime. The dotted lines denote fictitious ΔG^o_ad values for a GES collapsed to a single minimum.

The van’t Hoff plot demonstrates an adiabatic equilibrium for the phenyl-bridged compounds and a nonadiabatic one for the xylyl-bridged compounds. In other words, there is no evidence for thermal energy transfer at constant pressure for the phenyl-bridged compounds, i.e., q_p = ΔH^o = 0 kJ mol⁻¹ (Table 2). In contrast, the strong temperature dependence for 1x and 2x emanates from an enthalpically favored (ΔH^o = −7.0 kJ mol⁻¹) and unfavored (ΔH^o = +7.9 kJ mol⁻¹) electron-transfer equilibrium, respectively. These data represent a notable contribution to the literature as calorimetric characterization of intramolecular electron transfer is difficult to obtain and most discussions of adiabatic vs. nonadiabatic electron transfer are subjective, i.e., adiabaticity is inferred from rate constants or other observations.

Extrapolation of the xylyl-bridged data in the van’t Hoff plot to higher temperatures suggests that a common equilibrium constant would be reached for the xylyl- and phenyl-bridged compounds around 350 K. At this temperature, thermal motion in the xylyl bridge is expected to provide sufficient coupling to access an adiabatic electron-transfer pathway; however, the boiling point of CH₃CN precluded experimental confirmation of this. Notwithstanding the possibility of a slope change at higher temperature for xylyl-bridged compounds, the van’t Hoff analysis indicated a small entropic contribution, |ΔS°| = 2 ± 3 J mol⁻¹⋅K⁻¹. For the phenyl-bridged compounds |ΔS°| = 17 ± 3 J mol⁻¹⋅K⁻¹ and provides the predominant contribution to ∆G°. The enthalpies and entropies for the adiabatic and nonadiabatic reactions are presented in Table 2.

Free-Energy Loss due to Coupling.

Significantly, the van’t Hoff data reveal that |ΔG^o| was smaller for the adiabatic equilibrium of both phenyl-bridged compounds over the entire 80° temperature range. This finding naturally raises two interrelated questions of relevance to maximizing the free energy stored in artificial photosynthesis: (i) How much free energy can be lost due to coupling? and (ii) What amount of coupling is necessary to collapse the double-minimum GES into a single minimum? The second question could be rephrased to ask, when does H_DA become so large that the electron is delocalized over both redox centers such that equilibrium no longer has any physical meaning? The answers to these questions depend on the magnitudes of ΔG^o, H_DA, and the reorganization energy λ (10, 11). Fortunately, the ground- and excited-state GESs can be calculated exactly with Eq. 4 that has been previously reported (see also SI Appendix) (10, 11).

$${\text{G}}_{\pm }=\frac{\left[\lambda \left(2X^2-2X+1\right)+\mathrm{\Delta }{\text{G}}^{\text{o}}\right]}{2}\pm \frac{{\left[{\left(\lambda \left(2X-1\right)-\mathrm{\Delta }{\text{G}}^{\text{o}}\right)}^2+4{\text{H}}_{\text{DA}}^2\right]}^{1/2}}{2}.$$ [4]

The first derivative of the lower GES expression, G₊, provides x intercepts that indicate the reaction coordinate X positions for the two minima and the transition state (provided that one exists) which can then be analyzed. An example is given below.

Consider 2x and 2p whose GESs, shown in Fig. 2, are generated from Eq. 4 with λ = 0.6 eV and ΔG^o = −70 mV, H_DA = 0 eV for 2x, and H_DA = 0.17 eV (1,350 cm⁻¹) for 2p. When H_DA increased from 0 to 1 eV, the nonadiabatic ΔG^o = −70 mV characteristic of 2x remains essentially constant until about H_DA = 0.040 eV (Fig. 4B). With increasing H_DA values, the adiabatic ΔG^o_ad monotonically decreases and eventually the GES collapses to a single minimum, at the point where the solid lines become dashed in Fig. 4B, i.e., Class II → Class III behavior. At this point about 25% of the free energy is lost. Interestingly, the double-minimum GES survives at much larger H_DA when λ is increased to 1.0 eV. SI Appendix, Figs. S3 and S4 shows that H_DA value necessary for collapse increases linearly with λ. We note that Dutton and coworkers have shown that a λ of 0.6 eV for proteins and 1.0 eV for aqueous solution is sufficient to model much electron-transfer data regardless of the medium that separates the A and D (28–30). When |ΔG^o| is greater than 70 mV, Class III behavior occurs at weaker electronic coupling. Indeed, for self-exchange reactions, when ΔG^o = 0, the double minimum survives to H_DA = 0.5 eV for λ = 0.6 eV (SI Appendix, Fig. S4B). However, in self-exchange reactions, the products and reactants are the same and a free-energy gradient for vectorial electron transport is lost. Nevertheless, concentration gradients have been successfully used to transport charge toward an electrode for solar cell applications (31). In summary, this analysis indicates that the magnitude of |ΔG^o| lost to electronic coupling is significant and should be considered in artificial photosynthesis design. As the open-circuit photovoltage V_oc represents the maximum Gibbs free energy a regenerative solar cell can produce, the loss of >10 mV is highly significant. Indeed, a 3-mV loss in V_oc was recently reported when a donor–acceptor adduct was formed and it is likely that this enhanced coupling turned on an adiabatic pathway (32).

It is worthwhile to consider how natural photosynthesis utilizes electronic coupling to control the flow of electrons. In purple bacteria, H_DA is sufficient for adiabatic electron transfer in the special pair and the subsequent electron-transfer steps are nonadiabatic (2, 3, 5, 33). Other photosystems also show decreased electronic coupling when the redox-active groups are more spatially separated from the excited state (2–5, 33). Presumably these photosystems evolved to efficiently transfer electrons when a kinetic competition with excited-state decay existed and the subsequent vectorial electron-transfer steps occurred nonadiabatically to minimize free-energy loss (2, 3, 5, 33). These particular molecules have been used in artificial photosynthesis, specifically in dye-sensitized solar cells (14). It was found that the strong coupling afforded by the phenyl bridge resulted in more delocalized orbitals that promoted faster recombination with the injected electrons with the oxidized molecules. It is now clear that a weakly coupled secondary donor should be employed with a small free-energy gradient to translate the charge further from the interface. Therefore, natural and artificial photosynthesis utilize adiabatic pathways for electron-transfer reactions that occur in kinetic competition with fast excited-state relaxation processes and nonadiabatic pathways to shuttle redox equivalents to catalytic or other redox active sites. The data reported herein indicate that the magnitude of the electronic coupling should be carefully tuned so as to minimize free-energy loss.

The demonstration of a K_eq value closer to unity––or reduced |ΔG^o|––for electron-transfer reactions that follow adiabatic, relative to nonadiabatic, pathways has broad implications. Taube indicated that adiabatic electron transfers were possible whenever H_DA > 2kT (34, 35), and thus are potentially relevant to many classes of electron transfer in biology and chemistry, including redox titrations that are commonly performed in undergraduate laboratories. Such bimolecular chemistry, and others in general, involves diffusion of the A and the D to form an encounter complex prior to electron transfer (11, 36). The free-energy change associated with the encounter complex formation is small in polar solvents, but becomes more significant in low dielectric media (37). If coupling within the encounter complex is strong at the instance of electron transfer, an adiabatic pathway may be operative that is expected to decrease the yield of products from that calculated based on formal reduction potentials. Indeed, a recent literature report of light-driven bimolecular electron transfer in acetonitrile and ionic liquids with H_DA values between ∼100 and 1,500 cm⁻¹ showed that the rate constants could only be satisfactorily modeled when the ΔG^o values were lower than those measured electrochemically (38). This behavior is consistent with coupling lowering the free-energy change. Indeed, when any encounter complex is sufficiently coupled, such as those that occur by an inner-sphere mechanism where an atom, ion, or molecule, bridge the donor and acceptor, a loss in free energy should be anticipated.

Conclusions

In summary, light-initiated kinetic measurements have provided temperature-dependent equilibrium constants for fundamental adiabatic and nonadiabatic electron transfer. It was found that the absolute value of ΔG^o decreased for the adiabatic equilibria as was predicted theoretically decades ago (10, 11). A virtue of adiabatic electron transfer is that equilibrium is rapidly achieved, but the data described herein show that this comes with a loss in free energy and more delocalized wavefunctions that can promote undesired reactions. Subtle structural changes were found to dramatically influence electron-transfer reactions on the adiabatic/nonadiabatic borderline, and the results presented here teach how this influences fundamental chemical equilibrium. The data indicate that adiabatic pathways provide a more rapid approach to equilibrium that comes at the expense of some free-energy loss (17). On the other hand, the slower nonadiabatic path ultimately conserves more free energy in redox equilibrium and in vectorial transport chains for natural and artificial photosynthesis.

Experimental

All materials and reagents were used as received from the indicated commercial suppliers: acetonitrile (CH₃CN, spectrophotometric grade; Burdick & Jackson); lithium perchlorate (LiClO₄, ≥99.99%; Sigma-Aldrich); glass microscope slides (1-mm thick; Fisher Scientific); fluorine-doped SnO₂-coated glass (FTO, 2.3-mm thick, 15 Ω/cm²; Hartford Glass Co. Inc.). All compounds were synthesized as previously described (14).

Experimental methods for sample preparation, UV-vis and NIR absorption, transient absorption, electrochemistry, and DFT calculations are presented in SI Appendix.