Significance
Neurons fire action potentials to transfer information through synaptic release of neurotransmitter. At presynaptic terminals, the pattern of action potential discharge is integrated through dynamic Ca2+ signaling by the presynaptic machinery which triggers the release of neurotransmitter. It is generally accepted that the rate and the temporal precision of action potential firing support information transfer between neurons. Here, we show that in contrast to rate and temporal coding, giant mossy fiber terminals count the number of action potentials during trains to trigger CA3 pyramidal cell firing. Our results shed light on the synaptic signal transfer mechanisms supporting an additional information coding strategy in the brain.
Keywords: short-term plasticity, presynaptic release, mossy fiber, hippocampus
Abstract
Neuronal communication relies on action potential discharge, with the frequency and the temporal precision of action potentials encoding information. Hippocampal mossy fibers have long been recognized as conditional detonators owing to prominent short-term facilitation of glutamate release displayed during granule cell burst firing. However, the spiking patterns required to trigger action potential firing in CA3 pyramidal neurons remain poorly understood. Here, we show that glutamate release from mossy fiber terminals triggers action potential firing of the target CA3 pyramidal neurons independently of the average granule cell burst frequency, a phenomenon we term action potential counting. We find that action potential counting in mossy fibers gates glutamate release over a broad physiological range of frequencies and action potential numbers. Using rapid Ca2+ imaging we also show that the magnitude of evoked Ca2+ influx stays constant during action potential trains and that accumulated residual Ca2+ is gradually extruded on a time scale of several hundred milliseconds. Using experimentally constrained 3D model of presynaptic Ca2+ influx, buffering, and diffusion, and a Monte Carlo model of Ca2+-activated vesicle fusion, we argue that action potential counting at mossy fiber boutons can be explained by a unique interplay between Ca2+ dynamics and buffering at release sites. This is largely determined by the differential contribution of major endogenous Ca2+ buffers calbindin-D28K and calmodulin and by the loose coupling between presynaptic voltage-gated Ca2+ channels and release sensors and the relatively slow Ca2+ extrusion rate. Taken together, our results identify a previously unexplored information-coding mechanism in the brain.
Neurons encode and transmit information in the frequency and temporal precision of action potentials (APs) they discharge (1, 2). Presynaptic terminals are key elements involved in the translation of electrical signals to neurotransmitter release and further electrical signaling in the target postsynaptic cell (3). The distinct spatial assembly of voltage-gated Ca2+ channels (VGCCs), Ca2+ buffers and vesicular Ca2+ release sensors confers specific properties to presynaptic terminals (4). As such, neurotransmitter release is dynamically modulated during trains of APs and can be facilitated, depressed, or remain constant. This dynamic modulation of neurotransmitter release is thought to support the neuronal code used to transfer information (5). However, it remains generally unknown how a given presynaptic terminal leverages its attribute to transfer information to its postsynaptic partners.
During active states, several types of neurons fire in bursts. For example, hippocampal granule cells fire infrequently, but discharge bursts of APs with highly variable frequencies (6, 7). Remarkably, the probability of CA3 pyramidal cell firing increases several fold during granule cell burst firing in vivo (8). This increase in firing probability is supported by the extensive short-term facilitation observed at this synapse both in vitro (9–11) and in vivo (12). However, how presynaptic mossy fiber bouton (MFB) terminals decode the frequency and the number of APs in incoming bursts to transmit information remains poorly understood.
To probe how MF terminals integrate bursts of APs, we combined electrophysiological measurements in acute hippocampal slices with rapid presynaptic two-photon Ca2+ imaging and experimentally constrained modeling. We show that giant MFB terminals count the number of APs during bursts through a distinctive interplay between local and global presynaptic Ca2+ dynamics and buffering and Ca2+-triggered vesicular release and replenishment. This leads to postsynaptic CA3 pyramidal cell firing which is independent of the average burst frequency in the granular cell and only depends on the number of spikes and on the interspike interval between the two last APs in the burst. Altogether, our results elucidate how MFBs integrate incoming bursts of APs to propagate information to CA3 pyramidal neurons.
Results
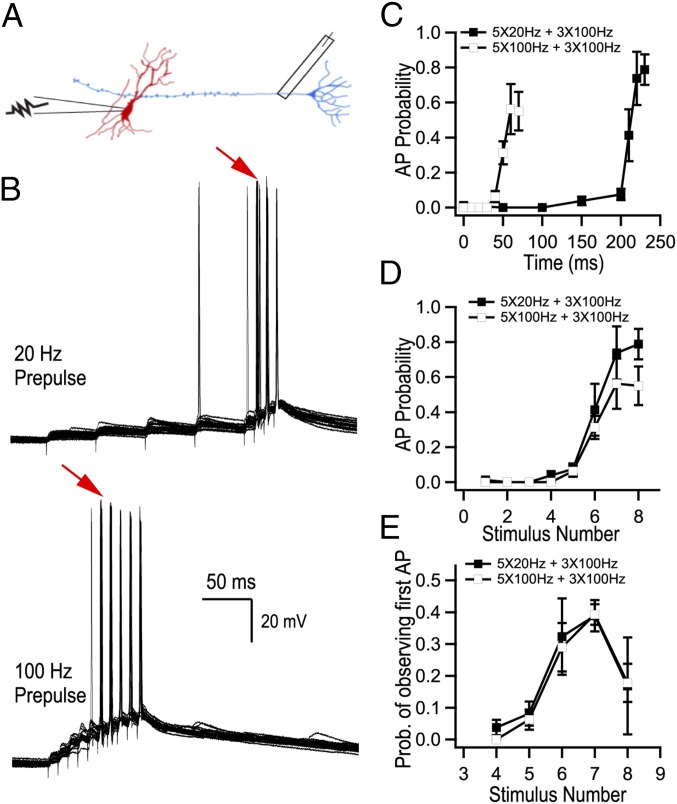
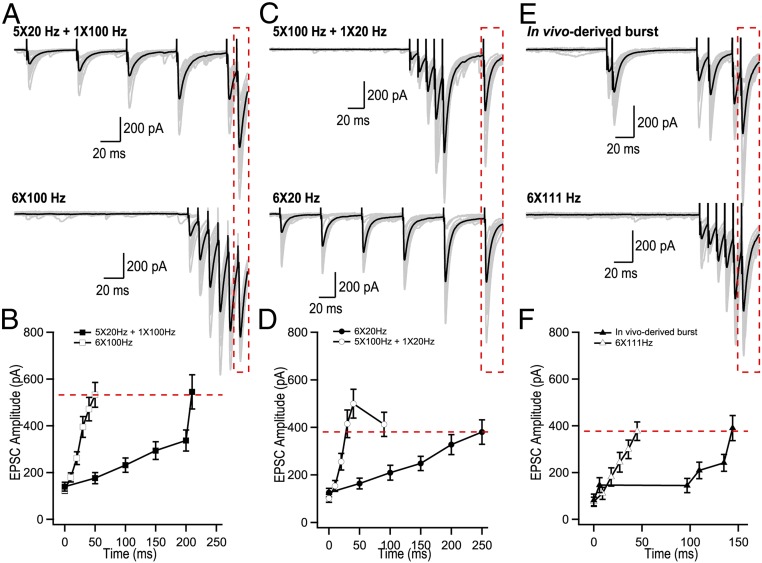
We first aimed to determine how AP transmission to CA3 pyramidal cells is encoded by the frequency and the number of APs discharged by granule cells. We recorded CA3 pyramidal cells in current clamp and stimulated mossy fibers using trains of APs with the initial frequency of the first five stimuli delivered at 20 or 100 Hz and the last three stimuli fixed at 100 Hz (Fig. 1A). As expected, AP firing by CA3 cells progressively increased during mossy fiber stimulation (Fig. 1 B–D). The probability of observing the first postsynaptic spike sharply increased at the sixth stimuli (Fig. 1E). Both the probability of CA3 pyramidal cell firing at the sixth stimulus and the probability of observing the first AP were independent from the initial burst frequency (Fig. 1 D and E). This suggests that AP transmission at MFB terminals is mainly determined by the number of spikes within the train and not by the average train frequency. Glutamate release from MFBs is greatly amplified during trains of stimuli (10, 13, 14), however how the frequency and number of stimuli are translated to specific patterns of glutamate release remains unknown. We varied the burst frequency and the number of stimuli to dissect the contribution of these two parameters. The sixth evoked postsynaptic current (EPSC) amplitude in a 5 × 20-Hz + 1 × 100-Hz burst was nearly identical to the sixth EPSC amplitude of a pure 100-Hz train (Fig. 2 A and B). Similarly, the sixth EPSC amplitude of a 5 × 100-Hz + 1 × 20-Hz burst closely matched the amplitude of the sixth EPSC in a 20-Hz train (Fig. 2 C and D). We next tested whether a burst derived from an in vivo recording of granule cell firing would result in the same phenomenon, by selecting a burst of six APs with inconstant frequencies (in vivo data supplied by György Buzsáki, New York University, New York). Our results show that the sixth EPSC from this in-vivo–derived burst was identical to the sixth EPSC from a pure 111-Hz train (Fig. 2 E and F). This supports the idea that the average frequency of the train is not a determining factor of the rate of glutamate release. Instead, the number of preceding stimuli and the timing of the last stimulus appear to dictate the efficiency of synchronous glutamate release at the last sixth spike. These data argue that MFB terminals use a counting logic. We confirmed that such counting logic was observed for any stimulus number between 2 and 10 (SI Appendix, Fig. S1 A and B) and for frequencies between 10 and 100 Hz (SI Appendix, Fig. S1C). Synaptic plasticity can be observed at various time scales and hence potentially can provide multiplexed coding strategies. We therefore investigated how post-tetanic potentiation (PTP) influences the number of presynaptic stimuli required to evoke a postsynaptic AP. In agreement with a recent report (15), we observed that PTP transiently reduces the number of presynaptic stimuli required to trigger a postsynaptic AP from 6 to 3, an effect which lasted on the order of ∼50 s (SI Appendix, Fig. S2). Thus, the counting logic in MFBs can be efficiently modulated by PTP. Ca2+-dependent neurotransmission involves both synchronous and asynchronous events. Although in our experimental conditions asynchronous release does not substantially contribute to the depolarization of a postsynaptic cell during short, high-frequency bursts of APs (SI Appendix, Fig. S3), our results argue that asynchronous release could further enhance the counting logic mediated by the synchronous component. Indeed, the linear dependency of the asynchronous component on the stimulation frequency (SI Appendix, Fig. S3B) implies that the number of quanta released between any two presynaptic APs (which is the product of the asynchronous release rate and interstimulus interval) should not depend on the stimulation frequency.
Fig. 1.
Transmission of information to CA3 pyramidal cells depends on the number of APs in bursts. (A) Cartoon based on an original drawing of Ramón y Cajal showing the recording configuration for experiments performed in Fig. 1 (replicated from ref. 41). Whole-cell recordings were obtained from CA3 pyramidal neurons and MF axons were electrically stimulated. (B) Representative current-clamp recordings from a CA3 pyramidal cell. The red arrows point to the sixth stimulus in the trains where postsynaptic AP probability increased sharply. (C and D) CA3 pyramidal cell firing probability as a function of time (C) and of the number of APs (D) during two stimulation paradigms. (E) Probability of observing the first AP. Both AP probability and the probability of observing the first AP are mainly determined by the number of preceding APs but not by the average burst frequency (B–E, n = 5 cells).
Fig. 2.
Glutamate release from MFB terminals operates through a counting logic. (A–F) Analysis of short-term facilitation at MFBs. (A, C, and E) Representative trains of EPSCs recorded using indicated stimulation paradigms. Gray traces, single trials; black traces, the averages of 20 trials. (B, D, and F) Summary graphs showing average EPSC amplitude as a function of time (n = 19 for 20 Hz; n = 15 for 5 × 20 Hz + 1 × 100 Hz; n = 25 for 100 Hz; n = 10 for 5 × 100 Hz+ 1 × 20 Hz; n = 9 for in-vivo–derived burst; n = 9 for 6 × 111 Hz).
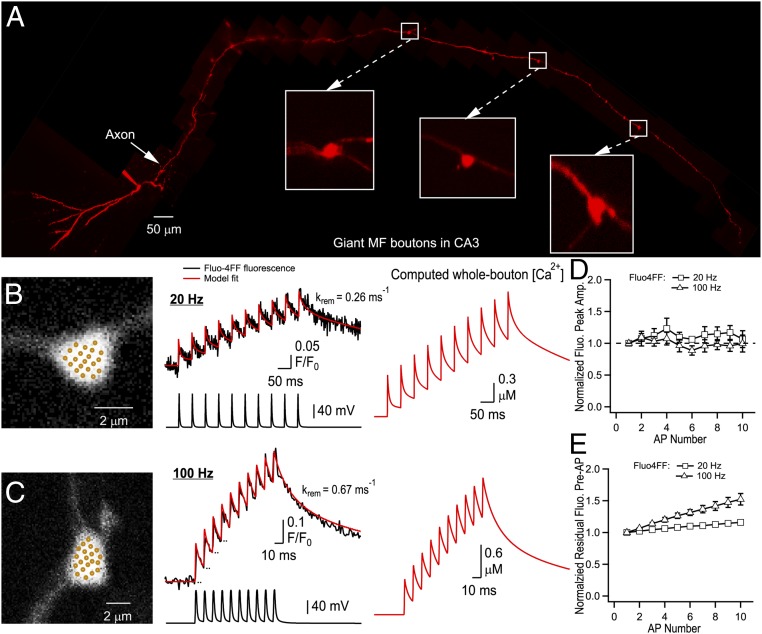
To gather insights on the presynaptic determinants of the counting logic, we next performed fast whole-bouton two-photon random-access Ca2+ imaging using the low-affinity Ca2+ indicator Fluo-4FF to measure the dynamic modulation of presynaptic [Ca2+] during AP trains (Fig. 3). We found that the amplitude of AP-evoked Ca2+-fluorescence transients remained constant during AP bursts (Fig. 3 B–E). This indicates that the total magnitude of AP-evoked Ca2+ influx does not change during 20- or 100-Hz stimulations and therefore, modulation of VGCC activity is unlikely to contribute to short-term plasticity in MFB terminals. We next explored the presynaptic Ca2+ dynamics by direct fitting of the experimental traces using a nonstationary single-compartment model (16, 17) (Fig. 3 B and C and Materials and Methods). The model, which incorporated three major endogenous Ca2+ buffers known to be present in MFBs [calbindin-D28K (CB), calmodulin (CaM), and ATP] provided close fits of the experimental data (Fig. 3 B and C and SI Appendix, Fig. S4). It is noteworthy that a similar model with a single fast high-affinity endogenous buffer (18) could not replicate the Ca2+ imaging data (SI Appendix, Fig. S5). The fitting allowed us to estimate Ca2+ removal rate in our experimental conditions ( range 0.2–0.7 ms−1), which was in close agreement with previous estimates obtained with high-affinity Ca2+ indicator Fluo-4 (16).
Fig. 3.
Ca2+ dynamics in MFB terminals. (A) Montage of multiple two-photon Z-stack maximal projections showing the axon anatomy of a typical granule cell filled with a morphological tracer AlexaFluor 594. The intact axon was followed to the CA3 region, where it formed giant MFB terminals (Insets). (B and C) Representative measurements of Ca2+ dynamics in two MFBs. (Left) Bouton morphology; dots indicate recording positions for random-access two-photon Ca2+ imaging. (Middle) Corresponding whole-bouton Ca2+ Fluo-4FF fluorescence elevations in response to 20- and 100-Hz AP stimulations (black traces, average of 140 and 133 sweeps, respectively). The red curves represent the nonstationary single-compartment model fit corresponding to Δ[Ca2+]total = 33.3 μM; model-predicted values of are shown for each bouton. (Right) Corresponding AP-evoked whole-bouton [Ca2+] transients computed using the nonstationary model. (D and E) Normalized peak amplitude of AP-evoked Fluo-4FF fluorescence (D) and residual Fluo-4FF fluorescence (E) as a function of AP number (n = 7 MFBs for both 20- and 100-Hz stimulation).
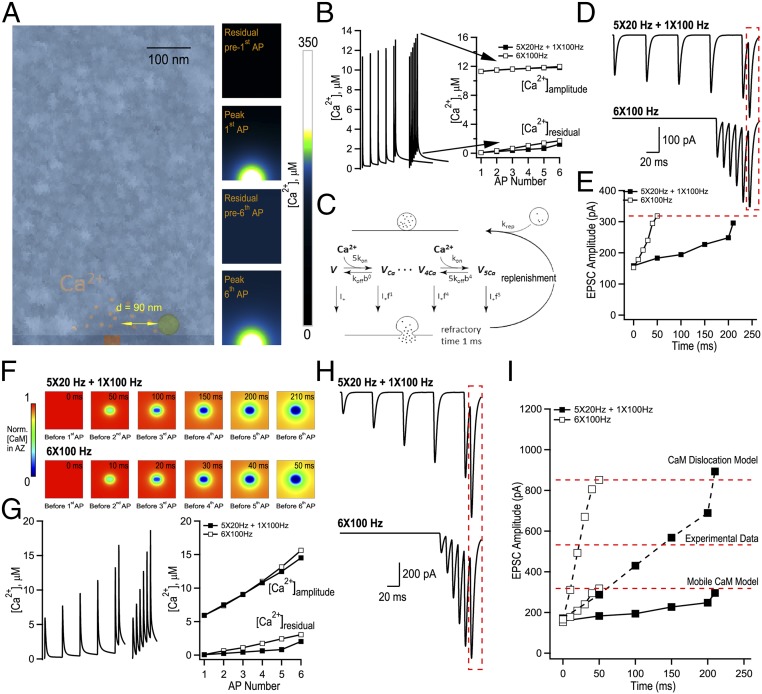
To understand whether the interplay between presynaptic Ca2+ dynamics and endogenous Ca2+ buffering can lead to AP counting, we performed quantitative modeling of AP-evoked Ca2+ influx, buffering and diffusion, and glutamate release in MFBs. The 3D model incorporated key ultrastructural and functional properties of MFBs including multiple release sites, experimentally constrained presynaptic Ca2+ dynamics, and loose coupling between VGCCs and vesicular release sensors (16, 18–20) (Fig. 4 and Materials and Methods). The simulation unit, which represented a part of MFB with a single release site, was modeled as a parallelepiped of size 0.5 µm × 0.5 µm × 0.79 µm with a single VGCC cluster in the middle of the bottom base (Fig. 4A). As in the case of the single-compartment model, we assumed the presence of three major MFB endogenous Ca2+ buffers: CB, ATP, and CaM. At physiological conditions CaM is known to be distributed between membrane-bound and mobile states, and this distribution is regulated by intracellular [Ca2+] (21–23). We first considered a limiting case of “Mobile CaM” model. We simulated spatial MFB Ca2+ dynamics in response to bursts of APs and used the obtained transients at the release site (90 nm away from the VGCC cluster, Fig. 4B) to perform simulations of vesicular release using a Monte Carlo implementation of Ca2+-activated vesicle fusion model (20) (Fig. 4C and SI Appendix, Fig. S6). To account for vesicle replenishment during AP bursts we included a vesicle replenishment step in the model and experimentally constrained the replenishment rate constant ( 20 s−1) (SI Appendix, Fig. S7). We found that Mobile CaM model indeed replicated the AP counting during mixed 20- and 100-Hz AP trains (Fig. 4 D and E and SI Appendix, Fig. S8). What mechanisms underlie the counting logic? The model predicted that the peak values of Ca2+ transients () were gradually augmented during AP bursts which was mainly attributed to the increase in residual and was mostly independent of the stimulation frequency (Fig. 4B). This argues that EPSC facilitation predicted by Mobile CaM model was due to accumulation and not due to endogenous Ca2+ buffer saturation [which normally leads to a progressive increase of the amplitudes of individual AP-evoked Ca2+ transients (18)]. Indeed, the model revealed that fast and low-affinity CaM N lobe did not show progressive saturation. However, slower and high-affinity buffers CB and CaM C lobe did saturate during AP bursts (SI Appendix, Fig. S9). This at first sight contradictory observation was fully in line with the dominant effect of CaM N lobe on release site Ca2+ dynamics and vesicle fusion (21) (SI Appendix, Fig. S10).
Fig. 4.
Modeling of evoked presynaptic Ca2+ dynamics and vesicular release reveals a plausible mechanism for AP counting logic in MFB terminals. (A, Left) Geometry of a parallelepiped-shaped modeling unit (0.5 µm × 0.5 µm × 0.79 µm) used in VCell simulations representing part of an MFB containing a single AZ with a 40 nm × 80 nm VGCC cluster, overlaid with a representative electron microscopy image that depicts part of an MFB with a single AZ (see Materials and Methods for details). (A, Right) Snapshots of VCell-computed spatial [Ca2+] profiles in the central XZ modeling unit plane during 6 × 100-Hz AP stimulation in the limiting case of Mobile CaM model. (B, Left) VCell-computed [Ca2+] transients at the release site located at 90 nm away from the VGCC cluster during 6 × 100 Hz and 5 × 20 + 1 × 100-Hz AP trains. (B, Right) Plot of corresponding residual [Ca2+]residual and amplitude [Ca2+]amp = [Ca2+]peak − [Ca2+]residual respectively, before and after each AP in the trains. (C) Schematics of the modified allosteric model of Ca2+-driven vesicle release and replenishment (20). (D) Simulated EPSCs, average of M = 60,000 Monte Carlo runs for each paradigm scaled for RRP of size m = 125. (E) Summary graph showing simulated EPSC amplitude as a function of time for the two stimulation paradigms shown in D. (F) Snapshots of spatial distribution of normalized total [CaM] (which accounts for all CaM molecules irrespective of their Ca2+ binding state) in the AZ plane, illustrating progressive dislocation of CaM from the membrane during AP stimulation predicted by CaM dislocation model (21) (see Materials and Methods for details). (G) VCell-computed [Ca2+] transients at the release site during 6 × 100 Hz and 5 × 20 Hz + 1 × 100 Hz AP trains and (H) corresponding simulated EPSCs for the case of CaM dislocation model. (I) Summary graph showing that experimentally observed short-term facilitation levels are likely to be explained by joint contribution of the two limiting cases represented by Mobile CaM (low facilitation) and by CaM dislocation (high facilitation) models that both allow AP counting logic.
Although Mobile CaM model replicated AP counting, the overall level of EPSC facilitation predicted by this model was ∼40% lower than the experimentally observed values (Fig. 2 B and D). Therefore, we considered another limiting case, “CaM dislocation” model. In this model (21) we considered that CaM was initially bound to the presynaptic membrane via interaction of its C lobe with neuromodulin and with other IQ-motif presynaptic membrane proteins (e.g., VGCCs) (21–23), while ATP and CB were considered as mobile buffers. The model assumed that Ca2+ binding by the CaM C lobe during AP bursts led to dissociation of CaM from its membrane binding partners and thus resulted in a stimulation-dependent reduction of Ca2+ buffering capacity in the active zone (AZ) (Fig. 4F). This in turn led to progressive increase of [Ca2+] transients at the AZ (Fig. 4G) and to facilitation of EPSCs (Fig. 4H). The progressive reduction of AZ Ca2+ buffering capacity predicted by the model did not depend on the frequency of AP bursts. Thus, CaM dislocation model also supported the counting logic at MFB terminals. In contrast to Mobile CaM model the dislocation model predicted substantial increase of local AP-evoked at the release site, which resulted in stronger EPSC facilitation (Fig. 4 G and I). Overall, the experimentally observed level of EPSC facilitation in MFB terminals is likely to be attributed to a joint contribution of the Mobile CaM and CaM dislocation limiting cases (Fig. 4I and SI Appendix, Fig. S11). Interestingly, the effect of somewhat stronger augmentation of on vesicular release at higher frequencies was compensated in both models by lower vesicle occupancy at the release site during high-frequency stimulation (SI Appendix, Fig. S12). This indicates that frequency-dependent differences in release site occupancy also contribute to the counting logic behavior of MFBs.
Discussion
We aimed to understand how granule cells generate CA3 pyramidal cell firing, which represents the first relay of information transfer in the hippocampus (24). This question is important because discharge of a single AP by a single CA3 pyramidal cell has dramatic network consequences as, for example, initiation of sharp-wave ripples (25). Our main finding is that MFBs count the number of APs during granule cell bursts with the temporal precision of only the last AP in the train being important to generate CA3 pyramidal cells firing. The counting logic can be explained by a combination of several structural and functional properties specific to MFB terminals. First, MFB is a synaptic terminal with loose coupling between VGCCs and Ca2+ vesicular release sensors (average coupling distance in the range of 70–100 nm) (18). Thus, AP-induced Ca2+ influx leads to only moderate amplitude at the release sites (∼10–15 µM). Therefore, in contrast to synapses with tight coupling, gradual accumulation of during AP bursts, in the range of ∼1–3 µM, significantly contributes to facilitation of glutamate release. Accumulation of is largely independent of stimulation frequency due to a relatively slow Ca2+ removal rate and therefore should contribute to AP counting mechanism. Another possible scenario that supports AP counting is Ca2+-dependent translocation of CaM molecules from the plasma membrane to the cytosol. CaM is a major presynaptic Ca2+ buffer and our model predicts that such CaM translocation should progressively reduce local Ca2+-buffering capacity in the AZ. This in turn should lead to facilitation of local at the release sites and as a consequence to facilitation of glutamate release. Again, CaM translocation mechanism is in line with AP counting because the model predicts that it should be largely independent of stimulation frequency. Further mechanisms could also contribute to short-term facilitation in MFB terminal, including the presence of release sites with different release probability (10), involvement of high-affinity Ca2+ sensors such as synaptotagmin 7 (26), different functional roles of VGCCs (11), presynaptic autoreceptor activation (27), Ca2+-induced Ca2+ release from intracellular stores (16, 28), as well as the mechanisms modulating synaptic vesicles dynamics in the activity-dependent manner (29, 30). It is likely that the above mechanisms also contribute to shaping short-term facilitation and AP counting in MFB. On the other hand, the AP broadening observed in MFBs is unlikely to significantly contribute to AP counting, given our observation that AP-evoked Ca2+ fluorescence transients remain constant during short (up to 10) trains of APs. This direct presynaptic measurement is consistent with less than 10% increase in presynaptic AP width observed for the 10th AP during 100-Hz trains (16, 31). Is there a postsynaptic contribution to AP counting? It is important to note that we cannot exclude possible postsynaptic mechanisms to CA3 pyramidal cell detonation. Indeed, the CA3 pyramidal cell needs to reach firing threshold, which requires sufficient membrane depolarization. Such postsynaptic factors may include a slow membrane time constant, efficient summation of EPSPs, and synaptic inputs from other sources which could play significant roles that will need to be explored in future studies. In this context, dissecting the role of postsynaptic factors would benefit from dynamic clamp experiments. However, as short-term facilitation is purely presynaptic at MF-CA3 synapses (10), we note that MF terminals can accomplish the counting function. Indeed, the experimentally constrained presynaptic release model presented here closely replicates the observed counting logic. This argues that the dynamic changes of and of Ca2+ buffering at release sites during AP bursts are the major contributors that determine short-term plasticity and AP counting in MFBs.
Synapses act as dynamics filters of information. It is commonly accepted that low-release probability synapses act as high-pass filters, while high-release probability synapses act as low-pass filters (32). Dynamic modulation of neurotransmitter release during bursts of APs further enriches the computational power of synapses (32). Short-term synaptic facilitation has been associated with the preferential transmission of information during burst-like activity (5, 33). In this regard, AP counting by MFBs appears to be an extreme example of burst detection for CA3 pyramidal cells for which the granule cell burst frequency structure is not important.
Dynamic modulation of neurotransmitter release during bursts of APs supports the neuronal code used by the presynaptic terminal (5, 33). AP counting by MFBs contrasts the rate and temporal codes observed in other types of synapses (2). In parallel, an AP counting mechanism was recently described in the Venus flytrap plant (34). What are the advantages, if any, of AP counting for the reliability and precision of information transfer? We propose that AP counting enforces both the reliability and precision of information transfer by allowing independent modulation of these two parameters. The reliability of CA3 pyramidal cell firing is largely gated by the number of APs in the granule cell burst, while the temporal precision of CA3 pyramidal cell firing depends solely on the timing of the last AP. This mechanism ensures burst detection and temporally precise information transfer. As a result, AP counting may ensure conditional and precise information transfer by eliminating possible errors associated with stochastic variations in intraburst frequencies.
Granule cells are known to discharge bursts of APs with variable frequency (35). However, our results highlight that the average burst frequency is not transferred to CA3 pyramidal neurons. Granule cells innervate 10 times as many interneurons than pyramidal cells through their filopodial extensions (36, 37). Interestingly, short-term plasticity at interneurons synapses varies in a target-specific manner (13). This may suggest that CA3 pyramidal cells and interneurons simultaneously receive different information from a granule cell burst (32, 33). In addition, the dynamics of information transfer between granule cells and their targets may be largely modulated by long-term plastic changes, with the count required for CA3 pyramidal cell detonation possibly altered in an activity-dependent manner (15, 38–40). Determining whether the counting logic is a unique property of hippocampal mossy fiber terminals or a feature shared by other strongly facilitating synapses will enhance our understanding of synaptic information transfer.
Materials and Methods
Electrophysiological Recordings in Acute Hippocampal Slices.
Acute hippocampal slices from P17–P25 male rats were prepared according to accepted procedures (10). Experiments involving the use of animals were performed in accordance with guidelines provided by the Animal Protection Committee of Laval University. The slice was perfused with oxygenated warmed recording artificial cerebrospinal fluid solution, containing (in millimolar): NaCl 124, NaHCO3 25, KCl 2.5, MgCl2 2.5, CaCl2 1.2, and glucose 10. The solution was oxygenated by bubbling a gas mixture composed of 95% O2 and 5% CO2. Temperature was maintained at 32 ± 1 °C throughout all experiments. The perfusion rate was adjusted to a constant 2 mL/min. Visually guided whole-cell patch-clamp recordings were obtained from CA3 pyramidal cells with a solution containing: K-gluconate 120, KCl 20, Hepes 10, MgCl2 2, Mg2ATP 2, NaGTP 0.3, phosphocreatine 7, EGTA 0.6 (pH = 7.2, 295 mOsm).
Random-Access Two-Photon Calcium Imaging.
A titanium:sapphire laser (Chameleon Ultra II, Coherent) tuned at 800 nm provided the two-photon excitation source (80 MHz, 140-fs pulse width and with an average power >4 W). The laser beam was redirected by a pair of acoustooptic deflectors (A-A Opto Electronics) to enable random access over the field of view. The laser beam was focused on the brain slice through a high-N.A. water-immersion objective (25× objective, with an N.A. = 0.95). Detailed procedures for two-photon calcium imaging experiments can be found in the SI Appendix, Supplementary Materials and Methods.
Nonstationary Single-Compartment Model of Presynaptic Ca2+ Dynamics.
Experimental Ca2+ fluorescence traces were analyzed using a nonstationary single-compartment model (16, 17), which assumes spatial homogeneity of [Ca2+] in the nerve terminal. SI Appendix, Supplementary Materials and Methods describes the details of the model.
Spatial VCell Model of MFB Ca2+ Dynamics.
Three-dimensional modeling of AP-evoked presynaptic Ca2+ influx, buffering, and diffusion was performed in the Virtual Cell (VCell) simulation environment (vcell.org) using the fully implicit adaptive time-step finite-volume method on a 10-nm meshed geometry. The detailed modeling procedures can be found in SI Appendix, Supplementary Materials and Methods.
Modeling of Ca2+-Triggered Synaptic Vesicle Fusion.
We assumed that the vesicular Ca2+ release sensor was located at coupling distance 90 nm from the edge of VGCC cluster (Fig. 4A). To simulate glutamate release we used profiles obtained in VCell at this location for each specific AP firing pattern in Monte Carlo simulations (implemented in MATLAB) based on the six-state allosteric Ca2+ sensor model (20) (Fig. 4C). The model also contained a stochastic repriming step, which was preceded by a short refractory period (1 ms) immediately after vesicle fusion. The model parameters were 100 µM−1 s−1, 4 × 103 s−1, 0.5, 31.3, 2 × 10−4 s−1. The repriming rate 20 s−1 was constrained using the experimental data for 50 stimuli applied at 100 Hz (SI Appendix, Fig. S7). For each stimulation paradigm, we performed 60,000 independent Monte Carlo runs with a time step 10−6 s and thus determined distribution for the vesicle fusion time during AP burst. Simulated EPSC response was calculated as , where 125 is the average readily releasable pool size and is the average quantal EPSC which was determined using voltage-clamp recoding during the asynchronous phase of release (200–300 ms after the last AP in the burst).
Supplementary Material
Acknowledgments
We are grateful to D. M. Kullmann for reading the manuscript and providing feedback. We thank György Buzsáki for the in vivo granule cell firing data. The study was supported by Canadian Institutes of Health Research Grant MOP-81142 and Natural Sciences and Engineering Research Council of Canada (NSERC) Grant RGPIN-2015-06266 (to K.T.), NSERC and CTRN PhD fellowships (to S.C.), and by the Medical Research Council and the Wellcome Trust (K.V.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1720659115/-/DCSupplemental.
References
- 1.Adrian ED, Zotterman Y. The impulses produced by sensory nerve-endings: Part II. The response of a single end-organ. J Physiol. 1926;61:151–171. doi: 10.1113/jphysiol.1926.sp002281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stein RB, Gossen ER, Jones KE. Neuronal variability: Noise or part of the signal? Nat Rev Neurosci. 2005;6:389–397. doi: 10.1038/nrn1668. [DOI] [PubMed] [Google Scholar]
- 3.Del Castillo J, Katz B. Quantal components of the end-plate potential. J Physiol. 1954;124:560–573. doi: 10.1113/jphysiol.1954.sp005129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Regehr WG. Short-term presynaptic plasticity. Cold Spring Harb Perspect Biol. 2012;4:a005702. doi: 10.1101/cshperspect.a005702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tsodyks MV, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci USA. 1997;94:719–723. doi: 10.1073/pnas.94.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pernía-Andrade AJ, Jonas P. Theta-gamma-modulated synaptic currents in hippocampal granule cells in vivo define a mechanism for network oscillations. Neuron. 2014;81:140–152. doi: 10.1016/j.neuron.2013.09.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pilz GA, et al. Functional imaging of dentate granule cells in the adult mouse hippocampus. J Neurosci. 2016;36:7407–7414. doi: 10.1523/JNEUROSCI.3065-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Henze DA, Wittner L, Buzsáki G. Single granule cells reliably discharge targets in the hippocampal CA3 network in vivo. Nat Neurosci. 2002;5:790–795. doi: 10.1038/nn887. [DOI] [PubMed] [Google Scholar]
- 9.Urban NN, Henze DA, Barrionuevo G. Revisiting the role of the hippocampal mossy fiber synapse. Hippocampus. 2001;11:408–417. doi: 10.1002/hipo.1055. [DOI] [PubMed] [Google Scholar]
- 10.Chamberland S, Evstratova A, Tóth K. Interplay between synchronization of multivesicular release and recruitment of additional release sites support short-term facilitation at hippocampal mossy fiber to CA3 pyramidal cells synapses. J Neurosci. 2014;34:11032–11047. doi: 10.1523/JNEUROSCI.0847-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chamberland S, Evstratova A, Tóth K. Short-term facilitation at a detonator synapse requires the distinct contribution of multiple types of voltage-gated calcium channels. J Neurosci. 2017;37:4913–4927. doi: 10.1523/JNEUROSCI.0159-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Klausnitzer J, Manahan-Vaughan D. Frequency facilitation at mossy fiber-CA3 synapses of freely behaving rats is regulated by adenosine A1 receptors. J Neurosci. 2008;28:4836–4840. doi: 10.1523/JNEUROSCI.3729-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Toth K, Suares G, Lawrence JJ, Philips-Tansey E, McBain CJ. Differential mechanisms of transmission at three types of mossy fiber synapse. J Neurosci. 2000;20:8279–8289. doi: 10.1523/JNEUROSCI.20-22-08279.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Salin PA, Scanziani M, Malenka RC, Nicoll RA. Distinct short-term plasticity at two excitatory synapses in the hippocampus. Proc Natl Acad Sci USA. 1996;93:13304–13309. doi: 10.1073/pnas.93.23.13304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vyleta NP, Borges-Merjane C, Jonas P. Plasticity-dependent, full detonation at hippocampal mossy fiber-CA3 pyramidal neuron synapses. eLife. 2016;5:e17977. doi: 10.7554/eLife.17977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Scott R, Rusakov DA. Main determinants of presynaptic Ca2+ dynamics at individual mossy fiber-CA3 pyramidal cell synapses. J Neurosci. 2006;26:7071–7081. doi: 10.1523/JNEUROSCI.0946-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ermolyuk YS, et al. Differential triggering of spontaneous glutamate release by P/Q-, N- and R-type Ca2+ channels. Nat Neurosci. 2013;16:1754–1763. doi: 10.1038/nn.3563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vyleta NP, Jonas P. Loose coupling between Ca2+ channels and release sensors at a plastic hippocampal synapse. Science. 2014;343:665–670. doi: 10.1126/science.1244811. [DOI] [PubMed] [Google Scholar]
- 19.Bischofberger J, Geiger JR, Jonas P. Timing and efficacy of Ca2+ channel activation in hippocampal mossy fiber boutons. J Neurosci. 2002;22:10593–10602. doi: 10.1523/JNEUROSCI.22-24-10593.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lou X, Scheuss V, Schneggenburger R. Allosteric modulation of the presynaptic Ca2+ sensor for vesicle fusion. Nature. 2005;435:497–501. doi: 10.1038/nature03568. [DOI] [PubMed] [Google Scholar]
- 21.Timofeeva Y, Volynski KE. Calmodulin as a major calcium buffer shaping vesicular release and short-term synaptic plasticity: Facilitation through buffer dislocation. Front Cell Neurosci. 2015;9:239. doi: 10.3389/fncel.2015.00239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kumar V, et al. Structural basis for the interaction of unstructured neuron specific substrates neuromodulin and neurogranin with Calmodulin. Sci Rep. 2013;3:1392. doi: 10.1038/srep01392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Alexander KA, Wakim BT, Doyle GS, Walsh KA, Storm DR. Identification and characterization of the calmodulin-binding domain of neuromodulin, a neurospecific calmodulin-binding protein. J Biol Chem. 1988;263:7544–7549. [PubMed] [Google Scholar]
- 24.Andersen P, Bliss TV, Skrede KK. Lamellar organization of hippocampal pathways. Exp Brain Res. 1971;13:222–238. doi: 10.1007/BF00234087. [DOI] [PubMed] [Google Scholar]
- 25.Bazelot M, Teleńczuk MT, Miles R. Single CA3 pyramidal cells trigger sharp waves in vitro by exciting interneurones. J Physiol. 2016;594:2565–2577. doi: 10.1113/JP271644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jackman SL, Turecek J, Belinsky JE, Regehr WG. The calcium sensor synaptotagmin 7 is required for synaptic facilitation. Nature. 2016;529:88–91. doi: 10.1038/nature16507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lauri SE, et al. A role for Ca2+ stores in kainate receptor-dependent synaptic facilitation and LTP at mossy fiber synapses in the hippocampus. Neuron. 2003;39:327–341. doi: 10.1016/s0896-6273(03)00369-6. [DOI] [PubMed] [Google Scholar]
- 28.Emptage NJ, Reid CA, Fine A. Calcium stores in hippocampal synaptic boutons mediate short-term plasticity, store-operated Ca2+ entry, and spontaneous transmitter release. Neuron. 2001;29:197–208. doi: 10.1016/s0896-6273(01)00190-8. [DOI] [PubMed] [Google Scholar]
- 29.Sakaba T, Neher E. Calmodulin mediates rapid recruitment of fast-releasing synaptic vesicles at a calyx-type synapse. Neuron. 2001;32:1119–1131. doi: 10.1016/s0896-6273(01)00543-8. [DOI] [PubMed] [Google Scholar]
- 30.Taschenberger H, Woehler A, Neher E. Superpriming of synaptic vesicles as a common basis for intersynapse variability and modulation of synaptic strength. Proc Natl Acad Sci USA. 2016;113:E4548–E4557. doi: 10.1073/pnas.1606383113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Geiger JR, Jonas P. Dynamic control of presynaptic Ca(2+) inflow by fast-inactivating K(+) channels in hippocampal mossy fiber boutons. Neuron. 2000;28:927–939. doi: 10.1016/s0896-6273(00)00164-1. [DOI] [PubMed] [Google Scholar]
- 32.Abbott LF, Regehr WG. Synaptic computation. Nature. 2004;431:796–803. doi: 10.1038/nature03010. [DOI] [PubMed] [Google Scholar]
- 33.Gerstner W, Kreiter AK, Markram H, Herz AV. Neural codes: Firing rates and beyond. Proc Natl Acad Sci USA. 1997;94:12740–12741. doi: 10.1073/pnas.94.24.12740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Böhm J, et al. The venus flytrap dionaea muscipula counts prey-induced action potentials to induce sodium uptake. Curr Biol. 2016;26:286–295. doi: 10.1016/j.cub.2015.11.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Henze DA, Buzsáki G. Action potential threshold of hippocampal pyramidal cells in vivo is increased by recent spiking activity. Neuroscience. 2001;105:121–130. doi: 10.1016/s0306-4522(01)00167-1. [DOI] [PubMed] [Google Scholar]
- 36.Amaral DG, Dent JA. Development of the mossy fibers of the dentate gyrus: I. A light and electron microscopic study of the mossy fibers and their expansions. J Comp Neurol. 1981;195:51–86. doi: 10.1002/cne.901950106. [DOI] [PubMed] [Google Scholar]
- 37.Acsády L, Kamondi A, Sík A, Freund T, Buzsáki G. GABAergic cells are the major postsynaptic targets of mossy fibers in the rat hippocampus. J Neurosci. 1998;18:3386–3403. doi: 10.1523/JNEUROSCI.18-09-03386.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pelkey KA, Topolnik L, Lacaille JC, McBain CJ. Compartmentalized Ca(2+) channel regulation at divergent mossy-fiber release sites underlies target cell-dependent plasticity. Neuron. 2006;52:497–510. doi: 10.1016/j.neuron.2006.08.032. [DOI] [PubMed] [Google Scholar]
- 39.Castillo PE, Weisskopf MG, Nicoll RA. The role of Ca2+ channels in hippocampal mossy fiber synaptic transmission and long-term potentiation. Neuron. 1994;12:261–269. doi: 10.1016/0896-6273(94)90269-0. [DOI] [PubMed] [Google Scholar]
- 40.Rebola N, Lujan R, Cunha RA, Mulle C. Adenosine A2A receptors are essential for long-term potentiation of NMDA-EPSCs at hippocampal mossy fiber synapses. Neuron. 2008;57:121–134. doi: 10.1016/j.neuron.2007.11.023. [DOI] [PubMed] [Google Scholar]
- 41.Ramón y Cajal S. 1917. Recuerdos de mi vida (Madrid Imprenta y Librería de N. Moya, Madrid). Spanish.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.