California's carbon market and energy prices: a wavelet analysis

Abstract

Carbon price is a key variable in management and risk decisions in activities related to the burning of fossil fuels. Different major players in this market, such as polluters, regulators and financial actors, have different time horizons. We use innovative multivariate wavelet analysis tools, including partial wavelet coherence and partial wavelet gain, to study the link between carbon prices and final energy prices in the time and frequency dimensions in California's carbon market, officially known as the California cap-and-trade programme. We find that gasoline prices lead an anti-phase relation with carbon prices. This result is very stable at lower frequencies (close to 1-year period cycles), and it is also present before mid-2015 in the 20–34 weeks frequency band. Regarding electricity, we find that at about a 1-year period, a rise in carbon prices is reflected in higher electricity prices. We conclude that the first 5 years of compliance of the California cap-and-trade programme show that emissions trading is a significant measure for climate change mitigation, with visible rising carbon prices. The quantitative financial analytics we present supports the recent decision to extend the current market to 2030 without the need for complementary carbon pricing schemes.

This article is part of the theme issue ‘Redundancy rules: the continuous wavelet transform comes of age’.

1. Introduction

In the current economic context with climate change concerns, variations of energy prices and numerous emission trading schemes that have multiplied around the world, there is an urge to develop quantitative tools to model and understand the origins of variations in carbon prices and their effect on energy prices. Information on the movement of these variables has operational and political implications highly relevant to the main players in the market: polluters, regulators and financial actors. While the latter are mostly interested in knowing daily connections between commodity prices, the polluting industries and regulators are also interested in longer cycle tendencies.

Previous work on carbon prices proliferated after 2008 and focused on the European Emission Trading Scheme (EU ETS). Studies of the Californian ETS were mostly concerned with market design features [1–5]. The exceptions are Bushnell [6] and Sousa & Aguiar-Conraria [7], who looked into the impact on daily electricity prices using vector autoregressions.

This paper adds two critical perspectives to the current research on carbon price dynamics. First, we study the California carbon market, a recent and different example in terms of design features. Second, we study relations between variables in cycles of different periodicities.

The ETS in California, created under the Assembly Bill 32 (AB32), as intended by the Western Climate Initiative (WCI), was signed in 2007. Operational since 2012, it is an important instrument to meet the goal of reaching the state's 1990 greenhouse gas (GHG) levels by 2020 and it was recently extended to 2030. The California market has significant structural differences from the EU ETS that should allow us to control previously encountered EU market misconceptions. Namely, containment mechanisms, such as price floor for auctions and an allowance price containment reserve, are used to mitigate price volatility and over-allocation of licences. Another relevant difference between EU ETS and the California ETS features concerns the sectors included and their point of regulation. The California programme is a mixed regulation scheme, with both downstream and upstream regulation of entities, including electricity importers, and, since 2015 (second phase), also road sector transport activities, such as suppliers of natural gas, liquid petroleum gas (LPG), reformulated blendstock for oxygenate blending (RBOB) and distillate fuel oil. In Europe, GHG emissions from road transport activities are controlled by other carbon pricing mechanisms.

Whereas there has been extensive research on carbon prices, built mainly on data from Europe, we present a new analysis of the California Carbon Allowances (CCA), representing one metric tonne of CO₂ equivalent, and the relationship with final energy consumers after 2014 when Québec joined the Californian market.

The second critical perspective concerns the methodology where we rely on multivariate continuous wavelet analysis to understand how carbon and energy prices relate at different cycle lengths.

Initial studies on carbon prices mostly explained the price or volatility of one variable in terms of others. They used Granger causality methods to find unidirectional relations between pairs of variables, including daily carbon and energy prices [8,9]. More recently, new studies have considered effects between variables—also daily energy and carbon prices—but in both directions. They include vector autoregressive studies, with multivariate analysis, and estimate impulse-response functions that show the daily impact of innovations of a variable, namely carbon [10–14]. Other carbon price issues, such as volatility, risk premiums and forecasting, have lately been the focus of attention; e.g [15,16].

Following previous studies, we relate CO₂ prices to final energy prices, electricity and RBOB for gasoline, which connect final consumers to the carbon cost. These are critical variables for carbon markets that include both electricity generators and suppliers of fuels for the transport sector, in a mixed upstream and downstream regulation.

In line with [17], we rely on multivariate wavelet analysis (MWA) and work in the time–frequency domain, estimating how carbon price relationships behave at different frequencies and how they evolve over time. We chose to work with MWA mainly for two reasons. First, it is important to use methods that do not require stationarity as Kyrtsou et al. [18] showed that energy prices are strongly non-stationary. Second, we note that decisions of market regulators include long-term plans, and also that decisions of investment and management strategy in power and transport supply on a large scale are neither easy nor quick. Therefore, it makes sense to consider the presence of short- and long-term decisions, meaning that these relations should be studied simultaneously at different frequencies. This can be easily performed with wavelet analysis. We go further than [17] as we also estimate the partial wavelet gain, which is akin to estimating regression coefficients in the time–frequency domain. Therefore, we estimate not only the strength of the relations, but also their magnitude. The papers [19–23] have already relied on wavelets to study the evolution of energy prices, including oil, gasoline, natural gas, biofuels and other commodities. To the best of our knowledge, the only previous work concerned specifically with carbon markets and performed in the time–frequency domain is [17].

The paper proceeds as follows. Section 2 provides a description of the methodology. Section 3 describes our data and the Californian carbon market. Section 4 contains our empirical results. Finally, §5 concludes and discusses some policy implications of our findings.

2. Continuous wavelet analysis

The first wavelet applications in economics and finance are due to Ramsey & Lampart [24,25], who were then followed by Gençay et al. [26–29], Wong et al. [30], Connor & Rossiter [31], Fernandez [32], Gallegati & Gallegati [33] and Gallegati et al. [34]. This first wave of applications relied on the discrete wavelet transform (DWT). Crowley [35] provides an excellent review of economics and financial applications of DWT and sets the ground for new researchers to the field. After this wave of DWT applications, there was another wave of applications to economics and finance which relied on the continuous wavelet transform (CWT): Aguiar-Conraria et al. [36], Baubeau & Cazelles [37], Crowley & Mayes [38], Rua & Nunes [39], Aguiar-Conraria & Soares [40,41], Jammazi [20], Vacha & Barunik [21], Alvarez-Ramirez et al. [42] and Aguiar-Conraria et al. [43] provide economic applications using these tools. The field is growing and it is now impossible to keep track of all papers applying CWT to economic data. Verona [44], Flor & Klarl [45] and Bekiros et al. [46] are just three nice examples among dozens that could be given. For a person seeking intuition on CWT, the political science applications of Aguiar-Conraria et al. [47,48] are good starting points.

(a). Continuous wavelet transform

Time-scale wavelets are characterized in reference to a mother wavelet, ψ(t), a function of a real variable t. For a function to qualify to be a mother wavelet it has to satisfy a certain admissibility condition which, in practice, amounts to requiring that the function integrates to zero and also has fast decay towards zero. The fact that ψ tends quickly to zero means that we can view it as a window function; on the other hand, demanding that ψ integrates to zero implies that ψ must be oscillatory, enabling us to associate a certain frequency to this function.

The mother wavelet ψ provides a source function for generating a family of daughter wavelets, ψ_τ,s; these functions are obtained from the mother by performing two operations, scaling by s and translation by τ:

The scaling parameter s controls the width of the wavelet and the translation parameter τ controls the location of the wavelet along the t-axis. For |s| > 1, the windows ψ_τ,s become larger (hence, correspond to functions with lower frequency) and, for |s| < 1, the windows become narrower (hence, become functions with higher frequency).

Given a time series x(t), its continuous wavelet transform with respect to the wavelet ψ is a function of two variables, W_x(τ, s), given by

In the above formula and throughout the paper the over-bar is used to denote complex conjugation.

The specific wavelet we use in this paper is a complex-valued function selected from the so-called Morlet wavelet family, first introduced in [49],

and corresponds to the particular choice of ω₀ = 6. Although, strictly speaking, the above function is not a true wavelet, because it has no zero mean, for sufficiently large ω₀, namely for the value used in this paper, ω₀ = 6, for numerical purposes it can be considered as a wavelet; see [50] and also [51] for some properties of this wavelet which justify our choice.¹

Remark 2.1

As for the wavelet transform, all the wavelet quantities we are going to introduce below are functions of two variables, time (τ) and scale (s). To simplify the notation, we will describe these quantities for a specific value (τ, s) of the argument which will be omitted from the formulae.

(b). Univariate wavelet tools

In analogy with the terminology used in the Fourier case, the (local) wavelet power spectrum of series x(t), denoted by (WPS)_x, is defined as

The wavelet power spectrum (sometimes called scalogram or wavelet periodogram) indicates the variance distribution of the time series in the time–scale (time–frequency) plane.

When the wavelet ψ(t) is chosen as a complex-valued function, as in our case, the wavelet transform W_x is also complex-valued and therefore can be separated into its real part, ℜ(W_x), and imaginary part, ℑ(W_x); alternatively, the transform can be expressed in polar form as

The angle ϕ_x is known as the (wavelet) phase.² For real-valued wavelet functions, the imaginary part is zero and the phase is undefined. Therefore, to separate the phase and amplitude information of a time series, it is necessary to use complex wavelets.

(c). Bivariate wavelet tools

In many applications, one is interested in detecting and quantifying the time–frequency relations between two non-stationary time series. Generalizations of the wavelet tools, appropriate for this purpose, are now briefly described; for more details, the reader is referred to e.g. [51].

Given two time series, y(t) and x(t), we define their cross-wavelet transform (or cross-spectrum), W_yx, by

2.1

where W_y and W_x are the wavelet transforms of y and x, respectively. The absolute value of the cross-wavelet transform, |W_yx|, will be referred to as the cross-wavelet power.

We also define the complex-wavelet coherence of y and x, ϱ_yx, by

where S denotes a smoothing operator in both time and scale.³ For notational simplicity, we will denote by S_yx the smoothed cross-wavelet transform of two series y and x and also use σ_y and σ_x to denote, respectively, and 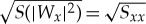. With these notations, the formula for the complex coherence is written simply as

By analogy with the Fourier case, we define the wavelet coherence, R_yx, of two series y and x as the absolute value of their complex wavelet coherence, i.e.

With a complex-valued wavelet, we can compute the wavelet phases of both series and, by computing their difference, we are able to obtain information about the possible delays of the oscillations of the two series, as a function of time and frequency. It follows immediately from (2.1) that the phase difference, which we will denote by ϕ_yx, can also be computed simply as the phase angle of the cross-wavelet transform. The obtained values for the phase difference may be interpreted as follows. If ϕ_yx = 0, then the series are completely in-phase, while if ϕ_yx = π, the series show a complete anti-phase relationship; if ϕ_yx lies between 0 and π/2, then the series are in-phase, but the variable y leads x; if ϕ_yx is between −π/2 and 0, the series are also in-phase, with x leading; when ϕ_yx is between −π and −π/2 or between π/2 and π, the series show an anti-phase relation and, in the first case, y leads x, while in the second case, it is x which leads.

Remark 2.2

The wavelet phase difference is sometimes defined as the phase angle of the complex wavelet coherence; although this is not fully consistent with the difference between the individual phases, because it is affected by the smoothing, the results obtained are not substantially different; this alternative definition has the advantage of being simpler to generalize to the multivariate case.

Finally, we define the complex wavelet gain of y over x, denoted by , by

and, following Mandler & Scharnagl [52], we define the wavelet gain of y over x, which we denote by G_yx, as the modulus of . Recalling the interpretation of the Fourier gain as the modulus of the regression coefficient of y on x at a given frequency (see e.g. [53]), it is perfectly natural to interpret the wavelet gain of y over x as the modulus of the regression coefficient in the regression of y on x, at each time and frequency.

(d). Multivariate wavelet tools

Some wavelet tools specially designed to use when more than two series are involved, namely the so-called partial wavelet coherence and partial phase difference, are also available; see e.g. [54] for the case of three series and [51] for the more general case. More recently, in [55], the authors introduced the concept of partial wavelet gain, a generalization of the wavelet gain for the case of more than two variables. Here, we will only display the formulae for the case of three variables, which are the ones we use in this paper. For the other cases, the reader is referred to the appendices of the aforementioned references [51,55].

Given a series y(t) and two other series x(t) and z(t), the squared multiple wavelet coherence between the series y(t) and the other two series, denoted by R²_y(xz), is given by

and the multiple wavelet coherence R_y(xz) is defined as the positive square root of the above quantity.

The complex partial wavelet coherence between y and x after controlling for z, denoted by ϱ_yx.z, is the quantity given by

The partial wavelet coherence of y and x after controlling for z, denoted by R_yx.z, is simply the absolute value of the complex partial wavelet coherence, and the partial phase difference of y over x, given z, denoted by ϕ_yx.z, is the phase angle of ϱ_yx.z.

The complex partial wavelet gain of y over x after controlling for z, denoted by , is given by

and the partial wavelet gain of y over x after controlling for z, denoted by G_yx.z, is simply the absolute value of . The partial wavelet gain G_yx.z can be interpreted as the coefficient (in modulus) in the multiple linear regression of y in the explanatory variables x, z, at each time and frequency.

(e). Statistical significance

Naturally, it is important to assess the statistical significance of the computed wavelet measures. Torrence & Compo, in their influential paper [56], were among the first authors to discuss this issue. Based on a large number of Monte Carlo simulations, Torrence & Compo concluded that the wavelet power spectrum of a white or red noise process, normalized by the variance of the time series, is well approximated by a chi-squared distribution. This problem was reconsidered more recently by Zhang & Moore [57]. For the specific case of the use of a wavelet ψ_ω0 from the Morlet family, Zhang & Moore established, analytically, that the wavelet power spectrum of a Gaussian white noise with variance σ² is distributed as

where X₁ and X₂ are independent standard Gaussian distributions. In the case of a Morlet wavelet with parameter ω₀ > 5, we have e^−ω2₀ ≈ 0, and hence we obtain confirming, for this specific type of wavelet and particular underlying process, the result obtained by Torrence & Compo. To assess the significance of the wavelet power spectrum, we will rely on this theoretical distribution.

References [58–60] have some important theoretical results on significance testing for the wavelet coherence. The results, however, are for specific ways of smoothing (namely in the time domain only) and do not apply directly to our case. To our knowledge, no work has been done on significance testing for the partial wavelet coherence. All our significance tests are obtained using surrogates. We fit an autoregressive moving-average ARMA(1,1) model to the series and construct new samples by drawing errors from a Gaussian distribution with a variance equal to that of the estimated error terms. For each time series (or set of time series), we perform the exercise 5000 times, and then extract the critical values at 5% and 10% significance.

Related to the phase difference (or partial phase difference), there are no good statistical tests. This is because it is very difficult to define the null hypothesis. In fact, Ge, in [58], argues that one should not use significance tests for the phase difference. Instead, one should complement its analysis by inspecting coherence, and only focus on phase differences whose corresponding coherence is statistically significant. The same kind of procedure should be used when interpreting the gain (or partial gain).

3. The carbon market in California and our data

The California cap-and-trade system, called California ETS for simplification, took effect in early 2012 and is linked to Québec's since January 2014. The first period occurred during 2012–2014, with compliance since 2013; the second compliance period started in 2015, and lasted until 2017, including suppliers of transportation fuels, natural gas and other fuels; and 2018–2020 covers the third period. In line with global tendencies of carbon pricing, the cap-and-trade programme of California was recently extended until 2030 [61], along with similar intentions from the linked markets of Québec and Ontario [62]. The California–Québec–Ontario cap-and-trade programme now forms the third largest carbon market in the world following China and the European Union.

California is one of the largest economies in the world. The state has a consumption of 7676 trillion BTU (2015), producing internally around 2353 trillion BTU of primary energy (crude oil and natural gas account for 49% and 11%, nuclear electric power 8% and renewables 31%).⁴ California's electricity system generates more than 290 TWh per year. The installed capacity shares in 2016 included approximately 54% natural gas, 18% hydroelectric, 25% other renewables and 3% nuclear. In fact, California produces 70% of the electricity it uses. The remaining amount is imported.⁵

The California challenge on electricity under AB32 is to secure supply with 33% of renewable sources, while reducing GHG emissions. California has an emission goal of 427 MMT CO₂e (million metric tonnes of CO₂ equivalent) in 2020, i.e. equalling 1990 estimated emissions, and aims for an 80% reduction in 2050 below 1990 levels. In 2015, California emitted a total of 440 MMT CO₂e, from which 39% originates in transportation, 23% from industrial sources and 19% from electricity generation (8% imported plus 11% in state).⁶

CCAs, each corresponding to one tonne of CO₂ equivalent, are traded on the Intercontinental Futures Exchange US (The ICE Futures US), a leading exchange for commodity markets. Currently, traded products are CCAs Vintage Futures for 2017, and corresponding options on futures, available as product number 6747558 at The ICE.⁷ Monthly contract sets for the current year plus 3 years.

An important difference between the California cap-and-trade programme and the European ETS regards the inclusion of importers of electricity from out of state (through its primary energy source mix), and of distributors of transportation fuels, natural gas and other fuels, which do not exist in Europe. All other CA trading sectors are, in their essence, energy-intensive and/or high-emission sectors, such as the EU sectors. Sectors included in the carbon trading since 2013 are: first deliverers of electricity (in state and imported) and large industrial facilities (such as petroleum refineries; crude petroleum and natural gas extraction; cement; industrial gas; mineral mining and lime; fruit and vegetable canning; glass; paper; dairies; iron, steel and aluminium; chemical, biological and pharmaceutical; breweries, wineries and juice). Since 2015 the market also includes suppliers of natural gas, suppliers of RBOB and distillate fuel oil, suppliers of LPG in California and suppliers of liquefied natural gas. This means that distributors of intermediate materials to produce gasoline and diesel are now considered. Sousa & Aguiar-Conraria [7] and the International Carbon Action Partnership (icapcarbonaction.com) provide further comparisons between the EU ETS and the CA ETS.

Considering the above-mentioned CA ETS fundamentals and other previous work on European CO₂ prices causality, namely, [8,10,14,63–66], our model considers three variables associated with the energy and carbon markets in California; namely, carbon (CCA), and the two most relevant final energies covered, electricity prices and RBOB fuel oil prices (RBOB is used to produce gasoline), which is used as a proxy for the effects in the transport sector.

The AB32 programme covers nearly 600 emitting facilities, responsible for 85% of CA emissions, which is a great feature of this market that contrasts, for example, with the 45% of the European market. On carbon prices, we use the available series on the CCA Futures of The ICE End-of-Day Front Report at the California Carbon Info.⁸ Data in figure 1 include 1452 observations, starting in 2014. The average value was of US$ 12.93 per CCA, reaching a maximum level of US$ 15.43 and a minimum of US$ 11.66. The bottom limit on the US$ axis is intentionally US$ 10, representing the minimum CCA value at auctions (figure 2).

Figure 1.

California carbon prices, 2014/2017. (Data source: The ICE, retrieved from California Carbon Info.)

Figure 2.

California selected energy prices, 2014/2017. (The left axis refers to gasoline and the right axis refers to electricity prices. Data sources: US EIA.)

Regarding the electricity variable, we considered the wholesale day - ahead price of SP15 EZ Generation Hub, located in California. The data source is The ICE exchange.⁹ Prices are in US$/MWh and were included from 2 January 2014 to 24 October 2017. RBOB fuel prices regard the Los Angeles Reformulated RBOB Regular Gasoline Spot Price, also available at the US EIA information page, in Dollars per Gallon.¹⁰ These prices relate to the Los Angeles area, and though no other RBOB prices were available for the remaining areas of California, and bearing in mind the socio-economic dimension of Los Angeles, we assumed the collected information to be representative of the overall State's prices. For an easier perception of the impact of RBOB fuel oil prices we refer to them as RBOB gasoline prices, as stated by the EIA, or, merely gasoline prices. We discarded the possibility of seasonally adjusting the data because it typically only affects electricity prices.

4. Our results

In figure 3, we perform a preliminary analysis with our data.¹¹ On the left, we plot the monthly returns of CCA, and the monthly rate of price increases of electricity and gasoline. On the right, we plot the wavelet power spectra. Our data are weekly and run from the beginning of 2014 until the 42nd week of 2017 (mid-October).¹²

Figure 3.

(a) Plot of the monthly rate of return of each time series, and (b) the corresponding wavelet power spectrum, for cases (i) CCA, (ii) electricity, and (iii) gasoline. The black/grey contour designates the 5%/10% significance level. The cone of influence, which is the region affected by edge effects, is indicated with a black line. The colour code for power ranges from blue (low power) to red (high power). The white lines show local maxima of the wavelet power spectrum.

The wavelet power indicates the variance of the time series for each moment and frequency. In the plots of the wavelet power, the black conic line identifies the region (usually referred to as the cone of influence, COI) where edge effects—unavoidable artefacts appearing when computing the continuous wavelet transform for a finite series—are important; outside this line, the results should be interpreted with caution; see e.g. [51] for more details. The degree of variability is distinguished by a colour spectrum, ranging from dark blue (low variability) to red (high variability). The white lines in the power spectra indicate local maxima. The black contours signify 5% significance levels, while the grey contours represent 10% significance levels. These were computed using the theoretical distribution already referred to for the power, assuming a flat spectrum as the null.

In the case of carbon prices, the volatility is spread across the sample, but it is stronger at higher frequencies. The red regions correspond to cycles of period smaller than 17 weeks.

It is interesting to note that in the case of electricity prices there are two dominant cycles that coexist at the same time. One cycle has a 24-week (about half-year) period and it became apparent in the second half of 2015. There is also a 1-year cycle that appeared in the beginning of 2015.

Finally, in the case of gasoline, most of the volatility is concentrated in the middle of the sample, between late 2014 and late 2016, especially at high frequencies. However, even for lower frequencies, the wavelet power spectrum is still statistically significant.

Based on the preliminary analysis of the wavelet power spectra, it is difficult to discern any interrelations between these markets. Figure 4 helps us on this task and tells us when and at which frequencies these interrelations are the strongest. We estimate the multiple coherence between CO₂ and the other two variables, electricity and gasoline. There are no relevant regions of high coherence after 2017. This possibly relates to the uncertainty of the future of the California carbon market, that characterized the year of 2016, and resulted in a steep decrease in the carbon allowance futures sold in the California–Quebéc joint auctions. In consequence, 1-year cycles of prices of CCA futures stopped reflecting market principles, namely, their relation to energy prices. Until then, we identify three main regions with statistically significant coherence. The most important one is located at low frequencies (corresponding to cycles of about 1 year periodicity) and runs from the beginning of the sample until the third quarter of 2016. In the 20–34 week frequency band, there are two regions of statistically significant coherence. One runs from 2014 until the third quarter of 2015. The other, smaller, occurs near mid-2016. Multiple coherence tells us how important the strength of the relation between energy prices (electricity and gasoline) and CO₂ is. However, just with that information one cannot differentiate the impact of both variables. For that purpose, one must rely on the partial coherence, which we do next.

Figure 4.

Wavelet multiple coherence between CO₂ and energy (electricity and gasoline) prices. The black/grey contour designates the 5%/10% significance level. The colour code for coherence ranges from blue (low coherence—close to zero) to red (high coherence—close to one).

In figure 5, we have our most important set of results. We estimate the partial coherence between CO₂ prices and each of the energy variables (after controlling for the other), the partial phase difference, and the partial wavelet gain, which will give us information about the magnitude of the impact that a shock in one variable will have on the other.

Figure 5.

(a) Partial wavelet coherence: (i) carbon versus electricity prices controlling for gasoline prices, and (ii) carbon versus gasoline prices controlling for electricity prices. The black/grey contour designates the 5%/10% significance level. The colour code for coherence ranges from blue (low coherence—close to zero) to red (high coherence—close to one). (b) Partial phase differences: (i) carbon versus electricity controlling for gasoline, and (ii) carbon versus gasoline controlling for electricity. (c) Partial wavelet gain: (i) carbon versus electricity controlling for gasoline, and (ii) carbon versus gasoline controlling for electricity.

To facilitate the presentation, we display the mean values for the phase differences and partial gains corresponding to the two considered frequency bands, namely for cycles of period 20–34 weeks and 46–58 weeks. For the phase differences, which are measured on a circular scale, the mean is computed as a circular mean, which is the appropriate notion of mean in this case; see e.g. [67].

In figure 5a(i),b(i),c(i), we have the partial coherence between CO₂ price returns and electricity. There are three important regions of high coherence that overlap with the high coherences estimated in figure 4. The first one is located in the 20–34 week frequency band, and runs from the beginning of the sample until the third quarter of 2015 (in some areas, it is only significant at 10%). The second is located at lower frequencies (46–58 week period) and runs from mid-2015 until the end of 2016. In both regions, the phase difference is between 0 and π/2, showing that price returns of both variables are in-phase, with CO₂ leading. Finally, there is a third region, again at higher frequencies (in the 20–34 week frequency band, to be more precise) in the second half of 2016. In that region, the phase difference is between −π and −π/2. This means that, at this frequency, changes in the CO₂ prices still lead changes in electricity; however, the relation is now negative. This result illustrates one of the main advantages of using wavelets in finance and economics. Economists have always known that some relations are time-varying. With wavelets, now they can also estimate frequency varying relations.

In figure 5a(ii), it is interesting to note the impressive similarity between the partial wavelet coherence of CO₂ and gasoline and the picture of the multiple wavelet coherence. The two main statistically significant regions that we found in figure 4 can also be seen in figure 5a(ii). In those regions of high partial coherence, the partial phase difference between CO₂ and gasoline is between π/2 and π, suggesting an anti-phase relation, with the gasoline prices leading. Economically, this means that, at these frequencies, an increase in the gasoline price is followed by a decrease in CO₂ prices in the financial markets. The partial gain is very stable at both frequency bands, with a value close to 0.1, about twice as large as the partial gain between CO₂ and electricity.

5. Concluding remarks and policy implications

In this paper, we present an analysis of the carbon prices in the California emission market. After describing the main market features, we studied the interaction between carbon prices and final energy prices, RBOB gasoline and electricity.

We applied MWA tools, including the partial wavelet coherence, with the purpose of analysing the relation between the various prices at different frequencies, and the partial wavelet gain to assess the magnitude of such a relation. Energy prices are non-stationary, so it is important to use methods that do not require stationarity. MWA tools allow for the study of cycles of different lengths as, on the one hand, decisions of power supply investments on a larger scale are neither easy nor quick, and on the other hand, regulator actions are also planned for the long term. Therefore, it makes sense to consider the presence of long-term decisions, or at lower frequencies, i.e. relations in longer temporal cycles. MWA provides additional information to usual energy data analysis that only considers pure time-domain methods, such as value at risk (VAR) or generalized autoregressive conditional heteroscedasticity (GARCH) models. The results we obtained in MWA for lower frequencies are of particular relevance for the above-mentioned actors, because they provide a perception of the annual relationships between decision variables. Of course, given the time span of our data (less than 4 years), it is unrealistic to study cycles of periods longer than a year.

In our studies on California, we found the most important result in the relationship between gasoline and carbon prices, with gasoline leading an anti-phase relation. This result is very stable at lower frequencies (close to 1-year period cycles), and it is also present before mid-2015 in the 20–34 weeks frequency band. By contrast, previous studies have shown that European carbon prices mostly reflect economic developments, and influence the price of electricity [7,17]. Regarding electricity, in California, the results may reflect the low price elasticity of electricity in the short run, as a rise in carbon prices is only reflected in higher electricity prices within a year. This contrasts with the relationship between carbon and gasoline.

The reading of our results regarding the interaction between the three variables is that the carbon market counterweights the reduction in prices of energies with high emission levels, such as gasoline, penalizing them via carbon prices. However, this result does not impact electricity prices with similar intensity due to the energy-mix features of power generation, which includes renewable energies, and also the sector's lower share of emissions in the carbon market. It is evident in the analysis that the weight of the emissions from the transport sector, together with the reduction in gasoline prices, had effects on the carbon price, which were stronger than the effects of the electricity prices on the carbon market. We recall that the transport sector corresponds to 39% of California's total emissions, versus 19% of electricity production and 23% of the industrial sector (2015 data, from the California Air Resources Board). This conclusion is confirmed in the results of multiple coherence and may be the reason for the rise of carbon prices in 2017. As a result, this will put pressure on consumers to seek less emitting products, and thus their production and distribution. An option that would not damage the overall environmental goal, but that would mitigate the economic impact, would be to channel the licences not used by the power utilities to the fuels sector.

In conclusion, we suggest that the first 5 years of compliance of the California–Québec cap-and-trade programme advocates emissions trading as a significant measure for climate change mitigation, with visible rising carbon prices. The quantitative financial analytics we present supports the recent decision to extend the current market to 2030 without the need for complementary carbon pricing schemes.

Data accessibility

This article has no additional data.

Author's contributions

L.A.-C. and R.S. conceived and designed the study. M.J.S. programmed the Matlab toolbox used to analyse the data. The three authors were involved in the preparation of the final manuscript. L.A.-C. and R.S. performed the data analysis and drew the policy implications. R.S. wrote the mathematical section. All the authors approved the manuscript contents.

Competing interests

The authors declare that they have no competing interests.

Funding

Research at NIPE has been carried out within the funding with COMPETE reference number POCI-01-0145-FEDER-006683, with the FCT/MEC's (Fundação para a Ciência e a Tecnologia, I.P.) financial support through national funding and by the ERDF through the Operational Programme on ‘Competitiveness and Internationalization—COMPETE 2020’ under the PT2020 Partnership Agreement.