A wavelet neural control scheme for a quadrotor unmanned aerial vehicle

Abstract

Wavelets are designed to have compact support in both time and frequency, giving them the ability to represent a signal in the two-dimensional time–frequency plane. The Gaussian, the Mexican hat and the Morlet wavelets are crude wavelets that can be used only in continuous decomposition. The Morlet wavelet is complex-valued and suitable for feature extraction using the continuous wavelet transform. Continuous wavelets are favoured when high temporal and spectral resolution is required at all scales. In this paper, considering the properties from the Morlet wavelet and based on the structure of a recurrent high-order neural network model, a novel wavelet neural network structure, here called a recurrent Morlet wavelet neural network, is proposed in order to achieve a better identification of the behaviour of dynamic systems. The effectiveness of our proposal is explored through the design of a decentralized neural backstepping control scheme for a quadrotor unmanned aerial vehicle. The performance of the overall neural identification and control scheme is verified via simulation and real-time results.

This article is part of the theme issue ‘Redundancy rules: the continuous wavelet transform comes of age’.

1. Introduction

Wavelet analysis decomposes a general function or signal into a series of basis functions called wavelets, which have different frequency and time location. Wavelets have the ability to decompose a signal or a time series across different levels. As a result, this decomposition brings out the structure of the underlying signal, including periodicities, singularities, trends or jumps that cannot be observed in the original time series.

Wavelets are designed to have compact support in both time and frequency, giving them the ability to represent a signal in the two-dimensional time–frequency plane. The Haar wavelet, which has a discontinuity, was among the first ones to be conceived. The Morlet wavelet, also known as the Gabor wavelet, is complex-valued and suitable for feature extraction using the continuous wavelet transform (CWT), while Daubechies wavelets, which are discrete, real-valued and have compact support, are widely used in signal denoising and compression using the discrete wavelet transform. In general, the choice of a particular wavelet is usually driven by the application [1,2]. The Gaussian, the Mexican hat and the Morlet wavelets are crude wavelets that can be used only in continuous decomposition. The Morlet wavelet does not have compact support, meaning that it does not decay in finite time and therefore does not satisfy the admissibility condition. Thus, it is not a wavelet in the strictest sense [3]. The Morlet wavelet is simply a complex wave within a Gaussian envelope. Other types of wavelets that do not have Gaussian envelopes cannot be expected to improve on the time–frequency localization of the Morlet wavelet [4]. The Fourier transform of the Morlet wavelet is a Gaussian function centred at the frequency of oscillation of a mother wavelet. The Morlet wavelet has an additional parameter that enables us to control the width of the Gaussian envelope and hence the number of periods, a feature that is useful experimentally because this can be performed independently of the oscillation frequency. An important feature of the CWT is the ability to choose a wavelet that best suits the problem at hand [4]. Wavelet transform analysis has now been applied in the investigation of a multitude of diverse physical phenomena, from video image compression to the compression of medical signal records, from heart monitoring to the condition monitoring of rotating machinery, from seismic signal denoising to the denoising of astronomical signals and images, from climate analysis to the analysis of financial indices, from surface characterization to the characterization of turbulent intermittency, and so on [5]. The applications of wavelet transforms to a variety of pertinent problems in engineering include the analysis of fundamental dynamical behaviour and chaotic motions, machining processes, non-destructive testing of structural elements and the condition monitoring of machinery, and the characterization of surfaces and fibrous materials. The choice of the most appropriate wavelet for use in the analysis of a particular engineering problem depends on the nature of the data itself. Continuous wavelets are favoured when high temporal resolution is required at all scales [5]. A number of studies have been carried out over recent years concerning the application of wavelet-based analytical techniques to the investigation and modelling of dynamical systems. Applications include the evaluation of dynamic properties and system characteristics, the modelling and control of dynamical behaviour, and the partitioning or decoupling of multiple responses [6]. Additional details about theoretical aspects of CWTs, state-of-the-art examples of wavelet applications in modelling and control, and future directions on this branch are provided in [6,7].

Robotic arms are basically positioning systems; therefore, the trajectory tracking control problem for that kind of robot manipulator has been a challenging problem to be solved in recent years. In this regard, the field of artificial neural networks (ANNs) has been playing an interesting role and a great challenge in its implementation in real time. Neural control schemes in continuous time have been proposed using the filtered error (FE) algorithm as training law for a recurrent high-order neural network (RHONN) [8,9]. In these works, identification and control were carried out online at the same time. The wavelet neural networks (WNNs) structure arises from combining the wavelet concept with the ANNs approach in order to achieve a better identification performance [10–17]. WNNs are a class of networks that combine the classical sigmoid neural networks and wavelet analysis. WNNs simultaneously possess the advantages of ANN learning ability and wavelet decomposition ability. Their applications and growth have come from many areas, including statistics, computer science, pattern recognition, communication and finance [18]. WNN-based control systems have been adopted widely for control of complex dynamical systems owing to their fast learning properties and good generalization capability. Moreover, recurrent wavelet neural networks (RWNNs), which combine properties such as dynamic response of recurrent neural networks and the fast convergence of WNNs, have been proposed to identify and control nonlinear systems [19–26]. An intelligent control system using a recurrent wavelet-based Elman neural network for position control of a permanent magnet synchronous motor servo drive was proposed in [27]. In [28], a self-recurrent WNN structure was proposed in order to identify a synchronous generator and the nonlinearities introduced in the system due to actuator saturation. Some research has been carried out in real time with interesting results, such as in [29], where an adaptive RWNN uncertainty observer was proposed to estimate the required lumped uncertainty and a backstepping approach was used to control the motion of a linear synchronous motor drive system. In [30], an intelligent control system based on a four-layer RWNN comprising Gaussian wavelet functions was proposed to solve the trajectory tracking problem for an unmanned aerial vehicle (UAV). Adaptive tuning laws for the RWNN, trained via a gradient descent method, were derived using a sliding-mode approach. The performance of the intelligent controller was validated through simulation results.

The use of WNNs and RWNNs is not new in the literature [31–35]; however, the implementation of these structures involves the use of multiple layers with multiple neurons. The use of offline training algorithms and some early applications in real time have generated a major motivation in the development of our proposal. The Gaussian and Mexican hat wavelets, together with classical sigmoid activation functions, are commonly used in the structure of WNNs and RWNNs. There is a lack of works about the use of the Morlet wavelet in the structure of WNNs. There are a few works about the use of WNNs and RWNNs in control theory. Most of the works about the use of WNNs and RWNNs are focused on estimation and time-series prediction [18]. For all of the above, here we explore the performance of the Morlet wavelet in the identification process of the dynamics of nonlinear systems. In this work, we propose a continuous-time wavelet neural identification scheme based on the structure of a RHONN model where classical activation functions are replaced by Morlet wavelet activation functions, i.e. classical sigmoid functions are excluded. The resulting structure has been called a recurrent Morlet wavelet neural network (RMWNN), also known as a recurrent wavelet first-order neural network, from which the design of a decentralized controller in order to solve the trajectory tracking problem for a quadrotor UAV is carried out using the backstepping approach. The training for the RMWNN is performed online in a series–parallel configuration using the FE algorithm, shaping a new neural structure of a single layer with a single neuron, where its capacity for identification of more complex dynamics increases with the implementation of the Morlet wavelet. The performance of the proposed scheme is validated via numerical simulation and experimental results. Besides, in this work also a decentralized RHONN controller for a quadrotor UAV is designed and taken as baseline controller. The backstepping controller derived from the RMWNN model is used because the structure for the RHONN model is considered as given in the same form as that for the RMWNN, namely in the form of a strict feedback system, but with sigmoid activation functions and high-order connections between them.

This paper is organized as follows: properties and applications of the CWT and the state of the art of WNNs have been provided above in this section; the fundamentals are described in §2; §3 provides the mathematical model for a quadrotor UAV and describes the design of the neural control scheme proposed via a backstepping approach; simulation and real-time results are provided in §4 in order to evaluate the viability of the wavelet neural control scheme proposed; and finally the conclusion is given in §5.

2. Fundamentals

(a). Recurrent Morlet wavelet neural network

Consider the RHONN model [36], where the state of each neuron is governed by a differential equation of the form

2.1

where xⁱ_j is the state of the ith neuron, aⁱ_j and bⁱ_j are positive real constants, wⁱ_jk is the kth adjustable synaptic weight connecting the jth state to the ith neuron, L represents the total number of weights used to identify the plant behaviour, and y_j is the activation function for each one of the connections. Each y_j is either an external input or the state of a neuron through a sigmoidal function, i.e. y_j = s(xⁱ_j), where s( · ) is a sigmoidal nonlinearity. In a recurrent second-order neural network, the total input to the neuron is not only a linear combination of the components y_j; it may also be the product of two or more elements represented by triplets y₁y₂y₃, quadruplets, etc. {I₁, I₂, …, I_L} is a collection of L not-ordered subsets of {1, 2, …, i + j} and d_j(k) are non-negative integers. This class of neural network forms a RHONN.

The input vector for each neuron is given by

2.2

where u = [u¹ u² · s u^j]^→ p is the vector of external control inputs to the network; the superscript → p denotes the transposed vector.

Introducing an L-dimensional vector z, defined as

2.3

the RHONN model (2.1) can be rewritten as

2.4

Replacing now the vector z by a wavelet vector ψ and considering that higher-order terms will not be used, the RHONN model (2.1) can be rewritten as

2.5

Defining the adjustable parameter vector as wⁱ_jk = bⁱ_j[wⁱ_j1 wⁱ_j2 · s wⁱ_jL]^→ p, so (2.5) becomes

2.6

where the vectors wⁱ_jk represent the adjustable weights of the network, while the coefficients aⁱ_j for i = 1, 2, …, n are part of the underlying network architecture and are fixed during training. The structure in the form (2.6) here is called a RMWNN.

To guarantee that each neuron xⁱ_j is bounded-input bounded-output (BIBO) stable, we assume that aⁱ_j > 0. The dynamic behaviour of the overall network is described by expressing (2.6) in vector notation as

2.7

where , 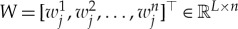and is a diagonal matrix. As aⁱ_j > 0, ∀ i = 1, 2, …, n, A is Hurwitz.

This RMWNN, i.e. a neuron with a single connection of first order, is the most simple structure for a RHONN and is an expansion of the first-order Hopfield [37] and Cohen–Grossberg [38] models. The sigmoidal activation function s( · ) is replaced by the real version of the modified Morlet wavelet [39,40] of the form ψ(x) = e^−x2/βcos(λx), with parameters β and λ representing expansion and dilation, respectively. Properties of this wavelet function are described in [5,6].

(b). Approximation properties of the recurrent Morlet wavelet neural network

In the following, the problem of approximating a general nonlinear dynamical system by a RMWNN is described. The input–output behaviour of the system to be approximated is given by

2.8

where is the input to the system, is the state of the system and is a smooth vector field defined on a compact set , where i and j are constants. The approximation problem consists of determining, using the wavelet activation function for continuous time, if there exist weights wⁱ_jk such that (2.6) approximates the input–output behaviour of an arbitrary dynamical system of the form (2.8). Assume that F( · ) is continuous and satisfies a local Lipschitz condition such that (2.8) has a unique solution and for all t in some time interval J_T = {t:0≤t≤T}, where J_T represents the time period over which the approximation is performed. From (2.1) and (2.2), it is clear that z(x, u) is in the standard polynomial expansion with the exception that each component of the vector x is preprocessed by a sigmoid function s( · ). As shown in [41], preprocessing of an input via a continuous invertible function does not affect the ability of a neural network to approximate continuous functions. Based on the above assumptions, the next theorem, which is strictly an existence result and does not provide any constructive method in order to obtain the optimal weights w*ⁱ_jk, proves that if a sufficiently large number of weights are allowed in (2.6), then it is possible to approximate any dynamical system to any degree of accuracy.

Theorem 2.1

Suppose that the system (2.8) and the RMWNN model (2.6) are initially at the same state χⁱ_j(0) = xⁱ_j(0). Then, for any ε > 0 and any finite T > 0 there exists an integer L and a vector such that the state xⁱ_j(t) of the RMWNN model (2.6), with L number of weights whose values wⁱ_jk = w*ⁱ_jk, satisfies:

Proof. —

See [42]. ▪

(c). Filtered error training algorithm

Under the assumption that the unknown system is exactly modelled by a RMWNN architecture of the form (2.6), the weight adjustment law and the FE training algorithm for this RMWNN are next summarized. Based on the assumptions of no modelling error, there exist unknown weight vectors w*ⁱ_jk such that each state χⁱ_j of the unknown dynamical system (2.8) satisfies

2.9

where χⁱ_j0 is the initial state of the system. As is standard in systems identification procedures, in this paper it is assumed that the input uⁱ(t) and the state χⁱ_j(t) remain bounded for all t≥0. Based on the definition for ψⁱ_jk(χⁱ_j, uⁱ) given by (2.3), this implies that ψⁱ_jk(χⁱ_j, uⁱ) is also bounded. In the sequel, unless there exists confusion, the arguments of the vector field ψ will be omitted. Next, the approach for estimating the unknown parameters w*ⁱ_jk of the RMWNN model (2.9) is described.

Considering (2.9) as the differential equation describing the dynamics of the unknown system, the identifier structure is chosen with the same form as in (2.6), where wⁱ_jk is the estimate of the unknown weight vector w*ⁱ_jk. From (2.6) and (2.9), the identification error ξⁱ_j = xⁱ_j − χⁱ_j satisfies

2.10

2.11

which can be rewritten as

2.12

where denotes the parametric error [43]. The weights wⁱ_jk are adjusted according to the learning law

2.13

where the adaptive gain is a positive definite matrix. Stability and convergence properties for the weight adjustment law given above are analysed in [44]. The following theorem establishes that this identification scheme has convergence properties with the gradient method for adjusting the weights.

Theorem 2.2 —

Consider the filtered error RMWNN model given by (2.12), whose weights are adjusted according to (2.13). Then

• (i) ξⁱ_j, (i.e. ξⁱ_j and are uniformly bounded);

• (ii) .

Proof. —

See [45]. ▪

3. Neural backstepping controller design

In this work, a miniature four-rotor helicopter is considered, having two of these rotors rotating clockwise, and two rotating anticlockwise. Each rotor consists of a direct current brushless motor with propeller. Forward motion is accomplished by increasing the speed of the rear rotor while simultaneously reducing the forward rotor by the same amount. Backward, leftward and rightward motion can be accomplished in the same way. Finally, yaw motion can be performed by accelerating the two clockwise-turning rotors, while decelerating the anticlockwise ones.

The equations describing the attitude and position of a quadrotor are those of a rotating rigid body with six degrees of freedom [46]. They can be separated into kinematic and dynamic equations [47]. The dynamic equations can be obtained around the centre of mass

3.1

and

3.2

where m_q denotes the quadrotor mass, V_b is the velocity in the body frame, ω is the angular rate of the quadrotor, J = diag{J_x, J_y, J_z} is the inertia matrix, the external force takes into account the quadrotor weight, the total thrust and the aerodynamic force, whereas the external torque considers the difference of thrust and torque exerted by the two pairs of rotors as well as the aerodynamic moment vector.

The equations of motion for a quadrotor, assuming low speeds, are given by Bouabdallah et al. [48] as

3.3

3.4

3.5

3.6

3.7

3.8

Here x, y and z are the coordinates of the centre of mass in the inertial frame; θ, ϕ and ψ are Euler angles representing pitch, roll and yaw, respectively; s( · ) and c( · ) denote the sin( · ) and cos( · ) functions; J_x, J_y and J_z are moments of inertia in the directions of the three-dimensional Cartesian coordinates; l represents the distance between the rotors with respect to the centre of mass (centre of gravity) of the quadrotor; ϖ_r = − ϖ₁ + ϖ₂ − ϖ₃ + ϖ₄ is the sum of angular velocity of the rotors; and J_r represents the inertia of the rotating rotors, which is considered the same parameter for all four motors.

Consider that the system (3.3)–(3.8) can be divided into N subsystems of the form [49]

3.9

where i = 1, 2, …, N, only depends on local variables, represents interconnection effects, χⁱ₁, represents the position and velocity from the ith subsystem, respectively, is the input for each subsystem, is the state vector of the system and is the input vector of the system. For this purpose, the governing equations can be expressed in the state equation through the selection of a set of state variables given by

3.10

Then, the system dynamics can be divided in a decentralized way as

3.11

3.12

3.13

3.14

3.15

3.16

Thus, the neural identification problem for the whole system can be simplified through the use of six second-order subsystems, namely one second-order subsystem for each coordinate.

In this work, as a continuation of [43], a decentralized RMWNN trained via FE algorithm (2.12) with weights adjustment law (2.13) is proposed for identification and control of a quadrotor UAV. From (2.6), the decentralized RMWNN model is given as follows:

3.17

with k = 1 for the wⁱ_jkψⁱ_jk( · ) term, where j = 1, 2 is for the number of states of the ith RMWNN model; χⁱ₁ represents the measurable local translational (angular) position and χⁱ₂ is for the calculated local translational (angular) velocity; uⁱ is the control input. It must be noted that this decentralized neural scheme is in the form of a strict feedback system; then, the use of the backstepping approach is suitable for the design of the neural controller. For each ith subsystem, the identification error between the neural identifier and the coordinate is defined as ξⁱ₁ = xⁱ₁ − χⁱ₁ for the translational (angular) position and ξⁱ₂ = xⁱ₂ − χⁱ₂ for the translational (angular) velocity. To update online the synaptic weights, the adaptive learning laws are given by

and

with Γⁱ_jk > 0 as the adaptive gain and

and

with β₁ = β₂ = 20 and λ₁ = λ₂ = 0.01.

Next, our objective is to design a feedback control law uⁱ to force the system output to follow a desired trajectory. The decentralized neural control scheme is based on the following.

Denoting ξⁱ = |χⁱ − xⁱ| as the identification error and the trajectory tracking error between the states of the neural network for position and the desired trajectory as ϵⁱ = |xⁱ − χⁱ_d|, the output tracking error is rewritten as

3.18

Consequently, the error dynamics is given as

3.19

Proposing the Lyapunov-like function

that stabilizes ξⁱ, then the time derivative of Vⁱ( · ) is given by

which evaluated along the trajectories (2.12) and (2.13) becomes

3.20

Now, from the neural structure (3.17) proposed, we proceed with the design of the controller that stabilizes ϵⁱ. To this end, defining the trajectory tracking errors of the RMWNN as

3.21

the error dynamics are given by

3.22

and

3.23

From (3.22), considering ϵⁱ₂ as virtual control input, we proceed with the design of a control ϵⁱ₂ = αⁱ₂ in order to stabilize the origin ϵⁱ₁ = 0.

Therefore, choosing

3.24

the nonlinear terms are cancelled. Consequently,

3.25

Now, proposing the augmented Lyapunov-like function

3.26

the time derivative of (3.26) is given by

3.27

From (3.25), (3.27) can be written as

3.28

or equivalently

3.29

Thus, the origin of is globally exponentially stable.

From the backstepping approach, applying the variable change

3.30

then

3.31

Substituting (3.31) in (3.22) yields

3.32

Continuing with the backstepping approach, the time derivative of (3.24) results in

3.33

From (3.32), (3.33) can be written as

3.34

The time derivative of (3.30) gives

3.35

From (3.23) and (3.34), (3.35) is written as

3.36

Thus, from (3.32) and (3.36), the system takes the form

3.37

and

3.38

Proposing the augmented Lyapunov-like function

its time derivative, along the trajectories (3.37)–(3.38), is then given by

Expanding and rearranging terms yields

Thus, selecting the control law as

3.39

it yields

Hence, the control law (3.39) asymptotically stabilizes the system.

The block diagram for the decentralized Morlet wavelet neural controller, proposed here, is shown in figure 1. Figure 2 shows the block diagram for the RMWNN controller.

Figure 1.

Decentralized Morlet wavelet neural control scheme. (Online version in colour.)

Figure 2.

RMWNN controller. (Online version in colour.)

4. Results

In this work, the Unmanned Vehicle Systems (UVS) Laboratory from Quanser is used as experimental set-up [50]. The QBall 2 is a quadrotor helicopter enclosed in a carbon fibre cage to protect the vehicle, ensuring safe operation in an indoor laboratory environment (figure 3). To measure on-board sensors and drive motors, the QBall 2 uses Quanser's on-board avionics data acquisition card and a wireless embedded computer. The QBall 2 operates using a host–target structure. The controllers are developed on the ground station computer (host) using Matlab/Simulink. The QUARC control software downloads real-time code from the host to the QBall 2 embedded computer (target), and allows users to run, modify and monitor the code remotely from the host. The controllers on-board the QBall 2 are open architecture and fully modifiable. The position of the QBall 2 in the workspace is tracked and accurately measured using an infrared camera localization system, fully integrated with QUARC. The parameters of the QBall 2 are given as J_x = J_y = 0.03 kg m², J_z = 0.04 kg m², l = 0.2 m and m_q = 1.79 kg [51].

Figure 3.

The Unmanned Vehicle Systems (UVS) Laboratory from Quanser provides a turn-key, integrated environment for exploring a wide range of advanced research applications. Integrating the Quanser QBall 2 system with additional QBall and QBot ground robot units allows researchers to build a flexible, open architecture, multi-agent platform for research. Image used with permission from Quanser.

First, the performance of the decentralized RMWNN control scheme is evaluated through numerical simulation. To compare the performance of the RMWNN control scheme, a decentralized RHONN control scheme is also proposed here. Figure 4 shows the trajectory tracking task performed by the quadrotor UAV under both decentralized neural control schemes. The reference trajectory is defined by χ^x_1d = 0.5cos(0.251t) and χ^y_1d = 0.5sin(0.251t). Table 1 exhibits the mean squared errors (MSEs) from the online identification of the quadrotor's dynamics during the performance of the circular trajectory tracking task. It can be seen from table 1 that the decentralized control based on RMWNNs exhibits the smallest values for the MSEs. From table 2, it can be seen that the performance for trajectory tracking is better under the decentralized control scheme using RMWNNs in contrast with that using RHONNs. Figure 5 shows the tracking task performed by the quadrotor UAV under both decentralized neural control schemes but for a square-shaped trajectory. For this latter task, a second-order low-pass filter, with damping ratio of 0.9 and natural frequency of 0.55, is used to the reference trajectories χ^x_1d and χ^y_1d in order to minimize the effect of its derivatives. Table 3 exhibits the MSEs from the online identification of the quadrotor's dynamics during the performance of the square-shaped trajectory tracking task. It can be seen from table 3 that the decentralized RMWNNs controller exhibits the smallest values for the MSEs with the exception of the z- and ψ-coordinates. From table 4, it can be seen that the performance for the tracking task when describing a square-shaped trajectory is also better under the decentralized control scheme when using RMWNNs. From figure 6, it can be seen that the decentralized RMWNN control scheme performs well in spite of the presence of a disturbance occurring at 10 s for the roll angle, measurement noise from 20 to 30 s for the pitch angle and parametric variation of 15% for J_z, from its nominal value, occurring at 35 s and beyond.

Figure 4.

(a) Circular trajectory tracking performed by the decentralized neural controllers and (b) dynamics of the attitude angles.

Table 1.

MSEs from the identification of the quadrotor's dynamics during the performance of circular trajectory tracking.

	subsystem
control scheme	x	y	z	θ	ϕ	ψ
via RMWNNs	0.000213	0.000171	0.001289	0.000112	0.000085	0.000097
via RHONNs	0.003908	0.003906	0.008341	0.003905	0.003892	0.008178

Table 2.

MSEs from the circular trajectory tracking.

	subsystem
control scheme	x	y	z	θ	ϕ	ψ
via RMWNNs	0.075974	0.004960	0.111253	0.003503	0.002553	0.000274
via RHONNs	0.068455	0.022092	0.111574	0.006181	0.004629	0.007953

Figure 5.

(a) Square-shaped trajectory tracking performed by the decentralized neural controllers and (b) dynamics of the attitude angles.

Table 3.

MSEs from the identification of the quadrotor's dynamics during the performance of square-shaped trajectory tracking.

	subsystem
control scheme	x	y	z	θ	ϕ	ψ
via RMWNNs	0.000155	0.000155	0.001001	0.000038	0.000033	0.000101
via RHONNs	0.003025	0.003021	0.001001	0.003015	0.003012	0.000101

Table 4.

MSEs from the square-shaped trajectory tracking.

	subsystem
control scheme	x	y	z	θ	ϕ	ψ
via RMWNNs	0.002440	0.002872	0.086096	0.002018	0.002119	0.000223
via RHONNs	0.005785	0.004694	0.086096	0.003100	0.003013	0.000223

Figure 6.

(a) Square-shaped trajectory tracking performed by the decentralized RMWNN controller when considering the presence of disturbance, measurement noise and uncertainty and (b) dynamics of the attitude angles.

Second, the performance in real time of the decentralized neural controller based on RMWNNs for the case in which the quadrotor UAV must describe an upward vertical displacement until it reaches a reference value for hover condition, maintain a constant height for a while, and then go back to the starting point is shown in figures 7–11. Figure 7 shows the dynamics described by the quadrotor UAV when pursuing the task of interest. From figure 8, it can be seen that there is no significant deviation from the x-coordinate. However, a deviation of about 20 cm from the y-coordinate is present when reaching the desired height. Figure 9 shows the error signal for the x- and y-coordinates. Figure 10 shows the error signal for the z-coordinate. It can be seen that the decentralized RMWNN controller reaches the desired height for hover condition, maintaining the flight during 6 s. Also, from figure 10, it can be seen that the control signal is proportional to the weight of the QBall 2, i.e. u^z is the required thrust to maintain the quadrotor UAV in flight and it is obtained from the control law related to the neural subsystem for the z-coordinate. Figure 11 shows that the error signal for the yaw angle exhibits a slight deviation from zero. Figures 12 and 13 show the error signal for the pitch and roll angle, respectively. It should be noted that regulation of the θ- and ϕ-coordinates could not be achieved through their respective RMWNN controllers; instead sliding-mode controllers, where the angular velocity from the yaw angle is taken into account in one of its terms, are used for these subsystems. In spite of the error signal for the yaw angle showing a slight deviation from zero (figure 11), its amplitude is almost the same in comparison with that for the roll angle. Table 5 shows the MSEs from performing the tracking task in real time.

Figure 7.

Real-time trajectory tracking performed by the decentralized RMWNN controller.

Figure 11.

(a) Error signal for the angular coordinate ψ and (b) control signal for the yaw movement.

Figure 8.

(a) Real-time translational displacement by the decentralized RMWNN controller in the (x, z)-plane; (b) real-time translational displacement by the decentralized RMWNN controller in the (y, z)-plane.

Figure 9.

(a) Error signal for the x-coordinate and (b) error signal for the y-coordinate.

Figure 10.

(a) Error signal for the z-coordinate and (b) control signal for the vertical thrust.

Figure 12.

(a) Error signal for the angular coordinate θ and (b) control signal for the pitch movement.

Figure 13.

(a) Error signal for the angular coordinate ϕ and (b) control signal for the roll movement.

Table 5.

MSEs from the real-time trajectory tracking.

subsystem
x	y	z	ψ
0.018176	0.130199	0.156589	0.038071

5. Conclusion

From the simulation results presented here, it is shown that our proposed method achieves an improved identification of the quadrotor's dynamics in contrast with one based on RHONNs, i.e. our method exhibits a faster response and smaller identification errors. Also, it requires small adaptation gain values in contrast to those for the RHONN scheme. The real-time results indicate that the decentralized RMWNN controller exhibits good performance for the z- and x-coordinates. However, an offset for the y-coordinate was present when reaching the desired height. This offset could not be cancelled, so the performance of our controller does not seem so good. The decentralized RMWNN controller shows a slight deviation from the ψ-coordinate. It should be noted that the θ- and ϕ-coordinates could not be controlled by the decentralized RMWNN controller; sliding-mode controllers were used for these subsystems. As is common, in practice, in this work the control for three translational coordinates and one rotational coordinate is achieved in contrast to those where the control for three rotational coordinates and one translational coordinate is reported. Hence, the real-time results validate the viability of the proposed continuous-time decentralized wavelet neural control scheme reported here.

Data accessibility

This article has no additional data.

Author's contributions

S.L. designed the study, carried out the experiments and performed the data analysis. F.J. conceived of and designed the study, performed the data analysis and drafted the manuscript. Both authors read and approved the manuscript.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was supported by CONACYT, Mxico, and by TecNM Projects.