Abstract
Theoretical and practical advances in time–frequency analysis, in general, and the continuous wavelet transform (CWT), in particular, have increased over the last two decades. Although the Morlet wavelet has been the default choice for wavelet analysis, a new family of analytic wavelets, known as generalized Morse wavelets, which subsume several other analytic wavelet families, have been increasingly employed due to their time and frequency localization benefits and their utility in isolating and extracting quantifiable features in the time–frequency domain. The current paper describes two practical applications of analysing the features obtained from the generalized Morse CWT: (i) electromyography, for isolating important features in muscle bursts during skating, and (ii) electrocardiography, for assessing heart rate variability, which is represented as the ridge of the main transform frequency band. These features are subsequently quantified to facilitate exploration of the underlying physiological processes from which the signals were generated.
This article is part of the theme issue ‘Redundancy rules: the continuous wavelet transform comes of age’.
Keywords: signal processing, continuous wavelet transform, electromyography, electrocardiography
1. Introduction
Physiological signals are characterized by oscillations that exhibit a range of frequencies, from the high frequencies of electroencephalography (EEG) and electromyography (EMG), to the medium frequencies of electrocardiography (ECG), and to the low frequencies of blood flow and intracellular mechanisms. Studying the dynamics of these oscillations at varying temporal resolutions can provide new insights into physiological processes [1]. Frequency analysis based on the Fourier transform (FT) is generally the first step in determining frequency content. However, FT assumptions, including stationarity, do not apply to complex physiological signals, which are generally non-stationary and contain transient components. Consequently, time–frequency techniques, which allow analysis in both time and frequency and do not require the assumptions of the FT, have proven to be successful in studying the dynamics of physiological systems. For instance, the short-time Fourier transform (STFT), which computes the FT in short, sliding time windows, was introduced for decomposition in both time and frequency [2]. A limitation of this method is that it only allows fixed time–frequency window sizes, and therefore the exact frequency of a component cannot be determined at an exact time [1]. Although fixed-size Gaussian windows can be used to alleviate this shortcoming, they only provide optimal time resolution at low frequencies. Consequently, other time–frequency approaches, such as wavelet analysis, were introduced to address these problems.
The continuous wavelet transform (CWT) represents the time–frequency space of a signal as a matrix whose magnitude values can be readily visualized as a heat map to reveal important features, transients and anomalies. In addition to facilitating new insights through visualization, the CWTs of multiple signals can be employed to assess the relationships of their frequency contents over time through the cross-wavelet transform, and to estimate the correlation between time–frequency features through wavelet coherence and phase coherence [3,4].
Many wavelet functions are available for the CWT, including the ‘Mexican hat’, the Paul wavelet and, in particular, the Morlet wavelet, which, because of its desirable properties and straightforward relationship to the FT, has been widely employed in many applications [3–7]. The current paper focuses on the analysis of real physiological signals collected from human subjects using an analytic CWT with generalized Morse wavelets, henceforth called the MsCWT. This wavelet family addresses some of the shortcomings of the complex analytic Morlet wavelet. In this paper, the MsCWT is applied to two types of physiological signals: (i) EMG, which measures the electrical activity of skeletal muscles, and (ii) ECG, which measures the electrical activity of the heart. One of the advantages of these wavelets is that rigorous methods exist to identify important features in the transform that can be subsequently quantified and subjected to statistical analysis. In the first experiment, the MsCWT is used for isolating events in EMG to study the activity of groups of muscles during skating. Regions of influence around maxima in the transform are computed for each muscle, as described in §2d, and the areas of overlap in the regions between two muscles are calculated and analysed with respect to skating speed. In the second experiment, the relationship between ECG and muscle sympathetic nerve activity (MSNA) is assessed through joint ridge analysis, described in §2c, with the goal of quantifying heart rate variability (HRV) [6,8]. These experiments employed a known orthostatic stressor, namely lower body negative pressure (LBNP), to increase sympathetic tone. Although many intuitive metrics in the time and frequency domains can be computed from the HRV record, this study proposes using the rich information provided in the original ECG record for complementary complexity metrics that can yield further insights into physiological processes [6].
For the EMG signals, regions of overlap between isolated events in the MsCWTs of pairs of muscles are quantified as a proxy measure related to co-contraction to assess how frequency content relates to skating speed. For the ECG signals, complexity measures are used to quantify the complexity and variability of the joint ECG and MSNA ridge occurring at the main heartbeat frequency to complement traditional HRV measures. The results of resting (baseline) and experimental (LBNP) conditions were compared. This analysis extends the work presented in [6,9], which employed the complex Morlet CWT, to employ a rigorous ridge identification algorithm developed for the MsCWT to quantify variability in both frequency and wavelet power as a function of time.
The purpose of this paper is not primarily to report new physiological findings or to draw possible clinical conclusions, but rather to employ the generalized Morse analytic wavelet transform as an exploratory tool. Thus, the work presented in this paper can be considered to be a precursor to definitive characterization of physiological dynamics and interactions [1].
2. The analytic wavelet transform
(a). Mathematical background
The MsCWT comprises a family of complex-valued transforms [10]. A complex-valued analytic signal x+(t) has only positive frequency components, expressed in polar coordinates as
 |
2.1 |
where a+ and ϕ+ are the canonical amplitude and canonical phase, respectively. The instantaneous frequency in radians (where the Nyquist frequency is represented by π radians) is given as 
, and in hertz as 
[11].
Analytic wavelets are wavelets whose FT Ψ(ω) is zero for ω < 0. The analytic CWT using ψ(t) as the basis (mother) wavelet is therefore a function of time t and scale s, given by Lilly & Olhede [10]:
 |
2.2 |
Note that the lower bound of integration is zero. An analytic wavelet has a ‘peak frequency’ ωβ,γ = (β/γ)1/γ, where Ψ(ωψ) attains its maximum amplitude.
For time-varying spectrum estimation, a class of wavelets, known as generalized Morse wavelets [12], have properties that make them particularly useful for signal analysis, including ridge extraction [10,13] and extracting isolated, time-localized events [14].
The Morse family of wavelets, ψβ,γ(t), is parametrized by a shape parameter γ > 0, an oscillation control parameter β > 0, and an order parameter 
. For a given β and γ, k allows the construction of increasingly oscillatory wavelets that are orthogonal to ψβ,γ [12,15]. Additionally, the number of oscillations in the wavelet (inverse bandwidth) is represented as 
. The time duration of a Morse wavelet (the ‘wavelet footprint’) at an angular frequency ω is given as 
. This quantity can be used to compute the cones of influence [3], which delineate transform regions with inaccurate values due to edge effects [14]: for a signal x(t) of length N and a specified ω, the transform values are only considered to be accurate in the range (Lβ,γ(ω)/2, N − Lβ,γ(ω)/2).
Morse wavelets are defined in the frequency domain as [12,15]:
 |
2.3 |
where U(ω) is the Heaviside function, and 
is a normalization constant [10] ensuring a peak frequency of 2 [10]. Examples of magnitude frequency responses of Morse wavelets at various β and γ are shown in figure 1. Time-domain Morse wavelets are shown in figure 2.
Figure 1.
Frequency responses Ψβ,γ(ω) at different β and γ for ω∈(0, π], generated through equation (2.3) and scaled with aβ,γ = 2(eγ/β)β/γ so that the peak frequency is 2. (Online version in colour.)
Figure 2.
Morse wavelets in the time domain, scaled to unit peak: (a) β = 8, γ = 3, (b) β = 4, γ = 8 and (c) β = 8, γ = 12. (Online version in colour.)
(b). Comparison of the Morse and Morlet continuous wavelet transforms
A distinct benefit of the widely used Morlet CWT is its simple construction. It was designed to be a zero-mean function with desirable Gaussian properties. For values of the central frequency of the Morlet mother wavelet ω0 > 5, it is a complex sinusoid in a symmetric Gaussian window [5]. Setting ω0 = 6 is generally preferred [3], as the wavelet becomes skewed for ω0 < 5 (see [5] for a discussion of the mathematical properties of the Morlet CWT). Owing to its simplicity, the complex Morlet CWT has a straightforward linear relationship to the Fourier period and intuitive time–frequency representation [3,6,9]. More complex wavelet shapes yield representations with spurious components.
Conversely, a difficulty associated with generalized Morse wavelets vis-à-vis the Morlet wavelet is conversion of wavelet scale to frequencies. The peak frequency, energy frequency and central instantaneous frequency differ in generalized Morse wavelets [16]. However, toolboxes such as jLab [17] can be used to perform these conversions.
In some cases, the Morlet CWT does not perform well for time localization [15]. Because it is only approximately analytic, it has support for negative frequencies, leading to interference terms and degrading the resulting transform. Although, in practice, the parameter ω0 of the Morlet CWT does not vary, the robustness of results to the choice of Morlet wavelet is also questionable [16]. Furthermore, given the variety of analytic wavelets, the question remains as to which one is most appropriate for general use (or for a specific purpose), making the selection of a particular wavelet appear to be arbitrary [6,15].
Generalized Morse wavelets are particularly useful for analysing modulated signals (signals that contain time-varying amplitude and frequency characteristics) and transient, short-duration, localized discontinuities and events. Because they are parametrized by two values (β and γ), they are more versatile than the Morlet wavelet (with one parameter). The parameters of the generalized Morse wavelet allow adjustments for refining localization in frequency and time. They have been shown to encompass eight distinct families of analytic wavelets, including Cauchy or Klauder wavelets when γ = 1, Paul wavelets for the case of γ = 1 and 
, and derivative of Gaussian (DoG) wavelets when γ = 2 [15,16]. However, setting γ = 3 results in the most symmetric and most Gaussian wavelets (‘Airy’ wavelet family), having many of the advantages of Morlet wavelets while avoiding their deficiencies, and have been recommended as an initial basis for general signal analysis [15].
Additionally, wavelet coherence [3,4] generally relies on simulations to obtain statistical properties, and assume joint stationarity. Orthogonal Morse wavelets are conducive for estimating the true wavelet coherence [18].
There is a growing literature on applications of Morse wavelet analysis. For instance, it was used to study intracellular neurophysiological time-series recordings via multi-wavelet coherence [19]. Another study found that, in studying high-frequency oscillations in intracranial EEG recordings, the Morse wavelet transform was the most appropriate to describe the temporal organization of the frequency content of the signals, compared to the DoG and Morlet wavelet transforms, and the Wigner–Ville distribution [20]. Ridge analysis of the Morse CWT was also combined with spatial (phase) information to detect sleep spindles in EEG recordings [21].
(c). Wavelet ridge analysis
Wavelet ridges are useful for determining instantaneous frequencies and amplitudes of signal components [5]. Ridge analysis assumes that oscillatory properties can be represented by wavelet ridge curves in time–frequency space, and are based on characteristics discerned from the wavelet transform [22–24]. An estimator for a modulated oscillatory signal is then obtained through the MsCWT values evaluated along the ridge. In practice, ridge curves (specifically, amplitude ridge curves) are represented as a collection of ridge points, which satisfy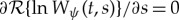 
and 
[10,13,25], ensuring that an amplitude ridge point corresponds to the scale at which a local maximum in the transform magnitude occurs at a specific time t. A ridge curve s(t) is then a scale curve as a function of time consisting of the contiguous individual ridge points, defined over some time interval T. The ridge-based signal estimate 
is then [10]
 |
2.4 |
As the MsCWT is complex-valued, phase-based wavelet ridge curves can also be defined in an analogous manner [10]. For practical implementations (such as found in jLab [17]), the individual ridge points determined through local maxima in the wavelet transform are chained together to form the curves. Finally, because the MsCWT is only computed at a discrete scale, quadratic interpolation is applied to increase the accuracy of the MsCWT values and frequencies at which they occur along ridges, based on the exact ridge location [13].
Ridge extraction from the MsCWT can also be extended to the multivariate case. Given a set of D real-valued signals, x(t) = [x1(t) x2(t) … xD(t)]T, the multivariate MsCWT is then: wψ(t, s) = [W1,ψ(t) W2,ψ(t) … WD,ψ(t)]T. Analogous to the univariate case, an amplitude ridge point satisfies ∂∥wψ(t, s)∥/∂s = 0 and ∂2∥wψ(t, s)∥/∂s2 < 0, and the amplitude ridge is constrained so that |ds(t)/dt| < ∞ [25].
(d). Transient and isolated wavelet features
A transform maximum point is defined as the two-dimensional point 
where the local maximum of the wavelet transform modulus is attained. Isolated maxima and confidence regions (regions of influence or ROIs) for these maxima in the MsCWT time–frequency representation can also be determined (see [14] for a thorough mathematical development).
A real-valued signal x(t) comprising N events can be written as [14]
 |
2.5 |
where the 
determine the amplitude and phase of the nth event at time tn and scale ρn. The xϵ denote a zero-mean noise process. In this equation, μ is a parameter that plays the same role as β in equation (2.3), but can take the value of β = 0. The MsCWT wβ,γ(τ, s) can then be computed for x(t), as described in equation (2.5), which is essentially computing the MsCWT for a weighted sum of Morse functions. Transform maxima in the time–frequency domain occur at coordinates 
that satisfy [14]
 |
2.6 |
The values of the MsCWT at these maxima can be computed through a modified wavelet function. This function is the wavelet transform, using ψβ,γ of another wavelet, ψμ,γ, where the parameter μ was introduced in equation (2.5) [14].
In the absence of noise and with sufficient separation of the N events, the coefficients cn, scales ρn and time locations tn of the events can be calculated from the maxima of the MsCWT. When noise is present, the MsCWT of the noise can be used to determine the rate of false positive maxima due to the noise processes, which, in turn, leads to a threshold for determining spurious maxima. Expected ROIs associated with each of the remaining statistically significant maxima ensure that they are isolated from each other [14]. An ROI is a curve encompassing a region in the time–frequency domain where the MsCWT modulus has decreased to a fraction λ of its peak value. As expected, smaller λ values result in larger ROI curves.
3. Materials and methods
(a). Electromyography skating experiments
Six female varsity ice hockey players gave informed written consent to participate in the study approved by the University of Ontario Institute of Technology Research Ethics Board. The anthropometrics are: mean age 19.5 ± 1.5 yr, height 168.0 ± 6.1 cm and mass 83.0 ± 8.3 kg. Seven dynamic skating trials, ranging in duration from 5 to 13 s, were completed. In this paper, only the results of the forward sprint (FS) and backward sprint (BS) are discussed.
Video with a 30 Hz frame rate was used to determine start and end times. Bilateral surface EMG (mV) was recorded of the following muscles: right and left tibialis anterior (RTA/LTA), lateral gastrocnemius (RLG/LLG), vastus lateralis (RVL/LVL) and biceps femoris (RBF/LBF); using a wireless system (Myomonitor IV®, Delsys Inc., Natick, MA, USA) and recorded to a personal laptop computer. Data were recorded at 1000 Hz and were bandpass filtered between 20 and 450 Hz. Skin preparation and electrode placements followed accepted standards. The EMG were downsampled to 500 Hz to facilitate MsCWT calculation. As the main EMG burst frequencies of interest are under 100 Hz, this downsampling is not considered to be detrimental to subsequent analyses.
The MsCWT of the EMG signals for forward and backward skating for each pair of muscles on both sides (e.g. RTA/RBF, LTA/LBF) and corresponding muscles on the left and right sides (e.g. RTA/LTA, RBF/LBF) for each subject were calculated with β = 8 and γ = 3. The former value was chosen because of the oscillatory nature of the EMG, and because it empirically revealed important features in the transform, and the latter value because of the advantages of γ = 3 discussed in §2. Element analysis, as described in §2d, was employed to determine the ROIs around the local transform maxima. The parameters were set to μ = 1 and λ = 3/4. ROIs not completely outside of the cone of influence were not considered in subsequent analyses.
For the NM1 ROIs for muscle M1 and the NM2 ROIs for muscle M2, the area of overlap OM1, OM2∈[0, 1] for each of the comparisons was computed as:
 |
3.1 |
(b). Skating regions of influences
For the skating EMG transforms, the regions of influence for the isolated local maxima for pairs of muscles were compared by quantifying the overlap of the ROIs for each pair. Because EMG bursts consist of events that are temporally close, λ was set to 3/4, a relatively large value. An example of the MsCWT and corresponding ROIs for a skating trial is shown in figure 3.
Figure 3.
EMG (top graphs) and corresponding MsCWT computed with β = 8 and γ = 3 (bottom plots) of a forward skating trial. (a) Entire skating trial. (b) MsCWT as in (a), but zoomed to 24 to 36 s, and from 0.2 to 12.3 Hz to show main regions of activity. ROIs are represented with black curves enclosing the events. The thick white lines at the sides of the transform denote the boundary of the cone of influence. (Online version in colour.)
(c). Electrocardiography–heart rate variability–muscle sympathetic nerve activity–lower body negative pressure experiments
Experiments were performed on nine healthy subjects (n = 9: seven men, two women, 27 ± 5 years of age, 171 ± 3 cm in height and 79 ± 9 kg in weight) at the University of Western Ontario in London, Canada. All subjects provided informed written consent for the experimental protocol as approved by the University of Western Ontario Health Sciences Research Ethics Board.
During the LBNP experiments, the participants completed 5 min baseline and LBNP (−20 mmHg) conditions in a supine posture. Analogue signals for standard three-lead ECG and microneurography (MSNA) were collected with an online acquisition and analysis system (PowerLab®, ADInstruments, Castle Hill, New South Wales, Australia). ECG records were collected for 300 s, digitized to 200 Hz and bandpass filtered at 10–25 Hz to remove noise and baseline wander. Rapid ectopic beats were filtered out. HRV signals were calculated from the processed and resampled ECG signal [6]. From these, the standard deviation of normal-to-normal (SDNN), the root mean square of successive differences in normal-to-normal intervals (RMSSD), the standard deviation of successive differences between adjoining normal cycles (SDSD), the number of successive differences of intervals that differ by more than 50 ms (NN50) and the percentage of NN50 of the total number of ECG cycles analysed (pNN50) were computed. In the frequency domain, a 1024-point fast Fourier transform (FFT) was applied to calculate the LF/HF ratio. Frequency bands were 0–0.04 Hz (VLF), 0.04–0.15 Hz (LF) and 0.15–0.4 Hz (HF) [6]. For MsCWT computation, the ECG signals were downsampled to 50 Hz, as the main frequency band of interest is around 1 Hz, and a lower sampling frequency is more appropriate for analysing HRV metrics [6].
(d). Band metrics
The 1 Hz ECG band in the MsCWT, corresponding to the heartbeat and consistently containing the highest spectral power, was analysed. This band resembles the HRV signal derived from the raw ECG, but, in the MsCWT, also provides the power of the ridge components and phase information [6]. In previous work, roughness, entropy and approximate entropy were used to analyse this band [6,9]. In this study, the mean value, as well as dispersion measures (standard deviation, interquartile range (IQR), mean absolute difference, relative mean absolute difference and distance variance) [26] and entropy were determined for the ridge of the main frequency band of each CWT. Dispersion metrics have proven very useful for quantifying band complexity [26]. The joint ECG–MSNA ridges were verified to have exactly one ridge value for each t. In a small number of cases, overlapping ridge segments in the main band were joined by using the segments that produced the smoothest ridge when joined.
(e). Complexity and dispersion measures
Entropy (H) is an important measure of uncertainty, or disorder, in a random variable [27], and was used in previous work to quantify ‘unpredictability’ or ‘randomness’ of the main CWT frequency band ridge [6]. Entropy is computed as
 |
3.2 |
where xi is a discrete sample of x(t), and p denotes an estimate of the probability density of x(t), which was estimated with an Epanechnikov kernel (which is optimal in the asymptotic mean integrated squared error sense) at 500 equally spaced points between the minimum and maximum values over all experiments.
Statistical dispersion quantifies the variability, scatter or spread of a distribution. Variance, standard deviation and IQR (a robust measure of scale that is relatively unaffected by a small number of outliers) are three such measures. The mean absolute difference (MD), also known as the Gini mean difference [28], is a relatively new dispersion measure. While standard deviation is defined in terms of central tendency, MD is twice the second L-moment (a statistic for quantifying population asymmetry and tailedness [29]). For a sequence of sample values xi, i = 1, …, N, MD is estimated by
 |
3.3 |
The relative mean absolute difference (RMD), or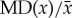 
, is a measure of dispersion when the probability distribution has a non-zero mean. The distance covariance (DV) is a non-negative quantity that characterizes the independence of random vectors in arbitrary dimensions [30], and is a special case of the distance covariance where the two vectors are equal [31]:
 |
3.4 |
where 
. Here, ai,j is the ith row, j is the column of the distance matrix, and 
, 
and 
, respectively, denote the jth row mean, kth column mean and overall mean of the distance matrix.
(f). Implementation
Custom processing, analysis, statistics and visualization programs were written in the Matlab® environment (The Mathworks, Natick, MA, USA), and were used in conjunction with the open source jLab framework for analytic continuous wavelet analysis [17].
4. Results
(a). Skating electromyography
Examples of overlap in regions of influence between pairs of muscle groups with high overlap, as well as regions excluded due to being fully or partially contained within the cone of influence, are shown in figure 4. The time duration of trial (inversely related to speed) was regressed against the overlap for the ROIs of each pair of muscles within each side, and of corresponding left and right muscles. The R2 values for the four pairs with the highest values are shown in figure 5. However, for these experiments, most muscle pairings for both forward and backward skating had R2 < 0.5, which may be attributable to the low number of participants (n = 6).
Figure 4.
Overlap for ROIs extracted from the MsCWT (β = 8, γ = 3) of EMG. The grey curved line represents the border of the cone of influence. ROIs affected by the cone of influence are displayed as hollow curves. (a) 25.74% overlap of ROIs for right and left biceps femoris muscles. (b) 24.09% overlap of ROIs for left lateral gastrocnemius and left vastus lateralis muscles. (Online version in colour.)
Figure 5.
Plots for forward (FS) and backwards (BS) skating duration versus overlap for the four highest R2 values. (Online version in colour.)
(b). Electrocardiography and muscle sympathetic nerve activity results
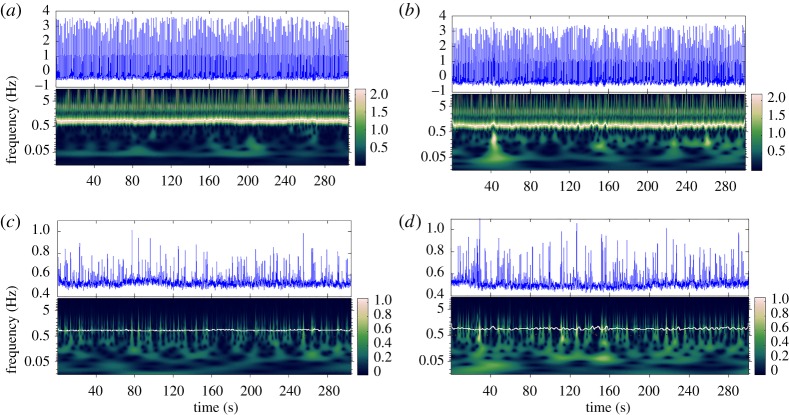
An example of joint ridges for resting and LBNP ECG/MSNA is shown in figure 6. It is seen from this figure that the joint ridge for the LBNP condition (figure 6b,d) is more variable and complex than for the resting condition (figure 6a,c). Paired-sample Student T-tests were performed for 
versus 
at the α = 0.05 significance level, where ϕ represents a variability metric. The p-values from the T-tests comparing resting and LBNP for each of the (β, γ) combinations are shown in tables 1–3.
Table 2.
Dispersion measures and entropy p-values for ECG and MSNA joint ridges (β = 4, γ = 8).
| ridge | mean | s.d. | IQR | MD | RMD | DV | entropy |
|---|---|---|---|---|---|---|---|
| joint | 0.001 | 0.002 | 0.007 | 0.001 | 0.003 | 0.009 | 0.014 |
| ECG ridge | 0.001 | 0.003 | 0.006 | 0.004 | 0.024 | 0.013 | 0.002 |
| MSNA ridge | 0.001 | 0.309 | 0.025 | 0.112 | 0.649 | 0.111 | 0.046 |
| ECG |Wψ| | 0.987 | 0.002 | 0.007 | 0.002 | 0.295 | 0.006 | 0.003 |
| MSNA |Wψ| | 0.003 | 0.171 | 0.035 | 0.041 | 0.854 | 0.123 | 0.005 |
Figure 6.
ECG, MSNA (top graphs), and their MsCWT representations computed with β = 4 and γ = 3 (bottom plots) for one subject, showing the main heart rate band at approximately 1 Hz. The ridge for this band is displayed as a white line. (a) ECG baseline (resting), (b) ECG LBNP, (c) MSNA baseline and (d) MSNA LBNP. (Online version in colour.)
Table 1.
Dispersion measures and entropy p-values for ECG and MSNA joint ridges (β = 4, γ = 3).
| ridge | mean | s.d. | IQR | MD | RMD | DV | entropy |
|---|---|---|---|---|---|---|---|
| joint | 0.001 | 0.052 | 0.333 | 0.055 | 0.104 | 0.140 | 0.056 |
| ECG ridge | 0.001 | 0.049 | 0.019 | 0.033 | 0.176 | 0.158 | 0.006 |
| MSNA ridge | 0.001 | 0.287 | 0.509 | 0.665 | 0.974 | 0.819 | 0.518 |
| ECG |Wψ| | 0.985 | 0.007 | 0.000 | 0.005 | 0.223 | 0.008 | 0.001 |
| MSNA |Wψ| | 0.006 | 0.292 | 0.023 | 0.076 | 0.918 | 0.149 | 0.010 |
Table 3.
Dispersion measures and entropy p-values for ECG and MSNA joint ridges (β = 8, γ = 12).
| ridge | mean | s.d. | IQR | MD | RMD | DV | entropy |
|---|---|---|---|---|---|---|---|
| joint | 0.000 | 0.001 | 0.011 | 0.001 | 0.001 | 0.011 | 0.000 |
| ECG ridge | 0.001 | 0.001 | 0.006 | 0.001 | 0.002 | 0.011 | 0.000 |
| MSNA ridge | 0.000 | 0.284 | 0.010 | 0.037 | 0.138 | 0.027 | 0.006 |
| ECG |Wψ| | 0.989 | 0.025 | 0.025 | 0.019 | 0.219 | 0.037 | 0.008 |
| MSNA |Wψ| | 0.006 | 0.079 | 0.073 | 0.027 | 0.812 | 0.065 | 0.018 |
The T-test analysis of the standard HRV time- and frequency-domain metrics performed in previous work (baseline − LBNP > 0, α = 0.05) demonstrated significance for all metrics (p < 0.025) except for SDNN (p = 0.441), indicating that resting HRV metrics showed higher variability than in the experimental condition [6]. This is the expected result, as, under stressed conditions, the heart generally beats more rapidly, but with a more regular, metronomic pattern. However, the metrics computed from the joint ridge of the main frequency band in the MsCWT showed higher complexity in the experimental condition, also as seen previously [6]. The CWT ridge analysis, therefore, provided complementary information about the complexity of the main frequency band that was not evident from the standard metrics.
The mean ridge value is significantly higher for LBNP because of the higher heart rate in the stressed condition. LBNP resulted in more ridge dispersion and complexity for the joint ridge, the ECG and MSNA frequency ridges, and, for the most part, the CWT coefficient values at the ridge. For all three combinations of (β, γ), the mean values of the CWT coefficient power showed no significant differences between conditions. The (β = 4, γ = 8) and (β = 8, γ = 12) transforms had more significant differences between resting and LBNP than the (β = 4, γ = 3) transforms. The statistical analysis presented here generally agrees with the results in [6], but the wavelet magnitude along the ridge and the joint ECG/MSNA ridge were also considered in the current study.
5. Discussion
(a). Electromyography event analysis
A strong relationship between activation of pairs of muscle groups and skating performance was not observed. The four pairs with higher R2, shown in figure 5, indicate that the ROI overlap of the tibialis anterior and vastus lateralis groups on both the left and right sides increases with speed (or decreasing duration) in FS, and that the converse effect is seen for the right and left vastus lateralis and biceps femoris for BS.
For FS, the strides are generally antiphase, and muscle activation patterns for the left and right legs are not concurrent. Therefore, low correlation between L and R of the same muscle is expected, and the ROI results shown here support this observation. The results also do not indicate a consistent relationship between ipsilateral synergistic muscles (e.g. gastrocnemius and vastus lateralis). Furthermore, bilateral variability is high within and between individuals, indicating two possibilities: (i) The activation bursts of synergistic muscles are occurring in such a way as to be considered uncorrelated with this technique, possibly due to the small overlap. The two muscles may be temporally contracting at the same time, but at different frequencies. To find consistent correlations between synergistic muscles, time-domain methods are preferred. (ii) Successful forward sprinting can be achieved by a range of synergistic activation patterns that cannot be easily classified. The participants are skilled skaters with only small differences in sprint times, and, consequently, gross motor differences related to speed were not observed.
For BS, leg antiphase movement is less certain. In general, there was not a strong relationship bilaterally for each muscle. The notable exception was the second slowest backward skater, with strong bilateral relationships for tibialis anterior and biceps femoris, respectively. However, the slowest skater exhibited a moderately strong relationship between the left and right vastus lateralis, but no other bilateral muscles. There are likely a range of motor patterns that will produce successful, skilled backward skating that result in variable relationships and correlations. As ice skating (both forward and backward) is a complicated motor output (i.e. multi-segmental and bilateral), it is possible for an indeterminate number of motor coordination patterns to effectively achieve the desired outcome [32]. The analytical technique employed in this study is a first step in using spatio-temporal analysis of multiple EMG signals, but additional work is required to gain further understanding of any potential functional implications as it relates to motor output.
(b). Electrocardiography–muscle sympathetic nerve activity ridge analysis
Most HRV research employs time-domain HRV metrics (e.g. RMSSD, SDNN, etc.) [8]. In the presence of stressors, such as LBNP, these metrics are expected to show decreased HRV [8], as was also observed in previous work [6]. However, the results in this paper, building on those of the previously cited study, found that the frequency content of ECG is more variable and complex in the stressed (LBNP) condition, notwithstanding the standard metrics exhibiting the expected behaviour. The differences in complexity require further investigation, but in [6] and [9], it was speculated that the large deviations from the mean heart rate in the LBNP condition (characterized by spikes in the MsCWT) may correspond to transient adjustments of the autonomic nervous system to compensate for fluctuations in blood pressure. Furthermore, as the link between autonomic nervous system activation and heart rate activity is very complex, the standard time-based metrics used in HRV analysis cannot capture the time at which these transient fluctuations occur, nor their rate of occurrence, and therefore cannot be related to specific events [6].
6. Conclusion
This study demonstrates the utility of identifying and quantifying features in the CWT to explore frequency characteristics that may be undetected in the time domain. The analytic CWT, implemented with the Morse family of wavelets, is conducive to mathematical and algorithmic approaches to identifying such important features, such as ridges in ECG transforms and regions of influence around local maxima in transforms of EMG bursts. Although the number of participants was relatively small for both experiments, and there are no clinical implications at present, the results and intuitive visualizations facilitated by MsCWT ridge and element analysis indicate potential areas for further processing, investigation and interpretation.
Future work includes combining the ROI overlap approach described in this paper with MsCWT magnitude and phase coherence. Investigations will also need to be carried out at the physiological level to determine potential causes of what was seen in the present exploratory phase. Although this paper employed recently proposed analytic methods for MsCWT ridge and feature detection, rigorous comparisons with Morlet CWT approaches need to be performed to assess potential clinical applicability. Finally, performing MsCWT analysis on a larger number of subjects over a wider range of conditions is necessary to draw any physiological or ultimately clinical conclusions.
Supplementary Material
Supplementary Material
Acknowledgments
The authors thank Dr J. Lilly for making the Matlab jLab software available [17], and for helpful correspondence. They also thank the anonymous reviewers for helpful comments, suggesting corrections and constructive criticisms.
Ethics
For the ECG/MSNA LBNP experiments, all subjects provided informed written consent for the experimental protocol as approved by the University of Western Ontario Health Sciences Research Ethics Board. For the UOIT skating experiments, informed written consent for the experimental protocol was provided as approved by the University of Ontario Institute of Technology Research Ethics Board.
Data accessibility
The anonymized raw EMG and ECG signals are accessible as electronic supplementary material. For inquiries concerning the EMG, contact K.E.P. at kevinp@mun.ca. For inquiries concerning the ECG/MSNA data, contact M.J.J. at michel.johnson@umoncton.ca. For information about the postprocessing and analysis code, contact the corresponding author.
Author's contributions
M.P.W. conceived of and designed the study, developed the software, performed the computations, led the analysis and drafted the manuscript. R.W.-S. also performed the analysis, assisted in preparing the graphics and edited the manuscript. M.J.J. and D.C.H. directed and performed the ECG/MSNA experiments, and assisted with editing the manuscript. D.C.H., K.E.P. and F.M.W.-B. directed and performed the skating EMG experiments and assisted with editing the manuscript. All authors read and approved the manuscript.
Competing interests
We declare we have no competing interests.
Funding
M.P.W. was supported by the Natural Sciences and Engineering Research Council of Canada (386586-2011). M.J.J. and D.C.H. were supported by a grant from the Atlantic Innovation Fund.
References
- 1.Clemson P, Lancaster G, Stefanovska A. 2016. Reconstructing time-dependent dynamics. Proc. IEEE 104, 223–241. ( 10.1109/JPROC.2015.2491262) [DOI] [Google Scholar]
- 2.Gabor D. 1946. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng.-Part III: Radio Commun. Eng. 93, 429–441. ( 10.1049/ji-3-2.1946.0074) [DOI] [Google Scholar]
- 3.Torrence C, Compo GP. 1998. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78. () [DOI] [Google Scholar]
- 4.Grinsted A, Moore JC, Jevrejeva S. 2004. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 11, 561–566. ( 10.5194/npg-11-561-2004) [DOI] [Google Scholar]
- 5.Addison P, Watson J, Feng T. 2002. Low-oscillation complex wavelets. J. Sound Vib. 254, 733–762. ( 10.1006/jsvi.2001.4119) [DOI] [Google Scholar]
- 6.Wachowiak MP, Hay DC, Johnson MJ. 2016. Assessing heart rate variability through wavelet-based statistical measures. Comput. Biol. Med. 77, 222–230. ( 10.1016/j.compbiomed.2016.07.008) [DOI] [PubMed] [Google Scholar]
- 7.Addison PS. 2017. The illustrated wavelet transform handbook: introductory theory and applications in science, engineering, medicine and finance. Boca Raton, FL: CRC Press. [Google Scholar]
- 8.Acharya UR, Joseph KP, Kannathal N, Lim CM, Suri JS. 2006. Heart rate variability: a review. Med. Biol. Eng. Comput. 44, 1031–1051. ( 10.1007/s11517-006-0119-0) [DOI] [PubMed] [Google Scholar]
- 9.Wachowiak M, Hay D, Johnson M. 2015. Quantification of wavelet band metrics for assessing heart rate variability. In World Congress on Medical Physics and Biomedical Engineering, 7–12 June 2015, Toronto, Canada, pp. 1026–1029. Berlin, Germany: Springer. [Google Scholar]
- 10.Lilly JM, Olhede SC. 2010. On the analytic wavelet transform. IEEE Trans. Inf. Theory 56, 4135–4156. ( 10.1109/TIT.2010.2050935) [DOI] [Google Scholar]
- 11.Cohen L. 1995. Time–frequency analysis. Englewood Cliffs, NJ: Prentice Hall. [Google Scholar]
- 12.Olhede SC, Walden AT. 2002. Generalized Morse wavelets. IEEE Trans. Signal Process. 50, 2661–2670. ( 10.1109/TSP.2002.804066) [DOI] [Google Scholar]
- 13.Lilly J, Gascard JC. 2006. Wavelet ridge diagnosis of time-varying elliptical signals with application to an oceanic eddy. Nonlinear Process. Geophys. 13, 467–483. ( 10.5194/npg-13-467-2006) [DOI] [Google Scholar]
- 14.Lilly JM. 2017. Element analysis: a wavelet-based method for analysing time-localized events in noisy time series. Proc. R. Soc. A 473, 20160776 ( 10.1098/rspa.2016.0776) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lilly JM, Olhede SC. 2012. Generalized Morse wavelets as a superfamily of analytic wavelets. IEEE Trans. Signal Process. 60, 6036–6041. ( 10.1109/TSP.2012.2210890) [DOI] [Google Scholar]
- 16.Aguiar-Conraria L, Soares MJ. 2014. The continuous wavelet transform: moving beyond uni- and bivariate analysis. J. Econ. Surv. 28, 344–375. ( 10.1111/joes.12012) [DOI] [Google Scholar]
- 17.Lilly J. 2017. jLab: a data analysis package for Matlab, v. 1.6.5. See http://www.jmlilly.net/jmlsoft.html.
- 18.Cohen EA, Walden AT. 2010. A statistical analysis of Morse wavelet coherence. IEEE. Trans. Signal Process. 58, 980–989. ( 10.1109/TSP.2009.2033645) [DOI] [Google Scholar]
- 19.Brittain JS, Halliday DM, Conway BA, Nielsen JB. 2007. Single-trial multiwavelet coherence in application to neurophysiological time series. IEEE Trans. Biomed. Eng. 54, 854–862. ( 10.1109/TBME.2006.889185) [DOI] [PubMed] [Google Scholar]
- 20.Worrell GA, Jerbi K, Kobayashi K, Lina JM, Zelmann R, Le VanQuyen M. 2012. Recording and analysis techniques for high-frequency oscillations. Prog. Neurobiol. 98, 265–278. ( 10.1016/j.pneurobio.2012.02.006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.O'Reilly C, Godbout J, Carrier J, Lina JM. 2015. Combining time–frequency and spatial information for the detection of sleep spindles. Front. Hum. Neurosci. 9, 70 ( 10.3389/fnhum.2015.00070) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Carmona RA, Hwang WL, Torrésani B. 1997. Characterization of signals by the ridges of their wavelet transforms. IEEE Trans. Signal Process. 45, 2586–2590. ( 10.1109/78.640725) [DOI] [Google Scholar]
- 23.Addison PS, Watson JN. 2004. Secondary transform decoupling of shifted nonstationary signal modulation components: application to photoplethysmography. Int. J. Wavelets Multiresolut. Inf. Process. 2, 43–57. ( 10.1142/S0219691304000329) [DOI] [Google Scholar]
- 24.Mallat S. 2008. A wavelet tour of signal processing: the sparse way. New York, NY: Academic Press. [Google Scholar]
- 25.Lilly JM, Olhede SC. 2009. Wavelet ridge estimation of jointly modulated multivariate oscillations. In 2009 IEEE Conf. Record of the Forty-Third Asilomar Conf. on Signals, Systems and Computers, pp. 452–456. [Google Scholar]
- 26.Wachowiak-Smolikova R, Wachowiak MP, Johnson MJ. 2017. Exploratory ECG analysis of driving events using wavelet band metrics. In 2017 IEEE Int. Conf. on Information and Digital Technologies (IDT), pp. 423–428. [Google Scholar]
- 27.Cover TM, Thomas JA. 1991. Entropy, relative entropy and mutual information. In Elements of information theory, ch. 2, pp. 12–49. New York, NY: Wiley-Interscience ( 10.1002/0471200611.ch2) [DOI] [Google Scholar]
- 28.Yitzhaki S. 2003. Gini's mean difference: a superior measure of variability for non-normal distributions. Metron – Int. J. Stat.LXI (2), 285–316. See https://ideas.repec.org/a/mtn/ancoec/030208.html. [Google Scholar]
- 29.Hosking JR. 1990. L-moments: analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. B (Methodol.) 52, 105–124. ( 10.2307/2345653) [DOI] [Google Scholar]
- 30.Székely GJ, Rizzo ML. 2012. On the uniqueness of distance covariance. Stat. Probab. Lett. 82, 2278–2282. ( 10.1016/j.spl.2012.08.007) [DOI] [Google Scholar]
- 31.Szekely GJ, Rizzo ML. 2014. Partial distance correlation with methods for dissimilarities. Ann. Stat. 42, 2382–2412. See https://projecteuclid.org/euclid.aos/1413810731. [Google Scholar]
- 32.Bernstein N. 1967. The co-ordination and regulation of movements: conclusions towards the study of motor co-ordination. In Biodynamics of Locomotion, pp. 104–113. New York, NY: Pergamon. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The anonymized raw EMG and ECG signals are accessible as electronic supplementary material. For inquiries concerning the EMG, contact K.E.P. at kevinp@mun.ca. For inquiries concerning the ECG/MSNA data, contact M.J.J. at michel.johnson@umoncton.ca. For information about the postprocessing and analysis code, contact the corresponding author.