Predicting protein–DNA binding free energy change upon missense mutations using modified MM/PBSA approach: SAMPDI webserver

Abstract

Motivation

Protein–DNA interactions are essential for regulating many cellular processes, such as transcription, replication, recombination and translation. Amino acid mutations occurring in DNA-binding proteins have profound effects on protein–DNA binding and are linked with many diseases. Hence, accurate and fast predictions of the effects of mutations on protein–DNA binding affinity are essential for understanding disease-causing mechanisms and guiding plausible treatments.

Results

Here we report a new method Single Amino acid Mutation binding free energy change of Protein–DNA Interaction (SAMPDI). The method utilizes modified Molecular Mechanics Poisson-Boltzmann Surface Area (MM/PBSA) approach along with an additional set of knowledge-based terms delivered from investigations of the physicochemical properties of protein–DNA complexes. The method is benchmarked against experimentally determined binding free energy changes caused by 105 mutations in 13 proteins (compiled ProNIT database and data from recent references), and results in correlation coefficient of 0.72.

Availability and implementation

http://compbio.clemson.edu/SAMPDI

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein–DNA interactions are essential for functions of living cells and are involved in many important cellular processes such as transcription, replication and recombination. For example, the expression level of genes is regulated by a wide number of proteins named transcription factors, which have DNA-binding domains recognizing a specific sequence of DNA (Orphanides and Reinberg, 2002; Roeder, 1998). Protein–DNA binding is mediated by many factors such as DNA sequence, hydrogen bonds, van der Waals contacts, DNA shape, protonation states, flexibility and many others (Hogan and Austin, 1987; Jones et al., 1999; Luscombe et al., 2001; Peng and Alexov, 2017; Rohs et al., 2009; Slutsky and Mirny, 2004). While DNA–backbone interactions are important for the stability of protein–DNA complexes, proteins recognize specific DNA sequence by forming hydrogen bonds between amino-acid side chains and DNA bases (Luscombe et al., 2001; Rohs et al., 2009, 2010, 2010). Therefore, mutations occurring in DNA binding proteins that alter the physicochemical properties of the binding interfaces will affect binding specificity and affinity (Luscombe and Thornton, 2002; Trelsman et al., 1989). Such mutations are frequently involved in many diseases like neurological disease, heart disease and cancer. Hence, understanding their molecular effects is crucial for deciphering disease origins and pursuing treatment (Chahrour et al., 2008; Garg et al., 2005; Peng et al., 2015; Vousden and Lane, 2007).

Significant fractions of diseases are caused by the alteration of native binding affinities, which can be quantitatively described by the binding free energy change (Peng and Alexov, 2016; Petukh et al., 2015a,b). There are many experimental techniques capable of measuring protein–DNA binding free energy such as isothermal titration calorimetry (ITC) (Velazquez-Campoy et al., 2004), fluorescence resonance energy transfer (FRET) (Hillisch et al., 2001), nuclear magnetic resonance(NMR) (Campagne et al., 2011), surface plasmon resonance(SPR) (Teh et al., 2007) and many others. However, these experimental methods are usually time consuming and non-applicable for large-scale studies. Recently, the available experimental data of protein–DNA binding free energy changes caused by amino acid substitutions was compiled and organized in a database, the ProNIT database (Kumar, 2006).

Computational approaches can complement experimental techniques and permit large-scale investigations. Among them, the free energy perturbation (FEP) and the thermodynamic integrations (TI) are the most rigorous, but require intensive calculations, which limit their applicability for large-scale analysis. Alternatively to FEP and TI, different physical models and optimized knowledge-based potentials have been developed to carry out fast predictions of protein–DNA binding affinities achieving a good correlation with experimental measurements (Donald et al., 2007; Jones et al., 2003; Liu, 2005; Morozov, 2005; Zhang et al., 2005). A structured based approach, the mCSM method, was developed (Pires and Ascher, 2017; Pires et al., 2014) and was shown that it achieves correlation coefficient of 0.673 in benchmarking test against ProNIT database. Very recently, mCSM was upgraded (mCSM-NA) and reported to achieve correlation coefficient of 0.72 (Pires and Ascher, 2017). Even so, the existing approaches for fast prediction of protein–DNA binding affinity changes upon mutations are still very limited, comparing with approaches developed for protein–protein interactions.

The Molecular Mechanics/Poisson Boltzmann Surface Area (MM/PBSA) approach is a widely applied method to calculate binding free energies of macromolecules by combining molecular mechanics calculations and continuum solvation models (Hou et al., 2011a,b; Lee et al., 2000). The MM/PBSA method computes a linear combination of energy terms for molecular mechanics, polar and non-polar solvation energy and shows high computational efficiency comparing with the rigorous methods such as FEP and TI methods. In this work, we developed a new approach termed SAMPDI (Single Amino acid Mutation binding free energy change of Protein–DNA Interaction) to perform fast predictions of binding free energy changes of protein–DNA complexes caused by single mutations on the proteins. Our approach combines modified MM/PBSA based energy terms with additional knowledge based terms. The method is implemented in a webserver (http://compbio.clemson.edu/SAMPDI/), which allows the users to upload the corresponding protein–DNA structural file, to specify the mutations and to obtain the predicted binding free energy change.

2 Materials and methods

2.1 Dataset preparation

We constructed a dataset, containing experimentally measured binding free energy change upon missense mutations and corresponding PDB structures, by combining the ProNIT database (Kumar, 2006) and data from recent references. We applied three criteria in constructing the dataset: (i) Mutations affecting protein DNA binding, but not the quaternary structure of the corresponding protein, like dimerization. (ii) The binding site of DNA (DNA sequence of the interface) used in the experiment is exactly identical to the DNA sequence of the corresponding PDB structure. (iii) The structures with modified DNA, like methylation were removed and not considered in this study. Finally, the constructed dataset for this study included 105 missense mutations from 13 proteins (The constructed dataset used in this study is shown in the Supplementary Material and can be downloaded from URL: http://compbio.clemson.edu/downloads).

2.2 NAMD simulation protocols

The structures of protein–DNA complexes were downloaded from RCSB Protein Data Bank (PDB) (Rose et al., 2015). The biological units were retained and ligands, except ions, were removed from the initial structures. The missing heavy atoms were fixed using the default parameters of the profix module in Jackal package (https://honiglab.c2b2.columbia.edu/software/Jackal/Jackalmanual.htm). The mutant (MT) structures were generated by the VMD Mutator plugin (Humphrey et al., 1996) using the topology files from CHARMM36 force field (Best et al., 2012; Denning et al., 2011). The energy minimization was performed with the NAMD program, version 2.11b (Phillips et al., 2005) using the conjugate gradient algorithm. The default minimization steps were set to 5000 steps but longer minimization was applied if the variation of the total energy was more than 0.5 kcal/mol. In the minimization, the Generalized Born implicit solvent (GBIS) model and CHARMM36 force field (Best et al., 2012; Denning et al., 2011) were used. The dielectric constant of the implicit solvent was set to 80 and the various values of the protein–DNA dielectric constant were tested (see Results section). Finally, the minimized structures were used to calculate the relevant energies.

2.3 Electrostatic energy calculations

Delphi with the Gaussian-based smooth dielectric function (Jia et al., 2017; Li et al., 2013, 2014) was used to calculate the electrostatic component of the binding free energy in the Protein–DNA binding interaction using the following parameters: scale = 2 grid/Å; percentage of filling for the protein–DNA complex structures = 70%; dielectric constant = 80 for the solvent; salt concentration = 0.15 mol/L; Gaussian with sigma = 0.93, srfcut = 20 and non-linear Poisson-Boltzmann equation (PBE) (non-linear PBE was used because of the high charge of the DNA). Grid box for protein and DNA monomers were set exactly identical as for their complex by specifying the grid box size and center.

2.4 Binding free energy calculations

This study combines a modified MM/PBSA approach and knowledge based energy terms to calculate the protein–DNA binding free energy change upon single amino acid substitution. MM/PBSA is a widely used approach to calculate the receptor–ligand binding free energy and the thermodynamic cycle of computing the binding free energy change upon single amino acid change is shown in Figure 1. In our approach, the unbound monomer structures are taken from the corresponding complex, thus assuming no structural changes upon the binding (called rigid body approach). In addition, a set of knowledge based energy terms, which are derived from analysis of physicochemical properties of the corresponding protein–DNA structures, are combined with the MM/PBSA approach [more details are provided in refs (Getov et al., 2016; Petukh et al., 2015a,b)]. All individual energy terms are combined via weighted linear scoring function and optimal weighted coefficients are determined via multiple linear regression against experimental data. Below, we will describe the protocols of computing each energy terms, including the MM/PBSA and knowledge based ones.

Fig. 1.

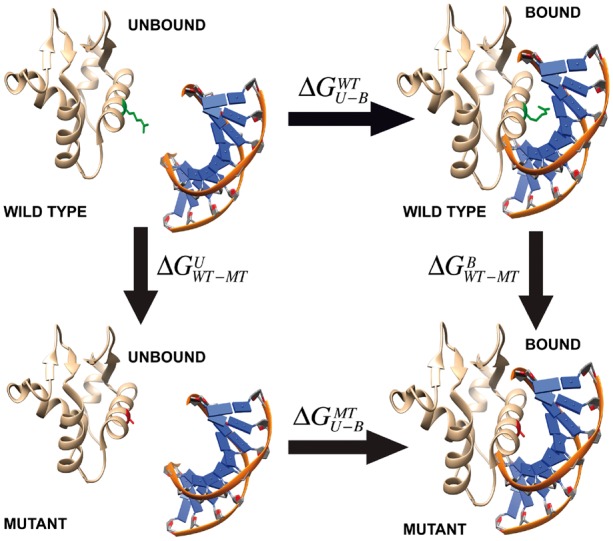
Thermodynamic cycle for binding free energy change calculations. The side chain of wild type and mutant residues are show in green and red color, respectively

2.4.1 The MM/PBSA-based energy terms

The MM/PBSA components of the change of the binding free energy are in a linear combination of the five components shown in the following equation:

$$\Delta \Delta G^{MM/PBSA}=w_0+w_1\cdot \Delta \Delta IE+w_2\cdot \Delta \Delta CE+w_3\cdot \Delta \Delta PS+w_4\cdot \Delta \Delta VE+w_5\cdot \Delta \Delta NS,$$ (1)

where IE is the internal energy, CE is the Coulombic energy, PS is the polar component of the solvation energy, VE is the van der Waals energy, NS is the non-polar component of the solvation energy and wi are weight coefficients. The energy difference for each energy term is computed using the following equation:

$$\Delta \Delta E=(E_{complex}^{MT}-E_{protein}^{MT}-E_{DNA}^{MT})-(E_{complex}^{WT}-E_{protein}^{WT}-E_{DNA}^{WT}),$$ (2)

where MT and WT represent the mutant and wild-type structures. The structures of unbound protein and DNA are taken from the complex structures. Below we describe each energy component [more details can be found in Petukh et al. (2015a,b)].

IE and VE energies were calculated using the NAMD program. Since the rigid body approach was applied and no structural changes are considered in the binding, ΔΔIE calculated by equation (2) will result in zero. In our methodology development, we have tried to minimize the complex structure and unbound monomer structure separately to take into account the structural changes induced by the binding. However, the results showed weaker correlation between the predicted value and experimental data comparing with applying the rigid body approach, thus w1 was set to zero. VE energy was obtained with NAMD by subjecting the corresponding minimized structure to an one step equilibration.

CE and PS were calculated using the Delphi program with Gaussian-based smooth dielectric function, an accurate and fast Poisson-Boltzmann Equation (PBE) solver (Li et al., 2013, 2014). In Gaussian Delphi, the solute and water phase are treated as an inhomogeneous dielectric medium by using a smooth Gaussian-based dielectric function, which showed better performance comparing with the traditional two-dielectric model (the traditional two dielectric model treats biomolecule and water as two distinctive media with two different dielectric constants with a sharp dielectric border between the two media). The performance of the traditional two-dielectric model and the smooth Gaussian-based model were tested and the Gaussian-based model showed better results as benchmarked against experimental data.

NS was calculated via the solvent accessible surface area (SASA) using the equation (3). The SASA was computed using the NACCESS software with default atom radius parameters (Hubbard, 1993). The constants α and β in equation (3) were incorporated into to the weight coefficient in equation (1).

$$\text{NS}=\alpha \text{SASA}+\beta$$ (3)

2.4.2 Knowledge-based energy terms

Many knowledge-based energy terms were tested in this study among which entropy (S) and hydrogen bond (HB) showed highest impact. The impact was evaluated based on the P-test indicating that S and HB are the terms showing highest correlation with experimental measured binding free energy changes (see Supplementary Material). Finally, the knowledge-based energy terms (ΔΔGKW) are a linear combination of the two components shown in the following equation:

$$\Delta \Delta G^{KW}=w_1\cdot \Delta \Delta S+w_2\cdot \Delta \Delta HB,$$ (4)

where S is the entropy, and HB is the number of hydrogen bonds. The energy differences for each term are also computed using equation (2).

The entropy of protein’s residue is calculated using the following empirical formula originally developed in our previous work (Petukh et al., 2015a,b).

$$S=\ln [rSASA(i)\cdot (R(i)-1)+1],$$ (5)

where rSASA(i) represents the relative solvent accessibility of residue i [calculated by the NACCESS software (Hubbard, 1993)]. Small rSASA(i) values (close to 0) indicate that the residue is buried and only a few side chain rotamers can be sampled resulting in a small entropy contribution. R(i) is the maximum number of the rotamers for residue i [R(i) for all types of residues are shown in the Table 1]. The entropy change upon mutation is calculated by subtraction of the entropy for the wild-type residue and mutant residue.

Table 1.

Max number of the rotamers for all types of amino acids taken from (Shapovalov and Dunbrack, 2011)

Residue	A	C	D	E	F	G	H	I	K	L
Rotamer	1	3	18	54	18	1	36	9	81	9
Residue	M	N	P	Q	R	S	T	V	W	Y
Rotamer	27	36	2	108	81	3	3	3	36	18

The number of hydrogen bonds (HBs) is calculated using the VMD plugin with a cut-off distance 3.0 Å and a cut-off angle of 30 degrees. We tried two protocols to compute the number of HB: (i) compute the total number of the HBs for the entire structures (including intra and inter HBs); (ii) only compute the number of HBs near the mutation site and choose to count the HBs within 6 Å of the mutation site (different cut-off values were tested and 6 Å showed the best correlation). The second protocol was applied in our calculation since it showed much better correlation with the experimental ΔΔG in the P-test (see Supplementary Material).

3 Results

3.1 Finding optimal value of dielectric constant

In our protocol we used an implicit model to minimize protein–DNA structures and to calculate the MM/PBSA energy terms. Different dielectric constant values affect the energy minimization and the energy terms calculated with both Delphi and NAMD programs. Our previous works showed that selecting an optimal dielectric constant value for proteins results in improved correlation coefficient for binding/folding free energy calculation (Getov et al., 2016; Petukh et al., 2015a,b). Here, we tested various dielectric constants for the protein–DNA complex to identify the optimal value corresponding to the highest correlation coefficient against experimental data. Figure 2 shows the dependence of correlation coefficient on the value of the dielectric constant of the protein–DNA complex. We varied the dielectric constant of protein–DNA from 1 to 5 for NAMD program (this was done for testing purposes, while understanding that dielectric constant value of 1 is physically sound) and 1 to 20 for Delphi program with a step of 1. Multiple linear regression was performed for each set of values of dielectric constants using VDW energy, Coulomb energy and the polar component of the solvation energy to obtain the correlation coefficient (Fig. 2). The results indicate the dielectric constant value used in NAMD modeling highly affects the correlation coefficient (Fig. 2). Summarizing, the correlation coefficient reaches the highest value with a dielectric constant for NAMD = 1 and for Delphi = 14 and these values will be used in our protocol.

Fig 2.

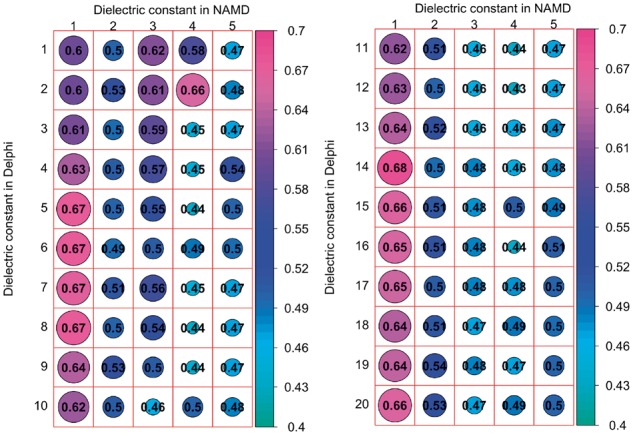
The correlation coefficient calculated with various dielectric constants used in Delphi and NAMD. The left panel shows the dependence of correlation coefficient when dielectric constant was varied from 1 to 5 in NAMD and 1 to 10 in Delphi, while the right panel shows the same for dielectric constant varied from 1 to 5 in NAMD and 11 to 20 in Delphi. The size of the circles are proportional to the magnitude of the correlation coefficient which is also indicated by the corresponding color (see the color scheme of the right)

3.2 Determination of optimal values of the weight coefficients

As discussed in the Materials and methods section, the linear function of binding free energy changes contains 6 terms and 7 weight coefficients:

$$\Delta \Delta G=w_0+w_1\cdot \Delta \Delta CE+w_2\cdot \Delta \Delta PS+w_3\cdot \Delta \Delta VE+w_4\cdot \Delta \Delta SASA+w_5\cdot \Delta \Delta S+w_6\cdot \Delta \Delta HB$$ (6)

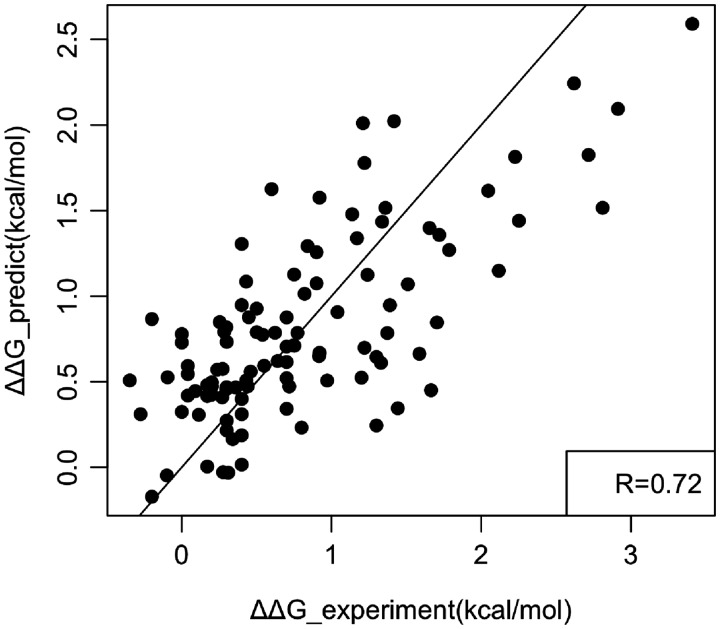
Then, the weighted coefficients are determined from the multiple linear regression (MLR) between experimentally measured ΔΔG and calculated binding free energy changes. The resulting optimized weight coefficients are shown in Table 2. The correlation coefficient from MLR is 0.72 over 105 cases. The plot of experimentally measured binding free energy changes and predicted binding free energy changes is shown in Figure 3.

Table 2.

The weight coefficients of the linear function for binding free energy changes determined from MLR

	CE	PS	VE	NS	S	HB	Y-intercept
Coefficient	0.078	0.048	0.088	−0.0012	0.14	−0.043	0.445
P-value	2E−05	1E−05	7.13E−08	0.4	0.041	0.10	8.92E−08
Correlation coefficient		0.72		Number of cases		105

Note: The corresponding P-values are shown as well.

Fig. 3.

A plot of experimentally measured binding free energy changes and predicted binding free energy changes. The corresponding linear fit and correlation coefficient are shown as well

3.3 Performance and validation

3.3.1 Five-fold cross validation

In our study the datasets used for training and testing are relatively small due to limited available experimental data. To address the problem of overfitting, we further performed 5-fold cross validation by randomly partitioning the dataset into five subgroups of approximately equal sizes. For each round, four subgroups are used for training and the rest one is used for testing. The results are shown in the Table 3 and Figure 4A. The Root Mean Square of the Error (RMSE) in each fold varies a little and the resulting average is 0.54 kcal/mol. At the same time, Pearson correlation coefficient (CC) varies significantly probably due to the limited number of data points (20 data points for each fold and the corresponding CC shows significant variation even if with roughly same RMSE). We also analyzed the variation of the weighting coefficients for each energy terms in 5-fold cross validation and the results are shown in Supplementary Table S3. The standard deviations of the weighting coefficients are relative small and indicate that the variations are not significant across each fold. We further compared the average weighting coefficients in 5-fold cross validation with the weighting coefficients from MLR and the results show that the differences for all the energy terms are very small (Supplementary Table S3). Overall, the testing indicates that overfitting is not significant.

Table 3.

5-fold cross validation for the dataset used for the SAMPDI approach

	Root Mean Square of the Error (kcal/mol)	Pearson correlation coefficient
Fold 1	0.53	0.33
Fold 2	0.57	0.7
Fold 3	0.48	0.76
Fold 4	0.64	0.6
Fold 5	0.49	0.52
Average	0.54	0.58

Fig. 4.

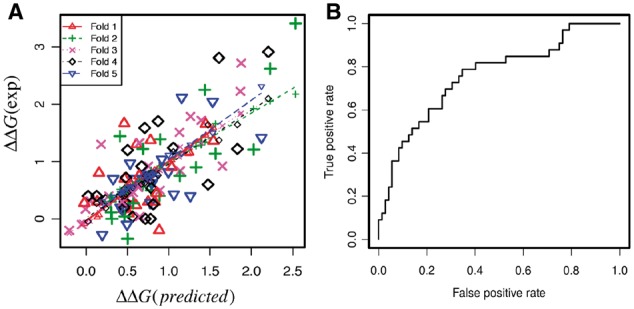
(A) Plot of predicted ΔΔG and experimental ΔΔG in 5-fold cross validation (see Table 3 for details). (B) Receiver operating characteristic curve of classification of large effects (|ΔΔG| > 1 kcal/mol) and small effects (|ΔΔG| < 1 kcal/mol)

3.3.2 Receiver operating characteristic (ROC)

To evaluate the performance of SAMPDI, we further performed ROC analysis to distinguish large and small effects on binding free energy changes. Here, we classify the large effects as |ΔΔG| > 1 kcal/mol and small effects as |ΔΔG| < 1 kcal/mol. Figure 4B shows the ROC curve of SAMPDI for 105 experimentally measured binding free energy changes. The area under the curve is 0.76, indicating the capability of SAMPDI to distinguish different types of mutations.

3.3.3 Multicollinearlity analysis

It may be anticipated that some energy terms may reflect similar phenomena. To address such a possibility, we performed multicollinearlity analysis to study the correlation across each term and the variance inflation factors (VIF) from MLR. The results shown in Table 4 indicate a strong correlation between CE and PS. This is due to the well know fact that the PS originates from the CE. In addition, SASA has relative high correlation with VDW, CE and PS. The rest, the VIFs of SASA, VDW, S and HB are within relative low multicollinearlity (VIF < 4). Removing highly correlated terms from eq. (5) results in decrease of prediction accuracy, but the change is not large. For example, removing the CE in the MLR leads to the decrease of correlation coefficient from 0.72 to 0.65. Thus, these highly conserved terms were kept in our final protocol to achieve optimal accuracy.

Table 4.

Correlation matrixes and variance inflation factors (VIF) for the energy terms in SAMPDI

Correlation matrixes calculated with Pearson correlation
	SASA	VDW	CE	PS	S	HB
SASA	1
VDW	0.7	1
CE	0.64	0.29	1
PS	0.61	0.26	0.99	1
S	0.32	0.41	0.2	0.2	1
HB	0.31	0.44	0.17	0.15	0.44	1
Variance inflation factors (VIF)
	SASA	VDW	CE	PS	S	HB
VIF	3.31	2.43	47.72	45.03	1.35	1.38

Note: Terms with high correlation and VIF values (CC > 0.5 and VIF > 4) are underlined.

3.3.4 Case studies: consistent and inconsistent predictions comparing with experimental data

To further investigate the factors affecting the predictions, representative examples of consistent and inconsistent predictions will be discussed below. The results of six single mutations shown in Table 5 will be discussed.

Table 5.

Cases of consistent and inconsistent predictions

Protein PDB (Mutation)	ΔΔG (EXP)	ΔΔG (PRED)	ΔΔSASA	ΔΔVE	ΔΔCE	ΔΔPS	ΔΔS	ΔΔHB
1B3T (R469A)	3.4	2.6	260.7	16.0	−61.4	106.9	1.8	−11.0
1B3T (Y518A)	2.6	2.2	72.6	14.3	1.3	−0.9	1.2	−9.0
1MSE (C130I)	0.3	0.2	3.6	−2.0	−2.3	3.8	0.0	0.0
1MSE E141A	−0.1	−0.1	0.8	−1.8	7.6	−19.4	0.0	0.0
1TN9 K54A	1.3	0.6	−18.0	−3.5	−20.5	38.4	0.9	−2.0
2A0I E187A	2.1	1.2	24.3	7.4	7.1	−11.5	0.5	0.0

Note: Mutations in protein 1B3T and 1MSE are the cases of consistent predictions (underlined), while the rest are inconsistent prediction cases. The ΔΔGs are in kcal/mol and positive value indicates destabilization (lowering protein–DNA affinity) while negative indicates stabilization. The ΔΔE for each terms is shown as MT-WT.

• Predictions consistent with experimental data

Epstein-Barr nuclear antigen 1 (EBNA1) binds to the recognition site of the minimal origin of latent DNA replication of Epstein-Barr virus and results in activation of the latent-phase replication of the viral genome (Bochkarev et al., 1998). Here, we outline two single mutations (R469A and Y518A) of a permanganate-sensitive DNA site bound by EBNA1. Both mutations occur on the binding interface (PDB: 1B3T, Fig. 5A) and dramatically destabilize the protein–DNA binding according to the experimental measurement (3.4 and 2.6 kcal/mol, respectively). The wild type residue R469 interacts with the DNA backbone and forms strong electrostatic interactions upon binding. Our calculations predict that a substitution to ALA will result in dramatic energy change of 61.44 kcal/mol of CE and 16.02 kcal/mol of VE upon binding along with a large effect on the SASA, HB and S (Table 5). Taking all together we predicted that R469A would cause decrease of 2.6 kcal/mol of binding free energy, which is very close to experiment. Another mutation, Y518A is also located at the binding interface, which leads to a large change of VE along with decrease of HB and S. For both mutations, the experimental measured free energy changes are dramatic and destabilize DNA binding, which is reproduced by the SAMPDI. Another representative example are two single mutations (C130I and E141A) in the structure of a specific DNA complex of the Myb DNA-binding domain with cooperative recognition helices (PDB: 1MSE, Fig. 5B) (Ogata et al., 1994). Both mutations are not in the binding interface and experimental measurement indicates minimal effects on the binding affinity. As shown in our energy calculations (Table 5), no large changes were computed for all energy terms resulting in minimal binding free energy change predictions, which is consistent with experiment.

Fig. 5.

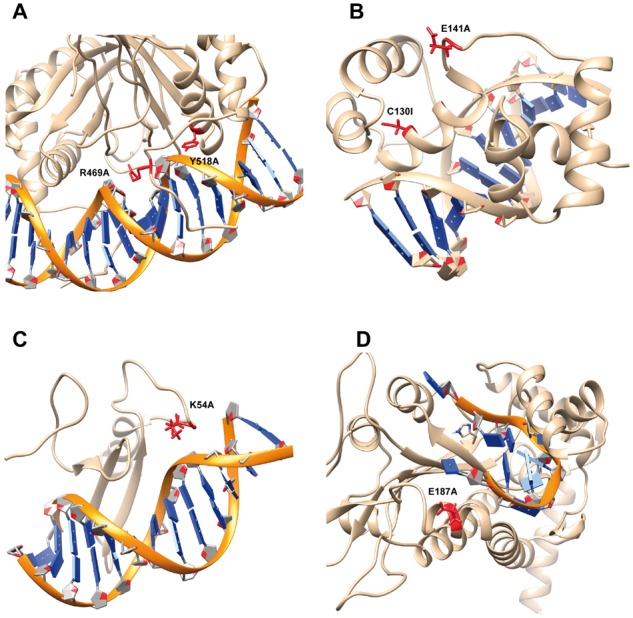
Case study of consistent and inconsistent predictions. The backbone of DNA is marked as orange while protein is shown as brown. Mutation site is labeled as red along with the side chain of the wild-type residue. (A) The estrogen receptor DNA-binding domain bound to DNA (PDB: 1HCQ). (B) DNA complex of the Myb DNA-binding domain (PDB: 1MSE). (C) TN916 integrase n-terminal domain/DNA complex (PDB: 1TN9). (D) F Factor TraI Relaxase Domain bound to F oriT Single-stranded DNA (PDB: 2A0I)

• Predictions inconsistent with experimental data

The first case is the mutation K54A in the structure of the Tn916 integrase-DNA complex (PDB: 1TN9, Fig. 5C) (Wojciak et al., 1999). Experimental measurement indicated destabilization of binding and our calculation underestimated the binding free energy change by 0.72 kcal/mol (Table 5). In the wild-type structure, K54 is located in a flexible loop and does not directly form H-bond with nearby residue. It is feasible that K54 forms H-bonds in unbound protein or other specific interactions, which would not be captured in our rigid-body protocol and this could be the reason for discrepancy between experiment and modeling. Another case is the single mutation E187A in the complex structure of F Factor TraI Relaxase Domain bound to F oriT Single-stranded DNA (PDB: 2A0I, Fig. 5D). The experimental data indicates that the mutation destabilizes the binding by 2.12 kcal/mol while the effect is underestimated by SAMPDI. The corresponding reference (Larkin et al., 2005) reporting the structure of protein–DNA complex indicates that there is significant uncertainty for the position of the Glu187 side chain. It is indicated that such a large free energy change is unexpected as the Glu187 side chain appears to only contact with Thy1 5-methyl with its carboxylate (Larkin et al., 2005). The SAMPDI is a structure-based approach and thus strongly depends on the accuracy of the experimental structures.

The reasons that in some cases SAMPDI predictions are good or bad, as compared with experimental data stem from various sources. It should be reiterated that the SAMPDI protocol is a structure-based rigid-body approach and the accuracy is expected to be sensitive to the conformational changes upon binding and the resolution of experimental structures. Thus, mutations that do not induce large conformation changes are expected to be predicted with higher accuracy compared with mutations causing significant conformational changes. Another reason could be that the protocol does not take into account some non-specified experimental conditions, as non-reported specific ion binding, proton release/uptake and many others.

4 Implementation

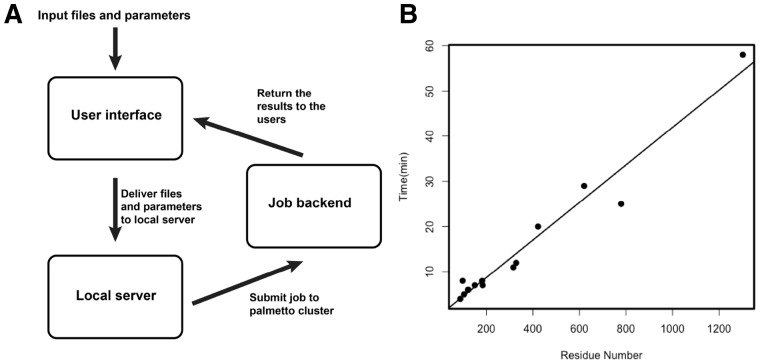
4.1 SAMPDI webserver architecture

The design of SAMPDI webserver consists of three components: the user interface, the local server and the job backend (The flowchart is shown in Fig. 6A). The user interface is implemented using the HTML (http://compbio.clemson.edu/SAMPDI/), which provides users with a webpage interface to upload all required input files and fill in parameters for the free energy calculations. In the webpage, users are firstly asked to upload an input PDB file from a local computer. In addition, the job parameters including chain ID, mutation position, original amino acid and mutated amino acid are provided by the users. Detailed descriptions of all the input parameters are provided as tooltips. Once the job is submitted, users are provided with an URL link to the result page, which will automatically refresh itself every 30 s to return the latest results from the backend. The local server part is run on a light-duty computer server, which obtains the PDB files and parameters from the user interface. All the jobs in the backend are executed on the Clemson University Palmetto Cluster. The jobs are executed using multiple nodes with MPI parallel runs to attain the capability for large-scale analysis. Large arrays of independent jobs are permitted to be submitted to the server and are sequentially executed on the Palmetto cluster according to the order of submission.

Fig. 6.

(A) Work flowchart of SAMPDI webserver. (B) Performance of SAMPDI webserver showing the execution time for different size proteins

4.2 Webserver performance

To verify the capability of the SAMPDI server for large-scale analysis, we tested the execution time for different sizes of the proteins ranging from tens of residues up to more than 1000. The execution time linearly increases with the size of proteins (Fig. 6B). For proteins with less than 200 residues, the results are returned to users within ten minutes. Execution time for middle size proteins is about 20 to 30 minutes and reaches maximum of an hour for large proteins with about and more than 1300 residues.

5 Discussion

Development of computational approaches for large-scale predictions of effect of mutations on macromolecular binding is not a trivial problem (Petukh et al., 2015a,b; Pires et al., 2014). There are multiple available tools and servers for predicting protein–protein binding affinity changes upon single mutations (Brender et al., 2015; Dehouck et al., 2013; Li et al., 2016; Petukh et al., 2015a,b; Pires et al., 2014; Schymkowitz et al., 2005). However, there is still lack of resources for predicting affinity changes of protein–DNA complexes. Currently, the only available method capable of quantitatively predicting binding affinity changes upon single mutation of protein–DNA binding, is the mCSM method (Pires et al., 2014) and its recent improved version mCSM-NA (Pires and Ascher, 2017). The mCSM was benchmarked against the ProNIT database (Kumar, 2006) and was reported to result in a correlation coefficient of 0.673/072. However, the benchmarking was done on the entire ProNIT database without taking into consideration that in ProNIT database (i) some proteins interact with DNA as dimers and mutations could indirectly affect the binding by altering the quaternary structure of the corresponding protein dimer instead of altering the binding; (ii) in some cases, the binding affinity energy change upon mutations was experimentally measured using DNA which does not match the sequence of DNA in ProNIT database. This may indicate that mCSM is not very sensitive to the DNA sequence and may be over fitted, and thus alternative resources are needed. In this work, we developed a new approach named SAMPDI, and benchmarked it against purged experimental data from the latest verison of ProNIT database and data from recent references. Comparing with existing mCSM and mCSM-NA approaches, SAMPDI provides additional structural information, the relative contribution of various energy terms and achieves correlation coefficient similar to mCSM-NA, but obtained on consistent experimental data (see Method section). The SAMPDI method was implemented in a user-friendly webserver, which is fast and allows for large-scale analysis.

The SAMPDI applies the so-called rigid body approach, which is based on the assumption that the structures do not undergo conformational changes upon binding. It should be mentioned that in the development of the SAMPDI method we also tested a scenario such that, complex protein–DNA structure and unbound monomeric structures were separately minimized to take into account plausible structural changes induced by the binding. However, the results were worse and thus the rigid body approach was applied. In the standard MM/PBSA approach, long time-consuming MD simulations are required to explore the conformational space and intensive sampling of the entire conformation space is still very challenging. The SAMPDI approach is a trade-off between extensive conformational sampling and execution time since one of the main goals of the SAMPDI method is to allow for large-scale analysis. Future expansion of the method could include fast conformation sampling method for protein and DNA to improve the accuracy of prediction.