Image-Based Modeling of Acute Myocardial Ischemia Using Experimentally Derived Ischemic Zone Source Representations

Abstract

Background

Computational models of myocardial ischemia often use oversimplified ischemic source representations to simulate epicardial potentials. The purpose of this study was to explore the influence of biophysically justified, subject-specific ischemic zone representations on epicardial potentials.

Methods

We developed and implemented an image-based simulation pipeline, using intramural recordings from a canine experimental model to define subject-specific ischemic regions within the heart. Static epicardial potential distributions, reflective of ST segment deviations, were simulated and validated against measured epicardial recordings.

Results

Simulated epicardial potential distributions showed strong statistical correlation and visual agreement with measured epicardial potentials. Additionally, we identified and described in what way border zone parameters influence epicardial potential distributions during the ST segment.

Conclusion

From image-based simulations of myocardial ischemia, we generated subject-specific ischemic sources that accurately replicated epicardial potential distributions. Such models are essential in understanding the underlying mechanisms of the bioelectric fields that arise during ischemia and are the basis for more sophisticated simulations of body surface ECGs.

Graphical abstract

2. Introduction

The electrocardiogram (ECG) is the most commonly used clinical tool for detecting and diagnosing myocardial ischemia, yet errors in ECG-based diagnosis¹ suggest a general lack of understanding regarding its underlying electrophysiology. Myocardial ischemia is a potentially life-threatening condition² that arises in response to a blood supply deficit within cardiac tissues leading to electrophysiological changes within the heart. Reduced blood flow within ischemic tissues inhibits the ability of cells to produce ATP. Reductions in available ATP, in turn, lead to depressed Na⁺/K⁺ and Ca⁺⁺ pump activity—resulting in altered local ionic concentrations and causing subsequent changes in tissue electrophysiology, such as reduced action potential amplitude, decreased action potential duration, and less-negative resting membrane potential.^3,4 The resulting extracellular potential differences that arise between healthy and ischemic tissues cause ECG recordings that deviate from normal. Clinically, ST segment shift is used as a marker for detecting the presence of ischemia;^5,6,7 however, ECG-based detection exhibits wide sensitivity and specificity ranges,¹ resulting in diagnostic error. In an effort to avoid the potentially severe consequences of misdiagnosis,² medical professionals have adopted aggressive admissions policies at the expense of elevated false positives, with only 50–60% of admitted patients actually experiencing an ischemic event.^1,8

Errors associated with the clinical detection of myocardial ischemia stem, at least in part, from an incomplete understanding of its mechanistic origins. Current clinical dogma assumes that ischemia develops as geometrically simple, contiguous regions of injured tissue that are anchored along the endocardial wall.⁷ While the presence of a single, fixed ischemic region provides a simple approach for interpreting ischemic disease, it is often a gross oversimplification of a far more complex condition. Recent experimental studies, for example, showed that subendocardial patterns of ischemia were not common—appearing in only 6% to 13% of all observed cases.⁹ In all other cases, ischemia formed over numerous, spatially distributed regions within the thickness of the myocardium, creating multiple isolated zones that expanded independently of each other under conditions of prolonged stress.⁹

These novel findings led us to develop an equally novel, experiment-based simulation pipeline to more fully elucidate the effects of ischemic disease on cardiac potentials.¹⁰ To this end, we previously constructed a subject-specific, image-based model of the heart, using, as a source, measured intracardiac potentials sampled from the anterior left ventricle, to simulate epicardial potential distributions during the ST segment for multiple ischemic episodes. Simulated epicardial potentials correlated strongly with those measured during experimentation.¹⁰ However, a partial sampling of the extracellular potentials of the intramyocardial space is only one possible representation of the ischemic source, and, although it closely resembles our experimental findings, a more natural and potentially more powerful option is to represent the injury in terms of ischemic zones. Once adequately characterized, such zones offer a path to parametrization, forming a much simpler representation of ischemia than a distributed set of potentials in space, much like a propagating wave encapsulates important behavior that is both intuitive and more easily interpreted than a set of electrograms. The result would be a reduction in complexity of the ischemic source descriptions from our previous model¹⁰ that offers a completely novel, physiologically motivated approach to locating and visualizing the impact of ischemic stress on the heart. The goal of this study, therefore, became to characterize ischemic zone sources, based on measured intramyocardial potentials, and to evaluate the ability of zone-based simulations to replicate measured epicardial potentials.

We, therefore, augmented our original simulation pipeline¹⁰ to explore the influence of biophysically justified, subject-specific ischemic zone representations on computed epicardial potentials. Using experimental measurements from canine models of induced ischemia, we extracted subject-specific ischemic zone geometries from measured intramural extracellular potentials during conditions of elevated ischemic stress. We imposed these zones within our image-based cardiac models, which we tuned to replicate measured epicardial potentials. This tuning consisted primarily of semi-empirically adjusting the various parameters of the ischemic border zone, i.e., the thin layer of hypoperfused tissue that separates healthy from ischemic tissues. Border zone tuning led to consistent and predictable changes in simulated outcomes. Our results showed improved accuracy in terms of epicardial potential distributions for simulations using zone-based source representations when compared to our previous studies, which incorporated directly measured, distributed, intracardiac potential values as boundary conditions.¹⁰ These results suggest that it is, indeed, possible, and in many ways preferable, to represent ischemia in terms of discrete zones. These findings encourage further exploration of zone-based modeling approaches, particularly with respect to the parameter space used to define them, in order to increase our understanding of the underlying biophysical mechanisms that drive myocardial ischemia and, consequently, to improve noninvasive localization and monitoring of acute myocardial ischemia.

3. Material and Methods

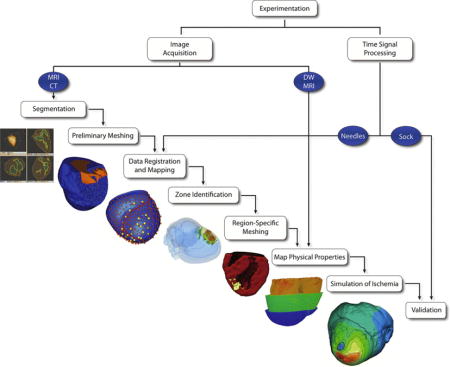
The overall approach in this study was to simulate static epicardial potentials associated with subject-specific ischemia models using an augmented implementation of our previously defined image-based modeling pipeline.^10,11 Figure 1 illustrates our overall approach in which image-based geometries, physical properties, and time-signal data were extracted from experimental canine models of acute ischemia.⁹ These were used to create subject-specific computational models, from which simulated epicardial potentials were computed and validated.¹⁰

Figure 1.

Ischemia Simulation Pipeline. Electrogram and imaging data were extracted from experimental preparations of induced acute ischemia in dogs. From imaging data, subject-specific geometric models were generated that contained conforming, subject-specific cardiac fibers definitions and ischemic zone geometries. Intramural electrical potentials were mapped within the geometric models. Intramural and epicardial electrical potentials (recorded from plunge needle and sock electrodes) were also mapped in order to define subject-specific is-chemic regions and to validate simulation results, respectively.

3.1. Experimental Methods and Data Processing

Unipolar intramural and epicardial electrograms were collected from open-chest canine models in which controlled, acute ischemia was induced, as described previously.^9,12 In brief, we regulated coronary blood flow through the left anterior descending artery (LAD) of anesthetized canine models (supply ischemia) while independently elevating heart rate and metabolic demand (demand ischemia), via right atrial pacing, to generate episodes of acute, transient ischemia. Our data includes examples of both supply and demand ischemia, which, for purposes of simulation, we consider to be equivalent. Electrogram recordings were concurrently captured using both a high-resolution customized sock (epicardial potentials)¹³ and plunge needle electrodes (intramural potentials)¹⁴ placed within the anterior portion of both ventricles. Potential values were extracted from each electrogram, using the Pfeifer open-source software package,¹⁵ at ST40%—a lead-independent time point defined as 40% of the interval between the end of the QRS complex (QRS_off) and the peak of the T wave (T_peak) of the global root mean squared signal, which considered all sock and needle electrograms together. ST40% was chosen to capture deflections in the ST segment while avoiding interference from T wave upstroke. Six distinct episodes, or interventions, of induced ischemia, acquired from two canine subjects, were considered for this study. Each episode lasted 6–8 minutes and consisted of stepwise increases in ischemic stress. ST40% potentials were corrected against control recordings taken prior to each induced ischemic episode to isolate the acute affects of ischemia.^9,12

Each heart was excised postexperiment and scanned using magnetic resonance imaging (MRI) and Diffusion Weighted MRI (DW-MRI) modalities (7 Tesla Bruker BIOSPEC 70/30, Billerica, MA) to identify cardiac geometries and fiber directions, respectively.¹⁰ Cardiac and blood volume geometries were segmented using the Seg3D open-source software package (www.seg3D.org) as were plunge needle electrode locations. DW-MRI images were used to define principal eigenvectors associated with each voxel within the heart volume, which corresponded to fiber orientation within the heart.¹⁶

3.2. Geometric Processing and Model Setup

3.2.1. Meshing

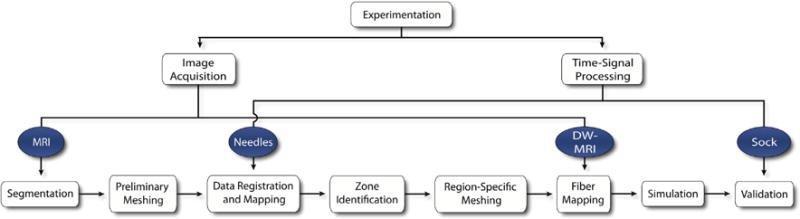
To enable numerical simulation, we implemented a two-phase meshing protocol to generate subject-specific tetrahedral meshes containing conforming geometries representing the heart, blood pool, and ischemic zones.¹⁰ Phase I meshes were generated using the open-source BioMesh3D software package¹⁷ and consisted of three-dimensional tetrahedral representations of cardiac and blood pool geometries. Recorded intramural electrograms were registered to, and interpolated within, phase I meshes using a thin-plate-spline, radial basis interpolation algorithm (Figure 2 A). Interpolated electrograms that registered elevated intramyocardial ST40% potentials were classified ischemic and thresholded to identify ischemic zone geometries within each phase I mesh (Figure 2 B). Thresholded phase I meshes provided inputs to the BioMesh3D package with which phase II meshes were generated—containing heart, blood, and ischemic zone geometries. Figure 2 C contains an example of the resulting mesh, with conformal heart tissues, blood volumes, and subject-specific ischemic regions.

Figure 2.

Region Identification and Conformal Mesh Generation. Intramural measurements were mapped within phase I meshes (A) on which thresholds were applied to extract potential zone volumes (B), which we merged to generate the final conformal phase II meshes (C) for use in finite element simulations.

3.2.2. Anisotropic Conductivities

Subject-specific anisotropic conductivities, which represented both intracellular and extracellular spaces, were identified and assigned within each phase II mesh in a manner similar to that in our previous studies.¹⁰ Briefly, fiber orientation vectors were identified on a voxel-by-voxel basis within each cardiac volume using DW-MRI images. These vectors were mapped to each element of their respective phase II meshes and used to define longitudinal and transverse conductivity values that were scaled to reflect both intracellular ( ${\overline{\sigma }}_{il}$ and ${\overline{\sigma }}_{it}$) and extracellular ( ${\overline{\sigma }}_{el}$ and ${\overline{\sigma }}_{et}$) spaces¹⁸ (see Table 1). We assumed that cross-fiber components ( ${\overline{\sigma }}_{it}$ and ${\overline{\sigma }}_{et}$) were radially isotropic in all transverse directions. Conductivities within ischemic regions were also altered to reflect bulk conductivity changes resulting from the ischemia condition as reported by Stinstra et al.¹⁸ Table 1 summarizes the resulting conductivity ratios we used for both healthy and ischemic tissue regions.

Table 1.

Ratios applied to tensor conductivity values within healthy and ischemic regions. The first subscript indicates the tissue domain (e = extracellular, i = intracellular, b = blood) and the second subscript the direction (l = longitudinal, t = transverse) relative to the local fiber direction.

Conductivity Labels	Healthy Conductivity Values	Ischemic Conductivity Values
σel	1	1/2
σil	1	1/10
σet	1/3	1/4
σit	1/10	1/1000
σb	3	3

3.2.3. Ischemic Source Model

We defined ischemic source models by assigning fixed transmembrane potential differences between the ischemic regions of phase II meshes and the otherwise healthy tissues surrounding them. A piecewise continuous border zone (BZ) representing hypoperfused, or partially ischemic, tissues¹⁹ was defined by decaying transmembrane potentials that varied as a function of distance, d, from the edge of the ischemic region. We assumed that as the distance from the boundary increased, the profile of the BZ voltage, V_BZ, transitioned from a Gaussian to a linear decay function as proposed by Swenson et al.²⁰

$$V_{BZ}(d)=\{\begin{array}{ll}{V}_m{e}^{\frac{-d^2}{2{\sigma }^2}}\hfill & d<S_1\hfill \\ V_m{e}^{\frac{-{(S_1)}^2}{{\sigma }^2}}\left(1--\frac{d-S_1}{S_2-S_1}\right)\hfill & S_1\le d<S_2\hfill \\ 0\hfill & d\ge S_2\hfill \end{array}$$ (1)

where V_m represents the transmembrane potential relative to that of the healthy tissue, S₁ corresponds to the distance at which the BZ function transitions from Gaussian to linear, and S₂ defines the distance at which the border zone ends. The values of V_m, S₁, S₂, and the Gaussian variance, σ², were expected to vary for each episode of ischemia. Accordingly, we estimated each value using a semi-empirical, multivariate approach, which consisted of, first, providing an initial guess for each variable based on values extracted by Swenson et al.²⁰ We then applied an automated perturbation scheme to each parameter to create 625 unique, uniformly distributed collocated parameter sets. Finally, for each parameter set, we compared simulation outcomes against their respective experimental epicardial measurements. In this manner, we generated individualized parameter sets for each ischemic episode that were optimized against experimental findings.

3.3. Mathematical Modeling

Acute ischemia was modeled using a passive bidomain description of the heart

$$\nabla ·({\overline{\sigma }}_e+{\overline{\sigma }}_i)\nabla {\varphi }_e=-\nabla ·{\overline{\sigma }}_i\nabla V_m,$$ (2)

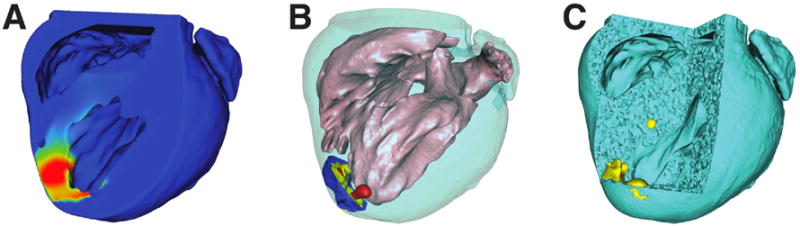
where ${\overline{\sigma }}_e$ and ${\overline{\sigma }}_l$ represent extracellular and intracellular anisotropic conductivity tensors, respectively, and V_m and ϕ_e represent transmembrane source potentials and extracellular potential throughout the heart. Boundary conditions that define the physical constrains of the model included a no-flow Neumann boundary condition along the epicardial surface and Cauchy boundary conditions (i.e., normal current flow coupled with continuity of potentials) along the endocardium as shown in Figure 3 and Equation 3:

$$\{\begin{array}{ll}{\overrightarrow{n}}_{\mathit{epi}}·({\overline{\sigma }}_e+{\overline{\sigma }}_i)\nabla {\varphi }_e=0\hfill & x\in \partial {\Omega }_{H,\mathit{epi}}\hfill \\ {\overrightarrow{n}}_{\mathit{endo}}·({\overline{\sigma }}_e\nabla {\varphi }_e)={\overrightarrow{n}}_{\mathit{endo}}·({\overline{\sigma }}_b\nabla {\varphi }_b)\hfill & x\in \partial {\Omega }_{H,\mathit{endo}}\hfill \\ {\varphi }_e={\varphi }_b\hfill & x\in \partial {\Omega }_{H,\mathit{endo}}\hfill \\ {\varphi }_i=0\hfill & x\in {\Omega }_b,\hfill \end{array}$$ (3)

where ϕ_e and ϕ_b are the potentials within the extracellular cardiac tissue and blood domains, respectively, and Ω_H represents the cardiac volume, which is bounded by the epicardial (∂Ω_H,epi) and endocardial (∂Ω_H,endo) surfaces with their respective surface normal unit vectors ${\overrightarrow{n}}_{\mathit{epi}}$ and ${\overrightarrow{n}}_{\mathit{endo}}$ (Figure 3). We assigned conductivity values (Table 1)¹⁸ for each domain to the labeled phase II mesh and defined transmembrane potentials (V_m) throughout the cardiac volume. A V_m value of 0 mV was assigned to healthy tissues to reflect control-corrected values as described previously.⁹ The epicardial subset of the computed ϕ_e values was subsequently compared to measured values from the sock electrodes in order to validate simulated solutions.

Figure 3.

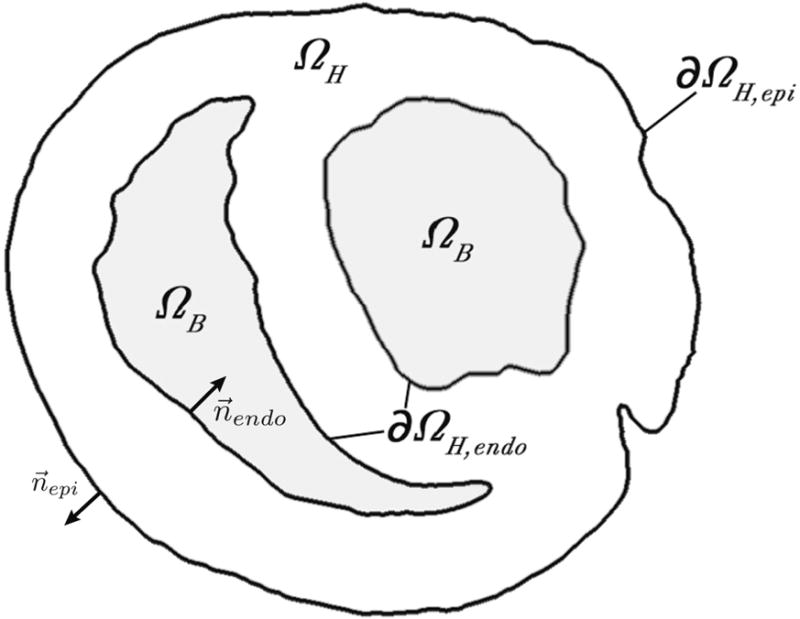
Model Boundary Conditions. The passive current flow bidomain equation (Equation 2) governed the cardiac tissue Ω_H, which was bounded by the epi- and endocardium—∂Ω_H,epi and ∂Ω_H,endo with their respective surface normal unit vectors ${\overrightarrow{n}}_{\mathit{epi}}$ and ${\overrightarrow{n}}_{\mathit{endo}}$. Extracellular currents were allowed to flow into the blood volume Ω_B along the endocardial boundary. All other currents along the boundaries maintained no-flow conditions (Equation 3).

3.4. Numerical Methods

By applying Green’s divergence theorem to Equation 2, the following finite element, weak formulation was generated:

$${\displaystyle \int (({\overline{\sigma }}_e+{\overline{\sigma }}_i)\nabla {\varphi }_e(\overline{x}))·\nabla \psi (\overline{x})d\overline{x}=-{\displaystyle \int ({\overline{\sigma }}_i\nabla V_m(\overline{x}))·\nabla \psi (\overline{x})d\overline{x},\forall \psi \in \Omega ,}}$$ (4)

where Ω represents the linear finite element mesh of the heart (Section 3.2) that consisted of $\overline{x}$ elements represented by local basis functions, ψ. By applying this formulation to the mesh, we reduced Equation 4 to a system of linear equations:

$$A{\varphi }_e=-R{V}_m,$$ (5)

where A and R represent stiffness matrices defined by $A_{j,k}={\langle \nabla {\psi }_j,({\overline{\sigma }}_e+{\overline{\sigma }}_i)\nabla {\psi }_k\rangle }_{\Omega }$.and $R_{j,k}={\langle \nabla {\psi }_j,{\overline{\sigma }}_i\nabla {\psi }_k\rangle }_{\Omega }$ ²¹. An iterative solver was used to compute ϕ_e from Equation 5 using a conjugate gradient method with a Jacobi preconditioner within the SCIRun problem-solving environment.²²

3.5. Validation

Simulation results were validated against experimental findings, as described previously, by comparing simulated epicardial potentials with measured sock electrodes recorded during experiments.¹⁰ Pearson’s correlation coefficient (PCC), RMS error (RMSE), and absolute error (AE) values were used to quantify agreement between experimental and simulation results as follows:

$$\begin{array}{l}\text{PCC}=\frac{\mathbb{E}[({\varphi }_s-{\mu }_{{\varphi }_s})({\varphi }_m-{\mu }_{{\varphi }_m})]}{S{D}_{{\varphi }_s}S{D}_{{\varphi }_m}}\\ \text{RMSE}=\sqrt{\mathbb{E}({({\varphi }_s-{\varphi }_m)}^2)}\\ \text{AE}=\left|{\varphi }_s-{\varphi }_m\right|,\end{array}$$ (6)

where ϕ_s and ϕ_m represent simulated and measured potential values, respectively, while $S{D}_{{\varphi }_s}$ and $S{D}_{{\varphi }_m}$ are their associated standard deviations. The covariance between ϕ_s and ϕ_m is represented in terms of expected value, $\mathbb{E}$, and the respective means, ${\mu }_{{\varphi }_s}$ and ${\mu }_{{\varphi }_m}$, of the simulated and observed potential fields. Absolute error, in addition to providing the epicardial maximum error measurement (AE_max = ‖ϕ_s − ϕ_m‖_∞), was also used to determine what percentage of the epicardium experienced errors larger than 1 mV as a measure of overall prevalence of error along the epicardium (AE_%).

4. Results

4.1. Ischemic Zone Characterization

Each ischemic region extracted from intramyocardial electrograms exhibited spatial complexity that did not reflect the simple schematic geometries that are the basis for the clinical dogma described in the Introduction. Figures 4 and 5 support this assertion and demonstrate the implications of modeling ischemia with subject-specific zone geometries. Each image shows: 1) subject-specific ischemic regions derived from intramurally measured extracellular potentials, 2) simulated solutions produced using each region, and 3) measured epicardial potentials taken from the same experiment (i.e., true epicardial potentials).

Figure 4.

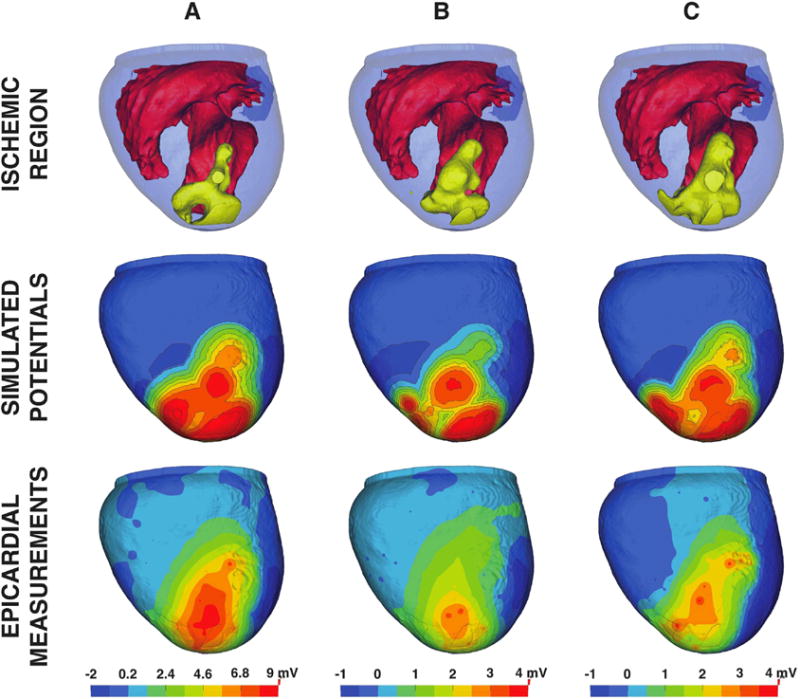
Subject-specific simulation results for experiment 1. Subject-specific ischemic regions from experiment 1 (row 1) are shown in yellow and were used to generate simulated epicardial potentials (row 2), which were subsequently validated against measured epicardial potentials (row 3). Columns A, B, and C depict samples acquired during 3 different interventions, each separated by a 30 minute recovery period.

Figure 5.

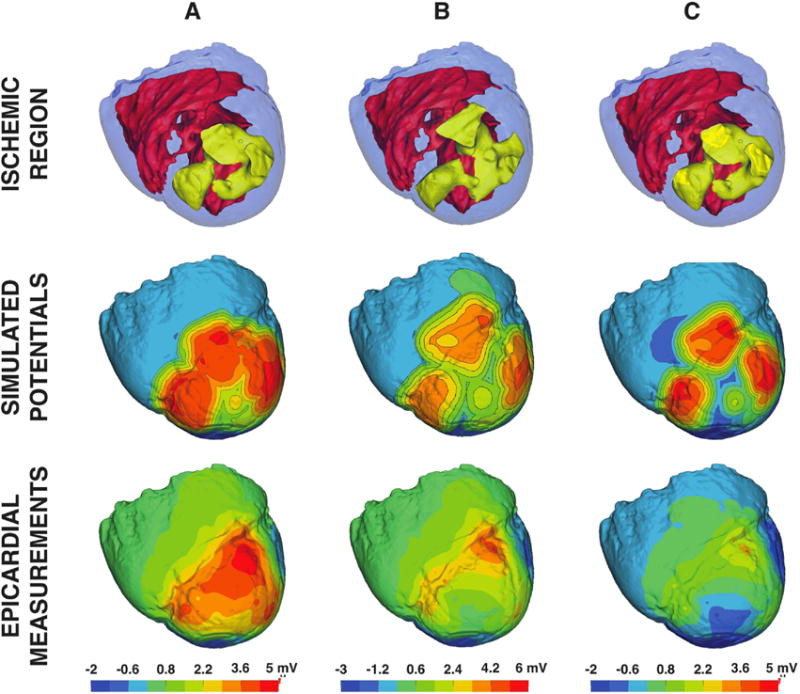
Subject-specific simulation results for experiment 2. Subject-specific ischemic regions from experiment 2 highlighted in yellow (row 1) were used to simulate epicardial potentials (row 2) that were subsequently validated against measured epicardial potentials (row 3). Columns A, B, and C depict samples acquired during 3 different interventions, each separated by a 30 minute recovery period.

Figure 4 depicts results from three distinct ischemic episodes within a single experiment (experiment 1).⁹ Each simulation is ordered sequentially, that is, episode A occurred before episode B, which occurred before episode C. The heart was allowed a 30-minute recovery period between episodes. Simulated epicardial potentials (Figure 4 middle) produced elevations that mirrored the major appendages of each ischemic region, particularly those that approached, or broke through to, the epicardial surface. Regions that were distant from the surface (i.e., more subendocardial) tended to produce weaker elevations. Experimental measurements (Figure 4 bottom) also revealed elevated potentials overlying subepicardial ischemic zone appendages; however, the more endocardial areas, such as those observed near the septoapical region, did not produce equally strong elevated potentials as were observed in simulations.

Slightly depressed potentials (dark blue) were also present in both simulated and measured electrograms. In both cases, epicardial depressions flanked the ischemic zone, manifesting in the basal regions and along the lateral, or free wall, areas of the left and right ventricles. Similar depressions were also observed along the inferoapical region of the heart, which are not visible in Figure 4 but are apparent in Figure 5. Measured depressions over the lateral and inferoapical areas, in particular, were also present in sock recordings.

Figure 5, like Figure 4, shows ischemic zones, simulated results, and measured epicardial potentials associated with a sequence of ischemic episodes from a second experiment (experiment 2). Again, the epicardial-most regions of the ischemic zones produced the largest simulated epicardial potentials. However, the measured potentials showed a different pattern as ischemic episodes were repeated (row 3 of columns A–C in the figure). Large elevated regions overlying the ischemic zone in early stage episodes (column A) dropped in amplitude and were encroached on by deep flanking depressions (column C).

4.2. Border Zone Characterization

Border zone construction relied on four major parameters, as dictated by Equation 1. These parameters consisted of the initial transmembrane potential difference between healthy and ischemic tissues (V_m), the variance of the Gaussian transitional region (σ²), the distance from the ischemic zone boundary to the edge of the Gaussian transitional region (S₁), and the total width of the border zone (S₂), where S₂ was, by definition, greater than S₁. Manipulation of these parameters produced consistent and predictable changes to epicardial solutions. We generated and analyzed 625 possible BZ parameter sets for each ischemic episode in order to identify simulations that were strongly correlated with measured epicardial electrograms and produced the least amount of RMS error as defined by Equation 6.

Figure 6 shows the influence of each parameter on simulated epicardial po tentials. In observing the trends of each of the parameters, we assumed that all other parameters remained static. That is, as we analyzed the affect of V_m, we assumed that σ², S₁, and S₂ remained unchanged. As expected, changes in V_m scaled the epicardial potential ranges meaning that, as V_m increased, epicardial maxima increased while minima decreased. Gaussian variance was inversely related to both epicardial minimum and maximum values i.e., a smoother transition of potential reduced the gradient in the border zone and hence the epicardial potential amplitudes. Changes in S₁ produced no significant changes in the epicardial potential range; however, it provided essential blurring, which improved correlation between simulated and measured potentials (Section 4.3). S₂ values were directly proportional to epicardial minima and inversely proportional to epicardial maxima, but in varying measure. Epicardial minima were strongly influenced by S₂ whereas maxima were only weakly affected. In short, border zone parameters were used to scale (V_m), translate (σ²), and fine tune (S₁ and S₂) simulation outcomes to match measured epicardial potentials. Using the optimal border zone definitions obtained from each simulation (N=6), we generated Table 2, which provides a list of averages and standard deviations for each parameter.

Figure 6.

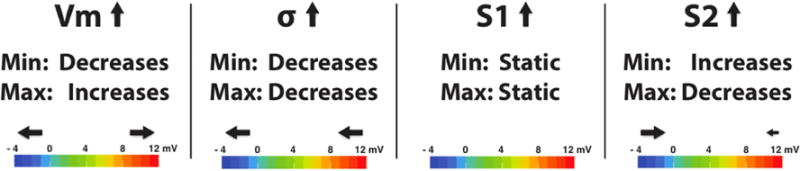
Effects of border zone parameters on epicardial potentials. Epicardial potentials can be scaled and translated by manipulating V_m and σ values, respectively. Manipulating BZ edge definitions (S₁ and S₂) can be used to fine tune simulated outcomes to more accurately reflect epicardial potentials.

Table 2.

Optimal values in border zone construction.

Label	Definition	Value
Vm	Transmembrane potential	15 ±.5 mV
σ	Gaussian variance	4.9 ± 0.8
S1	Gaussian transition width	8 ±2.3 mm
S2	Total BZ width	10.5 ± 2.1 mm

4.3. Quantitative Analysis

After establishing the best set of BZ parameters for each ischemic episode, we compared PCC, RMSE, and absolute error metrics across the entire epicardium and computed errors between simulated and measured epicardial potentials, as summarized in Table 3. These values are also juxtaposed against equivalent quantitative measures extracted from simulations, described previously,¹⁰ that were generated using the intracardiac potentials measured with needle electrodes as boundary conditions.

Table 3.

Quantitative validation metrics for simulations of epicardial potentials produced during ischemia using source models generated from both subject-specific ischemic zones (Zone-Based) and measured intracardiac potentials from needle electrodes (Needle-Based).¹⁰

Statistical Measure	Experiment 1A Zone-Based	Experiment 1A Needle-Based	Experiment 2A Zone-Based	Experiment 2A Needle-Based
PCC	0.86	0.73	0.84	0.68
RMSE	1.20 mV	1.54 mV	0.80 mV	0.79 mV
AEmax	7.78 mV	7.61 mV	4.56 mV	5.43 mV
*AE%	15.1%	52.6%	12.3 %	15.0%
Statistical Measure	Experiment 1B Zone-Based	Experiment 1B Needle-Based	Experiment 2B Zone-Based	Experiment 2B Needle-Based
PCC	0.81	0.59	0.68	0.47
RMSE	0.59 mV	0.88 mV	0.94 mV	0.78 mV
AEmax	3.27 mV	4.58 mV	6.54 mV	6.13 mV
AE%	6.3%	21.8%	16.0%	15.1%
Statistical Measure	Experiment 1C Zone-Based	Experiment 1C Needle-Based	Experiment 2C Zone-Based	Experiment 2C Needle-Based
PCC	0.65	0.44	0.65	0.49
RMSE	0.63 mV	0.69 mV	0.90 mV	0.43 mV
AEmax	3.96 mV	3.96 mV	5.22 mV	3.47 mV
AE%	6.3%	12.6%	11.1%	6.3%

^*AE_% represents the percentage of the epicardial surface with 1 mV of absolute error or greater.

Considering only zone-based models (i.e., the leftmost columns in each experimental pairing of Table 3), PCC values indicated a strong correlation between simulation results and measured potentials—agreement that was also qualitatively evident in Figures 4 and 5. Half of the simulated episodes produced correlation values greater than 0.8, and none produced PCC values less than 0.65, which is indicative of strong overall correlation. RMSE was also relatively low among all simulations. Error values lay between 11–13% of the total epicardial potential range. Absolute error (AE) was less predictable in isolation, but when considered as a percent error of the entire epicardial surface (AE_%), it provided a spatial metric for assessing the size of regions with error that exceeded 1 mV. Spatially, AE was generally low across the epicardium, rising above 1 mV primarily in regions that flanked sites with the most elevated ST potentials (not shown).

In comparing each approach, we found that zone-based methods consistently generated simulation outcomes that were more strongly correlated with experimentally measured epicardial potentials than were their needle-based counterparts. In all simulated cases, correlation was significantly stronger for zone-based models (p = 0.05), which reached levels as high as 0.86 while needle-based simulations only reached PCC values of 0.73 and were, in general only moderately correlated (i.e., 0.5 ≤ PCC< 0.7). RMSE and AE measures, however, were less indicative of simulation improvements using zone-based methods, with simulations failing to show a consistent and significant differences between the two approaches (Table 3).

5. Discussion

The goal of this study was to characterize ischemic zone sources, based on experimental methods, in order to develop subject-specific simulation approaches that accurately predicted epicardial potentials associated with acute myocardial ischemia. To this end, we employed an image-based simulation pipeline that included capturing both geometric (imaging) and electrogram (time-signal) data from canine experiments in which acute transient ischemia was induced (Figure 1).^11,10 These data were converted into whole-heart geometric models within which zone-based, ischemic source models were defined and used to reconstruct epicardial ST potentials that strongly agreed with those measured during experiments.

Errors associated with ECG-based detection of myocardial ischemia,¹ in conjunction with our own experimental findings,⁹ motivated us to reevaluate longstanding theory regarding the formation of ischemia within the heart and its influence on epicardial potentials.¹⁰ It is still broadly accepted that myocardial ischemia originates as a subendocardially anchored, relatively concentric, region of injured tissue that extends transmurally with prolonged ischemic stress.⁷ Our recent experimental findings, however, suggest, instead, an alternate notion that ischemia develops as a complex of smaller isolated zones—distributed within the midmyocardium—that converge to form larger transmural regions.⁹ Such observations offer a potential explanation for the broad deviations in accuracy recorded by ECG-based diagnosis.

Previously, we developed and validated a subject-specific simulation pipeline in which we used high-resolution, multielectrode, needle-based, intramyocardial extracellular measurements as direct source representations for the ischemic condition.¹⁰ This approach generated accurate outcomes, particularly in cases of severe ischemic stress; however, spatial sampling of the electrodes was limited by physical and practical constraints inherent in experimental models and was, therefore, not sufficient to document ST deviations that arose outside of the region occupied by our intramural electrodes (e.g., the entire posterior aspects of the heart). In the present study, we explored a new approach aimed at addressing this limitation by augmenting our simulation framework to incorporate zone-based source representations.^23,24

We found that zone-based computational simulations generated ST potential distributions that showed strong agreement, both qualitatively and quantitatively, with measured epicardial potentials. Furthermore, we compared our zone-based simulated results with our previously developed extracellular (“needle-based”) source potential model¹⁰ and found that zone-based methods consistently generated epicardial ST potential distributions that were more strongly correlated with measured epicardial potentials than those produced using needle-based sources (p = 0.05). Where needle-based approaches failed to detect ST deviations that were not directly recorded, zone-based models provided additional information, e.g., predicting ST depressions along the lateral boundaries of the ischemic zone and essentially reintroducing ST deviations that lay outside the measured region. This occurrence is a well-documented outcome of zone-based modeling in which anisotropic conduction, coupled with transmembrane potential source models, lead to elevated ischemic regions that are flanked by ST depressions.^23,24 In our studies, we found that PCC values were significantly and consistently higher in zone-based simulations (0.65 ≤ PCC≤ 0.86) than they were in simulations using needle-based approaches (0.44 ≤ PCC≤ 0.73), which reflected a strong spatial agreement that is apparent in Figures 4 and 5.

The improved performance of zone-based ischemic sources over needle-based estimates was less consistent when we used statistical comparisons based on potential amplitudes (i.e., RMSE and AE) rather than spatial patterns of the epicardial potentials (i.e., PCC). RMSE associated with zone-based simulations reached a maximum value of 1.20 mV while the needle-based equivalent reported 1.54 mV; however, as shown in Table 3, not all zone-based simulations outperformed their needle-based counterparts. For example, improvements in model outcomes, expressed in terms of RMSE, were observed in experiment 1, but not in experiment 2. Similarly, AE_% was markedly lower using the zone-based approaches for all experiment 1 simulations but not for all experiment 2 simulations where only one of three episodes exhibited lower AE_%. Differences in AE_% between zone and needle-based approaches can be attributed to the lack of flanking ST depressions in needle-based models. The majority of this error arose in the inferoapical and posterior regions (not shown) where ST depressions that were present in both measured and zone-based were not generated in needle-based approaches.

We consistently observed that errors in epicardial potentials depended heavily on how we set border zone parameters. The distributions of extracellular potentials in the border zone have yet to be well characterized but our results support other studies^19,25,20 that show they play an important role in ischemia simulation. Swenson et al. proposed an ischemic border zone definition that integrated two zone models with differing profiles (Equation 1), and which generated more accurate outcomes²⁰ than models using only linear or smooth BZ definitions. We built on this approach by optimizing border zone parameters to fit measured epicardial potentials. Our findings (Table 2) agreed approximately with those presented by Swenson et al.,²⁰ who estimated the thicknesses of the two BZ regions to be S₁ = 10 and S₂ = 13 mm while using a constant σ value of 2 and a transmembrane potential difference of V_m = 30. Despite general agreement with these previous findings, transmembrane potentials for our models were much lower than those used by Swenson et al.; however, our V_m values fell within the range of those used in other zone-based^24,20,26 and ionic distribution models.²⁷

In characterizing the border zone, we also identified the influence of each BZ parameter on the resulting epicardial potential magnitudes. Figure 6 illustrates the influence of each of the four border zone parameters on epicardial potentials and further shows how a) changes in V_m scaled the epicardial potential ranges, b) changes in σ translated those same ranges (e.g.,making them globally more negative or more positive), and c) fine tuning of epicardial potentials was achievable via manipulation of S₁ and S₂. Swenson et al. observed that, “most simulations fail to match the potential magnitudes seen in experimental data.” However, we find that by precisely manipulating the border zone parameters to generate good alignment between simulated and experimental potential magnitudes, we simultaneously improved correlation and reduced error in our validation metrics. This is not particularly surprising for RMSE and AE statistical measures, which, for properly registered experimental data, would in theory, generate less error. However it is somewhat unexpected for PCC measures, which are both scale and shift invariant.

Although our zone-based simulation approaches proved to be generally accurate, unavoidable confounding factors contributed to uncertainties in simulated outcomes. For example, insufficient needle coverage or missing electrodes (coverage error) may have lead to incomplete intramyocardial zone definitions; electrode misalignment (registration error) may have been the cause variations in statistical error; and uncertainty in experimental recordings (recording errors) due to time-sensitive degradation of tissues during prolong experimental procedures had the potential to introduce inconsistencies within our experimental measurements, which would, in turn, affect validation outcomes.¹⁰ These limitations were mitigated in the following ways. Coverage error was reduced by exposing as much of the LAD perfusion bed as possible prior to needle placement and distributing needles within the exposed region such that the perfusion bed was well covered. Registration errors were reduced using a two-phase registration process, as described previously,¹⁰ in which both postexperiment digitized points and activation times were used to position cardiac meshes and epicardial sock electrodes to fall within 1 cm of the original, digitized positions.¹⁰ Recording errors were mitigated by implementing sophisticated experimental protocols that ensured accurate data acquisition and measurement.⁹

A more fundamental limitation of any zone-based ischemia model is the selection of the zone itself. As discussed in the Introduction, current clinical dogma assumes a continuous, geometrically simple, subendocardial ischemic zone. Most computational models have adopted this paradigm, imposing spherical, hexahedral, or semi-ellipsoidal subendocardial ischemic regions,^24,26,27 surrounded by narrow border zones.²⁰ Our previous findings suggest that these assumptions are limited to only a small subset of possible ischemic regions.⁹ We defining our ischemic regions by setting thresholds based on semi-empirical processes, explained above, and found strong agreement between measured and simulated potentials. Ongoing studies will reveal the sensitivity of simulations to these threshold assumptions. Additionally, full-torso forward simulations are currently under development that further aim to characterize the effect of our subject-specific ischemic models on body surface potentials thereby relating our simulated findings to clinical outcomes.

1. Highlights.

• Experimental models have shown that myocardial ischemia develops as a complex distributed region rather than as a simple subendocardial zone.

• We have characterized these experimental findings and used them to develop a subject-specific simulation pipeline.

• We also present specific border zone (BZ) parameter sets for constructing accurate epicardial potentials, while also identifying in what way these BZ parameters influence epicardial potentials in translating, scaling, and refining simulated epicardial potential distributions.

• Results from our pipeline correlate strongly with measured epicardial potentials.