A Signal Detection-Item Response Theory Model for Evaluating Neuropsychological Measures

Abstract

Introduction

Models from signal detection theory are commonly used to score neuropsychological test data, especially tests of recognition memory. Here we show that certain item response theory models can be formulated as signal detection theory models, thus linking two complementary but distinct methodologies. We then use the approach to evaluate the validity (construct representation) of commonly used research measures, demonstrate the impact of conditional error on neuropsychological outcomes, and evaluate measurement bias.

Method

Signal detection-item response theory (SD-IRT) models were fitted to recognition memory data for words, faces, and objects. The sample consisted of US Infantry Marines and Navy Corpsmen participating in the Marine Resiliency Study. Data comprised item responses to the Penn Face Memory Test (PFMT; N = 1,338), Penn Word Memory Test (PWMT; N = 1,331), and Visual Object Learning Test (VOLT; N = 1,249), as well as self-report of past head injury with loss of consciousness.

Results

SD-IRT models adequately fitted recognition memory item data across all modalities. Error varied systematically with ability estimates, and distributions of residuals from the regression of memory discrimination onto self-report of past head injury were positively skewed towards regions of larger measurement error. Analyses of differential item functioning revealed little evidence of systematic bias by level of education.

Conclusions

SD-IRT models benefit from the measurement rigor of item response theory—which permits the modeling of item difficulty and examinee ability—and from signal detection theory—which provides an interpretive framework encompassing the experimentally-validated constructs of memory discrimination and response bias. We used this approach to validate the construct representation of commonly used research measures and to demonstrate how non-optimized item parameters can lead to erroneous conclusions when interpreting neuropsychological test data. Future work might include the development of computerized adaptive tests and integration with mixture and random effects models.

Introduction

Models from signal detection theory (SDT; Wickens, 2002) are commonly used to score both clinical and experimental test data in neuropsychology (e.g., Delis et al., 2000; Kane et al., 2007; Thomas et al., 2013). Although SDT originated in engineering, applications to psychological research, especially testing paradigms used in psychophysics (e.g., Green & Swets, 1966) and recognition memory (Lockhart & Murdock, 1970; Snodgrass & Corwin, 1988), are widespread.

DeCarlo (1998; 2011) demonstrated that some SDT models can be formulated as generalized linear models. In this paper, we extend this work to show that, because certain psychometric approaches also fall under the category of generalized linear models (de Boeck & Wilson, 2004), a restricted form of a popular item response theory (IRT; Lord, 1980) model can be shown to be equivalent to a popular SDT model. In doing so, we link a valuable body of psychometric research and technical literature from IRT to the measurement of a general class of cognitive constructs. We then demonstrate how methods from IRT can be used to address two applied measurement concerns raised by the Standards for Educational and Psychological Testing: conditional error and measurement bias (AERA, APA, & NCME, 2014).

Signal Detection Theory

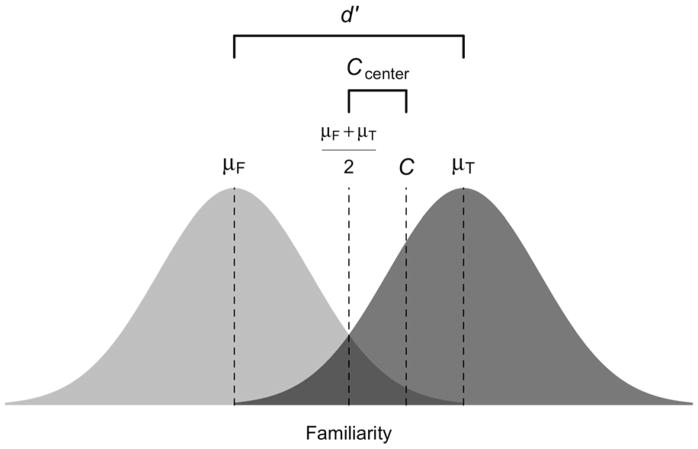
The SDT model shown in Figure 1 assumes that the presentation of repeated or old items (targets) and non-repeated or new items (foils) during the recognition period of testing evokes familiarity that can be represented by underlying probability distributions: typically normal but also logistic. Under one version of the model, target and foil items are assumed to follow unimodal, symmetric distributions of familiarity with equal variances¹ but different means. In SDT terms, the distribution of familiarity for targets corresponds to the signal plus noise intensity distribution on a sensory continuum; and the distribution of familiarity for foils corresponds to the noise intensity distribution. A larger distance between the mean of the target distribution(μ_T) and the mean of the foil distribution (μ_F) implies greater target familiarity, and thus a higher probability of accurate responding. This distance is a measure of memory discrimination and is defined as

Figure 1.

Equal variance, signal detection theory model. μ_T = mean of the distribution of familiarity for targets; μ_F = mean of the distribution of familiarity for foils; d′ = μ_T minus μ_F (memory discrimination); C = criterion; C_center = value of the criterion relative to the midpoint between μ_T and μ_F (bias).

$$d^{\prime }=\frac{{\mathrm{\mu }}_{\mathrm{T}}-{\mathrm{\mu }}_{\mathrm{F}}}{D},$$ (1)

where D is a scale parameter, reflecting the common standard deviation, and is often fixed to 1.0 for simplicity. Familiarity drives recognition; however, because familiarity follows a probability distribution, and because the familiarity distributions of targets and foils often overlap, the SDT model assumes that examinees must establish a criterion, C, representing the level of familiarity beyond which they will classify test items as targets. This criterion is centered relative to the midpoint between μ_T and μ_F, using:

$$C_{\text{center}}=C-\frac{{\mathrm{\mu }}_{\mathrm{T}}+{\mathrm{\mu }}_{\mathrm{F}}}{2}.$$ (2)

Typically, closed-form solutions are used to estimate values of d′ and C_center for individual examinees given their observed true and false positive rates (see Snodgrass & Corwin, 1988). In doing so, an examinee’s ability to recognize previously studied information (d′) can be disentangled from their bias towards conservative or liberal responding (C_center). That is, estimates of memory strength (d′) can be compared across subjects with liberal, neutral, and conservative response biases.

SDT’s appeal in applied work lies in its ability to provide researchers and clinicians with an experimentally validated interpretive framework for multiple latent abilities presumed to underlie recognition memory test performance. Studies have bolstered this position by showing that manipulations of environmental and stimulus factors have predictable effects on d′ and C_center. Snodgrass and Corwin (1988), for example, used a word recognition memory task to show that manipulating word imagery strength had an effect on d′ but not C_center. By contrast, manipulating payoff (i.e., preferentially punishing false positive or false negative responses) had an effect on C_center but not d′. SDT parameters have also shown unique diagnostic utility. Although memory deficits—low values of d′— associated with Alzheimer’s and other forms of dementia are well known, Alzheimer’s patients also show abnormally liberal response biases—negative values of C_center (Budson, Wolk, Chong, & Waring, 2006): a clinical finding not shared by patients with primary memory disorders such as Korsakoff’s syndrome (Snodgrass & Corwin, 1988).

Item Response Theory

IRT comprises a collection of models and techniques used to evaluate psychological measures (Embretson & Reise, 2000; Lord, 1980; McDonald, 1999). Among other benefits, IRT improves upon the classical approach by explicitly assessing conditional measurement error, improving the quantification, scaling, and equating of scores, more effectively identifying item bias, and facilitating the development of advanced measurement tools such as computerized adaptive tests (Embretson & Hershberger, 1999). IRT is now widely used in personality and psychiatric symptom measurement (Reise & Waller, 2009), and is garnering increased attention in neuropsychological measurement (e.g., Mungas, Reed, Marshall, & González, 2000; Pedraza, Sachs, Ferman, Rush, & Lucas, 2011; Thomas et al., 2013).

Many applications of IRT assume unidimensional measurement models; however, multidimensional models (Reckase, 2009) are often more plausible in cognitive testing. One popular model is the compensatory extension of the two-parameter (2P) model, where low ability on one latent trait can be compensated by high ability on another latent trait. The slope-intercept form of the 2P model assumes two types of item parameters: threshold (τ) and discrimination (α). The number of person parameters—or abilities (θ)—is defined by theory or by exploratory methods, and will be denoted M. IRT models are typically fitted to the entire item response matrix over all examinees and items. Compensatory multidimensional 2P IRT models can be expressed as:

$$\mathrm{f}\left(\mathrm{P}\left(X_{\text{ij}}=1|{\mathrm{\tau }}_{\mathrm{j}},{\mathbf{\alpha }}_{\mathrm{j}},{\mathbf{\theta }}_i\right)\right)={\mathrm{\tau }}_{\mathrm{j}}+{\mathbf{\alpha }}_{\mathrm{j}}{\mathbf{\theta }}_i,$$ (3)

where X_ij is the response of examinee i on item j (X_ij =1 for a correct response and X_ij =0 for an incorrect response), τ_j is the threshold of item j, θ_i is the column vector of abilities for examinee i [θ_i1, θ_i2, … θ_iM], and α_j is the row vector of discrimination parameters for item j related to each of these abilities [α_j1, α_j2, … α_jM]. The function f links the probability (P) of a correct response (left side of Equation 3 within parentheses) to the linear predictor (right side of Equation 3). Two commonly used link functions are the logit the inverse of the cumulative distribution function for the logistic distribution—and the probit—the inverse of the cumulative distribution function for the normal distribution (see Madsen & Thyregod, 2011). Whereas the predicted value of the probit is a z-score associated with P, the predicted value of the logit is the log-odds. However, the choice between these link functions is arbitrary, as a scaling constant can be multiplied into the linear predictors when the logit is used to achieve a metric that is nearly equivalent to the normal model, or divided into the linear predictors when the probit is used to achieve a metric that is nearly equivalent to the logistic model (Camilli, 1994; de Ayala, 2009). The parameter τ_j is interpreted as item easiness, and is negatively related to item difficulty (β_j). The row vector α_j conveys the extent to which item j can discriminate between different levels of ability; that is, higher values convey better discrimination and, all things equal, more precise measurement. The column vector θ_i conveys the standing of each examinee on the latent psychological constructs thought to systematically influence item performance.

In comparison to classical test theory, IRT provides users with more accurate and rigorous methods for studying the precision of ability estimates (Embretson & Hershberger, 1999). In IRT, precision is defined by the information about the true values of θ that items are expected to provide (Reckase, 2009). Stated differently, if the item score changes along with θ, the item is informative (precise); if the item score does not change along with θ, the item is non-informative (imprecise). The information function for an entire test is the sum of all item information functions. Information values are difficult to interpret directly; however, one over the square root of information is equal to standard error of estimate (SE_θ): the standard deviation of the maximum likelihood estimate of θ. SE_θ is typically a U-shaped function of θ with the low point of the function corresponding to the overall difficulty of the item (or test). That is, items and tests are most informative, and thus produce the lowest standard error, when ability and difficulty are closely matched. For example, Pedraza, Sachs, Ferman, Rush, and Lucas (2011) used IRT to show that most items from the Boston Naming Test have difficulty values located in the average to below average range of ability. Consequently, precision is relatively high within the low-average range of ability but low within the above average range of ability. Results such as these are commonly used to guide test development and refinement, especially computerized adaptive tests (e.g., Cella et al., 2007), and to identify strengths and weaknesses of existing instruments.

Applications of IRT are becoming increasingly common in neuropsychology, with papers now appearing in the Journal of Clinical and Experimental Neuropsychology (e.g., Jahn, Dressel, Gavett, & O’Bryant, 2015), Neuropsychology (e.g., Kenzik et al., 2015), and the Archives of Clinical Neuropsychology (e.g., Li, Root, Atkinson, & Ahles, 2016) among other current periodicals. Nonetheless, the methodology is still somewhat rare in comparison to other domains of clinical assessment (Thomas, 2017). This could reflect a disconnect between models that are common in IRT and models that are common in neuropsychology, such as the equal variance SDT model. This paper thus serves as link towards greater integration of IRT applications in neuropsychology.

Motivation for the Signal Detection-Item Response Theory Model

Motivation for a combined signal detection-item response theory model (hereafter referred to as the SD-IRT model) lies in the observation that rarely, if ever, are cognitive test scores thought to reflect strictly unidimensional constructs. Modern neuroscience acknowledges that complex cognitive functions are due to interactions among brain networks (Sporns, 2011), models from cognitive psychology habitually assume several coordinated, but distinct, cognitive processes (Lewandowsky & Farrell, 2011), and in neuropsychological assessment it is recognized that deficits in one domain (e.g., attention) often lead to deflated scores in measures of separate domains (e.g., memory; Lezak, Howieson, Bigler, & Tranel, 2012). Many clinicians and applied researchers have embraced this complexity as a tool that can be leveraged into informative understandings of complex human behavior (Brown, Lohr, Notestine, Turner, Gamst, & Eyler, 2007). Methodologists, as well, have touted the benefits of models that convey complex psychological narratives (Mislevy, Levy, Kroopnick, & Rutstein, 2008).

Although psychometric models need not mimic the full complexity of cognitive neuroscience, the added difficulty that comes with simultaneously measuring multiple latent dimensions is formidable nonetheless. As in factor analysis, multidimensional IRT models must contend with rotational indeterminacy; that is, there are infinite combinations of θ and α that would all produce the same likelihood given certain rotations of the multidimensional space. Whereas finding an interpretable rotation across a battery of tests can be comparatively simple—being that psychologists typically have a priori beliefs about the domains assessed by distinct tests (e.g., Patt et al., 2017)—it is often more challenging to interpret multidimensionality at the item level. Moreover, whereas exploratory solutions to rotational indeterminacy may be suitable for psychometric development of tests, applied research often demands consistent interpretation of measured constructs in order to facilitate repeatability and comparability of results across studies.

What is needed is an empirically validated, theory-based solution to the problem of rotational indeterminacy. As shown below, because certain IRT and SDT models can be formulated as generalized linear models (DeCarlo, 1998; de Boeck & Wilson, 2004), the equal variance version of the SDT model and the compensatory multidimensional 2P IRT model can be expressed as the same generalized linear model: the SD-IRT model. This model, as shown below, provides one solution to the problem of rotational indeterminacy and allows us to bring IRT’s rigorous approach to studying measurement precision to bear on the understanding of latent constructs defined by SDT.

Formulation of the Signal Detection-Item Response Theory Model

In the SDT model, the probability of responding to a foil can be expressed as the area to the right of the criterion under the foil distribution, and the probability of responding to a target as the area to the right of the criterion under the target distribution (see Figure 1). Using derivations presented in DeCarlo (1998), these probabilities can be expressed with the following:

$$\mathrm{f}\left(\mathrm{P}\left(U=1|\text{Foil}\right)\right)=\frac{{\mathrm{\mu }}_{\mathrm{F}}-C}{D},$$ (4)

and

$$\mathrm{f}\left(\mathrm{P}\left(U=1|\text{Target}\right)\right)=\frac{{\mathrm{\mu }}_{\mathrm{T}}-C}{D},$$ (5)

where f is either a logit or a probit link function² and U is a binary variable that takes on a value of 1 for a positive response and 0 for a negative response. Equations 4 and 5 can be combined into a single expression by introducing a variable Z that equals 1 if the test item is a target and −1 if the test item is a foil:

$$\mathrm{f}\left(\mathrm{P}\left(U=1|Z\right)\right)=\frac{{\mathrm{\mu }}_{\mathrm{T}}-C}{D}\left(\frac{Z+1}{2}\right)+\frac{{\mathrm{\mu }}_{\mathrm{F}}-C}{D}\left(\frac{1-Z}{2}\right).$$ (6)

Fixing the scale parameter D to 1, as is common in SDT, and simplifying produces the formula that appears in Appendix A of DeCarlo (1998):

$$\mathrm{f}\left(\mathrm{P}\left(U=1|Z\right)\right)=-C_{\text{center}}+\frac{d^{\prime }}{2}Z.$$ (7)

Two changes are needed to align SDT with IRT. First, as in IRT, the SDT model must be formulated to predict the probability of a correct response (X = 1) rather than the probability of a positive response (U = 1). Using the property that f(1-P) = −f(P) for both the probit and the logit link functions, and knowing that positively responding is correct when a target is presented whereas negatively responding is correct when a foil is presented, Equation 7 yields:

$$\{\begin{array}{l}\mathrm{f}\left(\mathrm{P}\left(X=1|\text{Target}\right)\right)=\mathrm{f}\left(\mathrm{P}\left(U=1|\mathrm{Z}=1\right)\right)=-C_{\text{center}}+\frac{d^{\prime }}{2}\hfill \\ \mathrm{f}\left(\mathrm{P}\left(X=1|\text{Foil}\right)\right)=\mathrm{f}\left(1-\mathrm{P}\left(U=1|\mathrm{Z}=-1\right)\right)=C_{\text{center}}+\frac{d^{\prime }}{2}\hfill \end{array}.$$ (8)

These equations are combined into:

$$\mathrm{f}\left(\mathrm{P}\left(X=1|Z\right)\right)=-Z{C}_{\text{center}}+\frac{d^{\prime }}{2}.$$ (9)

Second, to account for item differences in easiness and person differences in ability, the equation was modified as follows:

$$\mathrm{f}\left(\mathrm{P}\left(X_{ij}=1\right)|Z\right)={\mathrm{\tau }}_j-Z_j{C}_{\text{center},i}+\frac{d_i^{\prime }}{2},$$ (10)

where τ_j represents the easiness of item j, Z_j is equal to 1 if item j is a target and −1 if item j is a foil, C_center,i is the criterion parameter or tendency for responding of examinee i, and d_i′ is the ability of examinee i for discriminating between foils and targets. Using notations common to IRT, Equation 10 can be re-expressed as a compensatory multidimensional 2P IRT model:

$$\mathrm{f}\left(\mathrm{P}\left(X_{\text{ij}}=1|{\mathrm{\tau }}_{\mathrm{j}},{\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}},{\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}},{\mathrm{\theta }}_{C_{\text{center}},\mathrm{i}},{\mathrm{\theta }}_{{\mathrm{d}}^{\prime },\mathrm{i}}\right)\right)={\mathrm{\tau }}_{\mathrm{j}}+{\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}}{\mathrm{\theta }}_{C_{\text{center}},\mathrm{i}}+{\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}}{\mathrm{\theta }}_{{\mathrm{d}}^{\prime },\mathrm{i}},$$ (11)

where τ_j is the easiness of item j, θ_Ccenter,i and θ_d′,i are the abilities of examinee i corresponding to their bias toward responding positively and capacity for discriminating between targets and foils, respectively; and α_Ccenter,j and α_d′,j are the discrimination parameters of item j corresponding to these two abilities. In contrast to a 2P IRT model, where all of these parameters would be estimated from the data, the two discrimination parameters in the SD-IRT model are fixed to values based from derivations of the SDT model:

$$\begin{gathered} {\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}}=\{\begin{array}{ll}+1.0\hfill & \text{If}\text{item}j\text{is}\mathrm{a}\text{Foil}\hfill \\ -1.0\hfill & \text{If}\text{item}j\text{is}\mathrm{a}\text{Target}\hfill \end{array} \\ {\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}}=+\mathrm{0.5}. \end{gathered}$$ (12)

Note that α_Ccenter,j is determined by –Z and α_d′,j is set to 0.5 to account for the division by 2 in Equation 10. In applied research, this difference is important because it forms a known basis for interpreting parameters in line with the experimental cognitive and clinical literatures using SDT. Moreover, fixing these parameters solves the rotational indeterminacy problem for the compensatory multidimensional 2P IRT model. That is, the SD-IRT model forces a specific rotation of the latent multidimensional space by fixing, rather than freely estimating, the α values. Alternative expressions for Equation 11 are reported in the appendix.

Applications

Analyses were conducted within the context of an ongoing study of neurocognitive outcomes within a large sample of US Infantry Marines to be deployed overseas to Afghanistan. We explored potential applications of the SD-IRT approach by determining whether the models could adequately fit recognition memory item data collected across measures of multiple modalities. Specifically, our analyses focused on the Penn Face Memory Test (PFMT), the Penn Word Memory Test (PWMT), and the Visual Object Learning Test (VOLT): recognition memory measures of faces, words, and objects, respectively, from the Penn Computerized Neurocognitive Battery (CNB) (Gur et al., 2001, 2010). The Penn CNB is a popular research measure that has been used in large-scale and longitudinal studies of several clinical populations including individuals suffering from psychosis, suicidality, and posttraumatic stress (e.g., Irani et al., 2012; Moore, Reise, Gur, Hakonarson, & Gur, 2015), as well as in healthy and usually high-performing populations such as NASA astronauts (Basner et al., 2015).

The PFMT, PWMT, and VOLT are scored and interpreted with respect to the same assumed measurement framework: the equal variance SDT model. We sought to validate the meaning and interpretability of these scores (i.e., their construct representation) by fitting the SD-IRT model to item data. We compared two models: (1) A SD-IRT model with item intercepts constrained to be equal and item discrimination parameters fixed according to Equation 12; and (2) A SD-IRT model with unconstrained item intercepts and item discrimination parameters fixed according to Equation 12. The τ constrained model produces estimates of θ_d′ and θ_Ccenter that are consistent with d′ and C_center estimates based on closed-form solutions. However, this model does not allow variation in item difficulty, and thus is expected to poorly fit the item data. The τ unconstrained model, in contrast, allows item effects, and thus is expected to fit the item data much better.

Additionally, we aimed to demonstrate the practical utility of the SD-IRT model for use in neuropsychological research and practice. We focus on two specific concerns highlighted by the Standards for Educational and Psychological Testing (AERA, APA, & NCME, 2014). The first concerns the reporting of standard error of measurement (SEM) for scores. Although methods for estimating SEM vary, the most commonly referenced expression in clinical assessment derives SEM from reliability. As such, SEM is often reported as a single value for the sample of scores considered in an analysis. However, due to the fact that most psychological measures employ categorical response options (e.g., correct vs. incorrect), measurement error often varies systematically. Standard 2.14 notes that, “When possible and appropriate, conditional standard errors of measurement should be reported at several score levels unless there is evidence that the standard error is constant across score levels” (Standard 2.14; AERA, APA, & NCME, 2014).

Concerns related to conditional error are particularly relevant to the Penn CNB. Unlike standardized measures, the Penn CNB is commonly adapted for the specific populations under investigation in order to prevent floor and ceiling effects (i.e., loss of test score variance in the extremes of the performance distribution). Precisely characterizing patterns of measurement error in relation to the latent constructs of the SD-IRT model (i.e., θ_d′ and θ_Ccenter) could thus serve as a guide to future studies. The SD-IRT model provides a method for determining whether neuropsychological tests produce conditional errors for the latent constructs assessed. Specifically, the standard error of estimate for the jth item, SE_θ, can be expressed as:

$${\text{SE}}_{\mathrm{\theta }}=\frac{1}{{\left(\text{PQ}\left({\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}}^2+{\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}}^2\right)\right)}^{1/2}},$$ (13)

where P is the probability of responding correctly and Q is the probability of responding incorrectly³. Equation 13 is a general expression that applies to most multidimensional IRT models (see Reckase, 2009). Notably, the probability of responding to an item correctly (P) and incorrectly (Q), as well as the item discrimination parameters, all appear in the denominator. In the SD-IRT model, the discrimination parameters are fixed, and thus only person ability (θ_d′ and θ_Ccenter) and item difficulty or easiness (τ_j) will differentially impact error (i.e., via their impact on P and Q). More specifically, to the extent that that ability and difficulty are closely matched, and thus P and Q are close to 0.5, SE_θ will become smaller; conversely, to the extent that ability and difficulty are mismatched, and thus P and Q are close to 0.0 or 1.0, SE_θ will become larger.

A second concern highlighted in the Standards for Educational and Psychological Testing relates to fairness, and specifically measurement bias, in testing. The Standards (Chapter 3) stress that it is important to identify and account for measurement bias when it exists. A method that has grown in popularity involves using IRT to assess items for differential item functioning (DIF). DIF exists when examinees from separate populations have different probabilities of responding to an item correctly, even when they have the same value on the underlying ability measured (Millsap, 2011). That is, DIF does not simply indicate a group difference in ability, but rather an unfair or unintended performance advantage for one or more groups.

A common use of DIF methodology, including in neuropsychology, is to determine whether item properties differ by groups defined by high versus low education (e.g., Kim et al., 2017; Teresi et al., 2009). The implicit, if not explicit, assumption of this work is that a certain, qualitative level of education (e.g., college education in the United States) is more likely attained by individuals with higher levels of acculturation, social privilege, and wealth (Jez, 2014), and that these factors might artificially inflate scores. That is, the concern is not that education is correlated with ability, but rather that education serves as a proxy for variables that affect test scores, but are irrelevant to ability. On the PWMT, for example, it is possible that certain words are more familiar to college educated examinees, and that this familiarity conveys an unfair advantage in recognition memory. In the context of the SD-IRT model, the relevant question is whether examinees with different levels of education or race, who nonetheless have the same θ_d′ and θ_Ccenter values, have different response probabilities. This can be detected through DIF analyses that assess whether τ parameters vary by group.

Methods

Participants

The Marine Resiliency Study II (MRS-II; Oct 2011-Oct 2013) Neurocognition project is a prospective, longitudinal investigation of neurocognitive performance in Infantry Marines and Navy Personnel deployed to Afghanistan. Data for the current study come from participants’ initial pre-deployment baseline assessments. The study was approved by the institutional review boards of the VA San Diego Research Service and the Naval Health Research Center. Written informed consent was obtained from all participants. Data from a total of 1,441 individuals were included in the analyses. Demographic characteristics of the sample are reported in Table 1. Females were not eligible for Infantry Battalions at the time of testing thus the subject pool is all male.

Table 1.

Demographic Characteristics

	Face	Word	Object
Sample Size	1,338	1,331	1,249
Age M (SD)	22.18 (2.91)	22.20 (2.91)	22.19 (2.89)
Education M (SD)	12.40 (0.95)	12.40 (0.96)	12.39 (0.97)
Ethnicity
Not Hispanic or Latino	74%	75%	74%
Cuban	< 1%	< 1%	< 1%
Mexican	15%	15%	15%
Puerto Rican	2%	2%	2%
South or Central American	3%	3%	3%
Other Spanish culture/origin	5%	4%	4%
Race
Black or African American	4%	4%	4%
American Indian or Alaskan	2%	2%	2%
Asian	2%	2%	2%
Hawaiian or Pacific Islander	1%	1%	1%
White	91%	91%	91%

Note. Face = Penn Face Memory Test; Word = Penn Word Memory Test; Object = Visual Object Learning Test. All participants were male.

Measures

As previously noted, cognitive tests were administered as part of the Penn CNB, a 45-min neurocognitive battery designed for efficient computerized assessment with minimal proctoring (Gur et al., 2001, 2010; Moore, Reise, Gur, Hakonarson, & Gur, 2015). The PFMT measures episodic memory for faces. The test begins by showing examinees 20 faces that they will be asked to identify later. Faces are shown in succession for an encoding period of 5 seconds each. After this initial learning period, examinees are immediately shown a series of 40 faces—20 targets and 20 foils—and are asked to decide whether they have seen each face before. Penn Face Memory Test foil faces are matched to targets for age, ethnicity, and gender. The PWMT measures episodic memory for words. The test is identical to the Penn Word Memory Test (above), except that the participant is asked to memorize words instead of faces. Penn Word Memory Test foil words are matched to targets for length, frequency, imageability, and concreteness. The VOLT measures episodic memory for objects. The test is identical to the Penn Face Memory Test and Penn Word Memory Test (above), except that the participant is asked to memorize 10 Euclidean shapes and tested for recognition using 10 targets and 10 foils.

Analyses

We first examined scree plots (eigenvalues for eigenvectors) based on principle axis factoring of the polychoric item correlation matrices for each test. Although the SD-IRT modeling approach suggests that a 2-factor model ought to fit the recognition memory item data, we wanted to determine whether an exploratory technique would support this assumption. A simple and common interpretative approach is to infer dimensionality based on the number of factors that fall above the “elbow” of eigenvalues plotted from highest to lowest (Cattell, 1966). Importantly, we used this as a descriptive tool meant to support the a priori theory of two factors within the SDT model, and not as a guide to determine the final number of factors to retain.

Modeling analyses were conducted using the mirt package for R (Chalmers, 2011). Models were fitted to data using an expectation maximization (EM) algorithm.⁴ Ability estimates were taken as maximum a posteriori (MAP) values. Data included accuracy scores from each test. Only complete and valid data were analyzed (Face = 97%; Word = 97%; Object = 91%). Models were compared using Akaike information criterion (AIC) and Bayesian information criterion (BIC) values. AIC and BIC penalize overparameterized models and become smaller with better fit (see de Ayala, 2009). Absolute fit was determined by examining root mean square error of approximation (RMSEA; values range from 0 [good fit] to 1 [poor fit] with values < .06 commonly regarded as acceptable). Item fit (dependence) was evaluated by residual correlations between pairs of items (i.e., known in IRT as Q3; Yen, 1993).

To explore the impact of SE_θ on substantive analyses, we regressed MAP estimates of θ_d′ onto self-report of past head injury with loss of consciousness (LOC). Specifically, head injury with LOC was measured as an ordinal variable with 5 levels: no LOC (n = 1,016), LOC < 1min (n = 226), LOC 1–15 min (n = 143), LOC 16–30 min (n = 14), and LOC > 30 min (n = 45). LOC was based on the most severe head injury participants reported during their pre-deployment assessment (i.e., encompassing injuries associated with prior deployments, prior non-deployment related injuries, and injuries acquired prior to joining the military). We regressed estimates of θ_d′ from each test (PFMT, PWMT, and VOLT) onto head injury with LOC, plotted distributions of residuals, and examined associations with SE_θ.

Finally, we examined the tests for DIF based on education. Participants were split into two groups based on whether or then had completed any years of college (n = 206; focal group) or not (n = 872; reference group). Methods for evaluating DIF assume that the metrics of item parameters estimated in the reference and focal groups have been linked. We used the all-others-as-anchors (AOAA) approach, which has been shown to have high statistical power and well-controlled Type I error (Wang & Woods, 2017). In the approach, a series of model comparisons are first used to identify anchor items (i.e., by rank ordering likelihood-ratio test statistics [χ²_LR] based on models that free vs. fix τ across groups, and then choosing items that produced the lowest 20% of values). Next, fitting models that fix anchors to be equal between groups, but freely estimate ability means in the focal group, likelihood-ratio tests were used to determine whether individual items could be fixed across groups without significantly deteriorating model fit. The false discover rate was controlled using the Benjamini-Hochberg procedure.

Results

Dimensionality

Scree plots for all tests based on principal axis factoring of the polychoric correlation matrices are shown in Figure 2. Both the Penn Face Memory Test and the Penn Word Memory Test appear to have two meaningful dimensions. The Visual Object Learning Test, in contrast, appears to have only one.

Figure 2.

Principle factor analysis scree plot for all recognition memory tests.

Parameter estimates and model fit

Model fit statistics are reported in Table 2. For all tests, the unconstrained model produced better AIC and BIC statistics when compared to the constrained model. Although the unconstrained model consistently produced acceptable RMSEA values, the constrained model consistently produced poor values. Supplemental Figure 1 plots ability estimates produced by closed-form SDT expressions (d′ and C_center) versus constrained model MAP estimates (θ_d′ and θ_Ccenter). The estimates are very similar. Differences are due to the estimators’ unique methods for handling perfect response strings.

Table 2.

Model Fit Statistics

Test	Model	ln L	AIC	BIC	RMSEA
Face	Constrained	−25,050.90	50,111.80	50,137.80	0.14
Face	Unconstrained	−22,046.16	44,178.31	44,401.87	0.03
Word	Constrained	−21,815.30	43,640.60	43,666.57	0.13
Word	Unconstrained	−19,132.78	38,351.55	38,574.88	0.03
Object	Constrained	−13,332.64	26,675.28	26,700.93	0.12
Object	Unconstrained	−11,749.63	23,545.25	23,663.25	0.03

Note. Face = Penn Face Memory Test; Word = Penn Word Memory Test; Object = Visual Object Learning Test. Constrained – an signal detection-item response theory model with item intercepts constrained to be equal and item discrimination parameters fixed according to Equation 10; Unconstrained – an signal detection-item response theory model with unconstrained item intercepts and item discrimination parameters fixed according to Equation 10. ln L = log-likelihood; AIC = Akaike information criterion; BIC = Bayesian information criterion; RMSEA = root mean square error of approximation.

For the Penn Face Memory Test, 68% of the residual correlations were less than .05, 95% were less than .10, and 99% were less than .15. For the Penn Word Memory Test, 72% of the residual correlations were less than .05, 95% were less than .10, and 99% were less than .15. For the Visual Object Learning Test, 49% of the residual correlations were less than .05, 88% were less than .10, and 99% were less than .15. Detailed item fit values for the unconstrained model are shown in Supplemental Figure 2.

Standard error of estimate

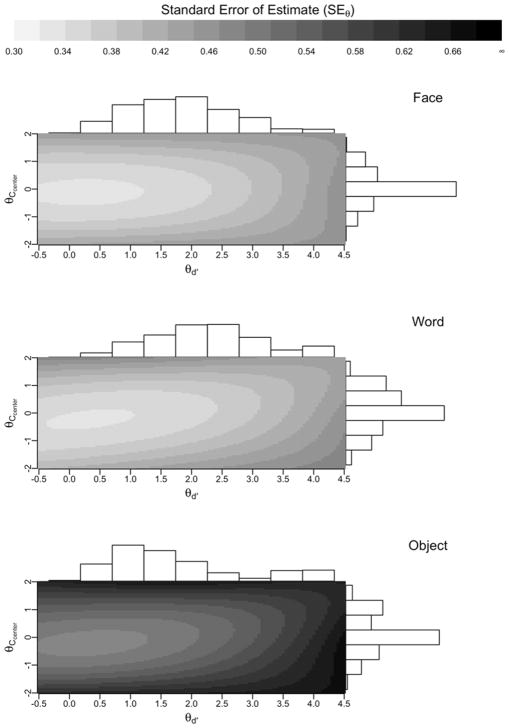
SE_θ functions for the unconstrained models fitted to each test are shown in Figure 3. The figure also shows the distribution of each construct within the sample. All tests are expected to provide the best precision (lowest SE_θ) near the 0 points of both θ_d′ and θ_Ccenter. Conversely, the tests are expected to provide worse precision (highest SE_θ) at high values of θ_d′. Thus, the tests are expected to measure examinees with low memory discrimination ability better than examinees with high memory discrimination ability. The Penn Face Memory Test and the Penn Word Memory Test have very similar SE_θ functions; however, the distribution of θ_d′ for the Penn Word Memory Test has a higher mean value than the distribution of θ_d′ for the Penn Face Memory Test (which is consistent with mean item accuracies of 85% and 82% respectively). The Visual Object Learning Test has the worst SE_θ among the tests, which is explained by the Visual Object Learning Test having fewer items.

Figure 3.

Standard error of estimate functions for the signal detection-item response theory models. Face = Penn Face Memory Test. Word = Penn Word Memory Test. Object = Visual Object Learning Test.

Regression analyses

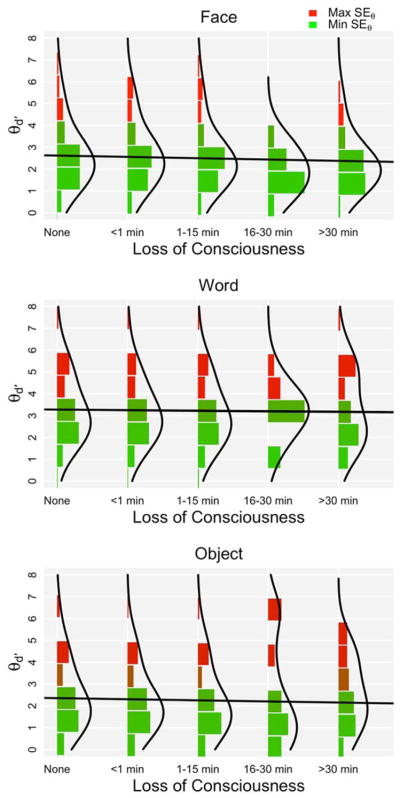
Figure 4 plots the regression of θ_d′ onto head injury with LOC for each test. Although the associations were consistently negative, suggesting that greater duration of LOC was associated with poorer memory discrimination, the effects were weak and non-significant (PFMT b = −0.06, SE = 0.04, p = 0.13; PWMT b = −0.02, SE = 0.04, p = 0.56; VOLT b = −0.05, SE = 0.05, p = 0.27). The distributions of residuals are positively skewed towards regions of higher ability and greater measurement error, suggesting that associations between memory discrimination and head injury were artificially weakened for participants with high versus low ability.

Figure 4.

Regression of estimates of memory discrimination (θ_d′) onto self-report of head injury with loss of consciousness with distributions of residuals. SE_θ = standard error of estimate. Face = Penn Face Memory Test. Word = Penn Word Memory Test. Object = Visual Object Learning Test.

Differential item functioning (DIF)

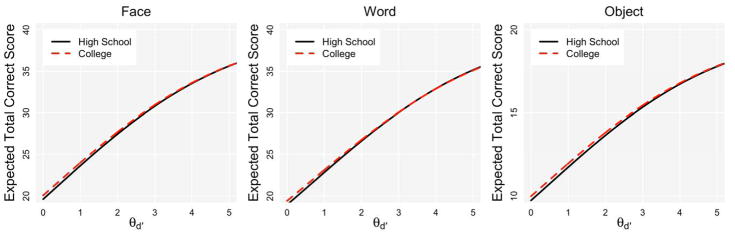
After establishing anchor items for the CPF (7, 9, 11, 12, 13, 26, 34, and 39), CPW (4, 6, 10, 13, 16, 27, 28, and 38), and VOLT (6, 7, 11, and 19), 1 item on the CPF, 2 items on the CPW, and 0 items on the VOLT were significant for DIF. Moreover, none of the CPF or CPW DIF p values survived an adjustment for the false discover rate. The results provide no strong evidence of biased measurement by education. To further examine this point, Figure 5 plots test response functions for the CPF, CPW, and VOLT, with separate functions for the two education groups. The test response functions plot expected total scores at varying levels of θ_d′ (holding θ_Ccenter to a constant value of 0 [unbiased]). The figures are based on models where only parameters for anchor items were forced to be equal between groups. Thus, any systematic differences in the estimated τs between groups would lead to discordant functions. As can be seen, the expected total correct scores are nearly identical for the two education groups across a wide range of θ_d′, thus further indicating that there is little evidence of DIF on the tests.

Figure 5.

Test response functions allowing item parameters to vary by groups defined by college versus high school education. Face = Penn Face Memory Test. Word = Penn Word Memory Test. Object = Visual Object Learning Test.

Discussion

In this paper, we provided formal expressions for a combined signal detection-item response theory (SD-IRT) model, and then demonstrated its application to the scoring and evaluation of neuropsychological test data. SDT defines a specific latent measurement structure; namely, that test performance is determined by memory discrimination and response bias. In an empirical example, we supported potential applications of the SD-IRT model by showing that restrictions imposed by this model can be appropriate for recognition memory item data across multiple modalities. We then demonstrated two applications of the modeling approach in terms of quantifying and comparing measurement error across tests scored according to the same cognitive model, and by assessing items for bias. Measurement error was systematically related to estimates of latent ability, which may have led to a missed opportunity to detect subtle consequences of brain injury. Analyses of differential item functioning, on the other hand, suggested little or no evidence of bias between groups defined by education.

Model fit to measures of face, word, and object recognition memory

Exploratory analyses (scree plots) suggested that the face and word memory tests had two meaningful dimensions along which individual differences could be characterized—which is consistent with past findings (Thomas et al., 2013) and supports the SDT interpretation of response processes. The object learning data, in contrast, appeared to have just one meaningful dimension. This may not preclude SDT-like scoring of the Visual Object Learning Test, but it does suggest that individual differences in memory discrimination (θ_d′) and/or response bias (θ_Ccenter) are less distinct than for the Penn Face Memory Test and Penn Word Memory Test.

The SD-IRT model with item intercepts constrained to be equal—which is simply a re-expression of an equal variance SDT model—poorly fitted the item data. However, freeing the item intercepts—that is, allowing items to vary in difficulty—substantially improved fit. Acceptable fit of the model with unconstrained item intercepts was not unequivocal. Residual correlation statistics suggested that a minority of items were not fitted well by the model. Given the large sample size, these residuals are likely not chance fluctuations in the data. They may, however, be few enough to be safely ignored in the process of scoring test data without seriously biasing results. Alternatively, the results could suggest limitations with the SDT model that might be accounted for by a more elaborate theory of recognition memory.

The equal variance SDT model is just one representation of cognitive processes involved in testing. The mathematical modeling literature in cognitive psychology is sophisticated and mature, but also unsettled (e.g., Pazzaglia, Dube, & Rotello, 2013; Wixted, 2007). For many areas of cognition, there is no consensus model. Batchelder and Alexander (2013) argue that it is important to distinguish between scientific goals and measurement goals when selecting a modeling approach. If the investigator’s goal is to develop or advance scientific theory about the measured construct itself, particularly as it relates to experimental paradigms, the approach discussed in this paper may not be optimal. However, if the investigator’s goal is to measure cognitive abilities in a way that approximates correct scientific theory, and yet is also flexible, SDT models are an attractive option.

Model applications

Conditional measurement error

The Standards for Education and Psychological Testing encourage test developers to report conditional standard errors of measurement when possible and appropriate (Standard 2.14; AERA, APA, & NCME, 2014). Neuropsychologists have reported conditional standard errors using IRT methodology for some measures, but widespread adoption of the approach is lacking. The SD-IRT model provides a mechanism for determining whether neuropsychological tests produce conditional standard errors. In the current study, SE_θ functions (Figure 3) suggested that all tests evaluated are most capable of discerning individual differences in θ_d′ (or d′) for examinees with relatively poorer memory discrimination.

A well-known axiom of psychometric theory demonstrates that associations between variables are attenuated to the extent that measures of those variables are unreliable (Haynes et al., 2011; Spearman, 1904). For example, measurement error attenuates group differences in test performance between samples of cognitively impaired versus healthy examinees (Thomas et al., 2017). Moreover, the risks of interpreting differential deficits based on measures of distinct cognitive abilities with unequal reliabilities have been well documented (e.g., Chapman & Chapman, 1973).

In the current study, we demonstrated that higher measurement error was systematically related to residuals from analyses that regressed θ_d′ onto self-report of head injury with LOC. Specifically, associations between head injury and cognitive performance appeared to be attenuated as a function of ability, artificially suggesting stronger effects in low versus high ability participants. Not only does this imply that the overall relationship between history of head injury and memory discrimination was diminished, it raises concerns about interpreting relative change in performance. That is, to the extent that participants in the Marine Resiliency Study were to experience future deployment-related head injuries resulting in cognitive deficits, changes in cognition could appear somewhat smaller in individuals with higher baseline levels of cognition (a similar argument has been made in the context of assessing cognitive declines associated with dementia; cf. Mungas & Reed, 2000). Although the SD-IRT model cannot retroactively fix such problems, it can warn neuropsychologists against a possible misinterpretation of results. We suspect these problems are common to measures of recognition memory, but have not been fully explored due to a lack of methods for quantifying conditional measurement error.

Conditional measurement error can be identified by classic approaches that are not dependent on IRT methodology, and neuropsychological texts (e.g., Mitrushina, Boone, Razani, & D’Elia, 2005) commonly warn about ceiling and floor effects. However, IRT is generally considered advantageous in this respect, in that the approach provides a more fine-grained analysis of error, including the ability to separately quantify the impact of error across multiple latent dimensions. For example, while common descriptions of floor and ceiling effects tend to suggest that precision becomes poor only in the extremes of performance, Figure 3 makes clear that conditional error is fluid, varying throughout the full range of ability. Figure 3 also demonstrates how conditional error varies as a function of both response bias and ability. Finally, IRT, and thus the SD-IRT model in particular, can be used to develop computerized adaptive tests (e.g., Gershon, Cook, Mungas, Manly, Slotkin, Beaumont, & Weintraub, 2014), where information about items, combined with IRT estimates of SE_θ, θ_d′, and θ_Ccenter, can be used to tailor item administration in order to prevent conditional error.

Measurement Bias

Bias exists when examinees from separate populations have different probabilities of responding to an item correctly, even when they have equal ability. Here, we assessed whether item easiness parameters (τ) systematically varied, and thus advantaged one group or the other. Controlling for the false discover rate, we found no evidence that τ parameters varied by groups defined based on high versus low education. Thus, there is no evidence of bias on the Penn Face Memory Test, Penn Word Memory Test, or Visual Object Learning Test. We did not examine other potential sources of bias, such as bias by race or gender, due to limited sample size and demographic characteristics of the sample. Nonetheless, the methodology presented here is easily replicated with standard IRT software. It is possible that the impact of level of education on DIF might be more nuanced than a simple no college versus some college distinction. As an alternative, methods that do not assume a priori known classes of individuals might be more effective in identifying biased items (e.g., Cohen & Bolt, 2005).

Interpretation of latent constructs

SD-IRT models can lessen ambiguity associated with interpreting latent constructs measured by certain cognitive tests. Typically, constructs are interpreted using exploratory methods along with a program of research comparing constructs to observed variables as well as to other constructs in order to form a nomological network (Cronbach & Meehl, 1955). Although these methods are effective, they primarily concern the significance of constructs rather than their meaning. For this reason, Embretson (Whitely 1983; Embretson, 1998) introduced the concept of construct representation, which concerns defining the meaning of constructs through the identification of latent psychological abilities, processes, and strategies that underlie item responses. The SD-IRT model, through the process of fixing item discrimination parameters according to SDT, helps define the construct representation, and thus meaning of latent constructs measured by some cognitive tests.

A contribution of the SD-IRT model is in providing a solution to the problem of rotational indeterminacy for some multidimensional item response models. The application of multidimensional measurement models at the item level is more challenging than the application of these models at the test level. This is because whereas tests are developed with the goal to assess distinct domains of cognition (e.g., attention vs. memory), test items are often thought to be homogenous, and may differ only with respect to their relative weighting, or discrimination, of cognitive subdomains. In unrestricted models, there are infinite combinations of equally likely ability and discrimination parameters given different rotations of the multidimensional ability space. Thus, final parameter estimates are often based on some type of rotation method that attempts to find simple structure: a pattern of item discrimination parameters where items are indicators of just one dimension. The SD-IRT model defines aspects of the latent ability space a priori based on SDT.

Future directions

Further evaluation of the SD-IRT model, including applications to tests from other domains of assessment, is needed before widespread use of the approach can be recommended. This includes not just measures of recognition memory (e.g., Delis et al., 2000), but also measures of other cognitive domains where the SDT scoring framework has been applied such as N-back tests of working memory (Kane et al., 2007), continuous performance tests of sustained attention and vigilance (Conners, 1994), and tests of emotion recognition (Gur et al., 2010) among others.

This paper has demonstrated two of the many applications of the SD-IRT model. As noted, the approach combines SDT scoring with IRT methods for evaluating tests and estimating scores. Thus, the full array of IRT applications (see Thomas, 2017) can be considered in future work. We envision several extensions of the approach. First, the SD-IRT model could be used to develop computerized adaptive tests (CATs). Analyses revealed that the PFMT, PWMT, and SVOLT all provide optimal precision (lowest SE_θ) for estimates of ability for individuals with average to below average memory functioning. Thus, the tests appear to be very well designed for their purpose of quantifying neurocognitive impairments. However, as is typical, the tests were less capable of discerning individual differences in the above average range of memory functioning, which would require an extended upper range of difficulty. It is challenging to design fixed item tests that include a wide range of item difficulty and yet are also tolerable and efficient. Because of this, a growing chorus of researchers argues that neuropsychological measures should take advantage of adaptive testing methodology, where item difficulty is tailored in real-time to the ongoing performance of individual examinees (Linden & Glas, 2010). A primary challenge in the development of CATs is in calibrating item parameters. Item parameters typically need to be pre-calibrated in large, diverse samples of many hundreds or thousands of participants, which can be expensive and impractical in many research settings. The SD-IRT model helps lessen the burden of calibration by defining item discrimination parameters a priori. Thus, the SD-IRT model could simplify the development of CATs for some neuropsychological measures.

Second, because the multidimensional IRT model described in this work is also a reparametrized confirmatory factor model, other latent variable methods such as structural equation modeling, in general, and latent growth curve models, mixed effects models, and mixture models, in particular, can be added on to the SD-IRT framework. This might be particularly valuable in longitudinal studies and randomized controlled trials. Mixture IRT models, where examinees are assumed to belong to one of several latent subpopulations, are increasingly popular in psychometric applications (de Ayala & Santiago, 2017). In samples where examinees might belong to subpopulations based on unknown clinical variables—such as individuals who are or are not at risk for developing dementia—mixture IRT models might prove to have diagnostic or predictive utility by estimating latent class membership. The SD-IRT model presented in this work effectively assumed one known class of examinees. However, extensions of the approach based on mixture IRT methodology are readily implemented.

Finally, there is also a growing trend that involves combining cognitive and psychometric models for developing, evaluating, and scoring neuropsychological tests (e.g., Batchelder, 2010; Brown, Patt, Sawyer, & Thomas, 2016; Brown, Thomas, & Patt, 2017; Thomas et al., 2015; van der Mass, Molenaar, Maris, Kievit, & Borsboom, 2011). Combining measurement models from cognitive and psychometric theories allows researchers to assess precision and other aspects of measurement using modern psychometric approaches while interpreting the meaning of latent constructs within the context of strong, experimentally validated psychological theories. This paper contributes one additional model to this effort. Additional studies are needed that demonstrate the practical advantages of this methodology when compared to more typical psychometric approaches.

Summary

In this paper, we demonstrated that certain IRT models can be formulated as SDT models, thus linking two complementary but distinct methodologies. We successfully fitted the SD-IRT model to measures of recognition memory across three distinct modalities (faces, words, and objects). We then demonstrated two applications of the approach that directly tied to professional standards for psychological assessment. Further evaluations of the SD-IRT model are needed, but our preliminary work suggests that the approach could prove valuable in neuropsychological research and practice.

Appendix

The logistic-ogive signal detection-item response theory model can also be expressed as

$$\mathrm{P}\left(X_{\text{ij}}=1|{\mathrm{\tau }}_{\mathrm{j}},{\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}},{\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}},{\mathrm{\theta }}_{C_{\text{center}},\mathrm{i}},{\mathrm{\theta }}_{{\mathrm{d}}^{\prime },\mathrm{i}}\right)=\frac{1}{1+exp\left(-\left({\mathrm{\tau }}_{\mathrm{j}}+{\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}}{\mathrm{\theta }}_{C_{\text{center}},\mathrm{i}}+{\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}}{\mathrm{\theta }}_{{\mathrm{d}}^{\prime },\mathrm{i}}\right)\right)},$$ (A1)

and the normal-ogive signal detection-item response theory model can also be expressed as

$$\mathrm{P}\left(X_{\text{ij}}=1|{\mathrm{\tau }}_{\mathrm{j}},{\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}},{\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}},{\mathrm{\theta }}_{C_{\text{center}},\mathrm{i}},{\mathrm{\theta }}_{{\mathrm{d}}^{\prime },\mathrm{i}}\right)=\mathrm{\Phi }\left({\mathrm{\tau }}_{\mathrm{j}}+{\mathrm{\alpha }}_{C_{\text{center}},\mathrm{j}}{\mathrm{\theta }}_{C_{\text{center}},\mathrm{i}}+{\mathrm{\alpha }}_{{\mathrm{d}}^{\prime },\mathrm{j}}{\mathrm{\theta }}_{{\mathrm{d}}^{\prime },\mathrm{i}}\right),$$ (A2)

where Φ is the cumulative distribution function for the normal distribution.