Contribution of left ventricular residual stress by myocytes and collagen: existence of inter-constituent mechanical interaction

Abstract

We quantify the contribution of myocytes, collagen fibers and their interactions to the residual stress field found in the left ventricle (LV) using both experimental and theoretical methods. Ring tissue samples extracted from normal rat, male and female, LV were treated with collagenase and decellularization to isolate myocytes and collagen fibers, respectively. Opening angle tests were then performed on these samples as well as intact tissue samples containing both constituents that served as control. Our results show that the collagen fibers are the main contributor to the residual stress fields found in the LV. Specifically, opening angle measured in collagen-only samples (106.45°±23.02°) and myocytes-only samples (21.00°±4.37°) was significantly higher and lower than that of the control (57.88°±12.29°), respectively. A constrained mixture (CM) modeling framework was then used to infer these experimental results. We show that the framework cannot reproduce the opening angle found in the intact tissue with measurements made on the collagen-only and myocytes-only samples. Given that the CM framework assumes that each constituent contributes to the overall mechanics simply by their mere presence, this result suggests the existence of some myocyte–collagen mechanical interaction that cannot be ignored in the LV. We then propose an extended CM formulation that takes into account of the inter-constituent mechanical interaction in which constituents are deformed additionally when they are physically combined into a mixture. We show that the intact tissue opening angle can be recovered in this framework.

1 Introduction

Among the many constituents found in the myocardium, myocytes and collagen fibers are arguably the two most prominent ones for the following reasons. First, myocytes account for the vast majority of the myocardial mass. Second, collagen fibers are significantly stiffer (when fully stretched) and form the extracellular matrix (ECM) scaffold that provides strength for the myocardium. Collectively, these two constituents contribute to the myocardium’s overall mechanical and functional behaviors found under physiological and pathophysiological conditions.

A key mechanical feature of the myocardium is the existence of residual (or internal) stresses in the intact left ventricle (LV). Its existence can be inferred using the classical “opening angle test” (Chuong and Chuong 1986), where radially cutting a ring sample excised from the LV will produce a sizable opening angle. While residual stress fields have been measured in the LV of rats (Omens and Fung 1990), canine (Costa et al. 1997) and embryonic chick (Taber et al. 1993), neither the relative contribution of myocytes and collagen fibers nor the sex effects on the resultant stress fields have been investigated. As such, there is currently a void in our understanding of how myocytes and collagen fibers individually affect the residual stress that plays an important role in LV mechanics (Genet et al. 2015; Nevo and Lanir 1994).

In relation to this, the constrained mixture (CM) theory remains a useful (and popular) way to account for the separate contribution of myocytes and collagen fibers to the LV’s mechanical behavior. Application of the CM theory can be found in a number of microstructural models of ventricular mechanics (Horowitz et al. 1988; Avazmohammadi et al. 2017). In these models, the myocardial tissue mechanical behavior is described based on the weighted sum of each constituent’s strain energy density function that characterizes the constituent’s mechanical behavior. That description implicitly assumes that each constituent contributes to the overall mechanics simply by their mere presence, without accounting explicitly for any physical or mechanical interactions between them. It is, however, very difficult to reconcile this assumption given that scanning electron microscopy images have revealed a tight physical connection between collagen fibers and myocytes in the myocardial tissue (Weber 1989).

While it is fairly obvious that the ECM interacts mechanically with myocytes given that they are microstructurally enmeshed together in the cardiac tissue (Macchiarelli et al. 2002), to the best of our knowledge, little has been done to characterize the mechanical interactions between these constituents at the tissue level. Related works are mostly confined to in vitro characterization of the cell–cell and cell–matrix adhesion occurring at the microscopic level (Bowers et al. 2010; McCain et al. 2012), which are difficult to extrapolate macroscopically to the tissue level. Most related studies also focus on the biochemical signaling arising from inter-constituent mechanical interaction. Our knowledge of the direct mechanical and physical interaction between collagen fibers and myocytes, and how this interaction contributes to the LV mechanics therefore remains rudimentary.

For these reasons, we seek here to experimentally isolate and quantify the contribution of these two key myocardial constituents to the residual stress fields found in the normal rat LV. To infer the existence of any direct mechanical interaction between the two constituents, we employed these measurements to inform a CM modeling framework that takes into account the contribution of myocytes and collagen fibers to the LV mechanical behavior simply by their presence. Specifically, we seek to test the hypothesis that this modeling framework can reproduce the measured opening angle found in the LV. The rationale is as follows: if the hypothesis is validated, it would imply that the myocyte– collagen mechanical interaction only has negligible effects (if any) on the myocardial tissue mechanics, while conversely, if the hypothesis is invalidated, it would imply that the resultant LV mechanical behavior cannot be described by the constituent’s mere presence. We show that our results imply the latter, suggesting the existence of myocyte–collagen mechanical interaction that cannot be ignored in describing LV mechanics. We then propose and show that this discrepancy can be resolved in an extended CM formulation with the introduction of a mapping that is associated with the constituent’s deformation arising from their interaction.

2 Method

2.1 Sample preparation

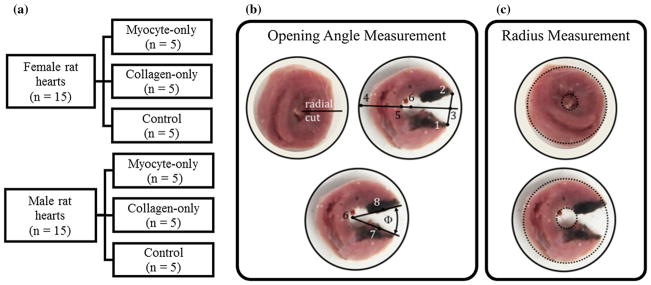
Healthy adult male (n = 15) and female (n = 15) Sprague Dawley rats (Charles River Breeding Laboratories, Portage, MI) were euthanized with pentobarbital (60–80 mg/kg i.p.), and their hearts were dissected. All animal protocols used in this study were approved by MSU Institutional Animal Care and Use Committee. Two lateral ring samples showing the LV and right ventricle (RV) were excised from each heart with an approximate thickness of 4.4 mm. Ring samples obtained from each sex were subdivided equally into three test groups, which were the (1) myocyte-only (n = 5), (2) collagen-only (n = 5) and (3) control (n = 5) groups (Fig. 1a).

Fig. 1.

a Distribution of tissue samples. Definitions of the b opening angle and c inner and outer radius of the ring tissue samples

Ring samples from the control group were soaked in a Krebs–Henseleit buffer solution containing 2,3-butanedione monoxime (BDM), a myosin inhibitor that inhibits cross-bridge formation (Hajjar et al. 1994) by interfering with Ca²⁺ – troponin interaction (Mulieri et al. 1989). On the other hand, ring samples in the myocyte-only group were first soaked in the same buffer + BDM for 15 min before being soaked for 96 h in a buffer solution (10 mg/l Sigma- Aldrich Chemicals) containing CaCl₂ and crude bacterial collagenase, a collagen-disrupting enzyme that breaks down the collagen fiber network. The chemical CaCl₂ was added to the solution because collagenase requires calcium to activate the enzymatic degradation (MacKenna et al. 1994). After the treatment (~ 96 h), the samples were moved back to a Krebs–Henseleit buffer solution containing BDM. Finally, ring samples in the collagen-only group were first soaked (for 15 min) in a heparinized saline solution before being transferred to and soaked for 96 h in a 10% sodium-dodecyl sulfate solution to remove the cells and cellular residua, leaving only the ECM scaffold. Thereafter, these samples were soaked in deionized water for 15 min and then in a 10% Triton X-100 solution for 30 min before testing (Ott et al. 2008). The efficacy of these treatments has been validated via analysis of histological images; see Sect. 2.3.

2.2 Opening angle experiment

Of the two ring samples acquired from each heart, after soaking in their corresponding solution (~ 96 h to remove the collagen fibers and myocytes) as described in Sect. 2.1, one was fixed for histological analysis (see Sect. 2.3), while an opening angle test was performed on the other. The opening angle test consists of making a radial cut through the LV lateral wall in the ring slices, which led to the samples opening up as they approach a near stress-free configuration. Pictures of the samples were taken immediately before and after the radial cut and at an interval of 3 min in the first 15 min after the cut. The interval was increased to 15 min for another 75 min before the test was terminated. The total test duration was 90 min and was based on a terminating criteria that the rate of change of the opening angle is less than 0.2°/min for all samples.

The opening angle was calculated from these pictures using ImageJ (Schneider et al. 2012) and a method described in Omens and Fung (1990) (Fig. 1b). First, a centerline (Line 3–4) extending through the RV was established using the middle of the opening line (Line 1–2). Then, this line was used, along with the inner radius measured from the pre-cut pictures to locate the LV center (Point 6). From this center point, two lines (Lines 6–7 and 6–8) connecting the center to either side of the cut were created. The opening angle was defined to be the angle between these two lines. On the other hand, inner and outer radii were determined by inscribing a circle on the inner and outer surface of the cut and uncut ring samples, respectively (Fig. 1c).

2.3 Histology and microstructural analysis

Histological analyses were conducted on the ring samples from each test group. Specifically, the samples were fixed in a 10% formalin solution in an unloaded state for an hour and then stored at room temperature in 30% ethanol before being embedded in paraffin and sectioned. Masson’s trichrome and Picrosirius red staining were then applied to quantify the amount of collagen (shown in blue in the Masson’s trichrome stain and red in the Picrosirius red stain) and myocytes (cytoplasm is shown in pink in the Masson’s trichrome stain and yellow in the Picrosirius red stain) (Bellini et al. 2014). We also applied and imaged H&E stains to verify the integrity of the cells in the control and myocytes-only samples. On the other hand, Picrosirius red-stained samples were imaged with polarized light to confirm that the collagen was intact in the control and collagen-only samples and was degraded in the myocytes-only samples. Area fractions of the myocytes and collagen fibers were quantified at four different regions that were located 90° from each other in each sample based on hue, saturation and lightness (HSL) thresholding with custom MATLAB routines (Bellini et al. 2014;Bersi et al. 2012). The constituent’s mass fraction (ϕ^c, ϕ^m) in each experimental group was taken to be the average of the computed area fractions.

Finally, we performed scanning electron microscopy (SEM) imaging on both the decellularized and collagenase-treated samples using a modified version of the protocol described in MacKenna et al. (1994). Briefly, samples were fixed at 4°C for 1–2 h in 4% glutaraldehyde buffered with 0.1 M sodium phosphate at pH 7.4. Following a brief rinse in the buffer, samples were dehydrated in an ethanol series (25, 50, 75, 95%) for 1 h at each gradation and with three 1 h changes in 100% ethanol. Then, samples were mounted on aluminum stubs using adhesive tabs (M.E. Taylor Engineering, Brookville, MD) and coated with 60 s of Iridium (roughly 5.5 nm thickness). Finally, samples were examined in a JEOL 6610LV (tungsten hairpin emitter) scanning electron microscope (JEOL Ltd., Tokyo, Japan).

2.4 Modeling

An extended version of the CM modeling framework with inter-constituent mechanical interactions was developed. We refer this as the CM with inter-constituent mechanical interaction (CMMI) modeling framework.

2.4.1 Kinematics

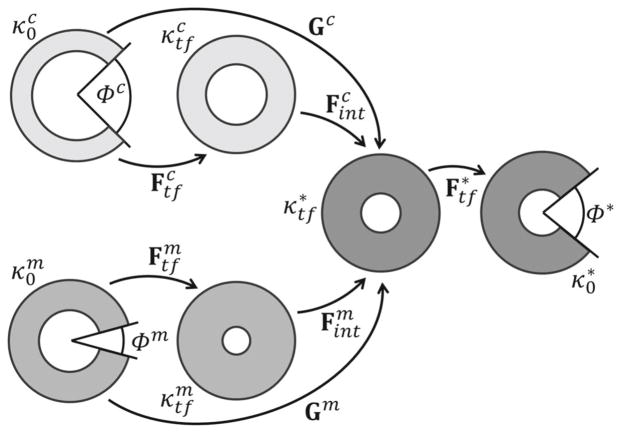
The kinematics associated with the CMMI modeling framework (Fig. 2) was defined by the following mappings.

Fig. 2.

Schematic representation of the configurations of interest in the CMMI modeling framework. From left to right, ${\kappa }_0^m$ and ${\kappa }_0^c$ represent the cut and stress-free configurations, and ${\kappa }_{tf}^m$ and ${\kappa }_{tf}^c$ represent the uncut and traction-free configurations for the myocytes (superscript m) and the collagen fibers (superscript c), respectively. The uncut, traction-free configuration and the cut, equilibrated configuration of the mixture are represented by ${\kappa }_{tf}^{\ast }$ and ${\kappa }_0^{\ast }$ respectively

1. ${\kappa }_0^{\xi }\to {\kappa }_{tf}^{\xi }$: Maps between the cut, nearly stress-free configuration ${\kappa }_0^{\xi }$ (with coordinates R^ξ, Θ^ξ, Z^ξ) to the uncut, traction-free configuration ${\kappa }_{tf}^{\xi }$ (with coordinates ρ^ξ, θ^ξ, z^ξ) of the myocyte-only (ξ= m) and collagen-only (ξ= c) tissue samples, respectively. The corresponding deformation gradient tensors are

   $$\left[{\mathbf{F}}_{\text{tf}}^{\xi }\right]=\text{diag}\left[\frac{\partial {\rho }^{\xi }}{\partial R^{\xi }};\frac{{\rho }^{\xi }}{R^{\xi }}\frac{2\pi }{2\pi -{\mathit{\Phi }}^{\xi }};{\mathit{\Lambda }}_z^{\xi }\right],\text{for}\xi =m,c.$$ (1)
2. ${\kappa }_{tf}^{\ast }\to {\kappa }_0^{\ast }$: A map between the mixture uncut, traction-free configuration ${\kappa }_{tf}^{\ast }$ (with coordinates ρ, θ, z) to its cut and equilibrated configuration ${\kappa }_0^{\ast }$ (with coordinates R, Θ, Z). The corresponding deformation gradient tensor is

   $$\left[{\mathbf{F}}_{\text{tf}}^{\ast }\right]=\text{diag}\left[\frac{\partial R}{\partial \rho };\frac{R}{\rho }\frac{2\pi -\mathit{\Phi }}{2\pi };{\mathit{\Lambda }}_z\right].$$ (2)
3. ${\kappa }_{tf}^{\xi }\to {\kappa }_{tf}^{\ast }$: Maps between constituent-specific, uncut configurations ${\kappa }_{tf}^m$ and ${\kappa }_{tf}^c$ to the uncut, traction-free configuration of the mixture ${\kappa }_{tf}^{\ast }$. These maps are associated with a mechanical interaction between the constituents when combining them into a mixture. For simplicity, the deformation gradient tensors corresponding to these map were defined to be isotropic and characterized by a prescribed interaction parameter α^ξ, i.e.,

   $$\left[{\mathbf{F}}_{int}^{\xi }\right]={\alpha }^{\xi }\text{diag}\left[\frac{\partial \rho }{\partial {\rho }^{\xi }};\frac{\rho }{{\rho }^{\xi }};{\lambda }_z\right],\text{for}\xi =m,c.$$ (3)

   Accordingly, the constituent ξ is stretched in the interaction when α^ξ> 1.00 or is compressed in the interaction when α^ξ< 1.00. On the other hand, when the myocytes and the collagen fiber network apply only negligible mechanical interaction on each other, the interactions parameters are α^m = α^c = 1.00. This specific case corresponds to the standard CM modeling framework. We also note that it is also possible to prescribe a non-homogeneous mechanical interaction where α^ξ depends on the radial coordinate ρ^ξ. To characterize such a non-homogeneous mechanical interaction will, however, require additional local measurements that are beyond the scope of our experimental setup.

By enforcing incompressibility in each kinematic mappings, the radial position of each configuration ( ${\kappa }_0^{\xi },{\kappa }_{tf}^{\xi }$ and ${\kappa }_{tf}^{\ast }$) is given as follows

$$R^{\xi }=\sqrt{{\left(R_i^{\xi }\right)}^2+\frac{2\pi }{2\pi -{\mathit{\Phi }}^{\xi }}{\mathit{\Lambda }}_z^{\xi }\left({\left({\rho }^{\xi }\right)}^2-{\left({\rho }_i^{\xi }\right)}^2\right)},\text{for}\xi =m,c;$$ (4a)

$${\rho }^{\xi }=\sqrt{{\left({\rho }_i^{\xi }\right)}^2+\frac{{\lambda }_z}{{\left({\alpha }^{\xi }\right)}^3}\left({\rho }^2-{\rho }_i^2\right)},\text{for}\xi =m,c;$$ (4b)

$$R=\sqrt{{(R_i)}^2+\frac{2\pi }{2\pi -\mathit{\Phi }}{\mathit{\Lambda }}_z\left({\rho }^2-{\rho }_i^2\right)}.$$ (4c)

In the above equation, $R_i^m,R_i^c$, R_i, ${\rho }_i^m,{\rho }_i^c$, and ρ_i are inner radius of the ${\kappa }_{tf}^m,{\kappa }_{tf}^c,{\kappa }_{tf}^{\ast },{\kappa }_0^m,{\kappa }_0^c$, and ${\kappa }_0^{\ast }$ configurations, respectively; Φ^m, Φ^c and Φ are the opening angles in the ${\kappa }_0^m,{\kappa }_0^c$ and ${\kappa }_0^{\ast }$ configurations, respectively.

2.4.2 Mechanical equilibrium conditions

Mechanical equilibrium was enforced in each of the non stress-free configurations to compute the mixture opening angle Φ with given interaction parameters α^ξ. To do so, Cauchy stress in each configuration was generalized as

$$\mathit{t}=-p\mathbf{I}+\sum _{\xi =m,c}2{\varphi }^{\xi }{\mathbf{F}}^{\xi }\frac{\partial W^{\xi }}{\partial {\mathit{C}}^{\xi }}{\left({\mathbf{F}}^{\xi }\right)}^T,$$ (5)

where p is the Lagrange multiplier (for enforcing incompressibility), ϕ^ξ is the mass fraction for the constituents (collagen: ξ= c; myocytes: ξ= m), F^ξ is the mapping taken with respect to the constituent’s stress-free configuration, C^ξ = (F^ξ)^T F^ξ is the corresponding right Cauchy–Green deformation tensor, and W^ξ is the prescribed strain energy density function of the constituents. Mechanical equilibrium was then enforced sequentially in each of the configurations detailed below to solve for the unknowns in the kinematic mappings.

1. ${\kappa }_{tf}^{\xi }$: Force equilibrium equations in the radial and axial direction are given by

   $$\underset{{\rho }_i^{\xi }}{\overset{{\rho }_o^{\xi }}{\int }}\frac{1}{{\rho }^{\xi }}\left(t_{\theta \theta }^{\xi }-t_{\theta \theta }^{\xi }\right)d{\rho }^{\xi }=0;$$ (6a)

   $$\underset{{\rho }_i^{\xi }}{\overset{{\rho }_o^{\xi }}{\int }}\left[2t_{zz}^{\xi }-\left(t_{\theta \theta }^{\xi }+t_{\rho \rho }^{\xi }\right)\right]{\rho }^{\xi }d{\rho }^{\xi }=0,$$ (6b)

   where ( $t_{\rho \rho }^{\xi },t_{\theta \theta }^{\xi },t_{zz}^{\xi }$) are, respectively, the radial, circumferential and longitudinal components of the Cauchy stress tensor associated with the collagen-only configuration t^c = t(ϕ^m = 0, ϕ^c = 1) and myocyte-only configuration t^m = t(ϕ^m = 1, ϕ^c = 0). After substituting F^ξ for ${\mathbf{F}}_{\text{tf}}^{\xi }$ in Eq. (5), these equations and Eq. (4a) were solved for the internal radius ${\rho }_i^{\xi }$ and axial stretch ${\mathit{\Lambda }}_z^{\xi }$ using opening angle Φ^ξ and stress-free inner and outer radius, $R_i^{\xi }$ and $R_o^{\xi }$, measured experimentally in the collagen-only and myocytes-only samples.

2. ${\kappa }_{tf}^{\ast }$: Force equilibrium equations in the radial and axial direction are given by

   $$\underset{{\rho }_i}{\overset{{\rho }_o}{\int }}\frac{1}{\rho }\left(t_{\theta \theta }-t_{\rho \rho }\right)\mathrm{d}\rho =0;$$ (7a)

   $$\underset{{\rho }_i}{\overset{{\rho }_o}{\int }}\left[2t_{zz}-\left(t_{\theta \theta }+t_{\rho \rho }\right)\right]\rho \mathrm{d}\rho =0.$$ (7b)

   After substituting F^ξ for ${\mathbf{F}}_{int}^{\xi }{\mathbf{F}}_{\text{tf}}^{\xi }$ in Eq. (5), these equations, together with Eqs. (4a) and (4b), were solved for the internal radius ρ_i and axial stretch λ_z in the uncut mixture traction-free configuration with prescribed interaction parameters α^ξ. In solving for these quantities, experimental measurements ( $R_i^{\xi },R_o^{\xi }$, Φ^ξ) as well as quantities ( ${\rho }_i^{\xi },{\mathit{\Lambda }}_z^{\xi }$) from the previous mechanical equilibrium solution of the ${\kappa }_{tf}^{\xi }$ configuration were used. We would like to point out that with α^ξ = 1 (no mechanical interaction), λ_z = 1, ${\rho }_i={\rho }_i^{\xi }$, and ${\rho }_o={\rho }_o^{\xi }$ (i.e., ${\mathbf{F}}_{int}^{\xi }=\mathbf{I}$) is the solution for this problem.

3. ${\kappa }_0^{\ast }$: Force equilibrium equations in the radial and axial directions, as well as the bending moment equilibrium equation, are given by

   $$\underset{R_i}{\overset{R_o}{\int }}\frac{1}{R}(t_{\mathit{\Theta }\mathit{\Theta }}-t_{RR})\mathrm{d}R=0;$$ (8a)

   $$\underset{R_i}{\overset{R_o}{\int }}[2t_{ZZ}-(t_{\mathit{\Theta }\mathit{\Theta }}+t_{RR})]R\mathrm{d}R=0;$$ (8b)

   $$\underset{R_i}{\overset{R_o}{\int }}R{t}_{\mathit{\Theta }\mathit{\Theta }}\mathrm{d}R=0.$$ (8c)

   After substituting F^ξ for ${\mathbf{F}}_{\text{tf}}^{\ast }{\mathbf{F}}_{int}^{\xi }{\mathbf{F}}_{\text{tf}}^{\xi }$ in Eq. (5), these equations, together with Eqs. (4a), Eq. (4b) and Eq. (4c), were solved for the internal radius R_i, axial stretch Λ_z and opening angle Φ in the cut mixture configuration. These equations were solved using $R_i^{\xi },R_o^{\xi }$ and Φ^ξ that were measured experimentally with ${\rho }_i^{\xi },{\mathit{\Lambda }}_z^{\xi }$, ρ_i and λ_z computed from the two previous mechanical equilibrium solutions.

More details about the CMMI framework solution in “Appendix 2.”

2.4.3 Constitutive relationship

Mechanical behaviors of the myocytes and collagen fibers were both prescribed by an exponential function of the first invariant of the right Cauchy–Green tensor C^ξ taken with respect to their natural stress-free configuration, i.e.,

$$W^{\xi }=c^{\xi }\left(exp{k}^{\xi }(I_1({\mathbf{C}}^{\xi })-3)-1\right),\text{for}\xi =m,c.$$ (9)

This choice was based on previous uniaxial test measurements made on single myocyte (Brady 1984), which showed that its stress–strain relationship is exponential. Our choice of using an exponential strain energy function to describe the mechanical behavior of collagen fibers was, however, motivated by the observation that the fibers are wavy in the cardiac tissue (Hanley et al. 1999) and has a linear stress–strain relationship upon fully straightened (Shen et al. 2008). Collectively, the stress–strain relationship of collagen fibers having varying degree of waviness would then become exponential (Horowitz et al. 1988). We also note that while the mechanical behavior of cardiac tissue is anisotropic with respect to the muscle fiber orientation that varies across the LV wall, we have, as a first approximation, neglected this feature here.

2.4.4 Parameterization with experimental measurements

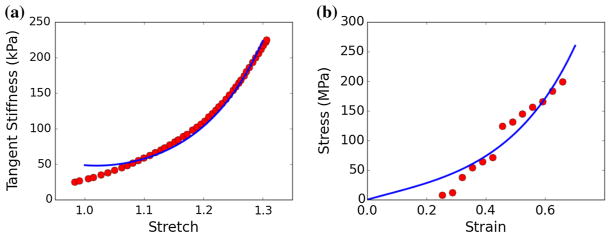
The CMMI framework was directly parameterized using geometrical and histological quantities measured in tissues with isolated collagen or myocytes (ϕ^ξ, $R_i^{\xi },R_o^{\xi }$, Φ^ξ) as well as those from the tissue mixture (Φ^*) as described in Sect. 2.2. A summary of the measurements used for parameterizing the framework is given in Table 1. Nonlinear regression was used to fit the parameters (c^c, k^c) and (c^m, k^m) in the constitutive relationship Eq. (9) to the previously published uniaxial mechanical test data on single myocyte (Brady 1984) and isolated collagen fiber (Shen et al. 2008). We note that strain E in the collagen fiber uniaxial test data was scaled by a straightening stretch of λ_s = 1.2 (i.e., $\stackrel{\sim }{E}=\frac{1}{2}((2E+1){\lambda }_s^2-1)$ to take into account of the fiber waviness found in the tissue (Hanley et al. 1999). The best-fit values were c^c = 11090 kPa, c^m = 4.36 kPa, and k^c = 2.22, k^m = 3.71 (Fig. 3).

Table 1.

Model parameters measured from experimental data

Model parameters	Experimental measurements	Test groups
$R_i^m,R_i^c$	Inner radius of cut samples	Myocyte-only and collagen-only
$R_o^m,R_o^c$	External radius of cut samples	Myocyte-only and collagen-only
Φm, Φc	Opening angle of cut samples	Myocyte-only and collagen-only
Φ*	Opening angle of cut sample	Intact tissue
ϕm, ϕc	Area fraction of constituents	Intact tissue

Fig. 3.

Fitting the strain energy density function parameters using uniaxial mechanical test data from a isolated myocyte (Brady 1984) and b individual collagen fibril (Shen et al. 2008). Dots: data points of the experimental measurements. Line: stress–strain relationship with the best-fit parameter values. Stress: first Piola Kirchhoff stress. Strain: Green-Lagrange strain. Tangent stiffness: $\frac{d\text{PK}1}{d\lambda }$ where λ is the stretch

2.4.5 Types of mechanical interaction

We considered four different types of mechanical interaction, namely (a) no interaction (α^c = α^m = 1.00), (b) isotropic compression of the collagen fibers while keeping the myocytes undeformed (α^m = 1.00, α^c < 1.00), (c) simultaneous isotropic compression of the collagen fibers and tension of the myocytes with a constant overall volume (α^c < 1.00, α^m = 1/α^c > 1.00) and (d) isotropic compression of the myocytes (α^m < 1.00). We note that interaction type (a) corresponds to the standard CM modeling framework, in which the collagen fibers and myocytes are not deformed when “combined” to form a mixture in the intact tissue. Correspondingly, should the standard CM modeling framework (parameterized with experimentally measured quantities) be able to reproduce the opening angle measured in the tissue mixture would suggest that any explicit inter-constituent mechanical interaction is negligible. Conversely, should the framework fail to reproduce the measured opening angle it would suggest the existence of an inter-constituent mechanical interaction that cannot be neglected when describing the mechanics of LV.

3 Results

3.1 Histology and microstructural analysis

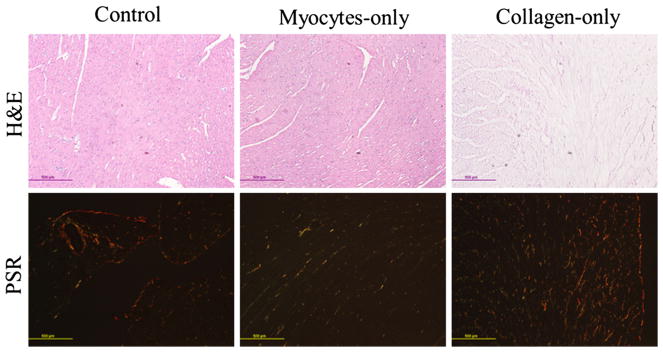
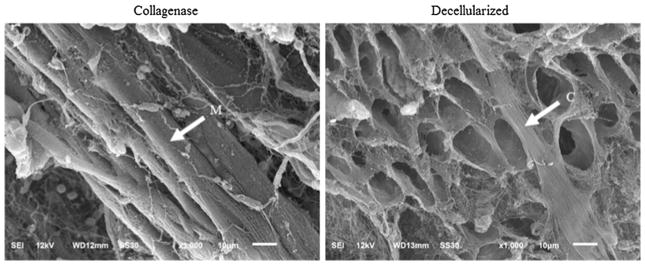
Samples stained with Picrosirius red showed a substantial decrease in the collagen content (red) in the myocyte-only group, and myocytes (yellow) in collagen-only group when compared to the control. Specifically, collagen accounts for 3 and 10% of the total area in the myocyte-only and control group, respectively. Myocyte, on the other hand, accounts for 11 and 90% of the total area in the collagen-only and control group, respectively. Figure 4 shows H&E samples and Picrosirius red under polarized light. The H&E-stained samples shows that myocytes are intact, in both control and collagenase-treated samples, while they are mostly digested in decellularized samples (Fig. 4, top). The polarized light images of Picrosirius red-stained samples show intact fibers (mostly red and yellow) in controls and decellularized samples, and degraded fibers (mostly green) in collagenase-treated samples (Fig. 4, bottom). Figure 5 shows the SEM images of both decellularized and collagenase-treated samples. The images confirm that the integrity of the myocytes and collagen network was not affected during collagenase treatment and decellularization, respectively.

Fig. 4.

Histology images of tissue samples from the male rats hearts. Top row: H&E (nuclei in purple and cytoplasm in pink); bottom row: Picrosirius red under polarized light (collagen fibers in red, yellow and green). Left: Intact samples, center: myocytes-only samples (collagenase-treated), and right: collagen-only samples (decellularized). Bar in each image represents 500 μm

Fig. 5.

SEM images of tissue samples from the male rats hearts. Left: myocyte-only samples (collagenase-treated) and right: collagen-only samples (decellularized). Bar in each image represents 10 μm

3.2 Opening angle experiment

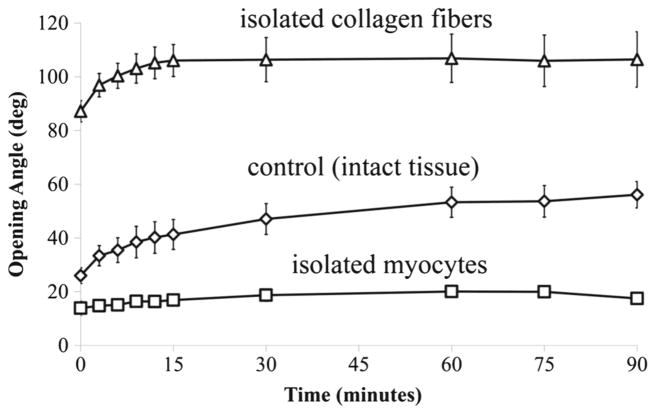
Our experiments showed that the opening angle increased with time and reached a steady state at about 15 min after the cut in the myocyte-only and collagen-only samples. The “control” samples took a longer time to reach steady state. Compared to the opening angle of the control samples taken from male rats (Φ^* = 57.88° ± 12.29°), the corresponding collagen-only samples have a larger opening angle (Φ^c = 106.45°±23.02°; p < 0.005), whereas the myocyteonly samples were found to possess a smaller opening angle (Φ^m = 21.00° ± 4.37°; p < 0.005) (Fig. 6). A similar behavior was also observed for the opening angle found in samples taken from the female rats, which is only statistically different (by ~ 10°) to that in the male rats for the myocyte-only samples (see “Appendix 1”).

Fig. 6.

Changes in opening angle at different time points after the radial cut in the samples from male rats

3.3 Model prediction

The CMMI model was parameterized using only quantities measured in tissue samples from the male rats.

3.3.1 No mechanical interaction

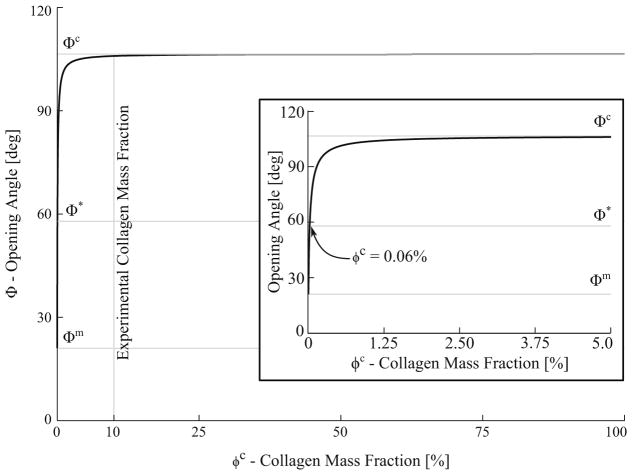
Figure 7 shows the model prediction of the mixture opening angle Φ as a function of collagen mass fraction ϕ^c without any inter-constituent interaction (i.e., α^c = α^m = 1). The model predicted an opening angle equal to that measured in the myocyte-only samples (Φ = Φ^m) when the tissue mixture does not contain any collagen (ϕ^c = 0). At the other extreme when the mixture is composed entirely of collagen (ϕ^c = 100%), the predicted opening angle is equal to that measured in the collagen-only samples (Φ = Φ^c). With mass fractions ϕ^c and ϕ^m equal to the measured values (i.e., ϕ^c = 10%), the model predicted the tissue mixture opening angle to be 106.45°, a value that is significantly higher than the measured value (57.88°) and close to that in the collagen-only tissue samples. Only when ϕ^c = 0.06% (i.e., collagen accounts for only 0.06% of the myocardium mass), did the model predict a tissue mixture opening angle equal to the measured value.

Fig. 7.

Opening angle Φ as a function of the collagen mass fraction ϕ^c without inter-constituent mechanical interaction. Φ^m, Φ^c and Φ^* denote measured values of the opening angle for myocytes-only, collagen-only and untreated tissue, respectively. Inset: close-up view (0 ≤ ϕ^c ≤ 5%) showing that the measured mixture opening angle is recovered by the model when ϕ^c = 0.06%

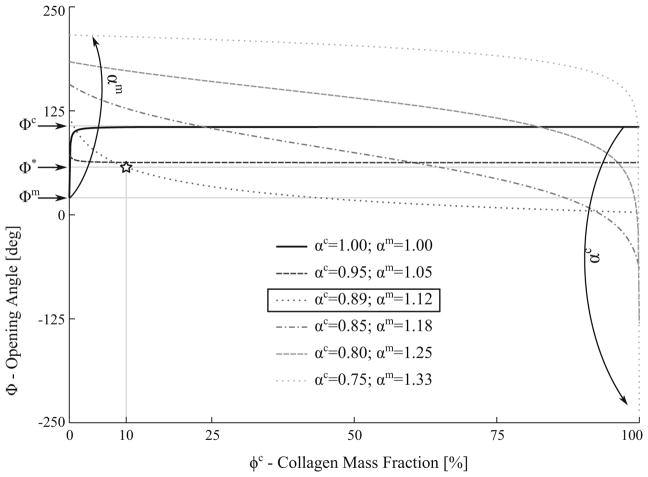
3.3.2 Compression of the collagen fibers only

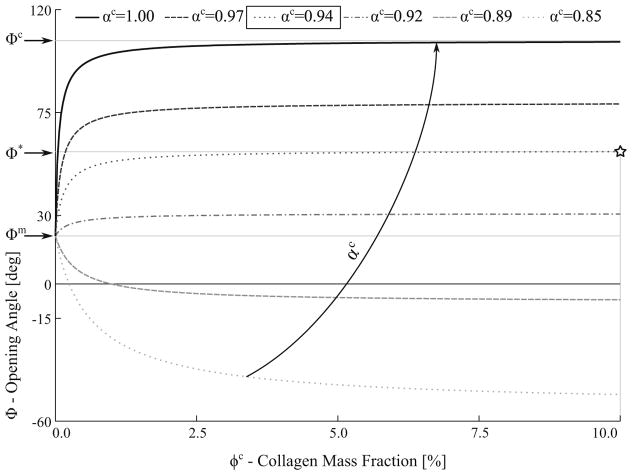
Figure 8 shows the effects on the relationship between the mixture opening angle Φ and the collagen mass fraction ϕ^c when the collagen fiber network is compressed isotropically (i.e., α^c < 1.00) and the myocytes are undeformed (α^m = 1.0) in the interaction. Correspondingly, when only myocytes are present (ϕ^c = 0) in the mixture, the model predicted an opening angle equal to that measured in the myocyte-only samples (i.e., Φ = Φ^m). To recover the measured opening angle Φ^*, the values of the interaction parameters are α^c = 0.94 and α^m = 1.00.

Fig. 8.

Effects of isotropic collagen compression on the mixture opening angle. Curves represent mixture opening angle Φ relationship with the collagen mass fraction ϕ^c at different compression level α^c. Φ^m, Φ^c and Φ^* denote measured values of the opening angle for myocytes-only, collagen-only and untreated tissue, respectively. Note that the graph is truncated at ϕ^c = 10% because all the curves plateau to a constant value when ϕ^c > 10%

3.3.3 Compression of collagen fibers and tension of myocytes

Figure 9 shows the effects on the relationship between the mixture opening angle Φ and the collagen mass fraction ϕ^c when the interaction led to an isotropic compression of the collagen fibers (α^c < 1.00) and tension of the myocytes (α^m > 1.00). To keep the overall mixture volume constant, the two interaction parameters were constrained by α^m · α^c = 1.00. The model predicted that a mechanical interaction producing simultaneous increase in collagen fiber compression and myocyte tension will lead to a decrease in the mixture opening angle at high collagen mass fraction ϕ^c. Conversely, the mixture opening angle was increased at high myocyte mass fraction (low ϕ^c). To recover the measured opening angle Φ^*, the values of the interaction parameters are α^c = 0.89 and α^m = 1.12.

Fig. 9.

Effects of mixture opening angle caused by simultaneous collagen compression (α^c < 1.0) and myocyte tension (α^m > 1.0) in the interaction. Curves represent mixture opening angle Φ relationship with the collagen mass fraction ϕ^c with different combinations of α^c and α^m. Φ^m, Φ^c and Φ^* denote measured values of the opening angle for myocytes-only, collagen-only and untreated tissue, respectively

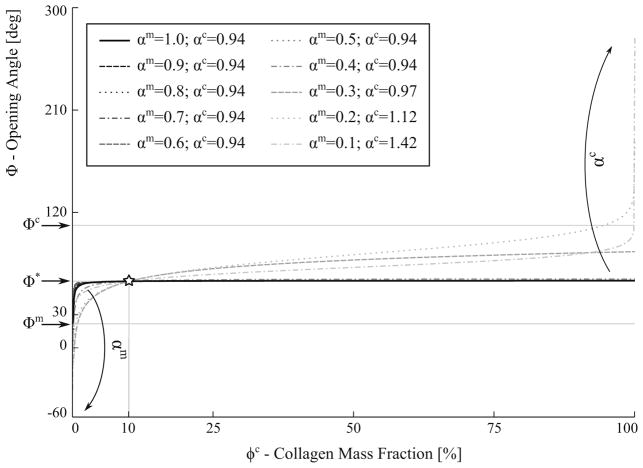
3.3.4 Isotropic compression of the myocytes

Figure 10 shows the effects on the Φ–ϕ^c relationship when the interaction led to an isotropic compression of the myocytes (α^m < 1). Here, the value of α^c was found for each value of α^m so that the model recovers the measured mixture opening angle (Φ^* = 57.88°) at ϕ^c = 10% (i.e., measured collagen mass fraction). Simply, all the curves found in this figure are solutions to the problem of finding interaction parameters that reproduces the measurements. Under this type of interaction, the model predicted that the collagen interaction parameter ϕ^c is constant at 0.94 over a wide range of myocyte compression (i.e., α^m = 1.0 – 0.4). Only when the myocytes are severely compressed (α^m < 0.3), did the model predict the collagen fibers to be in tension in order for the model to be consistent with the experiments.

Fig. 10.

Effects of mixture opening angle caused by isotropic myocyte compression (α^m < 1.0). Collagen interaction parameter α^c determined so that Φ = Φ^* at ϕ^c = 10%. Curves represent mixture opening angle Φ relationship with the collagen mass fraction ϕ^c at different combinations of α^c and α^m

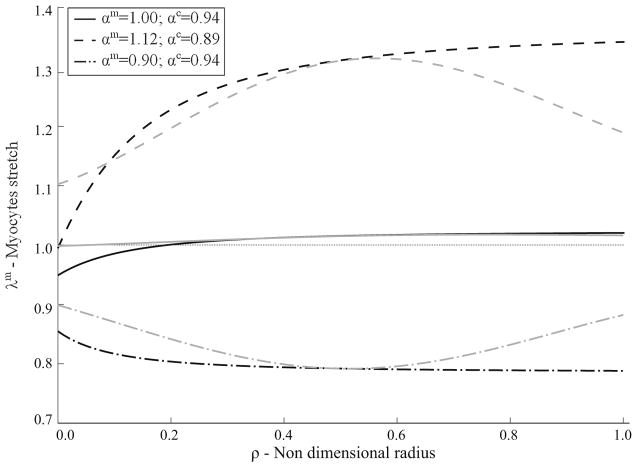
Finally, Fig. 11 represents the values of the stretches in the myocytes across the wall in the intact tissue, uncut, traction-free configuration ${\kappa }_{tf}^{\ast }$. Black lines in the figure represent stretches in the circumferential direction, while gray lines represent stretches projected along the direction of the myocytes across the ventricular wall. The effects of the three different interactions are also represented in the figure.

Fig. 11.

Comparison of the three different mechanical interactions considered. Myocytes and collagen interaction parameters, α^m and α^c, determined so that Φ = Φ^* at ϕ^c = 10%. Curves represent myocytes stretch in the circumferential (black) and in the direction of the myocytes across the wall (gray)

4 Discussion

While residual stress fields in the LV have been measured across many species (Taber et al. 1993; Omens and Fung 1990;Costa et al. 1997;Genet et al. 2015; Omens et al. 2003), none of these studies have, to the best of our knowledge, quantified those associated with the individual constituents of the LV. Neither are there studies investigating sex difference in the residual stress fields. We have addressed these issues here. By performing opening angle experiments on tissues isolated with collagen fibers and myocytes, our results showed that the two constituents contribute disproportionately to the LV residual stress fields. Measurements made on the tissue mixture containing these two constituents revealed an opening angle Φ^* = 57.88° that is comparable to those measured in previous studies, namely Omens and Fung (1990) (Φ^* = 45°), Omens et al. (1996) (~ 51° ± 11°) and Rodriguez et al. (1993) (~ 45° ± 15°). A Welch’s t test was also performed and showed no significant difference between our measurements and those from the latter study (α > 0.8). Unlike here where we measured the opening angle over a 90-min period as it reaches a steady state, the opening angle reported in these studies was measured (without BDM in Omens and Fung 1990) within 30 s of radial cutting before the onset of ischemic contracture. Given that the steady-state opening angle found here (57.88°) is well below that found under full contracture (180°) as reported in Omens and Fung (1990), our measurements should correspond to a state at which the muscle is mostly relaxed.

In comparison with that found in the tissue mixture, collagen-only samples have a significantly higher opening angle, whereas myocytes-only samples have a smaller opening angle. The opening angle increased progressively with time until reaching a steady state in all experimental groups, a feature that is associated with the tissue viscoelastic behavior (Zhang et al. 2008; Rehal et al. 2006). We also note that the collagen-only tissue samples appears to be similar to that found in the hydrated cartilage tissue, which is composed of a dense elastic ECM network with fluid-filled pores. As such, we expect these samples to also possess viscoelastic behavior as exhibited in the variation of opening angle with time. Correspondingly, these results suggest that the collagen fiber network is the major contributor to the LV residual stress fields, despite accounting for only about 10% of the cardiac tissue volume as estimated from the histological analyses.

Our finding that the tissue opening angle appears to be positively related to the collagen content is also compatible with those found in the arteries. First, opening angle of the arteries, which contains more collagen (ϕ^c ~ 50%) than the LV, is substantially larger (in excess of 100°) (Chuong and Fung 1986). Second, degradation of collagen using collagenase also reduces the opening angle (Durney et al. 2009) in the arteries, which is consistent with our findings.

To interpret these experimental findings further, we have developed a CMMI modeling framework that takes into account the inter-constituent mechanical interactions arising from combining the constituents into a mixture. In this framework, we introduced a mapping ${\mathbf{F}}_{int}^{\mathrm{m}}$ and ${\mathbf{F}}_{int}^{\mathrm{c}}$ that, respectively, represent the deformation of the myocyte and collagen when they are combined. We attribute that mapping to a mechanical interaction between the two constituents. We parameterized the CMMI model with measurements made on both untreated tissues and treated tissues with only myocytes or collagen fibers. Consequently, we showed that, without the presence of this mechanical interaction ( ${\mathbf{F}}_{int}^{\mathrm{m}}={\mathbf{F}}_{int}^{\mathrm{c}}=\mathbf{I}$), the model predicted a significantly larger opening angle in the tissue mixture than what was measured in the experiments. To reproduce the opening angle would require a collagen mass fraction that is significantly lower than that measured here (10%) and reported previously (Medugorac and Jacob 1983; Omens et al. 1998). Altogether, these findings suggest that the contribution of collagen fibers and myocytes to the overall LV mechanical behavior cannot be described simply by only taking into account of the constituent’s mere presence in the mixture (as in the standard CM model).

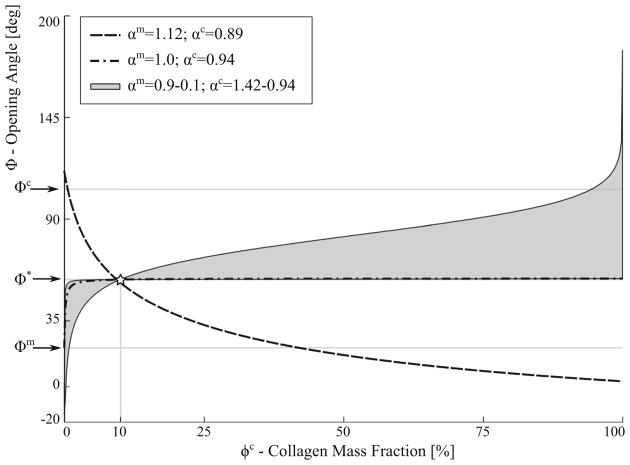
Different forms of mechanical interaction leading to the compression or tension of the collagen fibers and myocytes were investigated using the CMMI model. We showed that the form of mechanical interaction necessary for the model to be consistent with the measurements is not unique, as shown in Fig. 12. Specifically, consistency with the measurements can be achieved when the interaction results in a compression of the collagen fiber network and tension of the myocytes, or vice-versa. Because of the substantially higher stiffness found in the collagen fiber, however, the myocytes have to be severely compressed in the interaction (with a characteristic length < 0.3 of its pre-compressed length) for the model to be consistent with the experiments. In comparison, this consistency can be achieved with only moderate compression of the collagen fiber network. Correspondingly, our results suggest that the LV mechanics is more sensitive to the interaction-induced collagen fiber deformation than that of the myocytes.

Fig. 12.

Summary of the effects of three different types of mechanical interactions on opening angle. Myocytes and collagen interaction parameters, α^m and α^c, determined so that Φ = Φ^* at ϕ^c = 10%. Curves represent mixture opening angle Φ relationship with the collagen mass fraction ϕ^c at different combinations of α^c and α^m

In support of the CMMI model’s prediction that the collagen fibers are likely to be compressed by its interaction with the myocytes, previous studies have observed that the collagen fibers in cardiac tissues are not completely straightened (and wavy) even at physiological end-diastolic pressure (MacKenna et al. 1996; Omens et al. 1997). Moreover, a larger residual stress has also been shown to be associated with an increase in the LV compliance (Genet et al. 2015), suggesting that the substantial contribution of collagen fibers to the residual stress field may aid the passive filling of LV.

Moreover, given that the opening angle measured in the intact (mixture) tissue ~ 58° ± 12° is comparable with those found in similar studies by Omens and Fung (1990) (~ 45°±10°, without ischemic contracture) and Omens et al. (1996) (~ 51° ± 11°), we expect the transmural stretch gradient to be similar to those found in Rodriguez et al. (1993). We have also computed the transmural stretch in the muscle fiber direction, as well as in the circumferential direction. While the circumferential stretch follows an expected pattern of compression at the inner radius and tension at the outer radius, the stretch in the direction of the fibers follows a different distribution. This could be explained by choice of model description (isotropic vs orthotropic).

While the CM modeling framework has been used extensively to describe tissue mechanics in relation to its structural composition (Humphrey 2003), this framework may be inadequate (at least where cardiac mechanics is concerned) as our finding suggests the existence of some inter-constituent mechanical interactions in the LV. Evidence of such mechanical interaction was also reported very recently by Avazmohammadi et al. (2017). Although reaching the same conclusion, that study, however, differs from ours in two aspects. First, the conclusion was reached by Avazmohammad et al. based on their findings that the standard CM modeling framework was inadequate to fit the biaxial test measurements on the RV tissue. This is in contrast to our study, where the measurements of the LV opening angle form the experimental basis of our conclusion. Second, Avazmohammad et al. modeled the mechanical interaction by introducing an additional “myo-collagen coupling” strain energy density function into the CM modeling framework. This differs from our proposed (CMMI) framework, in which an inter-constituent mechanical interaction mapping from the isolated constituent configuration to the mixture configuration was introduced. Despite these differences, the fact that the same conclusion was reached in two independent studies using different approaches lend support to the importance of accounting for the inter-constituent mechanical interaction in describing LV mechanics.

4.1 Limitations

There are several limitations associated with this study. First, while it has been established previously that key features (e.g., weaves, struts and coils) of the collagen fiber network were preserved after decellularization (suggesting that it has minimal impact on the ECM’s structural, functional and mechanical properties) (Ott et al. 2008), it is still possible that the collagen fibers were damaged during decellularization treatment. Similarly, the myocytes may also be damaged during collagenase treatment although it was previously established that the treatment is unlikely to do so (MacKenna et al. 1994).

Second, it is possible that bathing the tissue in solutions containing BDM may not prevent ischemic contracture of all the myocytes in the control and myocytes-only groups. However, the fact that the opening angle measured here in the control group is comparable to those previously measured in fully relaxed tissue (Omens and Fung 1990; Omens et al. 1996) and is also well below that found in fully contracting tissue (Omens and Fung 1990) would suggest that the myocytes are mostly relaxed after treatment here.

Third, descriptors of the myocyte and collagen fiber mechanical behavior used here are highly simplified, which were characterized using previous uniaxial tension test data on isolated myocytes and individual collagen fibril. As a first approximation, we have also neglected any anisotropy of the cardiac tissue and focus primarily on the disparity in mechanical stiffness of the myocyte and collagen fiber (when straightened), which is the key contributor to our findings. Using anisotropic constitutive laws to describe the mechanical behavior of the tissue constituents will, no doubt, increase the realism of the CM model. This will, however, not only require biaxial mechanical test results of cardiac tissues isolated with myocytes and collagen fibers, but also detailed information of the microstructural arrangement of these constituents in the tissue ring samples. Therefore, we believe that until such data become available, using the simplest possible constitutive law is the most appropriate choice here

Last, we have assumed that the mechanical interaction deformation is isotropic and homogeneous. As a result, the form of mechanical interaction applied to the CMMI modeling framework to fit the measurements is not unique. While other forms can be prescribed in the CMMI framework, it will be fruitless to do so unless more microstructural information is available to constrain the form of interaction.

4.2 Conclusion

In conclusion, we have showed that the collagen fibers are key contributor to the residual stress fields found in the LV of normal rat. Our theoretical analysis on the experimental measurements also suggests the existence of some quantifiable inter-constituent mechanical interactions that must be taken into account when describing LV mechanics. Whether this interaction is altered under pathological conditions will be addressed in future studies.

Appendix 1

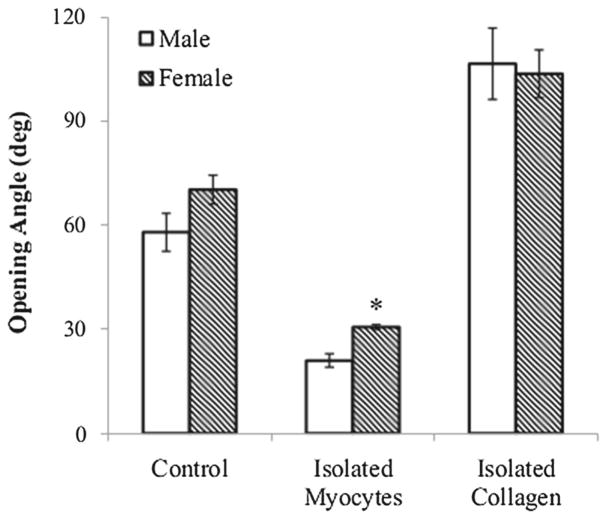
Only a significant difference in the steady-state opening angle between the male and female rats was found in the myocyte-only group (female: Φ^m = 30.63°±1.50° vs. male: Φ^m = 21.00° ± 4.37°, p < 0.005) (Fig. 13). Sex difference was not statistically significant in the collagen-only (female: Φ^c = 103.58° ± 15.43° vs. male: Φ^c = 106.45° ± 23.02°) and control (female: Φ^* = 70.15° ± 9.30° vs. male: Φ^* = 57.88°±12.29°) groups. These results therefore suggest that how collagen fibers and myocytes contribute to the LV residual stress is not different across sex.

Fig. 13.

Comparison of opening angle between male and female rats

Appendix 2

The following steps describe how the system of equations presented in Sect. 2 was solved. All the ODE systems described below were solved using Romberg’s algorithm.

1. We first solved the system described in Eqs. (6) for each constituent separately (ξ= m, c). This is a 2-equation (circumferential and axial equilibrium in the ${\kappa }_{tf}^{\xi }$ configuration) and 2-unknown ( ${\rho }_i^{\xi },{\mathit{\Lambda }}_z^{\xi }$) ODE system. The deformation gradient for each constituent is ${\mathbf{F}}^{\xi }={\mathbf{F}}_{tf}^{\xi }$ as defined in Eq. (1). Radius in the ${\kappa }_{tf}^{\xi }$ configuration ρ^ξ was written as a function of the radius in the ${\kappa }_{tf}^{\xi }$ configuration R^ξ by inverting Eq. (4a), where $R_i^{\xi },R_o^{\xi }$, and Φ^ξ were informed by experimental data and, ${\rho }_i^{\xi }$ and ${\mathit{\Lambda }}_z^{\xi }$ are unknowns of the problem. The deformation gradient ${\mathbf{F}}^{\xi }\left({\rho }_i^{\xi },{\mathit{\Lambda }}_z^{\xi }\right)$ was then used to evaluate the stresses in the ${\kappa }_{tf}^{\xi }$ configuration using Eq. (5), where W^ξ is given in Eq. (9). The stresses, as a function of ${\rho }_i^{\xi }$ and ${\mathit{\Lambda }}_z^{\xi }$, were then substituted in the equilibrium equations, i.e., Eqs. (6). The quantities computed in this first step are ${\rho }_i^{\xi }$ and ${\mathit{\Lambda }}_z^{\xi }$ and the experimental values employed here are $R_i^{\xi },R_o^{\xi }$, and Φ^ξ.

2. We then solved the system described in Eqs. (7), in which the 2 constituents are combined to form the mixture. This is also a 2-equation (circumferential and axial equilibrium in the ${\kappa }_{tf}^{\ast }$ configuration) and 2-unknown (ρ_i, λ_z) ODE system. The deformation gradient for each constituent is now equal to ${\mathbf{F}}^{\xi }={\mathbf{F}}_{\mathit{int}}^{\xi }{\mathbf{F}}_{tf}^{\xi }$, as defined in Eqs. (1) and (3). We then used Eq. (4b) to express the radius ρ^ξ of each constituent-specific uncut configuration ${\kappa }_{tf}^{\xi }$ as a function of the coordinate ρ and the quantities ρ_i, and λ_z (unknowns in the problem). We also expressed radius R^ξ in each constituent-specific cut configuration ${\kappa }_0^{\xi }$, as a function of ρ^ξ, ${\rho }_i^{\xi }$ and ${\mathit{\Lambda }}_z^{\xi }$, (evaluated in step 1), and $R_i^{\xi }$ and Φ^ξ (measured from the experiments) as described in Eq. (4a). The interaction parameters α^m and α^c were fixed accordingly based on the type of interaction. The stretches were then used to evaluate the stresses in the ${\kappa }_{tf}^{\xi }$ configuration as described by Eq. (5), where W^ξ is given in Eq. (9). Finally, these stresses were substituted into the equilibrium equations described in Eqs. (7) to solve for ρ_i and λ_z.

3. In the final step, we solved the system described by Eqs. (8). This is a 3-equation (circumferential, axial, and bending equilibrium in ${\kappa }_0^{\ast }$ configuration) and 3-unknown (R_i, Λ_z, and Φ) ODE system. The deformation gradient for each constituent was defined as ${\mathbf{F}}^{\xi }={\mathbf{F}}_{tf}^{\ast }{\mathbf{F}}_{\mathit{int}}^{\xi }{\mathbf{F}}_{tf}^{\xi }$. We then used Eq. (4c) to write the radius in the cut configuration of the mixture ${\kappa }_0^{\ast }$, as a function of ρ and ρ_i (evaluated in step 2), and R_i, Λ_z and Φ (problem unknowns). We also used Eq. (4b) to write each ρ^ξ in the constituent specific intact configuration ${\kappa }_{tf}^{\xi }$ as a function of ρ, ρ_i, and λ_z (evaluated in step 2) and α^ξ(that depends on the interaction type). Finally, we employed Eq. (4a) to express R^ξ in the constituent-specific cut configuration ${\kappa }_{tf}^{\xi }$, as a function of ρ^ξ, ${\rho }_i^{\xi }$ and ${\mathit{\Lambda }}_z^{\xi }$ (evaluated in step 1), and $R_i^{\xi }$ and Φ^ξ (measured from the experiments). These stretches were then used to evaluate the stresses in the ${\kappa }_0^{\ast }$ configuration as described by Eq. (5), where W^ξ is expressed by Eq. (9). Finally, these stresses were substituted in Eqs. (8) as a function of R_i, Λ_z, and Φ.

The opening angle of the intact tissue (Φ) is a key quantity computed from the above steps. We considered the interaction parameters α^m and α^c be the “solution” when the computed opening angle in the cut, mixture configuration κ₀ assumes the value Φ^* = 57.88° with a collagen mass fraction of 10% and myocyte mass fraction of 90% (measured experimentally).