Imaging the three-dimensional orientation and rotational mobility of fluorescent emitters using the Tri-spot point spread function

Abstract

Fluorescence photons emitted by single molecules contain rich information regarding their rotational motions, but adapting single-molecule localization microscopy (SMLM) to measure their orientations and rotational mobilities with high precision remains a challenge. Inspired by dipole radiation patterns, we design and implement a Tri-spot point spread function (PSF) that simultaneously measures the three-dimensional orientation and the rotational mobility of dipole-like emitters across a large field of view. We show that the orientation measurements done using the Tri-spot PSF are sufficiently accurate to correct the anisotropy-based localization bias, from 30 nm to 7 nm, in SMLM. We further characterize the emission anisotropy of fluorescent beads, revealing that both 20-nm and 100-nm diameter beads emit light significantly differently from isotropic point sources. Exciting 100-nm beads with linearly polarized light, we observe significant depolarization of the emitted fluorescence using the Tri-spot PSF that is difficult to detect using other methods. Finally, we demonstrate that the Tri-spot PSF detects rotational dynamics of single molecules within a polymer thin film that are not observable by conventional SMLM.

Fluorescence microscopy has been widely used for imaging living cells due to the genetic specificity provided by tagging or protein engineering, its single-molecule (SM) sensitivity, and its minimal toxicity compared to other high-resolution imaging techniques. Super-resolution microscopy has recently broadened its capabilities, enabling images of dynamic living processes to be created with 1 nm spatial resolution^1–3 and 10 ms temporal resolution.⁴ One class of super-resolution methods, termed single-molecule localization microscopy (SMLM), constructs high-resolution images by repeatedly measuring the positions of blinking molecules over time.^5–7 Beyond measuring molecular positions, SM imaging systems have also been augmented to measure molecular orientation,^8,9 which is not only critical for ensuring the accuracy of SMLM,^8,10–12 but is also helpful in elucidating a wide variety of biological processes.¹³ By measuring the orientation and the rotational mobility of SMs, researchers have gained insights into DNA bending and tangling,^9,14,15 molecular motor dynamics,^16–18 and structures of polymer chains.^19–21

Although the orientations of a molecule's absorption and emission dipole moments are not necessarily parallel,²² optical methods are capable of measuring the orientations of both vectors. These techniques leverage (1) the absorption dipole moment's sensitivity to the polarization of the pumping light, (2) the polarization of the emitted fluorescence relative to the emission dipole moment, and/or (3) the dipole's anisotropic emission pattern. Since the probability of absorption is proportional to the square of the dot product between the absorption dipole moment and the local illuminating electric field, absorption-based methods measure an emitter's fluorescence in response to varying the polarization of excitation light.^9,16,17 Similarly, the orientation of an emission dipole can be calculated by taking the ratio of photons detected between two or more polarized detection channels.^23,24 The combination of multiple excitation polarizations and polarized detection channels has been used to measure 3D orientation and rotational mobility,²⁴ but the need for multiple polarization modulators, polarizing beam splitters, and synchronized cameras complicates the adaptation of these methods for SMLM. Recently, the orientation of SM emitters has been measured using their emission pattern, either directly, with modulation by a phase mask, or with modulation by a polarization filter.¹³ However, a continuing challenge exists to design an instrument capable of simultaneously resolving the 3D orientation and the rotational mobility (or rotational diffusion or constraint) of SMs without angular degeneracy,²⁵ while still being compatible with SMLM for localizing the position of those SMs across a large field of view.

Here, we demonstrate a method, termed the Tri-spot point spread function (PSF), for measuring all degrees of freedom related to 3D molecular orientation and rotational mobility. We model a fluorescent molecule as a dipole-like emitter with orientation $\mathit{\mu }={[{\mu }_x,{\mu }_y,{\mu }_z]}^T={\left[\text{sin}\theta \text{cos}\varphi ,\text{sin}\theta \text{sin}\varphi ,\text{cos}\theta \right]}^T$, which can be parametrized as ${\mu }_x$, ${\mu }_y$ and ${\mu }_z$ in Cartesian coordinates or as the polar angle $\theta$ and the azimuthal angle $\varphi$ in spherical coordinates.

The recorded image can then be represented using the orientational second-moment vector $\mathit{M}=\left[⟨{\mu }_x^2⟩,⟨{\mu }_y^2⟩,⟨{\mu }_z^2⟩,⟨{\mu }_x{\mu }_y⟩,⟨{\mu }_x{\mu }_z⟩,⟨{\mu }_y{\mu }_z⟩\right]$^9,26–30

$${\mathit{I}}_{\text{img}}=I_0\left[{\mathit{X}\mathit{X}}_{\text{img}},{\mathit{Y}\mathit{Y}}_{\text{img}},{\mathit{Z}\mathit{Z}}_{\text{img}},{\mathit{X}\mathit{Y}}_{\text{img}},{\mathit{X}\mathit{Z}}_{\text{img}},{\mathit{Y}\mathit{Z}}_{\text{img}}\right]{\left[⟨{\mu }_x^2⟩,⟨{\mu }_y^2⟩,⟨{\mu }_z^2⟩,⟨{\mu }_x{\mu }_y⟩,⟨{\mu }_x{\mu }_z⟩,⟨{\mu }_y{\mu }_z⟩\right]}^{\mathrm{T}},$$ (1)

where ${\mathit{I}}_{\text{img}}$ is the image of the dipole emitter captured with the camera and ${\mathit{X}\mathit{X}}_{\text{img}}$, …, ${\mathit{Y}\mathit{Z}}_{\text{img}}$ are termed the basis images of the microscope, that is, the image produced by an emitter exhibiting each orientation component. The basis images can be computed for any imaging system using vectorial diffraction models.²⁹ A cascade of events produces each recorded photon: (1) an SM absorbs a photon at a certain orientation ${\mathit{\mu }}_{\text{abs}}$; (2) it diffuses rotationally during the molecule's excited state lifetime; and (3) it emits a photon while at an orientation $\mathit{\mu }$. Summing multiple fluorescence photons results in a second-moment vector $\mathit{M}$ of the molecule's orientation trajectory integrated over one camera frame. The angle brackets $⟨·⟩$ denote the temporal average or the equivalent ensemble average taken over the orientation domain. Furthermore, if the molecule's rotational diffusion is symmetric around a certain average orientation $\left[{\overline{\mu }}_x,{\overline{\mu }}_y,{\overline{\mu }}_z\right]$ and the rotational relaxation time is much shorter than the fluorescence lifetime, the elements of $\mathit{M}$ can be represented using 4 parameters, ${\overline{\mu }}_x$, ${\overline{\mu }}_y$, ${\overline{\mu }}_z$ and the rotational constraint $\gamma$³¹ (see supplementary material 3.1). If the rotational correlation time is longer than the fluorescence lifetime, then $\gamma$ may be interpreted as an effective rotational constraint or anisotropy factor that depends on both the molecular rotation and the illumination polarization.³¹ A rotational constraint $\gamma$ of unity represents a completely immobile emitter, while for the case of a freely rotating emitter, $\gamma =0$ and all the cross terms ${⟨{\mu }_i{\mu }_j⟩}_{i\ne j}$ in $\mathit{M}$ are equal to zero.

Our imaging system [Fig. S1(a)] includes a polarization beam splitter (PBS) to separate light into two imaging channels, and the Tri-spot phase mask [Fig. 1(a)] is placed in the back focal plane (BFP) in both channels. Due to the geometry of our imaging system and the reflective spatial light modulator, the PSF in the x-polarized channel [Fig. S1(c)] is rotated clockwise by 90° relative to that in the y channel [Fig. S1(d)]. The fluorescence in both channels is captured by the same image sensor.

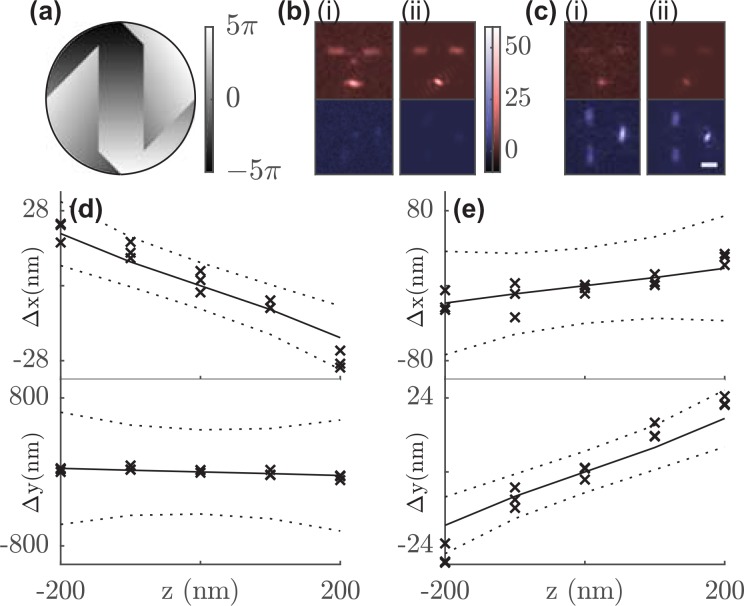
FIG. 1.

(a) Tri-spot Phase mask. Colorbar: phase (rad). Orientation measurements of Atto 647N (b) molecule 1 and (c) molecule 2. Representative (i) captured and (ii) fitted Tri-spot PSF image of each SM. Red: x-polarized channel; Blue: y-polarized channel. Scale bar: 1 μm; Color bar: detected photons/pixel. Measured localization bias (cross) along the x-axis in the x-polarized channel and the y-axis in the y-polarized channel at different z positions for (d) molecule 1 and (e) molecule 2 using the standard PSF. The solid line represents the predicted lateral translation from the Tri-spot's orientation measurements, and the dashed line marks the experimental localization precision (±1 std. dev.).

For analyzing the images of the Tri-spot PSF, we integrate the total photons contained within the 3 spots in each polarized image, resulting in six photon measurements of each molecule. The resulting six-element image vector $\mathit{I}\left(I_0,{\overline{\mu }}_x,{\overline{\mu }}_y,{\overline{\mu }}_z,\gamma \right)=I_0\mathit{B}\mathit{M}\left({\overline{\mu }}_x,{\overline{\mu }}_y,{\overline{\mu }}_z,\gamma \right)$ is a linear combination of the six-by-six basis-image matrix $\mathit{B}$. The Tri-spot PSF was designed such that each column of $\mathit{B}$ is linearly independent and has similar energy (Fig. S3), which guarantees a one-to-one correspondence between $\mathit{I}$ and $\mathit{M}$ and maximizes the precision of measuring each second moment. We built a maximum-likelihood (ML) estimator to estimate the average orientation ${\overline{\mu }}_x$, ${\overline{\mu }}_y$, ${\overline{\mu }}_z$ and the rotational constraint $\gamma$ from any image $\mathit{I}$ (see supplementary material 2.1). When the estimator is unbiased at a sufficiently high signal-to-background ratio (Fig. S5), its performance using simulated images of emitters with various orientations is close to the theoretical limit given by the Cramér-Rao lower bound (CRLB).³² For 3000 photons captured from a fixed SM with 10 background photons/pixel, the Tri-spot PSF achieves an average orientation ${\overline{\mu }}_x$ measurement precision of 0.06 (7° polar angle and 8° azimuthal angle in spherical coordinates) and a rotational constraint $\gamma$ measurement precision of 0.20 (to provide some physical intuition, this $\gamma$ is equivalent to a cone half-width uncertainty of 14° for a molecule uniformly diffusing within a cone).

We measured the orientation of single Atto 647N molecules embedded in a thin layer (87 ± 15 nm [mean ± std.] thickness) of polymethyl methacrylate (PMMA) on a glass coverslip using the Tri-spot PSF in focus. We then used the measured orientation to the correct dipole-induced localization bias when using the standard PSF in SMLM. When rotationally fixed, dipole radiation patterns from SMs lead to a systematic lateral (xy) localization bias that increases with defocus (z).^10,33,34 The size and the direction of this bias are a function of molecular orientation. Thus, accurately measuring a molecule's orientation enables this mislocalization bias to be calculated and removed using a post-processing algorithm.⁸

We used our ML estimator to measure the orientation of each SM and found that the fitted Tri-spot images [Figs. 1(b), 1(c-ii), and S8(d)] match closely with the camera images [Figs. 1(b), 1(c-i), and S8(c)]. The orientation measurements [Figs. S8(e) and S8(f)] were used to predict each molecule's localization bias ($\mathrm{\Delta }x$, $\mathrm{\Delta }y$) as a function of z using our vectorial diffraction model. Since each detection channel in our microscope is linearly polarized, we expect localization biases in the x-polarized channel to be the largest along the x direction and biases along the y direction to be the largest in the y channel (Fig. S9). ThunderSTORM³⁵ was used to localize the standard PSF image of each molecule at each defocus position, thereby quantifying each SM's experimental localization bias. The predicted localization bias matches the experimentally measured bias [Figs. 1(d), 1(e), S8(g), and S8(h)] to within the experimental localization precision for 95% of all z positions and molecules. We observed localization biases as large as 30 nm for ±200 nm defocus [Figs. 1(d) and 1(e)]. Applying the Tri-spot's localization correction reduces this bias to 7 ± 6 nm (mean ± std.), which is within the localization precision of 13 nm for 2500 photons detected at $z=\pm 200\hspace{0.17em}$ nm, thereby restoring the localization accuracy of the imaging system.

Since emission anisotropy causes the localization biases quantified above, it is important to characterize the anisotropy of any emitter used for measuring and calibrating optical aberrations.^36–39 It is widely assumed that fluorescent beads behave as ideal point sources, especially those that are smaller than the diffraction limit (∼$\lambda /2NA\approx 250\hspace{0.17em}\text{nm}$), but very little is known about their emission anisotropy or heterogeneity. The Tri-spot PSF is ideally suited for quantifying this anisotropy, because the second-moment vector M measured from each individual bead directly represents the orientation distribution of the ensemble of molecules contained within it. Measuring M as a function of excitation polarization provides additional insights into depolarization behaviors among the fluorophores within each bead.

Using the Tri-spot PSF, we imaged 20-nm and 100-nm diameter beads embedded in a thin layer (34 ± 14 nm) of polyvinyl alcohol (PVA) sequentially pumped by x- and y-polarized light [Figs. 2(a) and 2(b)]. Using our ML estimator, we measured a larger effective rotational constraint for 20 nm beads (median $\gamma =0.52$) than that for 100 nm beads [median $\gamma =0.38$, Fig. 2(c)]. This measurement is consistent with the expectation that the fewer number of fluorophores within the smaller bead results in fluorescence emission anisotropy more similar to that of a fixed SM, and hence a larger effective rotational constraint. Interestingly, both 100-nm and 20-nm beads do not exhibit emission patterns characteristic of isotropic emitters (i.e., $\gamma$ close to zero). In fact, the measured effective rotational constraint of 20-nm beads suggests that they could exhibit a localization bias of ∼50 nm when defocused by 200 nm [Fig. S9(c)].

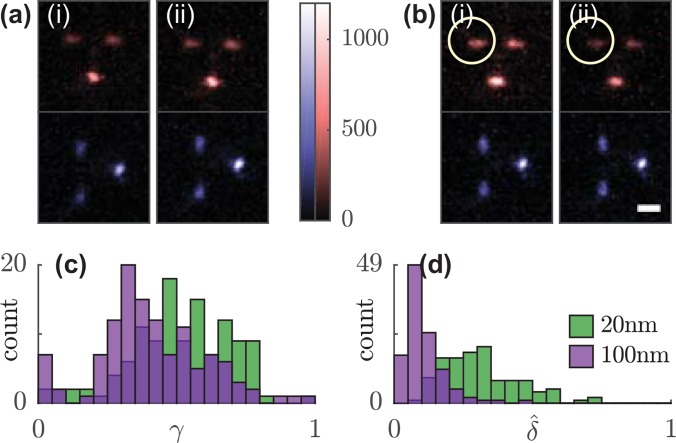
FIG. 2.

Anisotropy and rotation of the orientational second moment vector of fluorescent beads in response to linearly polarized excitation. Sum of 100 Tri-spot PSF images of a single (a) 100-nm and (b) 20-nm bead using (i) x- and (ii) y-polarized excitation. Circle highlights the change in spot brightness. (c) Rotational constraint $\gamma$ and (d) normalized rotation $\widehat{\delta }$ in response to x- and y-polarized excitation of 118 fluorescent beads. Green, 20-nm beads; purple, 100-nm beads. Scale bar: 1 μm; color bar: detected photons/pixel.

The measured anisotropy factor $\gamma$, or the effective rotational constraint, of fluorescent beads is a convolution of the distribution of molecular orientations within the bead with the probability of pumping those molecules with polarized light. However, within many material or biological systems, such as fluorescent beads, nanoscale emitters are not accurately modeled by a symmetrically rotating dipole with a certain rotational constraint. We therefore utilize direct basis matrix inversion to measure the full emission anisotropy, i.e., all six second moments, of the fluorescent beads given by $\mathit{M}={\mathit{B}}^{-1}\mathit{I}/I_0$.

The Tri-spot PSF image of a typical 100-nm bead does not change significantly under different pumping polarizations; the normalized change in spot brightnesses between x-polarized and y-polarized pumps $\left|\frac{{\mathit{I}}_{\mathrm{x}-\text{pump}}}{\left|{\mathit{I}}_{\mathrm{x}-\text{pump}}\right|}-\frac{{\mathit{I}}_{\mathrm{y}-\text{pump}}}{\left|{\mathit{I}}_{\mathrm{y}-\text{pump}}\right|}\right|=5\%$ [Fig. 2(a)]. However, that of a typical 20-nm bead changes much more [14%, Fig. 2(b)]. To further quantify this effect, we define $\delta$, the angular rotation of the second-moment vector $\mathit{M}$ in response to a rotation in pumping polarization given by

$$\delta ={\text{cos}}^{-1}\frac{{\mathit{M}}_{\mathrm{x}-\text{pump}}·{\mathit{M}}_{\mathrm{y}-\text{pump}}}{\left|\right|{\mathit{M}}_{\mathrm{x}-\text{pump}}\left|\right|\left|\right|{\mathit{M}}_{\mathrm{y}-\text{pump}}\left|\right|},$$ (2)

where ${\mathit{M}}_{\mathrm{x}-\text{pump}}$ and ${\mathit{M}}_{\mathrm{y}-\text{pump}}$ are the second-moment vectors measured in response to x-polarized and y-polarized excitation light, respectively. We generally expect $\delta$ to decrease as $\gamma$ increases; that is, for a fixed SM emitter ($\gamma =1$), there is no change in the emission pattern when changing pump polarization (${\delta }_{\text{fix}}=0$, Fig. S10, see supplementary material Discussion). We expect that an isotropic emitter (i.e., an ensemble of independent fixed fluorescent molecules) should emit with varying orientational second moments depending on how they are pumped (${\delta }_{\text{iso}}=50.48°$, supplementary material 3.2); that is, anisotropic pumping causes an isotropic emitter to emit anisotropically. Interestingly, our measurements of normalized $\widehat{\delta }=\delta /{\delta }_{\text{iso}}$ [Fig. 2(d)] show that 20-nm beads exhibit a larger second-moment rotation (median $\widehat{\delta }=0.29$) than 100-nm beads (median $\widehat{\delta }=0.08$). This measurement suggests that there is a depolarization mechanism between molecules within the 100-nm beads, such as homo-Förster Resonance Energy Transfer⁴⁰ or rotational relaxation during the fluorescence lifetime,³¹ that causes polarized excitation to result in emitted fluorescence that is more isotropic than expected. This depolarization effect is much weaker within 20-nm beads. The Tri-spot PSF is capable of detecting this depolarization because its orientation measurements are independent of excitation polarization, and unlike conventional fluorimeters, the Tri-spot PSF is sensitive enough to detect the emission anisotropy of single fluorescent nanoparticles and SMs.

Single-particle tracking is commonly used in materials science and biophysics to provide insights into the modes of motion of the target object, which may be diffusive, confined, or even motor-directed. Differentiating translational motions from rotational ones has revealed, for example, the fundamental mechanics of the movement of individual molecular motors.¹⁸ The strength of the Tri-spot PSF is its capability to simultaneously measure the rotational and translational diffusion of many SMs within a field of view. To demonstrate, we used the Tri-spot PSF to image single Atto 647N molecules embedded in a thin polyvinylpyrrolidone (PVP) film (54 ± 15 nm) in 10-min intervals as they were exposed to humid air.

When the PVP film is exposed to humid air, the spots of the Tri-spot PSF change dramatically in relative brightness [Figs. 3(i) and 3(ii)], thereby demonstrating changes in molecular orientation (supplementary material 3.1). The decreasing effective rotational constraint of embedded fluorescent probes over time, for example, from 10 to 60 min for molecule 1, is evidence of the polymer network softening and swelling as the moisture slowly penetrates the film. Interestingly, the heterogeneity across SMs in their measured rotational constraints [Figs. 3(iii) and S13(c)–S13(g)] suggests that the swelling is non-uniform across the film, even at long timescales. SMs have exhibited increasing translational diffusion when exposed to increasing humidity.⁴¹ However, we observe no correlation between rotational anisotropy and lateral diffusion, measured as the average displacement jump $\Delta r$ between frames using Tri-spot images [Figs. 3(iii) and S13(c)–S13(g), supplementary material 4.1]. The effective rotational constraint $\gamma$ of molecules 1 and 2 decreased by 0.05 and 0.01 over 50 min [an increase of 15° and 7° in the cone half-width if the molecule uniformly diffuses within a cone, Figs. 3(iii)], while no significant increase in translational diffusion over the same time period was observed.

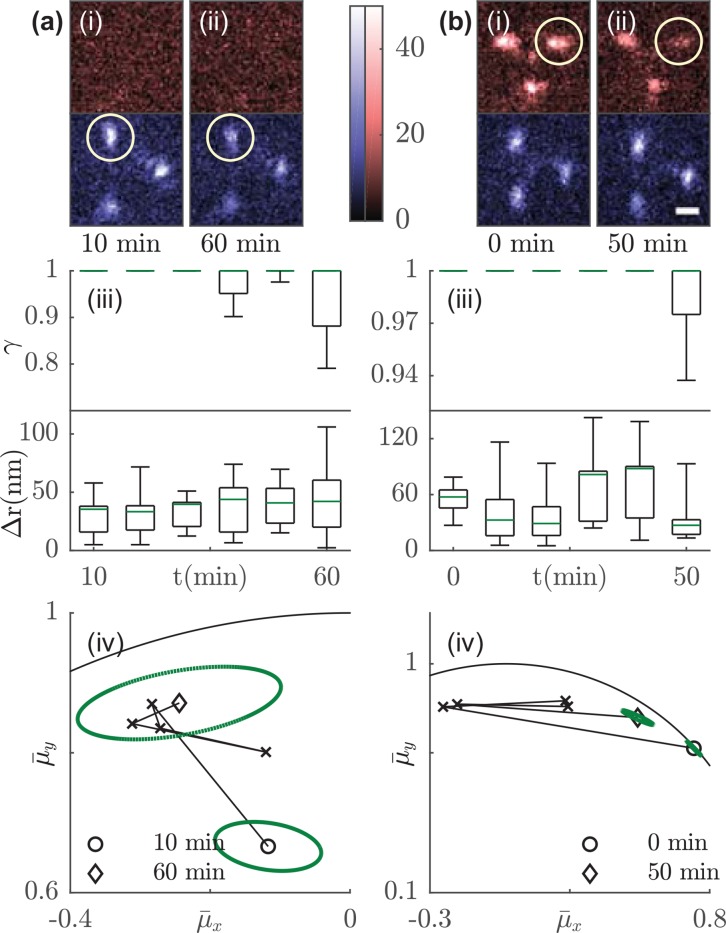
FIG. 3.

Effective rotational constraint, lateral diffusion, and orientation tracking of Atto 647N molecules embedded in a thin PVP film under continuous exposure to humid air. Tri-spot images of (a) molecule 1 and (b) molecule 2 at the (i) beginning and (ii) end of time-lapse imaging. Circle highlights the change in spot brightness. The change in (iii) the measured anisotropy factor $\gamma$ and the lateral movement $\mathrm{\Delta }r$ over 50 min. The estimated rotational constraint has a cutoff value of 1 (supplementary material 4.4). Green: median; Box: first and third quartile; Error bar: minimum and maximum. (iv) The orientation trajectory over 50 min. Circle represents the beginning and diamond represents the end of the time-lapse measurement. Dashed green ellipse represents the covariance matrix in the estimated orientation $\left({\overline{\mu }}_x,{\overline{\mu }}_y\right)$ measured at the beginning and end points. Molecule 1 rotates from $\left(-0.12\pm 0.06,\hspace{0.17em}0.67\pm 0.03\right)$ (mean ± std.) to $\left(-0.24\pm 0.12,\hspace{0.17em}0.87\pm 0.04\right)$, and molecule 2 rotates from $\left(0.73\pm 0.03,\hspace{0.17em}0.66\pm 0.03\right)$ to $\left(0.51\pm 0.05,\hspace{0.17em}0.78\pm 0.03\right)$ over 50 min. Solid curve marks the orientation domain ${\overline{\mu }}_x^2+{\overline{\mu }}_y^2\le 1$. Scale bar: 1 μm; color bar: detected photons/pixel.

Our time-lapse imaging also tracked the average orientation of each molecule [Figs. 3(iv) and S13(c)–S13(g)], quantifying rotational diffusion over both slow timescales (∼minutes between each interval) and faster timescales [∼seconds across camera frames, depicted as ellipses drawn at the initial and end time points in Figs. 3(iv) and S13(c)–S13(g)]. This slow-scale rotation is distinct from our measurements of anisotropy factor $\gamma$, which quantify rotational diffusion within a single camera frame (50 ms). The rotational constraint of molecule 1 $\{\gamma =0.95\pm 0.07$ [mean ± std.], 15° cone half-angle, Fig. 3(a-iii), t = 60 min} is similar to that of molecule 2 [$\gamma =0.99\pm 0.02$, 7° cone half-angle, Fig. 3(b-iii), t = 50 min], but molecule 1 rotates much less than molecule 2 does over 50 min [23° for molecule 1, Fig. 3(a-iv), vs. 63° for molecule 2, Fig. 3(b-iv)]. Observations of other molecules also show that smaller effective rotational constraints $\gamma$ within a single frame does not necessarily lead to more rotation over long timescales [Figs. S13(c)–S13(g)]. Interestingly, molecule 7 rotates by 80° within 1 h although its rotational constraint is not significantly larger than that of molecules 3–6, which all rotate less than 50°. Therefore, the unique strength of the Tri-spot PSF is its capability of quantifying both average orientation between camera frames and rotational movement within each camera frame, rather than requiring multiple acquisitions as in absorption-based measurements. It also allows measurements of rotational diffusion of many molecules simultaneously across a large field of view compared to higher-speed methods that measure these orientational parameters one molecule at a time.⁴² This ability is enabled by our direct engineering of the Tri-spot PSF to encode all 6 components of the second-moment vector M into its images with maximum sensitivity.

In summary, we report the design of a Tri-spot PSF that accurately and precisely measures the 3D orientation and the rotational mobility of fluorescent emitters within one camera frame. The Tri-spot PSF achieves an average orientation precision of 5° and an average precision of 0.20 in the rotational constraint (a cone-width precision of 14°) for 3000 photons detected from a single molecule. We demonstrated experimentally that the Tri-spot's orientation measurements are sufficiently accurate to reduce the anisotropy-induced localization bias from 30 nm to 7 nm for an SM 200 nm out of focus. The Tri-spot's sensitivity to all orientational degrees of freedom shows that both 100-nm and 20-nm diameter fluorescent beads do not emit light isotropically and reveals that the larger beads exhibit stronger depolarization effects. The Tri-spot PSF is also compatible with SMLM and SM-tracking techniques and measured the rotational and translational diffusion of dye molecules embedded within a softening polymer film. The ability to fully quantify the 3D orientation, the rotational constraint, and the translational diffusion of SMs could significantly benefit nanoscale studies across biology and materials science, including interrogating protein-protein interactions, elucidating mechanisms of cargo transport along and across cell membranes, and understanding interactions between fluorophores and nanoparticles.⁴³ Further refinements will make it possible to measure the z position of point-like emitters, such that SMLM with the Tri-spot PSF will provide super-resolved images of 3D location, 3D orientation, and rotational constraint of any molecules or nanoparticles of interest.

See supplementary material for materials and methods, design of the Tri-spot PSF, a theoretical image formation model, detection and estimation of the Tri-spot PSF, and additional discussion and figures.