Data Analysis for Total Internal Reflection Fluorescence Microscopy

Abstract

In the microscopes we use to analyze total internal reflection fluorescence (TIRF), the emitted fluorescence is split chromatically, using dichroic filters, into either two or three different colors (“channels”). In our two-color instrument, the green emission wavelengths (405–488 nm; for imaging green fluorescent protein [GFP]-tagged proteins) and far-red emission wavelengths (650–800 nm; for imaging Alexa-647-labeled microtubules) are projected onto the upper and lower halves, respectively, of a single camera. A single filter can be swapped to collect near-red wavelengths (561–640 nm; for imaging mCherry, or Alexa-568-labeled microtubules) instead of far-red. Our three-color instrument is very similar except that the green, near-red, and far-red color ranges are projected onto three separate cameras. In either case, the different colors can be imaged simultaneously. Typically, we collect images at 10 frames/sec for ~200 sec. We have developed a series of semiautomated image analysis programs, written in LabView, to obtain the brightness, residence time, and mobility of individual particles bound to single microtubules. The basic analysis steps are straightforward and could also be implemented using ImageJ or Matlab. For convenience, this protocol describes the analysis of a single microtubule. Data from many microtubules across many experimental trials are needed to obtain robust conclusions that are independent of stochastic and trial-to-trial variability.

MATERIALS

Equipment

Data analysis program (e.g., Igor Pro, Matlab, or Microsoft Excel; see Step 7) EMCCD camera (iXon DV887 from Andor)

Image analysis programs custom written in LabView (see Gestaut et al. 2010)

Copies of our programs are available for free upon request.

Microscope (Ti-U from Nikon or equivalent)

METHOD

For appropriate sample preparation procedures, see Protocol: Coverslip Cleaning and Functionalization for TotaI internal Reflection Fluorescence Microscopy (Kudalkar et al. 2015a) and Protocol: Preparation of Reactions for Imaging with Total Internal Reflection Fluorescence Microscopy (Kudalkar et al. 2015b).

1. Trace the contour of a microtubule by hand using a multisegment line tool (Fig. 1A).

   The filaments in the experiments described here should remain stationary on the coverslips. Assuming negligible drift, the contours traced in an early image will apply to the entire duration of the time-lapse experiment.

2. Map the microtubule contour automatically onto the other color channel(s), and use it to generate a kymograph(s) showing the arrival of particles on the microtubule, their movement along the filament, and their release (Fig. 1B).

   Accurate mapping from one color channel to another usually requires coordinates to be translated (i.e., moved along x and y directions) and also slightly rotated. Depending on the microscope setup, slight magnification changes might also be needed. The required mapping operation can be determined empirically using reference particles that fluoresce in all the channels.

3. For each particle visible on the kymograph, estimate its location along the microtubule by finding the brightest pixel at each time point.

4. Map the one-dimensional estimate of location versus time from Step 3 back onto the original, two-dimensional particle image using the contour from Step 2.

5. Obtain the pixel coordinates of the particle in each image by using a two-dimensional search for the brightest pixel within a small square (7 × 7 pixels) centered on the estimated position from Step 4.

   Alternatively, fit a two-dimensional Gaussian function to the intensity distribution within the small square. A Gaussian fit is more time-consuming and generally does not improve localization accuracy for single GFP molecules imaged at 10 frames/sec in our microscopes. However, in cases where more photons are collected per frame, Gaussian fitting may improve localization accuracy.

6. After coordinates are obtained in Step 5, compute particle brightness at each time point by integrating pixel intensities over a small square, centered on the particle position. Estimate background levels by integrating over a larger concentric square area, excluding the central small square (Fig. 1C).

7. For every particle, save a file containing the pixel coordinates, integrated brightness, and background level at each time point (Fig. 1D).

   Once the particle data are saved, we use another graphing and data analysis program, Igor Pro, to carry out the subsequent analysis steps. These steps could also be performed using Matlab or Microsoft Excel.

8. Examine plots of brightness versus time for each event to confirm the arrival and release times, and to identify photobleaching steps.

9. Compute the residence times for each event from the start and end times obtained in Steps 7 and 8. Plot a distribution of residence times, either in the form of a histogram (e.g., see Gestaut et al. 2008 or Powers et al. 2009) or as a cumulative survival probability versus time (e.g., see Sarangapani et al. 2013).

   Histograms are more intuitive, but cumulative distributions avoid the need for binning and facilitate comparisons because many can be overlayed onto a single graph without loss of clarity.

10. Note that the residence time distribution is often (but not always) well described by a single exponential decay, except that the lowest bins (corresponding to the shortest residence times) may be underpopulated due to the finite time resolution of the instrument. Invert the mean from the best-fit exponential (excluding the lowest bins) or, equivalently, its time constant, τ, to give the off rate, k_off = τ⁻¹ (e.g., in units of sec⁻¹).

11. For each event, also calculate a mean squared displacement along the microtubule long axis, <x²>, for every possible time lag, Δt. Average the <x²> values across many events to generate a plot of <x²> versus Δt for a population (each individual binding event contributing equally to the population average).

12. Compute the one-dimensional diffusion coefficient, D, from the slope, m, of a linear fit to the plot according to D = (1/2)m = (1/2) <x²> Δt⁻¹.

FIGURE 1.

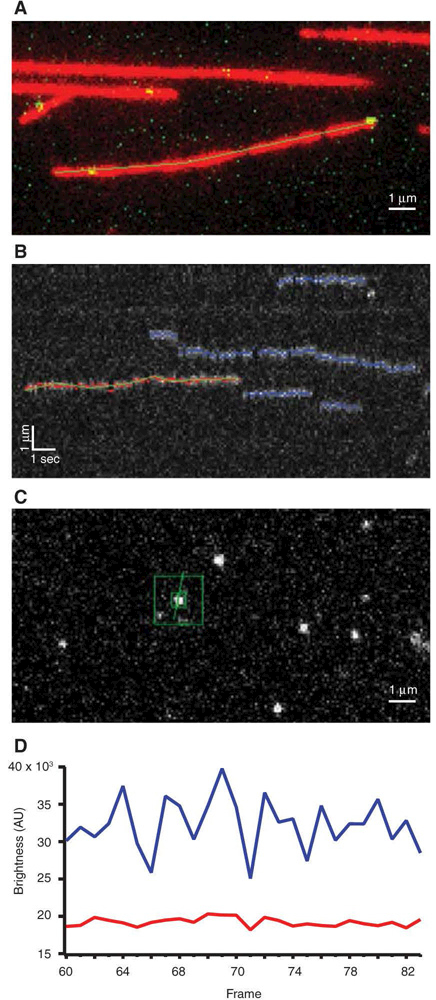
TIRF data analysis. (A) Overlapping green and red channels depict a microtubule (red) that was traced by hand using a multisegmented tool. Yellow spots show GFP-tagged proteins binding to the microtubule. (B) Kymograph created from a traced microtubule as in A. Red dots and green line indicate the currently selected binding event, blue lines show previously selected events, and untraced events are shown in gray. (C) Particle brightness is computed at each time point of event from B. Integrated brightness is measured using small green box surrounding particle and larger green box is used to calculate background intensity. (D) Example plot of pixel brightness (blue trace) and background level (red trace) over time generated from C.