Direct Evidence for the Effect of Glycerol on Protein Hydration and Thermal Structural Transition

Abstract

The mechanisms of protein stabilization by uncharged solutes, such as polyols and sugars, have been intensively studied with respect to the chemical thermodynamics of molecular crowding. In particular, many experimental and theoretical studies have been conducted to explain the mechanism of the protective action on protein structures by glycerol through the relationship between hydration and glycerol solvation on protein surfaces. We used wide-angle x-ray scattering (WAXS), small-angle neutron scattering, and theoretical scattering function simulation to quantitatively characterize the hydration and/or solvation shell of myoglobin in aqueous solutions of up to 75% v/v glycerol. At glycerol concentrations below ∼40% v/v, the preservation of the hydration shell was dominant, which was reasonably explained by the preferential exclusion of glycerol from the protein surface (preferential hydration). In contrast, at concentrations above 50% v/v, the partial penetration or replacement of glycerol into or with hydration-shell water (neutral solvation by glycerol) was gradually promoted. WAXS results quantitatively demonstrated the neutral solvation, in which the replacement of hydrated water by glycerol was proportional to the volume fraction of glycerol in the solvent multiplied by an exchange rate (β ≤ 1). These phenomena were confirmed by small-angle neutron scattering measurements. The observed WAXS data covered the entire hierarchical structure of myoglobin, ranging from tertiary to secondary structures. We separately analyzed the effect of glycerol on the thermal stability of myoglobin at each hierarchical structural level. The thermal transition midpoint temperature at each hierarchical structural level was raised depending on the glycerol concentration, with enhanced transition cooperativeness between different hierarchical structural levels. The onset temperature of the helix-to-cross β-sheet transition (the initial process of amyloid formation) was evidently elevated. However, oligomerization connected to fibril formation was suppressed, even at a low glycerol concentration.

Introduction

Glycerol is a simple polyol compound that is widely used as a nontoxic additive in various industrial products as a preservative, humectant, and thickening stabilizer; it is also used as a cryoprotectant for storing enzymatic reagents, bacteria, nematodes, mammalian embryos, and other materials. The function of protein stabilization by glycerol has been studied for a long time. An early study of the effect of glycerol on proteins using the densitometric measurement by Gekko et al. reported that the preferential hydration of proteins in glycerol-water mixture minimizes the surface of contact between proteins and glycerol to stabilize those native structures (1). A study hydrogen exchange of myoglobin conducted by Calhoun et al. indicated a negligible influence of glycerol solvents on protein fluctuation (2). On the other hand, a static light scattering study of bovine pancreatic trypsin inhibitor conducted by Farnum et al. suggested that the repulsive intermolecular force increases with glycerol concentration, which was explained by the incorporation of a layer of structured water that was enhanced by the presence of glycerol (3). A molecular dynamics (MD) simulation study by Vagenende et al. reported that the preferential hydration of proteins in glycerol-water mixtures originates mainly from electrostatic interactions that induce the orientation of glycerol molecules at the protein surface, which excludes the interaction of additional glycerol molecules (4). The same authors also suggested that glycerol may prevent protein aggregation by inhibiting protein unfolding and by stabilizing aggregation-prone intermediates through preferential interactions with hydrophobic surface regions that favor amphiphilic interface orientations of glycerol. A Raman and quasi-elastic inelastic neutron-scattering study by Caliskan et al. showed that the rapid conformational fluctuations, low-frequency vibrations, and temperature variations of proteins are very sensitive to the behavior of solvents (5). The recent rheometer study by Ronsin et al. on the effect of glycerol on the dynamics of collagen re(de)naturation suggested the presence of a nanometer-thick, glycerol-free hydration layer where glycerol is completely expelled (6). Despite this collective data, there is little direct evidence showing the effect of glycerol on the protein structure, its preferential hydration (solvation) layer, and thermal stability.

On the other hand, it is known that the stabilities of proteins in aqueous solutions are affected by changes in temperature and pressure and by the addition of salts and neutral substances (7, 8). The presence of osmolytes, such as sugars and polyols, affects the structural stability of proteins in aqueous solutions because of the preference to be solvated by either water or osmolyte (9, 10). The effect of osmolytes on protein structural stability has been explained by several physicochemical factors, including specific binding between proteins and osmolytes and changes in solvent viscosity (11, 12). A molecular-crowding environment might affect the equilibrium state of proteins from the physicochemical point of view, although this remains debatable. In addition, hydration is the key determinant of the isothermal and concentration-dependent effects on protein equilibria (13, 14). Inelastic neutron scattering analyses (15, 16, 17, 18) have revealed that the dynamics of proteins are coupled with and/or governed by surrounding water molecules. Therefore, it is important to clarify the theoretical and experimental relationships between protein hydration and the molecular-crowding environment, even for low molecular weight molecules.

Physicochemical interpretations of the crowding effect of small molecules on proteins (10, 11, 13, 19) have revealed that a change in the chemical potential of bulk water due to highly concentrated crowding molecules causes a difference in chemical potential with water at the protein interface, which generates osmotic stress. To relax the distortion due to osmotic stress, the surface structure and the exclusion area (preferential hydration area) of the protein change, producing a shift to a different equilibrium state from the state in the dilute solution. At the same time, the changes in the diffusive motion (translational/rotational motion, internal motion) and in the intermolecular interaction are also induced. However, direct observation and characterization of protein structures and their solvation in solutions in which large quantities of other molecules coexist are usually difficult because the significant increase of background scattering from cosolutes interferes with the statistically accurate acquisition of data from a protein. Therefore, most experimental studies of protein structure and stability are conducted in dilute solutions (7, 8).

Despite these hurdles, the remarkable progress of MD simulations has provided fruitful insights on the effect of molecular crowding on protein structure and hydration. Dastidar et al. demonstrated a sharp decrease in the interaction energy between the water layers and protein beyond 4 Å from the protein surface (20). The study of the effect of protein crowding on the structure and dynamics of water by Harada et al. suggested significant changes in both the structure and dynamics of water under highly crowded conditions (21). An all-atom MD simulation study by Wang et al. on the influence of the size of the crowding proteins on the hydration structure indicated changes in the accessible volumes and water locations in three well-defined regions, whereas the water densities as a function of the distance from protein surfaces remained the same (22). These studies suggest the importance of quantitative experimental evidence to compare with theoretical and simulation results.

In this study, we clarified the effect of glycerol on both the hydration shell and thermal structure transition of myoglobin using synchrotron radiation wide-angle x-ray scattering (SR-WAXS) and small-angle neutron scattering (SANS). Myoglobin has proven to be a good model in studies of protein folding (7) because it displays a cross-β transition that accompanies amyloid aggregate formation (23, 24). SR-WAXS is a unique method that enables the observation of the entire hierarchical structure of proteins from their quaternary or tertiary structures to secondary structures in solutions (25). The details of the structural transition process of proteins can be analyzed separately at each hierarchical structure level (26). We have already clarified the initial process of amyloid formation of apomyoglobin using synchrotron radiation small-angle x-ray scattering (27) and the characteristics of the dynamics of apomyoglobin in the helix-to-sheet transition using a combined SR-WAXS and elastic incoherent neutron-scattering analysis (28). In the neutron-scattering measurements, we employed the inverse-contrast variation method, which is quite unique in its capability to selectively elucidate only the structures of the biological materials of interest (29, 30).

We successfully obtained scattering data of myoglobin with high statistical accuracy in concentrated glycerol solutions of approximately (∼here and hereafter) 75% v/v. Combined experimental results and theoretical solution-scattering simulations yielded direct evidence on the effect of glycerol on the hydration (solvation) shell of myoglobin and the thermal structural transition. These results clearly indicate that the function of glycerol as a stabilizer of proteins is related to the preservation of protein hydration by the preferential exclusion of glycerol from the hydration-shell region of the protein at glycerol concentrations lower than ∼40% v/v, which agrees well with previous studies using different techniques (1, 2, 3, 4, 5, 6). At glycerol concentrations above ∼50% v/v, the partial penetration or replacement of glycerol into or with the hydration shell of water molecules surrounding the protein surface appears to depend on the glycerol concentration. The trend of hydration or solvation of a protein in glycerol-water solutions can be explained quantitatively by the change from the preferential exclusion of glycerol (preferential hydration) to its neutral solvation of glycerol.

Materials and Methods

Myoglobin from horse skeletal muscle, glycerol, and deuterated glycerol (98 atom % D) were purchased from Sigma-Aldrich (St. Louis, MO) and were used without further purification. All other chemicals used were of analytical grade. Deuterium oxide (99.9 atom % D; Sigma-Aldrich) was used for neutron-scattering experiments. The buffer solvent used was 10 mM HEPES (N-(2-hydroxymethyl) piperazine-N′-(2-ethane-sulfonic acid)) at pH 7.4 (pD 7.0). Myoglobin was dissolved in the buffered solvent on the concentration of 5% w/v, which was used as the protein stock solution. Glycerol solutions with different concentrations were prepared. The stock protein solution and the various glycerol solutions were mixed to generate 2% (w/v) protein in 10, 20, 30, 40, 50, 60, or 75% (v/v) glycerol.

SR-WAXS measurements were done by using a BL-40B2 spectrometer at the Japan Synchrotron Radiation Research Institute (Harima, Japan) and by using a BL-10C spectrometer at the High Energy Accelerator Research Organization (KEK, Tsukuba, Japan). The x-ray wavelengths and the sample-to-detector distances were 51 cm for 0.75 Å x-ray and 4089 cm for 1.0 Å for x-ray at BL-40B2 as well as 190 cm for 1.49 Å x-ray at BL-10C. The x-ray scattering intensity was recorded by the R-AXIS IV (30 × 30 cm², 100 μm, (Rigaku, Tokyo, Japan)) at both facilities. The exposure times for BL-40B2 and BL-10C were 60 and 180 s, respectively. The temperature of the sample solutions contained in the sample cells was controlled in the temperature range from 25 to 85°C using a model mK2000 temperature controller (Instec, Boulder, CO). During the measurements, the sample solutions were slowly oscillated to avoid radiation damage. SANS measurements were carried out by using a D22 spectrometer at the research reactor of the Institut Laue-Langevin (ILL, Grenoble, France) and by using the BL15 TAIKAN spectrometer at the pulsed-neutron source of the Materials and Life Science (MLF) Experimental Facility of the Japan Proton Accelerator Research Complex (J-PARC, Tokai, Japan). The neutron wavelengths were 6 Å at ILL and 0.5–6.0 Å at J-PARC. At both facilities, the sample solutions were contained in the quartz cells with 1 mm path length. The exposure time was around 10–30 min. Just before the scattering measurements, the sample solutions were filtered to remove aggregates by using the centrifugal filter unit (Merck, Darmstadt, Germany) with a molecular weight cutoff of 50 kDa.

The background correction for SANS data was done conventionally (30). WAXS data correction was done as previously described (25, 26). The distance distribution function, p(r), was calculated by the Fourier inversion of the scattering curve I(q), as follows:

$$p\left(r\right)=\frac{1}{2{\pi }^2}{\int }_0^{\infty }rqI\left(q\right)\sin \left(rq\right)dq,$$ (1)

where q is the scattering vector (q = (4π/λ)sin(θ/2)), θ is the scattering angle, and λ is the x-ray wavelength. The radius of gyration, Rg, and the zero-angle scattering intensity, I(0), were determined by using the following equations (31):

$$R_g^2=\frac{{\int }_0^{D_{\max }}p\left(r\right)r^{2}dr}{2{\int }_0^{D_{\max }}p\left(r\right)dr},$$ (2)

$$I\left(0\right)=4\pi {\int }_0^{D_{\max }}p\left(r\right)r^{2}dr,$$ (3)

where D_max is the maximal diameter of the particle determined from the p(r) function, satisfying the condition p(r) = 0 for r > 0. The Rg and I(0) values were also calculated by using the Guinier plot (q² vs. ln I(q)).

Execution of a theoretical simulation of the solution scattering curve from a protein with known atomic structure or fitting the simulation to the experimental scattering curve obtained from x-ray or neutron scattering was done using the CRYSOL program for x-ray scattering and the CRYSON program for neutron scattering. Both programs were developed by Svergun et al. (32) based on a spherical harmonics series method (33), taking into account the existence of the hydration shell of a protein from its atomic structure registered in the Protein Data Bank. In both programs, the width of hydration shell is limited to 3 Å. Solvent scattering density and hydration-shell contrast were variables. The CRYSOL and CRYSON programs very accurately reproduce experimental SANS curves of proteins in solutions (34). However, a difficulty for both programs is that for WAXS to be counted as sufficient for analyzing WAXS data, two parameters (excluded volume and weights of the solvation layer) are essential (34).

Results and Discussion

Myoglobin structure depending on glycerol concentration observed by x-ray scattering

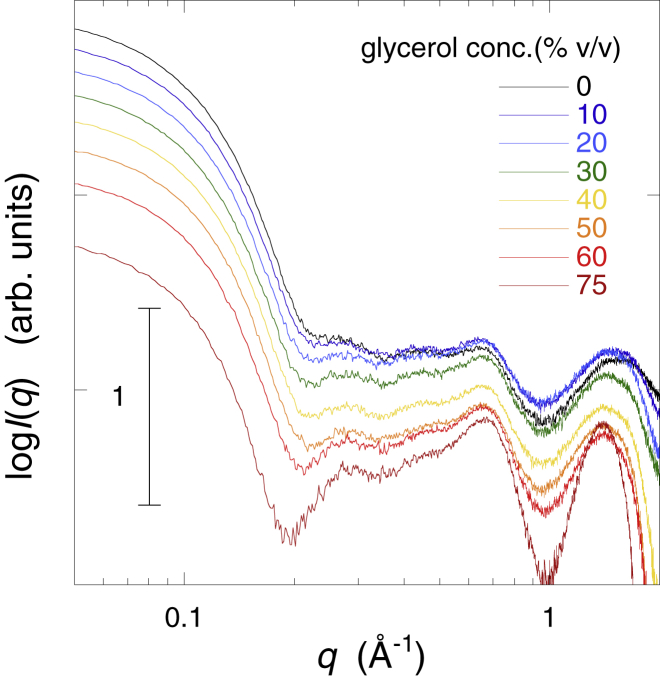
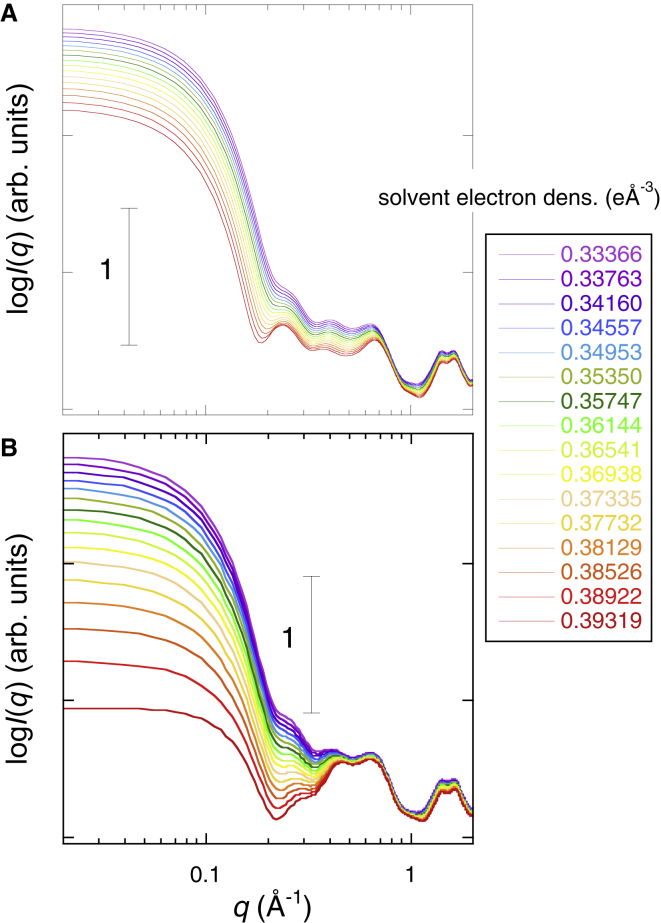
Fig. 1 shows the WAXS curves of myoglobin depending on the glycerol concentration (0, 10, 20, 30, 40, 50, 60, and 75% v/v). As shown previously (26, 27), the WAXS curves of a protein in the different scattering regions mostly reflect the complete characteristics of the protein in the different hierarchical structure levels. These characteristics include the quaternary and tertiary structures (q < ∼0.2 Å⁻¹), the interdomain correlation (∼0.25 Å⁻¹ < q < ∼0.5 Å⁻¹), the intradomain structure (∼0.5 Å⁻¹ < q < ∼0.8 Å⁻¹), and the secondary structure including the closely packed side chains (∼1.1 Å⁻¹ < q < ∼1.9 Å⁻¹), respectively. The scattering intensity of the particles in solutions depends on the difference between the scattering density of the solute particles and those of the solvent (33). This is the excess average scattering density, which is termed contrast $\left(\mathit{\Delta }\rho \right)$. With increasing glycerol concentration, the scattering intensity in the small q region below q = ∼0.2 Å⁻¹ decreases systematically because of the change of the contrast of myoglobin by the presence of glycerol (Fig. 1). However, there was no evident change of the slope in this region, suggesting the preservation of the globular tertiary structure. In contrast, the profile of the scattering curve in the q region from ∼0.25 to ∼0.8 Å⁻¹ changed gradually, which is attributable to the change of the contrast depending on glycerol concentration, as shown in the following theoretical simulation. The profile of the scattering curve in the q region from ∼1.1 to ∼1.9 Å⁻¹ was mostly constant. The data indicate the retention of the intramolecular and secondary structures of native myoglobin even in 75% v/v glycerol.

Figure 1.

Wide-angle x-ray scattering curve of myoglobin depending on glycerol concentration (0, 10, 20, 30, 40, 50, 60, and 75% v/v). The protein concentration is 2% w/v in 10 mM HEPES buffer at pH 7.4 and 25°C. To see this figure in color, go online.

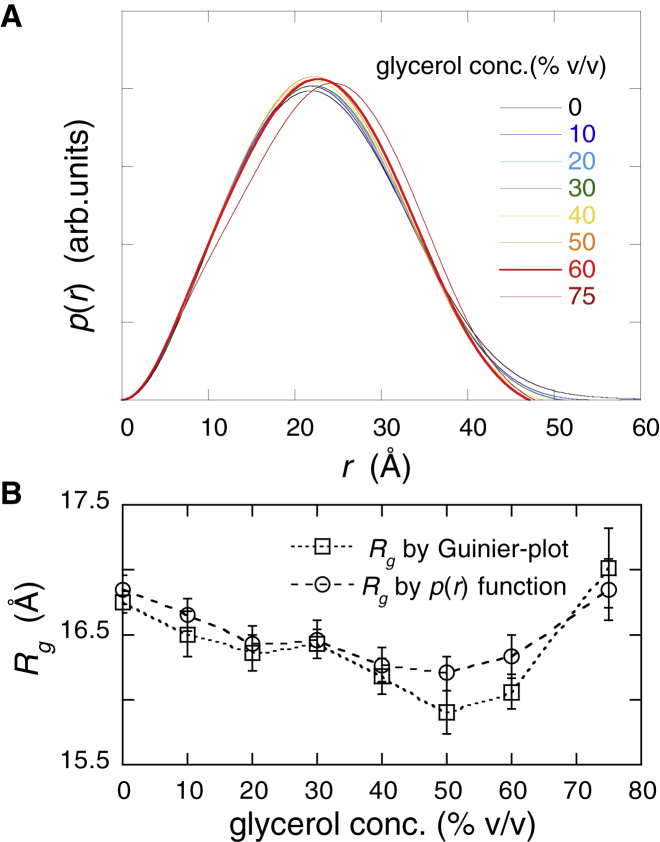
Fig. 2 depicts the distance distribution function, p(r), and the radius of gyration, R_g, of myoglobin obtained by the Fourier transform of the scattering curve in Fig. 1, where (A), p(r) and (B), R_g. The p(r) functions in Fig. 2 A were calculated using Eq. 1. The maximal diameter, D_max, of the protein decreased from ∼54 Å at 0% v/v glycerol to ∼47.5 Å at 50% v/v glycerol and slightly increased to ∼48.5 Å at 75% v/v. In contrast, the value of the peak position, p(r)_max, was mostly constant at ∼22 Å in the presence of up to 50% v/v glycerol and increased to ∼25 Å at 75% v/v glycerol. Fig. 2 B presents the values of the radius of gyration, R_g, obtained using the p(r) function (Eq. 2) and the Guinier plot. The R_g value once decreases from 16.9 ± 0.1 Å by using the p(r) function (16.8 ± 0.1 Å by Guinier plot) to 16.2 ± 0.1 Å by the p(r) function (15.9 ± 0.2 Å by Guinier plot) at 50% v/v glycerol, and it increases to 16.9 ± 0.2 Å by p(r) function (17.0 ± 0.3 Å by Guinier plot) at 75% v/v glycerol. The changing tendency of the R_g value agreed with that of the D_max value in Fig. 2 A. These WAXS results were reasonably explained by the WAXS simulation, as shown in the following section.

Figure 2.

Distance distribution function, p(r), obtained by the Fourier transform of the scattering curve in Fig. 1, and radius of gyration, R_g, of myoglobin. (A) depicts p(r), and (B) depicts R_g. In (B), R_g values obtained from Guinier plot and p(r) function are shown. To see this figure in color, go online.

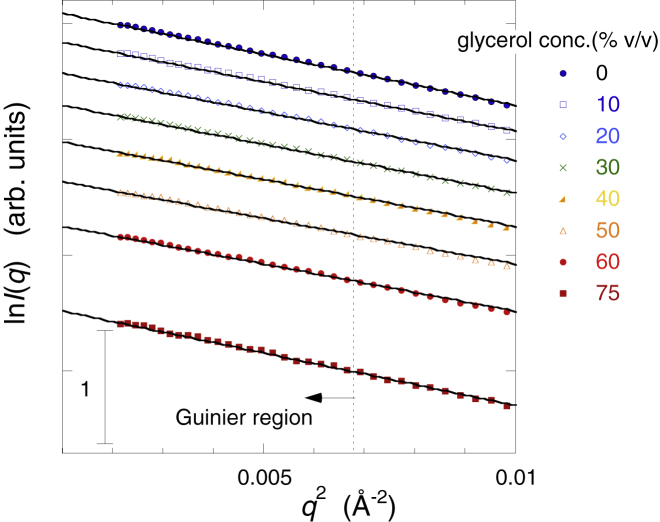
The Guinier plot is sensitive to the presence of aggregative or repulsive interparticle interactions. The light-scattering study of bovine pancreatic trypsin inhibitor by Farnum et al. (3) revealed that the repulsive intermolecular force between proteins is enhanced by glycerol. In addition, we used a solution with a relatively high protein concentration. Therefore, it is important to check for the effect of interparticle interaction on the observed scattering curves. Fig. 3 presents the Guinier plots of the scattering curves in Fig. 1. In Fig. 3, the lines represent the least-square fitting (q² vs. ln I(q)) using Guinier-region (q < ∼0.07 Å⁻¹). If attractive or repulsive interparticle interactions existed, deviation of the Guinier plot from linearity would have been seen. However, there was no trend of deviation, indicating that under these experimental conditions, any creation of interparticle interactions was not induced by glycerol.

Figure 3.

Guinier plots of WAXS curves in Fig. 1. The solid lines represent the least-square fitting (q² vs. ln I(q)) using the so-called Guinier region (q < ∼0.07 Å⁻¹). To see this figure in color, go online.

Simulation of x-ray scattering curve and radius of gyration of myoglobin in molecular-crowding solution based on the preferential solvation model and the preferential exclusion model

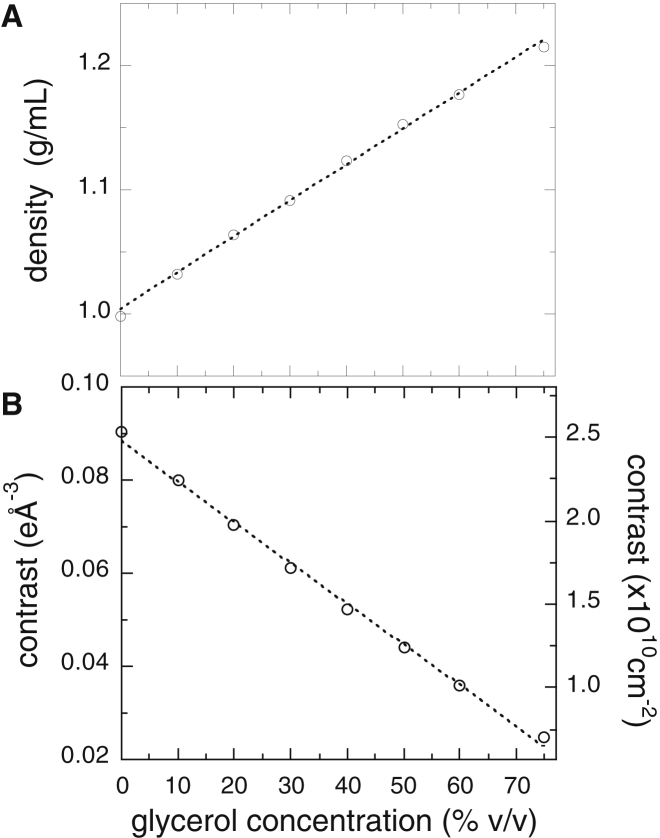
As described above, the observed scattering curve of the solute particle depends on the difference between the scattering density of the solute and that of the solvent, which is termed contrast, Δρ. In this experiment, the average scattering density of the solvent varies depending on the glycerol concentration. An x-ray scattering simulation requires an estimate of the variation of Δρ in mixed glycerol-water solutions. We have measured the mass densities of the glycerol solvents to determine those scattering densities. Fig. 4 A presents the observed densities of the water solvents containing different concentrations (% v/v) of glycerol using a model R200D electric balance (Sartorius, Göttingen, Germany). The mass density displayed good linearity across the range of concentrations. The average scattering densities (electron densities) of proteins are known to range from ∼11.7 to ∼12.0 × 10¹⁰ cm⁻² (∼0.416–0.427 eÅ⁻³) for x-rays (33). Based on the crystal structure of myoglobin (code number 1WLA registered in the Protein Data Bank (35)), the average scattering density of myoglobin was calculated as 11.9 × 10¹⁰ cm⁻² (0.424 eÅ⁻³) for x-rays. Fig. 4 B illustrates the glycerol concentration dependence of the x-ray contrast of myoglobin in cm⁻² and eÅ⁻³ units. The presence of glycerol in the solvent altered the contrast of the protein and results in the change of the scattering curve.

Figure 4.

Observed mass density of the water solvent containing glycerol at different concentrations (% v/v) and the estimated value of the excess average scattering density (contrast) for x-ray of myoglobin in glycerol solution. (A) presents mass density, and (B) presents contrast.

Comparison of the theoretical calculation of the scattering curve with the experimental observations revealed the details of the effect of glycerol on the protein structure observed experimentally. The theoretical WAXS simulations were executed by using the CRYSOL program (32). The amount of protein hydration corresponds to that of water molecules covering protein surface with at least two layers of water (the so-called strongly bound water layer and weakly bound water layer) (36). Therefore, the fixed 3 Å value of the hydration-shell width determined by the CRYSOL program reflects only the first hydration layer of protein. At first, theoretical WAXS simulations were performed by assuming the following two different models, which can happen to the hydration (solvation) shell surrounding the protein surface caused by glycerol. In the first model, the preferential replacement of hydration-shell water molecules with glycerol molecules occurs (preferential solvation model (37)). In this case, the preferential arrangement of glycerol molecules surrounding the protein surface will increase the scattering density of the solvation shell with the rise of glycerol concentration. In this model, the molar concentration of glycerol is always higher than in the bulk glycerol solvent. In the second model, glycerol molecules are preferentially excluded from the protein surface because of the hydration repulsion force. In this case, the hydration-shell density that is always higher than in bulk water is preserved and has a constant value even with increased glycerol (preferential exclusion model and preferential hydration model (1, 6)). Although the above models are extreme cases induced by cosolutes depending on physicochemical conditions, it is meaningful to elucidate qualitatively typical effects of cosolutes on the scattering curve of protein. In other words, the preferential solvation and exclusion/hydration models are equivalent to the assumptions of the partial replacement of hydrated water with glycerol and the nonpenetration of glycerol into the hydration shell, respectively. Fig. 5 provides a schematic diagram of the variation of the contrasts of protein and its hydration (solvation) shell depending on the glycerol concentration for the above models. In the figure, the electron densities of hydration shell and glycerol solvation shell are the same as in the following simulations, and the relative contrast values are displayed correctly. The case of this neutron-scattering measurement is also represented. For preferential solvation, the x-ray contrasts of protein and its solvation shell are always positive values at all glycerol concentrations. In the case of the preferential exclusion of glycerol (preferential hydration), the hydration shell contrast changed significantly from a positive to a negative value with increasing glycerol concentrations.

Figure 5.

Schematic picture of the variation of the contrasts of protein and its hydration (solvation) shell depending on the glycerol concentration used for WAXS simulation in Fig. 6. The relative values of the electron densities of the contrasts are displayed correctly. To see this figure in color, go online.

Fig. 6 depicts the simulated WAXS curves with the rise of the average scattering density (electron density) of the solvent, which is proportional to the glycerol concentration, where Fig. 6 A is the preferential solvation model and Fig. 6 B is the preferential exclusion model. The variable range of the average electron density of the solvent was compatible with that of glycerol concentration range from 0 to 75% v/v. In Fig. 6 A, the average electron density of the solvation shell was set at 1.1 times higher than in the glycerol solvent. In Fig. 6 B, the average electron density of the hydration shell was 1.1 times higher than in bulk water. The scattering curves using other values of the shell-electron densities were also simulated. Compared with the experimental scattering curve in the q-range from ∼0.2 to ∼0.3 Å⁻¹, the decreasing trend of the scattering intensity in Fig. 1 was more similar to that in Fig. 6 B than in Fig. 6 A. The change of the SANS intensity (q < 0.1 Å⁻¹) in Fig. 6 B with increased solvent electron density was much larger than in Fig. 6 A.

Figure 6.

Simulated WAXS curve depending on the average electron density of the solvent that corresponds to the glycerol concentration from 0 to 75% v/v in Fig. 1. The simulation using the CRYSOL program was done based on two different models. (A) depicts the preferential solvation model (preferential replacement of hydration-shell water by glycerol). (B) depicts the preferential exclusion model (preferential exclusion of glycerol molecules from the hydration-shell region of the protein). To see this figure in color, go online.

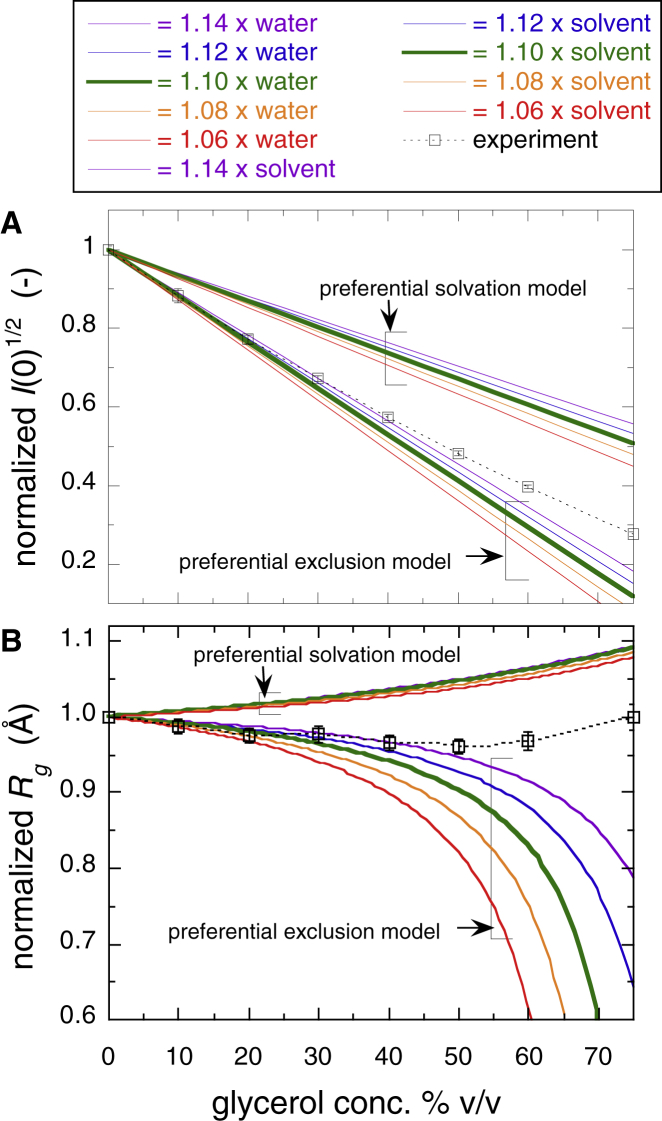
Fig. 7 presents the normalized values of the experimental and theoretical square root of the zero-angle scattering intensity (I(0)^1/2) and R_g, where Fig. 7 A displays I(0)^1/2 and Fig. 6 B displays R_g. The I(0)^1/2 value is known to be proportional to the product of the contrast and the volume of the solute particle (31). For the preferential solvation model, the solvation-shell electron density was set from 1.06 to 1.14 times higher than in the glycerol solvent. For the preferential exclusion model, the hydration-shell electron density was set from 1.06 to 1.14 times higher than in the bulk water. In Fig. 7 A, the theoretical I(0)^1/2 value for the preferential exclusion model was sharply decreased compared with that for the preferential solvation model. At glycerol concentrations lower than ∼40% v/v, the decreasing tendency of the experimental I(0)^1/2 and R_g with the increased glycerol concentration was mostly reproduced by the preferential exclusion model at the hydration-shell electron density of ∼1.1 in Figs. 7, A and B. However, at glycerol concentrations above ∼50% v/v, the deviation of the experimental I(0)^1/2 and R_g values from the theoretical ones based on the preferential exclusion model became evident. Of note, the theoretical R_g values based on the two different models clearly displayed opposite tendencies with increasing glycerol concentration.

Figure 7.

Normalized values of the experimental and theoretical square root of the zero-angle scattering intensity, I(0)^1/2 (A), and R_g (B). In the preferential solvation model, the solvation shell electron density is varied from 1.06 to 1.14 times higher than in the glycerol solvent. In the preferential exclusion model, the hydration-shell electron density is varied from 1.06 to 1.14 times higher than in bulk water. To see this figure in color, go online.

The results suggested that glycerol molecules were preferentially excluded from the protein surface region up to the glycerol concentration of ∼40% v/v, whereas at concentrations above ∼50% v/v, glycerol avidly penetrated into the hydration region of the protein. An MD simulation study by Vagenende et al. reported that the preferential interaction coefficient for a protein in glycerol-water mixture was essentially linear with respect to glycerol molality in glycerol concentrations from 0 to 40% v/v and mainly originated from electrostatic interactions that induced orientations of glycerol molecules at the protein surface such that glycerol was further excluded (4). The authors suggested that protein can be neutrally solvated, preferentially hydrated, or preferentially solvated by glycerol. Therefore, we executed another simulation based on the model (neutral solvation model), which posits that the replacement of hydrated water by glycerol is proportional to the volume fraction of glycerol multiplied by a certain exchange ratio. The electron density of hydration (solvation) shell is defined as follows:

$$D_{shell}=0413\beta V_f+0.367\left(1-\beta V_f\right),$$ (4)

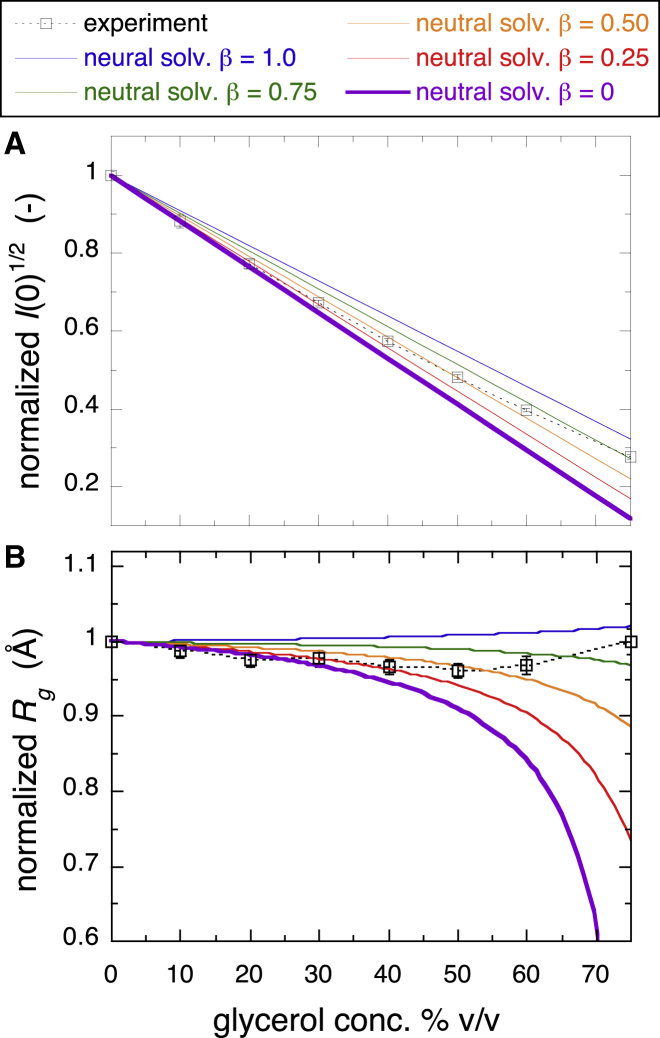
where D_shell, V_f, and β are the electron density of solvation shell, the volume fraction of glycerol, and the exchange rate (0–1), respectively. The average electron densities of glycerol and the hydration shell (1.1 times bulk water) are 0.413 and 0.367, respectively. β varied from 0 to 1 with a value of 0 corresponding to the preferential exclusion model at 1.10× water in Fig. 7. The β-value of 1 indicates that the replacement of hydrated water by glycerol is just proportional to the volume fraction of glycerol in the solvent. Fig. 8 summarizes the theoretical I(0)^1/2 and R_g values compared with the experimental values. Clearly, the changes in I(0)^1/2 and R_g depending on the glycerol concentration were mostly quantitatively explained by the neutral exchange rate, β. At glycerol concentrations below ∼40% v/v, β had a relatively small value, indicating that the preferential exclusion of glycerol was dominant. At glycerol concentrations above ∼50% v/v, β approached 1, meaning that the replacement of hydrated water by glycerol was simply proportional to the volume fraction of glycerol in the solvent. The following experimental and simulation results of neutron scattering strongly support the above WAXS results.

Figure 8.

Normalized values of the experimental and theoretical square root of the zero-angle scattering intensity, I(0)^1/2 (A), and R_g (B). Theoretical I(0)^1/2 and R_g values were obtained based on the neutral solvation model that the replacement of hydrated water by glycerol is proportional to the volume fraction of glycerol multiplied by a certain exchange ratio β. β was varied from 0 to 1. β = 0 corresponds to the preferential exclusion model at 1.10× water in Fig. 7. To see this figure in color, go online.

Effect of glycerol on protein structure observed by neutron scattering

In the case of neutron scattering, various types of the contrast-variation method are available to determine the structure of a particle in solution (38). We used the inverse-contrast variation method (29) to observe the effect of glycerol on the protein structure. This method uses deuterated materials, which can avoid or minimize the artificial effect on the scattering curves caused by the addition of cosolute molecules. The mixture of nondeuterated glycerol (h-glycerol) and deuterated glycerol (d-glycerol, 98 atom % D) was used. Because the molecular volume of glycerol was known from the mass density measurement, the average scattering densities of h-glycerol and 98% d-glycerol could be calculated. The average scattering density of the mixture of h-glycerol/98% d-glycerol = 21.25/78.75 (v/v) corresponds to that of 100% deuterated water (D₂O). This mixture can minimize both the coherent and incoherent background scatterings from glycerol molecules and hydrogen atoms. In addition, by the use of this mixture, the increase of the glycerol content does not change the contrast of the protein, as shown in Fig. 5. In contrast, for x-ray scattering, the change of the contrast is unavoidable, as shown in the above section. In other words, we are able to observe selectively only the protein structure including its hydration shell under the above experimental condition.

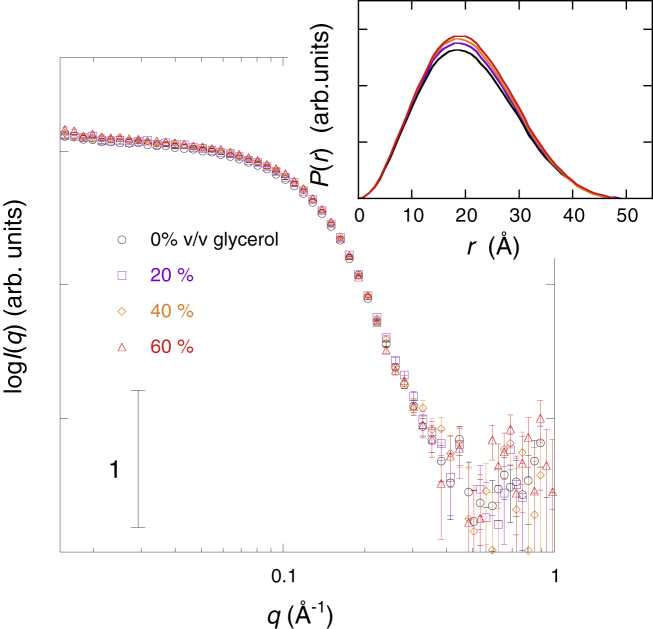
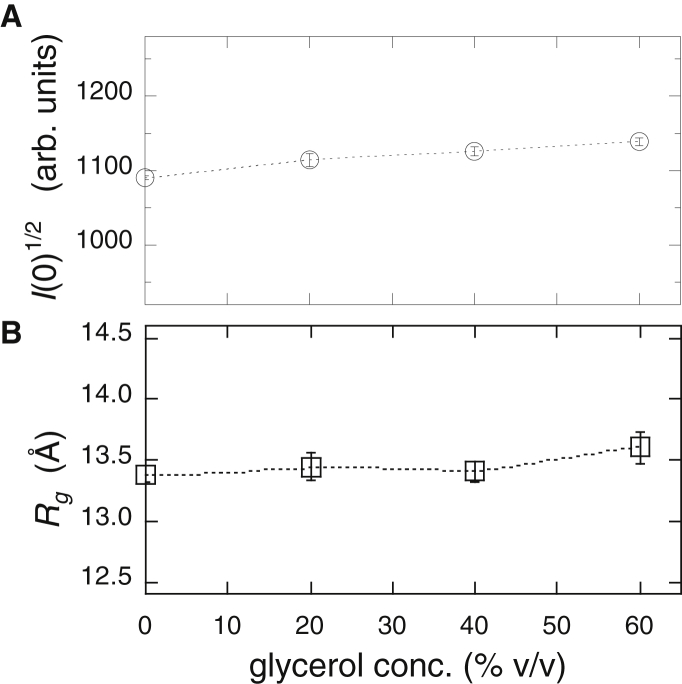
Fig. 9 illustrates the glycerol concentration dependence of the neutron-scattering curve of myoglobin, where the inset is the distance distribution function, p(r). Glycerol concentrations varied from 0 to 60% v/v. The maximal diameter, D_max, in the p(r) function was mostly maintained from 49 to ∼50 Å. Fig. 10 presents the square root of the zero-angle scattering intensity, I(0)^1/2, and the R_g value obtained from Fig. 9, where Fig. 9 A displays I(0)^1/2 and Fig. 9 B displays R_g. I(0)^1/2 increased by ∼4% at 60% v/v glycerol. This incremental increase suggests a change in the hydration-shell density by the preferential replacement of hydration-shell water molecules with glycerol molecules, as shown below. The R_g value by p(r) function changed from 13.4 ± 0.1 to 13.6 ± 0.1 Å. However, the difference in R_g was too small to be able to define a trend line. It should be noted that the difference between the absolute values of R_g obtained by SANS and SR-WAXS was essentially attributable to the difference in the contrast profile of myoglobin in D₂O (for SANS) and H₂O (for SR-WAXS).

Figure 9.

Neutron-scattering curve of myoglobin depending on glycerol concentration. The protein concentration is 2% w/v in 100% D₂O, 10 mM HEPES, at pH 7.4 and 25°C. Glycerol is the mixture of [h-glycerol]/[98% d-glycerol] = 21.25/78.75. The average scattering density of the glycerol mixture matches that of 100% D₂O. The inset shows the distance distribution function. To see this figure in color, go online.

Figure 10.

Square root of the zero-angle scattering intensity, I(0)^1/2 (A), and radius of gyration, R_g (B), obtained from Fig. 9.

Fitting by theoretical neutron-scattering curve and estimation of hydration-shell density

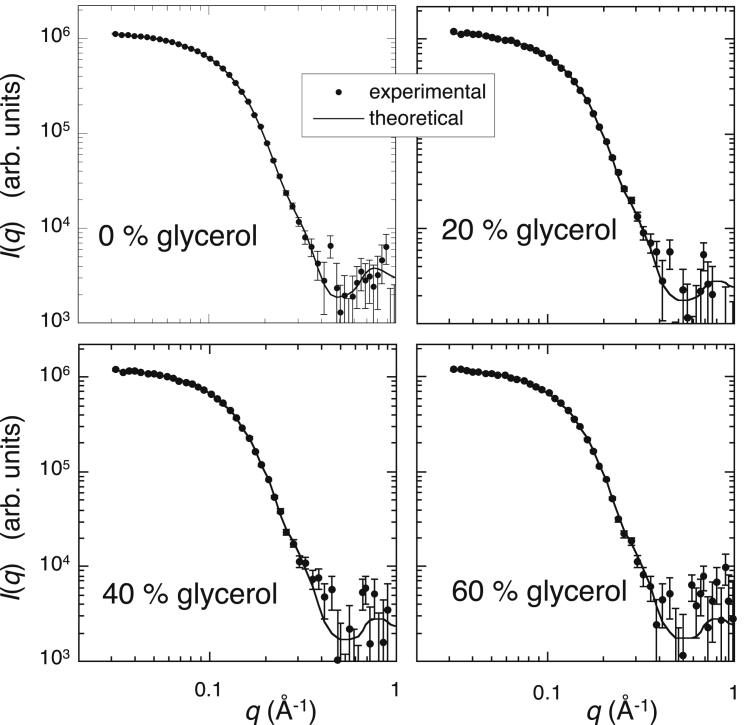
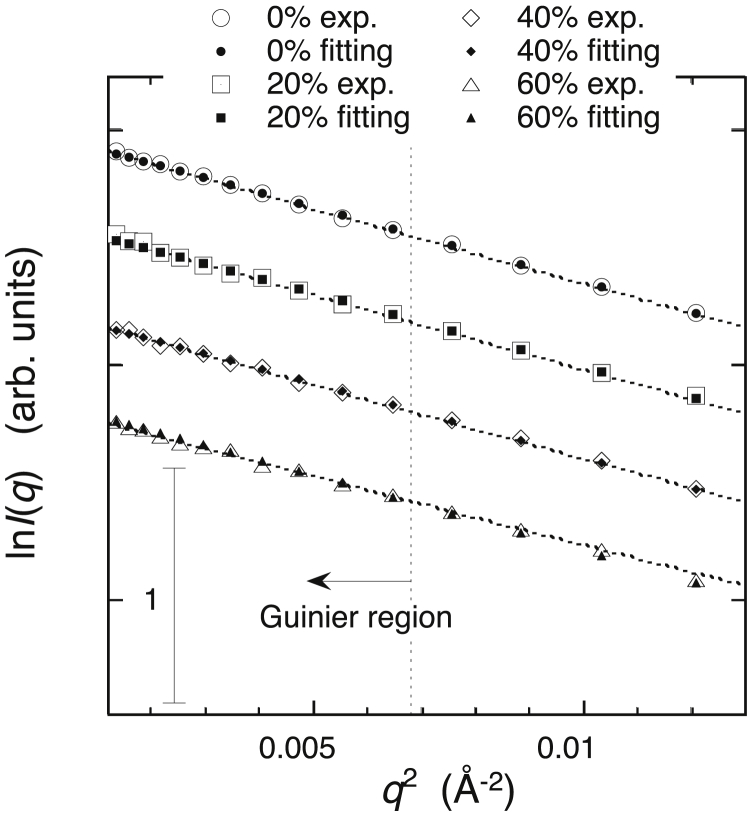
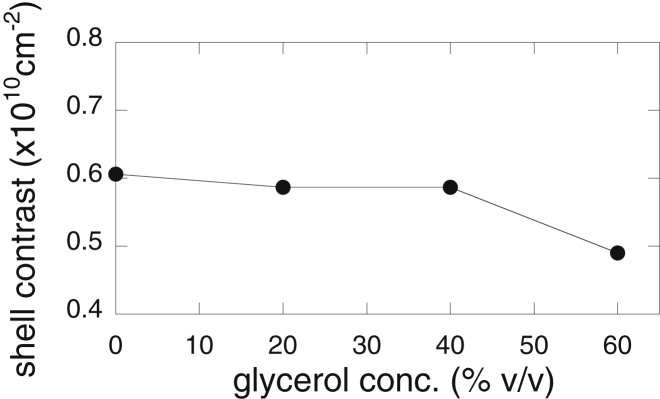
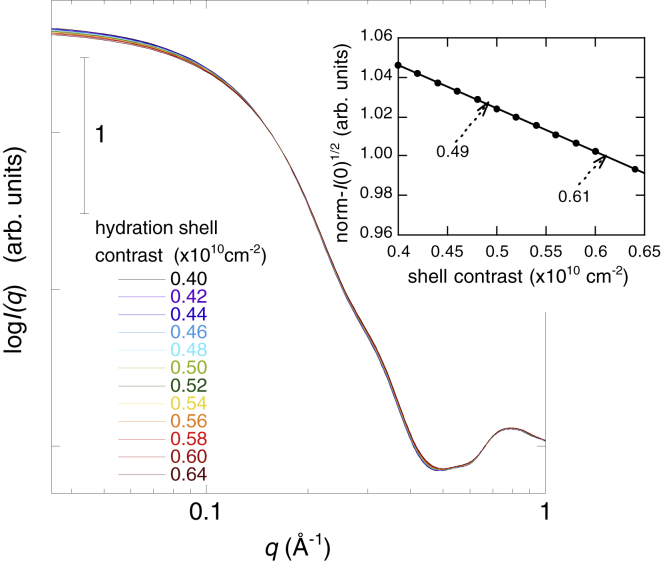
In this neutron-scattering experiment, we applied the inverse-contrast variation method to avoid an artificial change of contrast caused by the addition of glycerol. Thus, the average scattering density of the solvent and the contrast of the protein did not change with increasing glycerol concentrations. The theoretical fitting procedure could be effectively used to reproduce the experimental scattering curve by the CRYSON program. The CRYSON program is a reimplementation of CRYSOL and is adapted to work with SANS data. In the CRYSON fitting, we used the maximal order of harmonics of 50 and fixed the excluded volume to be 2.226 × 10⁴ ų, which was ∼4% larger than the dry volume of myoglobin. Fig. 11 depicts the optimized simulated neutron-scattering curve with the experimental curve at each glycerol concentration. The discrepancy between theoretical and experimental curves defined by χ² values ranged from 0.92 to 1.4. Fig. 12 presents the Guinier plot of Fig. 11, in which the experimental and theoretical scattering curves in Fig. 11 are shifted and replotted against q². The dotted lines represent the least-square fitting (q² vs. ln I(q)) using the Guinier region (q < ∼0.07 Å⁻¹). The Guinier plots show good linearity, demonstrating the absence of protein-protein interactions in the glycerol concentration from 0 to 60% v/v. It should be noted that both the CRYSOL and CRYSON programs can perform the fitting of the theoretical curve to the experimental data with the fixed value of the solvent scattering density and with the hydration-shell contrast, which varies from 0 to 22% higher than the average scattering density of the solvent. These SANS and WAXS results suggest the preferential exclusion of glycerol to preserve the hydration-shell density of the protein. Therefore, as shown in Fig. 5, in the case of WAXS measurements, the hydration-shell contrast changed from a positive to a negative value with increasing glycerol concentration. Thus, the estimation of the hydration-shell density by the CRYSOL fitting to experimental x-ray scattering is evidently inappropriate and impossible because this program does not assume that the hydrated shell density is lower than that of the solvent. On the other hand, in this SANS measurement, the contrast of the hydration shell was always positive. This is the reason why we successfully performed fittings of theoretical curves to experimental data to estimate the hydration-shell density by the CRYSON fitting. The estimated contrast of the hydration (solvation) shell by the CRYSON fitting is shown in Fig. 13. The hydration-shell contrast mostly preserved the value of 0.61–0.59 × 10¹⁰ cm^–2 (corresponding to 9.5% higher than the average scattering density of D₂O) up to 40% v/v glycerol and decreased to 0.49 × 10¹⁰ cm⁻² at 60% v/v glycerol. Under this experimental condition, the average scattering density of glycerol matched that of D₂O. Therefore, on the assumption that the excluded volume of the protein and the hydrated water density were affected little by glycerol, the decrease of the solvation-shell contrast from 0.61 to 0.49 × 10¹⁰ cm⁻² indicated that ∼20% of the solvation-shell volume was replaced by glycerol. From Fig. 8 of the WAXS simulation, the experimental values of I(0)^1/2 and R_g at a glycerol concentration of 60% v/v were located at the simulation values at β = ∼0.55. This value corresponds to the volume fraction of glycerol in the solvation shell, which is around 33%. The difference in the absolute values of the estimated volume-fractions of glycerol at 60% v/v would result from the difficulty of the fitting procedure for the determination of protein structures in solutions, as suggested by Makowski (39), that both factors—the excluded volume and the solvation layer—could affect scattering curves.

Figure 11.

Theoretical scattering curve fitting the experimental neutron-scattering curve in Fig. 9 obtained using the CRYSON program. The solid lines and the marks correspond to the optimized simulated neutron-scattering curves and the experimental data, respectively. The discrepancy defined by the χ² value is in the range of 0.92 to 1.4.

Figure 12.

Guinier plots of SANS experimental and theoretical-fitting curves in Fig. 11. Large and small marks correspond to experimental and theoretical data, respectively. The dotted lines represent the least-square fitting using the so-called Guinier region (q < ∼0.07 Å⁻¹).

Figure 13.

Estimated contrast of the hydration (solvation) shell obtained by the CRYSON fitting shown in Fig. 11.

The effect of the change in the hydration-shell contrast on the scattering curve was estimated by the scattering function simulation using the CRYSON program. In Fig. 14, the hydration-shell contrast varied from 0.64 × 10¹⁰ cm⁻² to 0.4 × 10¹⁰ cm⁻². When the hydration-shell contrast changed from 0.61 × 10¹⁰ cm^–2 to 0.49 × 10¹⁰ cm⁻², the I(0)^1/2 value increased by ∼3%. This incremental increase mostly agreed with the experimental value shown in Fig. 10 A. Thus, the neutron-scattering results also suggested that at glycerol concentrations below 40% v/v glycerol, the preferential exclusion of glycerol molecules from the protein surface dominated, whereas at 60% v/v glycerol, the neutral solvation by glycerol began to occur. These results agreed well with those obtained from the WAXS experiment and theoretical simulation in the above section.

Figure 14.

Theoretical neutron-scattering curve depending on the hydration-shell contrast obtained by the CRYSON program. The hydration-shell contrast varied from 0.64 × 10¹⁰ to 0.4 × 10¹⁰ cm⁻². The inset shows the I(0)^1/2 depending on the hydration-shell contrast. For the change of the hydration-shell contrast from 0.61 × 10¹⁰ to 0.48 × 10¹⁰ cm⁻² (as shown in Fig. 12), the I(0)^1/2 increases by ∼3%. To see this figure in color, go online.

Thermal structure stability and helix-to-sheet transition in glycerol solution

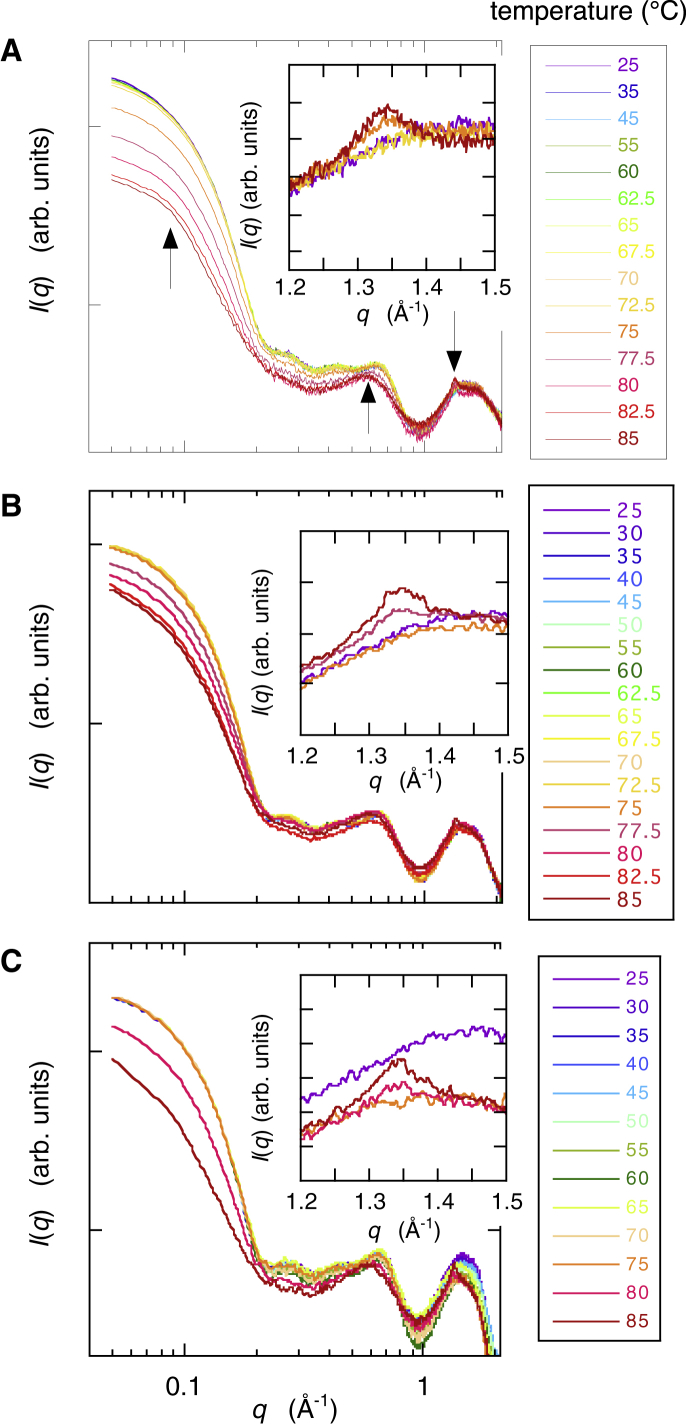
The above results clearly show the protective action of glycerol on the hydration shell of myoglobin. Therefore, it was interesting to study the effect of glycerol on the thermal structural transition of myoglobin because this protein has an amyloid fibril formation (23, 24). Fig. 15 shows the temperature dependence of the WAXS curve of myoglobin in 10 mM HEPES buffer at pH 7.4. Fig. 15, A–C depict results in water solvent, 10% v/v glycerol solvent, and 20% v/v glycerol solvent, respectively. The insets in Fig. 14 show selected WAXS curves for the secondary structure region at 25°C, just before and after helix-to-sheet (cross-β) transition, and at 85°C. As already mentioned in Myoglobin Structure Depending on Glycerol Concentration Observed by X-ray Scattering, the observed WAXS scattering data covered all distinct hierarchal structure levels of the protein. The scattering data at q < ∼0.2 Å⁻¹, at ∼0.25 Å⁻¹ < q < ∼0.5 Å⁻¹, at ∼0.5 Å⁻¹ < q < ∼0.8 Å⁻¹, and at ∼1.1 Å⁻¹ < q < ∼1.9 Å⁻¹ reflected the tertiary structure, the interdomain correlation, the intradomain structure, and the secondary structure, respectively. This allowed the separate analysis of the structural transition features of myoglobin at different hierarchical levels separately. In Fig. 15 A, the shoulder at q = ∼0.08 Å⁻¹, the hump at q = ∼0.58 Å⁻¹, and the peak at q = ∼1.34 Å⁻¹ became evident with the elevation of temperature above ∼75°C. As reported previously, these are typical features that appear in the initial process of amyloid transition, namely the oligomerization of myoglobin, the formation of the pleated sheet stacking, and the appearance of cross-β structure (helix-to-sheet transition), respectively (27, 28). The observed q-values in the positions of the hump and the peak corresponded to ∼10.8 and ∼4.69 Å, respectively, in real space distance. These values agreed with those reported previously within experimental errors (23, 24, 40). The change of the scattering curve by cross-β structure formation occurred between 70.0 and 72.5°C in water solvent, between 75.0 and 77.5°C in 10% glycerol solvent, and between 75.0 and 80.0°C in 20% glycerol solvent. Thus, the transition onset temperature, T_on, of the cross-β structure was in the middle of those temperatures. Fig. 16 shows the temperature dependence of the distance distribution function, p(r), obtained by applying Eq. 1 to the scattering curves in Fig. 15, where Fig. 15, A and B depict the results using water solvent and 20% v/v glycerol solvent, respectively. At low temperature, the p(r) function in the short-distance region displayed a bell-shape profile with a maximum at ∼20 Å and the first minimum at ∼45 Å, which reflected the gradual change of the structure of myoglobin monomer. With the rise in temperature, the p(r) function in the long-distance region began to show the second maximum in the case of water solvent at 75°C or displayed a tail in the case of 20% v/v glycerol solvent at 80°C, suggesting the presence of oligomeric aggregates, namely the formation of amyloid-like aggregates. As clearly shown in Fig. 16, the presence of glycerol suppressed both the thermal unfolding and oligomerization of the protein.

Figure 15.

Temperature dependence of the WAXS curve of myoglobin (2% w/v in 10 mM HEPES buffer (pH 7.4)) in water solvent (A), 10% v/v glycerol solvent (B), and 20% v/v glycerol solvent (C). The insets show selected WAXS curves for the secondary structure region at 25°C, just before and after helix-to-sheet (cross-β) transition, and at 85°C. The arrows indicate the typical features in the scattering curve that appear in the initial process of amyloid transition. The shoulder at q = ∼0.08 Å⁻¹ indicates oligomerization, the hump at q = ∼0.58 Å⁻¹ indicates pleated sheet stacking, and the peak at q = ∼1.34 Å⁻¹ indicates cross-β sheet structure formation. To see this figure in color, go online.

Figure 16.

Temperature dependence of the distance distribution function of myoglobin calculated from the WAXS curves in Fig. 15, A and C. (A and B) are water solvent and 20% v/v glycerol solvent, respectively. The appearance of the second maximum in (A) at 75°C or the tail in (B) at 80°C suggests the presence of oligomeric aggregates. To see this figure in color, go online.

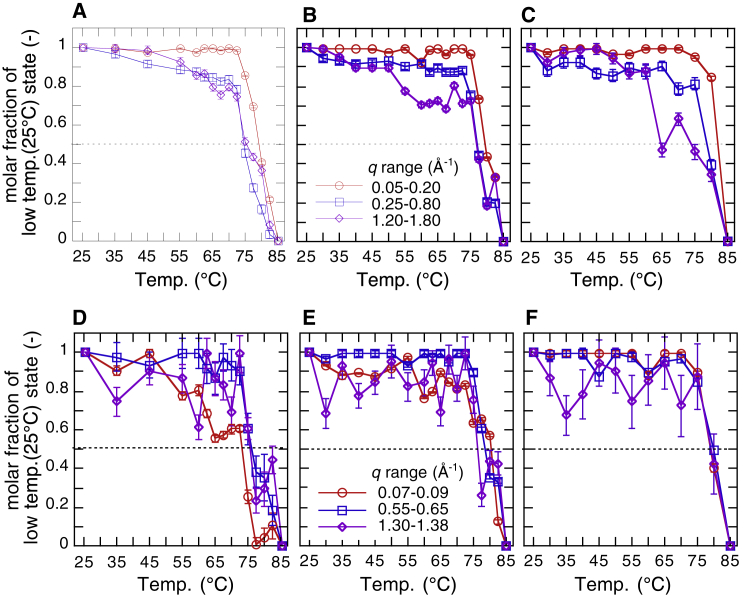
The transition-multiplicity analysis (TMA) (26, 41) is useful to characterize the thermal stability in the different hierarchical structure levels. The TMA method is based on the principle that the scattering curves in different q-regions correspond to the structures of an object in the different hierarchical structure levels. The structural transitions in the different hierarchical structure levels do not necessarily proceed cooperatively. By using Eq. 5, we could analyze the transition cooperativeness among different hierarchical structure levels (26, 41, 42).

$${\mathit{\Delta }}_{ij}=\sum _{q=q_i}^{q_j}\left[\frac{I\left(q,T\right)}{\sum _{q=q_i}^{q_j}I\left(q,T\right)}-\left\{{\alpha }_{ij}\frac{I\left(q,T_N\right)}{\sum _{q=q_i}^{q_j}I\left(q,T_N\right)}+\left(1-{\alpha }_{ij}\right)\frac{I\left(q,T_U\right)}{\sum _{q=q_i}^{q_j}I\left(q,T_U\right)}\right\}\right],$$ (5)

where $I\left(q,T_N\right)$, $I\left(q,T_U\right)$, and $I\left(q,T\right)$ are the scattering profiles at the initial, final, and intermediate temperatures in a defined q-range of qi–qj Å⁻¹, respectively. The scattering curve $I\left(q,T\right)$ in a defined q-range at an intermediate temperature was fitted by using a linear combination of${\alpha }_{ij}I\left(q,T_N\right)$ and $\left(1-{\alpha }_{ij}\right)I\left(q,T_U\right)$. The factor α_ij was determined by minimizing the ${\mathit{\Delta }}_{ij}$ value in Eq. 5. Thus, the α_ij-value corresponds to the molar fraction of the native protein structure in the hierarchical structure level covering the q-range of qi–qj Å⁻¹ at an intermediate temperature, T. As shown previously, the molar fraction of native structure determined in the q-range corresponding to the tertiary structure agreed well with that obtained by differential scanning calorimetry, namely by structural transition accompanying a large enthalpy change (41). Fig. 17 summarizes all results obtained using the TMA method, with Fig. 17, A and D displaying the results from water solvent, Fig. 17, B and E displaying the results from 10% v/v glycerol solvent, and Fig. 17, C and F displaying the results from 20% v/v glycerol solvent. From (A) to (C), the q-ranges selected for TMA analysis were from 0.05 to 0.2 Å⁻¹ and 0.25 to 0.8 Å⁻¹, which corresponded to the tertiary structure and the internal structure, respectively. From (D) to (F), the selected q-ranges were from 0.07 to 0.09 Å⁻¹, 0.55 to 0.65 Å⁻¹, and 1.30 to 1.38 Å⁻¹, which corresponded to the q-ranges defining typical features of amyloid transition, namely oligomerization, pleated sheet stacking, and cross-β structure, respectively. The transition midpoint temperature, T_m, was determined by the temperature at in Fig. 17. Table 1 presents a summary of T_m values at different hierarchal structure levels, where columns from A to E are T_m values obtained from Fig. 17, and column F presents the T_on values estimated from Fig. 15. The T_m values were determined by sight and by sigmoid function fitting. Both T_m values agreed well within estimation errors. Clearly, in columns A and B, increasing glycerol concentrations displayed a trend of rising T_m values of the tertiary and internal structures. The T_m value in column C suggests that the amyloid oligomerization was remarkably suppressed by glycerol compared with the pleated sheet stacking and the cross-β transition. The T_m and T_on values of the cross-β transition were systematically elevated depending on the glycerol concentration.

Figure 17.

Molar fraction α (α ≤ 1) of the native structure (at 25°C) of myoglobin at an intermediate temperature in the heating process determined from the scattering curves in different q-ranges by using the TMA analysis. (A) and (D) display data from water solvent, (B) and (E) display data from 10% v/v glycerol solvent, and (C) and (F) display data from 20% v/v glycerol solvent. From (A) to (C), the selected q-ranges are 0.05–0.2 and 0.25–0.8 Å⁻¹, which correspond to the tertiary structure and the internal structure, respectively. From (D) to (F), the selected q-ranges are 0.07–0.09, 0.55–0.65, and 1.30–1.38 Å⁻¹, which correspond to the q-ranges for typical features of amyloid transition, namely oligomerization, pleated sheet stacking, and cross-β structure, respectively. To see this figure in color, go online.

Table 1.

Midpoint and Onset Temperatures of Structural Transition at Distinct Hierarchical Structure Levels

	A Tertiary Structure q = 0.05–0.2 Å−1	B Internal Structure q = 0.25–0.8 Å−1	C Oligomerization q = 0.07–0.09 Å−1	D Sheet Stacking q = 0.55–0.65 Å−1	E Cross-β Structure q = 1.3–1.38 Å−1	F Cross-β Structure
By Sight
Tm (gly = 0% v/v)	79.0 ± 0.5°C	74.8 ± 0.5°C	73.2 ± 0.5°C	76.2 ± 0.5°C	75.8 ± 0.5°C	–
Tm (gly = 10% v/v)	79.4 ± 0.5°C	76.9 ± 0.5°C	80.3 ± 0.5°C	78.3 ± 0.5°C	76.2 ± 0.5°C	–
Tm (gly = 20% v/v)	82.2 ± 0.5°C	78.8 ± 0.5°C	80.0 ± 0.5°C	80.2 ± 0.5°C	80.2 ± 0.5°C	–
Ton (gly = 0% v/v)	–	–	–	–	–	73.8 ± 1.3°C
Ton (gly = 10% v/v)	–	–	–	–	–	76.3 ± 1.3°C
Ton (gly = 20% v/v)	–	–	–	–	–	77.5 ± 2.5°C
By Sigmoidal Fit
Tm (gly = 0% v/v)	79.3 ± 0.1°C	75.6 ± 0.4°C	70.4 ± 1.5°C	77.3 ± 0.5°C	78.1 ± 1.6°C	–
Tm (gly = 10% v/v)	80.0 ± 0.3°C	77.7 ± 0.3°C	79.9 ± 0.6°C	79.2 ± 0.3°C	79.2 ± 1.2°C	–
Tm (gly = 20% v/v)	81.0 ± 2.3°C	79.5 ± 0.4°C	79.3 ± 0.3°C	79.9 ± 0.4°C	80.0 ± 2.1°C	–

Summary of transition midpoint temperature, T_m, at different hierarchal structure levels. Columns A–E show T_m values obtained from Fig. 16, and column F shows T_on values estimated from Fig. 14. T_m values were determined both by sight and by sigmoid function fitting.

Conclusions

Although glycerol is considered to be generally excluded from the surfaces of proteins (1, 9, 10, 11), this is only a measure of the relative distribution of glycerol at the protein surfaces versus bulk. Further, no actual numbers of glycerol have been provided experimentally. By the complementary use of SR-WAXS and SANS methods and by the theoretical simulation of scattering functions, we have clarified the effect of glycerol molecules on the myoglobin structure, its hydration (solvation) layer, and thermal stability. To reproduce experimental data, we employed three different models in the WAXS simulations. In the first model, glycerol molecules preferentially surround the protein surface to form a high-density solvation shell in which the molar concentration of glycerol in the shell is higher than the concentration in the bulk glycerol solvent (preferential solvation model). In the second model, glycerol molecules are preferentially excluded from the protein surface to preserve the hydration-shell density, which is higher than the density in bulk water (preferential exclusion model or preferential hydration model). The second model can qualitatively describe WAXS and SANS results at glycerol concentrations lower than ∼40% v/v. However, there is an evident deviation from the second model at glycerol concentrations higher than ∼50% v/v. Based on the MD simulation result (4), we constructed a third model, in which the replacement of hydrated water by glycerol is proportional to the volume fraction of glycerol in the solvent multiplied by an exchange rate β (neutral solvation model). β would relate the preferential interaction coefficient defined in the MD simulations (4, 43, 44) that can be measured as the excess number of cosolvent molecules near the protein surface for a protein in a cosolvent-water mixture (1, 45, 46). Here, the exchange rate of glycerol was defined to be less than 1. β = 1 means a simple neutral solvation in which the replacement of hydrated water by glycerol is just proportional to the volume fraction of glycerol in the solvent. Experimental WAXS results at glycerol concentrations above ∼50% v/v were quantitatively described by the change of β-value. At the highest glycerol concentration of 75% v/v, the β-value approached 1. The SANS results clearly indicated that the hydration-shell density was preserved at glycerol concentrations below 40% v/v, whereas it decreased because of the replacement of hydrated water by glycerol at a glycerol concentration of 60% v/v. Both experimental and simulation results by WAXS and SANS suggest that at the concentrations lower than 40% v/v glycerol, molecules are preferentially excluded from the protein hydration layer and that at glycerol concentrations above 50% v/v, partial replacement by glycerol proceeds within the framework of the neutral solvation model. Having glycerol begin to enter the solvation layer and displace water in glycerol concentrations above 50% v/v suggests that glycerol is only weakly excluded from the protein surface. The energy of exclusion must be no more than the order of thermal energy (k_bT) if concentration alone can displace water from the hydration shell when the solute is volumetrically equivalent to the solvent. Gekko et al. suggested that free-energy change when protein is transferred to polyol solvent depends on the polyol concentration, and in the case of glycerol, the change of free energy becomes remarkable from the concentration of ∼5 [M] (∼40% v/v) (1, 9). These results mostly agree with the previous MD simulation results based on the framework of preferential interaction that is the measure of the preference of the protein surface for cosolvent as compared to the water molecules (4, 43, 44).

We also studied the effect of glycerol on the thermal structural transition of myoglobin. As the observed WAXS data covered all distinct hierarchal structure levels of the protein (the tertiary structure, interdomain correlation, intradomain structure, and secondary structure), we separately analyzed the structural transition feature at each hierarchical level using the TMA method (26, 41). With the rise of glycerol concentration, the amyloid-like oligomerization process was evidently suppressed. The onset temperature of the helix-to-sheet transition increased by ∼4°C. The transition midpoint temperatures at all hierarchal structure levels rose, with no difference between them, suggesting that the transition cooperativeness between different hierarchical structural levels was enhanced by glycerol. The above result was consistent with the finding in a prior study that the change in the standard free energy of denaturation brought by the addition of glycerol increases in aqueous solutions (9). Recently, Katina et al. demonstrated that A-, B-, E-, F-, and G-helices in the native apomyoglobin structure participate in intermolecular interactions in amyloids (47). Therefore, the suppression of amyloid-like oligomerization by glycerol observed at a relatively low concentration might suggest a specific interaction between glycerol and local domains of the protein to prohibit direct interaction between the proteins.

Finally, concerning studies of the crowding effects of low molecular weight cosolutes on protein structures, it should be noted that the combination of SR-WAXS and SANS inverse-contrast methods has a superior experimental advantage to elucidate both features of protein structures and their solvation.

Finally, it should be noted that this method by the combination of SR-WAXS and SANS inverse-contrast methods has a superior experimental advantage to elucidate the molecular origin of the various types of osmolyte (sugars, polyols, etc.)-dependent protein stability. In addition, recently, molecular crowding and the confinement effect on biological systems has been focused because in living cells, macromolecules occupy a significant fraction (typically 20–30%) of the total volume (48, 49). Therefore, because of the diversity of molecular species in living cells, further development and combination of experimental and theoretical methods treating macromolecular crowding environments is important. This method might offer a certain advantage for studying macromolecular crowding effects on biological complex systems.

Author Contributions

M.H. designed the research, performed the research, and analyzed the data. S.A. performed the research and analyzed the data. M.S. performed research at ILL and analyzed the data. H.I. performed research at MLF at J-PARC and analyzed the data. S.T. performed research at MLF at J-PARC and analyzed the data. N.S. performed research at PF at KEK and contributed analytic tools. N.I. performed research at PF at KEK and contributed analytic tools. A.M. performed research at ILL and contributed analytic tools. L.P. performed research at ILL and contributed analytic tools.

Editor: Jill Trewhella.