Abstract
Plant development and morphology relies on the accurate insertion of new cell walls during cytokinesis. However, how a plant cell correctly orients a new wall is poorly understood. Two kinesin class-12 members, phragmoplast orienting kinesin 1 (POK1) and POK2, are involved in the process, but how these molecular machines work is not known. Here, we used in vivo and single-molecule in vitro measurements to determine how Arabidopsis thaliana POK2 motors function mechanically. We found that POK2 is a very weak, on average plus-end-directed, moderately fast kinesin. Interestingly, POK2 switches between processive and diffusive modes characterized by an exclusive-state mean-squared-displacement analysis. Our results support a model that POK motors push against peripheral microtubules of the phragmoplast for its guidance. This pushing model may mechanically explain the conspicuous narrowing of the division site. Together, our findings provide mechanical insight into how active motors accurately position new cell walls in plants.
Introduction
Cytokinesis in plants is characterized by the insertion of a membranous cell plate in the center of a dividing parental cell. The assembly of the cell plate in the cell division plane is aided by a dynamic, plant-specific cytoskeletal scaffold structure called the phragmoplast (1). This phragmoplast apparatus arises from the mitotic spindle after chromosome segregation and consists of endoplasmic reticulum, filamentous (F)-actin, and bipolar microtubules oriented perpendicular to the division plane (1). These microtubules serve as tracks for Golgi-derived vesicles translocating cell-plate material toward the division plane, where vesicle fusion results in cell-plate formation. The phragmoplast expands centrifugally by virtue of microtubule polymerization at the outer/leading zone and depolymerization at the inner/lagging zone where the cell-plate assembly is achieved (1). The coordinated interplay of the phragmoplast dynamics and cell-plate assembly ends by the fusion of the cell plate with the parental plasma membrane at the cell-plate fusion site, completing the new cell wall (2). In land plants, the cell-plate fusion site is predicted by the cytoskeletal preprophase band during the gap 2 phase/mitosis transition (3). The cortical division zone, defined as the membrane region next to the preprophase band, remains at the cell cortex after the preprophase band disassembles. Memory of this region is kept throughout cell division, and its location coincides with the later division site (2). Furthermore, the narrowing of this region from an initially broad zone to a definite cell-plate fusion site during late cytokinesis occurs via a yet unknown mechanism (4, 5, 6, 7). The kinesin-12 phragmoplast orienting kinesin 1 (POK1), along with its dependents TANGLED (TAN) (5, 6) and RanGAP (8), localize to the division site throughout cell division (7). POK1 is functionally redundant with its homolog, POK2, as simultaneous impairment of both leads to loss of the TAN and RanGAP1 after preprophase band disassembly. Moreover, with the simultaneous impairment, newly formed cell plates position abnormally (7, 8, 9), presumably without proper guidance of the phragmoplast (7). Based on these findings, it was hypothesized that POKs might guide the phragmoplast by facilitating a mechanical communication between the division site at the cell cortex and microtubules of the phragmoplast leading edge (7).
Conventional kinesin-1 motors are dimers stepping in a rotary hand-over-hand mechanism along the microtubule lattice in an ATP-dependent, directed manner (10). Dimerization facilitates processive motion—the ability to take many directed steps without dissociation (11). During this continuous, processive stepping behavior, the kinesin heads switch between strongly and weakly bound states before detaching from the microtubule lattice. Apart from processive, directed motion, some kinesins interact in a diffusive manner with microtubules, such as human kinesin-13 MCAK (12) and kinesin-3 Kif1A (13). In addition, diffusive behavior has also been observed as an intermittent part of processive motion for Drosophila kinesin-14 Ncd using low-ionic-strength buffers (14, 15), Xenopus kinesin-7 CENP-E (16), human kinesin-5 Eg5 (17), human kinesin-8 Kif18B (18), and human kinesin-12 Kif15 (19). During one-dimensional diffusive motion, both heads are thought to be in weakly bound states (20) and therefore exhibit random backward and forward motion on the microtubule lattice. Here, we asked how POKs mechanically interact with the peripheral microtubules of the expanding phragmoplast.
Outside of plants, the closest relative of POKs, the tetrameric human kinesin-12 hKif15, has recently attracted attention (19, 21, 22, 23). hKif15 is partially redundant to the tetrameric kinesin-5 Eg5 and is required during cell division for proper maintenance of spindle bipolarity by assisting the formation of parallel microtubule bundles. Although hKif15 is the sole member of the human kinesin-12 family, Arabidopsis has an extended family comprising six members (24). Thus, due to this increase and different cellular context, it is unclear whether the Arabidopsis kinesin-12 family members have similar molecular properties compared to hKif15. Here, we used in vitro single-molecule imaging and optical-tweezers-based force spectroscopy to characterize single POK2 motor proteins from Arabidopsis thaliana. We found that POK2 motors exhibited both processive and diffusive motion and that individual motors frequently switched between the two modes. To quantify this switching behavior, we developed a mean-squared-displacement (MSD) analysis that accounts for the motor being exclusively in either the directed or diffusive state. This analysis can be robustly applied to a diverse range of other molecular machines. Additionally, to understand how POK2 would be able to guide the phragmoplast, we performed in planta imaging, visualizing the interaction of truncated POK2 motors with dynamic microtubules, the narrowing of the cortical division site, and the polarity of peripheral microtubules during late stages of cytokinesis. POK2 motors might pull on or push against these peripheral microtubules emanating from the expanding phragmoplast. Instead of intuitively pulling on the expanding phragmoplast for its guidance, our data supports the view that POK2 motors push against it.
Materials and Methods
Protein expression and purification
Porcine brain tubulin was purified and labeled with tetramethylrhodamine (Invitrogen, Carlsbad, CA) according to standard protocols (25). 10% rhodamine-labeled taxol-stabilized microtubules were polymerized as described previously (26). POK21–589 green fluorescent protein (GFP)-His and POK2183–589 GFP-His were expressed in SF9 insect cells (Expression Systems, Davis, CA) using baculovirus expression (flashBAC; Oxford Expression Technologies, Oxford, UK at Protein Facility, Max Planck Institute of Molecular Cell Biology and Genetics, Dresden). To pull on the tail domain of the kinesin in optical trapping experiments, the GFP was located at the C-terminus. The protein was purified via sequential chromatography. Cation exchange chromatography (HiTrap SP HP 1 mL; GE Healthcare, Little Chalfont, UK) followed by desalting (HiTrap desalting 5 mL; GE Healthcare) and subsequently affinity chromatography (HisTrap HP 1 mL; GE Healthcare) was performed. Cells were lysed in 50 mM HEPES, 150 mM NaCl, 5% glycerol, 0.1% Tween 20, 1.5 mM MgCl2, 3 mM EGTA, 1 mM dithiothreitol, 0.5 mM ATP, and protease inhibitors (pH 7.5). The cation wash buffer consisted of 20 mM HEPES, 150 mM NaCl, 5% glycerol, 1.5 mM MgCl2 (pH 7.5). The cation elution buffer consisted of the same except for the concentration of NaCl (600 mM) (pH 7.5). The desalting column was used to exchange the buffers to proceed toward metal affinity. The metal affinity wash buffer consisted of 50 mM phosphate buffer (pH 7.5), 300 mM NaCl, 10 mM imidazole, 10% glycerol, 1 mM MgCl2, 20 μM ATP, and protease inhibitors (pH 7.5). The metal affinity elution buffer consisted of the same except for the concentration of imidazole (300 mM) (pH 7.5). Protein stability was confirmed from the SDS-PAGE and Western blotting using anti-GFP antibody (mouse, Cat. 11814460001; Roche, Basel, Switzerland). The purified protein concentration was determined using a Bradford assay. Finally, the protein aliquots were snap frozen in liquid nitrogen and stored at −80°C. The protein concentrations were measured using a NanoDrop ND-1000 spectrophotometer (Thermo Fisher Scientific, Waltham, MA). The concentration for the colocalization experiment was validated with the Western blot.
Constructs
All the constructs used were amplified from the complementary DNA (cDNA) using standard polymerase chain reaction (PCR) techniques. The total RNA was extracted from Arabidopsis accession Columbia flower buds using an RNeasy Plant Mini Kit (74903; Qiagen, Hilden, Germany), and cDNA was generated using Superscript Reverse Transcriptase II and oligo deoxythymidine primers (18064-022; Invitrogen) as described previously (9). All the constructs used were amplified from the cDNA using Phusion DNA Polymerase (M0530L; New England Biolabs, Ipswich, MA) and standard PCR techniques. The cloning was performed using a Quick Ligation Kit (M2200L; New England Biolabs). The used primers are mentioned in Table 1.
Table 1.
Used Primers for All Constructs
| Not POK21–589 F | AATAATAACATGCGGCCGCaATGTCAAAGGAGACCAAGCTTTC |
| NotI POK2183–589 549F | AATAATAACATGCGGCCGCaATGGAAGATCCATCTTTCTGGATGGATCACAA |
| AscI POK2 R | AATAATAACATGGCGCGCCttaACTTGATGGCGAATCGACT |
| EB1b EcoRI F | gaattcAAAAATGGCGACGAACATT |
| EB1b XhoI R | ctcgagTTAAGTTTGGGTCTCTGCAGCA |
Microscopy assay and imaging conditions
The flow cell was constructed as described earlier (27), but the surface was rendered hydrophobic using chlorotrimethylsilane (Merck Millipore, Burlington, MA). The flow channels were washed four to five times with sterile filtered buffer BRB80 (80 mM PIPES, 1 mM MgCl2, 1 mM EGTA, 100 mM KOH, pH 6.9). This was followed by incubation with anti-β tubulin (T7816; Sigma Aldrich, St. Louis, MO) for 15–20 min at room temperature. Afterwards, the channels were washed once with BRB80 and blocked using 1% Pluronic F-127 in BRB80 (P2443; Sigma-Aldrich) for 20–25 min. This step was followed by five times washing with BRB80 and incubation with 10% rhodamine-labeled, taxol-stabilized microtubules for 15 min. The assay buffer (BRB80, 0.08 mg/mL casein, 1 mM ATP, 20 mM D-glucose, 250 nM glucose oxidase, 134 nM catalase, 0.5% β-mercaptoethanol, 10 μM taxol) containing the protein was added after a quick wash of the channel. The samples were imaged at 25°C on a custom-built total-internal-reflection-fluorescence (TIRF) microscope combined with epifluorescence (28). The TIRF microscope is equipped with a sCMOS camera (Orca Flash 4.0; Hamamatsu Photonics, Hamamatsu, Japan) and an oil-immersion, TIRF objective (60×, 1.49 numerical aperture; Nikon, Tokyo, Japan). To visualize motor movement, 40-s-long time-lapse videos were recorded at 10 fps using a continuous image acquisition mode at 100 ms exposure. The sample was excited using a 488-nm laser (LuxX 488-100; Omicron, Rodgau-Dudenhofen, Germany).
Polarity-marked microtubules
Guanosine-5'-[(α,β)-methyleno]triphosphate (GMP-CPP)-stabilized microtubule seeds were prepared using 2–3 μM unlabeled tubulin, 1 mM MgCl2, 1 mM GMP-CPP (Jena Bioscience, Jena, Germany), and BRB80 and incubating them for 1 hr at 37°C. Afterwards, microtubules were spun down and the pellet was resuspended in the same constituents but with 1–2 μM of 10% rhodamine-labeled tubulin. This reaction was incubated further for an hour at 37°C. Then, 1–2 μM of 10% rhodamine-labeled tubulin was added and incubated for another hour before they were spun down and resuspended in BRB80.
Photobleaching assay
The photobleaching assay was conducted in the same manner as the rest of the in vitro preparations except for the assay buffer. The assay buffer consisted of 0.08 mg/mL casein, 1 mM adenosine 5′-[β,γ-imido)triphosphate (AMP-PNP), 10 mM dithiothreitol, and BRB80 (pH 6.9). In the presence of AMP-PNP, motors are thought to bind with both heads in a strongly bound state. GMP-CPP-stabilized microtubules were used. The data was acquired at the same conditions mentioned earlier using a higher excitation laser power. Postacquisition, kymographs were generated, and intensity values were extracted from them, followed by an analysis via a custom-written, MATLAB (The Mathworks, Natick, MA)-based step-finding algorithm (20).
Microsphere preparation and force measurements
Microsphere functionalization and protein-microsphere coupling was performed as reported previously (29). The sample preparation and assay buffer for optical tweezers experiments were the same as mentioned above. All the measurements were performed on a custom-built, single-beam optical tweezers setup (30, 31). The setup has a millikelvin precision temperature control of the trapping objective, which was set to 29.200°C. The experiments were conducted with a trap stiffness of 0.01 pN/nm and recorded with a sampling rate of 4 kHz. Calibration was performed by analyzing the height-dependent power spectral density combined with a drag-force method as reported earlier (27, 32).
Single-molecule tracking and data analysis
Single molecules were tracked using FIESTA (33), which is based on two-dimensional Gaussian model fitting. The resulting position coordinates were subjected to a rotation and projection on the microtubule axis, and subsequently MSD values were calculated. The same set of data was also subjected to a speed correlation index (SCI) analysis (34). All the in vitro data were analyzed in MATLAB by using custom-written scripts. The kymographs were plotted using Fiji (http://fiji.sc) with a custom-written macro that autocontrasts. In vivo images were analyzed in Fiji.
Plant materials and growth conditions
A. thaliana plants, pok 1-1 pok 2-3 (7), microtubule marker line (7) were the base lines for this study. All other double-labeled transgenic lines were generated via crossing of single transgenic lines in accession Columbia (Col). All plants including seedlings were grown at 20–22°C with a 16 hr-light/8 hr-dark cycle. The seedlings used for the localization studies were grown on plates containing Murashige and Skoog medium (Sigma-Aldrich) and 1% agarose, incubated at the aforementioned conditions.
Tobacco leaf infiltration
Nicotiana benthamiana leaves of 4-week-old plants were infiltrated with Agrobacterium tumefaciens suspension culture (OD600 0.5) carrying respective plasmid DNA (GFP POK21–589). 48–72 hr postinfiltration, the leaf epidermis of transformed plants was imaged on a confocal microscope.
Cloning of pUBN:RFP-EB1b
EB1b was PCR amplified from Arabidopsis cDNA, accession Columbia, using primers EB1b EcoRI F and EB1b XhoI R and cloned into pgem T-vector (Promega, Madison, WI). Subsequently, the plasmid was digested with EcoRI and XhoI, and the Eb1b insert was ligated into the respective restriction sites in pENTR2B (Gateway, Irvine, CA). The resulting vector was recombined with destination vector pUBN:RFP (35) to obtain pUBN:RFP-EB1b. Transgenic lines were generated via A. tumefaciens mediated transformation as described earlier (36).
Accession numbers
The full-length sequences of POK2 and EB1b can be found at the Arabidopsis Genome Initiative or the European Molecular Biology Laboratory/GenBank databases using accession numbers GenBank: At3g19050 and At5g62500, respectively.
Confocal microscopy
Localization imaging used a Leica SP8 (Leica, Wetzlar, Germany) confocal microscope equipped with a resonant scanner. Imaging was carried out at room temperature using a 63× water immersion objective with a numerical aperture of 1.2. GFP and yellow fluorescent protein were excited at 488 and 514 nm using an argon and krypton laser, respectively, and were detected using Hybrid Detectors in the range of 500–550 and 520–550 nm, respectively. The excitation for red fluorescent protein was done using a 561 nm laser line, and the signal was detected by a Hybrid Detector in the range of 570–650 nm.
Results
POK21–589 is a plus-end-directed dimeric motor that switches motility modes
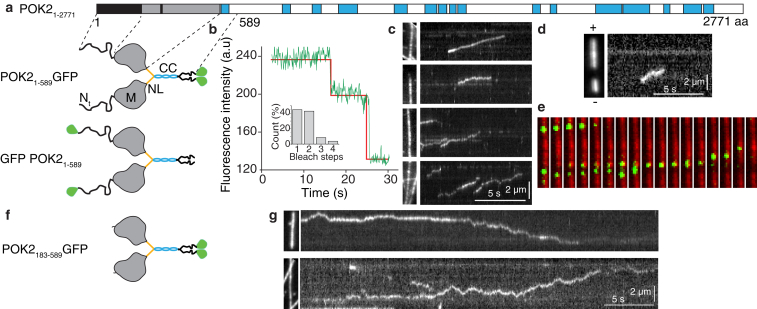
To investigate the underlying molecular mechanism using reconstituted assays, we expressed and purified truncated and fluorescently tagged POK2 motors. POK2 is the largest identified kinesin to date, with an extraordinary long and intrinsically disordered N-terminus (∼190 amino acids (aa) compared to 7 aa in conventional kinesin) preceding its motor domain (9). To focus on the motor functionality, we created a motor, POK21–589, truncated after the first predicted coiled coil and fused to a C-terminal GFP tag (Fig. 1 a; Fig. S1). To test whether the coiled coil was sufficient for the dimerization of the truncated motor, we performed photobleaching assays using a custom-built TIRF microscope (28). We immobilized taxol-stabilized and rhodamine-labeled microtubules at the cover glass surface and added purified POK21–589 molecules into the flow channel in the presence of AMP-PNP (Figs. S2 and S3). This nonhydrolyzable ATP analog causes kinesin motors to interact with microtubules in a strongly bound, nonmotile state. We recorded the fluorescence intensity of GFP-tagged motors that colocalized with microtubules as a function of time and found that most GFP molecules bleached in one or two steps (Fig. 1 b). For most of the single-step bleach events, the step amplitude was consistent with twice the amplitude of single-step bleach events, suggesting that two GFP fluorophores bleached simultaneously. Together, these data confirm that POK21–589 binds microtubules and is consistent with the notion that the first coiled-coil region is sufficient for homodimer formation.
Figure 1.
POK21–589 is a plus-end-directed dimeric motor. (a) The top shows the full-length POK2 domain organization: motor domain (gray, M) with ATP binding site (black strip in M), coiled coil (cyan, CC), and intrinsically disordered N-terminus region (black, Nt). The bottom shows a structural cartoon of the GFP-tagged truncated POK2 used in the in vitro (top) and in vivo (bottom) assays, where region Nt is followed by M, and a short neck linker (orange, NL) connecting M and CC. The domain organization and cartoon are based on a bioinformatics analysis (Fig. S1). (b) An example trace of the fluorescence intensity over time for a single POK21–589 bound to the microtubule in the presence of 1 mM AMP-PNP is shown. The relative frequencies of bleaching steps are represented in the inset (N = 105). (c) Representative kymographs showing motile single POK21–589 and their typical behavior on the microtubule lattice are shown. The left picture indicates respective microtubules. (d) An example kymograph for a single POK21–589 indicating its plus-end directionality is shown. The left picture shows a polarity-marked microtubule. (e) An image sequence of single POK21–589 (green) interacting with a microtubule (red) corresponding to the third panel of (c) is shown. Images are 4.75 μm high. The time between frames is 0.5 s. (f) A cartoon of the N-terminal truncation POK2183–589-GFP construct is shown. (g) Representative kymographs of POK2183–589 are shown. To see this figure in color, go online.
To characterize the motor functionality, we performed TIRF microscopy motility assays in the presence of ATP (1 mM). We found that POK21–589 is an active motor that robustly translocates on the microtubule lattice (Fig. 1, c–e; Video S1). Using polarity-marked microtubules, POK21–589 showed on average plus-end-directed motility, as expected for kinesins with an N-terminally located motor domain (Fig. 1 d). We did not observe any preference for or extended dwells at microtubule ends. Interestingly, although the overall motion of POK21–589 molecules was toward the plus end, we observed recurrent episodes of random, forward, and backward motion (Fig. 1, c–e) suggesting that POK21–589 motors switch between processive and diffusive modes while interacting with the microtubule lattice.
An image sequence of single POK21–589 (green) interacting with a microtubule (red) corresponding to the third panel of Fig. 1 c is shown. The still images are displayed in Fig. 1 e. The video is 11 μm wide and 17× real time.
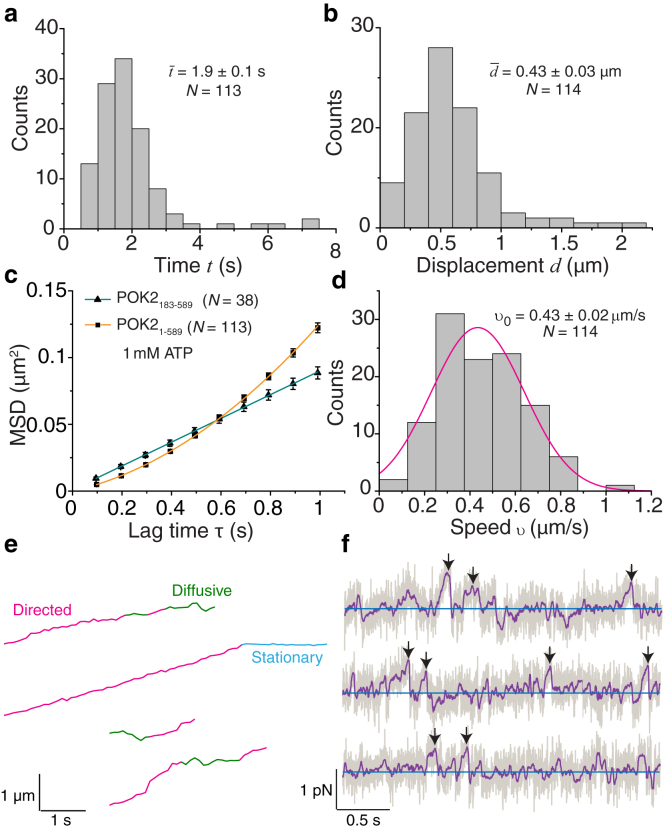
To test whether diffusion was due to the large N-terminal extension (Nte) of the motor (Fig. 1 a), we truncated the N-terminus and repeated the same motility assay for the POK2183–589 construct (Fig. 1, f and g). Surprisingly, POK2183–589 interacted with the microtubule lattice for a longer time of 11 ± 1 s (mean ± standard error (SE), N = 38) compared to 1.9 ± 0.1 s for POK21–589 (Fig. 2 a). Kymographs of POK2183–589 showed more diffusive motion (Fig. 1 g), suggesting that the Nte affected the processive mode. Furthermore, POK2183–589 had a much lower affinity to microtubules (Fig. S4 a). Therefore, we analyzed the Nte amino acid sequence and found a similarity to the ∼80 aa long Nte of BimC (Fig. S4 b). BimC is the founding member of the kinesin-5 family and has a secondary microtubule-binding site in its Nte (37). Interestingly, loss of the Nte in BimC also reduced the affinity of BimC to microtubules; however, the structural mechanism is not understood. Together, these findings suggest that the Nte of the POK2 affects the motor-microtubule interaction strength and promotes the processive over the diffusive mode.
Figure 2.
POK21–589 is a weak motor that switches between processive and diffusive modes. Distributions of total interaction time (a) and overall displacement (b) of POK21–589 on the microtubule lattice are shown. Mean values, ± SE, and total number of molecules are indicated. (c) The mean-squared displacement (MSD) of POK21–589 and POK2183–589 in 1 mM ATP plotted against the lag time is shown. The orange line is a fit of the Eq. 1 to the POK21–589 data, whereas the green line is a linear fit to the POK2183–589 data. The error bars are ± SE of squared-displacement values. (d) A speed histogram of directed segments has a Gaussian distribution (magenta line). Mean speed, ± SE and number of molecules are indicated. (e) Example trajectories of POK21–589 obtained via single-molecule tracking are shown. Mode switches were detected using an SCI algorithm (Supporting Material). Magenta, green, and cyan denotes directed, diffusive, and stationary segments, respectively. Note that stationary segments were not at the microtubule end. (f) Representative traces depicting the force of single POK21–589 molecules as a function of time (gray line, running median filter over 500 data points: purple line). The blue line marks zero force. Maximal forces are marked by black arrows. To see this figure in color, go online.
MSD for exclusive directed and diffusive states
To confirm the POK21–589 switching behavior, we tracked the motion of single POK21–589 motors on individual microtubules using an automated data analysis based on two-dimensional Gaussian models (33) (Fig. 1 e). Histograms of the total microtubule interaction time and overall displacement of single motors show peaked distributions (Fig. 2, a and b). Peaked distributions are indicative of multiple underlying processes, such as directed and diffusive modes. In contrast, exponential distributions are typical of a single, rate-limiting process (38). To quantify this behavior, we used a statistical approach to measure the spatial extent of motion over time: an MSD analysis. In our case, the MSD of a single POK21–589 motor as a function of lag time is best fitted by a parabola (orange line in Fig. 2 c) with significant linear and parabolic coefficients. The presence of both terms confirms that POK21–589 indeed has two motility modes. Although the linear term is related to diffusion, the quadratic term is due to directed motion (39, 40). Diffusion can occur simultaneously with directed motion, for example, when a particle is freely diffusing in three dimensions and subjected to a flow or drift. However, in our case, POK21–589 is exclusively either in the processive or the diffusive state. To the best of our knowledge, this scenario has not been addressed with respect to single molecular machines interacting with filaments in a one-dimensional diffusive system. Therefore, we derived the expected MSD as a function of lag time τ for a motor being either in the diffusive or in the processive state (Appendix A):
| (1) |
where ϕ is the fraction of the total interaction time the motor spends in the directed mode; υ0 and συ the mean speed and its standard deviation, respectively; D the diffusion coefficient; and ε an offset related to the tracking precision and image acquisition (41). Equation 1 accounts for the exclusive character of the states and the amount of time in the respective states avoiding an underestimation of both the speed and the diffusion coefficient (14, 18). Because five parameters enter Eq. 1, namely ϕ, υ0, συ, D, and ε, and a fit of Eq. 1 to the data only results in three independent coefficients of the parabola, the system is underdetermined. Thus, an MSD analysis alone cannot provide all the parameters. Therefore, in addition to the MSD, we used an SCI analysis. The SCI analysis is based on the temporal correlations of the speed of individual molecules, in which high amount of correlation signifies directed motion and no correlation indicates purely Brownian motion (34). The SCI algorithm optimized to our POK21–589 dataset identified transient switches in the POK21–589 trajectories between directed, diffusive, and stationary states (Appendix B). However, because of limited spatiotemporal resolution of the TIRF measurements, our SCI algorithm could only reliably determine the speed in the directed mode of 430 ± 170 nm/s (mean ± SD, N = 114, Fig. 2, d and e; Fig. S5). Using this speed υ0 and its standard deviation συ as an input for Eq. 1 (i.e., we provide and fix two out of the five parameters for the fit), the best-fit diffusion coefficient is 0.056 ± 0.008 μm2/s (mean ± SE), the relative time spent in the directed mode is 62 ± 2% (mean ± SE; Figs. S6–S8), and the constant offset is ε = 32 ± 3 nm, giving an estimate for the tracking precision. We also tracked single POK2183–589 molecules. In contrast to POK21–589, their MSD was best fit by a line (green line in Fig. 2 c) with no significant parabolic coefficient. Thus, the truncation of the Nte switched POK2 to a purely diffusive mode with a diffusion coefficient of 0.040 ± 0.001 μm2/s not significantly different from the value for POK21–589. The value for the diffusion coefficient of POK21–589 is intermediate between the reported values for other kinesins, such as Kip3 (26) and MCAK (12), of ∼0.004 and 0.4 μm2/s, respectively. Our MSD equation also quantitatively explains previous observations of motors switching between different states (18). Thus, with a combined SCI and MSD analysis approach, we could objectively quantify the two modes of the POK21–589 motor interaction with the microtubule lattice. Taken together, POK21–589 spends a large fraction—about two-thirds—of its time in the processive state, walking in a directed manner along microtubules.
POK21–589 is a weak motor
To assess whether POK2 motors are capable of generating force, we measured the maximal force that single machines could exert on artificial cargo using high-resolution optical tweezers (30, 42). As cargo, we used microspheres coupled to POK21–589 via its GFP tag, ensuring functional activity of the motor (29) (Fig. S2). Using a stationary trap, single motors displaced microspheres from the trap center with force increasing proportional to the displacement according to Hooke’s law (Fig. 2 f). Compared to conventional kinesin-1 and other kinesins (29), we observed that POK21–589 did not exhibit stalling behavior for extended periods. Instead, motor-coupled microspheres showed sudden and fast movements back to the trap center, consistent with a motor detachment from the microtubule or switching to a diffusive mode and slipping back on the microtubule (10, 43). We measured the maximal force before such events and found an average maximal force of 0.34 ± 0.02 pN (mean ± SE, N = 67, Fig. 2 f). Because POK2183–589 did not show any directed motility, we did not use this motor for trapping experiments. Thus, for POK21–589, even though the motor spent most of its time in the directed mode when no loads were applied, single motors were unable to generate large forces. Forces exceeding 1 pN could be measured when multiple POK21–589 motors were pulling on trapped microspheres (Fig. S9).
The peripheral microtubule plus ends point toward the putative cell-plate fusion site
Having characterized the POK21–589 motor activity in vitro, we wanted to confirm the microtubule interaction, functionality, and speed of POK21–589 in vivo. Therefore, we transiently expressed GFP-POK21–589 (Fig. 1 a) in N. benthamiana leaves. We found that POK21–589 colocalizes with microtubules (Fig. S10). The microtubule decoration changed dynamically, consistent with motors keeping up with dynamic microtubule ends growing with a speed of 74 ± 3 nm/s (mean ± SE, N = 41; Fig. S10) (44). However, the signal/noise ratio was insufficient to track the motility of single motors in vivo precluding direct measurements on peripheral microtubules emanating from the phragmoplast.
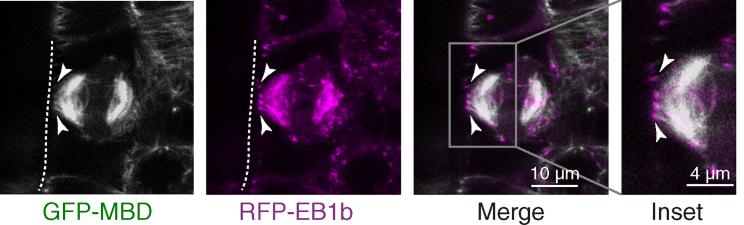
The polarity of peripheral microtubules at the phragmoplast leading zone approaching the cell cortex during late cytokinesis (7, 8) determines whether motors pull on or push against such microtubules and thereby the phragmoplast itself. The majority of phragmoplast microtubules, including the ones at the leading edge, are oriented with their polymerizing plus ends toward the division plane (45), suggesting that peripheral microtubules are also oriented with their plus ends toward the division site (46, 47). To confirm the polarity of the peripheral microtubules in Arabidopsis, we created an Arabidopsis transgenic line with GFP-labeled microtubules and red-fluorescent-protein-labeled EB1b, a microtubule plus-end tracking protein. We imaged 4–5-day-old seedlings using a confocal microscope and found that the leading edge of the phragmoplast indeed sends out peripheral microtubules with their plus ends directed toward the putative division site (Fig. 3). However, the presence of microtubule plus ends at the division site does not rule out that additional minus-end-directed microtubules are there as well. Yet, based on the overall structure and dynamics of the phragmoplast, we do not expect a high abundance of such microtubules. Suggested by the functional redundancy of POK1 and POK2, we assume that both POKs localize to the cortical division site (unpublished data by S.M. confirm the assumption for POK2) and function alike. Thus, POK2 motors likely push against peripheral microtubules rather than pull on them.
Figure 3.
Directionality of the phragmoplast peripheral microtubules. Arabidopsis root meristem stably expressing 35S:GFP-MBD and pUBQ:RFP-EB1b during late cytokinesis is shown. Plus ends (RFP-EB1b) marked with arrow heads of peripheral microtubules (GFP-MBD) from the leading edge of the phragmoplast reach out toward the putative division site. The cell boundary is marked with a dashed line. To see this figure in color, go online.
Discussion
Based on state-of-the-art single-molecule techniques and a combined MSD-SCI analysis, we have functionally characterized the plant kinesin-12 POK2 motor—without its long C-terminal tail—as a plus-end-directed, weak, and dimeric motor that switches between processive and diffusive modes. Because the long Nte before the motor domain appears to be required for the processive mode, this Nte domain seems to be involved in the switching process. As for BimC, the disordered region of the POK2 Nte might also have a microtubule-binding site that helps in the microtubule attachment, explaining the low affinity of the construct lacking the Nte (Fig. S4). Once bound, the Nte interaction with the motor domain may promote processivity at the cost of total microtubule interaction time.
Although MSD analyses are commonly applied to study mixed diffusive and directed motion, to the best of our knowledge, studies so far do not account for the mutually exclusive character of processive and diffusive states in case of molecular machines. Our MSD analysis (Eq. 1) not only accounts for this exclusive character of states but also for the inherent speed distribution of motors. Not accounting for the exclusive character and distribution leads to systematic errors in the motility parameters.
Compared to conventional kinesin-1 with a stall force of ∼5–6 pN (29), POK21–589 is one of the weakest kinesin motors across taxa. Reported weak motors belong to the kinesin-8 family with the members Kif18B, Kif18A, and Kip3 reaching maximal forces of ∼0.6, 0.8, and 1.1 pN, respectively (18, 43). For POK21–589, we attribute such low forces to the motor switching to a diffusive state similar to Kip3 that switches into a slip state (43). Because motors are weakly bound to the microtubules in the diffusive state, they can slide along the microtubule lattice with little resistance but without detachment when a force is applied (10, 20, 43). This sliding might enable the motor to dynamically link to microtubule plus ends in analogy to CENP-E (16, 48). CENP-E is almost as large as POK2, suggesting that a very long motor tail may enhance dynamic attachment to microtubules. Thus, we hypothesize that the function of the diffusive state and low force production is to provide a means of attachment to microtubules, allowing for a relative sliding motion with little resistance. Based on this hypothesis and the intrinsic motor properties, how does POK2 guide the expanding phragmoplast during cytokinesis?
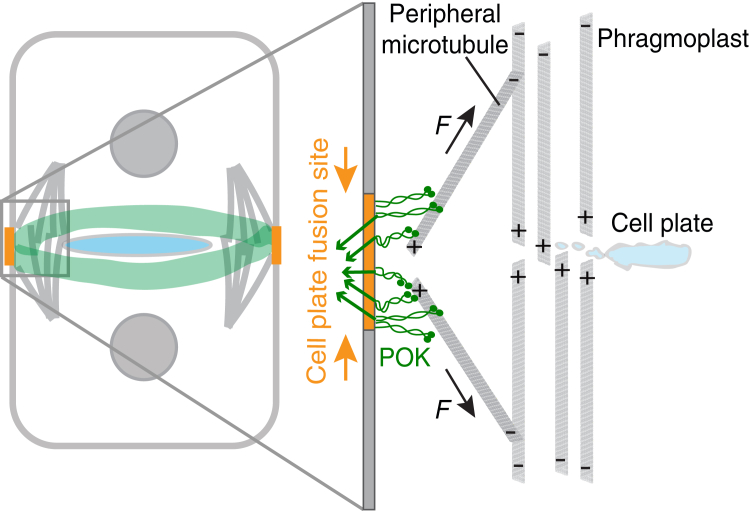
Our combined in vivo and in vitro results support a phragmoplast guidance model in which POK2 motors push against peripheral microtubules (Fig. 4). We validated the POK21–589 interaction with microtubules in planta and the polarity of the peripheral microtubules that appear to connect the putative division site, where POK motors are located, with the phragmoplast. Peripheral microtubules are oriented with their plus ends toward the putative cell-plate fusion site and likely probe the cell cortex in a “search and capture”-type mode (46). We propose that as the torus-shaped phragmoplast branches out plus-end-directed peripheral microtubules at the leading edge, POK2 full-length molecules at the division site (S.M., unpublished data) capture these microtubules and walk toward their plus ends. Because the motor speed (Fig. 2 d) is faster compared to the phragmoplast expansion speed (7), we expect that motors catch up with the microtubule plus ends. If motors are attached to the cell boundary, and because they walk toward the microtubule plus end, they counteract the microtubule expansion driven by the phragmoplast and, thus, push against the phragmoplast (Fig. 4). The POK2s’ enormous size and contour length may enhance an effective capture of incoming microtubules in analogy to CENP-E. Pushing may seem counterintuitive for phragmoplast guidance but, together with the unusual mechanics of these kinesin-12 motors, provides insight into the guidance mechanism. As POK21–589 motors exert little force, the forces of the expanding phragmoplast are expected to exceed the opposing pushing force of POK2 motors when they are in the processive state, even when multiple motors interact simultaneously. Once the motors switch to the diffusive state, they can then slide along the microtubule lattice. The switching rate to the diffusive mode of the motors may even increase under load conditions, as reported for the switching to the weakly bound slip state of kinesin-8 (43). POK2 motors would, thus, guide the phragmoplast in a manner similar to the dynamic and diffusive attachment of microtubules to the kinetochore or chromosomes, for example, via the Ndc80 complex (49, 50, 51) or CENP-E (48), respectively. We believe that POK1 motors function in a similar manner, as established by their functional redundancy with POK2 (7). Whether POK2 motors are regulated by importin-β during the cell cycle remains to be seen (52).
Figure 4.
Proposed model for phragmoplast guidance. POK motors (green) localized at the division site push against the leading edge of the expanding phragmoplast by capturing the peripheral microtubules and walk toward their plus ends, pushing against the expanding phragmoplast. The black arrow marks the direction of the pushing force. This model also supports the narrowing of the division site (orange, Fig. S11) to the cell-plate fusion site by a mechanical process. POK motors experience a counter force (green arrows). This force focuses the POKs to a precise spot, i.e., the cell-plate fusion site. To see this figure in color, go online.
During cytokinesis, pushing forces by POKs have an important consequence. According to Newton’s third law, there is a net force of equal magnitude and opposite direction acting on the anchoring points of the motors. Furthermore, due to the geometry of the connected peripheral microtubules, these opposing forces will focus the motors to a central spot, assuming that their membrane anchors are mobile within the lipid bilayer (Fig. 4). The small forces of a single motor are sufficient to drag an anchoring point through a fluid membrane. Also, when multiple motors interact simultaneously with a microtubule, the pushing forces of the expanding phragmoplast and counteracting motor forces are expected to be sufficient for moving the anchoring points in the membrane. This mechanical focusing could contribute to the poorly understood narrowing of POK1 and POK1-dependent components from the division site to a definite cell-plate fusion site during late cytokinesis (5, 7, 8, 53) (Fig. S11). Whether POK motor motility itself is required for in planta guidance, whether a diffusive tethering is sufficient, how motors switch to the diffusive state, and if and how much force is necessary for division site narrowing are unknown at the moment.
Interestingly, a few other microtubule-associated candidates occupy the division site, such as minus-end-directed kinesin-14 KCBP (54, 55), TAN (6), and MAP65-4 (56). What possible role they play during the cell-plate insertion process is also unclear at the moment. For example, forces generated by KCBP could accelerate phragmoplast guidance, or MAP65-4 could contribute to the cross-linking of peripheral microtubules.
Conclusions
In conclusion, our study offers mechanistic insights into the operating behavior of single plant kinesin-12 POK2 motors. We quantified the motors’ motility by a novel to our knowledge MSD analysis that can be utilized for other diverse molecular machines. POK2 is the first kinesin-12 motor among five other members in Arabidopsis to be characterized to our knowledge. The mechanical properties of POK2 provide a key step toward an active and dynamic understanding of the division site beyond what can be inferred from localization studies alone. Moreover, the phragmoplast guidance pushing model suggested here highlights the participation of active molecular machines needed for the accurate insertion of cell plates during plant cytokinesis and plausibly accounts for the narrowing of the division site to the cell-plate fusion site. In planta experiments, ideally with single-molecule resolution, are required to test the proposed hypothesis involving pushing forces. In other cells, pushing forces are thought to provide a more precise centering mechanism compared to pulling forces, for example, for centering of the mitotic spindle (57, 58). Here, pushing forces in combination with sliding of motors along microtubules dynamically attaching to their ends may lead to precise and accurate mechanical patterning and shaping of plant tissues.
Author Contributions
E.S., E.L., S.M., and M.C. designed the research. M.C. and M.R. performed in vitro experiments. M.B. assisted in force measurements and wrote MATLAB scripts. M.C., E.L., A.H., and S.M. performed in vivo experiments. B.R. and E.S. derived the MSD equation. M.C., M.R., M.B., E.L., S.M., and E.S. analyzed the data. M.C. and E.S. wrote the manuscript.
Acknowledgments
We thank Tobias Jachowski, Naghmeh Azadfar, and Mohammad Kazem Abdosamadi, Katharina Stuhrberg for technical assistance during the project and Suman De for building the TIRF microscope. We thank Pantelis Livanos and Christine Kiefer for comments on the manuscript and Martin Oettel for comments on the MSD equation.
M.C. and M.B. acknowledge financial support from the International Max Planck Research Schools from Molecules to Organisms, Max Planck Institute for Developmental Biology, Tübingen and the Rosa Luxemburg Foundation, respectively. This work was supported by the Deutsche Forschungsgemeinschaft in terms of the Collaborative Research Center 1101 project A04 from S.M. and E.S. and the University of Tübingen.
Editor: Stefan Diez.
Footnotes
Basudev Roy’s present address is Department of Physics, Indian Institute of Technology Madras, Tamil Nadu, India.
Eleven figures and one video are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30688-X.
Appendix A: MSD Analysis
The average MSD was plotted against lag time and fitted with a parabola because the motor exhibited diffusive as well as directed motion. For simultaneous one-dimensional diffusion and directed motion, the MSD as a function of lag time τ is given by the well-known equation
| (2) |
The first term refers to the directed motion, where υ is the speed. The second term is the contribution by the diffusive motion, where D is the diffusion coefficient. The last term is a constant related to the tracking precision and image acquisition (41). Although this equation yields the parameters D and υ, the motion occurs simultaneously. An example for such simultaneous motion is a particle diffusing in a liquid with an applied flow. However, such simultaneous motion is impossible for a molecular motor taking discrete steps. Steps are exclusively either directed or random. Furthermore, for kinesins, the average stepping rate in the diffusive mode is typically much larger compared to the directed mode. For example, a kinesin moving with a directed speed of 400 nm/s takes about 50 steps per second. Assuming the motor takes 8 nm steps during diffusion (20) and has a diffusion coefficient of 0.032 μm2/s, the diffusive stepping rate is 2D/δ2 = 1000 steps per second (δ = 8 nm), 20× higher compared to the directed state. Thus, the motor has distinct and different properties in the two modes. To account for the switching behavior, a modification to Eq. 2 is required. Therefore, the MSD equation that accounts for a motor being exclusively either in a diffusive or directed mode is derived in the following.
The motion of a motor that switches between the different modes is described by the Fokker-Planck equation
| (3) |
where p(x,t) is the probability density of the motor being at a position x at time t. η(t) is either 0 or 1, randomly switching between the two values as a function of time. The number indicates whether the particle is diffusing (η = 0) or translating (η = 1). Equation 3 is for one realization of η(t) and also assumes that the average switching rate is small compared to the stepping rate of the molecular motor, i.e., the time between switches is long compared to the time per step. The Fourier transform of Eq. 3 yields
| (4) |
where is the Fourier transform of p, k is the spatial frequency corresponding to the Fourier transform of x, and i is the imaginary unit. Separating variables, Eq. 4 can be written as
| (5) |
Integration of both sides of Eq. 5 yields
| (6) |
where is an integration constant, t0 is the initial time, and the time interval t − t0 can be set to the time lag τ. The parameter ϕ is the time average of η(t) over the time interval t − t0 and, thus, represents the time fraction the motor spends in the directed state. For ϕ = 1, the motor is purely in the directed mode, and for ϕ = 0, only diffusing. The equation holds for times large compared to the switching time, for which case the variance of ϕ is small. The last equation can be rewritten as
| (7) |
for which the inverse Fourier transform results in the probability density
| (8) |
The MSD is then defined by
| (9) |
which results in
| (10) |
where, as pointed out above, ϕ is the fraction of the time spent in the directed motion.
If the speed of an individual molecular motor is constant for an individual run but changes from molecule to molecule and run to run, then the average MSD of the individual MSDs of the individual runs differs from Eq. 10. The difference arises because of the nonlinear, i.e., quadratic, contribution of the speed to the MSD. We assume that the speed is normally distributed with a mean speed υ0 and standard deviation συ. If we denote the various MSDs for different runs as , where n is the index of the run, the expectation value of the average MSD for large n is calculated according to
| (11) |
The second moment of the speed, i.e., the mean-squared speed, is (note that the variance is ). If we denote the mean diffusion coefficient by , then the final result of the modified Eq. 10 is
| (12) |
where we have added again the offset 2ε2 related to the tracking precision and image acquisition. Because the MSD has a linear dependence on the diffusion coefficient, a distribution in the diffusion coefficients does not affect the equation. For a small variance in speed relative to the mean, Eq. 12 reduces to Eq. 10. Equation 12 corresponds to the MSD equation stated in the main text.
If the mean speed and standard deviation are known, the parameters D and ϕ can be calculated from a parabolic fit, MSD = A2τ2 + Bτ + C, to the overall MSD (Fig. 2 c in the main text) by the following relations
| (13) |
and
| (14) |
Appendix B: SCI Analysis
To determine the speed of the motor, we performed an SCI analysis (34). The SCI analysis relies on the temporal correlations of the speed of individual molecules. This correlation exists and persists for directed motion but disappears for Brownian motion. A MATLAB script was written to analyze the trajectories of each molecule. The SCI parameter is a normalized average over an optimal time window, which provides a local analysis whether speeds are correlated or not. In particular, the switch times between diffusive and directed segments were analyzed by defining a threshold for temporal correlations. The SCI analysis cannot distinguish between diffusive and stationary events. Thus, we identified the latter by comparing the root mean-squared positional noise σx of the segments with that of stationary motors taken from immotile POK2 bound to microtubules. For a threshold of σx < 32 nm, segments were classified as being stationary. For our frame time of 0.1 s, we used a window size of four data points with an SCI threshold of 0.8. From 113 original POK2 trajectories, 95 traces were long enough for the SCI analysis. The algorithm found 65 diffusive, 114 directed, and 21 stationary segments. The relative time POK2 spent in the diffusive, directed, and stationary mode were 29%, 63%, and 8%, respectively. All diffusive and directed segments are shown in Fig. S7. The mean duration of the diffusive and directed segments were 0.8 ± 0.1 s and 1.1 ± 0.1 s, respectively (Fig. S6). The mean speed and standard deviation of directed segments weighted by their number of data points was 430 ± 170 nm/s (Fig. 2 e). A Shapiro-Wilk test confirmed a normal distribution of speeds. An MSD analysis of only the diffusive segments yielded a diffusion coefficient of 0.015 ± 0.001 μm2/s (Fig. S5). However, the mean displacements of diffusive segments still showed a significant bias over time (Fig. S7). Such a bias is inconsistent with pure diffusion and indicates that the SCI analysis did not fully separate directed and diffusive segments. This bias remained for all tested combinations of SCI parameters, i.e., variations of window size and thresholds. Thus, our time resolution and tracking precision was not sufficient for the segmentation. Therefore, we conclude that POK2 sometimes switched between modes faster than or on time scales comparable to the data acquisition time. An observation consistent with this conclusion is the lack of short diffusive segments due to the SCI algorithm when comparing the distribution to the expected exponential distribution (Fig. S6). Apart from the cutoff at short times, segments containing very short periods of directed and diffusive motion are identified as diffusive segments by the algorithm. As a consequence, the diffusion coefficient obtained from the MSD analysis of the diffusive segments is underestimated, because during short directed periods, the motor takes far fewer steps compared to when it is in its diffusive mode (see Appendix A). Yet we expect that long directed segments and their parameters are reliably detected. One indication whether directed parameters are reliable is that the speed is normally distributed. The mean speed also corresponds to the mean speed that one obtains by manually analyzing the slopes of the kymographs. Thus, Eqs. 13 and 14 can be used to determine diffusion constant D and relative time in the directed mode ϕ. The derivation of Eq. 12 did not account for the possibility of a stationary state. However, such a state only adds a constant to the MSD and is effectively adsorbed in our constant parameter. Thus, using Eq. 13, the diffusion constant was calculated to be 0.056 ± 0.008μm2/s and, using Eq. 14, the relative time in the directed state excluding stationary segments was determined to be 62 ± 2%. To assess how the diffusion coefficient and speed depends on the relative time spent in the states, we plotted Eq. 13 as a function of the effective speed (Fig. S7). Not accounting for our standard deviation in speed of 170 nm/s would change the time fraction to about 67%, with an increase in the diffusion coefficient of about 10%. We expect to slightly underestimate the speed because the SCI algorithm misses short diffusive segments. In this case, ϕ-values might be higher and the diffusion coefficient lower. Because our parameters fall into the range of effective speeds, for which Eq. 13 flattens out, we do not expect a large difference in the true diffusion coefficient of the motor.
Supporting Material
References
- 1.Smertenko A.P., Piette B., Hussey P.J. The origin of phragmoplast asymmetry. Curr. Biol. 2011;21:1924–1930. doi: 10.1016/j.cub.2011.10.012. [DOI] [PubMed] [Google Scholar]
- 2.Smertenko A., Assaad F., Žárský V. Plant cytokinesis: terminology for structures and processes. Trends Cell Biol. 2017;27:885–894. doi: 10.1016/j.tcb.2017.08.008. [DOI] [PubMed] [Google Scholar]
- 3.Buschmann H., Zachgo S. The evolution of cell division: from streptophyte algae to land plants. Trends Plant Sci. 2016;21:872–883. doi: 10.1016/j.tplants.2016.07.004. [DOI] [PubMed] [Google Scholar]
- 4.Gunning B.E., Wick S.M. Preprophase bands, phragmoplasts, and spatial control of cytokinesis. J. Cell Sci. Suppl. 1985;2:157–179. doi: 10.1242/jcs.1985.supplement_2.9. [DOI] [PubMed] [Google Scholar]
- 5.Walker K.L., Müller S., Smith L.G. Arabidopsis TANGLED identifies the division plane throughout mitosis and cytokinesis. Curr. Biol. 2007;17:1827–1836. doi: 10.1016/j.cub.2007.09.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rasmussen C.G., Sun B., Smith L.G. Tangled localization at the cortical division site of plant cells occurs by several mechanisms. J. Cell Sci. 2011;124:270–279. doi: 10.1242/jcs.073676. [DOI] [PubMed] [Google Scholar]
- 7.Lipka E., Gadeyne A., Müller S. The phragmoplast-orienting kinesin-12 class proteins translate the positional information of the preprophase band to establish the cortical division zone in Arabidopsis thaliana. Plant Cell. 2014;26:2617–2632. doi: 10.1105/tpc.114.124933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xu X.M., Zhao Q., Meier I. RanGAP1 is a continuous marker of the Arabidopsis cell division plane. Proc. Natl. Acad. Sci. USA. 2008;105:18637–18642. doi: 10.1073/pnas.0806157105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Müller S., Han S., Smith L.G. Two kinesins are involved in the spatial control of cytokinesis in Arabidopsis thaliana. Curr. Biol. 2006;16:888–894. doi: 10.1016/j.cub.2006.03.034. [DOI] [PubMed] [Google Scholar]
- 10.Ramaiya A., Roy B., Schäffer E. Kinesin rotates unidirectionally and generates torque while walking on microtubules. Proc. Natl. Acad. Sci. USA. 2017;114:10894–10899. doi: 10.1073/pnas.1706985114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hancock W.O., Howard J. Processivity of the motor protein kinesin requires two heads. J. Cell Biol. 1998;140:1395–1405. doi: 10.1083/jcb.140.6.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Helenius J., Brouhard G., Howard J. The depolymerizing kinesin MCAK uses lattice diffusion to rapidly target microtubule ends. Nature. 2006;441:115–119. doi: 10.1038/nature04736. [DOI] [PubMed] [Google Scholar]
- 13.Lu H., Ali M.Y., Trybus K.M. Diffusive movement of processive kinesin-1 on microtubules. Traffic. 2009;10:1429–1438. doi: 10.1111/j.1600-0854.2009.00964.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Furuta K., Toyoshima Y.Y. Minus-end-directed motor Ncd exhibits processive movement that is enhanced by microtubule bundling in vitro. Curr. Biol. 2008;18:152–157. doi: 10.1016/j.cub.2007.12.056. [DOI] [PubMed] [Google Scholar]
- 15.Fink G., Hajdo L., Diez S. The mitotic kinesin-14 Ncd drives directional microtubule-microtubule sliding. Nat. Cell Biol. 2009;11:717–723. doi: 10.1038/ncb1877. [DOI] [PubMed] [Google Scholar]
- 16.Kim Y., Heuser J.E., Cleveland D.W. CENP-E combines a slow, processive motor and a flexible coiled coil to produce an essential motile kinetochore tether. J. Cell Biol. 2008;181:411–419. doi: 10.1083/jcb.200802189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kwok B.H., Kapitein L.C., Kapoor T.M. Allosteric inhibition of kinesin-5 modulates its processive directional motility. Nat. Chem. Biol. 2006;2:480–485. doi: 10.1038/nchembio812. [DOI] [PubMed] [Google Scholar]
- 18.Shin Y., Du Y., Ohi R. Biased Brownian motion as a mechanism to facilitate nanometer-scale exploration of the microtubule plus end by a kinesin-8. Proc. Natl. Acad. Sci. USA. 2015;112:E3826–E3835. doi: 10.1073/pnas.1500272112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Drechsler H., McHugh T., McAinsh A.D. The kinesin-12 Kif15 is a processive track-switching tetramer. eLife. 2014;3:e01724. doi: 10.7554/eLife.01724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bormuth V., Varga V., Schäffer E. Protein friction limits diffusive and directed movements of kinesin motors on microtubules. Science. 2009;325:870–873. doi: 10.1126/science.1174923. [DOI] [PubMed] [Google Scholar]
- 21.Sturgill E.G., Das D.K., Ohi R. Kinesin-12 Kif15 targets kinetochore fibers through an intrinsic two-step mechanism. Curr. Biol. 2014;24:2307–2313. doi: 10.1016/j.cub.2014.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Drechsler H., McAinsh A.D. Kinesin-12 motors cooperate to suppress microtubule catastrophes and drive the formation of parallel microtubule bundles. Proc. Natl. Acad. Sci. USA. 2016;113:E1635–E1644. doi: 10.1073/pnas.1516370113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mann B.J., Balchand S.K., Wadsworth P. Regulation of Kif15 localization and motility by the C-terminus of TPX2 and microtubule dynamics. Mol. Biol. Cell. 2017;28:65–75. doi: 10.1091/mbc.E16-06-0476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Richardson D.N., Simmons M.P., Reddy A.S. Comprehensive comparative analysis of kinesins in photosynthetic eukaryotes. BMC Genomics. 2006;7:18. doi: 10.1186/1471-2164-7-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hunter A.W., Caplow M., Howard J. The kinesin-related protein MCAK is a microtubule depolymerase that forms an ATP-hydrolyzing complex at microtubule ends. Mol. Cell. 2003;11:445–457. doi: 10.1016/s1097-2765(03)00049-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bugiel M., Böhl E., Schäffer E. The kinesin-8 Kip3 switches protofilaments in a sideward random walk asymmetrically biased by force. Biophys. J. 2015;108:2019–2027. doi: 10.1016/j.bpj.2015.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schäffer E., Nørrelykke S.F., Howard J. Surface forces and drag coefficients of microspheres near a plane surface measured with optical tweezers. Langmuir. 2007;23:3654–3665. doi: 10.1021/la0622368. [DOI] [PubMed] [Google Scholar]
- 28.Schellhaus A.K., Moreno-Andrés D., Antonin W. Developmentally regulated GTP binding protein 1 (DRG1) controls microtubule dynamics. Sci. Rep. 2017;7:9996. doi: 10.1038/s41598-017-10088-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bugiel M., Fantana H., Jannasch A. Versatile microsphere attachment of GFP-labeled motors and other tagged proteins with preserved functionality. J. Biol. Methods. 2015;2(4):e30. [Google Scholar]
- 30.Mahamdeh M., Schäffer E. Optical tweezers with millikelvin precision of temperature-controlled objectives and base-pair resolution. Opt. Express. 2009;17:17190–17199. doi: 10.1364/OE.17.017190. [DOI] [PubMed] [Google Scholar]
- 31.Mahamdeh M., Campos C.P., Schäffer E. Under-filling trapping objectives optimizes the use of the available laser power in optical tweezers. Opt. Express. 2011;19:11759–11768. doi: 10.1364/OE.19.011759. [DOI] [PubMed] [Google Scholar]
- 32.Tolić-Nørrelykke S.F., Schäffer E., Flyvbjerg H. Calibration of optical tweezers with positional detection in the back focal plane. Rev. Sci. Instrum. 2006;77:103101. [Google Scholar]
- 33.Ruhnow F., Zwicker D., Diez S. Tracking single particles and elongated filaments with nanometer precision. Biophys. J. 2011;100:2820–2828. doi: 10.1016/j.bpj.2011.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bouzigues C., Dahan M. Transient directed motions of GABA(A) receptors in growth cones detected by a speed correlation index. Biophys. J. 2007;92:654–660. doi: 10.1529/biophysj.106.094524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Grefen C., Donald N., Blatt M.R. A ubiquitin-10 promoter-based vector set for fluorescent protein tagging facilitates temporal stability and native protein distribution in transient and stable expression studies. Plant J. 2010;64:355–365. doi: 10.1111/j.1365-313X.2010.04322.x. [DOI] [PubMed] [Google Scholar]
- 36.Clough S.J., Bent A.F. Floral dip: a simplified method for Agrobacterium-mediated transformation of Arabidopsis thaliana. Plant J. 1998;16:735–743. doi: 10.1046/j.1365-313x.1998.00343.x. [DOI] [PubMed] [Google Scholar]
- 37.Stock M.F., Chu J., Hackney D.D. The kinesin family member BimC contains a second microtubule binding region attached to the N terminus of the motor domain. J. Biol. Chem. 2003;278:52315–52322. doi: 10.1074/jbc.M309419200. [DOI] [PubMed] [Google Scholar]
- 38.Moffitt J.R., Chemla Y.R., Bustamante C. Methods in statistical kinetics. Methods Enzymol. 2010;475:221–257. doi: 10.1016/S0076-6879(10)75010-2. [DOI] [PubMed] [Google Scholar]
- 39.Qian H., Sheetz M.P., Elson E.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991;60:910–921. doi: 10.1016/S0006-3495(91)82125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Saxton M.J., Jacobson K. Single-particle tracking: applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 1997;26:373–399. doi: 10.1146/annurev.biophys.26.1.373. [DOI] [PubMed] [Google Scholar]
- 41.Michalet X. Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;82:041914. doi: 10.1103/PhysRevE.82.041914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bugiel M., Jannasch A., Schäffer E. Implementation and tuning of an optical tweezers force-clamp feedback system. In: Gennerich A., editor. Optical Tweezers: Methods and Protocols. Chapter 5. Springer Press; 2017. pp. 109–136. [DOI] [PubMed] [Google Scholar]
- 43.Jannasch A., Bormuth V., Schäffer E. Kinesin-8 is a low-force motor protein with a weakly bound slip state. Biophys. J. 2013;104:2456–2464. doi: 10.1016/j.bpj.2013.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shaw S.L., Kamyar R., Ehrhardt D.W. Sustained microtubule treadmilling in Arabidopsis cortical arrays. Science. 2003;300:1715–1718. doi: 10.1126/science.1083529. [DOI] [PubMed] [Google Scholar]
- 45.Murata T., Sano T., Hasebe M. Mechanism of microtubule array expansion in the cytokinetic phragmoplast. Nat. Commun. 2013;4:1967. doi: 10.1038/ncomms2967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dhonukshe P., Mathur J., Gadella T.W., Jr. Microtubule plus-ends reveal essential links between intracellular polarization and localized modulation of endocytosis during division-plane establishment in plant cells. BMC Biol. 2005;3:11. doi: 10.1186/1741-7007-3-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wu S.Z., Bezanilla M. Myosin VIII associates with microtubule ends and together with actin plays a role in guiding plant cell division. eLife. 2014;3:e03498. doi: 10.7554/eLife.03498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gudimchuk N., Vitre B., Grishchuk E.L. Kinetochore kinesin CENP-E is a processive bi-directional tracker of dynamic microtubule tips. Nat. Cell Biol. 2013;15:1079–1088. doi: 10.1038/ncb2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hill T.L. Theoretical problems related to the attachment of microtubules to kinetochores. Proc. Natl. Acad. Sci. USA. 1985;82:4404–4408. doi: 10.1073/pnas.82.13.4404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Powers A.F., Franck A.D., Asbury C.L. The Ndc80 kinetochore complex forms load-bearing attachments to dynamic microtubule tips via biased diffusion. Cell. 2009;136:865–875. doi: 10.1016/j.cell.2008.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sarangapani K.K., Asbury C.L. Catch and release: how do kinetochores hook the right microtubules during mitosis? Trends Genet. 2014;30:150–159. doi: 10.1016/j.tig.2014.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ganguly A., DeMott L., Dixit R. Importin-β directly regulates the motor activity and turnover of a kinesin-4. Dev. Cell. 2018;44:642–651.e5. doi: 10.1016/j.devcel.2018.01.027. [DOI] [PubMed] [Google Scholar]
- 53.Stöckle D., Herrmann A., Müller S. Putative RopGAPs impact division plane selection and interact with kinesin-12 POK1. Nat. Plants. 2016;2:16120. doi: 10.1038/nplants.2016.120. [DOI] [PubMed] [Google Scholar]
- 54.Buschmann H., Dols J., Lloyd C.W. Arabidopsis KCBP interacts with AIR9 but stays in the cortical division zone throughout mitosis via its MyTH4-FERM domain. J. Cell Sci. 2015;128:2033–2046. doi: 10.1242/jcs.156570. [DOI] [PubMed] [Google Scholar]
- 55.Yamada M., Tanaka-Takiguchi Y., Goshima G. Multiple kinesin-14 family members drive microtubule minus end-directed transport in plant cells. J. Cell Biol. 2017;216:1705–1714. doi: 10.1083/jcb.201610065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Li H., Sun B., Liu B. Arabidopsis MAP65-4 plays a role in phragmoplast microtubule organization and marks the cortical cell division site. New Phytol. 2017;215:187–201. doi: 10.1111/nph.14532. [DOI] [PubMed] [Google Scholar]
- 57.Tolić-Nørrelykke I.M. Push-me-pull-you: how microtubules organize the cell interior. Eur. Biophys. J. 2008;37:1271–1278. doi: 10.1007/s00249-008-0321-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Howard J., Garzon-Coral C. Physical limits on the precision of mitotic spindle positioning by microtubule pushing forces: mechanics of mitotic spindle positioning. Bioessays. 2017;39(11) doi: 10.1002/bies.201700122. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
An image sequence of single POK21–589 (green) interacting with a microtubule (red) corresponding to the third panel of Fig. 1 c is shown. The still images are displayed in Fig. 1 e. The video is 11 μm wide and 17× real time.