Narcissist or Narcissistic? Evaluation of the Latent Structure of Narcissistic Personality Disorder

Abstract

We investigated the latent structure of narcissistic personality disorder (NPD) by comparing dimensional, hybrid, and categorical latent variable models, using confirmatory factor analysis (CFA), non-parametric (NP-FA) and semi-parametric factor analysis (SP-FA), and latent class analysis, respectively. We first explored these models in a clinical sample, and then pre-registered replication analyses in four additional datasets (with national, undergraduate, community, and mixed community/clinical samples) to test whether the best fitting model would generalize across different datasets with different sample compositions. A one-factor CFA outperformed categorical models in fit and reliability, suggesting the criteria do not serve to distinguish a “narcissist” class or subtypes; rather, a “narcissistic” dimension underlies the NPD construct. The CFA also outperformed hybrid models, indicating that people fall within the same continuous distribution, rather than composing homogenous groups of relative severity (NP-FA) or pulling apart into mixtures of discrete distributions (SP-FA) along that spectrum.

Narcissistic personality disorder (NPD) has received considerable attention in the past decade (Wright & Edershile, 2018). However, the latent structure of NPD remains unresolved. Research that has examined the structure of NPD has produced inconsistent results and fuels ongoing controversy. Some researchers have found support for “overt” and “covert” dimensions underlying the criteria (Fossati et al., 2005), whereas others have found evidence for a single latent factor (Miller et al., 2008). Although somewhat separate from this study, trait narcissism measured using the Narcissistic Personality Inventory shows evidence of dimensionality (Foster & Campbell, 2007). This evidence dovetails with the broader literature supporting dimensionality of other personality disorders (Haslam, Holland, & Kuppens, 2012) and the utility of dimensional measures, for instance, to improve statistical power, explain comorbidity patterns, and account for transdiagnosticity (Kotov et al., 2017).

Only one study has investigated whether the NPD criteria serve as markers for discrete classes of individuals, as the Diagnostic and Statistical Model of Mental Disorders (DSM) would suggest (Fossati et al., 2005). Fossati and colleagues found support for two latent classes using taxometric analyses, narcissistic and non-narcissistic individuals. Although they considered categorical and dimensional models within the same data, they could not compare these models directly as they did not use an estimator that allowed for such a comparison.

In addition to dimensional and categorical models, hybrid models incorporating both structures are worth investigating (Wright et al., 2013). Comparing these models in a data-driven approach could help resolve current debates about whether individuals are best classified (a) as members of a narcissist category (or categories), (b) according to their position on a narcissistic spectrum (or spectra), or (c) as members of categories defined by differences on dimensional measures (a hybrid model). Such structural analyses could serve either to support or refute the DSM’s NPD construct, which is based on the a priori assumption of a qualitatively distinct, homogeneous category. In contrast, evidence for a dimensional latent structure would call into question the use of the construct and terminology of a “narcissist,” which is common in scientific and lay publications.

We aimed to investigate the latent structure of the DSM’s NPD criteria using maximum likelihood estimation to compare the fit of categorical, dimensional, and hybrid models. The models under consideration included latent class analysis as a purely categorical model, factor analysis as a strictly dimensional model, and non-parametric and semi-parametric factor analysis as hybrid (factor mixture) models.

A latent class analysis (LCA) considers variation in responses to indicator variables to be explained by membership in latent subgroups or “classes,” whereas a factor analytic model posits one or more continuous latent dimensions (factors) that account for covariances among indicator variables. LCA captures patterns of item endorsement by modeling distinct classes. In a factor analytic model, respondents are assumed to fall at different points along a latent continuum within the same category, and parameters do not vary as a function of any underlying class (Hallquist & Wright, 2014).

Hybrid models explain different response patterns through both classes and factors, where classes explain why people vary across latent dimensions. Certain parameters (e.g., factor means) can be allowed to vary across classes depending on the type of mixture model. Non-parametric factor analysis (NP-FA) distinguishes among homogeneous classes of individuals based on their relative positions along a dimension (i.e., factor means), with within-class variance fixed at zero; as such, it can be considered a conceptual midpoint between LCA and FA (Hallquist & Wright, 2014).¹ Semi-parametric factor analysis (SP-FA) lies further towards the dimensional end of the spectrum than NP-FA.²

In the current study, we first estimated each of the four models in a clinical sample, then tested whether our initial results replicated across additional, large datasets – an undergraduate sample, large community sample, national epidemiological sample, and mixed community/clinical sample. The goal was to verify that a best-fitting model described the latent structure well enough to generalize across large samples with different compositions and different assessment approaches (e.g., self-report, clinical interview) and measures.

Methods

Pre-Registration

Initial analyses of the latent structure of NPD criteria were conducted in a single dataset and then used to generate predictions for the remaining datasets. To rigorously test replicability and generalizability of the results, we chose to use five datasets – a clinical sample (for the initial analyses), a community sample, an undergraduate sample, a national epidemiological sample, and a mixed community/clinical sample. The replication datasets were decided upon at the beginning of the study and obtained while the initial dataset was being analyzed. Thus, we pre-registered our initial results and predictions before commencing analyses on the replication datasets: https://osf.io/8s8c5/.

Datasets (See supplementary Tables S1-S5 for demographics details)

Computerized Adaptive Test of Personality Disorders Sample (CAT-PD)

The CAT-PD dataset is drawn from a NIH funded study (R01MH080086) to develop a new measure of personality disorders, and includes N=628 current or recent psychiatric outpatients. NPD criteria were assessed using an adapted version of the Structured Clinical Interview for DSM-IV Personality Disorders (SCID-II; First et al., 2002). This served as the clinical dataset in which our initial models were estimated. No diagnoses were exclusionary, and only participants appearing visibly intoxicated or who failed data validity checks were excluded. See Wright and Simms (2015) for a detailed summary of assessment procedures and further sample characteristics.

Personality Studies Lab Archival Data (PSL)

The PSL dataset was collected over five iterations of NIH funded grants (R01MH044672, R01MH056888) focusing on the diagnosis and prospective observation of participants with personality disorders. It includes 580 participants who were assessed for NPD criteria using the “Longitudinal, Expert, and All Data” standard. The dataset includes a mixed clinical-community sample, with psychiatric outpatients recruited from Western Psychiatric Institute and Clinic and community participants recruited through advertising, random-digit dialing telephone solicitations, and mailings to University of Pittsburgh staff and faculty. Exclusion criteria included a lifetime history of a psychotic disorder or any medical condition compromising the central nervous system. DSM-III-R criteria were used to assess the first 152 of the 580 participants, with the DSM-IV used to assess the rest of the sample. The DSM-III-R differs from the DSM-IV in one criterion. The DSM-III-R includes a “criticism sensitivity” criterion, whereas the DSM-IV includes an “arrogance” criterion. Therefore, the data for the arrogance criterion were unavailable for 152 participants and were treated as missing data in our models using maximum likelihood-based approaches.

Adult Health and Behavior (AHAB)

These data were derived from the University of Pittsburgh AHAB project, a registry of behavioral and biological measurements on non-Hispanic Caucasian and African-American individuals (30–54 years old) recruited in 2001–2005 via mass-mail solicitation from communities in southwestern Pennsylvania. Collection of the AHAB sample was supported, in part, by the NIH (PO1HL040962). A portion (N=931) of the total AHAB sample completed the Schedule for Non-Adaptive and Adaptive Personality (Clark, 1993), a self-report inventory including NPD criteria-based items.

Large Public University Undergraduates

This dataset was collected from a sample (N=2,924) of introductory psychology students at Pennsylvania State University as part of their course requirement. Participants completed the Personality Disorder Questionnaire (PDQ-4; Hyler, 1994), a self-report inventory of DSM personality disorder symptoms.

National Epidemiologic Survey on Alcohol and Related Conditions-Wave II (NESARC)

This national comorbidity survey (N=34,653) conducted by the National Institute on Alcohol Abuse and Alcoholism used the Alcohol Use Disorder and Associated Disability Interview Schedule–DSM–IV Version to collect data on alcohol and substance use disorders. The survey also collected data on 16 DSM-IV psychiatric disorders. The data represent a geographically and ethnically diverse national sample (Grant & Dawson, 2006).

Design

The aim of this investigation was to find the most likely latent structure of NPD criteria given the data in each dataset. For this purpose, we used maximum likelihood estimation to test the fit of a one-factor solution (for FA models), one through k_n-class solutions (for LCAs), where k_n is the number of classes in the model when fit begins to degrade, and the same number of classes along a single latent factor (for NP-FAs and SP-FAs). The relative fit of these competing models was determined based on the Bayesian Information Criterion (BIC). Each analysis was repeated with increased numbers of random starts to ensure at least 10 replications of the log-likelihood. Each LCA, NP-FA, and SP-FA was conducted with increasing numbers of classes until fit degraded (i.e. until the BIC of the model with k classes increased relative to the model with k – 1 classes). We selected the BIC as our metric for both the preliminary and replication analyses because of its conservatism in terms of parsimony and superior performance in simulation studies (Nylund, Asparouhov, & Muthén, 2007). A more liberal metric (i.e., which imposes a more modest penalty for increasing numbers of parameters), such as the AIC, risks overfitting to a particular dataset, jeopardizing replicability.

Because fit indices only indicate how well a model’s estimated parameters fit the observed data relative to other models, we also assessed model quality to determine which models were reliable enough for further consideration based on the BIC. An adequate (greater than 0.7) probability of correctly assigning individuals to classes and a large enough within-class sample size is needed to trust that the model is reliable and can support inferences about the classes it estimates (Wang & Wang, 2012). Reliable categorical and hybrid models then were evaluated based on the integrity and interpretability of their classes (i.e., whether members resemble each other and are distinguishable from non-members). Response probabilities can be used to determine whether class members reliably endorse or fail to endorse a given criterion together (“homogeneity” on a criterion); where a class responds reliably, it must also be separable from other classes based on the pattern of those characteristic criteria (Masyn, 2013). Low classification quality can also indicate within-class heterogeneity of responses or poor separation between classes (Muthen, 2004). Thus, both model quality and interpretability are vital indicators of whether classes are estimated based on distinct, reliable profiles (Kaplan & Depaoli, 2011).

Relative fit in one dataset may be an artefact of a sample’s characteristics. For instance, because LCA captures higher-order statistical moments (i.e., skewness and kurtosis) as well as the means and covariances captured by FA, it may be more likely to fit data that violate factor analytic assumptions (e.g., multivariate normality) by adding spurious classes which improve fit without adding interpretative utility (Bauer & Curran, 2004). Assumption violations will be discussed but were not used as an exclusion criterion.

Results

Initial CAT-PD Dataset Analyses and Predictions for Replication Samples

All models were estimated in Mplus Version 8 (Muthén & Muthén, 1998-2017). Initial analyses in the CAT-PD dataset favored dimensional solutions over categorical and hybrid (factor mixture) models by a considerable margin. See Table 1 for the summary of model fit for each model considered. We used these results to generate our prediction that one-factor dimensional models would provide the best relative fit for models estimated in the remaining datasets.

Table 1.

Summary of Initial Results in CAT-PD (Clinical) Sample

Model	Classes	Factors	BIC	Log-Likelihood	Number of Free Parameters
CFA	N/A	1	7032.844	−3458.569	18
SP-FA	2	1	7038.648	−3455.043	20
SP-FA	3	1	7050.604	−3454.593	22
NP-FA	2	1	7094.552	−3486.209	19
NP-FA	3	1	7048.531	−3456.771	21
NP-FA	4	1	7056.663	−3454.408	23
LCA	2	N/A	7094.551	−3486.208	19
LCA	3	N/A	7080.103	−3446.844	29
LCA	4	N/A	7115.213	−3432.259	39

Note. BIC=Bayesian Information Criterion.

Exploratory Analyses

Although some researchers have reported a two-factor model fitting their data better than a single dimension (Fossati et al., 2005), we did not consider multi-factor models for the pre-registered analyses. Fossati and colleagues posited an “overt” narcissism factor (encompassing grandiose self-importance, belief in one’s own uniqueness, entitlement, exploitativeness, arrogance, and lack of empathy) and a “covert” narcissism factor (encompassing fantasies, envy, and need for admiration). However, when we estimated a CFA based on this model in the CAT-PD dataset, we found the two factors correlated at r=.94, suggesting a single factor would be more parsimonious. The Fossati et al. model also fit our data worse than the single factor model.

We used exploratory factor analysis to evaluate a two-factor solution in the CAT-PD dataset and found one factor that included the six NPD criteria related to grandiose self-importance, fantasies, belief in one’s own uniqueness, envy, need for admiration, and arrogance. The second factor included entitlement, exploitativeness, and lack of empathy. These two factors failed to replicate the results of Fossati and colleagues (2005) and suggest an alternative interpretation, with Factor 1 capturing grandiosity and Factor 2, antagonism. A CFA based on this solution does offer an improved BIC (7018.923), although it capitalizes on the known structure of the data. Because the two-factor solution did not replicate previous work, we chose at the time of pre-registration not to make a priori predictions about two-factor models in the remaining datasets. We retained EFA analyses as an exploratory aim; however, no stable two-factor structure emerged (see supplementary Tables S6-S10).

Replication Analyses

Dimensional models performed much better than categorical models in our replication analyses (Tables 1–6). The one-factor CFA was favored among reliable models in all but the national dataset (NESARC), where it came in third place among reliable models. The CFA had the lowest BIC among all models (even before reliability exclusions) in the clinical (CAT-PD), community (AHAB), and community/clinical (PSL) datasets. It was also the best-fitting model in the undergraduate (PSU) dataset after reliability exclusions.³ All indicators loaded > 0.30 except envy in the AHAB dataset (Table 2, supplemental materials). Full tables for replication analyses are located in supplementary materials because of space restrictions.

Table 6.

Summary of Results in NESARC (National) Sample

Model	Classes	Factors	BIC	Log-likelihood	Number of Free Parameters
CFA	N/A	1	284180.895	−141996.369	18
SP-FA	2	1	Unidentified	Unidentified	20
SP-FA	3	1	Unidentified	Unidentified	22
NP-FA	2	1	286493.779	−143147.585	19
NP-FA	3	1	284127.573	−141954.029	21
NP-FA	4	1	283969.053	−141864.316	23
NP-FA	5	1	Unidentified	Unidentified	25
LCA	1	N/A	317185.519	−158545.721	9
LCA	2	N/A	286493.779	−143147.585	19
LCA	3	N/A	284118.010	−141907.434	29
LCA	4	N/A	283600.754	−141596.541	39
LCA	5	N/A	283480.650	−141484.223	49
LCA	6	N/A	283400.059	−141391.662	59
LCA	7	N/A	283376.339	−141327.536	69
LCA	8	N/A	283427.350	−141300.776	79

Note. BIC=Bayesian Information Criterion. CFA=Confirmatory Factor Analysis. SP-FA=Semi-Parametric Factor Analysis. NP-FA=Non-Parametric Factor Analysis. LCA=Latent Class Analysis.

Table 2.

CFA Factor Loadings

Criterion	CAT-PD (Clinical)	NESARC (National)	AHAB (Community)	PSU (Undergraduate)	PSL (Community/Clinical)
Grandiosity	0.53	0.60	0.39	0.40	0.68
Fantasy	0.53	0.59	0.43	0.54	0.67
Own Uniqueness	0.62	0.57	0.56	0.42	0.72
Need Praise	0.57	0.62	0.56	0.53	0.73
Entitlement	0.53	0.72	0.73	0.75	0.66
Exploitativeness	0.54	0.74	0.56	0.75	0.56
Lack Empathy	0.39	0.66	0.42	0.62	0.54
Envy	0.58	0.62	0.24	0.48	0.64
Arrogance	0.53	0.67	0.57	0.68	0.80

Note. All factor loadings significant at P < .001. CAT-PD=Computerized Adaptive Test of Personality Disorders, NESARC=National Epidemiological Survey on Alcoholism and Related Conditions, AHAB=Adult Health and Behavior Study, PSU=Pennsylvania State University, PSL=Personality Studies Laboratory.

The CFA outperformed (a) the second best-fitting model (after reliability exclusions) in the PSU dataset (a three-class NP-FA), by a difference greater than 12 in BIC (BIC = 25,619.3 vs. 25,631.8), (b) the second best-fitting model in the AHAB dataset (a two-class SP-FA) by a difference of nearly 10 (BIC = 15,208.4 vs. 15,217.1), and (c) the second best-fitting model in the PSL dataset (a two-class SP-FA) by a difference of about 3 (BIC = 4,650.7 vs. 4,653.7).

The CFA had the third best fit in the NESARC (national) dataset (BIC = 284,180.9), taking into account only the BIC and basic standards of model reliability. The three-class LCA (BIC = 284,118.0) and three-class NP-FA (BIC = 284,127.6) were the first and second best-fitting models, respectively. The three-class LCA and NP-FA were nearly identical in terms of their constituent members and endorsement probabilities, which all correlated at 0.95 and above between the two models. The three classes in both models maintained consistent relative positions across criteria with high, low, and very low endorsement probabilities (Classes 1, 2, and 3, respectively).

Class 1 constituted approximately 10% of the NESARC sample; it was typified by a high probability (> 0.70) of endorsing the uniqueness, entitlement, and lack of empathy criteria (grandiosity and envy were near this threshold – 0.68 and 0.67, respectively) and was heterogeneous on other criteria. Class 2 constituted approximately 50% of the sample and was typified by a low probability (< 0.30) of endorsing arrogance, exploitativeness, and need for admiration, whereas probabilities for the other criteria (except uniqueness) hovered slightly above that threshold (0.31 to 0.32). Class 3 constituted approximately 40% of the sample and was typified by low endorsement probabilities across all criteria. Thus, class 2 was different from Class 3 in that it was not well measured by the uniqueness criterion; however, the classes resembled each other in the infrequent endorsement of the other eight criteria.

Excluded Models

Certain models with competitive BICs were excluded from further consideration because of their unreliability. In the PSU (undergraduate) dataset, the two-class SP-FA’s smaller class had only a 0.52 average membership probability; moreover, Mplus had to fix one class’s factor mean for the model to converge, indicating that the parameter may have been underidentified. PSU’s four-class NP-FA had an unreliably classified class with only 34 people (about 1% of the sample) as well as a class whose members were heterogeneous on all criteria. The five-class NP-FA had one class with only 17 people (about 0.5%) and two with unreliable classification.

In the NESARC (national) dataset, the seven-class LCA had the lowest BIC, followed (in order) by the six, eight, five, and four-class LCAs. Relative gains in fit dropped off steeply after the addition of the third class, and model quality substantially degraded in terms of classification uncertainty. For instance, in the four-class LCA, the probability of correct classification of one intermediary class’s most likely members was only 0.49, with a 0.33 probability of being classified in a different intermediary class. SP-FA log-likelihoods failed to replicate even once, despite using dramatically higher random start values (20,000) than other models.

Discussion

Ultimately, the CFA was the most stable model of NPD criteria across a variety of samples, assessment approaches, and measures. A one-dimensional structure prevailed among reliable models in four of the five datasets and was arguably the best-fitting interpretable model in the fifth. Categorical models tended to have markedly worse fit and to extract ordered (severity-based) classes, an approximation of dimensionality. None of the models reflected patterns which would be expected if NPD were a distinct category or if qualitative subtypes of NPD existed.

Problems of Interpretability of the NESARC Classes

We would argue that the NESARC (national) results, which diverge from results in the other samples, do not pose a convincing challenge to our argument for a dimensional conceptualization of NPD. Results from the NESARC dataset were suggestive of an over-extraction of classes, with the BIC favoring models with implausibly large numbers of classes, many of which were poorly identified, statistically indistinguishable, and theoretically uninterpretable. NESARC’s substantially larger sample size relative to the other datasets means that enough people exist at the tail ends to support the estimation of classes, even if not the characterization of meaningful classes, to compensate for non-normality. Indeed, the sample is large enough that even 0.01% of its members can be extracted to form a class improving model fit. Because LCA can capture higher-order moments as well as means and covariances captured by FA, they have more flexibility to fit data which violate factor analytic assumptions by adding spurious, uninterpretable classes (Bauer & Curran, 2004).

Moreover, classes which maintain their relative position on endorsement probabilities across criteria may not reflect qualitatively distinct subgroups, but rather an approximation of dimensionality within a categorical framework (Lubke & Neale, 2009). The most obvious utility of a categorical or hybrid model is to reveal subgroups which have high endorsement probabilities in different sets of criteria—that is, qualitatively distinct classes. NESARC’s three-class LCA and NP-FA models, however, both described graded classes (Figure 1). Since two of the classes were not clearly separable, we see neither a strong statistical case nor any theoretical utility on behalf of a three-class model. It is difficult to conclude that the separability of the higher endorsement rating class from the two lower classes provides evidence of a distinct jump between non-narcissists and narcissists when the two-class LCA and NP-FA were the worst and second worst-fitting models. Both were outperformed by the CFA by an overwhelming margin, with a 2,312 difference in BIC. If a discrete jump between healthy and pathological groups existed, the categorical and hybrid models failed to capture that distinction without adding a spurious intermediary class.

Figure 1.

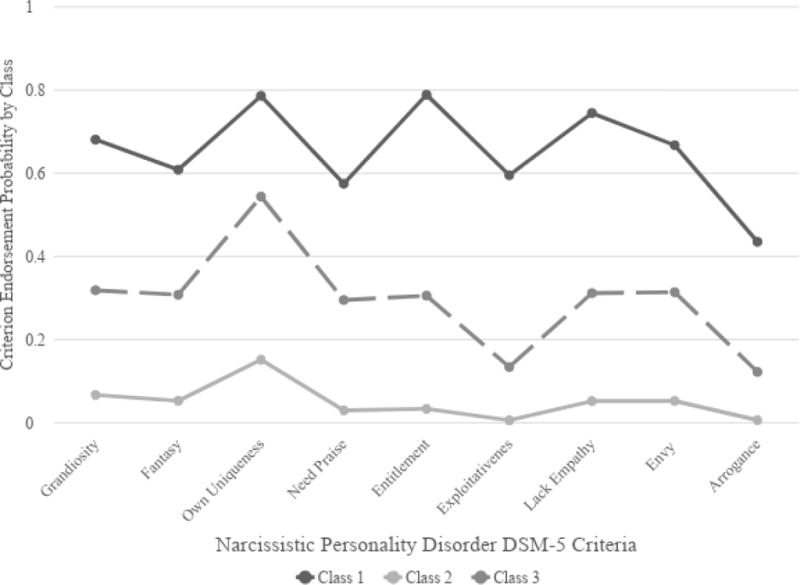
Plot of NESARC 3-class latent class analysis criteria endorsement probabilities.

Thus, the most likely explanation is that NESARC LCAs and NP-FAs reflect an approximation of non-normal dimensionality.⁴ We see no apparent utility of models whose graded classes provide no clear thresholds or compelling evidence of qualitatively distinct patterns. Individuals can still be usefully distinguished for clinical and research purposes in a dimensional framework, without imposing absolute thresholds, by investigating whether relatively high levels of factors may be contributing to impairment or other variables of interest. Moreover, imposing absolute, arbitrary thresholds has adverse clinical and empirical consequences, such as barriers to healthcare access and decreased statistical power. Moreover, dimensions may serve as better measurement tools to study symptomatology across time (e.g. for evaluation of treatment progress) and to develop more fine-grained accounts of between-person differences.

One limitation of this study was the use of binary and ordinal data. The availability of continuous measures would facilitate the use of dimensional modeling techniques that can better accommodate non-normality (e.g., skewed dimension factor analyses). A final consideration is that although narcissism may be a dimensional trait, function related to it may not be continuously distributed. Nevertheless, a move towards dimensional measures could contribute to the study of functional impairment by accounting for those who meet fewer than five criteria but experience substantial distress (Kotov et al., 2017).

Future Directions

The categorical conceptualization of NPD in the DSM-5 may not be the only problem in the current nosology. In our exploratory analyses, no stable multi-factor EFA solution emerged across datasets. Though DSM-5 criteria captured a general narcissism factor, they did not serve to distinguish among lower-order factors often described in the clinical literature (i.e., grandiosity and vulnerability). If the DSM-5 lacks coverage of salient aspects of narcissism such as vulnerability, a shift from categorical to dimensional framing would be insufficient. As investigations of narcissism’s structure progress, it may become clear that key ingredients are missing from the DSM-5 criteria. Indeed, this has been argued by clinical theorists and researchers (Ronningstam, 2011).

In the meantime, this study provides robust evidence of the dimensional nature of NPD. Moreover, our results are consistent with prior literature supporting dimensionality in other PDs and pathological personality traits. Though NPD criteria are currently conceptualized in the DSM-5 as indicators of a “narcissist” category, a narcissistic spectrum is what best explains the variability in endorsement of the NPD criteria from an empirical standpoint. The classification and diagnosis of patients and research participants should reflect this dimensionality.

Table 3.

Summary of Results in PSL (Community/Clinical) Sample

Model	Classes	Factors	BIC	Log-likelihood	Number of Free Parameters
CFA	N/A	1	4650.666	−2268.066	18
SP-FA	2	1	4653.735	−2263.237	20
SP-FA	3	1	4654.173	−2260.275	22
NP-FA	2	1	4666.214	−2259.932	19
NP-FA	3	1	4660.536	−2260.275	21
NP-FA	4	1	4673.441	−2276.272	23
LCA	1	N/A	5220.760	−2581.746	9
LCA	2	N/A	4673.441	−2276.272	19
LCA	3	N/A	4702.058	−2258.765	29

Note. BIC=Bayesian Information Criterion. CFA=Confirmatory Factor Analysis. SP-FA=Semi-Parametric Factor Analysis. NP-FA=Non-Parametric Factor Analysis. LCA=Latent Class Analysis.

Table 4.

Summary of Results in AHAB (Community) Sample

Model	Classes	Factors	BIC	Log-likelihood	Number of Free Parameters
CFA	N/A	1	15208.420	−7498.248	31
SP-FA	2	1	15217.097	−7495.750	33
SP-FA	3	1	15228.904	−7501.224	34
NP-FA	2	1	15296.535	−7538.887	32
NP-FA	3	1	15234.882	−7501.225	34
NP-FA	4	1	15234.941	−7494.418	36
LCA	1	N/A	16045.687	−7947.644	22
LCA	2	N/A	15346.842	−7519.605	45
LCA	3	N/A	15372.929	−7454.032	68

Note. BIC=Bayesian Information Criterion. CFA=Confirmatory Factor Analysis. SP-FA=Semi-Parametric Factor Analysis. NP-FA=Non-Parametric Factor Analysis. LCA=Latent Class Analysis.

Table 5.

Summary of Results in PSU (Undergraduate) Sample

Model	Classes	Factors	BIC	Log-likelihood	Number of Free Parameters
CFA	N/A	1	25619.288	−12737.824	18
SP-FA	2	1	Unidentified	Unidentified	20
SP-FA	3	1	25598.661	−12711.550	22
NP-FA	2	1	25801.243	−12824.811	19
NP-FA	3	1	25631.763	−12732.091	21
NP-FA	4	1	25604.122	−12710.291	23
NP-FA	5	1	25609.783	−12705.141	25
LCA	1	N/A	27399.296	−13663.738	9
LCA	2	N/A	25801.243	−12824.811	19
LCA	3	N/A	25664.170	−12716.375	29
LCA	4	N/A	25641.561	−12665.170	39
LCA	5	N/A	25651.632	−12630.306	49

Note. BIC=Bayesian Information Criterion. CFA=Confirmatory Factor Analysis. SP-FA=Semi-Parametric Factor Analysis. NP-FA=Non-Parametric Factor Analysis. LCA=Latent Class Analysis.

General Scientific Summary.

This study suggests that narcissistic personality disorder symptomatology does not reflect a “narcissist” category but rather a continuum of narcissistic pathology.