It’s Not (Only) the Mean that Matters: Variability, Noise and Exploration in Skill Learning

Abstract

Mastering a motor skill is typified by a decrease in variability. However, variability is much more than the undesired signature of discoordination: structure in both its distributional properties and temporal sequence can reveal control priorities. Extending from the notion that signal-dependent noise corrupts information transmission in the neuromotor system, this review tracks more recent recognitions that the complex dynamic motor system in its interaction with task constraints creates high-dimensional spaces with multiple equivalent solutions. Further analysis differentiates these solutions to have different degrees of noise-sensitivity, goal-relevance or additional costs. Practice proceeds from exploration of these solution spaces to then exploitation with further channeling of noise. Extended practice leads to fine-tuning of skill brought about by reducing noise. These distinct changes in variability are suggested as a way to characterize stages of learning. Capitalizing on the sensitivity of the CNS to noise, interventions can add extrinsic or amplify intrinsic noise to guide (re-)learning desired behaviors. The persistence and generalization of acquired skill is still largely understudied, although an essential element of skill. Consistent with advances in the physical sciences, there is increasing realization that noise can have beneficial effects. Analysis of the non-random structure of variability may reveal more than analysis of only its mean.

Variability and Noise in Skill Learning: Bad or Good?

Learning new motor skills is quintessentially human. Over our lifetime we learn to eat with knife and fork, ride a bicycle, and dance salsa, going far beyond the fundamental locomotory and reaching behaviors that all animals display. How can the neuromotor system achieve such extraordinary plasticity, flexibility, and creativity? Over the last decades there has been relatively little research in motor neuroscience on the acquisition of novel motor skills, in favor of research on more constrained movements under highly controlled conditions. For example, a widely used experimental platform has been reaching of a 2-link arm in the horizontal plane with meticulously designed perturbations that introduce force fields or visuomotor mappings to induce adaptation^1,2. When neuroimaging is involved, the tasks necessarily have to be further reduced to small finger and hand movements. While experimental reduction and control has a long history in motor neuroscience and is core to any empirical science, the perennial risk is that the real problems are “controlled away”. One such phenomenon that is intentionally attenuated by experimental control is variability. This review aims to draw attention to the fact that variability and noise in motor performance is not only a nuisance, but is a ubiquitous and informative biological feature that has meaning in itself, not only to the performer but also to the scientist who aims to understand movement control and coordination.

Trying to understand skill learning inevitably has to face variability. Mastering a new motor skill implies performing with increasing accuracy and diminishing variability, or “with maximum certainty and a minimum outlay of time or energy”^3–6. Similarly, recent work showed that skill improvement manifests in a shift of the speed-accuracy trade-off function^7,8: skilled individuals become less variable, while keeping the same tempo, or they can move faster without increasing variability. And yet, not even Olympic athletes ever perform with total certainty - like robots. In fact, this is what makes competitive sports interesting to watch. Why are humans not perfect? The complex neuromotor system has abundant noise and fluctuations at all levels^9,10, and even deterministic physiological processes at lower levels may manifest in overt unstructured “noise”. Hence, skill cannot, and probably should not completely suppress noise. Rather, it should “make noise matter less”^11,12, i.e., have little or no effect on task success. Further, variability is necessary when exploring solutions for a novel task. So, can noise be beneficial? The plethora of roles and meanings of variability is also reflected in a variety of seemingly similar and overlapping terms (see Table 1). While there are no strict definitions, the table attempts to reserve different labels for different aspects of variability. The fact that variability and noise is a phenomenon that is interesting and intricate has already been recognized by many other physical sciences¹³. This review aims to demonstrate and argue that variability is rich in information about control priorities in skill learning and maybe even more meaningful than the mean.

Table 1.

Overview of terminology with brief definitions

Variability and Variation	Umbrella terms for all sets or series of observations that are non-constant and may be also non-stationary.
Variance	Well-defined concept in statistics that measures spread of data from its mean, quantified as squared deviation of a random variable from its mean.
Noise	Unstructured variability, both in the temporal and spatial domain. In signal processing defined as a random signal with equal intensity at different frequencies, constant spectral density at all component frequency (white noise).
Colored noise or 1/f noise	Signals with power spectral densities proportional to 1/fβ; for Brownian noise β=2. Note, the signal is still noise, but has different degrees of predictability.
Uncertainty	Term originates in probability theory and Bayesian literature, defined as possible states or outcomes measured by assigning probabilities to each possible state or outcome, including probability density functions for continuous variables.
Fluctuations	Non-constant behavior over time that can be stochastic or deterministic. Time series with sinusoidal changes and more frequency terms are fluctuations, but are not stochastic. The degree of structure is measured with metrics, such as entropy.
Deterministic versus Stochastic processes	System or process whose outcome entirely determined by inputs and initial conditions, no randomness involved in the development of future states. Random sequence or selection of data that have no structure in the temporal or spatial domain.
Isotropic versus Anisotropic distributions	Distribution is uniform in all directions; Distribution is non-uniform in different directions.

Adaptation versus De Novo Learning

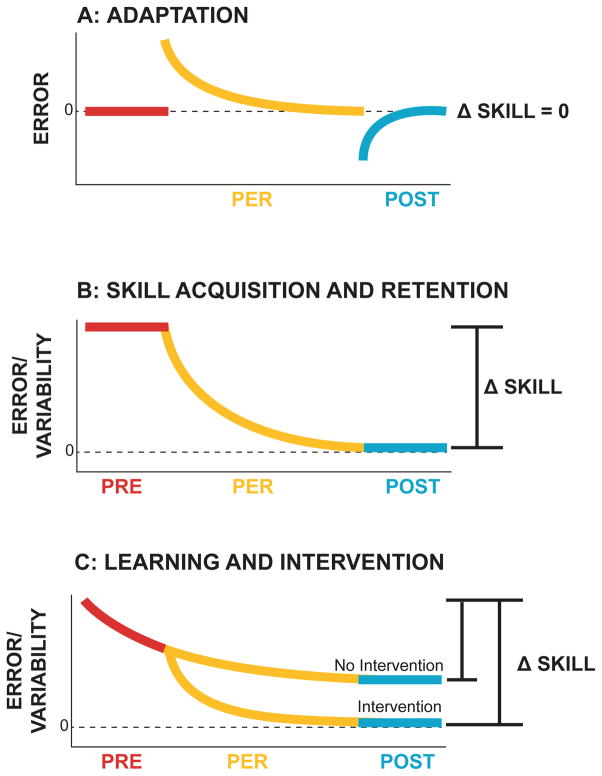
Before reviewing variability in skill acquisition, a distinction needs to be drawn between de novo learning and adaptation: Evidently, not every movement is a novel skill that needs practice to be mastered. Adaptation of well-established behaviors such as postural control, locomotion or reaching to altered environmental demands epitomizes an essential behavioral capacity ubiquitous in daily life. Adaptation has received much attention over recent decades in experimental paradigms such as prism, visuomotor, or force-field adaptations. However, it should not be confused with de novo learning as its behavioral manifestations are markedly different, suggesting different underlying processes. Figure 1A illustrates how adaptation occurs at a relatively short time scale: in laboratory experiments few trials are sufficient to approximate the new target and in real life it has to happen almost instantly and accurately, e.g. when grasping a cup that is fuller than expected. The process reduces an externally induced error back to zero-error performance, probably reducing sensory prediction errors, modeled by linear time-invariant systems¹⁴. This fast change contrasts to the weeks and months of practicing and fine-tuning a new skill, such as handwriting or learning to dance salsa (Figure 1B). An even longer process is motor development unfolding over the timescale of years^15,16. Several essential elements of skill acquisition play only a subordinate role in adaptation: Exploration of new solution spaces is relatively modest (see below¹⁷); generalization, essential for any learning, tends to be limited as adaptation occurs fast in new situations^18,19; adapted behaviors quickly vanish when the perturbation disappears²⁰, despite savings upon renewed exposures. For skills long-term retention is essential and any intervention not only aims to accelerate the slow process of improvement but also achieve retention (Figure 1C). Unlike in adaptation, variability plays many different roles in skill learning and is an umbrella term for a plethora of conceptually distinct observations that are non-constant and non-stationary (see Table 1).

Figure 1.

Behavioral change (Δ skill) in adaptation and skill acquisition. A: Adaptations to novel environmental or bodily conditions, such as wearing new shoes, starts with a behavior that is well-practiced, such as walking (pre-perturbation, error = 0). Wearing new hiking boots or high heels it usually only takes a short time to adapt the coordination pattern (per-perturbation, Δ skill ≠ 0). After changing back to the regular shoes, the walking pattern quickly returns to baseline behavior (post-perturbation, error = 0). For the baseline behavior, there is typically no gain in skill (Δ skill = 0). B: Skill learning, such as learning a new dance routine, starts with high levels of errors and variability (error ≫ 0). Consistent practice, with or without controlled conditions, such as detailed performance feedback, leads to a reduction of error and variability (Δ skill > 0). This is typically a much longer process and results in long-term retention of the skill (Δ skill ≈ 0). Riding a bicycle is a skill that is never forgotten. C: In sports coaching and therapeutic interventions, the goal is to aid and accelerate the process of reducing error and variability by including expert guidance, verbal feedback, clues, and technology-based assistance (Δ skill ≫ 0). The goal is to achieve long-lasting behavioral changes that should also generalize to other conditions.

This review focuses on acquisition of perceptual-motor behaviors that are novel, demanding and complex with inherent redundancy that offers a space of multiple solutions that need to be explored and learned. The review begins with the traditional notions of noise as unwanted signal corruption to more recent perspectives how motor variability can reveal the structure of control, and can characterize stages of learning, and finishes with how noise may be leveraged in training interventions.

Noise as Nuisance

Dating back to Woodworth²¹ in the late 1900’s and a prominent concept since the advent of information theory²² in the 1950’s, noise has been regarded central to understand communication in signal and symbol processing systems, such as the brain and the neuromotor system. Undisputedly, neural signals in the body have noise that can corrupt the information transmission. To assure veridical information transmission, it is necessary to minimize noise and thereby increase the signal-to-noise ratio. Directly motivated by information theory, Fitts’ seminal study showed how an increase in speed engendered higher variability and, where possible, variability is traded off against speed²³. Fitts’ Law was explicitly derived as an information-theoretic formulation, even though later research brought forth variations and new interpretations of the same observations²⁴. The view that signal-dependent noise is detrimental is pervasive and foundation to much current theorizing. For example, Wolpert and colleagues showed how reduction of signal-dependent noise and optimizing endpoint error/precision can produce several core features in motor control^25,26. While this perspective remains valid, noise is more than just a nuisance. As many other physical sciences have revealed, noise can have structure that is informative and beneficial (see Table 2 for a brief summary of different scientific directions). Capitalizing on these insights and developments, also research in motor control has adopted new perspectives where noise and variability started to play important roles.

Table 2.

Examples of positive effects of noise in physical and biological systems.

Phenomenon	Description	Examples in Sensorimotor Control
Stochastic resonance	Noise added to a weak signal raises the average signal level leading to better signal detection in a nonlinear system. Frequencies in the white noise corresponding to the signal's frequencies will resonate and amplify the original signal, thereby increasing the signal-to- noise ratio. Stability of nonlinear control systems, particularly oscillatory systems, can be enhanced by exploiting nonlinear mechanisms.	Insoles applying vibrations to the plantar foot surface showed that input noise can enhance sensory and motor function, via stochastic resonance95. Stochastic vibrotactile stimulation stabilizes respiratory rhythm in preterm infants, avoiding life-threatening apneas96. Perception of “subconscious” visual events ascribed to stochastic resonance, following enhanced neurons activation because of non- linearities in their processing97,98.
Fluctuations in physiological signal arising from spatial and temporal self- similarity	Long-range power law correlations over a wide range of time scales suggest that physiological systems operate far from equilibrium. Maintaining constancy (homeostasis) is not the goal of physiological systems.	Cortical neurons show dendritic arborization with self-similar (fractal) geometry. A variety of cardiac pathologies are characterized by long-range correlations in ECG signals99. Stride intervals in walking show altered scaling behavior and correlation properties in individuals with degenerative neurological disorders100–102.
Phase transitions in nonlinear dynamical system	Nonlinear dynamical systems with multiple stable states can undergo phase transitions between modes that are facilitated by noise (non-equilibrium phase transition). Robustness is defined as stability with respect to noise in parameters of a control	In rhythmic bimanual coordination, spontaneous transitions from anti-phase to in- phase movements are observed at a critical value of the control parameter movement frequency. Modeling these phase transitions with stochastic order parameter equation matches different time scales of behavior33. In speech recognition noisy data sets to train deep neural networks avoid over-fitting and
Inducing robustness	system. Noise can improve state estimation and thereby enhance robustness. See also persistent excitation.	performance degradation in noisy acoustic conditions103. To discover robustness of an operating system noise can be injected by a program that generates strings of characters104.
Exploration in Deep Reinforcement Learning	Noise can be added in the so-called action (state) or parameter space of the policy.	Parameter noise often results in more efficient exploration and in some cases allows for solving problems in which action noise is unlikely to succeed105.
Dithering	Intentionally applied form of noise used in digital signal processing to randomize error due to quantization. If quantization yields error that is repeating and correlated with the signal, the error may yield undesirable artifacts.	Image processing of a grey scale image routinely applies dithering to approximate the density of black dots to the average grey level in the original image. Color images achieve more depth if the limited color palette is extended by adding noise to available colors. In image classification, noisy or weakly correlated to the categories of their classification improves the performance of the classifier106. In mechanical systems, small high-frequency vibrations or random noise reduces static friction between moving parts as they move less jerky and more continuously. This transforms the system into smooth dynamics that can be controlled more easily with standard techniques. It can also reduce wear and tear.
Simulated annealing and noise in networks	Probabilistic technique used in large-scale networks with large search space with the goal to find the global optimum. This noise is abated after the system found the global optimum.

Variability and Stability in Complex Dynamical Systems

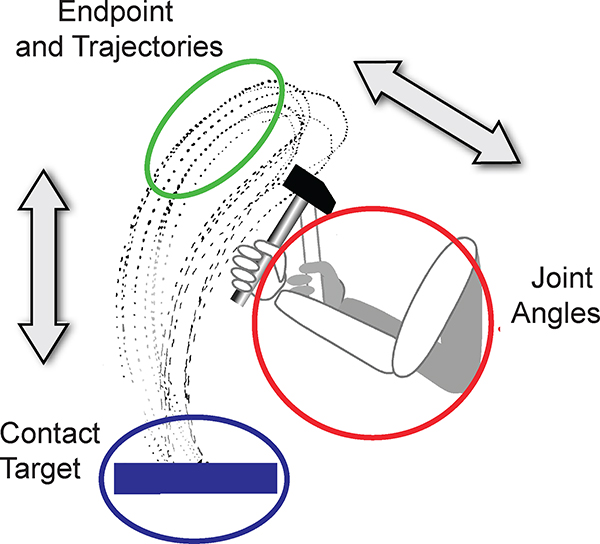
With the rise of nonlinear dynamics in the 1980’s in the physical sciences, a dynamical systems perspective was also applied to biological systems²⁷ and movement coordination in particular^28–30. Initially centered on bimanual rhythmic coordination, the focus of attention broadened and stability and variability became core concepts for theorizing about movement coordination^31–34. Variability can reflect the stability of a coordinative structure and fluctuations can induce phase transitions, i.e. discontinuous changes in behavior³⁵. Of central importance is that the dynamical system is high-dimensional and has redundancy such that any task goal can be achieved in multiple ways; this was introduced as the Bernstein problem^36–38. Figure 2 illustrates the different redundancies that arise in a motor task, here using Bernstein’s original example of hammering on an anvil. Intrinsic redundancy is defined by the redundant mapping of the joint degrees of freedom of the body onto the endpoint, e.g. the tip of the hammer. Extrinsic redundancy is defined by the multiple trajectories that can all hit the anvil at the same point. Further, the task can also offer redundancy as the anvil is not a single point but an area and allows an infinite set of successful hits. With these nested redundancies, the sensorimotor system does not have to select unique optimal solutions, but rather has families of solutions that achieve a task goal. In Bernstein’s words, there is “repetition without repetition”. Even at a highly skilled level, no movement is ever the same: there is always variability.

Figure 2.

Illustration of multiple redundancies with the example of hammering on an anvil. Intrinsic redundancy: An infinite number of combinations of the three joint angles of the arm can place the tip of the hammer in one location in the plane. Extrinsic redundancy: An infinite number of trajectories can hit the anvil at one point. Task redundancy: The anvil can be hit at an infinite number of contact points, as the target is not a single point but an area. The shown trajectories are the original recordings of Bernstein³⁸. Not shown is that similar intrinsic redundancies exist due to multiple muscles and muscle fibers achieving the same joint configuration.

As a consequence, variability no longer only represents corruptive noise, but rather the expression of flexibility and choice of the central nervous system and a motor for the self-organization in a dynamical system. Noise may have self-similar, fractal structure and it can be “colored”, characterized as power laws in its spectrum³⁹. These features take noise far beyond the well-understood normal or Gaussian distribution, quantified by its mean and standard deviations, as frequently included in simple models. Variability in a high-dimensional system is multi-dimensional and its extent can differ in different dimensions, i.e. be anisotropic. This structure, both in its spatial distribution and its temporal evolution, is informative. In motor neuroscience, it may inform about control priorities of the central nervous system and its relation to task constraints.

Structure of Variability in Redundant Solution Spaces

Since the emphasis on the human system as a multi-degree-of-freedom system, redundancy and the notion of null space, i.e. the manifold of task-equivalent solutions, has figured prominently. Starting point for analysis was variability from repeated executions with a focus on the shape of its distribution in the different dimensions of the solution space, i.e. its anisotropy. Three related methods have been developed to quantify this anisotropy of data sets: the Uncontrolled Manifold method (UCM), the Goal-Equivalent Manifold (GEM) approach, and the Tolerance, Noise and Covariation (TNC) approach. Figures 3 illustrates these three methods with an exemplary data distribution plotted in a schematic space spanned by 3 execution variables. The space may for example represent three joint angles mapping into one endpoint in extrinsic space, or different endpoints mapping into the task space. The set of executions that achieve a given result is represented by the nonlinear surfaces. For clarification, the three insets show a 2D section of the same data and manifold. While sharing a common objective, the three methods also differ in critical aspects, both theoretically and conceptually, as briefly summarized in the following.

Figure 3.

Overview of three methods to analyze variability in multi-dimensional spaces. The insets are 2D sections of the 3D space. A: UCM-method. A schematic space spanned by three execution variables and the associated result variable, defining task performance. The darker nonlinear surface denotes the solution manifold, the set of executions that achieve the task result with zero error. Using the schematic data set (yellow dots) the UCM-method anchors the analysis at the mean performance, and applies Jacobian analysis to estimate variance parallel to the null space, illustrated by the plane (red mesh), and orthogonal to it (red line). Note the light blue manifold signifies that the non-linearized manifold can be a nonlinear surface and can differ from the solution manifold describing zero error. B: GEM-method. The analysis applies the same decomposition, but also introduces a goal function that defines the solution manifold and affords calculation of the error-sensitivity of solutions on the manifold. This is indicated by the dark blue color shading. C: TNC-method. Assuming the same task as in A and B, the three data sets represent performance on three practice sessions. The largest distribution (yellow, identical to the data in A and B) represents initial data (Day 1) far from the solution manifold (same as in B). With more practice on Day 2, the set of trials (red) approaches the manifold (Tolerance-cost is small) and starts to covary with the solution manifold (Covariation-cost decreases); however, the distribution is still relatively broad. The Day 3 data set (green) represents performance after extended practice where the distribution has aligned with the manifold (Covariation-cost is small) and the dispersion is reduced (Noise-cost is small). Note that the numerical quantification of the TNC-costs does not assume Gaussian distributions.

The UCM approach defines skilled task performance as the ability of a time-varying dynamical system to maintain a relatively invariant state^40,41. Standard covariance (Jacobian) analysis parses variability into components parallel and orthogonal to the null space. In this stable or skilled state variations across repetitions show low variance in directions that affect the result, compared to larger variance in directions that do not affect the result. Figure 3A illustrates this method by showing a data set (yellow dots) and its null space as a plane (red grid) and the orthogonal space as a line normal to the null space (red line). A ratio between the variances projected onto the orthogonal and parallel directions captures the degree of “skill”, with more variance in the null space signifying higher skill. The null space is a linearization around the mean point, which can differ from the full set of solutions with the same result, if this is nonlinear (like the surface shown in light blue). This manifold can also be separate from the manifold of solutions with zero error. Note that the Jacobian is calculated around the mean of the data. If the mean differs from zero error, this goes unnoticed. In this case, there is another manifold that defines zero error (shown in dark blue). The inset shows a 2D section with the data mean on the light blue manifold and the zero-error solution as a dark blue manifold. The two lines illustrate the null space and its orthogonal direction.

The UCM analysis has been applied to several motor skills and has shown evidence for the anisotropy, but predominantly focused on identifying controlled variables, rather than learning processes⁴². While the original analysis only decomposed variability around the mean performance, a recent extension introduced analysis of “motor equivalence” to decompose changes in execution variables in response to changes in task or perturbations⁴³. Note that when the UCM-method was applied to evaluate trajectories, the method requires the set of trajectories to be time-normalized and binned so that the UCM-analysis can be applied to the sets of data within each time bin. The analysis cannot deal with temporal evolution per se. One other caveat for this and other covariance-based variability analyses is that they are sensitive to the choice of coordinates⁴⁴.

The GEM-approach uses the same mathematical tools of covariance analysis to steady-state behavior⁴⁵. However, the GEM-approach also maps the observed dynamics of task performance onto an independently defined goal or solution space (Figure 3B). Knowing this goal function, small errors in execution variables can be mapped into result variables and the sensitivity of solution manifold can be quantified⁴⁶. Figure 3B shows the same two nonlinear manifolds but now the solution manifold has additional error sensitivity. Similar to UCM, one assumption is that the data are at steady state clustered around the zero-error performance. The method has been applied to tasks where this assumption was justified, such as walking or a simple shuffleboard tasks, where subjects had reached their asymptote in performance.

The TNC-analysis was explicitly developed to quantify structural changes in variability throughout practice to identify different learning processes^11,47–49. Figure 3C show the same initial non-Gaussian data set (yellow) that then translates towards the solution manifold over two days of practice. Initial changes are quantified by Tolerance-cost, defined as the change in location of the data in the result space. Covariation-cost quantifies the amount of performance improvements by covarying the dispersion with the solution manifold (covariation is calculated numerically and is distinct from covariance analysis). Noise-cost quantifies how minimizing the magnitude of stochastic dispersion achieves the best result. While Tolerance-cost describes initial exploratory changes, Covariation-cost and Noise-cost describe processes that come to prominence later in practice. Covariation-cost in particular correlates with the slow decrease in performance error and variability, but both processes continue to change in parallel over days of practice⁵⁰; however, a study on 16 days of practice showed that Noise-cost remained the highest cost to performance.

Unlike UCM and GEM, the TNC-analysis uses numerical tools that evaluate the entire result space (shown by different color shades in the inset of Figure 3C). Hence, sensitivity or tolerance is known for all locations in the result space, which is the basis for the cost calculations. The disadvantage of the numerical procedure is that it can become cumbersome for higher-dimensional spaces. Further, the goal function, i.e., the mapping between execution and result variables should be known or has to be approximated via regression. The most important conceptual difference to UCM and GEM, which analyze the data distributions in the space of the execution variables, is that the TNC-method projects the data into the space of the result variables and quantifies the costs in these units. Due to this projection, execution variables can have different units, such as position and velocity for the studied throwing task. Therefore, the analysis is in principle applicable to multi-modal problems. In contrast, the covariance methods of UCM and GEM require a metric, which necessitates the same units in the execution variables or some appropriate normalization.

In sum, despite the differences, all three methods concur in that variability consists of deterministic and stochastic processes and its structure reveals control processes in performance and learning. Skill learning is a multi-stage process of finding a stable solution where detrimental effects of the intrinsic neuromotor noise onto performance is reduced.

Sensitivity to Errors and Noise

While revealing, these analyses remain descriptive of the observed behavior if they are not supplemented by synthesis with a model that generates the observed structure of variability. One approach towards a generative model is to analyze the trial-to-trial changes in the space of execution variables⁵¹. Dingwell et al⁵¹ examined reaching tasks where different speed-amplitude profiles defined different GEMs. Analysis of trial-by-trial fluctuations in directions parallel and orthogonal to the solution manifold showed that subjects actively corrected deviations perpendicular to the manifold faster than deviations parallel to the manifold. With a focus on learning, Abe and Sternad⁵² analyzed a throwing task and quantified persistence and anti-persistence in successive throws over 6 days of practice. Subjects clearly became more sensitive to the direction of the execution space and the solution manifold. An iterative learning model replicated these results, although the most pronounced persistence and anti-persistence did not coincide exactly with the parallel and orthogonal directions. Testing different types of scaling of the embedding coordinates illustrated how such coordinate choices – or the coordinate of the CNS - might skew the direction in solution space.

Complementing studies on the same throwing task focused on the hand trajectory and the timing of ball release. A range of task variations showed that the hand trajectory increasingly aligned with the solution manifold, thereby creating longer timing windows for ball releases that all lead to task success^53–56. These error-tolerant timing windows relaxed the necessity to accurately time the ball release to achieve a good hit. Interestingly, this error- and noise-tolerant hand trajectory developed after the timing accuracy had reached a plateau. Similar trajectory changes were also observed in children with severe dystonia who thereby may have compensated for their high motor variability⁵⁷. A mathematical analysis of a simplified throwing task by Mahadevan and Venkasedan⁵⁸ demonstrated how the dynamics of the physical task and noise propagation from initial conditions to projectile landing determines error-sensitivity and thereby optimal throwing strategies. This analysis underscores how the task dynamics constrains control strategies before making any assumptions about the neuromotor system.

While all these studies focused on a throwing skill that involved an external degree of freedom, the ball, and a singular moment that determined task success, the release, sensitivity to noise and errors was also examined in a continuous reaching task that required navigating around an obstacle^59,60. Detailed analyses of the chosen paths and their error sensitivity in kinematics, inertia or admittance of a simple arm model revealed that humans favored paths around the obstacles that were less sensitive to error or at risk to collide with the obstacle. These studies on the modulation of reaching underscores the central role of sensitivity to errors and noise in coordination.

Variability for Exploration of the Solution Space

A topic conceptually distinct from the variability due to differential sensitivity of performance is the variability at the early stages of practice, typically labelled “exploration”. In a redundant solution space in addition to intrinsic redundancy in the effectors, it is not surprising that the learner needs to “experiment” to find the best possibilities for action. Spurred by this recognition of high-dimensional solution spaces and advances in reinforcement learning, exploration in learning has garnered recent interest again^61–64. Smith and colleagues examined learning in a series of reaching tasks, where either typical error feedback was provided or reward to shape a specific desired path⁶⁵. Several metrics computed at the end effector differentiated between task-specific and total variability and showed that subjects consistently reshaped the structure of their motor variability in a manner that promoted learning. Most noteworthy was that motor variability was correlated with the individual’s learning rate and therefore seemed to predict learning rate. These findings reinforced the importance of action exploration again and strongly implied that the CNS actively regulates and exploits variability to facilitate learning in both error-based and reinforcement scenarios.

While intriguing, the results could not be replicated in several follow-up studies. Wei and colleagues⁶⁶ conducted several experiments including visual perturbations, simulations with an optimal learner model, and a meta-analysis of extant data on reaching adaptation that all rendered divergent results. The authors surmised that multiple factors contributed to the observed variability, including sensory uncertainty, an incomplete forward model, noise in motor planning, execution and muscle noise. Hence, the rate of learning may be independent from initial variability measured at the endpoint. Extending the reaching paradigm to a redundant task where 4 joint angles mapped onto 2-dof target position in the horizontal plane, Singh and colleagues⁶⁷ again failed to replicate Wu et al.’s results, but also reported that the joint variability in null-space (task-irrelevant variability) in the baseline session did correlate with a measure of learning rate. Going beyond variability at the endpoint of a reaching task, two other recent studies on a pointing and bimanual task again failed to replicate the finding^68,69. Finally, Barbado and colleagues⁷⁰ examined the temporal structure of variability in a standing and a sitting postural task. As different initial performance levels correlated with learning rate, learners were separated by their initial performance level. Individuals with lower long-range correlations, measured by detrended fluctuation analysis (DFA), not only showed better performance, but also displayed a faster learning rate. The findings were interpreted as reflecting higher error sensitivity rather than exploration per se.

Stages of Learning Defined by Changing Roles of Variability and Noise

Given these divergent findings it becomes clear that exploration and exploitation of the solution space is a multi-faceted phenomenon. Note that in computer science and robotics many algorithms have been developed for exploration of non-convex high-dimensional space, e.g. the rapidly exploring random tree algorithm (RRT) that describes a differentiated branching path⁷⁴. Merging numerous findings, we would like to suggest that learning proceeds in stages that are characterized by different roles and contributions of variability. At the initial stage when the solution space is unknown the search for strategies to achieve a task might require random explorations that are nevertheless intentional. The information garnered is stored and used to build a representation of the solution space. Hence, these explorations are not necessarily Gaussian; for example research on a pole balancing task has shown a mixture of movements that include rare large deviations that lead to long tails in the distribution, i.e. to Levy distributions^71,72. At later stages, exploration may only require smaller-scale gradient search in a linearized environment before this process will transition to exploitation. The observed “exploratory” variability is always confounded with intrinsic noise and slow drifts that the CNS is unaware of, and therefore do not contribute to the representation of solution space. Importantly, in any human experiment there is also intentional switching of strategies for biomechanical reasons or to break psychological monotony⁷³. When approaching a performance plateau, the only way to further improve performance is by reducing the noise level.

Our own work on the decomposition of variability differentiates between three processes (TNC)^47–49: the first stage consists of finding the right location in the solution space which is quantified by Tolerance-cost. The fine-tuning stage proceeds by two intertwined processes: one consists of covarying the execution variables to align with the solution manifold, quantified by Covariation-cost. The second process consists of a general decrease of the variance of noise, quantified by Noise-cost. The data show differential emphasis of the three processes throughout practice, but also reflect that they are not strictly sequential. It is therefore safe to say that variability is a conglomerate of many different processes and sources.

In sum, before rushing to conclusions about exploratory variability based on simple variance measures, all these sources of variability need teasing apart. More behavioral research is needed to identify different facets of variability in learning. One focus should be to examine longer-term practice in longitudinal studies that afford teasing apart variability and its change over extended practice.

Mechanisms for Increasing and Decreasing Random and Exploratory Variability

Given these potential positive effects of variability, one may ask whether the human neuromotor system is able to increase the magnitude of the variability or random noise component. Although identified in birdsong^61,75, it remains an open question whether these intriguing mechanisms have an analog in humans whose anatomy and motor behaviors are undoubtedly very different. One study by Shadmehr and colleagues revealed some evidence for an “intentional” increase in variability and tied it to dopamine. When healthy control subjects performed fast reaching actions with different probabilities of reward, they increased their trial-to-trial variations when reinforcement was absent, presumably in search for more rewarding solutions⁷⁶. The fact that unrewarded trials were followed by larger changes suggests immediate corrections, as they were also accompanied by a bias. Interestingly, Parkinson patients showed smaller trial-by-trial changes and less sensitivity to reward prediction errors, suggesting that this variability was regulated by dopamine.

While increasing variability may be helpful for exploration, in the later stages of “exploitation” lower variability, at least at the task-relevant endpoint, remains desirable. Two recent studies on accurate throwing have shown that extensive practice with up to 2000 trials and more not only reduced error and variability by error corrections, but also lowered the residual unstructured noise^77,78. Several time series analyses and system identification methods ruled out short and longer-range correlational structure in the trial sequence. How, or whether the magnitude of random fluctuations can be suppressed by the individual remains an interesting open question. Potential explanations are more efficient generation of neural activation in the cortex or neuromodulator mechanisms, such as serotonin, that affect motor neuron excitability and gains in the descending drive^79,80.

Variability and Noise for Intervention

The previous summary emphasized that overt performance variability is determined by a plethora of factors in both the actor and the task. An initial search for gathering information is beneficial and necessary not only in reinforcement learning with sparse feedback but also error-based learning. Beyond exploration, other domains of science and engineering have long recognized the many positive roles that noise can play¹³ (see Table 2). In this spirit, several recent studies in motor control examined whether noise, inherent, amplified, or added to the neuromotor system, may have positive effects.

Two studies by Diedrichsen and colleagues tested the hypothesis that either amplifying intrinsic noise or adding extrinsic noise, uncorrelated with the individual’s fluctuations, can serve as teaching signal and guide the learner to solutions along the solution manifold^81,82. Using a redundant 3-dof reaching movement in the horizontal plane, where either reach direction or a specific joint configuration was the target task, two studies only rendered partial support for noise as an implicit teaching signal. While reach error was quickly reduced, i.e., error-feedback directed the system onto the solution manifold (zero error), adding noise as a teaching signal to additionally optimize error sensitivity or effort, was only successful if subjects were aware of the target direction. As the well-practiced reaching task might not have provided the right testbed for the hypothesized learning processes, Thorp and colleagues⁸³ examined subjects practicing a novel mapping between 4-dof hand postures to 2-dof cursor positions. When adding posture-dependent noise, subjects indeed acquired a control policy that minimized noise and avoided dimensions that increased noise. Importantly, they also generalized their newly-acquired mapping to other target postures. This countered expectations from Bayesian learning, where increased sensory uncertainty would lower the Kalman gain and slow down learning. It is conjectured that added noise may pressurize the system to quickly form an accurate control policy. If this is correct, then this may open an interesting route for clinical interventions.

Using their throwing task, Sternad and colleagues created noisy conditions by amplifying the task error with three different gains, with and without adding random noise⁷⁷. Following three days of baseline practice when subjects had reached a performance plateau, amplifying the error, both in stochastic and deterministic fashion, led to significant further improvements. System identification with three different stochastic iterative learning models revealed that amplification led subjects to not only error-correct, but also to decrease the variance of the random noise. As potential neurophysiological mechanisms for such systemic reduction of intrinsic noise neuromodulators, such as serotonin⁷⁹, are discussed. The successful use of manipulating variability for a clinical question was exemplified by Sanger and colleagues⁸⁴, who examined whether children with dystonia could improve their performance when their variability was experimentally lowered. Trial-to-trial variability in a virtual shuffleboard task was attenuated by replacing their veridical puck release velocities by the average over their previous throws. Children with dystonia improved their shuffleboard score significantly, documenting their sensitivity to their own seemingly uncontrolled variability.

A computational study by Ajemian and colleagues⁸⁵ highlighted the beneficial role of noise in a supervised neural network explicitly addressing the stability-plasticity dilemma, a well-known problem in artificial intelligence: a single task A can be perfected, but learning an additional task B may eradicate, or at least interfere with task A. This dilemma, how to adapt to new information (i.e., be plastic) without overwriting old information (i.e., be stable), was resolved by using both high levels of noise and high gains, a combination that is widely expected to induce instability. However, as demonstrated, this hyper-plastic network can learn two stable patterns by orthogonalizing the two vectors representing the two tasks in weight space. High levels of noise in weights maintain continued plasticity, while top down feedback avoids drift in task performance. This distinction between noise in weight space while network performance remains stable is similar to the distinction between stable endpoint and variability in the null space of joint angles. The simulations are complemented by experimental data that compare interleaved and blocked practice schedules and demonstrate that the old phenomenon of “contextual interference” can be explained with this hyperplastic network. Given the high dimensionality of the neural network and the continuous regeneration and turn-over in cortical neurons⁸⁶, this illustrates a viable supportive role for noise in the CNS.

Motor Memory – the Forgotten Aspect of Motor Learning

Nobody would dispute that skill learning includes generalization and long-term persistence of the skill. Indeed, Schmidt confined the term “learning” to permanent changes in behavior, in contrast to fast improvements in laboratory sessions that may only reflect short-term adaptations or physiological changes⁸⁷. Hence, strictly speaking, true learning can only be inferred from retention and generalization to different tasks. A recent study on error-based and reinforcement learning in cerebellar patients and control participants probed into this essential distinction: performing a visuomotor rotation task with and without visual error feedback revealed that in error-based learning error and variability of performance improved, but performance faded in the 100 retention trials much faster than under reinforcement learning conditions⁸⁸. A model including two noise sources, random motor noise and exploratory “noise” (random deviations that serve as reference for subsequent corrections) replicated the findings. Interestingly, cerebellar patients could improve with binary reinforcement, although noise interfered. While the results are convincing, it should be noted that the retention session followed the practice session immediately. Retention tests become more informative, but also harder to implement, when they are scheduled days or weeks after the practice session. Huber and colleagues manipulated reward during 6 days of practice of the throwing task⁷⁸. Increasing the threshold for reward led subjects to less variable behavior. Unexpectedly, when relaxing the reward requirements, subjects maintained their more precise performance over 5 retention days. Several time series analyses and a simple iterative stochastic model argued that trial-to-trial variability was no longer shaped by error corrections, but showed a significant decrease in the magnitude of noise.

Two long-term studies took retention to the extreme and tested performance of a novel polyrhythmic bimanual task in 20 practice sessions over 2 months and assessed retention after 3 and 6 months and after 8 years^89,90. As practice was largely self-guided with extremely sparse feedback, subjects developed their individual kinematic signatures in this relatively challenging task. Retention tests showed remarkable persistence of subtle kinematic variations, even after 8 years. Different metrics improved and persisted with different time scales, suggesting different mechanisms generating the complex behavior. One group that received additional auditory guidance showed more “forgetting” indicating that extrinsic information may destabilize the internal representation of the task.

Given the central position of memory, both declarative and procedural, in cognitive psychology, it is remarkable how few studies in motor neuroscience have paid attention to retention and memory. We all “know” that one never forgets how to ride a bicycle, but then, musicians need to practice every day to not lose their skill. Memory formation remains a fascinating process and retaining and forgetting need more attention.

Beyond Variability and Noise in Skill Learning

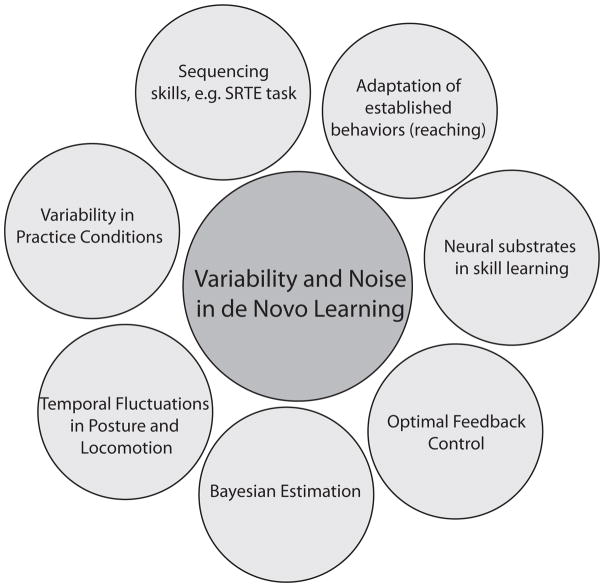
The role of variability and noise in skill acquisition, or de novo learning, is a vast area of research and any review has to set boundaries. Figure 4 overviews adjacent experimental and theoretical approaches that were excluded here, but that are covered in other excellent reviews: mixtures of deterministic and stochastic structure in temporal fluctuations in posture and locomotion⁹¹, the effect of varying practice conditions⁹², error-based learning and adaptation in well-established behaviors such as reaching, including implicit and explicit learning in SRT (serial response time) tasks¹⁴, Bayesian approaches, Kalman filter models and stochastic optimal feedback control⁹³, reinforcement learning⁶¹ and the neural substrate of skill learning⁹⁴.

Figure 4.

Overview of the current focus on skill acquisition and variability with related research areas and paradigms, both experimental and theoretical, in adjacent circles. These other areas are covered by other reviews on motor learning cited in the text.

This review aimed to highlight that variability not only reflects error corrections, but stems from a host of other processes at different time scales and from different levels of the complex high-dimensional system. This review progressed from noise as the unwanted corruption of a signal, to variability structured by the high dimensionality of the body and the task, including random searches for exploration of this solution space, noise as a means to induce plasticity and flexibility, and to shape behavior and form flexible and long-lasting skills.

While variability and noise attracts increasing attention, a host of questions are open and still unaddressed. How can we differentiate between desired and undesired noise? Is there a mechanism that turns on and turns off noise? What are the control mechanisms that channel variability into task-irrelevant directions? How can we use external noise to shape learning for clinical applications? Evidently, we are still far from understanding the positive and negative roles of variability and more methodological and theoretical approaches are needed to fully explore and exploit the information contained in overt variability.

Highlights.

• Analysis of variability provides information about control priorities

• Variability comprises a multitude of processes that contribute to skill improvement

• Stages of learning can be characterized by different roles of variability

• Skill learning aims to make intrinsic noise matter less in task performance

• Noise or unstructured variability can also be beneficial, e.g., exploration