Self-assembly of convex particles on spherocylindrical surfaces

Abstract

The precise control of assembly and packing of proteins and colloids on curved surfaces has fundamental implications in nanotechnology. In this paper, we describe dynamical simulations of the self-assembly of conical subunits around a spherocylindrical template, and a continuum theory for the bending energy of a triangular lattice with spontaneous curvature on a surface with arbitrary curvature. We find that assembly depends sensitively on mismatch between subunit spontaneous curvature and the mean curvature of the template, as well as anisotropic curvature of the template (mismatch between the two principal curvatures). Our simulations predict assembly morphologies that closely resemble those observed in experiments in which virus capsid proteins self-assemble around metal nanorods. Below a threshold curvature mismatch, our simulations identify a regime of optimal assembly leading to complete, symmetrical particles. Outside of this regime we observe defective particles, whose morphologies depend on the degree of curvature mismatch. To learn how assembly is affected by the nonuniform curvature of a spherocylinder, we also study the simpler cases of assembly around spherical and cylindrical cores. Our results show that both the intrinsic (Gaussian) and extrinsic (mean) curvatures of a template play significant roles in guiding the assembly of anisotropic subunits, providing a rich design space for the formation of nanoscale materials.

TOC image

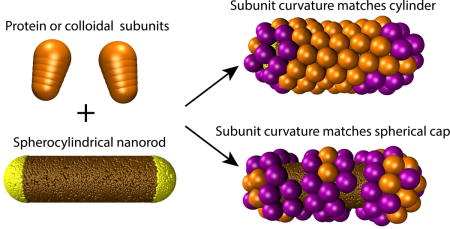
I. INTRODUCTION

Achieving molecular-scale control over the surface morphology of nanoscale particles is essential for many nano-materials and drug delivery applications. A promising route to this end is self-assembly, in which local interactions between subunits drive the emergence of particular large-scale morphologies [1–16]. However, assembly can be frustrated when the subunit-subunit interactions are incompatible with the surface geometry. For example, the densest 2D packing of spheres or discs, a six-fold coordinated hexagonal lattice, requires a minimum of 12 five-fold coordinated disks to cover a spherical surface [17, 18]. This frustration is metric in origin, arising because a hexagonal lattice is incompatible with the positive intrinsic (Gaussian) curvature of a sphere. Intrinsic curvature frustration has been the subject of intense experimental and theoretical investigation [17–45]. In contrast, there has been much less attention on extrinsic (mean) curvature, since it plays no role in the assembly of subunits that are isotropic (e.g. spheres) or live entirely in the surface tangent plane (i.e. a film of zero thickness). However, finite-thickness layers of flexible ligands undergo microphase separation or ordering on surfaces with mean curvature [5, 6, 10, 46–52]. Similarly, anisotropic subunits such as proteins or aspherical colloids have a preferred (spontaneous) mean curvature, and their assembly can be frustrated when the spontaneous curvature differs from that of the substrate on which they assemble [53].

In this article we computationally investigate assembly when both forms of geometric frustration occur simultaneously, during the assembly of anisotropic subunits on a spherocylindrical template. The inhomogeneous curvature of a spherocylinder ensures that the preferred subunit curvatures (mean and Gaussian) cannot globally match those of the template. Moreover, we show that anisotropy between the two principal curvature directions provides an additional source of frustration, even on surfaces such as cylinders for which the Gaussian curvature is zero.

Our study is motivated by recent experiments in which the capsid proteins of brome mosaic virus (BMV, a small, single-stranded RNA, icosahedral plant virus) assembled around spherocylindrical nanorods [1]. The assembly of viral capsid proteins around spherical cores has been studied for several systems [12–14, 54–57], including the assembly of BMV proteins around spherical charge-functionalized gold nanoparticles [3, 4, 58–62]. The experiments on spherical cores showed that the core size influences the protein organization, since as the core size increased, the proteins assembled larger icosahedral shells [4]. Yet, relatively little is known about viral protein assembly around nanoparticles with lower symmetry such as spherocylinders. Bancroft and coworkers [63] showed that BMV proteins form bacilliform particles around calf-thymus DNA, while Mukherjee et al. [64] showed that the capsid proteins of cowpea chlorotic mottle virus (CCMV, closely related to BMV) form tubular structures around double-stranded DNA. However the detailed arrangements of proteins in these complexes is unknown.

Zeng et al. [1] showed that BMV proteins can assemble closed shells around spherocylindrical gold nanorods whose surfaces are functionalized with negative charge. Using AFM, they visualized the arrangement of protein capsomers (pentamers or hexamers of the capsid protein) on the nanorod surfaces. While pentamer and hexamer capsomers formed partial icosahedral shells on the endcaps, particles exhibited hexagonal packing of capsomers on the cylindrical region of nanorods. Different alignments of the hexagonal lattice relative to the cylinder axis were observed, including both achiral geometries and a range of chiral angles. In addition to closed shells, the experiments identified particles with a variety of defects, several examples of which are shown in Fig. 1. The presence of defects was correlated to the nanorod dimensions.

FIG. 1.

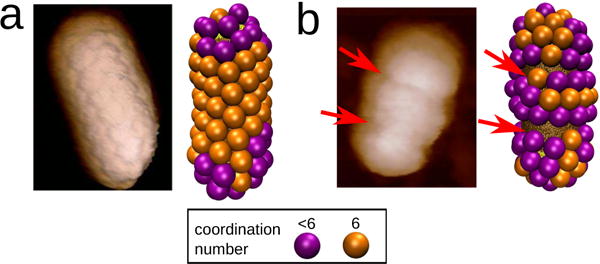
Comparison between AFM images of BMV capsid proteins assembled around gold spherocylindrical nanoparticles and simulation outcomes. The images show typical examples of (a) complete particles and (b) particle with defects, with red arrows indicating defects. Parameters for the simulation outcomes are: nanorod radius $R_{\text{scyl}}^{\prime }=11\text{nm}$, nanorod length L_cyl = 45nm, and subunit spontaneous curvature radius R_cone = 14.0 (top) and R_cone = 9.5 (bottom). In all figures, capsomers with six neighbors are shown in orange, and capsomers with 5 or fewer neighbors in purple.

While insightful computational and theoretical studies have modeled the packing of spherical subunits on spherical [65–68] or spherocylindrical templates [69–71], spherical subunits do not possess a preferred mean curvature. In studies that did consider the effects of mean curvature, Yu et al. [53] showed that rodlike particles, with a preferred mean curvature of zero, form faceted structures on a spherical template, while other studies modeled the assembly of anisotropic subunits into icosahedral shells on spherical templates [72–78]. However, to our knowledge none have yet considered assembly around templates with inhomogeneous curvature.

In this article we examine the effect of preferred subunit curvature on assembly around templates with inhomogeneous curvature. We have developed a minimal coarse-grained model in which conical subunits with short-range lateral subunit-subunit attractions assemble on the surface of a spherocylindrical nanorod (Fig. 2). The preferred curvature of the assemblage is controlled by the subunit cone angle. Depending on the relative values of the subunit preferred curvature and the template curvature, our simulations predict a rich array of particle morphologies, including many of the structures observed in experiments such as complete shells and particles with circular vacancies, or ring defects (Fig. 1). To understand the physics underlying these results, we develop a continuum-theory description for the assembly of a triangular lattice with spontaneous curvature on a surface with arbitrary curvature. The theory shows that the assembly outcomes depend on mismatches between the mean curvatures of the subunits and nanorod, as well as the curvature anisotropy of the nanorod (i.e. difference between the two principal curvatures) even when the Gaussian curvature is zero. These results highlight the key role played by extrinsic curvature incompatibilities in the assembly of proteins and colloids on curved substrates.

FIG. 2.

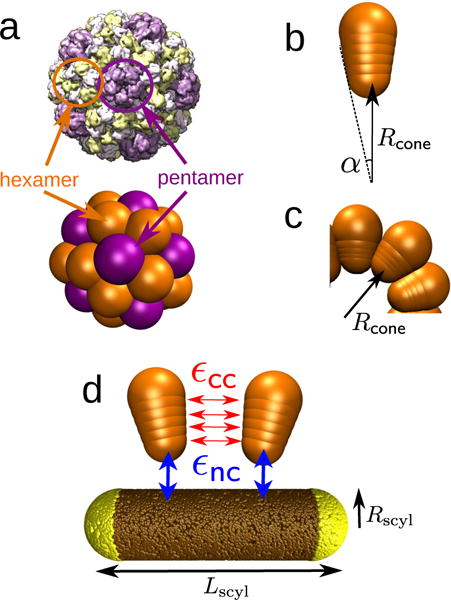
(a) Brome mosaic virus (BMV) capsid structure obtained from cyoEM (PDB ID: 3J7M) [79], compared with a capsid assembled from conical subunits in the absence of a nanoparticle. Each conical subunit represents a capsomer, and both pentamers (five neighbors, in purple) and hexamers (six neighbors, in orange) can be identified, showing icosahedral organization consistent with T=3 symmetry [22, 80]. (b,c) The cone angle α (b) sets the capsid spontaneous curvature radius R_cone (c), defined as the radial position of the capsomer bottom bead in the lowest energy capsid. (d) Capsomer model for R_cone = 9.5nm. Each of four interior beads (indices n = 1 … 4) interacts through a Morse potential of depth ε_cc with its counterparts in neighboring capsomers (red). The bottom capsomer bead experiences attractive interactions of strength ε_nc with the nanoparticle beads (blue). The equilibrium distance of the Morse potential between nanoparticle and capsomer beads, $r_{\text{eq}}^{\text{nc}}$, must be considered in the template curvature. The effective template radius is then given by $R_{\text{scyl}}^{\prime }=R_{\text{scyl}}+r_{\text{eq}}^{\text{nc}}$.

II. COMPUTATIONAL METHODS

Capsomer model

We seek a minimal, general, model capable of investigating the relationship between template curvature, subunit spontaneous curvature, and assembly morphologies. Motivated by these objectives and the limited resolution of the AFM experiments in Ref. [1], we employ a model in which the basic assembly unit corresponds to a protein capsomer (either a hexamer or pentamer). The model is sufficiently general to describe anisotropic colloidal subunits as well as proteins.

We have adapted the model from the conical subunits described in Chen et al. [69], which showed that conical subunits can self-assemble into monodisperse aggregates. Each subunit consists of a linear array of six beads with increasing radius, characterized by the cone angle α (Fig. 2b). For certain magic cone angles, the equilibrium structures exhibit icosahedral symmetry.

We modify the Chen et al. model by truncating the cones, so that in bulk (with no nanorod present) they assemble into empty shells with geometries that closely resemble viral capsids. We index the beads within a given capsomer by n = 0 … 5, with n = 0 corresponding to the bead with the smallest radius, which sits at the inner surface of an assembled capsid. Each of the four interior beads (n = 1 … 4) in a capsomer interacts with its counterpart (bead with the same index) in a nearby capsomer through a Morse potential (Eq. (9)), which drives lateral assembly of the subunits. Other pairs of beads experience excluded volume interactions (Eq. (10)).

Our subunit dimensions and aspect ratio roughly match those of BMV capsomers. The bead sizes within a subunit set the cone angle α and correspondingly the preferred capsid radius, i.e., the capsomer spontaneous curvature radius, R_cone. In an ideal shell, the innermost bead of each capsomer is located at a radial distance from the shell center R_cone, and the outer capsomer bead is located at R_out = R_cone + h, where h is the ‘height’ of a capsomer. The four interior beads are uniformly distributed between the inner and outer beads, so that the spacing between neighboring beads is h/5. The cone angle α is then determined by the criteria that beads of the same index in neighboring capsomers should be separated by a distance equal to their diameter (the equilibrium distance of their interaction potential). This requirement determines the bead radius as a function of index and cone angle as: $r_n^{\text{eq}}=(R_{\text{cone}}+nh/5)\sin \alpha /2$. Specifying values for h, one bead diameter, and α thus completely determines the dimensions of the model capsomers. In our simulations we fix h = 4 nm and the diameter of the outermost bead to σ_cone = 2r₅ = 7.7 nm, and we vary α to tune the spontaneous curvature.

To model the native BMV capsid structure, we set the cone angle α = 33.1°, so that in bulk simulations we obtain spherical shells consisting of 32 subunits and inner radius R_cone ≈ 9.5nm, in good agreement with the native BMV capsid [79]. Because we consider only a single subunit geometry, which represents both hexamer and pentamer capsomers, we find that only 40% of the assembled shells have perfect icosahedral symmetry. Robust formation of T=3 capsids with icosahedral symmetry was previously shown to require two capsomer diameters (with ‘pentamer’ subunits being smaller than those corresponding to hexamers) [67]. Moreover, the preferred curvature of individual BMV capsomers could differ from those observed in assembled capsids. Similarly, interactions with a substrate (such as the functionalized nanorod surface) could drive conformation changes that adjust the capsomer spontaneous curvature. To address these possibilities, we performed simulations over a range of cone angles α, corresponding to spontaneous curvature radii R_cone = 4.0 – 21.0nm. The inner radii of assembled capsids closely correspond to R_cone throughout this range.

Nanoparticle template

The nanoparticle is represented as a rigid body formed from many spherically symmetric pseudoatoms (or beads). In the case of spherocylinders (Fig. 2a), a central cylindrical body of length L_cyl and radius R_scyl is fused with two spherical caps also with radius R_scyl. The total length of the spherocylinder is then L_scyl = L_cyl + 2R_scyl. For studying spherical nanoparticles, we set L_cyl = 0. For cylindrical nanoparticles, we turn off the attractive interaction between the spherical caps and capsomers. We randomly distribute beads on the nanoparticle surface with a high and homogeneous density (ρ=13 beads/nm² regardless of the nanoparticle dimensions), so that the capsomers interact with a roughly homogeneous surface. In the experimental system, positive charges on the inner surface of BMV capsomers are attracted to functionalized negative charge on the nanoparticle surface. We qualitatively represent this attractive interaction by implementing a Morse potential between the bottom bead (n = 0) of each capsomer and the nanoparticle surface beads. To account for excluded volume between capsomers and the nanoparticle, the outer three beads in each capsomer n = 3 … 5 experience a repulsive Lennard-Jones potential with nanoparticle surface beads. When considering the nanoparticle curvature, we must account for the interaction distance between the nanoparticle and capsomer beads, roughly given by the Morse potential equilibrium distance $r_{\text{cn}}^{\text{eq}}=1.0\text{nm}$. Thus, we define an effective nanoparticle radius as $R_{\text{scyl}}^{\prime }=R_{\text{scyl}}+1.0$

Simulations

We performed simulations in HOOMD[81], which uses GPUs to accelerate molecular dynamics simulations [82]. In our simulations, all physical units are expressed relative to the thermal energy k_BT, mass m, and a reference length σ. The maximum diameter of a subunit is σ_cone = 7.7σ and its height (h, center-to-center distance between beads 0 and 5) is h = 4σ. By comparison with the actual height and diameter of a BMV capsomer h ≈ 5nm and d ≈ 8nm [79], we can map the length scale of our simulations into that of real viruses by setting σ ≈ 1nm. Accordingly, to facilitate comparison with experiments, we express all distances in nanometers.

Motivated by the experiments, we performed all simulations within the nanoparticle-directed assembly regime, meaning that assembly only occurs on the nanoparticle surface. To this end, we set the depth of the Morse potential for interactions between capsomer beads to ε_cc = 2k_BT. For such weak interactions, nucleation of assembly in bulk was not observed at the simulated capsomer concentration. We set the well-depth of the Morse potential for the nanoparticle-capsomer interaction to ε_nc = 0.3k_BT, which gives an average interaction energy of 6.65k_BT/capsomer (each capsomer interacts with many nanoparticle pseudoatoms). This value promotes adsorption of capsomers onto the nanoparticle surface, resulting in a sufficiently high local capsomer concentration to drive assembly nucleation [76]. Our results are qualitatively unchanged for ε_nc ∈ [0.2, 0.5]k_BT; for smaller adsorption energies the density of adsorbed capsomers is too low to promote rapid assembly nucleation, whereas for higher ε_nc capsomer adsorption becomes effectively irreversible, leading to malformed assemblies [83]. We found that achieving a homogeneous absorption free energy on the nanorod surface required slightly weakening the interaction between capsomers and nanoparticle surface beads on the spherical endcaps, ε_{nc, sph} = 0.98ε_{nc, cyl}. This reflects coupling between curvature and the finite size of the nanorod pseudoatoms.

Depending on the nanoparticle size, we considered two system sizes: for small nanoparticles (L_cyl < 45.0) we initialized 300 capsomers in a 130×130×130nm box, and for larger nanoparticles (L_cyl < 45.0) we used 500 capsomers in a 154×154×154nm box. For these system sizes the ratio of free to adsorbed capsomers was always higher than 5:1, thus ensuring results were not affected by depletion of free capsomers. The simulated capsomer concentration corresponds to approximately 220 μM. Our results were qualitatively insensitive to varying capsomer concentration provided that we remained in the nanoparticle-directed assembly regime.

We integrated the positions and orientations of capsomers using the HOOMD Brownian dynamics algorithm for rigid bodies for 1.5 × 10⁷ timesteps, with a timestep duration of Δt = 0.005. The nanoparticle position and orientation were fixed. Based on the energy and visual inspection of particle morphologies, simulations have equilibrated (or at least reached long-lived metastable minima) by 5 × 10⁶ timesteps.

III. CONTINUUM THEORY FOR A TRIANGULAR LATTICE WITH SPONTANEOUS CURVATURE

A. Derivation of the continuum description

In this section we elucidate the effects of mean and Gaussian curvature on assembly morphologies, by deriving a continuum approximation for the bending energy of a triangular lattice of subunits on a surface with arbitrary curvature. Our calculation is general, and extends calculations of bending energy for triangulated membrane models (e.g. Seung and Nelson [44] and Gompper and Kroll [45]) to lattices with spontaneous curvature and arbitrary template curvature. We will see that allowing for spontaneous curvature makes the relevant physics more transparent as well as increasing generality.

We consider a hexagonal lattice of subunits on a patch of surface with principal curvatures c₁ and c₂. We assume that particles maintain hexagonal close packing density at some neutral surface located at a distance h_ns above the surface, and that the long axis of each subunit points along the local surface normal. For now we neglect the presence of disclinations in the hexagonal lattice due to non-zero Gaussian curvature; we will discuss their contribution below. To make the derivation concrete, we assume the interaction potential used in our computational model. However, the derivation is easily extendable to other interaction forms and the results are generic.

We consider a reference state in which $c_1^{\text{ref}}=c_2^{\text{ref}}=1/R_{\text{cone}}$, so that all pseudoatoms pairs are separated by their equilibrium distance $d_n^{\text{eq}}=2r_n^{\text{eq}}$. We then calculate the change in the interaction energy between a pair of subunits (to quadratic order) as the curvatures vary:

$$U(c_1,c_2)-U_{\text{ref}}=\frac{1}{2}{\displaystyle \sum _{n=1}^4{k}_n{(d_n(c_1,c_2)-2r_n^{\text{eq}})}^2}$$ (1)

with d_n the distance between neighboring pairs of pseudoatoms with index n, and $k_n={\frac{\partial U_{\text{Morse}}(d)}{\partial d^2}|}_{d=2r_n^{\text{eq}}}$.

Distances within the shell can be calculated using the metric associated with the nanorod surface, but to make the role of curvature transparent we calculate the deviation from the reference state displacement between a pair of pseudoatoms separated by lattice vector $\widehat{\mathrm{k}}$ as:

$$d_n-2r_n^{\text{eq}}\approx {\sigma }_{\text{ns}}(h_n-h_{\text{ns}})\left(c_{\mathrm{N}}(\widehat{\mathrm{k}})-\frac{1}{R_{\text{cone}}}\right).$$ (2)

with σ_ns the equilibrium separation distance at the neutral surface, h_n the height of pseudoatom n above the surface, and c_N the normal curvature along $\widehat{\mathrm{k}}$:

$$c_{\mathrm{N}}(\widehat{\mathrm{k}})=c_1{\cos }^2(\theta )+c_2{\sin }^2(\theta ).$$ (3)

with θ the angle between $\widehat{\mathrm{k}}$ and the principal direction associated with c₁.

Substituting Eq. (2) into Eq. (1), summing over all particles and bonds, and using the hexagonal close-packing density ${\rho }_{\text{HCP}}=\frac{2}{\sqrt{3}{\sigma }_{\text{ns}}^2}$ yields a result independent of θ:

$$U_{\text{bend}}=A\kappa \left[\frac{1}{2}{(2H-c_0)}^2+\frac{1}{4}{(c_1-c_2)}^2\right]$$ (4)

with A the template surface area, H = (c₁ + c₂)/2 the mean curvature and c₀ = 2/R_cone the shell spontaneous curvature. The effective bending modulus is given by

$$\kappa =\frac{\sqrt{3}}{2}{\displaystyle \sum _{n=1}^4{k}_n{(h_n-h_{\text{ns}})}^2}.$$ (5)

Eq. (4) can also be written as

$$U_{\text{bend}}=A\kappa \left[\frac{1}{2}{(2H-c_0)}^2+(H^2-K)\right],$$ (6)

with K = c₁c₂ the Gaussian curvature. Eqs. 4 and 6 are the central result of this section.

There are several points worth noting about this result. Firstly, the energy, to quadratic order, is independent of lattice orientation, as shown by Seung and Nelson [44]. However, note that the energy does become orientation-dependent if higher order terms are considered in Eq. (1). Secondly, the first term in Eq. (6) has the standard Helfrich form for deviations between the mean and spontaneous curvatures [85], but the second term (H² − K) arises from curvature anisotropy (c₁ ≠ = c₂). When this term is accounted for, the bending modulus κ is seen to be independent of surface geometry; i.e., in contrast to the suggestion in Ref. [45], the triangulated membrane model does not have a different bending modulus value on a sphere and a cylinder. Thirdly, we see that the Gaussian modulus is equal to the negative of the bending modulus, κ_G = −κ as found for lipid bilayers [86].

The contribution from the Gaussian curvature is constant if particles are uniformly covered, since the integrated Gaussian curvature is 4π regardless of the nanorod dimensions according to the Gauss-Bonnet theorem [87]. However, this contribution will change for particles which have vacancies on portions of the surface with non-zero K, and thus affects the relative favorability of assembling on the end caps or shaft. More interestingly, the curvature mismatch term H² − K is zero on the spherical caps, but is nonzero on the cylindrical shaft and does depend on R_scyl.

Finally, regions with non-zero Gaussian curvature (e.g. the spherical caps) require disclinations in the hexagonal packing, which give rise to an additional energy U_d. This energy has been discussed at length for spherical packings (e.g. [17–22, 25, 30, 33, 35–45]). For our small spherical caps we can expect the total disclination energy to be proportional to U_d ∼ 12·4ε_cc since there are 12 five-fold coordinated subunits with 4 attractive pseudoatoms.

B. Implications of the continuum theory for assembly morphologies

To assess the relative favorability of assembly on the cylindrical or spherical portions of the nanorod, we use Eq. (6) to write the energy (per particle) due to bending and disclinations for the two surface geometries as

$$\begin{gathered} u_{\text{sphere}}=\frac{\kappa }{{\rho }_{\text{HCP}}}\frac{1}{2}{\left(\frac{2}{R_{\text{scyl}}^{\prime }}-\frac{2}{R_{\text{cone}}}\right)}^2+\frac{U_d}{4\pi {(R_{\text{scyl}}^{\prime })}^2{\rho }_{\text{HCP}}} \\ {u}_{\text{cyl}}=\frac{\kappa }{{\rho }_{\text{HCP}}}\left[\frac{1}{2}{\left(\frac{2}{R_{\text{scyl}}^{\prime }}-\frac{2}{R_{\text{cone}}}\right)}^2+\frac{1}{4}{\left(\frac{1}{R_{\text{scyl}}^{\prime }}\right)}^2\right] \end{gathered}$$ (7)

Comparing these expressions shows that there is a threshold value of the curvature ratio γ_nr above which assembly on the cylinder becomes more favorable than on a sphere:

$${\gamma }_{\text{nr}}\ast =8/(5+U_d/\pi {\rho }_{\text{HCP}})$$ (8)

Finally, to apply these results to our model, we set the pseudoatom height h_n = nh/5, the neutral surface height h_ns = h/2, cone angle α = 33.1°, Morse strength ε_cc = 2, and Morse potential width ${\alpha }_n=12/2r_n^{\text{eq}}$, resulting in κ = −κ_G = 38.3k_BT. To maintain the simplification of a harmonic interaction, we are neglecting the excluded volume repulsions from the Lennard-Jones potential (Eq. (10)), which apply only when the pseudoatom displacement is less than the equilibrium distance.

IV. RESULTS

All simulations resulted in extensive adsorption of capsomers onto the nanoparticle. To clearly illustrate the capsomer packing on the nanoparticle surface, in all figures we render only the outermost attractive bead of each capsomer (n = 4), and only show capsomers located within 5 nm of a nanoparticle surface bead. We render capsomers with six neighbors in orange, and capsomers with 5 or fewer neighbors in purple. We compute the coordination number of each capsomer from the number of neighbors within a distance $1.25r_4^{\text{eq}}$, where $r_4^{\text{eq}}$ is the equilibrium distance between the outermost attractive beads in neighboring capsomers. Due to this threshold-based definition, we never observe capsomers with 7 or more neighbors. Consistent with Luque et al. [71], we observe hexagonal packing of capsomers on the cylindrical portion of complete particles and 5-fold defects on the spherical caps.

To understand how assembly morphologies depend on mismatches in curvature, we consider results in terms of the ratio between the capsomer spontaneous curvature radius and the nanoparticle radius, ${\gamma }_{\text{nr}}\equiv R_{\text{cone}}/R_{\text{scyl}}^{\prime }$. The mean curvature, defined as $H=\frac{1}{2}(c_1+c_2)$ with c₁ and c₂ the principle curvatures, differs for the spherical endcaps and the cylindrical shaft. The ratio of mean curvatures on endcap and shaft is thus 1/γ_nr and 2/γ_nr respectively. Also note that the curvature anisotropy term in Eq. (6), (H² − K), is zero on the endcap but equal to $1/{(2R_{\text{scyl}}^{\prime })}^2$ on the cylinder.

A. Spherocylinders: simulation outcomes

We first studied the assembly of conical capsomers around spherocylindrical nanoparticles of different length and radius. We focused on nanoparticles of similar dimensions to those studied in experiments, R_scyl ∼ 5 – 15 nm and L_cyl = 5 – 45 nm. Because the BMV capsid protein spontaneous curvature is not known for certain, and to understand the effect of varying γ_nr, we explored capsomer spontaneous curvature radii in the range R_cone = 5 – 21nm.

Within the simulated range of nanoparticle dimensions, we identify six classes of assembly outcomes (Fig. 3): incomplete III, with capsomers assembled into three isolated clusters; partial III, three partially connected domains; incomplete II, two isolated clusters; partial II, two partially connected clusters; complete capsids with capsomers homogeneously covering the entire nanoparticle surface; and incomplete, in which capsomers do not homogeneously cover the surface. We observe incomplete morphologies for very low radii of curvature (typically ≤ 5nm), suggesting that assembly is frustrated by the high substrate curvature.

FIG. 3.

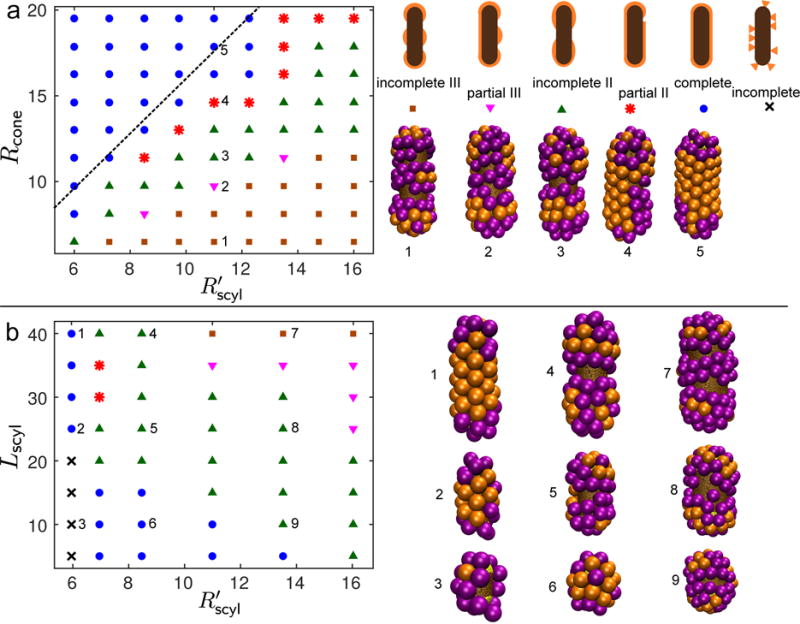
(a) Phase diagram of the most frequent simulation outcomes as a function of the capsomer spontaneous curvature radius R_cone and spherocylinder radius $R_{\text{scyl}}^{\prime }$, for a spherocylinder length of L_cyl = 40nm. On the right, we show a schematic for each class of assembly outcome along with a representative example from the simulations. The outcomes are numbered the same as the corresponding parameters on the phase diagram. The dashed line shows the threshold above which the continuum theory (Eq. (8)) predicts that assembly is more favorable on the cylindrical shaft than on the spherical end caps. (b) Phase diagram of the most frequent outcomes as a function of the spherocylinder length L_cyl and radius R_scyl, for constant R_cone = 9.5nm. Legend as in (a). On the right we show some typical simulation snapshots for relevant spherocylinder aspect ratios. We performed 5-10 independent simulations at each parameter set. The distribution of outcomes for representative parameter values is shown in the supplemental figure [84].

Fig. 3a shows the most frequent morphology as a function of capsomer and nanoparticle radius, for fixed spherocylinder length L_cyl = 40nm. The phase diagram can be divided into two main regions: complete particles for $R_{\text{cone}}\gtrsim 8/5R_{\text{scyl}}^{\prime }$ (i.e. γ_nr ≳ 8/5) and incomplete particles otherwise. Among incomplete particles, for 1.2 < γ_nr < 1.5 we observe incomplete II particles, and for γ_nr < 1.2 only incomplete III particles. If we consider a cut of constant spherocylinder dimensions $(e.g.R_{\text{sycl}}^{\prime }=10\text{nm})$, as we increase R_cone the size of the capsomer domains increases and therefore the number of isolated domains that grow on the nanoparticle decreases. In this sequence, morphologies gradually change from incomplete III particles, to incomplete II and eventually complete particles, as shown in the snapshots of Fig. 3a. For parameter sets away from outcome transition boundaries, independent trajectories result in the same outcome class. However, for parameter sets near transition boundaries we observe up to three distinct outcomes at a given parameter set. The supplemental figure [84] shows the distribution of outcomes for representative parameter sets.

These results suggest that shell bending energy due to curvature mismatch and anisotropy is the key factor determining the presence and number of defects. In particular, the dashed line in Fig. 3a shows the threshold curvature ratio γ_nr∗ = 8/5 predicted by Eq. (8) (neglecting the contribution from disclinations, i.e. U_d = 0), above which assembly on the cylinder is more favorable than on the spherical endcaps. We see this matches the boundary between complete and incomplete particles reasonably well. Moreover, Fig. 4 plots the difference between bending energy on the cylinder and sphere, Δu = u_cyl − u_sphere (Eq. (7)), and we see that the contours roughly track the boundaries between different assembly morphologies. We discuss in section IV B 2 how the circular ‘ring’ defects can be understood in terms of the bending energy. However, in addition to these equilibrium effects, we observed instances in which kinetics played a role in defect generation. In a few trajectories, clusters independently nucleated on both end caps, after which their growth edges met with incompatible orientations.

FIG. 4.

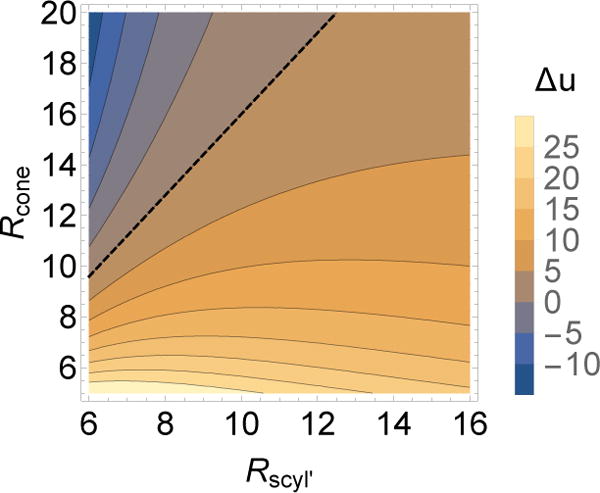
Comparison of bending energy on cylindrical and spherical surfaces. The difference in bending energy per particle predicted by the continuum theory, Δu = u_cyl −u_sphere (Eq. (7)), is shown as a function of $R_{\text{scyl}}^{\prime }$ and R_cone for κ = 38.3k_BT. The dashed line shows the threshold above which assembly is favored on the cylinder over the sphere (Eq. (8)).

Fig. 3b shows the most frequent morphology as a function of spherocylinder radius and length, for fixed capsomer radius R_cone = 9.5nm. In this case, the nanoparticle length determines the number of capsomer domains assembled. For small L_cyl, capsomers homogeneously assemble around the whole surface even for small R_cone. As we increase the nanoparticle length, two and eventually three domains are observed. The figure shows a slight coupling between radius and length; e.g. for the same L_cyl we observe incomplete II particles for $R_{\text{scyl}}^{\prime }=8.5\text{nm}$ and incomplete III for $R_{\text{scyl}}^{\prime }\ge 10\text{nm}$. The case of highest curvature $R_{\text{scyl}}^{\prime }=6\text{nm}$ exhibits a different behavior, with many vacancies and a low assembly yield for the shortest spherocylinders, presumably due to the high curvature of the template. However, as we increase the spherocylinder length we obtain complete particles. These results can be understood in terms of the relationship between the typical shell domain width and γ_nr discussed in section IV B 2.

B. Assembly around templates with uniform curvature

To understand how the interplay between the cylindrical and spherical portions of the nanoparticle effects assembly morphology, we performed independent sets of simulations in which assembly occured on spherical or cylindrical templates.

1. Spherical nanoparticles

We first consider capsomer assembly around a perfectly spherical nanoparticle, with a radius consistent with the T=3 capsid obtained in bulk, $R_s^{\prime }=9.5\text{nm}$. We explore a range of capsomer curvature radii, 5.0 ≤ R_cone ≤ 15.5nm, so that the ratio of preferred capsid size to nanoparticle size varies from 0.5 ≲ γ_nr ≲ 1.75. Representative assembly outcomes are shown in Fig. 5a for cases in which the spontaneous curvature radius is smaller than, equal to, or larger than the nanoparticle size. For γ_nr ≈ 1 we obtain complete particles which consist of 32 capsomers, although icosahedral symmetry is observed in a lower proportion (20%) of simulations than in bulk (40%). As the preferred curvature radius deviates from the template size, assembled particles exhibit vacancies and defects. For γ_nr > 1 capsomers tend to form larger shells, leading to the formation of two large, flat caps whose assembly eventually stalls when the capsomers in the cap can no longer reach the nanoparticle surface. For smaller radii, γ_nr < 1, the capsomer curvature does not allow a well-formed assemblage to cover the entire nanoparticle surface, and instead we usually observe two small caps.

FIG. 5.

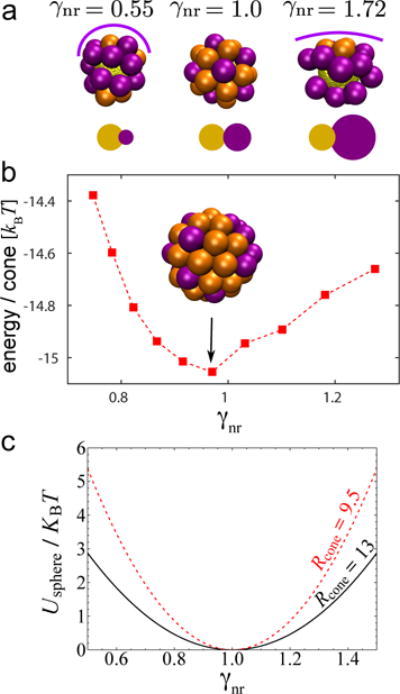
(a) Representative examples of capsomers assembled around spherical nanoparticles with radius $R_{\mathrm{s}}^{\prime }=9.5$. From left to right, R_cone = 5.0, 9.5 and 15.5nm. The line over each capsid approximately shows its preferred curvature. Below each snapshot we show a schematic of the relative size between the nanoparticle (yellow) and the protein capsid in bulk (purple). (b) Energy per capsomer assembled around spherical nanoparticles as a function of ${\gamma }_{\text{nr}}\equiv R_{\text{cone}}/R_{\mathrm{s}}^{\prime }$.In the simulations for (b), we kept the capsomer radius ≡ constant R_cone = 13.0nm and changed the nanoparticle size. (c) Continuum result for bending energy / capsomer on a spherical surface, u_sphere (Eq. (7), as a function of curvature ratio for indicated values of the spontaneous curvature radius R_cone.

In both limits (γ_nr > 1 and γ_nr < 1) the incompatibility between capsid and template curvature eventually frustrates assembly, leading to a gap between two caps. However, Yu et al. [53] showed that cylindrical rods assembling on spherical nanoparticles form ordered faceted particles. It is conceivable that the same result would be recovered in the limit γ_nr → ∞. In general we expect that the existence of gaps and the number of faces could depend on the degree of curvature mismatch and whether capsomer-capsomer interactions are sufficiently strong to drive assembly once a cap separates from the nanoparticle surface (recall that these simulations are performed in the limit of weak capsomer-capsomer interactions).

To quantitatively describe how the ‘quality’ of assembly depends on the curvature mismatch, we show the average energy per capsomer in Fig. 5b. For this calculation we fixed the capsomer spontaneous curvature radius at R_cone = 13nm, and then varied the nanoparticle in the range R_s ∈ [9.0, 16.0]. In this parameter regime all assembled capsids were defect-free, simplifying the interpretation of the capsomer energy. The simulation results are qualitatively consistent with the continuum theory (Eq. (6), Fig. 5c) — the energy is minimized at γ_nr ≈ 1, when the capsomer and nanoparticle curvatures match, and increases as the capsomer curvature radius deviates from the template size.

2. Cylindrical nanoparticles

To investigate assembly on the cylindrical portion of the nanoparticle, we performed simulations with long nanoparticles (L_cyl = 75nm), with attractions turned off between capsomers and the surface beads in the spherical caps. Thus assembly morphologies near the middle of the cylindrical region were essentially independent of end effects. As shown in Fig. 6, we observe well-formed hexagonal lattices that uniformly cover the cylindrical surface for γ_nr ≳ 1.4, with optimal assembly for γ_nr ≈ 1.5. This is roughly consistent with the behavior predicted by Eq. (6) as shown below.

FIG. 6.

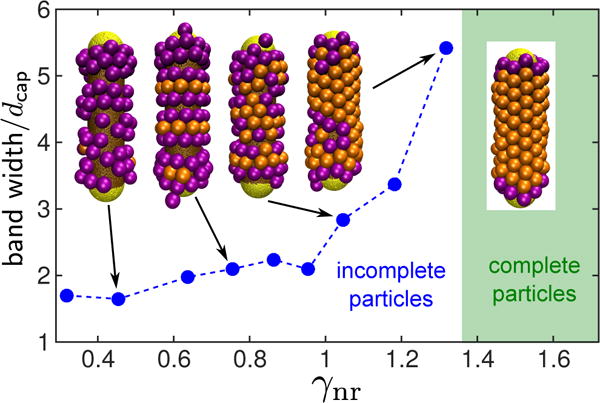
Average normalized width of clusters (in the cylinder axis direction) formed by capsomers assembled around cylinders, for increasing ${\gamma }_{\text{nr}}\equiv R_{\text{cone}}/R_{\text{scyl}}^{\prime }$ and constant L_cyl = 75nm.

For smaller capsomer curvature radii, we observe capsomers assembled into ‘bands’ separated by gaps, with the width of the bands depending on γ_nr. Capsomers at the edge of a band tilt along the cylinder axis, effectively allowing for shell curvature along the cylinder axis. To quantify the band width, we define w as as the maximum distance along the cylinder axis direction $\widehat{z}$ between two beads belonging to the same cluster, w_l = (max(z_i) − min z_i) / σ_cone for all capsomer beads i in a given cluster l. Here we have normalized the band with by the diameter of the outer capsomer bead σ_cone = 7.7, so that the normalized band width roughly equals the number of capsomers per cluster in the axial direction. The normalized cylinder length is then L_cyl/σ_cone = 9.7.

Fig. 6 shows the average band width as a function of γ_nr, along with representative assembly outcomes. For a low curvature ratio γ_nr ≈ 0.4 – 0.5, capsomers assemble poorly on the cylinder, forming very narrow bands consisting of just 1-2 capsomers. Bands become thicker with increasing γ_nr, until w ≈ 5 for γ_nr ≈ 1.3 meaning that only two domains fit on the cylinder. The system then gradually transitions to a complete hexagonal lattice for γ_nr ≳ 1.4. Due to the finite length of our nanoparticle, we cannot determine whether the band width remains finite (but larger than the cylinder length), or if capsomers could assemble infinite domains with hexagonal packing. However, the energy calculations discussed next suggest that assembly is minimally frustrated for γ_nr ≈ 1.5, suggesting that the band width would be infinite (except for defects arising due to entropy in this effectively 1D geometry).

The increasing band width as a function of γ_nr can be qualitatively understood from (Eq. (4)). For small γ_nr both the mean curvature and curvature anisotropy terms are unfavorable because the principle curvature is zero along the cylinder axis. Tilting of capsomers near the edge of a band allows for nonzero curvature along this direction, with higher curvature for smaller bands. In particular, the typical band width for small γ_nr is comparable to R_cone.

We note that the bands in our simulations superficially resemble bands observed in the context of spherical colloids assembling around spherical nanoparticles in recent experiments [33] and simulations [68]. However, the physics driving band formation differs. The bands in our system arise due to curvature anisotropy and a mismatch between the extrinsic (mean) curvatures of the capsomer and template. In contrast, the spherical surfaces in Refs. [33, 68] have isotropic curvature, and the spherical colloids undergoing assembly have no spontaneous curvature. Bands arise because isotropic growth of a crystal with hexagonal order becomes frustrated by the intrinsic (Gaussian) curvature of the spherical surface.

To evaluate assembly quality, Fig.7a shows the average energy per capsomer for fixed R_cone = 13.0 and cylinder radius R_scyl = 7.5 – 15.0nm. We observe a minimum at γ_nr = 1.5, when capsomers form highly ordered hexagonal lattices. As the curvature ratio increases beyond γ_nr = 1.5, the energy increases and both visual inspection of simulation snapshots and analysis of the mean square deviations of capsomer-capsomer distances confirmed that the packings become less ordered (e.g. see Fig.7b for γ_nr = 2.05). This result is qualitatively consistent with the continuum theory. Minimization of the energy per particle on a cylinder (u_cyl, Eq. (7)) as a function of $R_{\text{scyl}}^{\prime }$, at fixed R_cone, gives an optimal cylinder radius $R_{\text{scyl}}^{\prime }=3/4R_{\text{cone}}$ corresponding to γ_nr = 4/3. This is qualitatively consistent with the minimum in Fig.7a, as is the variation of u_cyl with γ_nr (Fig.7c). This result highlights the importance of the curvature anisotropy; analysis of mean curvature mismatch only would predict optimal assembly on a cylindrical surface for γ_nr = 2.0. Note however that if one varies R_cone at fixed $R_{\text{scyl}}^{\prime }$ the energy per particle is optimal for γ_nr = 2.0, since the curvature anisotropy term is independent of R_cone.

FIG. 7.

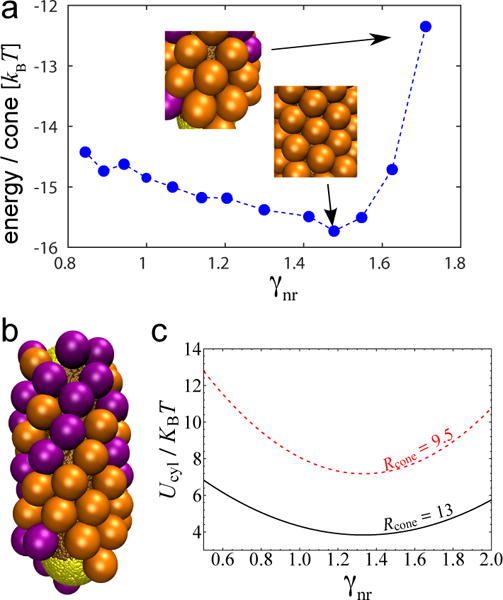
(a) Energy per capsomer assembled around cylindrical nanoparticles, for different capsomer/cylinder curvature ratios γ_nr. The insets show examples of ordered hexagonal packing at γ_nr = 1.5 and irregular hexagonal packing at γ_nr = 2.0. In these simulations the attractive interaction between capsomers and the spherical caps is turned off. Parameter values are L_cyl = 45.0, R_cone = 13.0 and R_scyl = 7.5–15.0nm. (b) Typical example of assembly morphology around a cylinder for γ_nr = 2.05. (c) Continuum result for bending energy / capsomer on a cylindrical surface, u_cyl (Eq. (7), as a function of curvature ratio for indicated values of the spontaneous curvature radius.

C. Chirality

AFM imaging showed that capsid proteins form hexagonal lattices on the cylindrical region of the nanorod [1]. The particle lattice orientations relative to the nanorod were quantified by determining θ as the smallest angle between any of the lattice vectors and the long axis (Fig. 8). Following the nomenclature of Luque et al. [70, 71], there are two achiral geometries denoted as “ring” (θ = 0°) or “zigzag” (θ = 30°), while angles between 0° < θ < 30° correspond to chiral (or “skew”) configurations. The experimental particles exhibit the complete range of angles, but favor the “zigzag” configuration.

FIG. 8.

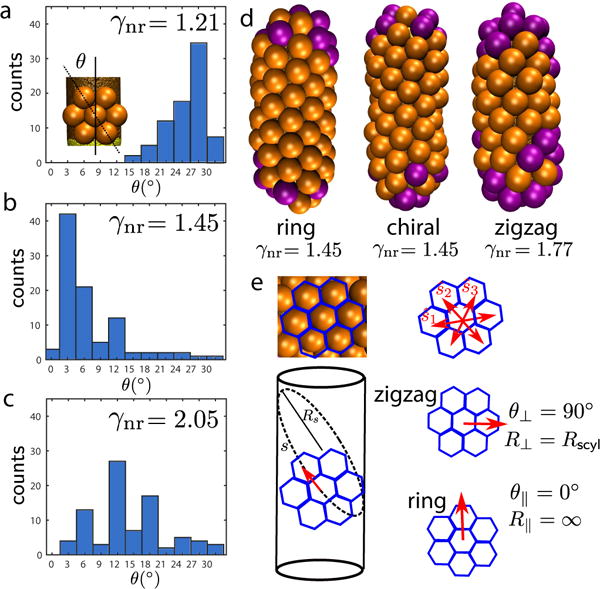
Chirality of the hexagonal lattice assembled on spherocylinders with L_cyl = 45nm and $R_{\text{scyl}}^{\prime }=9\text{nm}$, and variable R_cone. (a) Angle distribution for γ_nr = 1.21. The inset shows how the chiral angle θ is defined. (b) Angle distribution for γ_nr = 1.45. (c) Angle distribution for γ_nr = 2.05. (d) From left to right, representative examples of particles with hexagonal lattice orientations that are approximately ring, chiral, and approximately zigzag. (e) Schematic of the hexagonal lattice orientation. Each capsomer interacts with six neighbors, with interaction directions given by the vectors ${\widehat{s}}_i$. Capsomers experience three different interaction directions, each one along a different curve s on the cylinder, with curvature radius R_s (for simplicity only one is shown). In zigzag particles, the perpendicular orientation presents the minimum curvature radius R_⊥ = R_scyl. Ring particles experience the lowest curvature radius, R_║ = ∞.

Our simulation trajectories also result in a range of chiral angles (Fig. 8), with the preferred angle depending on γ_nr. We calculate the chiral angle θ as the minimum angle formed by the nanoparticle axis and any of the three orientation vectors of the hexagonal lattice (see Fig. 8), averaged over all the beads adsorbed onto the cylindrical face with 6 neighbors. We computed the angle distribution from 105 independent simulations at each of three parameter sets corresponding to different curvature ratios (see Fig. 8). For γ_nr = 1.21, adsorbed capsomers tend to form bands in which the hexagonal lattice is perpendicular to the cylinder axis (e.g. see several examples in Fig. 6). The angle distribution in Fig. 8a then exhibits a peak at θ ∼ 30°. For γ_nr = 1.45, we observed complete particles in which the hexagonal lattice aligns with the axis, and the angle distribution in Fig. 8b shows a clear preference for ring particles, with only a few chiral particles and generally of angle < 15°. As described in Section IV B 2, this regime corresponds to optimal hexagonal packing. For γ_nr = 2.05, we observe formation of both chiral and zigzag particles with disordered hexagonal packing (Fig. 8c); there is no identifiable pattern in the angle distribution.

The chiral angle distribution in simulations is most consistent with that observed in the experiments for γ_nr = 1.21 [1], implying a capsomer preferred curvature more closely matching the spherical end cap rather than the cylindrical region of the nanorod. A key difference in this regime is that the simulation model cannot capture the ability of the experimental capsomers to form complete particles in this regime. This difference may arise because the simulations only consider one subunit geometry while the BMV proteins form both pentameric and hexameric capsomers with different preferred curvatures.

To test whether the chiral angle is sensitive to kinetic effects (i.e. whether growth starts from the hemispherical caps or on the cylinder) we performed a set of 60 simulations for each chiral angle in which capsomers only interacted with the cylindrical surface. These simulations resulted in very similar angle distributions, suggesting the chiral angle primarily arises from energetic rather than kinetic effects. This result can be explained at least in part by the coupling between anisotropic curvature on the cylinder surface and the discrete nature of the capsomer lattice. As noted in section III the bending energy is independent of lattice orientation to quadratic order, but becomes orientation-dependent when nonlinearities are included. We have not performed a detailed analysis of the continuum theory at higher order, but the simulation results can be qualitatively understood as follows. As shown in Fig. 8d, the three lattice vectors ${\widehat{s}}_i$ define three curves s_i on the cylinder, with different curvature radii R_si. The anisotropy in the curvatures of the three lattice directions strongly depends on the lattice orientation. Zigzag configurations allow a direction with the smallest curvature radius (for θ_⊥ = 90°, R_⊥ = R_scyl), while ring particles have the highest radius of curvature (for θ_║ = 0°, R_║= ∞). For preferred capsomer curvature radii matched to the spherical end cap (γ_nr ≈ 1), capsomers avoid the flat axis direction and preferentially orient perpendicular to the axis, resulting in a curvature radius along the perpendicular contour R_⊥ = R_cyl ∼ R_cone. For γ_nr ∼ 1.5, ring orientations allow for the curvature along two directions to nearly match that of the capsomer (for θ_s = 30°, R₃₀° = R_scyl/3 R_cone), although one lattice vector must then orient along the unfavorable flat axis direction.

D. Nucleation & kinetics

Although we have focused on long-time assembly morphologies thus far, the simulations also allow studying assembly dynamics. Figs. 9a,b shows the evolution of the number of capsomers adsorbed onto the cylindrical and spherical regions of the nanoparticle as a function of time for high and low curvature ratios. Note that the first adsorbed capsomers are typically isolated and randomly distributed, and hence the adsorption probability is equal for the cylindrical and spherical regions until nucleation occurs. Fig. 9c shows the density of adsorbed capsomers on each region at t = 6 × 10⁵ as a function of γ_nr.

FIG. 9.

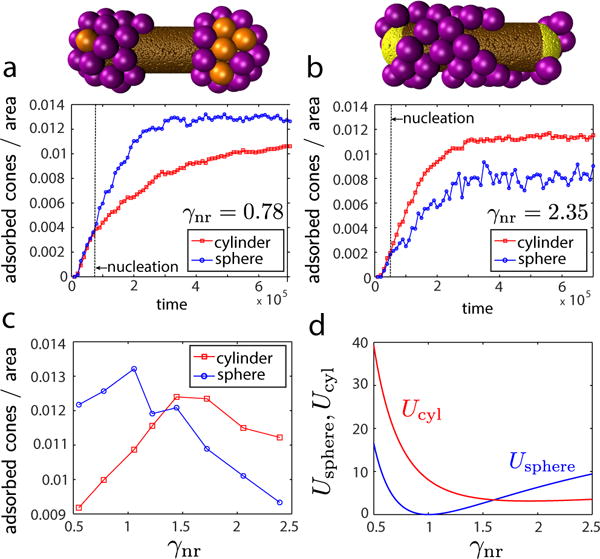
Comparison of assembly kinetics on spherical and cylindrical surfaces. (a), (b) Density of adsorbed capsomers on spherical (○ symbols) and cylindrical (□ symbols) nanoparticles as a function of time for curvature ratios below and above the threshold: (a) γ_nr = 0.8 and (b) γ_nr = 2.3. The black dashed line in each plot indicates the time point at which nucleation occurred. The image above each plot is a snapshot from a representative trajectory at (a) t = 4.5 × 10⁴ and (b) t = 3 × 10³. Each curve represents the average over ten independent simulations. (c) The average density of adsorbed capsomers on cylindrical and spherical nanoparticles as a function of γ_nr. (d) The bending energy per capsomer on spherical and cylindrical surfaces calculated from continuum theory (Eq. (7)) as a function of curvature ratio. In all cases the spherocylinder radius is fixed at $R_{\text{scyl}}^{\prime }=9.5\text{nm}$and R_cone is varied. In the simulations L_cyl = 40.0nm.

Recall that the continuum theory predicts a threshold γ_nr∗ ≈ 8/5 above which there is a transition from preferential assembly on spherical surfaces to cylindrical surfaces. The dependence of the relative driving force for assembly on either surface can be estimated from the dependence of curvature energies for each geometry shown in Fig. 9d. The simulation trajectories are strongly consistent with the continuum predictions. For low γ_nr nucleation preferentially occurs on end caps, whereas nucleation occurs in the cylindrical region for high γ_nr. The crossover between these regimes, where nucleation occurs uniformly throughout the nanorod, occurs at γ_nr∗ (within error). Moreover, the adsorbed density is correlated to the bending energy, with a maximum in the density on the spherical region at γ_nr = 1 corresponding to the minimum in u_sphere.

Consistent with these results, experimental evidence in Zeng et al. [1] suggests both that the preferred capsomer curvature is consistent with the spherical end-caps (i.e. γ_nr ≈ 1) and that experimental trajectories initiate at the end-caps.

V. DISCUSSION & CONCLUSIONS

We have studied a phenomenological computational model motivated by experiments in which capsid proteins from an icosahedral virus assemble around spherocylindrical nanorods [1]. By varying a single parameter, the ratio of the preferred curvature of the subunits to the template curvature, the simulations reproduce most of the experimentally observed assembly outcomes. These results highlight the importance of the coupling between the curvatures of subunits and substrate, demonstrating that particle asymmetry adds an important control parameter for assembly confined on curved surfaces. Our subunit model is sufficiently general that it also could be realized experimentally by synthesizing conical-shaped colloidal particles.

It is well known that packing of particles with a circular cross-section on a spherical surface is frustrated due to the incompatibility of hexagonal order on surfaces with Gaussian (intrinsic) curvature. Here, we see that the assembly of anisotropic particles on a curved surface results in an additional forms of geometric frustration: when there is a mismatch between the preferred extrinsic (mean) curvature of the particles and the template, or a mismatch between curvature anisotropy of the particles and template. It was previously shown that a mismatch in mean curvatures of subunits and substrate on a spherical surface leads to line defects and faceting [53]. Here, we see a similar behavior on a cylindrical surface, with bands separated by line defects when the capsomer spontaneous curvature is sufficiently large in comparison to that of the cylindrical region of the nanorod. In contrast to a spherical surface, curvature is anisotropic on a cylinder, and our simulations show that this anisotropy can provide an additional control parameter, allowing tuning of the preferred lattice orientation on the cylinder. Thus, the class of systems described by our simple computational model could allow for designing a rich variety of particle geometries.

The simulation results suggest that measuring the width w of bands between defects could provide an estimate of the spontaneous curvature radius of the adsorbed particles (w ∼ 2R_cone), a parameter which is in general difficult to measure in bulk experiments. However, the simulations also suggest a coupling between domain width and cylinder radius, and thick cylinders may lead to underestimation of R_cone.

Finally, while the minimal model used in this work seems to capture the key physical principles dictating the assembly of anisotropic particles on curved surfaces, the model also has limitations relative to the motivating experimental system [1]. In particular, while the model reproduces the experimentally observed morphologies, different values of the subunit spontaneous curvature are required to match the experimental observation that complete particles can form on both short and long nanorods. We speculate that this discrepancy arises because, for simplicity, the model considers only a single subunit geometry, whereas BMV proteins adopt different ‘quasi-equivalent’ conformations allowing them to form pentameric or hexameric capsomers. It is likely that hexameric capsomers have a larger preferred curvature radius than pentamers, which would allow them to more readily assemble on the cylindrical region of the nanorod. However, comparison of several results between the simulations and experiments still suggests that the subunits have a spontaneous curvature which more closely matches the spherical end caps than the cylinder. In particular, the distribution of chiral angles and the fact that trajectories initiate on end-caps in this regime are both consistent with experimental observations [1].

VI. APPENDIX

Our model is defined by pairwise potentials describing capsomer-capsomer and capsomer-nanoparticle interactions. The capsomer-capsomer potential, U_cc, consists of two terms, $U_{\text{cc}}=U_{\text{cc}}^{\text{att}}+U_{\text{cc}}^{\text{ex}}$. The attractive interaction between the four interior pseudoatoms of the capsomers, n = 1 … 4 is modeled by a Morse potential. Beads are attracted only to their counterparts (with the same index n) on neighboring capsomers, and the equilibrium distance of the potential depends on the bead radius, $r_n^{\text{eq}}$:

$$U_{\text{cc}}^{\text{att}}={\displaystyle \sum _{i,j<i}{\displaystyle \sum _{n=1}^4{\epsilon }_{\text{cc}}\left(e^{-2{\alpha }_n(r_{i,j,n}-2r_n^{\text{eq}})}-2e^{-{\alpha }_n(r_{i,j,n}-2r_n^{\text{eq}})}\right)}}$$ (9)

with i and j indexing capsomers, n indexing beads within a capsomer, r_ij,n the distance between the pair of beads with index n in capsomers i and j, and ε_cc = 2k_BT. The potential width parameter is ${\alpha }_n=(12.0/2r_n^{\text{eq}})$, and the cutoff radius is set to $r_n^{\text{cut}}=2r_n^{\text{eq}}+1.5$. The Morse potential is used for these interactions largely for historical reasons, although in principle it offers the advantage over a Lennard-Jones interaction of allowing independent control over the pseudoatom size and the width of the potential well.

All pairs of capsomer pseudoatoms that are not on the same subunit and do not mutually attract (Eq. (9)) have excluded volume interactions represented by a WCA potential [88]

$$U_{\text{cc}}^{\text{ex}}={\displaystyle \sum _{i,j<i}{\displaystyle \sum _{n\ne m}4{\epsilon }_{\text{ex}}\left[{\left(\frac{{\sigma }_{nm}}{r_{ij,nm}}\right)}^{12}-{\left(\frac{{\sigma }_{nm}}{r_{ij,nm}}\right)}^6\right]}}$$ (10)

with r_ij,nm the distance between bead n in capsomer i and bead m in capsomer j, ε_ex = 1.0, and the cutoff distances $r_{nm}^{\text{cut}}={\sigma }_{nm}=r_n^{\text{eq}}+r_m^{\text{eq}}.$

The interaction potential between the nanoparticle and capsomers, U_nc, can be also split into contributions from attractions and excluded volume. The bottom bead of each capsomer experiences an attractive interaction with nanoparticle beads, described by a Morse potential:

$$U_{\text{cc}}^{\text{att}}(r)={\displaystyle \sum _{i=1}^{N_{\text{nr}}}{\displaystyle \sum _{j=1}^{N_{\text{cone}}}{\epsilon }_{\text{nc}}\left(e^{-2{\alpha }_{\text{nc}}(r_{i,j,0}-2r_{\text{nc}}^{\text{eq}})}-2e^{-{\alpha }_{\text{nc}}(r_{i,j,0}-2r_{\text{nc}}^{\text{eq}})}\right)}}$$ (11)

with the sum running over all N_nr nanorod beads and the bottom beads of all N_cone capsomers, r_ij,0 the distance between nanorod pseudoatom i and the bottom bead of capsomer $j,r_{\text{nc}}^{\text{eq}}=0.5$, and the interaction width parameter set to α_nc = 3.0. The well-depth parameters are set to ε_nc = 0.3k_BT for beads on the cylindrical portion of the NR, and ε_nc = 0.294k_BT for beads on the spherical endcap to ensure a uniform driving force for subunit adsorption everywhere (see section II). In addition, all nanoparticle beads interact through excluded volume with the three outermost capsomer beads:

$$U_{\text{nc}}^{\text{ex}}={\displaystyle \sum _{i=1}^{N_{\text{nr}}}{\displaystyle \sum _{j=1}^{N_{\text{cone}}}{\displaystyle \sum _{n=3}^{5}4{\epsilon }_{\text{ex}}\left[{\left(\frac{{\sigma }_n^{\text{nr}}}{r_{ij,n}}\right)}^{12}-{\left(\frac{{\sigma }_n^{\text{nr}}}{r_{ij,n}}\right)}^6\right]}}}$$ (12)

with r_ij,n the distance between nanorod pseudoatom i and bead n of capsomer j, _ex = 1.0 and cutoff radius $r_n^{\text{cut}}={\sigma }_n^{\text{nr}}=r_{\text{nc}}^{\text{eq}}+r_n^{\text{eq}}.$